Structured models of infectious disease: inference with discrete data

Abstract

The usage of structured population models can make substantial contributions to public health, particularly for infections where clinical outcomes vary over age. There are three theoretical challenges in implementing such analyses: i) developing an appropriate framework that models both demographic and epidemiological transitions; ii) parameterizing the framework, where parameters may be based on data ranging from the biological course of infection, basic patterns of human demography, specific characteristics of population growth, and details of vaccination regimes implemented; and iii) evaluating public health strategies in the face of changing human demography. We illustrate the general approach by developing a model of rubella in Costa Rica. The demographic profile of this infection is a crucial aspect of its public health impact, and we use a transient perturbation analysis to explore the impact of changing human demography on immunization strategies implemented.

1. Introduction

Structured population models have particular relevance in human epidemiology because both contact patterns and severity of disease are strongly age-dependent. Theoretically, there are three linked challenges to making age-structured models relevant to the epidemiological setting. First, the model framework must reflect both demographic and epidemiological transitions (Anderson and May, 1991; Klepac and Caswell, 2010; Schenzle, 1984), which requires taking into account the different time-scales of epidemiological rates and human demography. Second, the model must be parameterized from diverse public health data that are usually crude with respect to age structure (since cases are often binned into broad age classes), age-specific mixing, and sparse with respect to time (since data are often aggregated at intervals greater than the natural time-scale of infection). Third, parameterized models must be able to evaluate various public health strategies in the face of current and projected changes in demography. We illustrate these three linked challenges by developing a structured model for rubella in Costa Rica – an infection for which disease severity is particularly age-dependent.

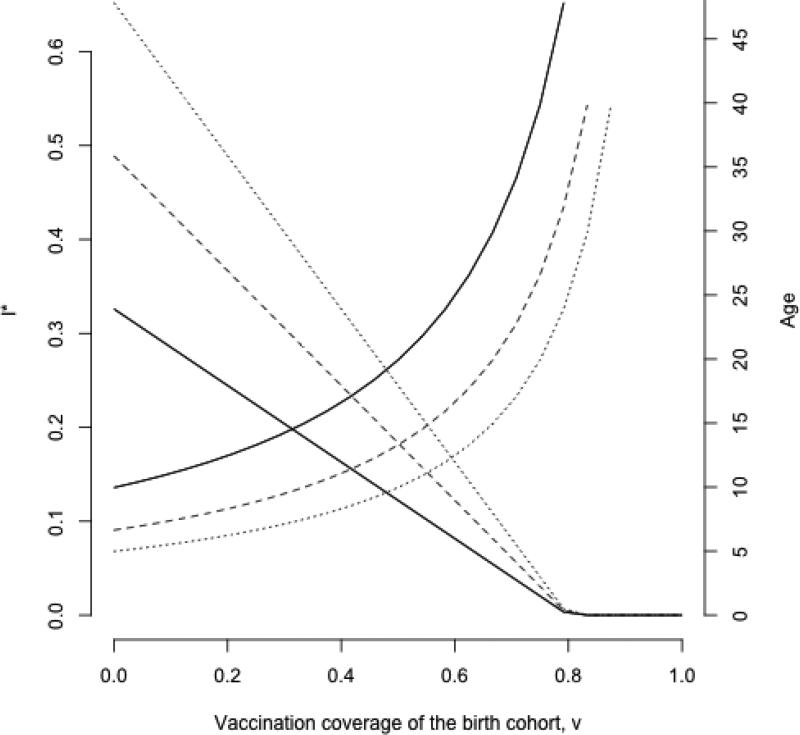
Rubella is a directly transmitted and strongly immunizing infection that generally causes a mild childhood disease. However, infection during the first trimester of pregnancy may cause fetal death or congenital rubella syndrome (CRS). The latter entails a range of impairments, including deafness, cataracts and blindness, and congenital heart disease. Since routine vaccination generally decreases the force of infection (FOI, the rate at which susceptible individuals become infected), it will increase the average age of infection unless coverage is high enough to achieve elimination. Mass vaccination may therefore potentially have the negative side effect of increasing CRS incidence (Anderson and May, 1983; Anderson and May, 1985; Anderson and May, 1991; Edmunds et al., 2000b; Vynnycky et al., 2003). Dynamically speaking, mass vaccination is analogous to reducing the birth rate, if vaccine-induced immunity conveys life-long protection (Earn et al., 2000). Consequently, a secular reduction in fertility rates is another factor that will increase the mean age of infection. In the simplest analysis, an unstructured susceptible-infected-recovered (SIR) model indicates that rubella immunization activities must attain sufficiently low equilibrium incidence to offset the increase in the average age of infection in the birth rate context of interest (Fig. 1). Perturbations due to changes in human demography or vaccination coverage mean that reality will rarely reflect the simple case. Understanding age-structured dynamics combining both changing demography and epidemiology in this context is thus key, and for this, developing structured models is essential (Tuljapurkar and John, 1991).

Figure 1.

In a classic SIR framework (here, dS/dt = μ(1 – v) – βSI – μS and dI/dt = βSI – gI – μI, where μ is the birth and death rate (total population size as taken as N=1), v is vaccination coverage of the birth cohort, and g is the generation time of the infection) the equilibrium proportion of infected individuals I* (y axis, left) is defined by I* = μ[(1 – v)R₀ – 1]/β and thus declines with increasing vaccination coverage of the birth cohort (x axis). The average age of infection A increases (y axis, right), approximately following R₀=G/A where G is the inverse of the birth rate. Different lines reflect 20, 30 or 40 births per 1000 (solid, dashed and dotted lines, respectively); other parameters are g is 18 days⁻¹, and β=R₀/(g+μ) with R₀=5.

From the point of view of public health, the dynamics of rubella in Costa Rica following vaccination are particularly interesting. Theoretical concerns about increases in the CRS incidence following introduction of rubella vaccination (Knox, 1980) appear to have been to some degree born out in the country (Morice et al., 2009). Vaccination was introduced at first at low coverage levels, and following years of low incidence, large outbreaks in older individuals occurred in 1987 and 1999. This was matched by an increase of susceptibility in older age groups (Jimenez et al., 2007) as well as an increase in CRS incidence. However, interpreting the impact of vaccination on CRS incidence in Costa Rica is complicated by the dramatic concurrent declines in the population birth rate.

Globally, introduction of the rubella vaccine is increasingly being considered, particularly given large-scale efforts currently underway towards measles eradication (World Health Organization, 2011). Understanding the contexts that might lead to problems by better understanding what occurred in Costa Rica is of considerable applied as well as theoretical interest. We use a structured modeling approach and sensitivity analysis to explore the determinants of the observed patterns, and to detail the impact of vaccination coverage under changing human demography. Below, we first introduce the model framework. We then describe data sources available, and approaches that can be used to parameterize the model, and finally use a perturbation analysis to explore how outcomes are altered given the changing human demographic context. We conclude by discussing the impact of changing human demography on the impact of rubella immunization strategies.

2. Model framework

We use a discrete-time model that incorporates both epidemic and demographic transitions (Klepac and Caswell, 2010; Klepac et al., 2009) by structuring the population into age classes, and epidemiological classes (‘maternally immune’ M, ‘susceptible’ S, ‘infected’ I, ‘recovered’ R, and ‘vaccinated’ V, taken to indicate the successfully vaccinated, and only applied to susceptible individuals). We can frame the joint processes of aging and infection as a matrix of demographic and epidemiological transitions. We structure the population into age strata (1, 2, ...., z; where z is the total number of age strata, here taken as z=37 with yearly age strata from age 1 to age 34, and decadal age strata thereafter up to age 64), and epidemiological classes (M, S, I, R, and V). Initially ignoring demographic transitions (survival and aging), within each age class a transitions between epidemiological categories occur according to:

$${\mathbf{A}}_{a,t}=\left(\begin{array}{ccccc}\hfill 1-d_a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill d_a\hfill & \hfill 1-{\phi }_a\left(\mathbf{n}\left(t\right)\right)(1-v_a)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\phi }_a\left(\mathbf{n}\left(t\right)\right)(1-v_a)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill v_a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$$ (1)

The five rows and columns represent the M, S, I, R, and V categories, respectively, and the matrix contents capture transitions between them. The time-step is taken as the approximate generation time of rubella (the latent plus infection period of the infection). Discrete time approaches that use the generation time of the infection as a time-step go back to Bailey's chain-binomial model (Bailey, 1957), and have received general support from analysis of a range of immunizing childhood infections with generation times similar to that of rubella (Bjørnstad et al., 2002; Metcalf et al., 2009). In the transition matrix d_a is the probability of losing maternal immunity, φ_a is the probability of becoming infected, and v_a is the probability of being vaccinated. The infection probability φ (also called the force of infection, FOI) is a function of n(t), a vector describing the population at time t

$$\mathbf{n}\left(t\right)={(M_{1,t},S_{1,t},I_{1,t},R_{1,t},V_{1,t},M_{2,t},\dots ,V_{z,t})}^{\mathrm{T}}$$ (2)

according to

$${\phi }_a\left(\mathbf{n}\left(t\right)\right)=1-\exp [-\sum _j{\beta }_{a,j,t}{I}_{j,t}^{\gamma }∕\sum \mathbf{n}\left(t\right)]$$ (3)

where z is the total number of age classes, β_a,j,t is the rate of transmission between individuals in age classes a and j, referred to as the Who-Acquires-Infection-From-Whom or WAIFW matrix, and γ captures heterogeneities in mixing not directly modeled (Bjørnstad et al., 2002; Finkenstadt and Grenfell, 2000) and the effects of discretization of the underlying continuous time process (Glass et al., 2003). Here we fix γ at 0.97 (except when calibrating R₀; see below), reflecting values obtained for measles in England and Wales (Bjørnstad et al., 2002). Discrete-time models that do not incorporate this exponent (i.e., γ=1) result in dynamics that are unrealistically unstable and prone to frequent extinction. Total population size appears as a denominator of number of infected individuals in each age class since previous experience with rubella indicates that transmission appears to scale in a frequency dependent manner (Metcalf et al., 2011b) as expected when social clique size is relatively independent of population size (Ferrari et al., 2011).

Seasonality in transmission often play an important role in the dynamics of childhood infections (Ferrari et al., 2008; Schenzle, 1984), and is generally observed for rubella (Metcalf et al., 2011a; Metcalf et al., 2011b). In the absence of detailed data, we chose to model seasonal fluctuations as a trigonometric function (e.g., (Schenzle, 1984)), i.e., transmission to individuals in age strata a, from individuals in age strata j at time t are defined by β_a,j,t = β_1,a,j (1 + β₂ cos(2πt)) where β_1,a,j is mean transmission from individuals in age strata j to age strata a, and β₂ is a parameter controlling the magnitude of seasonal fluctuations.

We construct the full transition matrix A(n(t)) to project the entire population forwards via aging, mortality and infection dynamics according to:

$$\mathbf{A}\left(\mathbf{n}\left(t\right)\right)=\left(\begin{array}{ccccc}\hfill s_1(1-u_1){\mathbf{A}}_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill s_1{u}_1{\mathbf{A}}_1\hfill & \hfill s_2(1-u_2){\mathbf{A}}_2\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill s_2{u}_2{\mathbf{A}}_2\hfill & \hfill s_3(1-u_3){\mathbf{A}}_3\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill s_3{u}_3{\mathbf{A}}_3\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill .s_z{\mathbf{A}}_z\hfill \end{array}\right)$$ (4)

where s_a is the probability that an individual in age class a survives to the next time step, u_a is the rate of aging out of age class a, and A₁, A₂, etc., are defined in equation (1), time-subscript dropped for convenience. The dynamics of the population as a whole can be projected forward according to the density dependent matrix model:

$$\mathbf{n}(t+1)=\mathbf{A}\left(\mathbf{n}\left(t\right)\right)\mathbf{n}\left(t\right)+{\mathbf{B}}_t$$ (5)

where B(t) is a vector representing the number of births at time t

$${\mathbf{B}}_t={(B_t,0,0,\dots ,0)}^{\mathrm{T}}.$$ (6)

Initial conditions were taken as values corresponding to the quasi-stationary distribution of the stochastic model for each set of parameters (obtained by iteration).

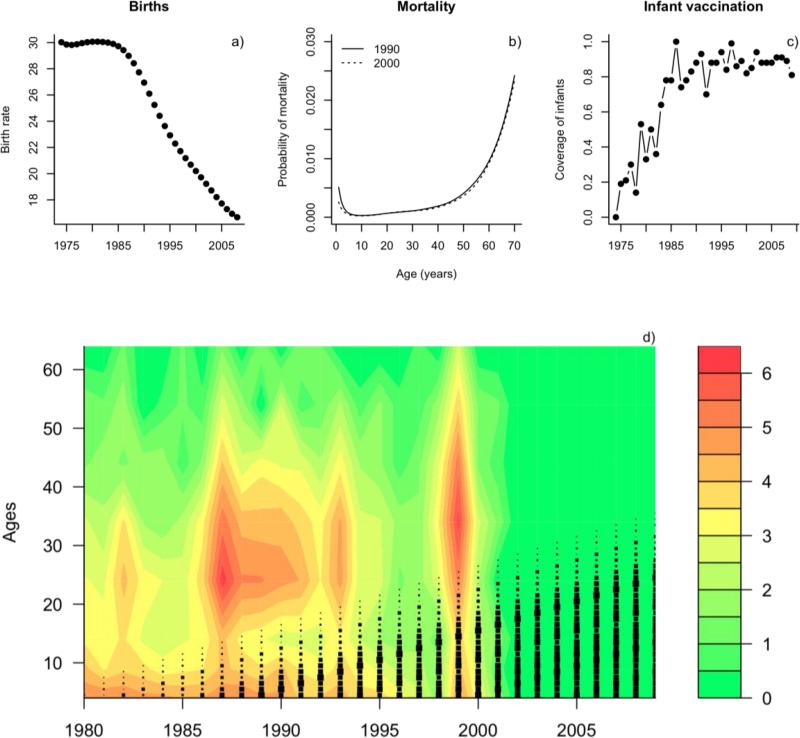
Our matrix model structure (eqn 4) implicitly assumes that demographic transitions relating to survival precede epidemiological transitions. The impact that this will have on dynamics is likely to be minimal since survival is very high across the chosen serial interval. The separation of births from the overall demographic and epidemiological transitions (eqn 5) also assumes that epidemiology precedes this aspect of demography. Given the gradual nature of the change in birth rates modeled (Fig. 2) this will have some effect on initial conditions, but will be minimal subsequently.

Figure 2.

Demographic, vaccination and infection characteristics of Costa Rica over the time-span considered including a) birth rate (from http://data.worldbank.org); b) mortality over age in 1990 and 2000 (from http://apps.who.int/ghodata/?vid=720; c) variation in coverage via infant vaccination through time; and d) rubella incidence over age across Costa Rica on a log scale (legend) in years following the introduction of vaccination. Black squares indicate the fraction of each cohort covered by routine infant vaccination (reflecting Fig. 1b). Older age outbreaks start at the upper limit of this line.

With this framework, we can calculate the basic reproductive ratio, R₀ (the number of cases that would result from the introduction of a single infected individual into a completely susceptible population), as the dominant eigenvalue of the next generation matrix taken at the disease free equilibrium (Allen and van den Driessche, 2008; Diekmann et al., 1990; Klepac and Caswell, 2010). In this case, R₀ is undefined for γ<1 so for its evaluation we set γ=1. This is necessary because we need an approximate next-generation value for R₀ to calibrate our transmission matrix (see below). We use γ=0.97 for all dynamic simulations (for reasons discussed above).

We can extended the model to be stochastic and to include an immigration rate according to,

$$\mathbf{n}(t+1)=S[\mathbf{A}\left(\mathbf{n}\left(t\right)\right),\mathbf{n}\left(t\right)]+{\mathbf{B}}_t+{\mathbf{M}}_t$$ (7)

where in the stochastic setting, S[A(n(t)), n(t)] is a vector resulting from the sum of stochastic draws from multinomial distributions defined according to each column of the matrix A and the number of individuals in each category, n(t); B_t is a vector with zeros corresponding to all but the first class (cf eqn 6), which in the stochastic setting is taken as a draw from a Poisson distribution around the time-varying mean birth rate, and M_t is a vector with zeros corresponding to all but the infected classes, and a draw from a random Poisson distribution with mean ι for each of the infected classes (that is, we make the simplifying assumption that the immigration rate is the same for all age classes). Large values of ι correspond to high mobility and low coverage of adjacent locations; small values of ι correspond to low mobility and effective vaccination in adjacent locations.

3. Parameterizing the model

Informing structured populations can be more straightforward than informing un-structured models, because it is often easier to match data inputs (e.g., age specific vaccination and death rates) to appropriate parameters in the model than in cases where population structure is oversimplified or ignored. Here, birth rates and population size of Costa Rica changed substantially over the period considered (1972-2000, Fig. 2a). We incorporate this directly into the model. Survival over age was less variable (Fig. 2b) and also directly incorporated into the model using the average rate over the time-course considered (Fig. 2b), again scaled to the generation time of rubella. The rubella vaccine was introduced in Costa Rica in 1972 and the measles-rubella vaccine (MR) was introduced into the childhood vaccination program in 1975 (Morice et al., 2003). Coverage increased gradually at a national scale (Fig. 2c). We include this in the model by allowing temporal variation in the vaccination rate of one year olds.

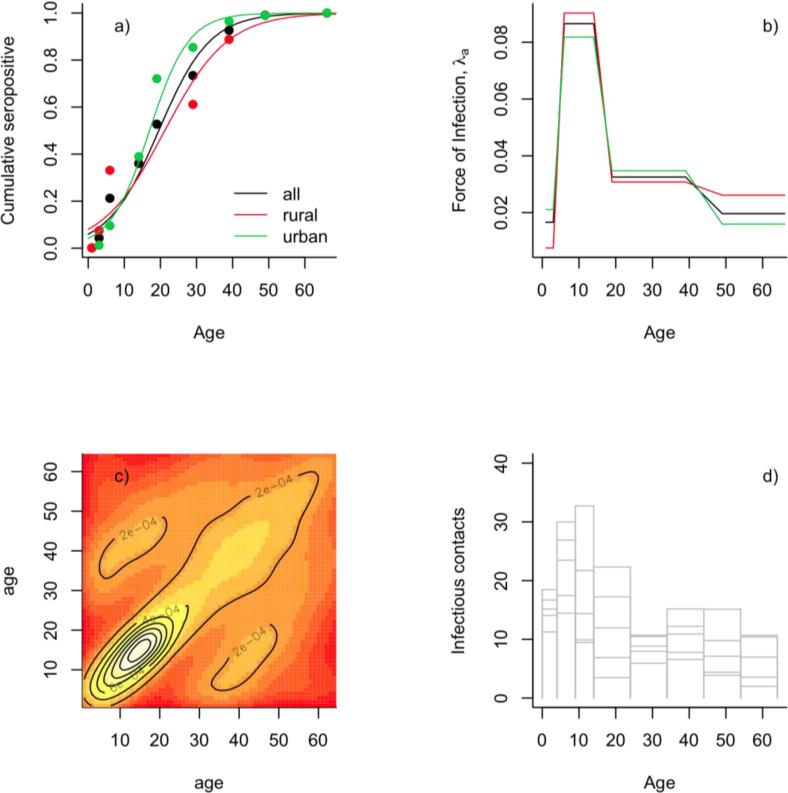
Magnitude and patterns of transmission over age may be informed by an array of data (Anderson and May, 1991). Sero-profiles (i.e. the age incidence of antibodies to rubella, indicating exposure to the infection, here available for rather broad age classes) taken before the start of vaccination (Villarejos et al., 1971) suggest that the pre-vaccination average age of infection, A was rather high (Fig. 3a), and shows slight regional differences. With life-expectancy of around L=66 in Costa Rica in 1969, using the relationship R₀~1+L/A (Anderson and May, 1991), this suggests a rather low R₀ (between 3 and 5), comparable with R₀ estimates of between 2 and 8 reported for rubella Europe (Edmunds et al., 2000a; Edmunds et al., 2000b). To estimate the force of infection over age, we used the 'catalytic' model (Griffiths, 1974), so called because of it structural similarity to equations commonly used to study of chemical reactions (Grenfell and Anderson, 1985). For this model, the cumulative probability P(a), of infection by age a is given by:

$$P\left(a\right)=1-\exp [-{\int }_0^a\phi \left(a\right)da]$$ (8)

where φ(a) is the age-specific force of infection. We fit a piece-wise constant force of infection model to the data, with four age classes (0-3, 4-14, 15-39, 40-66); note that these are the age classes available in the data, and finer resolution is not available (each of these bins is captured in the finer 37 stage structure used in our dynamic model). The pattern over age indicates that infection is predominantly occurring in children of school age (Fig 2b).

Figure 3.

a) Seroprofiles (points) of rubella pre-vaccination in 1969 (Villarejos et al., 1971), fitted with a logistic regression (lines) for rural communities, urban communities, and the entire country; the corresponding average age of infection (defined as −β₀/β_s where β₀ is the intercept of the fitted logistic regression; and β_s the slope) ranges between 17 and 21; b) corresponding age-specific FOI fitted with a catalytic model; c) log pattern of observed contacts across age (Mossong et al., 2008); d) profile of the expected FOI over age obtained by combining the age structure of the Costa Rican population between 1980 and 1985 with the age structure of infected individuals and the contact matrix shown in c).

The most direct source of information on human age-patterns of contact is provided by the observational diary studies in Europe (Mossong et al., 2008). A strongly diagonal structure (indicative of considerable mixing within an age class) combined with 'whiskers' of contact between individuals in their early twenties and children (Fig 3c) characterizes these matrices (Mossong et al., 2008; Rohani et al., 2010). To explore whether this is an appropriate structure for the contact matrix in Costa Rica, we used the Europe-wide model (Mossong et al., 2008). We then calculated the expected age-specific force of infection by considering this contact matrix in combination with the age-specific prevalence (Fig. 3d), and compared this with the empirical pattern revealed by the catalytic analysis (Fig. 3b). The overall similarity of the two (Fig. 3b vs. Fig. 3d) suggests that the model of contacts obtained from Europe is an adequate first cut in the absence of Costa Rican contact data. We finally generated a WAIFW matrix (i.e., obtained values for β_1,a,j for all age classes) by scaling the contact matrix so that the resultant R₀ matched empirical estimates from the seroprevalence data. In preliminary analyses we also used the approach of (Farrington and Whitaker, 2005) to estimate the WAIFW matrix. However, since this method is quite complicated and all epidemiological conclusions derived were similar to those using contact data, we have not included this analysis in this paper.

In the absence of data at a finer than annual time scale during the pre-vaccination era, it is impossible to estimate the exact magnitude of seasonality in transmission. However, given no substantial evidence for large variation in transmission for other countries in the region (Metcalf et al., 2011a; Metcalf et al., 2011b), and evidence for transmission predominantly in school children (Fig. 3b), we set β₂=0.2. This value is sufficiently high to generate an annual peak in transmission observed throughout the range for rubella, but not of a degree to will result in highly nonlinear dynamics (Ferrari et al., 2008). In the absence of data, we assumed that seasonal variation in transmission affected all ages in the same way.

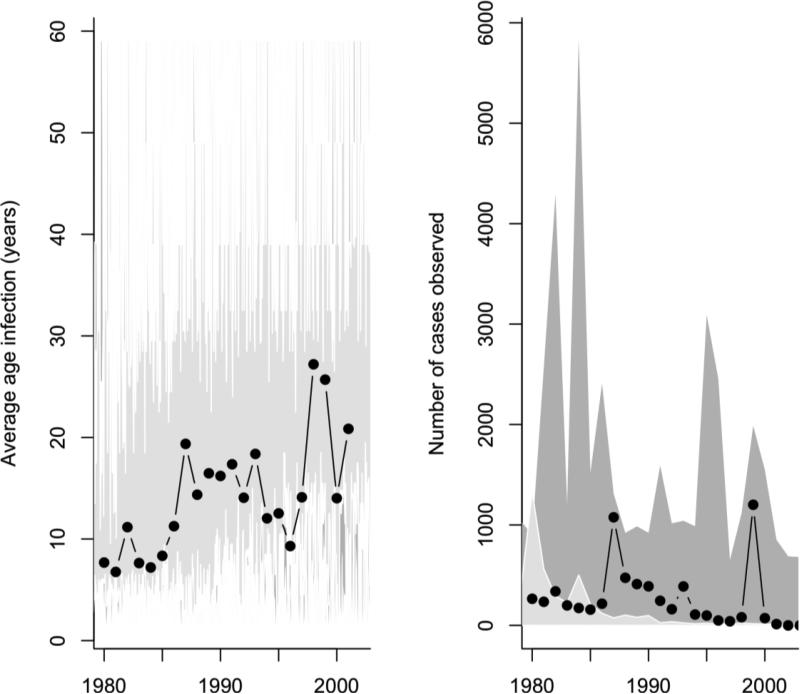
As well as allowing a straightforward way of incorporating epidemiological and demographic rates (i.e., births, vaccination, transmission, see above), structured models produce a diversity of outputs that can be compared to data. For instance, sero-surveys providing cumulative incidence by age, incidence data from surveillance systems, and rates of severe outcomes (e.g., CRS, death) can all be compared with model outputs and used in fitting procedures. Data from Costa Rica indicates that large, irregular outbreaks occurred prior to eradication, with the age structure shifting upwards (Jimenez et al., 2007; Morice et al., 2003) as predicted by epidemic theory (Anderson and May, 1991; Knox, 1980). Changes in the age-profile in serology are reviewed in (Morice et al., 2005), and overall indicate an increase in the age of infection, and proportion of women of child-bearing age at risk, also seen in the incidence reports (Fig. 2d). The signature of this has been documented in the burden of CRS (Morice et al., 2009). The pattern closely matches the cohorts unprotected by vaccination through time (Fig. 2d), and thus suggests that susceptibility is predominantly driven by vaccination rather than natural circulation over this period.

To develop an understanding of the dynamics linked to the age structure of susceptibility, we simulated stochastic dynamics for 20 years prior to 1973 to arrive at the pre-vaccination quasi-stationary distribution of the stochastic model, and then initiated vaccination following coverage levels defined in the data, assuming on average 1 infected immigrant a year across all age classes. Under reported levels of vaccination coverage, and in the absence of heterogeneity in coverage, although the age profile of incidence is well reflected (particularly its increase), total incidence is under-predicted, as rubella rapidly goes extinct. Cases that do occur are entirely due to introductions that fail to spread. Classical theory (Anderson and May, 1991) shows that circulation will cease in a homogenous population with coverage of more than 80% for an immunizing infection with an R₀ between 3 and 5 (the critical level of coverage require to attain herd immunity is, at its upper limit, 1-1/5 = 0.8). Heterogeneity in vaccination coverage indicated by coverage surveys in Costa Rica during this time period (Calvo et al., 2004) may have resulted in pockets of susceptible individuals, permitting the 1990's outbreaks to occur.

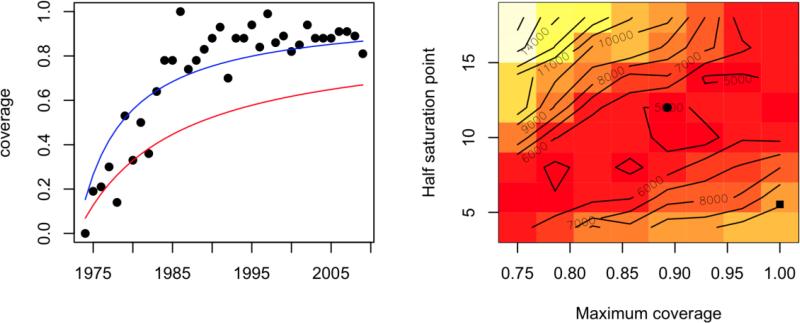
The potential for heterogeneity in coverage led us to explore the effects of lower effective coverage. To capture this, we fitted a saturating curve of the form y=ax/(b+x) to coverage through time and identified values of the parameters a and b corresponding to the lowest sum of squares separating log observed and log simulated age incidence over 10 simulations (Fig. 4). In these simulations, we assumed a reporting rate of 0.02 in 1973 that increases to near perfect reporting in 2008 to be consistent with the fact that surveillance for measles and rubella was targeted for improvement over this period with the introduction of standardized protocols, training of health personnel and use of quality surveillance indicators to evaluate surveillance. With this inferred vaccination profile, observed changes in the age profile are well reflected, as are overall changes in incidence (Fig. 5). Altering the exact timing and magnitude of changes in reporting slightly alters the best fitting vaccination profile, but the various combinations of reporting and vaccination coverage all permit the intermittent large outbreaks late in the time-series, indicating that the model can capture the broad qualitative patterns observed both with respect to age-incidence and temporal dynamics.

Figure 4.

Fitted curve (blue line, y=x/(5.53+x)) to reported vaccination coverage levels (black points) and curve reflecting the closest match between 15 simulated age-incidence profiles and the observed age incidence (red line, y=0.89x /(12+x)); the log sum of squares surface is shown on the right; parameters corresponding to the observed (square) and predicted (circle) shown. We assume that reporting rates increase gradually from 0.02 in 1980, reaching close to perfect reporting in 2008.

Figure 5.

The range of 50 stochastic simulations for R₀=4, assuming on average one infected immigrant a year and vaccination coverage levels adjusted as described above (dark grey polygon) or following the observed (light grey polygons) with the observed (black lines) average age of infection (left) and number of cases observed (right). Simulated case numbers are re-scaled for comparison with the observed (right) by calculating a reporting rate so that the average number of cases simulated in 1980 reflects the observed number of cases, corresponding to p_obs=0.02; we assume that this increases exponentially, reaching close to perfect reporting in 2008.

4. Perturbation analysis

To explore how the demographic context changes the impact of vaccination of rubella, we can use a deterministic perturbation analysis to estimate the transient sensitivity of total numbers of cases, and numbers of CRS cases to a change in vaccination coverage (Caswell, 2007). To establish this, we write

$$\frac{d\mathbf{n}(t+1)}{d{\theta }^T}=\left\{\mathbf{A}[\theta ,\mathbf{n}\left(t\right)]+({\mathbf{n}}^T\left(t\right)\otimes {\mathbf{I}}_s)\times \frac{\partial \mathrm{vec}\mathbf{A}[\theta ,\mathbf{n}\left(t\right)]}{\partial {\mathbf{n}}^T\left(t\right)}\right\}\frac{d\mathbf{n}\left(t\right)}{d{\theta }^T}+({\mathbf{n}}^T\left(t\right)\otimes {\mathbf{I}}_s)\frac{\partial \mathrm{vec}\mathbf{A}[\theta ,\mathbf{n}\left(t\right)]}{\partial {\theta }^T}$$ (9)

where θ refers to the parameter of interest, here vaccination coverage attained at age 1; A and n are as defined in equations (2) and (4); I_s is an identity matrix of dimension s corresponding to the dimensions of A (i.e., s=5z), and the vec operator transforms matrices into vectors with the columns stacked (Caswell, 2007; Henderson and Searle, 1979). To solve eqn 9, we first define a_i,j to include all appropriate transition components except vaccination for each cell of the matrix. The derivative of the transition matrix relative to coverage ∂A[θ,n(t)]/∂θ^T is then zero for transitions that do not include vaccination, a_i,j where vaccination occurred and −a_i,j where vaccination did not occur. This yields an s×s matrix that becomes an s²×1 matrix following the vec transform.

The vec-transformed derivative of the transition matrix relative to n(t), ∂vecA[θ,n(t)]/∂n^T(t) is an s²×s matrix where every column reflects the vec transformed derivative of the matrix A relative to each successive value in the vector n. To estimate this we require an expression of the derivative of the density dependent term φ_a(n(t)), to the number of individuals in each the population classes. For n ∈{M,S,R,V} this is

$$\frac{\partial {\phi }_a\left(\mathbf{n}\left(t\right)\right)}{\partial n}=-\frac{\sum _j{\beta }_{a,j,t}{I}_{j,t}^{\gamma }}{{(\sum \mathbf{n})}^2}\exp (-\sum _j{\beta }_{a,j,t}{I}_{j,t}^{\gamma }∕\sum \mathbf{n})$$

and for n ∈ {I},

$$\frac{\partial {\phi }_a\left(\mathbf{n}\left(t\right)\right)}{\partial I_i}=(1-{\phi }_a\left(\mathbf{n}\left(t\right)\right)\left(\frac{{\beta }_{a,i,t}\alpha I_{i,t}^{\gamma -1}\sum \mathbf{n}-\sum _j{\beta }_{a,j,t}{I}_{j,t}^{\gamma }}{{(\sum \mathbf{n})}^2}\right)$$

Since φ_a only appears for transitions out of susceptible stages (eqn 1), these will be the only transitions for which the derivative ∂vecA[θ,n(t)]/∂n^T(t) is not zero. For example for susceptible individuals of age a that are not vaccinated (corresponding to probability 1-v_a), that do survive (corresponding to probability s_a), remain in the same age class (corresponding to probability 1-u_a), and are not infected, relative to the number of maternally immune, susceptible, recovered or vaccinated individuals of any age class i (represented by n), the corresponding derivative of A[∂,n(t)] is

$$\left(s_a[1-v_a][1-u_a]\right)\times \frac{\partial {\phi }_a\left(\mathbf{n}\left(t\right)\right)}{\partial n}.$$ (10)

Relative to the number of infected individuals in age class a, the derivative is

$$\left(s_a[1-v_a][1-u_a]\right)\times \frac{\partial {\phi }_a\left(\mathbf{n}\left(t\right)\right)}{\partial I_a}$$ (11)

For the equivalent susceptible individuals that become infected, the relationships are the same, but multiplied by −1.

To evaluate ∂vecA[θ,n(t)]/∂n^T(t), we first define the derivative of the matrix A[θ,n(t)] using the above for each value in the population vector (M₁, S₁, ...). For each matrix derivative, we then take the vec transform. This defines the column in the ∂vecA[θ,n(t)]/∂n^T(t) matrix corresponding to the element in the population vector to which the derivative was calculated. All that remains is to define the initial state for dn(t)/dθ^T, here taken as zeros, since the parameters do not affect the initial population structure. Sensitivities of numbers of individuals in each age class can then be estimated using eqn 9; and numbers of infected individuals can be scaled by fertility in each age class to obtain the sensitivity of CRS burden to changes in vaccination coverage (Caswell, 2007; Klepac and Caswell, 2010). To obtain the cumulative burden over the years of vaccination (1975-2010), sensitivities or scaled sensitivities may be directly summed.

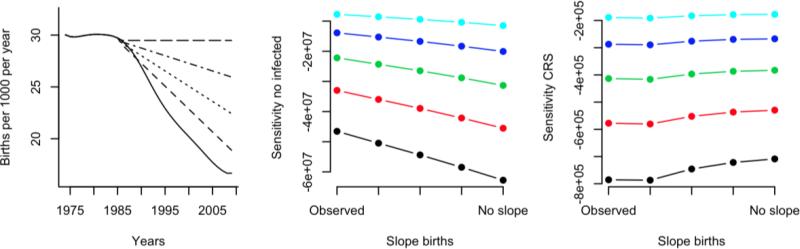
Increasing low coverage (Fig. 6, top row) averts more rubella cases for constant birth rates (Fig. 6a, horizontal line) than if birth rates are falling as seen in Costa Rica. This occurs because in a persistently high birth-rate context averting cases in an increased proportion of new-born individuals prevents transmission to many others, because of the functional equivalence between birth rate and transmission (Earn et al., 2000). For the CRS burden, the relationship is generally the opposite: increasing the proportion of the birth cohort vaccinated has a larger effect when birth rates are declining than if they are not, at least when coverage is low. This pattern occurs because declining birth rates are themselves increasing the burden, by increasing the average age of infection, so the impact of reducing incidence is larger. For sufficiently high coverage, this pattern is reversed, and the effect reflects that of numbers of infected individuals, since the reduction in incidence is large enough to overwhelm the effect of birth rate on the average age of infection.

Figure 6.

For birth-rate profiles ranging from that reported for Costa Rica (steep decline starting around 1985; solid line) to constant birth through the period (horizontal dashed line), we estimated the sensitivity of the cumulative number infected to vaccination coverage achieved in infants (y axis) for coverage levels of 0 (black line), 0.1 (red line), 0.3 (green line), 0.4 (blue line) and 0.5 (turquoise line); and likewise for the sensitivity for the number of CRS cases. For both, sensitivity is consistently <0 indicating that an increase in vaccination always reduces cumulative cases and cumulative CRS cases over this time-horizon; however, greater effect is observed for lower coverage levels, and for the CRS burden, the direction of effects may shift with coverage levels, see text.

5. Discussion

Epidemic dynamics of strongly immunizing childhood infections have been the focus of much research. Theoretical predictions of unstructured models and epidemiological surveillance data are often closely matched (Grenfell et al., 2002; Keeling et al., 2001). Seasonal variation in transmission generally stands in for differences in mixing over age in these unstructured models (Bjørnstad et al., 2002; Earn et al., 2000), for example via low transmission during times corresponding to school holidays. However, for infections like rubella where the age of infection is a critical aspect of the burden, extending models to incorporate demographic structure becomes essential. Additionally, unstructured models must generally disregard data on age-incidence as a source of information, and this may considerably weaken inference, especially where data is only available at a yearly time-scale, preventing direct parameterization of seasonal variation in transmission.

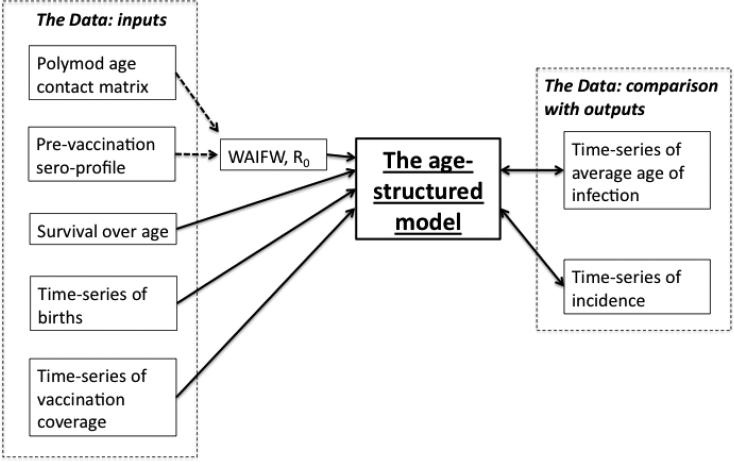
Here, we combine a diverse array of data to parameterize a model of rubella in Costa Rica (Fig. 7) that incorporates the age-dependent mechanisms we know to be operating (e.g., age variation in transmission, etc.). This framework provides insights into rubella dynamics in Costa Rica, but also points to uncertainties, such as the likely role of both changes in reporting rates over the time-scale of interest, and vaccination heterogeneity resulting in pockets of susceptible individuals (Fig. 4). Although our model has the potential to capture all the qualitative features of the transients affecting incidence and age structure in Costa Rica, the strongest quantitative fit to the empirical patterns is seen for lower vaccine coverage than reported. This inferred lower vaccine coverage may both capture the combined effect of changes in reporting and spatial heterogeneity in susceptibility, as well as potentially compensate for some aspect of model mis-specification, and thus may not necessarily be the true mechanism.

Figure 7.

Relationship between data and the age-structured model. Solid lines ending in arrows indicate either data or elements inferred from data (i.e., R₀, the appropriate structure of the WAIFW) that directly enter the model; double-ended arrows indicate data that is compared with model output for model validation.

From a public health perspective, since birth rates and coverage may vary through time (Fig. 2), and heterogeneity of transmission across age (Fig. 3) is likely to be the rule, structured models are also essential to assess the transient effects of shifts in demography and vaccination (Caswell, 2007). A key public health question that the Costa Rican experience can inform is whether the gradual introduction of coverage led to more cases of CRS than would have been observed with no introduction at all (given a specified time interval). Bearing the caveats outlined above in mind, across an array of values of R₀ (3-12) we find a negative sensitivity of the cumulative CRS burden on an increase in vaccination coverage (see, e.g., Fig. 6), which is retained across a range of birth scenarios. This indicates that for situations broadly resembling that of Costa Rica, introducing vaccination even at rather low levels is likely to largely result in positive outcomes relative to the CRS burden, and would therefore be recommended (although note that extending the time-horizon could eventually result in an increase in the cumulative burden (Metcalf et al., Submitted); and additionally, only deterministic rather than stochastic sensitivities were explored).

A second critical question in the current context of changing human demography is the degree to which changes in coverage are affected by changes in the birth rate. The relative magnitude of the effects of vaccination in a declining birth context vs in a constant birth context may be reversed for rubella incidence vs CRS incidence. The analysis of rubella in Costa Rica explicitly reveals the time-scales and magnitude over which such effects play out, emphasizing the importance of introducing the rubella vaccine into a declining birth situation, despite the relatively lower impacts of immunization in this context on overall incidence.

Structured population models and next-generation techniques have the potential to greatly inform public health questions: the age-structured approach is essential to prediction of age-structured outcomes, but also to exploiting the array of data sources available The more detailed reflection of underlying mechanism further simplifies parameterization but also reveals areas of important remaining uncertainty.