Abstract
Imaging depth of optical microscopy has been fundamentally limited to millimeter or sub-millimeter due to strong scattering of light in a biological sample. X-ray microscopy can resolve spatial details of few microns deep inside a sample but contrast resolution is inadequate to depict heterogeneous features at cellular or sub-cellular levels. To enhance and enrich biological contrast at large imaging depth, various nanoparticles are introduced and become essential to basic research and molecular medicine. Nanoparticles can be functionalized as imaging probes, similar to fluorescent and bioluminescent proteins. LiGa5O8:Cr3+ nanoparticles were recently synthesized to facilitate luminescence energy storage with x-ray pre-excitation and subsequently stimulated luminescence emission by visible/near-infrared (NIR) light. In this paper, we propose an x-ray micro-modulated luminescence tomography (XMLT, or MLT to be more general) approach to quantify a nanophosphor distribution in a thick biological sample with high resolution. Our numerical simulation studies demonstrate the feasibility of the proposed approach.
OCIS codes: (340.0340) X-ray optics, (100.3010) Image reconstruction techniques, (170.3880) Medical and biological imaging
1. Introduction
Systems biology is devoted to comprehensive studies of biological components with interrelated mechanisms across resolution scales over six orders of magnitude, involving molecules, sub-cellular features, cells, organisms, and entire species [1]. Living systems are highly complicated, dynamic, and often unpredictable. To understand and manipulate these systems, quantitative measurements of interacting components and clusters are necessary using systematic and microscopic technologies such as microscopies, genomics, proteomics, bioinformatics, in vivo or in situ imaging, and computational models. Regenerative medicine utilizes principles of biology and engineering to develop and transplant engineered substitute tissues and organs [2], with various protocols for cell seeding onto porous scaffolds during incubation [3]. These constructs are then expected to restore or regenerate functionality of diseased tissues or organs. Engineered tissue growths are rather sophisticated, and as natural biological counterparts they usually recapitulate normal developmental processes [4]. Hence, systematic and microscopic technologies are critical for evaluating engineered tissue prior and post implementation.
Molecular and cellular probes have versatile and sophisticated labeling capabilities, and are considered instrumental for systems biology, tissue engineering, and molecular medicine. There is a tremendous interest in biocompatible nanoparticles for in situ or in vivo molecular imaging, drug delivery, and therapy [5]. Optical imaging is a primary methodology to sensitively visualize nanoparticles tagged to specific molecules and cells [6, 7]. A typical example of their applications is cancer research [8, 9], which employs nanoparticles to deliver drug, heat, or light to cancer cells [10]. Another example is tissue engineering. With multi-functional nanoparticles, engineered tissue constructs can not only be monitored at cellular and molecular levels but also stimulated and regularized by multiple physical means for optimal functionalities. These nanoparticle ingredients are particularly important for the paradigm shift from 2D to 3D matrices in tissue engineering.
Microscopy is the principal observational tool and has made important contributions to our understanding of biological systems and engineered tissues [11]. However, imaging depth of optical microscopy has been fundamentally limited to millimeter or sub-millimeter due to multiple scattering of light in a biological sample. Conventional microscopy techniques utilize visible light or electron sources [12–14]. Optical microscopy divides into transmission (i.e., wide-field microscopies for snap-shot of 2D images in terms of light absorption, phase contrast, or dark-field signals) and emission modes (i.e., wide-field fluorescence microscopy, confocal laser scanning microscopy, and two-photon fluorescence microscopy). These microscopic modalities are good for in vitro and in vivo studies of cultured cell/tissue samples or small animals [15]. Inherently, image resolution of optical microscopy is diffraction-limited by ~200nm with single objective techniques and ~120nm with confocal techniques. With appropriate sample preparation, stochastic information and innovative interference techniques, ~100nm resolution is achievable. Three-dimensional image cubes can be obtained with optical sectioning of ~200nm lateral resolution and ~500nm axial resolution. Ultimately, multiple scattering prevents these techniques from imaging thick samples. Photoacoustic tomography permits scalable resolution at imaging depths up to ~7cm with a depth-to-resolution ratio ~200. Photoacoustic microscopy aims at millimeter imaging depth, micron-scale resolution and absorption contrast, which could be used to characterize the structure of the scaffold but it is generally not as sensitive and specific as fluorescence and bioluminescence imaging [15, 16].
Nanoparticles can be functionalized as imaging probes, similar to fluorescent and bioluminescent proteins. Unlike conventional nanoparticle probes, LiGa5O8:Cr3+ nanoparticles were recently synthesized to facilitate the luminescence energy storage with x-ray pre-excitation and subsequently stimulated luminescence emission by visible/near-infrared (NIR) light [17, 18]. LiGa5O8:Cr3+ nanoparticles are synthesized using a sol-gel method with lithium nitrate, gallium nitrate and chromium nitrate as precursors, followed by calcination and wet mechanical grinding. These particles are single-crystalline of 50–100nm in size. Upon UV or x-ray irradiation, they emit an intense photoluminescence band peaking at 716nm, attributing to the spin-forbidden 2E→4A2 transition of Cr3+ dopants. The energy stored in nanoparticles can sustain for 10 hours with detectable NIR persistent luminescence.
Our idea is to use a micro-modulated x-ray for engraving a distribution of nanophosphors which can then have luminescence energy stored for detailed tomographic imaging deeply in tissue samples. This imaging modality promises to reveal a distribution of LiGa5O8:Cr3+ nanoparticles targeting specific molecular and cellular aggregates, pathways and responses in engineered tissue samples of several millimeters in size and a few microns in resolution, overcoming the imaging depth limit of all other optical microscopic methods. In this micro-modulated luminescence tomography (MLT) process, tomographic data will be acquired via near-infrared (NIR) light stimulation and optical multiplexing. Needless to say, this MLT principle can be also used for luminescence tomography with traditional nanophosphors. In the following section, we will describe a system design, a photon transport model, and an image reconstruction algorithm for MLT. In the third section, we report our realistic numerical simulation results. In the last section, we discuss relevant issues and conclude the paper.
2. System prototyping
One embodiment of our proposed MLT system architecture consists of a micro-focus x-ray source, an x-ray zone plate, two EMCCD cameras, NIR laser stimulation sources, and a rotating stage, as shown in Fig. 1. All the components will be integrated on an optical table in a light-proof box made of aluminum posts and blackened panels [19, 20]. The x-ray source will be mounted on a horizontally-motorized linear stage (ILS300LM, Newport) for focal plane adjustment. The object to be studied will be placed on a rotational stage (URS75BCC, Newport) on a 3D combination of linear stages (VP-25XA, VP-5ZA, Newport) for x-y-z adjustment. NIR laser beams are expanded and controlled to stimulate nanoparticles for luminescence imaging. The EMCCD camera (iXon3 897, Andor Technology) has a sensitive 512 × 512 matrix with pixel size 16 × 16μm2. The two cameras are faced each other with the object in between for simultaneous data acquisition. An aluminum filter is used to block low energy x-rays and have a spectral peak at 10keV-20keV. The x-rays can be collimated into a narrow-angle cone-beam to irradiate the Fresnel zone plate. The zone plate is placed within a five axis lens positioner (IP-05A, Newport). As a standard x-ray microscopic imaging component, the zone plate focuses an incoming monochromatic x-ray beam onto a focal spot. The zone plate consists of multiple radially symmetric x-ray transparent rings. The width of a ring decreases with increment of its radius . The focal length of a zone plate depends on its diameter, outermost zone width and x-ray wavelength : [21–23]. Since an incoming beam from an ordinary x-ray tube is polychromatic, the x-rays are focused along a focal line segment. When an object intersects the x-ray focal line segment, the exposed nanophosphors in the object can be excited by x-rays and store some x-ray energy. Upon NIR light stimulation, the x-ray energy stored in the nanophosphors will be released via luminescence emission, and can be detected by the CCD camera. The intensity of luminescence emission reflects the nanophosphor concentration distribution.
Fig. 1.
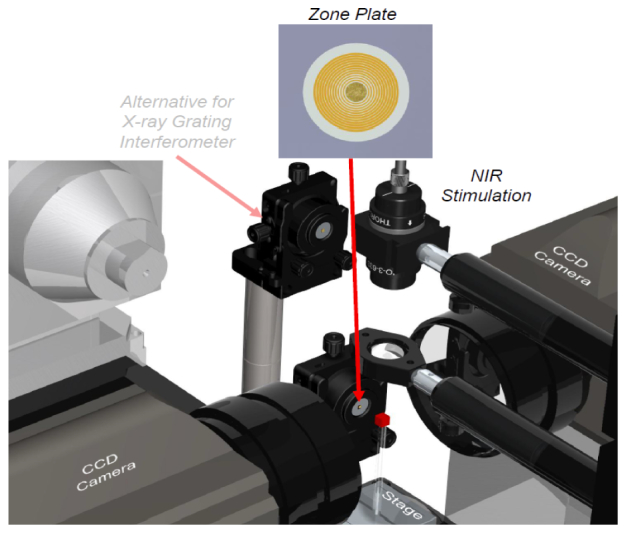
Micro-modulated luminescence tomography (MLT) system.
3. Photon transport model and reconstruction algorithm
3.1. Photon transport model
The measured light signal on the surface of a sample is closely related to the optical parameters of the sample. A practical method was already proposed for determination of optical parameters of tissues [24]. The reduced scattering coefficient [mm−1] relies on luminescence emission wavelength (nm) and can be approximated by an empirical function:
| (1) |
where a and b are respectively tissue-type-specific constants. The organ-specific values for a and b are in [24]. The tissue absorption is associated with local oxy-hemoglobin (HbO2), deoxy-hemoglobin (Hb) and water (W) concentrations, and the absorption coefficient [mm−1] is well approximated as the weighted sum of the three absorption coefficients , and , which are calculated from the corresponding absorbance spectra [24]:
| (2) |
where is the ratio between oxy-hemoglobin and total hemoglobin concentrations, and are scaling factors respectively.
MLT involves NIR light stimulation to make energy-stored nanophosphors emit luminescence photons. A light propagation model is needed to describe interactions of light photons with scattering and absorbing media, which is essential for MLT image reconstruction [25, 26]. For biological samples, the diffusion approximation model, a computationally-efficient approximation to the radiative transport equation (RTE), would break down with small sample size, strong absorbers, near sources, and across boundaries [27, 28]. In that case, either RTE itself or an alternative photon transport model will be needed to accurately describe the photon propagation in biological tissue [28, 29].
For the infinite-space medium, the solution can be obtained via the spherical harmonics approximation [30],
| (3) |
where and are defined as follows. From the initial conditions and , and the recursive formula, a polynomial can be derived: , where and are the n-th order absorption moment and the expansion coefficient of the phase function respectively. In the case of the Henyey-Greenstein phase function,, where g is an anisotropic factor. From the initial conditions and , the second polynomial can be obtained: . The polynomial equation gives a total of negative real-valued roots . These roots define the values and the coefficients
| (4) |
For optical imaging of biological samples, the tissue boundary must be taken into account when analyzing the photon propagation. A significant amount of photons go across the tissue boundary and can be detected by a highly sensitive CCD camera. In this scenario, the photon propagation process can be well modeled using a semi-infinite slab. For that purpose, we use the extrapolated boundary condition, which is simple and has been shown to agree well with the Monte Carlo (MC) simulation and physical measurement [31, 32]. An image source is used to construct a fluence rate solution such that holds at an extrapolated boundary at a distance above the surface of the sample, where and [32, 33]. The photon fluence at the boundary is the sum of the contributions from the source and its image,
| (5) |
where , and . Therefore, the NIR light propagation in the biological sample can be simulated using Eq. (5).
3.2. Few-view image reconstruction
The intensity of the NIR luminescence emission from nanophosphors is decaying with time, and is related to nanoparticle concentration [µg/mL], x-ray intensity [Watts/mm2], stimulating light intensity [Watts/mm2], and luminescence photon yield . The luminescence emission from nanophosphors can be formulated as
| (6) |
where is stimulation efficiency. X-ray beams can be focused by a zone plate, forming a pair of narrow-angle cones with a common vertex point. When a biological sample with a thickness of ~5mm is centralized around the focus region, several micrometer width x-rays go through the sample. For example, for a zone plate with a diameter of 0.35mm, an outer zone width of 100nm, and a zone height (gold) of 1600nm, the focal length is 258mm and the maximum width of x-ray beams through a sample is ~3.39µm. In practice, the intensity distribution of x-rays around the focal region can be measured using an x-ray detector. The narrow x-ray beam excites the nanophosphors in the sample, and the luminescence emission from the nanophosphors is measured on the surface of the sample by the CCD camera. The total intensity of the measured NIR light is related to the nanophosphor concentration on a narrow x-ray beam path, if we assume that all the nanophosphors in the excited region are completely depleted during each luminescence data acquisition step (otherwise, the total measurement is a weighted integral).
With the first generation CT scanning mode, we obtained a dataset with a parallel-beam excitation and different view angles for MLT reconstruction. To the first order approximation, we have a model to simulate the luminescence emission from nanophosphors. From Eqs. (5) and (6), we computed the intensity of luminescence emission from the nanophosphors on each x-ray path in the sample. Hence, we have a system of linear equations:
| (7) |
where is a vector of measured photon fluence rates, a vector of nanophosphor concentrations, and the system matrix. In the molecular imaging applications, molecular probes are attached to cells of a preferred type, and accumulated locally to form nanophosphor clusters. For reconstruction of a sparse image, an advanced compressive sensing (CS) method can produce excellent image quality from far fewer measurements than what is required by the Nyquist sampling theorem. The l0 norm regularization can ensure the sparsest image reconstruction. The equivalence between the l1 and l0 minimization procedures was previously established under the assumption of the restricted isometry property (RIP). Hence, the l1 norm is a valid sparsity measure of a signal, and is a convex function for efficient optimization. The reweighted ll minimization outperforms the l1 minimization for accurate image reconstruction in the case of even fewer measurements. This algorithm consists of solving a sequence of weighted l1-minimization problems. The recently developed few-view reweighted sparsity hunting (FRESH) scheme [34] was selected for MLT reconstruction.
4. Numerical simulation results
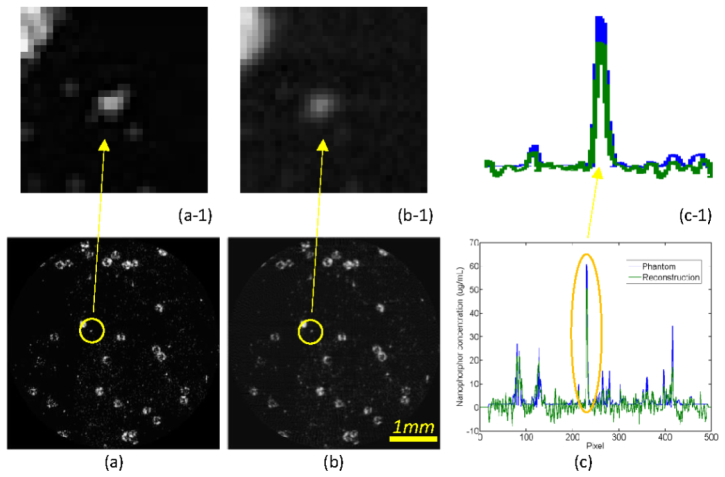
Using the proposed MLT methodology, we numerically studied a biological sample phantom of 5 × 5 × 5mm3. Biologically relevant optical parameters were assigned to the phantom: absorption coefficient µa = 0.01mm−1, scattering coefficient µs = 10mm−1 and anisotropy parameter g = 0.9. We assumed that the phantom included two patterns of nanophosphors at 2.5mm and 3.5mm in depth respectively, which were adapted from a STORM image [35], with 100µg/ml maximum concentration, as shown in Figs. 2(a) and 3(a). This phantom is representative for nanophosphor molecular probe accumulation, contrast and spatial resolution. An x-ray source of 5µm focal spot was filtered by a 0.4mm-thick aluminum plate for an energy spectrum of 10-20KeV. A Fresnel zone plate of 0.35mm diameter was utilized for x-ray focusing into a narrow beam of 10µm width. The phantom was steered with step size of 10µm for 512 translations to generate NIR light for a view angle, and rotated 100 times over a 180° angular range to excite nanophosphors in the phantom. NIR light stimulation steps were then applied to read out the stored luminescence energy. The x-ray excitation, NIR stimulation and luminescence emission were all simulated according to Eq. (5). In this work, all luminescence photons from a narrow x-ray beam were collected to define the associated integral, and a sinogram was formed. The simulated luminescence signals on the surface of the phantom were corrupted by 5% Gaussian noise to mimic a real measurement condition. The proposed MLT reconstruction method was applied to estimate the nanophosphor distribution from the simulated data. The reconstructed results were in an excellent agreement with the true phantom. Figure 2(b) shows the reconstructed nanophosphor distribution with resolution ~10µm at 2.5mm depth. Figure 3(b) is the counterpart distribution at 3.5mm depth. Figures 2(c) and 3(c) compare the reconstructed and true profiles at 2.5mm and 3.5mm depths respectively, confirming the quantification accuracy of the MLT reconstructions.
Fig. 2.
Modulated luminescence tomography simulation. (a) The true nanophosphor distribution at 2.5mm depth, (b) the reconstructed nanophosphor distribution with ~10µm resolution, and (c) the profile comparison along the vertical line at x = 160th pixel between the true and reconstructed nanophosphors concentrations. The top row images are the zoomed regions of interest in the bottom row.
Fig. 3.
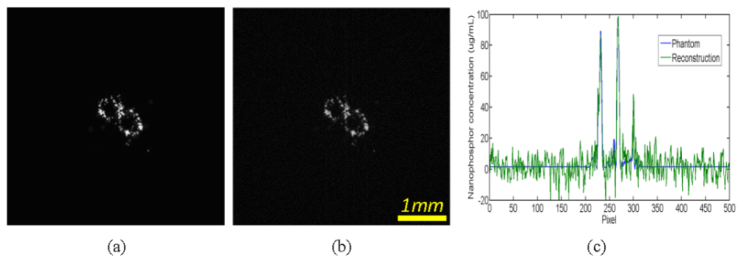
Modulated luminescence tomography simulation. (a) The true nanophosphor distribution at 3.5mm depth, (b) the reconstructed nanophosphor distribution, and (c) the profile comparison along the horizontal centerline between the true and reconstructed nanophosphors concentrations.
5. Discussions and conclusion
We have proposed the MLT modality to quantify a nanophosphor distribution in a biological sample of a thickness much greater than currently possible with existing optical microscopic techniques. Although we described LiGa5O8:Cr3+ nanoparticles for the above-reported embodiment of the MLT system, other types of nanophosphors including traditional ones used for x-ray luminescence tomography [36] can be used for MLT as well. Different from the conventional pinhole-based x-ray excitation mode adopted for x-ray luminescence tomography [36], which is difficult to be made at micron precision, and is subject to diffractive complication, the proposed MLT approach focuses x-rays into a narrow pattern with an x-ray zone plate or other similar elements such as gratings. A successful application of an x-ray zone plate is nano-x-ray computed tomography, which achieves nano-scale resolution routinely. Because of the deep penetration of well-modulated x-ray excitation, MLT is capable of achieving micron resolution image reconstruction deep into a sample. The NIR laser stimulation of stored luminescence energy further improves image resolution with an optimized optical or alternative readout sequence.
Because of targeted high resolution, this proposed imaging modality would take more imaging time in experiments than x-ray luminescence computed tomography [36] and stored luminescence computed tomography [20]. The cutting-edge compressive sensing (CS) method can recover a sparse image from rather fewer measurements. Hence, few-view tomography will be critical for MLT to minimize projection data and radiation dose.
In summary, our MLT approach has been conceptualized and formulated. The simulation results have demonstrated the feasibility and potential of the proposed approach. The MLT modality may find many utilities in investigating biological features and processes with tissue engineering and cancer imaging as two examples, monitoring drug delivery, assessing therapeutic responses, and other applications such as FRET-like imaging.
Acknowledgments
This work was partially supported by the National Institutes of Health Grant NIH/NHLBI HL098912. We thank very much Dr. Zhengwei Pan with University of Georgia for information and discussion on his novel nanoparticles.
References and links
- 1.Timpson P., McGhee E. J., Anderson K. I., “Imaging molecular dynamics in vivo - from cell biology to animal models,” J. Cell Sci. 124(17), 2877–2890 (2011). 10.1242/jcs.085191 [DOI] [PubMed] [Google Scholar]
- 2.Chien K. R., “Regenerative medicine and human models of human disease,” Nature 453(7193), 302–305 (2008). 10.1038/nature07037 [DOI] [PubMed] [Google Scholar]
- 3.Weinand C., Xu J. W., Peretti G. M., Bonassar L. J., Gill T. J., “Conditions affecting cell seeding onto three-dimensional scaffolds for cellular-based biodegradable implants,” J. Biomed. Mater. Res. B Appl. Biomater. 91B(1), 80–87 (2009). 10.1002/jbm.b.31376 [DOI] [PubMed] [Google Scholar]
- 4.Solanki A., Kim J. D., Lee K. B., “Nanotechnology for regenerative medicine: nanomaterials for stem cell imaging,” Nanomedicine 3(4), 567–578 (2008). 10.2217/17435889.3.4.567 [DOI] [PubMed] [Google Scholar]
- 5.Perrault S. D., Chan W. C., “In vivo assembly of nanoparticle components to improve targeted cancer imaging,” Proc. Natl. Acad. Sci. U.S.A. 107(25), 11194–11199 (2010). 10.1073/pnas.1001367107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Alivisatos P., “The use of nanocrystals in biological detection,” Nat. Biotechnol. 22(1), 47–52 (2004). 10.1038/nbt927 [DOI] [PubMed] [Google Scholar]
- 7.Shin S. J., Beech J. R., Kelly K. A., “Targeted nanoparticles in imaging: paving the way for personalized medicine in the battle against cancer,” Integr Biol 5(1), 29–42 (2013). 10.1039/c2ib20047c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gao X. H., Cui Y. Y., Levenson R. M., Chung L. W. K., Nie S. M., “In vivo cancer targeting and imaging with semiconductor quantum dots,” Nat. Biotechnol. 22(8), 969–976 (2004). 10.1038/nbt994 [DOI] [PubMed] [Google Scholar]
- 9.Nie S. M., Xing Y., Kim G. J., Simons J. W., “Nanotechnology applications in cancer,” Annu. Rev. Biomed. Eng. 9(1), 257–288 (2007). 10.1146/annurev.bioeng.9.060906.152025 [DOI] [PubMed] [Google Scholar]
- 10Ricci C., Moroni L., Danti S., “Cancer tissue engineering: new perspectives in understanding the biology of solid tumors: A critical review,” OA Tissue Eng. 1(1), 4 (2013). [Google Scholar]
- 11.Goy A. S., Unser M., Psaltis D., “Multiple contrast metrics from the measurements of a digital confocal microscope,” Biomed. Opt. Express 4(7), 1091–1103 (2013). 10.1364/BOE.4.001091 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jalili N., Laxminarayana K., “A review of atomic force microscopy imaging systems: application to molecular metrology and biological sciences,” Mechatronics 14(8), 907–945 (2004). 10.1016/j.mechatronics.2004.04.005 [DOI] [Google Scholar]
- 13.Pong W. T., Durkan C., “A review and outlook for an anomaly of scanning tunnelling microscopy (STM): Superlattices on graphite,” J. Phys. D Appl. Phys. 38(21), R329–R355 (2005). 10.1088/0022-3727/38/21/R01 [DOI] [Google Scholar]
- 14.Wongsrichanalai C., Barcus M. J., Muth S., Sutamihardja A., Wernsdorfer W. H., “A review of malaria diagnostic tools: Microscopy and rapid diagnostic test (RDT),” Am. J. Trop. Med. Hyg. 77(6), 119–127 (2007). [PubMed] [Google Scholar]
- 15.Wang L. V., “Multiscale photoacoustic microscopy and computed tomography,” Nat. Photonics 3(9), 503–509 (2009). 10.1038/nphoton.2009.157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cai X., Zhang Y. S., Xia Y., Wang L. V., “Photoacoustic Microscopy in Tissue Engineering,” Mater. Today 16(3), 67–77 (2013). 10.1016/j.mattod.2013.03.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Liu F., Yan W., Chuang Y. J., Zhen Z., Xie J., Pan Z., “Photostimulated near-infrared persistent luminescence as a new optical read-out from Cr³⁺-doped LiGa₅O₈,” Sci. Rep. 3, 1554 (2013). 10.1038/srep01554 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pan Z., Lu Y. Y., Liu F., “Sunlight-activated long-persistent luminescence in the near-infrared from Cr3+-doped zinc gallogermanates,” Nat. Mater. 11(1), 58–63 (2012). 10.1038/nmat3173 [DOI] [PubMed] [Google Scholar]
- 19.Cong W., Wang G., Kumar D., Liu Y., Jiang M., Wang L. V., Hoffman E. A., McLennan G., McCray P. B., Zabner J., Cong A., “Practical reconstruction method for bioluminescence tomography,” Opt. Express 13(18), 6756–6771 (2005). 10.1364/OPEX.13.006756 [DOI] [PubMed] [Google Scholar]
- 20.Cong W., Wang C., Wang G., “Stored luminescence computed tomography,” Int. J. Eng. Innovative Technol. (to be published).
- 21.David C., Gorelick S., Rutishauser S., Krzywinski J., Vila-Comamala J., Guzenko V. A., Bunk O., Färm E., Ritala M., Cammarata M., Fritz D. M., Barrett R., Samoylova L., Grünert J., Sinn H., “Nanofocusing of hard X-ray free electron laser pulses using diamond based Fresnel zone plates,” Sci. Rep. 1, 57 (2011). 10.1038/srep00057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Vila-Comamala J., Pan Y., Lombardo J. J., Harris W. M., Chiu W. K., David C., Wang Y., “Zone-doubled Fresnel zone plates for high-resolution hard X-ray full-field transmission microscopy,” J. Synchrotron Radiat. 19(5), 705–709 (2012). 10.1107/S0909049512029640 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wu S., Hwu Y., Margaritondo G., “Hard-X-ray zone plates: recent progress,” Materials 5(12), 1752–1773 (2012). 10.3390/ma5101752 [DOI] [Google Scholar]
- 24.S. A. Prahl, “Optical properties spectra,” Oregon Medical Laser Clinic, http://omlc.ogi.edu/spectra/index.html, 2001.
- 25.Klose A. D., Larsen E. W., “Light transport in biological tissue based on the simplified spherical harmonics equations,” J. Comput. Phys. 220(1), 441–470 (2006). 10.1016/j.jcp.2006.07.007 [DOI] [Google Scholar]
- 26.Kim A. D., Keller J. B., “Light propagation in biological tissue,” J. Opt. Soc. Am. A 20(1), 92–98 (2003). 10.1364/JOSAA.20.000092 [DOI] [PubMed] [Google Scholar]
- 27.Panasyuk G. Y., Markel V. A., Schotland J. C., “Superresolution and corrections to the diffusion approximation in optical tomography,” Appl. Phys. Lett. 87(10), 101111 (2005). 10.1063/1.2040010 [DOI] [Google Scholar]
- 28.J. Welch and M. J. C. Van Gemert, Optical and Thermal Response of Laser-Irradiated Tissue (Plenum, 1995). [Google Scholar]
- 29.A. Ishimaru, Wave Propagation and Scattering in Random Media (Oxford University, 1997). [Google Scholar]
- 30.Liemert A., Kienle A., “Analytical Green’s function of the radiative transfer radiance for the infinite medium,” Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 83(3), 036605 (2011). 10.1103/PhysRevE.83.036605 [DOI] [PubMed] [Google Scholar]
- 31.Rice B. W., Cable M. D., Nelson M. B., “In vivo imaging of light-emitting probes,” J. Biomed. Opt. 6(4), 432–440 (2001). 10.1117/1.1413210 [DOI] [PubMed] [Google Scholar]
- 32.Haskell R. C., Svaasand L. O., Tsay T. T., Feng T. C., McAdams M. S., Tromberg B. J., “Boundary conditions for the diffusion equation in radiative transfer,” J. Opt. Soc. Am. A 11(10), 2727–2741 (1994). 10.1364/JOSAA.11.002727 [DOI] [PubMed] [Google Scholar]
- 33.Schweiger M., Arridge S. R., Hiraoka M., Delpy D. T., “The finite element method for the propagation of light in scattering media: boundary and source conditions,” Med. Phys. 22(11), 1779–1792 (1995). 10.1118/1.597634 [DOI] [PubMed] [Google Scholar]
- 34.Chang M., Li L., Chen Z. Q., Xiao Y. S., Zhang L., Wang G., “A few-view reweighted sparsity hunting (FRESH) method for CT image reconstruction,” J. XRay Sci. Technol. 21(2), 161–176 (2013). [DOI] [PubMed] [Google Scholar]
- 35.Huang B., Wang W., Bates M., Zhuang X., “Three-dimensional super-resolution imaging by stochastic optical reconstruction microscopy,” Science 319(5864), 810–813 (2008). 10.1126/science.1153529 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Pratx G., Carpenter C. M., Sun C., Xing L., “X-ray luminescence computed tomography via selective excitation: a feasibility study,” IEEE Trans. Med. Imaging 29(12), 1992–1999 (2010). 10.1109/TMI.2010.2055883 [DOI] [PMC free article] [PubMed] [Google Scholar]