Nearly complete regression of tumors via collective behavior of magnetic nanoparticles in hyperthermia

Abstract

One potential cancer treatment selectively deposits heat to the tumor through activation of magnetic nanoparticles inside the tumor. This can damage or kill the cancer cells without harming the surrounding healthy tissue. The properties assumed to be most important for this heat generation (saturation magnetization, amplitude and frequency of external magnetic field) originate from theoretical models that assume non-interacting nanoparticles. Although these factors certainly contribute, the fundamental assumption of ‘no interaction’ is flawed and consequently fails to anticipate their interactions with biological systems and the resulting heat deposition. Experimental evidence demonstrates that for interacting magnetite nanoparticles, determined by their spacing and anisotropy, the resulting collective behavior in the kilohertz frequency regime generates significant heat, leading to nearly complete regression of aggressive mammary tumors in mice.

1. Introduction

Heat has a profound effect on biological systems, especially cancer [1]. However, the widespread clinical application of thermal therapy [2–5] for cancer has yet to be realized despite the knowledge of its biological effectiveness, including an understanding of many of the molecular and physiologic mechanisms that give rise to its tumoricidal effects [6, 7]. The principle barriers to clinical application of thermal therapies in oncology are technical. Specifically, for tumors located deep within the patient, it is a challenge to deliver heat selectively that is sufficient to uniformly raise the local (tumor) temperature to 42–45 °C, causing necrosis in the tumor, without overheating and damaging the surrounding normal tissues. An additional technical challenge is accurately determining the deposited heat dose, or dosimetry [8]. Magnetic nanoparticles, particularly those capable of being delivered selectively to a tumor, offer the potential to deliver site-selective, and even cell-specific, heat to the local or microscopic environment of a tumor [9, 3]. Because the magnetic nanoparticle can also be a contrast agent for magnetic imaging [10–12] or can be labeled with an imaging ligand, there exists the possibility to quantify the deposited heat dose to the tumor [3]. Correlating heat dose with tissue temperature rise and therapeutic outcome offers the tools clinicians require to develop and use prescriptive thermal treatment plans for their patients.

When exposed to an alternating magnetic field (AMF), magnetic materials generate heat via four possible loss mechanisms: (1) hysteresis, (2) eddy current, (3) Néel paramagnetic switching, and (4) friction from Brownian rotation [13]. It is quite possible that all four mechanisms may contribute to the total heat generated by a particular magnetic sample in an AMF, but it is expected that only one or two of the mechanisms will dominate. This is determined by the properties of the magnetic material, its environment (e.g. temperature), and the magnetic field. For example, the material often chosen for biomedical applications is magnetite, Fe₃O₄, because it exhibits a lower toxicity than other magnetic materials while still possessing useful magnetic properties [14, 15]. (Other iron oxide or iron/iron oxide [16] combination nanoparticles have been considered. However, bulk manufacturing processes are not well established for all these, and ageing becomes a serious issue for the combination materials because iron does not have a self-limiting oxide. Finally, there is very little clinical work on the combination materials.) For samples of this resistive oxide with dimension ≪1 µm that are exposed to an AMF in the intermediate radiofrequency region (f ∼ 10⁵ Hz), the heat generated by eddy current losses is likely negligible; instead, the dominant sources of heat are expected to be magnetodynamic (hysteresis, Néel switching, and frictional contributions) [17].

2. Nanoparticle design

Successful application of this technology requires synthesis of stable colloidal suspensions of magnetite nanoparticles in biocompatible fluids (water or saline solution) that maintain their stability in biological media such as blood or plasma [18–21]. The particles must also produce a predictable and sufficient amount of heat, or specific absorption rate (SAR) measured in W g⁻¹, at modest particle concentrations (in order to limit toxicity) when exposed to AMF amplitudes that can be applied safely to large regions of tissue [22]. Thus, the surface chemistry, size, and magnetic properties of the particles must be engineered to meet demanding, even competing, performance criteria.

Knowledge of the specific characteristics that are important for delivering the maximum heat dose per gram of injected material [4, 9] is limited to theoretical calculations that assume non-interacting magnetic nanoparticles [13] and a passive biological system that fails to react to the heat or presence of the particles. The most influential characteristics include the saturation magnetization, anisotropy, relaxation time of the magnetic moments, amplitude and frequency of the external AMF, and intratumor particle concentration and distribution. The distribution and amount of heat deposited to the tumor are related to each of these parameters and are integral to successful therapeutic outcome. There are practical limitations, however, to the achievable value of each parameter. Many of these limitations are due to physiologic constraints imposed by either tumor biology or toxicology. Saturation magnetization is determined by choice of material and nanoparticle size, but few magnetic materials with large saturation moments (e.g., Co) are biocompatible. The choice of particle size is constrained by the physical and physiologic realities of the application—large particles (e.g., > 100 nm) heat well but do not form a stable colloid nor do they easily penetrate and disperse inside the tumors [20, 21, 23]. Field amplitude and frequency can be increased, but the power required to generate the field can become prohibitive, particularly at high frequency. Also, the non-specific coupling of the AMF energy with tissue becomes detrimental [22]. Although these factors certainly contribute to the overall heat dose, the assumption that magnetic nanoparticles must be non-interacting in the models severely limits their utility because they guide the design of nanoparticles away from a potentially critical parameter. Data presented here demonstrate clearly that magnetic nanoparticles suitable for hyperthermia are strongly interacting, and that this interparticle interaction also influences their interaction with cells. In turn, the resulting particle distribution in tissues or cells dictates the distribution and degree of heat that is generated, ultimately determining therapeutic efficacy. Experimental evidence shows that the heat deposition that results from these strong interactions, i.e. increased temperature and more localized heat deposition, can provide hyperthermia treatment with nearly complete regression of mammary tumors in mice.

3. Interaction study

In previous work, we have described the development of a stable colloidal suspension of high SAR bionized nanoferrite (BNF) particles [24] that with appropriate surface modifications can be covalently conjugated with monoclonal antibodies and demonstrate selective uptake in mouse models of human breast cancer [25]. The BNF nanoparticle system was synthesized by high pressure homogenization according to the core/shell method outlined previously [24]. In this case, both steric stabilization and biocompatibility were achieved by adsorbing a polymer, dextran, to the particle surface [24, 20, 21]. Dextran was physically adsorbed onto the precipitated iron oxide particles under high pressure conditions followed by adsorption of an additional dextran (‘double layer’) under high temperature but different pressure conditions to yield the suspension studied (Lot 01350684G). In anticipation of animal trials¹¹, all material in this study was suspended in phosphate buffer saline with pH adjusted to the physiologic value of 7.4 for biocompatibility and was sterilized by passing through a 0.2 µm filter. The colloidal stability has been established for greater than twelve months.

Our primary interest in these particles is the therapeutic potential of the heat they generate. However, a complete characterization obtained by a thorough physical and chemical analysis of the particles is necessary to gain an understanding of the nature of such selective heating. Two components form the BNF nanoparticles: an iron oxide core and the dextran shell. The composition and size¹² of the core are critical to determining the heat output. Here, the iron oxide core (figure 1) was determined by Mössbauer spectroscopy to be composed of >98% magnetite (Fe₃O₄). Less than 2% of iron hydroxide was detected and was assumed to be limited to the surface of the nanoparticle core. We find that the diameter of just the iron oxide core of the dextran-coated spheres is 44 nm ±13 nm (figure 1), as determined by analytical ultra-centrifugation (AUC). Transmission electron microscopy images also confirm a core diameter of ≈50 nm, and electron beam diffraction suggests that each nanoparticle core is comprised of one or two grains with different crystallographic orientations.

Figure 1.

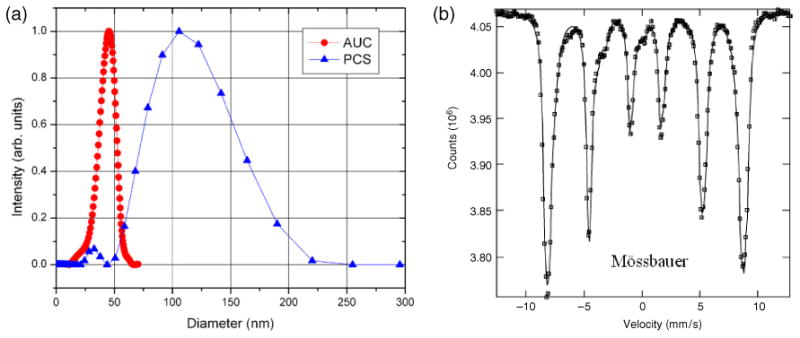
Characterization of size and composition of the BNF magnetic nanoparticles: (a) analytical ultra-centrifugation data (red circles) measured¹³ on an Optima XL-I from Beckman-Coulter, USA and photon correlation spectroscopy data (blue triangles) measured (see footnote 13) on a Zetasizer Nano ZS90 by Malvern Instruments, Inc. (b) Mössbauer spectroscopy measured on dried nanoparticles at 5 K.

The size of the nanoparticles is a critical parameter for biological performance and applications [2, 3, 9–22]. Furthermore, the overall size of the particles, with coating, determines the interparticle and particle-cell interactions. To determine the total particle size in suspension, very low concentrations (the non-interacting regime) are necessary (∼0.2 mg ml⁻¹). We used photon correlation spectroscopy (PCS), yielding a mean nanoparticle (core + shell), or ‘hydrodynamic’, diameter of 96 nm ±12 nm. Since AUC estimates the volume of a dense sphere while PCS estimates the hydrodynamic diameter of a model Stokes–Einstein sphere moving through the solvent, the dextran shell thickness can be estimated by the difference to be ≈26 nm. Given the mean molecular mass of dextran used was 40 000 Da, a mean radius of gyration of 26 nm [26] is reasonable.

In an apparent contradiction to both the TEM and AUC data, we infer a crystallite size of 9.5 nm ± 0.8 nm from x-ray diffraction. To better understand the origin of this discrepancy, and to understand the structure of the solution at concentrations relevant for biological applications, i.e. >10 mgml⁻¹, we used small angle neutron scattering (SANS). The SANS and ultra-SANS (USANS) experiments were conducted on the NG-3 beam line and the BT-5 thermal neutron double-crystal instrument [27] at the NIST Center for Neutron Research (NCNR). As seen in figure 2, the model best fitting the data assumes that the nanoparticle cores are comprised¹⁴ of [28] parallelepiped-shaped crystals of iron oxide that have dimensions 6.5 nm × 19 nm × 49 nm. This result correlates well with the ≈9 nm crystallite size determined from x-ray diffraction as well as with the small secondary PCS peak at 20–30 nm (see supplemental information available at stacks.iop.org/Nano/20/395103). This also correlates with the single-crystal nature of the nanoparticles seen by e-beam diffraction: as a result of the synthesis, the nanoparticles have one crystallographic axis aligned along the length of the parallelepiped.

Figure 2.

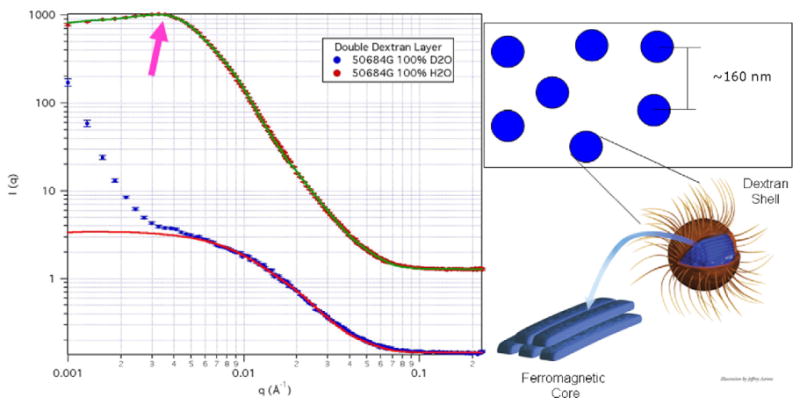
Detailed physical characterization using neutron scattering. SANS data taken with 0.84 nm wavelength neutrons in transmission using three detector settings in order to span the range of scattering vectors Q from 3 × 10⁻⁵ to 5 × 10⁻¹ Å⁻¹. USANS data taken with 0.24 nm wavelength neutrons in transmission over a Q (wavevector component in the horizontal plane) range sensitive to length scales from 1500 to 200 000 Å. The H₂O samples were held in 1 mm thick quartz cells while the D₂O samples were held in 4 mm thick quartz cells. SANS data and fits for the nanoparticle systems where the arrow highlights the interaction peak. The D₂O data highlights the dextran shell plus the magnetic structure of the iron oxide core, while the H₂O data highlights the magnetic and physical structure of the iron oxide core. Inset: schematic of the physical structure determined by SANS for both particle separation and internal structure. (Note: all graphs include the error bars.)

From existing hyperthermia theory, the most critical magnetic property of the material is the saturation magnetization (M_S). From the hysteresis loops (magnetization versus magnetic field measurements) at room temperature of the colloidal systems (normalized to the mass of particles present in the colloid), M_S = (41.08 ± 0.03) kA m² g⁻¹. This value is about half that of bulk Fe₃O₄, but some reduction in the magnetization is expected because of the diamagnetic properties of the hydrated dextran shell. However, the saturation magnetization alone does not yield any information about the anisotropy or interactions between the nanoparticles.

Since the nanoparticles are suspended in a fluid, we expect that they are free to move through the fluid and rotate, in a somewhat random manner, as has been observed in other magnetic nanoparticle systems [29, 30]. If this is the case, then no anisotropy, or directionality, would be measurable. An analysis (by vector magnetometry in a saturating field) of the directionality of the magnetic moments of the nanoparticles showed that they are neither able to freely rotate (uniaxial anisotropy) nor are they able to move freely (unidirectional anisotropy) as individual particles (figure 3). The uniaxial anisotropy was (186.1 ± 0.9) × 10⁻⁷ N m while the unidirectional anisotropy was (0.8 ± 0.3) × 10⁻⁷ N m, at a concentration of ≈25 mg particles ml⁻¹. This non-zero anisotropy in the BNF nanoparticles is a strong indication of interactions between these nanoparticles.

Figure 3.

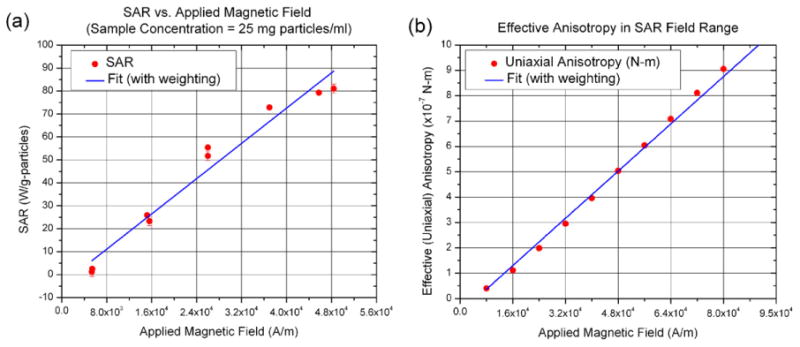
Characterization of magnetic and thermal properties of BNF nanoparticles (a) SAR heating curves, measured as described in [3]. (b) Vector magnetometry measurements at room temperature (298 K) under SAR field conditions (8–80 kA m⁻¹) measured (see footnote 13) using a VSM from ADE. The anisotropy is determined by fitting the raw data (magnetization as a function of field angle) to the same equation as in [29]. (Note: all graphs include the error bars.)

Fortunately, neutron scattering also characterizes the interactions of the nanoparticles in suspension, in contrast to magnetometry which simply confirms that they exist [31] (data not shown). Again, with modeling we can infer that the effective (or hard sphere interaction) radius of a BNF nanoparticle is 157 nm ± 4 nm (figure 2). This effective radius represents the average center to center distance between two nanoparticles, with smaller radii corresponding to stronger attractive potentials between the nanoparticles. If no interparticle interactions are present, we expect that the scattering data would be dominated by length scales corresponding to the individual particles, i.e. core, shell, and core-shell. That the scattering contains features describing a preferred interparticle spacing is an important indication that the magnetic dipole-dipole interactions are overall attractive and are counteracted by Brownian motion and polymer– polymer steric interactions. The extended length scales seen in SANS/USANS (concentration ≈ 25 mg particles ml⁻¹) are not apparent in the PCS data for the BNF nanoparticles because the latter technique is limited to sample concentrations of about 0.22 mg particles ml⁻¹ to overcome optical opacity (multiple scattering and iron absorption) of the sample. In the PCS regime, we expect and find that interparticle interactions are significantly reduced leading to ‘single-particle’ dominated dimensions.

Regardless of the nature of the particles suspension, it is the heating rate that is a primary consideration for thermal therapy applications. In particular, we desire a high heat output at a moderate amplitude and frequency of AMF. The SAR of the sample was measured (figure 3) in an external AMF with peak amplitude, H = 48 kA m⁻¹ and frequency f = (160 ± 0.5) kHz in a manner described previously [3] and reported [24, 32]. The temperature data were corrected for the thermal properties of the calorimeter and coil, and then the SAR was calculated using the specific heat of water and normalized to either particle or iron concentration. At a colloidal (particle) concentration of ≈25 mg particles ml⁻¹ of suspension, the measured SAR of the BNF particles is (81 ± 2) Wg⁻¹ particle. This results in a temperature rise for 1 g of water of 0.5 °C g⁻¹ of particles. Furthermore, the anisotropy is non-negligible and increases linearly over the same field range in which significant SAR develops nearly linearly (figure 3).

The SAR and non-zero anisotropy can be readily explained by interactions between the nanoparticles. At high concentrations (≫1 mg particle ml⁻¹ suspension), interactions between the nanoparticles permit the formation of chains [33] and these chains then have a uniaxial anisotropy along the length of the chain [29, 34]. However, the presence of a unidirectional component corresponds to the degree of entanglement (or congestion) of these chains, preventing the entire chain from being able to rotate freely. In fact, the unidirectional component decreases with decreasing concentration as determined from vector magnetometry measurements (data not shown).

The observed interparticle interactions may affect the heating in two ways: (1) the dipolar interactions would be significantly stronger enabling the nanoparticles to couple their behavior under an oscillating field (thereby amplifying the heating) and (2) the small interaction radius relative to the particle size allows more particles to group closer together, enhancing the local heat output in a smaller area by (a) increasing the concentration of energy and (b) enhancing the anisotropy (which will yield larger hysteresis losses at kHz frequencies). This latter effect is expected to show significant enhancement in vivo, as preliminary electron microscopy experiments have demonstrated clustering of the magnetic nanoparticles occupying both the interstitial and intracellular spaces in tumors after intratumoral injection (figure 4).

Figure 4.

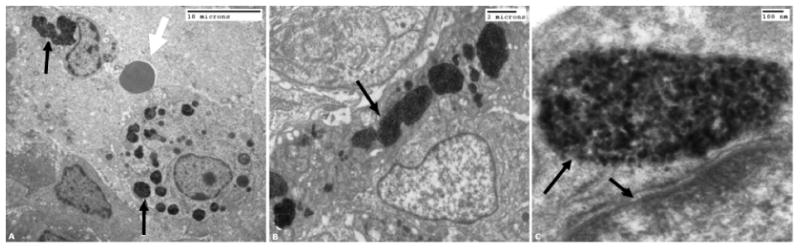
Electron microscope image of the nanoparticles in vivo. The nanoparticles were direct injected into the tumor, and then incubated for 18 h before preparing EM specimens. The round circular object in the left image (pointed out by white arrow) is a red blood cell to provide scale for the tumor cells. The center and right images are progressively higher magnifications that demonstrate the clustering of the nanoparticles (black objects) within the cells. The black arrows in all three images point out the presence of the nanoparticles encapsulated in sub-cellular structures.

4. Mouse trials

With an understanding of the physical properties of these nanoparticles, we now tested their effectiveness against breast tumors. In vivo mouse therapy was performed in an AMF inductor that confines high-amplitude magnetic fields to a 1 cm wide band of the interior of a 3.5 cm internal diameter induction coil [22, 4]. Twelve female mice (C3H/HeJ) bearing MTG-B murine breast tumors with volume 180 mm³ ± 40 mm³ were separated into three experimental groups of four each. They were anesthetized with a single peritoneal injection of ketamine/xylazine prior to therapy. Once anesthetized, the particle suspension was injected directly at a single site into the central region of the tumor using a sterile hypodermic needle and treated with varying AMF conditions. Each mouse received a normalized dose of (4.98 ± 0.03) mg Fe cm⁻³ tumor, and AMF therapy was varied by adjusting amplitude and duration of exposure, but always at a fixed frequency of 150 kHz and 100% duty. An additional cohort of six tumor-bearing mice received no particle injection, but were exposed to an AMF with amplitude H = 43.8 kA m⁻¹ at 150 kHz and 100% duty for 20 min. The study also contained a control cohort of five tumor-bearing mice that received no particles and no AMF exposure. Study conditions and results are summarized in table 1.

Table 1.

Animal trial groups.

AMF amplitude (kA m−1)	Mean tumor vol. mm3 (±S.D.)	AMF ON time s (±S.D.)	Dose ratea mW g−1 tumor	Total dosea J g−1 tumor (±S.D.)	Mean max. tumor temp. °C (±S.D.)	Mean max. rectal temp. °C (±S.D.)	Mean doubling time days (±S.D.)
31.8	140(10)	900(0)	706(1)	635(1)	37(1)	34(2)	4(2)
43.8	180(46)	900(200)	883(6)	800(200)	47(3)	40.2(0.2)	10(6)
55.7	220(40)	600(300)	969(4)	500(200)	52(2)	42.2(0.2)	50(15)b
43.8	190(40)	1200(0)	N/Ac	N/Ac	40(2)	39(3)	5(2)
0	180(30)	0	N/Ac	N/Ac	N/Ac	N/Ac	2.3(0.7)

^aValues estimated from particle SAR W g⁻¹ Fe, amplitude, and particle dose of 5 mg Fe g⁻¹ tumor.

^bThree out of four treated mice showed complete response (CR), i.e. no tumor re-growth was observed for the duration of the study (60 days).

^cNot applicable because either no AMF was used, or no particles were present in the tumor.

Therapy began when the tumor achieved a temperature of 40.5 °C, and was terminated [4] after 15 min, or when the rectal temperature of the mouse reached 41.5 °C, or the tumor temperature reached 55 °C. In some cases (55.7 kA m⁻¹ cohort) the rectal temperature continued to rise after therapy was terminated as heat from the skin was conducted inward [22]. Temperatures were continuously recorded at one-second intervals using fiberoptic temperature probes placed in the center of the tumor, immediately adjacent to the tumor, and in the rectum. Maximum tumor temperature correlated well with AMF amplitude, as expected, because the particle SAR [24] depends strongly on magnetic field amplitude if concentration and AMF frequency are constant (table 1). At higher field amplitudes, the heat dose rate or particle SAR created rapid heating leading to shorter duration treatments. Tumor response was monitored by calculating tumor volume from three orthogonal caliper measurements taken at regular intervals.

Therapeutic efficacy from animal studies was estimated by the time required for a tumor to grow to a volume equal to double (2×) its volume prior to treatment (figure 5). Exposure of tissues to AMF at the frequency used in this study is sufficient to deposit heat through induction of eddy currents. In general, this interaction of electromagnetic fields with tissues is well known, although relatively little study has been performed at the frequency–amplitude combinations used here [18].

Figure 5.

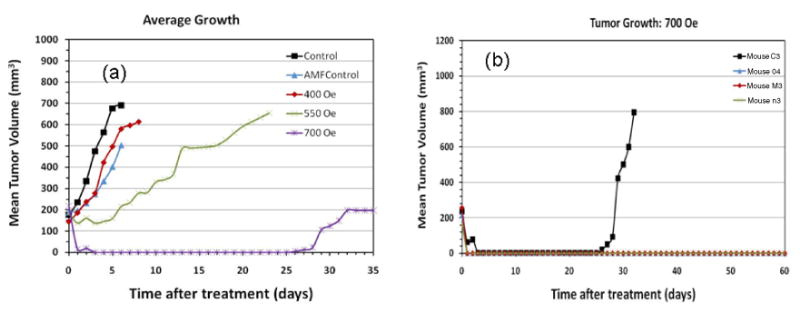
Therapeutic heating results in a pilot study demonstrated by (a) average growth curves for each of the groups in the study and (b) growth curves for each animal in the high field study which showed nearly complete regression after one treatment. (Note: the animals were sacrificed and the experiments ended when the tumor reached a certain size, in accordance with the IACUC rules, resulting in different study times after treatment for the different groups.) (Note: All graphs include the error bars.)

Exposure of the control tumors to a 43.8 kA m⁻¹ field for 20 min is sufficient to slow tumor growth comparably to particle-mediated interstitial heating in a 31.8 kA m⁻¹ field. Because duration of therapy differs in these cases, it is difficult to estimate an iso-therapeutic dose with the AMF alone. However, when nanoparticles are present in the tumor, the same 43.8 kA m⁻¹ field is required for about 15 min to achieve a doubling (response) time that is five-fold greater than the control, and about two-fold greater than with AMF alone for 20 min therapy.

When a 55.7 kA m⁻¹ field is used for therapy, the particle SAR increases dramatically to produce substantial intratumor heating. Non-specific heat deposition from eddy currents is also increased as seen by the rising rectal temperature. However, because the interstitial heating produced by the particles is substantially greater than at lower fields, a significantly greater therapeutic response results (figure 5, table 1) for shorter duration treatment. Indeed, three out of four mice displayed a complete response, defined as no tumor re-growth for the duration of the study (60 days). It is worth noting that the estimated total heat dose (J g⁻¹ tumor) given to this cohort is comparable to (but less than) that given to mice at 31.8 kA m⁻¹ (longer duration). Yet, because the particle SAR is much higher at 55.7 kA m⁻¹ than at 31.8 kA m⁻¹, the dose rate is correspondingly greater, resulting in higher intratumor temperatures [35]. Both animal and human clinical studies have shown that therapeutic efficacy from interstitial thermal therapy is related to thermal dose as defined [6, 8] by ‘time at temperature’. Thus, high SAR particles are a necessary component to the success of such an approach.

5. Conclusions

We have shown that it is possible to synthesize high SAR particles that possess strongly magnetic properties yielding significant heating in an AMF while also preserving colloidal stability. This achievement relies upon synthesis of magnetite particles comprising an aggregate core wherein the core contains (shape) anisotropic crystals. Biocompatibility and solution stability were achieved by steric stabilization of the colloid through adsorption of dextran. The balance among the magnetic dipole interactions, Brownian motion, and polymer– polymer steric interactions in this system causes a loose aggregation of particles to act like a large particle without the biological issues presented by rigid large particles, as seen from cell cultures of tumor tissue from the animal studies. This collective behavior enhances the efficacy of the interacting nanoparticles, leading to nearly complete regression of aggressive mammary tumors as shown in a pilot study on animals.