Summary
In biomedical research such as the development of vaccines for infectious diseases or cancer, measures from the same assay are often collected from multiple sources or laboratories. Measurement error that may vary between laboratories needs to be adjusted for when combining samples across laboratories. We incorporate such adjustment in comparing and combining independent samples from different labs via integration of external data, collected on paired samples from the same two laboratories. We propose: 1) normalization of individual level data from two laboratories to the same scale via the expectation of true measurements conditioning on the observed; 2) comparison of mean assay values between two independent samples in the Main study accounting for inter-source measurement error; and 3) sample size calculations of the paired-sample study so that hypothesis testing error rates are appropriately controlled in the Main study comparison. Because the goal is not to estimate the true underlying measurements but to combine data on the same scale, our proposed methods do not require that the true values for the errorprone measurements are known in the external data. Simulation results under a variety of scenarios demonstrate satisfactory finite sample performance of our proposed methods when measurement errors vary. We illustrate our methods using real ELISpot assay data generated by two HIV vaccine laboratories.
Keywords: assay comparison, inter-laboratory measurement error, multiple data sources, regression calibration
1 Introduction
In the development of an effective vaccine against a particular infectious disease or cancer, vaccine-induced immune responses are routinely assessed in Phase I and II preventive or therapeutic vaccine trials. Wherein trials of antibody-based vaccines typically evaluate vaccine-induced neutralization and/or binding antibody responses, trials of cell-mediated-immunity (CMI)-based vaccines typically evaluate vaccine-induced T-cell responses. When comparing two vaccine candidates or evaluating a single candidate, it is common that a certain immune response (e.g., the percent of vaccine-induced T-cells secreting Interferon-gamma among vaccinated subjects) is assessed by two different laboratories. This often occurs when collaboration across multiple laboratories is desirable or when one single laboratory is not feasible or optimal for expedited evaluation of a given vaccine candidate in a large multi-center trial. Because independent samples are tested by each laboratory, these studies are hereafter referred to as the “Independent two-sample” or the “Main” study. In these studies, however, the true underlying immune responses are unknown or cannot be observed exactly. Instead, along with random errors, the observed readouts may carry lab-specific and, possibly, sample-specific measurement errors. Ignoring these systematic errors, especially when pronounced, may misguide high-stake decisions on advancement of vaccine candidates from early to late stage clinical trials or on identification of immune correlates of protection in efficacy trials. While we use the vaccine evaluation as an illustrative example throughout, the discussion also pertains to other biomedical fields where interest lies in comparing or combining data collected from multiple sources.
Many other researchers have tackled the problem of correction for measurement error by using external or internal validation studies (e.g., [1] and [2]). These methods often assume that the true underlying responses, X, are measured in the validation studies and hence parameters in the measurement error models for the error-prone measurement, W, are identifiable. In addition, issues with data from multiple sources are usually not explicitly considered. In vaccine immunology, however, not only may data come from different sources, the accuracy of many of the immune responses, especially cellular responses cannot be evaluated due to the lack of human cell standards with known X values. Fortunately, the information or extra data needed to correct for inter-laboratory measurement error in W may be available. With the increasing awareness and willingness for collaboration across institutions or laboratories, considerable efforts have been devoted to assess the comparability of assays performed by different laboratories based on a common set of biological specimens. For example, the Association for Immunotherapy of Cancer (CIMT) generated large inter-laboratory immunological assay data from centrally prepared specimens by multiple laboratories under the CIMT Immunoguiding Program (CIP) ([3] and [4]); the Comprehensive T Cell Vaccine Immune Monitoring Consortium (CTC-VIMC) under the Bill & Melinda Gates Foundation funded Collaboration for AIDS Vaccine Discovery (CAVD) conducted several studies (e.g., [5] and [6]) to assess the comparability of both cellular and antibody-based assays across its clinical immunogenicity testing laboratories. Because the same specimen is usually divided equally and tested by each laboratory, these studies are hereafter referred to as the “Paired-sample” or “Assay-comparison” studies.
In this paper, we describe and evaluate methods to correct for measurement error in the Main study via integration of data from the Assay-comparison study. Specifically, in Section 2, we introduce methods to 1) normalize or calibrate individual level data in the Main study, 2) estimate and test mean differences in the Main study, and 3) calculate sample sizes for the Assay-comparison study. In Section 3, we study the characteristics and performance of the proposed methods based on simulation studies. In Section 4, we illustrate the proposed methods using a real data example. A discussion is provided in Section 5.
2 Methods
We first describe the notations for the two types of studies. Without explicit indication of replicates, noted observable variables in the following refer to either the average of replicates or a single measurement. In the Assay-comparison study, let X1, …, Xn denote a size n random sample from some population of true immune response levels. Two laboratories, lab 1 and lab 2, measure all n specimens separately. That is, for a given Xi = xi, i = 1, …, n, readouts from the two labs, and , i = 1, …, n, are independent. Xi, i = 1, …, n, are identical and independently distributed (i.i.d) with mean μ and variance , but are unobserved. Realizations of and , i = 1, …, n, carrying measurement error are observed from labs 1 and 2, respectively.
We assume an additive error model for V(1) and V(2) as
| (1) |
where and for j = 1, 2 and i = 1, …, n, with |xi denoting “given Xi = xi”. u(1) and u(2) represent lab-specific measurement error from labs 1 and 2 in a broad sense because they may be error related to measurement, instrument or sampling design. In the following, when the superscripts are dropped, V refers to either V(1) or V(2), and u refers to either u(1) or u(2).
Of note, the classical measurement error model often requires (e.g., [7] and [8]). Here, such a strict assumption is not necessary because our goal is not to estimate the true mean, μ, unbiasedly but to bring data from multiple laboratories to the same scale. Instead, we have a more general assumption that is equal to a constant (i.e., δj), which may or may not equal to 0. Such an assumption is more realistic in our situation because data from different laboratories may have different levels of nonzero mean shift. In addition, as long as the constant, δj, is not related to the specific sample or its value, but only to a specific lab, such an assumption has two important implications:
, using double expectation, and
-
Cov(u, X) = 0, since
Cov(u, X) = E(Cov(u|X, X|X)) + Cov(E(u|X), E(X|X)) = E(0) + Cov(δ, X).
Interestingly, as pointed out by [9] this holds true even if var(u|x) is a function of x.
Often times the Assay-comparison study includes mi replicate values Vi1, …, Vimi for each sample i. Besides the constant assumption on the unconditional mean, as shown in Remark 1 of [9], the unconditional variance of Vi is also constant for all i as long as mi is not a random variable, even when the conditional variance of ui may depend on xi or on any inherent variation associated with the unit i. That is, for all i:
-
, where τ2 = E(var(ui|xi)).
Implication (iii) holds true when the sampling design on replicates is a) associated with the unit (Definition 4 in [10]), b) fixed with each mi = m, or c) identically distributed for each selected unit. Because of this, without loss of generality, in this paper we demonstrate our methods by assuming that the conditional variance of ui is not related to the specific sample or its value, but only to a specific lab, i.e., for all i = 1, …, n and j = 1, 2. Consequently, let Δ = V(2) − V(1), we then have the mean and variance of Δ as E(Δ) = μΔ = δ2 − δ1 and .
In the Main study, let , …, and , …, denote two independent random samples of sizes n1 and n2 from a “population” of true immune response levels that are, respectively, measured by the same two laboratories, labs 1 and 2. , i = 1, …, n and j = 1, 2, are i.i.d with mean μj and variance . Instead of realizations of X(1) and X(2), realizations of W(1) and W(2) carrying lab-specific measurement error are observed from labs 1 and 2, respectively. Of note, the two independent samples may or may not be measured under the same study conditions, e.g., treatment or disease status.
Again, we assume an additive error for W(1) and W(2) as for V(1) and V(2). In addition, we assume the measurement error terms, u(1) and u(2) are transportable from the Assay comparison Study to the Main study. That is,
Consequently, the variance of the observable W(1) and W(2) are and , respectively.
2.1 Normalization of individual level data in the Main study
In the Main study, one may desire to understand the underlying responses X(1) and X(2), for example by studying their association with other study data, such as clinical outcomes or subject-specific characteristics. We propose to “normalize” or “calibrate” the observed, but error-prone individual level data to a common scale and use the normalized values for across-lab data inferences. Since it is often infeasible to have external validation data to estimate the distribution of the individual measurement error with unknown standards, we do not intend to estimate the absolute values of the X′s unbiasedly.
Without loss of generality, we choose lab 1 as the reference lab and carry out such a normalization process on the scale of lab 1 by assuming δ1 = 0. We assume the ( , ) pairs follow a bivariate normal distribution: (X(1), W(1))′ ∼ N ((μ1, μ1 + δ1)′, Σ) where
As shown earlier, X(1) and u(1) are uncorrelated regardless of the form of the measurement error variance. Therefore, we have . Then, the conditional distribution is as follows:
| (2) |
where μ1 and are the population mean and variance of X(1), is the variance of W(1), δ1 and are the unconditional mean and variance of u(1).
We construct individual level data x(1) as x̃(1) via its conditional distribution mean, E(X(1)|(W(1) = w(1))). We then substitute the sample counterparts for μ1 (= μ1 + δ1 because δ1 = 0), , and .
Let and denote the sample mean and variance, respectively, of . Under the aforementioned assumptions on the X′s and on the conditional mean and variance of u, it can be shown that E(w̅(j)) = μj + δj and (result 1 of [10] where E(u|x) = 0 is substituted by E(u|x) = δj in their proof), regardless of the type of heteroscedasticity of ui. Specifically, we can replace both μ1 and μ1 + δ1 with w̅(1), with and with lab 1 measurement error variance estimated via replicates from the Main study, the Assay comparison study or historical studies of the same assay from the same lab.
Similarly, we construct x(2) as x̃(2) by a sample estimator of the conditional mean, , where we replace μ2 + δ2 with the sample mean of w(2), δ2 with the sample counterpart of E(Δ), i.e., the sample average of (v(2) − v(1)) from the Assay comparison study, with and τ2 with measurement error variance estimated via replicates as for lab 1 data. After accounting for inter-lab measurement error in this normalization step, these individual level data estimates can then be directly used for across-lab inferences.
2.2 Estimation and testing of the mean difference in the Main study
Next, we estimate the mean difference, μ2 − μ1 of the true underlying responses in the Main study. Some simple derivations lead to an unbiased estimate of the mean difference without any assumption on the joint distribution of X and W. Specifically, because
taking expectation on both sides, we have
The mean difference, ε = μ2 − μ1 = E(X(2) − X(1)), can hence be expressed as
| (3) |
where W(1), W(2) and Δ are mutually independent. An unbiased estimate for ε is given by
| (4) |
where w̅(2) − w̅(1) and Δ̅ can be estimated from the observed Main study data and the Assay-comparison study data, respectively. The variance of ε̂ is expressed as
| (5) |
Because of equation (3), to test whether the mean difference is different from zero, i.e., H0 : μ1 − μ2 = 0 versus Hα : μ1 − μ2 ≠ 0, it is equivalent to testing H0 : E(W(2)) − E(W(1)) − E(V(2) − V(1)) = 0 versus Hα : E(W(2)) − E(W(1)) − E(V(2) − V(1)) ≠ 0. Under large sample theory, ε̂ follows a normal distribution with mean ε and variance . Therefore, the null hypothesis is rejected at the α level of significance if
| (6) |
where zα/2 is the upper (α/2)th quantile of the standard normal distribution.
2.3 Sample size requirement for the Assay-comparison study
When the Main study data are collected from different sources that may carry varying measurement error, it is often desirable to conduct an external study to assess the comparability of measurements between the data sources. Paired samples are mostly used in such comparison studies to minimize possible confounding factors and to increase efficiency of comparisons. It is important to plan for an appropriate sample size for such comparison studies in order to achieve satisfactory power for the Main study objectives.
Suppose the hypotheses of interest for the Main study are
Based on equations (5) and (6), under the alternative hypothesis that ε ≠ 0, the power of the above test is given by
| (7) |
after ignoring a small term of value ≤ α/2, where Φ is the cumulative standard normal distribution function. As a result, the sample size needed to achieve power 1 − β in the Main study can be obtained by solving the following equation
This leads to the folllowing sample size for the Assay comparison study:
| (8) |
Note that similar calculations can be made for a one-sided test.
3 Simulations
We assess the performance of our proposed methods in two separate simulation studies in the following two subsections.
3.1 Effect of individual-level data normalization
Main study
We consider case-control studies where biomarkers (e.g., vaccine-induced immune responses) are ascertained after the occurrence of the studied condition (e.g., HIV infection) on stored specimens from subjects with the condition (i.e., cases, D = 1) and those without the condition (i.e., controls, D = 0). Biomarker data, X(1) or X(2), from cases and controls (ratio=1:4) are associated with D in a logistic form:
where β0 = −2.9, β1 = log(2.0) or log(5.0); X|D = 0 are normally distributed with mean 5.0 and standard deviation 1.0 and X|D = 1 are normally distributed with mean (5.0 + β1) and standard deviation 1.0. A total of n1 + n2 = 250 (50 cases vs. 200 controls) or 1500 (300 cases vs. 1200 controls) are simulated with equal number of cases and controls measured by two laboratories, Lab 1 and Lab 2. The measurements follow an additive measurement error model, , i = 1, …, nj, j = 1, 2, where u(j) are normally distributed with mean δj = 0, 0.5 or 1.0 and standard deviation , 0.5 or 1.0.
Assay Comparison study
We assume X follows a normal distribution with mean of 5.0 and standard deviation of 1.0. The error-prone data, V(j) are collected from Lab 1 and Lab 2 on a common set of n = 100 or 500 specimens. These specimens are measured in triplicates from Lab 1 and Lab 2 following the additive error model, , i = 1, …, n, m = 1, 2, 3, j = 1, 2.
For each scenario, 1000 Monte Carlo simulations were performed. Tables 1 and 2 display the simulation results for n1 + n2 = 250 and 1500, respectively. Characteristics of the estimator for β1 including bias, mean standard error (MSE) and coverage of the 95% confidence intervals are reported from three models: regressing D on the underlying X (True), the normalized X̃ (Regression Calibration or RC) and the raw error-prone W (Naïve). The standard error of β̂1 from the RC models were estimated by bootstrap method of 1000 re-samplings stratified by lab. In Table 1 with n1 + n2 = 250, we observe that there is almost an uniform attenuation of the βl effect due to measurement error shown as a negative bias of β̂1 for the RC and the Naïve models, except when the measurement error is small (i.e., = 0.1) in few scenarios for the RC model. While the bias of the Naïve model can get seriously large when the measurement error is non-ignorable with sizable variance or mean-shift, the bias of β̂1 of the RC models is considerably lower than that from the Naïve model under all studied scenarios. Satisfactory performance of the RC model and improvement of the RC model over the (Naïve) model are also demonstrated based on the MSE quantities and the coverage of the estimates. Similar patterns are observed in Table 2 with n1 + n2 = 1500, where the finite sample performance of our method is improved over increased sample size with smaller Monte Carlo run errors. The performance of the RC method also improves slightly when we increased the size of the Assay-comparison study to n = 500 (results not shown).
Table 1.
Empirical characteristics of β̂1 in 1000 simulations with n = 100 in the Assay-comparison study and n1 = n2 = 250 in the Main case-control study for models regressing D on the underlying X (True), the normalized X̃ (RC) and the raw error-prone W (Naïve).
|
|
|
δ2 | eβ1 | Bias | MSE | Coverage | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True | RC | Naïve | True | RC | Naïve | True | RC | Naïve | ||||||
| 0.1 | 0.1 | 0 | 2.0 | 0.02 | 0.01 | −0.05 | 0.03 | 0.03 | 0.03 | 0.96 | 0.96 | 0.94 | ||
| 0.5 | 0.02 | −0.01 | −0.15 | 0.03 | 0.03 | 0.04 | 0.96 | 0.96 | 0.81 | |||||
| 1.0 | 0.02 | −0.02 | −0.24 | 0.03 | 0.04 | 0.07 | 0.96 | 0.96 | 0.56 | |||||
| 0.5 | 0.5 | 0.02 | −0.02 | −0.22 | 0.03 | 0.04 | 0.07 | 0.96 | 0.96 | 0.62 | ||||
| 1.0 | 0.02 | −0.03 | −0.29 | 0.03 | 0.04 | 0.10 | 0.96 | 0.95 | 0.35 | |||||
| 1.0 | 1.0 | 0.02 | −0.05 | −0.34 | 0.03 | 0.05 | 0.13 | 0.96 | 0.94 | 0.19 | ||||
| 0.1 | 0.1 | 5.0 | 0.05 | 0.00 | −0.10 | 0.06 | 0.06 | 0.06 | 0.96 | 0.96 | 0.90 | |||
| 0.5 | 0.05 | −0.08 | −0.34 | 0.06 | 0.06 | 0.15 | 0.96 | 0.93 | 0.54 | |||||
| 1.0 | 0.05 | −0.14 | −0.54 | 0.06 | 0.08 | 0.32 | 0.96 | 0.88 | 0.16 | |||||
| 0.5 | 0.5 | 0.05 | −0.15 | −0.51 | 0.06 | 0.08 | 0.29 | 0.96 | 0.87 | 0.20 | ||||
| 1.0 | 0.05 | −0.21 | −0.67 | 0.06 | 0.10 | 0.47 | 0.96 | 0.81 | 0.04 | |||||
| 1.0 | 1.0 | 0.05 | −0.26 | −0.79 | 0.06 | 0.13 | 0.64 | 0.96 | 0.74 | 0.00 | ||||
| 0.1 | 0.1 | 0.5 | 2.0 | 0.02 | 0.01 | −0.08 | 0.03 | 0.03 | 0.03 | 0.96 | 0.96 | 0.92 | ||
| 0.5 | 0.02 | −0.01 | −0.18 | 0.03 | 0.03 | 0.05 | 0.96 | 0.96 | 0.74 | |||||
| 1.0 | 0.02 | −0.02 | −0.26 | 0.03 | 0.04 | 0.09 | 0.96 | 0.96 | 0.45 | |||||
| 0.5 | 0.5 | 0.02 | −0.02 | −0.24 | 0.03 | 0.04 | 0.08 | 0.96 | 0.96 | 0.54 | ||||
| 1.0 | 0.02 | −0.03 | −0.31 | 0.03 | 0.04 | 0.11 | 0.96 | 0.95 | 0.28 | |||||
| 1.0 | 1.0 | 0.02 | −0.05 | −0.35 | 0.03 | 0.05 | 0.14 | 0.96 | 0.94 | 0.16 | ||||
| 0.1 | 0.1 | 5.0 | 0.05 | 0.00 | −0.19 | 0.06 | 0.06 | 0.08 | 0.96 | 0.96 | 0.82 | |||
| 0.5 | 0.05 | −0.08 | −0.42 | 0.06 | 0.06 | 0.21 | 0.96 | 0.93 | 0.35 | |||||
| 1.0 | 0.05 | −0.14 | −0.62 | 0.06 | 0.08 | 0.41 | 0.96 | 0.88 | 0.06 | |||||
| 0.5 | 0.5 | 0.05 | −0.15 | −0.56 | 0.06 | 0.08 | 0.34 | 0.96 | 0.87 | 0.13 | ||||
| 1.0 | 0.05 | −0.21 | −0.72 | 0.06 | 0.10 | 0.54 | 0.96 | 0.81 | 0.02 | |||||
| 1.0 | 1.0 | 0.05 | −0.26 | −0.81 | 0.06 | 0.13 | 0.68 | 0.96 | 0.74 | 0.00 | ||||
| 0.1 | 0.1 | 1.0 | 2.0 | 0.02 | 0.01 | −0.17 | 0.03 | 0.03 | 0.05 | 0.96 | 0.96 | 0.79 | ||
| 0.5 | 0.02 | −0.01 | −0.25 | 0.03 | 0.03 | 0.08 | 0.96 | 0.96 | 0.51 | |||||
| 1.0 | 0.02 | −0.02 | −0.32 | 0.03 | 0.04 | 0.11 | 0.96 | 0.96 | 0.24 | |||||
| 0.5 | 0.5 | 0.02 | −0.02 | −0.29 | 0.03 | 0.04 | 0.10 | 0.96 | 0.96 | 0.34 | ||||
| 1.0 | 0.02 | −0.03 | −0.35 | 0.03 | 0.04 | 0.13 | 0.96 | 0.95 | 0.16 | |||||
| 1.0 | 1.0 | 0.02 | −0.05 | −0.38 | 0.03 | 0.05 | 0.16 | 0.96 | 0.94 | 0.08 | ||||
| 0.1 | 0.1 | 5.0 | 0.05 | 0.00 | −0.39 | 0.06 | 0.06 | 0.18 | 0.96 | 0.96 | 0.42 | |||
| 0.5 | 0.05 | −0.08 | −0.59 | 0.06 | 0.06 | 0.37 | 0.96 | 0.93 | 0.08 | |||||
| 1.0 | 0.05 | −0.14 | −0.75 | 0.06 | 0.08 | 0.58 | 0.96 | 0.88 | 0.01 | |||||
| 0.5 | 0.5 | 0.05 | −0.15 | −0.67 | 0.06 | 0.08 | 0.47 | 0.96 | 0.87 | 0.03 | ||||
| 1.0 | 0.05 | −0.21 | −0.81 | 0.06 | 0.10 | 0.68 | 0.96 | 0.81 | 0.00 | |||||
| 1.0 | 1.0 | 0.05 | −0.26 | −0.88 | 0.06 | 0.13 | 0.79 | 0.96 | 0.74 | 0.00 | ||||
Note: and are the measurement error variances from Lab 1 and Lab 2, respectively; δ2 is the mean of the measurement error from Lab 2, and Lab 1 is regarded as the reference(i.e., δ1 = 0); eβ1 is the odds ratio of one increment increase of X from the underlying logistic regression model.
Table 2.
Empirical characteristics of β̂1 in 1000 simulations with n = 100 in the Assay-comparison study and n1 = n2 = 1500 in the Main case-control study for models regressing D on the underlying X (True), the normalized X̃ (RC) and the raw error-prone W (Naïve).
|
|
|
δ2 | eβ1 | Bias | MSE | Coverage | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True | RC | Naïve | True | RC | Naïve | True | RC | Naïve | ||||||
| 0.1 | 0.1 | 0 | 2.0 | 0.00 | 0.00 | −0.06 | 0.00 | 0.01 | 0.01 | 0.93 | 0.94 | 0.84 | ||
| 0.5 | 0.00 | −0.01 | −0.16 | 0.00 | 0.01 | 0.03 | 0.93 | 0.92 | 0.27 | |||||
| 1.0 | 0.00 | −0.02 | −0.24 | 0.00 | 0.01 | 0.06 | 0.93 | 0.91 | 0.02 | |||||
| 0.5 | 0.5 | 0.00 | −0.02 | −0.23 | 0.00 | 0.01 | 0.06 | 0.93 | 0.92 | 0.04 | ||||
| 1.0 | 0.00 | −0.04 | −0.29 | 0.00 | 0.01 | 0.09 | 0.93 | 0.90 | 0.00 | |||||
| 1.0 | 1.0 | 0.00 | −0.05 | −0.34 | 0.00 | 0.01 | 0.12 | 0.93 | 0.89 | 0.00 | ||||
| 0.1 | 0.1 | 5.0 | 0.01 | −0.04 | −0.14 | 0.01 | 0.01 | 0.03 | 0.94 | 0.92 | 0.65 | |||
| 0.5 | 0.01 | −0.11 | −0.36 | 0.01 | 0.02 | 0.14 | 0.94 | 0.75 | 0.02 | |||||
| 1.0 | 0.01 | −0.16 | −0.56 | 0.01 | 0.04 | 0.32 | 0.94 | 0.57 | 0.00 | |||||
| 0.5 | 0.5 | 0.01 | −0.17 | −0.53 | 0.01 | 0.04 | 0.29 | 0.94 | 0.53 | 0.00 | ||||
| 1.0 | 0.01 | −0.23 | −0.68 | 0.01 | 0.06 | 0.47 | 0.94 | 0.32 | 0.00 | |||||
| 1.0 | 1.0 | 0.01 | −0.27 | −0.80 | 0.01 | 0.08 | 0.64 | 0.94 | 0.20 | 0.00 | ||||
| 0.1 | 0.1 | 0.5 | 2.0 | 0.00 | 0.00 | −0.09 | 0.00 | 0.01 | 0.01 | 0.93 | 0.94 | 0.70 | ||
| 0.5 | 0.00 | −0.01 | −0.19 | 0.00 | 0.01 | 0.04 | 0.93 | 0.92 | 0.09 | |||||
| 1.0 | 0.00 | −0.02 | −0.27 | 0.00 | 0.01 | 0.08 | 0.93 | 0.91 | 0.00 | |||||
| 0.5 | 0.5 | 0.00 | −0.02 | −0.24 | 0.00 | 0.01 | 0.06 | 0.93 | 0.92 | 0.01 | ||||
| 1.0 | 0.00 | −0.04 | −0.31 | 0.00 | 0.01 | 0.10 | 0.93 | 0.90 | 0.00 | |||||
| 1.0 | 1.0 | 0.00 | −0.05 | −0.35 | 0.00 | 0.01 | 0.13 | 0.93 | 0.89 | 0.00 | ||||
| 0.1 | 0.1 | 5.0 | 0.01 | −0.04 | −0.22 | 0.01 | 0.01 | 0.06 | 0.94 | 0.92 | 0.29 | |||
| 0.5 | 0.01 | −0.11 | −0.45 | 0.01 | 0.02 | 0.21 | 0.94 | 0.75 | 0.00 | |||||
| 1.0 | 0.01 | −0.16 | −0.64 | 0.01 | 0.04 | 0.42 | 0.94 | 0.57 | 0.00 | |||||
| 0.5 | 0.5 | 0.01 | −0.17 | −0.57 | 0.01 | 0.04 | 0.33 | 0.94 | 0.53 | 0.00 | ||||
| 1.0 | 0.01 | −0.23 | −0.73 | 0.01 | 0.06 | 0.54 | 0.94 | 0.32 | 0.00 | |||||
| 1.0 | 1.0 | 0.01 | −0.27 | −0.82 | 0.01 | 0.08 | 0.68 | 0.94 | 0.20 | 0.00 | ||||
| 0.1 | 0.1 | 1.0 | 2.0 | 0.00 | 0.00 | −0.18 | 0.00 | 0.01 | 0.03 | 0.93 | 0.94 | 0.14 | ||
| 0.5 | 0.00 | −0.01 | −0.25 | 0.00 | 0.01 | 0.07 | 0.93 | 0.92 | 0.01 | |||||
| 1.0 | 0.00 | −0.02 | −0.32 | 0.00 | 0.01 | 0.10 | 0.93 | 0.91 | 0.00 | |||||
| 0.5 | 0.5 | 0.00 | −0.02 | −0.29 | 0.00 | 0.01 | 0.09 | 0.93 | 0.92 | 0.00 | ||||
| 1.0 | 0.00 | −0.04 | −0.35 | 0.00 | 0.01 | 0.12 | 0.93 | 0.90 | 0.00 | |||||
| 1.0 | 1.0 | 0.00 | −0.05 | −0.38 | 0.00 | 0.01 | 0.15 | 0.93 | 0.89 | 0.00 | ||||
| 0.1 | 0.1 | 5.0 | 0.01 | −0.04 | −0.41 | 0.01 | 0.01 | 0.18 | 0.94 | 0.92 | 0.00 | |||
| 0.5 | 0.01 | −0.11 | −0.60 | 0.01 | 0.02 | 0.37 | 0.94 | 0.75 | 0.00 | |||||
| 1.0 | 0.01 | −0.16 | −0.76 | 0.01 | 0.04 | 0.59 | 0.94 | 0.57 | 0.00 | |||||
| 0.5 | 0.5 | 0.01 | −0.17 | −0.68 | 0.01 | 0.04 | 0.47 | 0.94 | 0.53 | 0.00 | ||||
| 1.0 | 0.01 | −0.23 | −0.82 | 0.01 | 0.06 | 0.68 | 0.94 | 0.32 | 0.00 | |||||
| 1.0 | 1.0 | 0.01 | −0.27 | −0.89 | 0.01 | 0.08 | 0.80 | 0.94 | 0.20 | 0.00 | ||||
Note: and are the measurement error variances from Lab 1 and Lab 2, respectively; δ2 is the mean of the measurement error from Lab 2, and Lab 1 is regarded as the reference(i.e., δ1 = 0); eβ1 is the odds ratio of one increment increase of X from the underlying logistic regression model.
3.2 Estimation and testing of mean difference
We assume that X from the Assay-comparison study, X(1) and X(2) from the Main study for comparison, and the measurement error terms, u(1) and u(2) all follow normal distributions. We assume μ = 5, , δ1 = 0, . Based on these parameter values, similar to the previous simulation study, the same additive measurement error models were used to simulate V(j) in the Assay-comparison study and W(j) in the Main study. For different values of τ2 = 0.1, 0.5 or 1.0, δ2 = 0, 0.5, 1.0 or 2.0, Table 3 presents the probability of rejecting H0 : μ1 = μ2 under the null when μ1 = μ2 = 5.0 for n = 50, n = 100 and n = 200. Results from the following three methods are reported: comparing the observed data W(1) vs. W(2) in the Main study without any adjustment (“Raw”), comparing the observed data W(1) vs. W(2) with adjustment discussed in section 2.2 (“Adj”), and comparing the simulated unobservable values of X(1) vs. X(2) (“True”). We can see that the type I errors are well preserved in the true method, as expected. Type I errors from the Raw method are seriously off especially when the measurement error variance and/or mean shift becomes large. The Adj method provides satisfactory control of type I errors in all the studied scenarios, even when the sample size of the Assay-comparison study is as small as n = 50 and the sample size of the Main study is as small as n1 = n2 = 50.
Table 3.
Type I error rates under the null hypothesis of μ1 = μ2 = 5.0 from comparing the observed data in the Main study without any adjustment (“Raw”), comparing the observed data with adjustment discussed in section 2.2 (“Adj”), and comparing the simulated unobservable true values (“True”).
| n1 = n2 | τ2 | δ2 | n = 50 | n = 100 | n = 200 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Raw | Adj | True | Raw | Adj | True | Raw | Adj | True | |||
| 50 | 0.1 | 0 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| 200 | 0.05 | 0.06 | 0.05 | 0.05 | 0.05 | 0.06 | 0.05 | 0.05 | 0.05 | ||
| 1000 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | ||
| 50 | 0.5 | 0.66 | 0.05 | 0.05 | 0.66 | 0.05 | 0.05 | 0.66 | 0.05 | 0.05 | |
| 200 | 1.00 | 0.06 | 0.05 | 1.00 | 0.05 | 0.06 | 1.00 | 0.05 | 0.05 | ||
| 1000 | 1.00 | 0.05 | 0.05 | 1.00 | 0.05 | 0.05 | 1.00 | 0.05 | 0.05 | ||
| 50 | 1.0 | 1.00 | 0.05 | 0.05 | 1.00 | 0.05 | 0.05 | 1.00 | 0.05 | 0.05 | |
| 200 | 1.00 | 0.06 | 0.05 | 1.00 | 0.05 | 0.06 | 1.00 | 0.05 | 0.05 | ||
| 1000 | 1.00 | 0.05 | 0.05 | 1.00 | 0.05 | 0.05 | 1.00 | 0.05 | 0.05 | ||
| 50 | 0.5 | 0 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| 200 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.06 | 0.05 | 0.05 | 0.05 | ||
| 1000 | 0.05 | 0.06 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | ||
| 50 | 0.5 | 0.54 | 0.05 | 0.05 | 0.52 | 0.05 | 0.05 | 0.53 | 0.05 | 0.05 | |
| 200 | 0.98 | 0.05 | 0.05 | 0.98 | 0.05 | 0.06 | 0.98 | 0.05 | 0.05 | ||
| 1000 | 1.00 | 0.06 | 0.05 | 1.00 | 0.05 | 0.05 | 1.00 | 0.05 | 0.05 | ||
| 50 | 1.0 | 0.98 | 0.05 | 0.05 | 0.98 | 0.05 | 0.05 | 0.98 | 0.05 | 0.05 | |
| 200 | 1.00 | 0.05 | 0.05 | 1.00 | 0.05 | 0.06 | 1.00 | 0.05 | 0.05 | ||
| 1000 | 1.00 | 0.06 | 0.05 | 1.00 | 0.05 | 0.05 | 1.00 | 0.05 | 0.05 | ||
| 50 | 1.0 | 0.0 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| 200 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.06 | 0.05 | 0.05 | 0.05 | ||
| 1000 | 0.05 | 0.06 | 0.05 | 0.06 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | ||
| 50 | 0.5 | 0.42 | 0.05 | 0.05 | 0.42 | 0.05 | 0.05 | 0.42 | 0.05 | 0.05 | |
| 200 | 0.94 | 0.05 | 0.05 | 0.94 | 0.05 | 0.06 | 0.94 | 0.05 | 0.05 | ||
| 1000 | 1.00 | 0.06 | 0.05 | 1.00 | 0.05 | 0.05 | 1.00 | 0.05 | 0.05 | ||
| 50 | 1.0 | 0.94 | 0.05 | 0.05 | 0.94 | 0.05 | 0.05 | 0.94 | 0.05 | 0.05 | |
| 200 | 1.00 | 0.05 | 0.05 | 1.00 | 0.05 | 0.06 | 1.00 | 0.05 | 0.05 | ||
| 1000 | 1.00 | 0.06 | 0.05 | 1.00 | 0.05 | 0.05 | 1.00 | 0.05 | 0.05 | ||
Note: n1 and n2 are the sample sizes of the Assay comparison study from Lab 1 and Lab 2, respectively; τ2 is the measurement error variance for both labs; ρ is the correlation between the Lab 1 and Lab 2 measurements in the Assay-comparison study; δ2 is the mean of the measurement error from Lab 2, and Lab 1 is regarded as the reference(i.e., δ1 = 0); and n is the sample size of the Main Study.
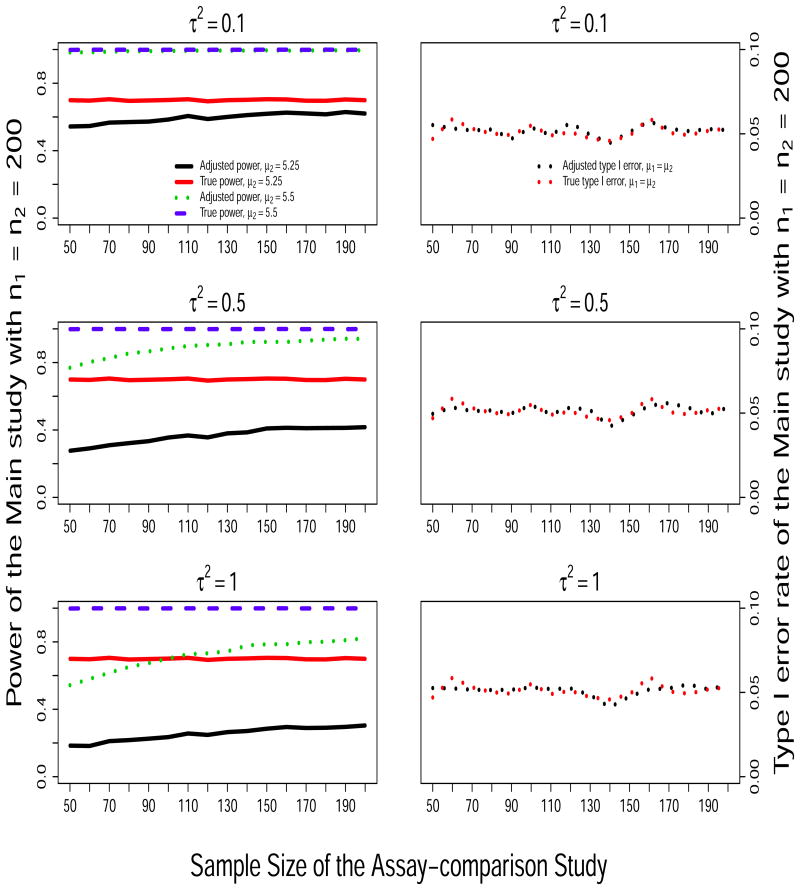
Figure 1 presents the probability of rejecting H0 based on the Main study data under H0 (right panels) and under the alternatives when (μ1 = 5, μ2 = 5.25) and (μ1 = 5, μ2 = 5.5) (left panels) as the sample size of the Assay-comparison study increases from n = 50 to 200. Results from the True and the Adj methods are included; the Raw method is excluded because the type I error was not preserved as shown in Table 3. On the left panels, we can see that the adjusted power for the Main study increases with the sample size of the Assay-comparison study because the precision of the measurement error estimates increases as the sample size of the Assay-comparison study increases. We also see that the adjusted power decreases as the variance of the measurement error increases from τ2 = 0.1 to τ2 = 1.0, but the power does not change when the measurement error mean shift changes from δ2 = 0 to δ2 = 0.5 (data not shown). This is expected because the power of the adjusted method is inversely related to σε but does not depend on δ2 as shown in equation (7). In addition, we observe that, when μ2 = 5.25 the adjusted power (solid black line) rests at low levels because it is limited by the sample size of the main study, the sample variance and the assumed small effect size, as much as is shown for the true power (solid red line). On the right panels, we observe that the Type I error is maintained for all the sample sizes.
Figure 1.
Simulation results: Empirical power of rejecting H0 : μ1 = μ2 under scenarios of (μ1 = 5.0, μ2 = 5.25) and (μ1 = 5.0, μ2 = 5.5) (left panels) and empirical type I error rate under H0 (right panels) in the Main study, as a function of the sample size of the Assay-comparison study.
4 Examples
We illustrate our methods of individual-level data normalization and testing of mean difference using real data collected from two HIV vaccine laboratories: the HIV Vaccine Trial Network (HVTN) Central Laboratory (Lab 1) and the Merck Co. Research Laboratory (Lab 2) in a Phase IIB HIV vaccine clinical trial as described previously ([11] and [12]). Although responses were measured from both vaccine and placebo recipients against multiple HIV peptide pools, for illustration we restrict both the Assay-comparison study and the Main study data to post-immunization ELISpot assay measurements only from vaccine recipients against the HIV Gag peptide pool. The assay readout is the number of spot forming cells (SFC) per million peripheral blood mononuclear cells (PBMCs). All responses were natural log transformed.
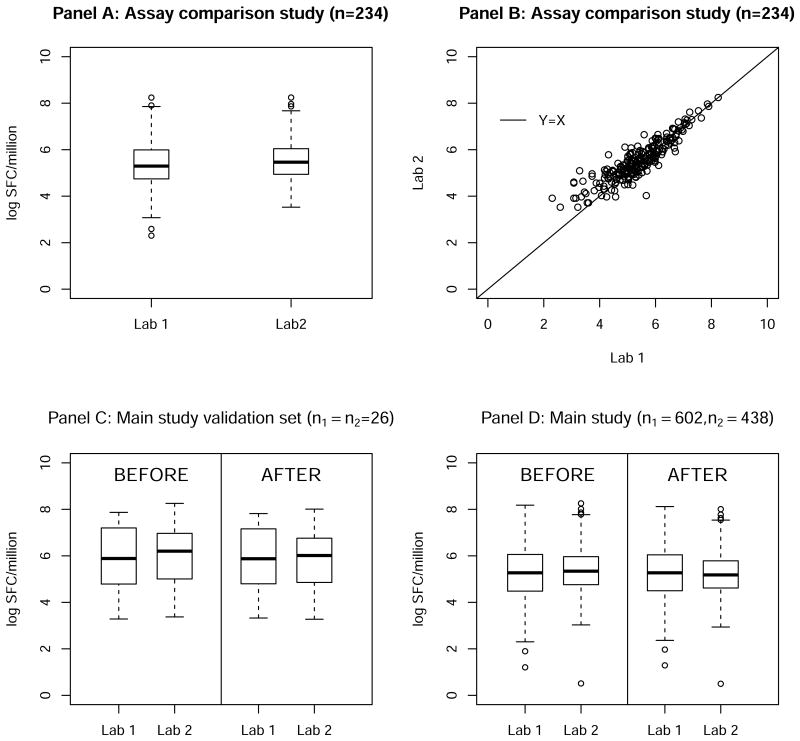
In the Assay comparison study, n = 234 specimens from vaccine recipients collected at 30 weeks after the first immunization were tested by both labs. In Figure 2, the upper panels show data from the Assay-comparison study of n = 234 samples: boxplots (panel A) of the average HIV Gag antigen stimulated responses over three replicates and a scatter plot (panel B) of these responses with an identity line (Y = X). These data have a mean of 5.36 and standard deviation of 1.02 from Lab 1 and mean of 5.52 and standard deviation of 0.87 from Lab 2. We assume δ1 = 0, and δ2 was hence estimated to be 0.16. τ1 and τ2 were estimated to be 0.17 based on triplicates available from Lab 1. No replicate data from Lab 2 was available. We can see that although measured on the same set of samples, Lab 2 measurements are noticeably higher than those from Lab 1.
Figure 2. ELISpot assay immune responses measured by two labs from a Phase IIB HIV vaccine clinical trial: distribution of the Assay-comparison study data (Panel A & B) and distribution of the Main study data before and after normalization (Panel C & D).
In the Main study, n1 = 602 and n2 = 438 specimens from vaccine recipients collected at the primary immunogenicity time-point, 8 weeks after the first immunization, were tested by Lab 1 and Lab 2, respectively. Among these, 26 specimens were measured by both labs. These 26 pairs of data from the Main study will be used as a small validation data set (referred as paired subset) to assess the performance of our proposed method for individual level data normalization.
First, we applied our method described in section 2.1 to normalize the data from the Main study, including the paired subset. Since the 26 data pairs were from the same set of specimens, we expect the “true” values after normalization to be similar. We can see that our proposed method did help to bring the measurements to a similar scale for the paired subset data (Figure 2 Panel C). Specifically, before normalization, the means were 5.81 and 6.03 from Lab 1 and Lab 2, respectively (paired t-test p-value= 0.03). Based on the normalized values, however, the means were 5.80 and 5.85, respectively (paired t-test p-value = 0.63). In Panel D, values before and after normalization from all samples in the Main study are displayed. Specifically, before normalization, the means were 5.30 and 5.35 from Lab 1 and Lab 2, respectively; after the normalization, the means were 5.30 and 5.18, respectively. These normalized values from Lab 1 and Lab 2 can then be pooled and used as either a covariate or outcome variable in subsequent analyses.
Second, assume in a Main study we are interested in comparing ELISpot immune responses induced by two vaccine candidates separately evaluated on n1 and n2 samples by Lab 1 and Lab 2, respectively. We applied the sample size calculation formula in (8) with , and as estimated from the data presented above for illustration. With n1 = n2 = 150, it turns out that n = 24 samples are needed in the Assay-comparison study in order to have least 90% (i.e., β = 0.1) power in the Main study to detect a half log change (i.e., ε = 0.5) in ELISpot responses between the two vaccine candidates at a two-sided type I error rate of α = 0.05.
5 Discussion
As the biomedical field and information technologies advance, it is increasingly desirable and feasible to collaborate across multiple entities and to consolidate data collected from multiple sources for comparison or merging purposes. However, if not handled appropriately, variation across data sources may pose serious problems to the validity of such combined data. We proposed a method for individual-level data normalization so that data from multiple sources are calibrated to the same scale for appropriate comparison or merging. This approach is often used in calibrating error-prone covariates in regression settings (e.g., [13], [14] and [15]). We extended this popular method to our context where data come from two sources bearing possibly different measurement error terms, and the true values of the error-prone measurements are never observed. We assumed a bivariate normal distribution for the true and observed variables, however, other context-driven distributions can be explored and the corresponding conditional mean can be used for calibration similarly. Of note, mixture distributions or a separate normalization for each condition can be considered when there is a mixture of responses collected under multiple conditions (e.g., treatment and control) from both the Assay Comparison study and the Main study. We also proposed a method for comparing data from multiple sources accounting for possible inter-source measurement error without assumptions on the joint distribution of the true and observed values. Unlike traditional methods for measurement error correction, our proposed methods do not require internal or external validation data where the true values for the error-prone measurements are observed. Instead, paired sample data, for example, of an Assay-comparison study collected from the same sources, are used to carry out the adjustment described in our methods. In addition, we provided sample size calculations for the Assay-comparison study in order to achieve desirable power for comparing samples between labs in the Main study. This is useful for researchers to consider before planning to compare data from multiple sources.
Besides using the conditional expectation of X|w for individual-level data normalization, alternatively, W1 and W2 can be re-scaled using inverse cumulative density functions (cdf). Let and denote the cdf of V1 and V2 from the paired-sample data. We could consider transforming W1 and W2 onto and so that they are comparable. More research is needed to better understand this approach.
Other issues remain to be addressed for comparing and combining data across multiple sources. For example, some bioassays have certain limit of detection where a mixture distribution may need to be considered for the error-prone measurements; such limit of detection may vary between data sources. In addition, the verification of the assumed transportability of the measurement error term may require using a subset of the same biomarker targets in both the Assay-comparison study and the Main study.
Acknowledgments
The authors thank Janne Abullarade, Cheryl DeBoer and Cindy Molitor for constructing the example data set. The authors also thank Dr. Holly Janes, and the anonymous reviewers and editors for their helpful comments. This work was supported by the Bill and Melinda Gates Foundation grant: Vaccine Immunology Statistical Center and the NIH grant (U01 AI068635-01): Statistical and Data Management Center for HIV/AIDS Clinical Trials Network.
References
- 1.Spiegelman D, Carroll R, Kipnis V. Efficient regression calibration for logistic regression in main study/internal validation study designs with an imperfect reference instrument. Statistics in Medicine. 2001;20:139–160. doi: 10.1002/1097-0258(20010115)20:1<139::aid-sim644>3.0.co;2-k. [DOI] [PubMed] [Google Scholar]
- 2.Thurston S, Williams P, Hauser R, et al. A comparison of regression calibration approaches for designs with internal validation data. J Stat Plann Inference. 2003;131:175–190. [Google Scholar]
- 3.Britten CM, Gouttefangeas C, Welters MJ, et al. The cimt-monitoring panel: a two-step approach to harmonize the enumeration of antigen-specific cd8+ t lymphocytes by structural and functional assays. Cancer Immunol Immunother. 2008;57:289–302. doi: 10.1007/s00262-007-0378-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mander A, Gouttefangeas C, Ottensmeier C, et al. Serum is not required for ex-vivo ifn-gamma elispot: a collaborative study of different protocols from the european cimt immunoguiding program. Cancer Immunol Immunother. 2010;59:619–627. doi: 10.1007/s00262-009-0814-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Dilbinder G, Huang Y, Levine L, et al. Equivalence of elispot assays demonstrated between major hiv network laboratories. PLoS ONE. 2010;5(12):e14330. doi: 10.1371/journal.pone.0014330. URL http://dx.doi.org/10.1371%2Fjournal.pone.0014330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Todd C, Greene K, Yu X, et al. Development and implementation of an international proficiency testing program for a neutralizing antibody assay for hiv-1 in tzm-bl cells. J Immunol Methods. 2012;375:57–67. doi: 10.1016/j.jim.2011.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fuller W. Measurement Error Models. Wiley; New York: 1987. [Google Scholar]
- 8.Buonaccorsi JP. Measurement error: models, methods, and applications. 1st. Chapman & HallCRC; Boca Raton, FL: 2010. [Google Scholar]
- 9.Staudenmayer J, Buonaccorsi J. Accouting for measurement error in linear autoregressive time series models. Journal of American Statistical Association. 2005;100:841–852. [Google Scholar]
- 10.Buonaccorsi J. Estimation in two-stage models with heteroscedasticity. International Statistical Review. 2006;74:403–415. [Google Scholar]
- 11.Buchbinder S, Mehrotra D, Duerr A, et al. Efficacy assessment of a cell-mediated immunity hiv-1 vaccine (the step study): a double-blind, randomised, placebocontrolled, test-of-concept trial. Lancet. 2008;372(9653):1881–93. doi: 10.1016/S0140-6736(08)61591-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.McElrath M, De Rosa C, Moodie Z, et al. Hiv-1 vaccine-induced immunity in the test-of-concept step study: a casecohort analysis. Lancet. 2008;372(9653):1894–1905. doi: 10.1016/S0140-6736(08)61592-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Prentice R. Covariate measurement errors in the analysis of cohort studies. In: Johnson R, Crowley J, editors. Survival Analysis, IMS Lecture Notes, Monograph Series 2. 1982. pp. 137–151. [Google Scholar]
- 14.Carroll R, Stefanski L. Approximate quasilikelihood estimation in models with surrogate predictors. Journal of the American Statistical Association. 1990;85:652–663. [Google Scholar]
- 15.Gleser L. Improvements of the Naïve approach to estimation in non-linear errors-in-variables regression models. In: Brown FWPJ, editor. Statistical Analysis of Measurement Error Models and Applications. American Mathematical Society; 1990. [Google Scholar]