Tomographic lifetime imaging using combined early- and late-arriving photons

Abstract

We present a novel, hybrid approach for time domain fluorescence tomography that efficiently combines lifetime multiplexing using late-arriving or asymptotic photons, with the high spatial resolution capability of early photon tomography. We also show that a decay amplitude-based asymptotic approach is superior to direct inversion of late-arriving photons for tomographic lifetime imaging within turbid media. The hybrid reconstruction approach is experimentally shown to recover fluorescent inclusions separated as close as 1.4 mm, with improved resolution and reduced cross talk compared to just using early photons or the asymptotic approach alone.

Time domain (TD) techniques offer the most comprehensive optical information about a turbid medium, since a short laser pulse contains all modulation frequencies, including the zero frequency or continuous wave (CW) component. Several methods have been proposed for the reconstruction of TD data, including direct TD inversion [1–3], derived data types such as Laplace transform [4,5], Mellin transform or moments [6], and asymptotic approach based on a multi-exponential analysis [7–9]. In particular, it has been shown that reconstruction using direct time points from early TD data can provide higher resolution than CW and late TD data [3], due to the minimal scattering experienced by early arriving photons. However, the early TD data offers poor lifetime sensitivity, resulting in significant lifetime cross talk and inaccurate localization of closely separated fluorophores with distinct lifetimes [7]. On the other hand, we have shown that an asymptotic TD (ATD) approach based on a multi-exponential analysis of the decay portion of TD data provides low cross talk and superior tomographic localization of multiple fluorophores with distinct lifetimes [10]. The ATD approach relies on the asymptotic factorization of the TD fluorescence into diffusive and pure exponential fluorescence decay components [7].

In this Letter, we present a novel, hybrid TD approach that combines the resolving power of early photon tomography with the lifetime multiplexing capability of the asymptotic approach into a single self-consistent inverse problem, thereby achieving high-resolution tomographic lifetime multiplexing. Experimental results from phantom measurements demonstrate that the hybrid method is able to separate targets as close as 1.4 mm apart with minimal cross talk and with distributions narrower than that obtained from any individual method. We also show that a direct TD inversion of late time gates results in poor separation of multiple lifetime components, while also being computationally far more intensive than the ATD approach.

Consider a diffuse medium embedded with N fluorophores, characterized by yield distributions η_n(r) and lifetimes τ_n. The fluorescence temporal point spread function (TPSF) for impulsive excitation at source position r_s and detection at r_d on the surface of a bounded transport medium of support Ω takes the form:

$$U_f({\mathbf{r}}_s,{\mathbf{r}}_d,t)=\sum _{n=1}^N{\int }_{\mathrm{\Omega }}{W}_n({\mathbf{r}}_s,{\mathbf{r}}_d,\mathbf{r},t){\eta }_n(\mathbf{r}){\mathrm{d}}^3\mathbf{r},$$ (1)

where W_n = G^x(r_s, r, t) ⊗ exp(−t/τ_n) ⊗ G^m(r, r_d, t) is the TD sensitivity function, expressed as a double convolution of the source and detector Green’s functions, G^x and G^m, for light transport in the medium [11] and a fluorescence decay term. Discretizing the medium volume into V voxels, Eq. (1) can be written as a linear matrix equation for M source-detector pairs, L time gates, and N lifetime components:

$$y=W\eta ,$$ (2)

where y is a (ML × 1) vector of the measured fluorescence data U_f, W = [W₁, …, W_N] is a (ML × VN) matrix of TD sensitivity functions, and η = [η₁, …, η_N]^T is a VN × 1 vector of yield distributions for all lifetimes. A direct inversion of Eq. (2) leads to the direct TD (DTD) approach, and the inverse problem is expressed in the standard way using Tikhonov regularization [12] to recover η:

$${\eta }^{\mathrm{D}\mathrm{T}\mathrm{D}}=W^T{(W{W}^T+\lambda I)}^{-1}y.$$ (3)

It is possible to recast the TD forward problem in an alternate form in the asymptotic limit, i.e., for times much longer than the intrinsic diffuse timescale τ_D of the medium [7], and assuming the widely held condition, τ_n > τ_D [13]. The W_n(t)’s in Eq. (1) can then be factored into a product of CW sensitivity functions and simple exponential decays [7] for arbitrary transport media. This allows the forward problem in Eq. (2) to be expressed as

$$y\stackrel{t\gg {\tau }_D}{=}A\mathrm{W̄}\eta ,$$ (4)

where A = [exp(−t/τ₁) * I,…, exp(−t/τ_N) * I] is a (ML × MN) basis matrix of exponential decays, I is a (M × M) identity matrix, and W̄ = diag(W̄_n) is a (MN × VN) block diagonal matrix containing CW weight matrices, W̄_n, which are evaluated with the background absorption reduced by 1/vτ_n [7,13].

A simple manipulation of Eq. (4) can allow a fundamentally different approach to solving the TD inverse problem in the asymptotic limit. Since A is a well-conditioned matrix, it can be first inverted without regularization by multiplication with its Moore–Penrose pseudoinverse A^†. The left-hand side of Eq. (4), after pre-multiplication withA^†, is then simply a linear least-squares solution for a multi-exponential analysis of U_f. In other words, A^†y = a, where a = [a₁, …, a_N]^T is a (MN × 1) vector of decay amplitudes for all source-detector pairs and lifetimes. In the next step, we apply Tikhonov regularization to invert the decay amplitudes:

$${\eta }^{\mathrm{A}\mathrm{T}\mathrm{D}}={\mathrm{W̄}}^T{(\mathrm{W̄}{\mathrm{W̄}}^T+\lambda I)}^{-1}{A}^{†}y.$$ (5)

This two-step inversion is a matrix representation of the previously derived asymptotic TD (ATD) approach [7–10,13]. It should be noted that, although the forward problems of DTD [Eq. (2)] and ATD [Eq. (4)] are equivalent for late time gates, the corresponding inverse problems [Eqs. (3) and (5)] are distinct and will produce different reconstructions even when applied to the same measurement. The key aspect of the ATD approach is that the basis matrix A is removed from the regularization step. This ensures that the measurements in y are directly separated using the exponential basis function of each fluorophore. Additionally, given the block diagonal nature of W̄, Eq. (5) essentially reduces to completely separate inverse problems for each yield distribution η_n. This should be contrasted with the DTD inversion in Eq. (3), where the inverse problem for each η_n is not separable. Consequently, the ATD approach results in significantly lower cross talk between the yields of multiple lifetimes than the DTD approach, as we will demonstrate using simulations below.

Although the DTD approach is suboptimal for lifetime multiplexing, the early and peak portions of the TD signal provide higher resolution and better noise statistics than the late photons [3]. In order to incorporate these advantages of early gates into the ATD approach, we consider inverting a “hybrid” data set consisting of early time gates and decay amplitudes, 𝓎 = [y(t₁), y(t₂), …, a₁, a₂, …]^T, using a hybrid weight matrix, 𝒲 consisting of the DTD and ATD weight functions (W_n and W̄_n). The hybrid TD (HTD) forward problem takes the form 𝓎 = 𝒲η or explicitly,

$$\left[\begin{array}{c}\hfill y(t_1)\hfill \\ \hfill y(t_2)\hfill \\ \hfill ⋮\hfill \\ \hfill a_1\hfill \\ \hfill ⋮\hfill \\ \hfill a_N\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill W_1(t_1)\hfill & \hfill \dots \hfill & \hfill W_N(t_1)\hfill \\ \hfill W_1(t_2)\hfill & \hfill \dots \hfill & \hfill W_N(t_2)\hfill \\ \hfill ⋮\hfill & \hfill \dots \hfill & \hfill ⋮\hfill \\ \hfill {\mathrm{W̄}}_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathrm{W̄}}_N\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\eta }_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\eta }_N\hfill \end{array}\right].$$ (6)

It is advantageous to impose a positivity constraint (see also [12]) on the Tikhonov cost functional, so that the inversion of the HTD approach is expressed as the minimization problem:

$${\eta }^{\mathrm{H}\mathrm{T}\mathrm{D}}=\text{arg}\underset{\eta \ge 0}{\text{min}}{\Vert 𝓎-𝒲\eta \Vert }_{C^{-1}}^2+\lambda {\Vert \eta \Vert }^2,$$ (7)

where C is a measurement covariance matrix that incorporates the distinct noise characteristics of the direct time points y and the amplitudes a within 𝓎. The positivity constraint reduces cross talk with the HTD approach by preventing negative yield values from spuriously reducing the ATD term of the HTD cost functional in Eq. (7).

Equations (6) and (7) are the central results of this Letter and present a novel approach for TD fluorescence tomography, particularly for lifetime multiplexing. We next quantified the above theoretical results using Monte Carlo simulations, performed using tMCimg [14]. The simulation medium was a 2 cm × 2 cm × 2 cm slab with optical properties of μ_a = 0.2 cm−1 and ${\mu }_s^{\prime }=10\mathrm{c}{\mathrm{m}}^{-1}$. Forty-nine equally spaced sources and detectors were located at z = 0 and z = 2 cm planes, respectively. The time step was set to 100 ps. Fluorescent inclusions (0.125 mm³) were placed at the center of the slab. A 2% shot noise was added to all forward data prior to reconstruction. Minimization of the HTD cost functional with positivity constraint was implemented using L-BFGS-B [15] in MATLAB (The Mathworks, Inc.). In all simulations, the regularization parameter λ was chosen corresponding to the least-mean-square error (MSE = ‖η_recon − η_true‖).

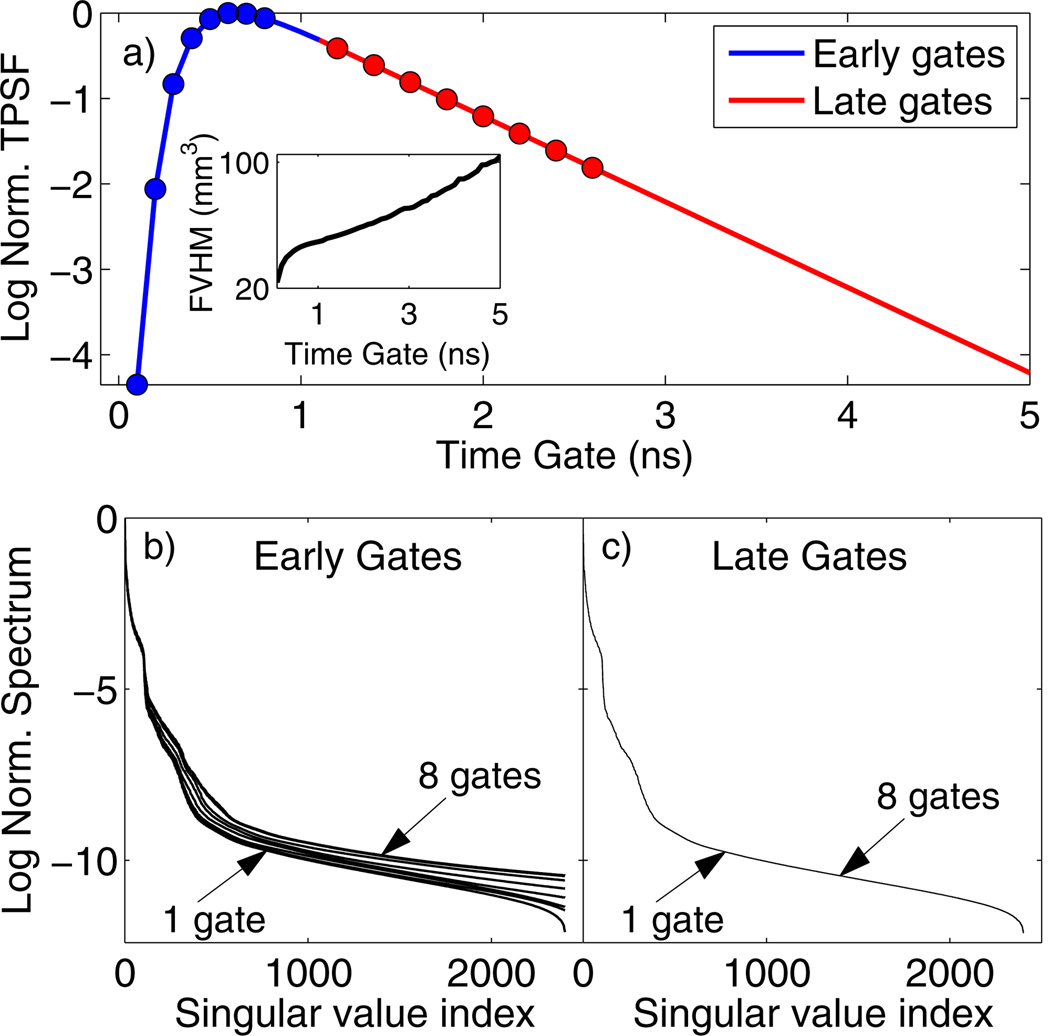
Figure 1 shows simulations for a single fluorescent inclusion using the DTD approach. The inset of Fig. 1(a) shows that the resolution, quantified by the full volume at half-maximum (FVHM) of the reconstructed yield, decreases with later time gates. Also, a singular value decomposition (SVD) analysis of the DTD sensitivity matrix shows distinct behavior for the early and late portions of the TPSF. The slope of the singular value spectra increased with the number of early time gates, indicating improvement in the conditioning of the inversion and gains in resolution [Fig. 1(b)]. However, the SVD spectra show negligible change for any combination of multiple late time gates [Fig. 1(c)]. This demonstrates the redundancy of using multiple gates in the asymptotic region for tomography, as we expect from the spatio-temporal factorization in Eq. (4).

Fig. 1.

(a) Fluorescence TSPF for a 2 cm thick diffusive slab with a fluorescent inclusion (τ = 1 ns) at the center. The inset shows the FVHM of the reconstructed yield for individual time gates. SVD spectra of the DTD weight matrix are shown for (b) one to eight early gates [indicated as blue circles in (a)] and (c) one to eight late gates [red circles in (a)]. The gates were stacked in order of decreasing intensity for both cases.

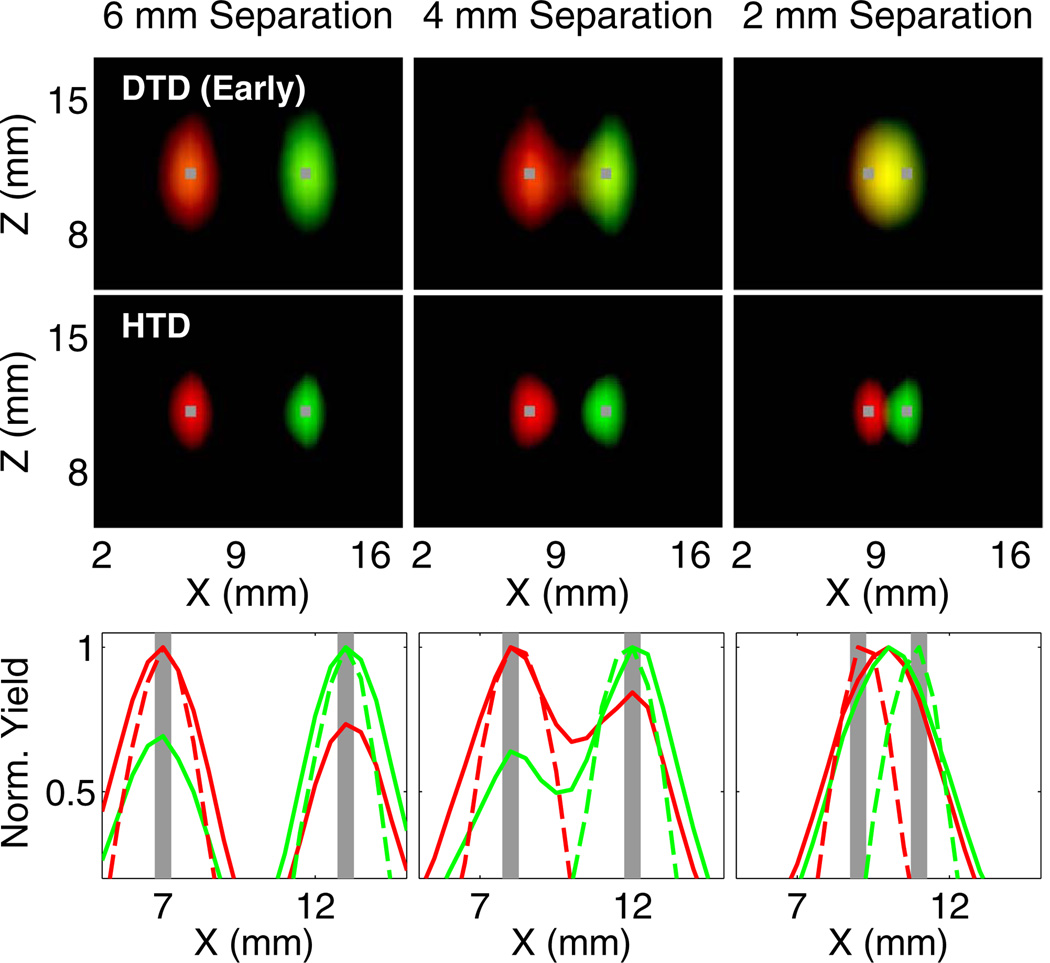
We next compared the imaging performance of DTD, ATD, and HTD methods using two inclusions with distinct lifetimes (τ = 0.87 ns and 1.27 ns) and with varying separations of 2–6 mm. Figure 2 shows a comparison of ATD with DTD applied to the same set of 12 late time gates. It can be seen from the line plots that there is significantly higher cross talk for reconstructions using DTD (Fig. 2, yellow indicates cross talk), which precludes accurate localization of the inclusions even for 4 mm separation. The ATD approach, however, provides minimal cross talk and correctly localizes the inclusions down to 2 mm separation.

Fig. 2.

Comparison of reconstructions obtained from applying ATD and DTD to the same set of 12 late time gates. Red and green corresponds to the yield distributions for 0.87 and 1.27 ns, respectively. The true locations of the inclusions are shown in gray. In the first two rows, the X–Z plots are generated by assigning the recovered yields to the red (0.87 ns) and green (1.27 ns) components of the RGB colormap. Each distribution is thresholded at 50% of its maximum. The bottom row shows line plots for ATD (dashed line) and DTD (solid line) along the x axis at the depth of the inclusion. The computation time for ATD was 21 times shorter than that for DTD.

Figure 3 shows reconstructions using the DTD approach with four early time gates. While the individual yield distributions are smaller than the ATD distributions in (Fig. 2), the cross talk is significantly higher than ATD for all separations, once again leading to inaccurate localization. Figure 3 also shows the reconstructions using the HTD approach with four early time gates and the decay amplitudes, which provides high resolution and accurate localization for all separations. We note that when the positivity constraint (Eq. 7) was not imposed, the cross talk of the HTD method was higher, but still lower than for DTD alone.

Fig. 3.

Comparison of reconstructions obtained from DTD applied to four early gates and the HTD method. The display parameters are consistent with (Fig. 2). The bottom row shows line plots for HTD (dashed line) and DTD (solid line) along the x axis at the depth of the inclusion.

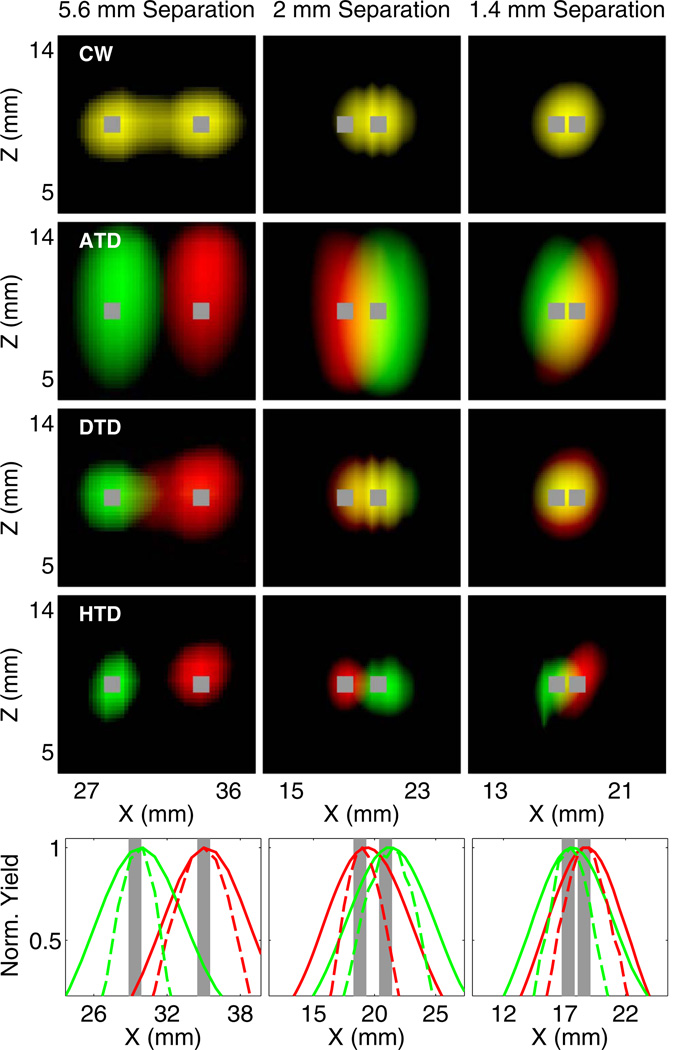
Finally, we validated the HTD approach using phantom experiments. Parallel tubes filled with two dyes (τ = 0.87 and 1.27 ns) and separated by 5.6, 2, and 1.4 mm were embedded in a scattering medium consisting of intralipid and nigrosin (μ_a = 0.1 cm⁻¹ and ${\mu }_s^{\prime }=10\mathrm{c}{\mathrm{m}}^{-1}$ ). Measurements were performed with a previously described TD fluorescence tomography system [9,10], consisting of a Ti-Sapphire laser for excitation and time-gated intensified CCD camera for detection. Full tomographic measurements were acquired for up to 84 sources and 84 detectors, and 46 time gates, with a gate width of 500 ps, CCD integration time of 100–200 ms, and step size of 150 ps. The results shown in Fig. 4 indicate that the ATD method is able to correctly localize the tubes for all separations, while DTD and CW cannot separate tubes closer than 5.6 mm. However, the HTD method applied to three early time gates and decay amplitudes is able to accurately localize the inclusions, with significantly narrower yield distributions compared to the ATD method. We note that the same regularization was applied to ATD alone as to the ATD component of the hybrid method, indicating that the improvement in resolution is due to the incorporation of early time gates in the reconstruction.

Fig. 4.

Experimental reconstruction of fluorophores with lifetime contrast in a dish phantom. X–Z and line plots for CW, ATD, DTD (three early and three late gates), and HTD combining ATD and DTD (three early gates) are shown. Red and green correspond to the yield distributions for 0.87 and 1.27 ns, respectively. Each distribution is thresholded at 70% of its maximum. The bottom row shows line plots for HTD (dashed line) and ATD (solid line) along the x axis at the depth of the inclusion.

In summary, we have presented a novel approach for TD fluorescence tomography that combines the use of early- and late-arriving photons, enabling high-resolution lifetime tomography in turbid media. We have also shown that direct inversion of late time gates can lead to erroneous localization, while also being computationally more cumbersome than an asymptotic approach using decay amplitudes. We have experimentally demonstrated the improved resolution and cross talk performance of the hybrid method in separating closely located targets. The spatial resolution of the HTD approach can be further improved using faster detectors that are capable of detecting photons arriving earlier than 100 ps. Future work will be focused on in vivo applications of this technology in animal models of disease.