Near-Contiguous Spin Echo Imaging Using Matched-Phase RF and Its Application in Velocity-Selective Arterial Spin Labeling

Abstract

Purpose

The minimum slice spacing in multislice imaging is limited by inter-slice crosstalk due to an imperfect slice profile. This study sought to minimize the slice spacing using matched-phase RF pulses and demonstrate its application in cerebral blood flow imaging using velocity-selective arterial spin labeling.

Methods

A spin-echo matched-phase 90°–180° RF pair was designed using Shinnar-Le Roux algorithm in order to improve the slice profile of longitudinal magnetization, which plays a more critical role in creating interslice crosstalk than transverse magnetization. Both transverse and longitudinal slice profiles were compared between matched-phase RF and sinc-based RF pulses in simulations and measurements. Velocity-selective arterial spin labeling was performed in normal volunteers using both RF pulses and standard deviation of cerebral blood flow time series was calculated to examine ASL signal stability.

Results

Using designed matched-phase RF, the longitudinal slice profile was sharpened without signal-to-noise ratio loss. In velocity-selective arterial spin labeling imaging, the temporal standard deviation of cerebral blood flow measurements was reduced from 48 mL/100 g/min to 32 mL/100 g/min by 33% using matched-phase RF pulses, and as a result, cerebral blood flow image quality improved.

Conclusion

This study reports that near-contiguous multislice imaging can be achieved using matched-phase RF pulses without compromising signal-to-noise ratio and signal stability.

Crosstalk between slices in multislice imaging is caused by an imperfect RF slice profile (1–4). No selective RF pulse has a perfectly rectangular profile in practice, and therefore partially excites the adjacent slices in contiguous multislice imaging. Unless a very long TR (>4–5 × T₁) is used, the perturbed magnetization in the adjacent slices will not fully recover to its equilibrium value before its own RF excitation. This pre-perturbation introduces errors into quantitative imaging such as measurements of T₁ or T₂ (5–8), alters the contrast between tissues in qualitative imaging which confounds clinical diagnosis (9–11), and reduces overall signal-to-noise ratio (SNR) (12). One simple method to avoid the pre-perturbation is to place a larger gap between slices (4) although this involves a risk of missing lesions in the acquired images. Another simple method is to use a longer TR to allow for a near-full relaxation of the perturbed magnetization. However, a long TR increases total scan time and a shorter TR is required in applications such as T₁-weighted imaging. Based on the similar idea of increasing time for relaxation, the order of slice acquisition can be interleaved (2,3,13,14), but the time for relaxation still may not be long enough to achieve full relaxation when a short TR is used. While crosstalk may be significantly reduced in gradient echo sequences using these methods, it is a more severe problem in spin-echo sequences because the profile of the 180° refocusing RF pulse or the 90°–180° combination is worse than that of the 90° RF pulse alone due to the peak RF limits. Spin-echo imaging is beneficial in many applications for its advantage of reducing susceptibility artifacts both those arising from anatomy (temporal/frontal regions) and from pathology/foreign bodies (blood products, clips, etc).

The typical goal of RF pulse design is to produce a sharp pulse profile in a minimum amount of time. The tradeoff is limited by the time-bandwidth (TBW) product, specific absorption rate, and peak B₁ of the RF pulse. In spin-echo imaging, matched-phase pulses can be used to improve RF excitation performance (15). Unlike conventional RF pulses, the individual 90° and 180° pulses in matched-phase RF pulses can have non-linear phase. However, these phases are designed to be matched to each other such that a linear phase is obtained at the end of the pulse pair. This creates more flexibility in RF pulse design, which can be utilized to sharpen the slice profile (or increase TBW product), reduce the echo time (TE), or lower peak B₁ for a given pulse duration.

In addition to improving transverse slice profile, we demonstrate that the profile of longitudinal magnetization can be sharpened using matched-phase RF pulses, and therefore inter-slice crosstalk is minimized. We simulate and measure slice profiles using the matched-phase RF and sinc-based RF pulses and show that matched-phase RF pulses achieve a sharper longitudinal slice profile than sinc-based RF pulses, allowing for a smaller slice spacing. We then apply matched-phase RF pulses to cerebral blood flow (CBF) measurements using velocity-selective arterial spin labeling (VSASL) (16). Because of the typical brain motion during image acquisition, higher interslice crosstalk increases a temporal variation in the ASL signal, leading to reduced ASL signal stability. We demonstrate that near-contiguous multislice imaging can be achieved using matched-phase RF pulses in ASL perfusion imaging without reducing stability of ASL signal.

METHODS

Pulse Design

Matched-phase RF pulses were designed using the Shinnar– Le Roux (SLR) algorithm (17). In the SLR algorithm, an RF pulse is represented by two complex polynomials α and β. The transverse component of magnetization after the 90° excitation is

$$M_{xy,90}=2{\mathrm{\alpha }}_{90}^{\ast }{\mathrm{\beta }}_{90}.$$ [1]

The transverse magnetization after the 180° refocusing pulse following the 90° excitation pulse is then given by

$$\begin{array}{l}{M}_{xy,180}=-{\mathrm{\beta }}_{180}^2{M}_{xy,90}^{\ast }\\ =-{\mathrm{\beta }}_{180}^2{(2{\mathrm{\alpha }}_{90}^{\ast }{\mathrm{\beta }}_{90})}^{\ast }\\ =-2{\mathrm{\alpha }}_{90}{\mathrm{\beta }}_{90}^{\ast }{\mathrm{\beta }}_{180}^2.\end{array}$$ [2]

Because the term α₉₀ has very little phase across the slice, most of the phase in M_xy,180 arises from ${\mathrm{\beta }}_{90}^{\ast }{\mathrm{\beta }}_{180}^2$. A simple solution to make this term have a linear phase would be

$${\mathrm{\beta }}_{90}=\frac{1}{\sqrt{2}}{\mathrm{\beta }}_{180}^2$$ [3]

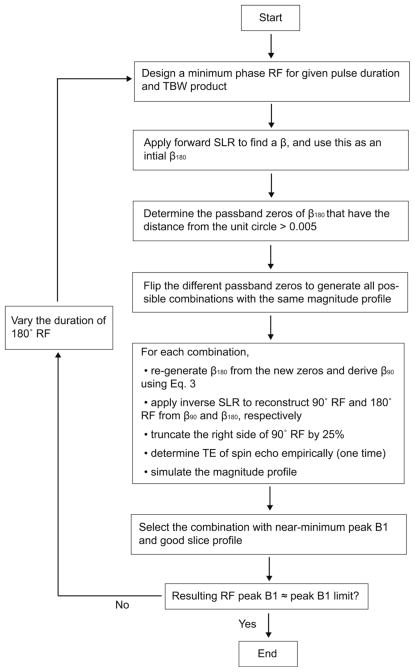
as described in Ref. 15. Note that the scalar is added to satisfy the equations, |β₉₀| = sin(90°/2) and |β₁₈₀| = sin(180°/2) in the passband. The polynomial β₁₈₀ was designed by beginning with a minimum phase RF. The 180° RF pulse design is then reduced to finite impulse response filter design using this initial β₁₈₀. With N time points in the 180° RF pulse, there are N-1 zeros in the polynomial β₁₈₀, mostly residing along the unit circle in the complex plane. The passband zeros were determined such that the distance from the unit circle was larger than a threshold, 0.005. The number of these passband zeros, M, is approximately same as the TBW product of the pulse, which corresponds to the number of zero-crossing of the RF pulse. Flipping (or taking a conjugate reciprocal of) any of the zeros of a β polynomial only scales the magnitude profile by a factor of one over magnitude of the corresponding zero but does not change the overall shape of magnitude profile (17,18). With the scalar compensation, we flipped the different zeros in the polynomial β₁₈₀ to generate 2^M of all possible combinations of flipped and nonflipped passband zeros. For each case, we regenerated β₁₈₀ from the combination of the new zeros and derived β₁₈₀ from β₁₈₀ using Eq. [3]. Furthermore, we truncated the right side of the 90° RF pulse by 25% without much signal loss, to avoid increasing TE. We then empirically determined the TE of a spin echo that produced a refocused phase across the slice. Once TE was found for one combination, it was the same for all other combinations. Note that, during zero-flipping, the magnitude of β₁₈₀ is preserved but the phase of β₁₈₀ is changed; however, the phase of β₁₈₀ is matched to the phase of β₁₈₀ in all cases such that a linear phase at the spin-echo is achieved. Among all combinations, we chose the one that obtained close-to-minimum peak B₁ with good slice profile. We repeated the whole design process several times with a different initial pulse duration for 180° RF until the resulting peak B₁ matched the target RF limit. The whole design steps are summarized in Figure 1, and the designed matched-phase 90°–180° pulse pair is shown in Figure 2.

FIG. 1.

Summary of RF design steps for the matched-phase RF pulses. Flipping zeroes of β₁₈₀ maintains the magnitude but varies the phase of β₁₈₀. From Eq. 3, β₁₈₀ also has a consistent magnitude but compensates for the phase variation of β₁₈₀ so that the linear phase can be achieved at the spin-TE. Most of the combinations of flipped zeros produce the desirable magnitude profiles, but one with minimum peak B₁ can be selected.

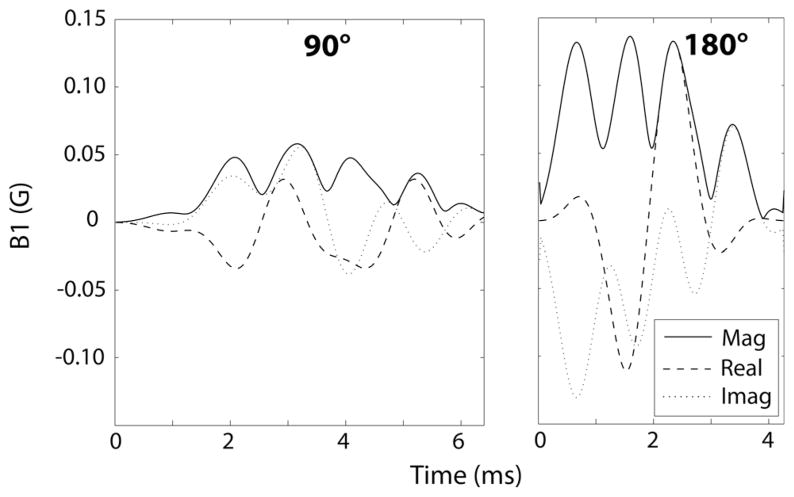
FIG. 2.

Designed matched-phase 90°–180° RF pulse pair with peak B₁ of 0.15 G. Time from start of RF pulse to spin-echo formation was only 2.5 ms longer compared to conventional RF pulses based on sinc or SLR design.

Slice Profile Simulations

We generated slice profiles in simulation using our matched-phase RF as well as conventional RF pulses based on sinc or SLR design for comparison. While the duration of the 90° and the 180° pulse was both 3.2 ms in the conventional RF pulses, it was 6.4 ms for the 90° RF and 4.3 ms for the 180° RF in the matched-phase RF pulses. Nevertheless, there was only 2.5 ms of difference in the minimum time from start of RF pulse to spin-echo formation because, with the matched-phase RF pulse, (1) the conventional rephasing gradient on the slice selection direction after the 90° RF was not required and (2) the empirically found TE was shorter than twice the time between centers of 90° and 180° RF pulses. The nominal slice thickness for 90° RF was 6 mm in both matched-phase and conventional RF pulses. The nominal slab thickness for 180° RF was the same as 90° excitation thickness in the matched-phase RF. For conventional RF pulses, however, a slab thickness larger than the 90° excitation thickness is preferred for the 180° RF because, in the profile of 180° RF, the plateau is much smaller than the prescribed slice thickness and therefore the refocusing is fully achieved only for the magnetization within this narrow range of the slice. A smaller 180° RF slab thickness will lead to lower SNR whereas a larger 180° RF slab thickness will create more perturbation of magnetization in the neighboring slices, leading to lowered initial magnetization for those slices. For fair comparison, the 180° RF slab thickness in conventional RF pulses was optimized in this study as follows. We performed multislice imaging in a phantom using sinc RF pulses with 6-mm slice thickness and 2-mm slice spacing and measured the average signal intensity in each slice while varying the refocusing slab thickness. As shown in Figure 3a, the average signals in all slices except for the first slice was maximized when the refocusing slab thickness was 1.6 times larger than the imaging slice thickness, and we used this ratio for the subsequent simulations and measurements. With this ratio, sinc-based RF pulses achieve rather consistent signal intensity across slices compared to larger ratios but obtain lower average signal intensity than matched-phase RF (Fig. 3b). The TBW product was eight for the 90° RF and four for the 180° RF in conventional pulses. The TBW product was eight for both 90° RF and 180° RF in matched-phase pulses. We also simulated the slice profiles in the presence of B₀ and B₁ inhomogeneity.

FIG. 3.

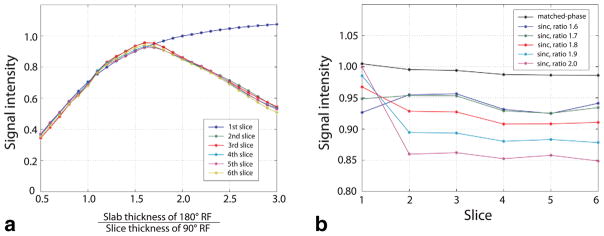
a: Signal intensity of each slice measured in multislice imaging using sinc-based 90°–180° RF pulses with 6-skip-2 slice configuration. For each slice, signal intensity was averaged and normalized by the signal intensity measured in single-slice imaging. For all slices except for the first slice, the signal intensity decreased as the 180° RF slab thickness became larger than 1.6 times the 90° RF slice thickness because of more magnetization perturbation from previous slices. b: Normalized signal intensity in each slice acquired using sinc-based RF with slab thickness ratio 1.6–2.0 and matched-phase RF. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Slice Profile Measurements

Slice profiles were measured in a phantom using matched-phase and sinc-based RF pulses. A cylindrical phantom was used with the long axis as a slice-selection direction. For each RF pulse type, slice profiles of both M_xy and M_z were measured. M_xy profile was measured by swapping the gradients of readout direction and slice-selection direction during image readout. M_z profile was measured by adding another RF excitation after the RF excitation to examine, with slice-selection directions perpendicular to each other. All slice profiles were normalized by nonselective profiles.

VSASL Perfusion Imaging

To evaluate the RF performance in a clinical application, matched-phase RF pulses were incorporated into CBF measurement sequence using VSASL. Thirty pairs of tagged/control images were acquired for signal averaging. The standard deviation (SD) of the CBF time series was calculated to estimate ASL signal stability (16). Scans were performed using matched-phase RF as well as sinc-based RF pulses for comparison. Two slice-thickness/ slice-spacing configurations were used; 6-mm slice thickness with 6-mm slice spacing (6-skip-6) and 6-mm slice thickness with 2-mm slice spacing (6-skip- 2). For sinc-based RF pulses, we used the slice thickness ratio of 1.6 with 6-skip-2, but used ratio of two with 6-skip-6 for higher SNR. This experiment was performed in five normal volunteers. Although demonstrated using VSASL imaging, matched-phased RF design can be used in ASL imaging with any other tagging schemes.

Experimental Setup

In all phantom and in vivo experiments, the imaging sequence was a 2D single-shot spiral spin-echo acquisition with TE = 16 ms, readout bandwidth = 125 kHz, 64 × 64 matrix size, FOV = 220 cm, and 6-mm slice thickness. For VSASL scans, the velocity-selective tagging was performed using double hyperbolic secant (sech) inversion pulses with a cut-off velocity of 2 cm/s. Background suppression was achieved using one saturation and two sech inversion pulses placed at 4453, 1623, and 463 ms prior to image acquisition respectively. Other parameters in VSASL scans included TR = 5 s and TI = 1630 ms. All experiments were performed on a GE MR750 3.0 T scanner (GE Healthcare, Waukesha, WI) with gradients supporting 50 mT/m amplitude and 200 mT/m/ms slew rate. The body coil and a standard eight-channel head coil were used for RF transmission and signal reception, respectively. All subjects provided informed consent in accordance with institutional policy.

RESULTS

Slice Profile Simulation

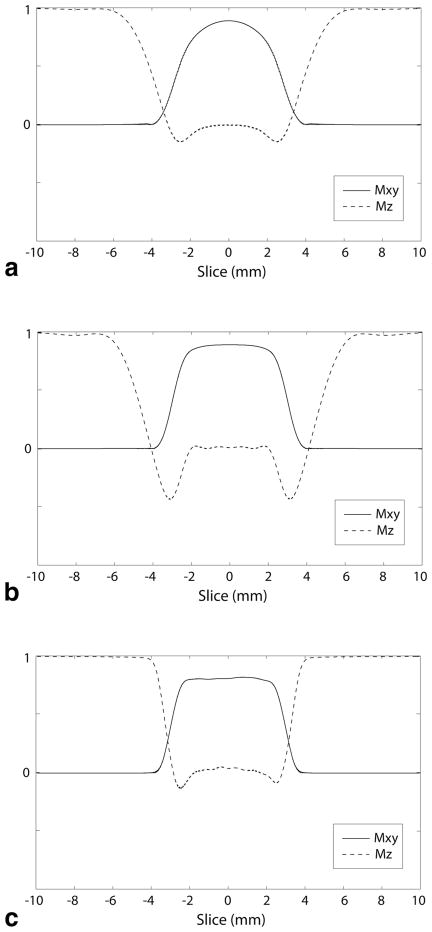
Figure 4a shows the slice profile with RF pulses designed using a sinc waveform. It can be seen that perturbation of magnetization in the neighboring slice arises primarily from longitudinal component (M_z) rather than transverse component (M_xy). Figure 4b shows the slice profile with RF pulses designed using SLR algorithm on 90° RF and 180° RF separately. SLR-designed RF pulses sharpen the M_xy profile, which depends mostly on 90° RF, but lead to similar or slightly worse M_z profile than sinc RF because the gain from the use of SLR design in 180° RF may be limited compared to 90° RF. The slice profile with matched-phase RF shown in Figure 4c illustrates that M_xy slice profile is as sharp as SLR RF pulses, but more importantly, M_z profile is improved such that the perturbation to the neighboring slices can be significantly reduced. Figure 5 shows the slice profiles of M_xy simulated in the presence of off-resonance of °100–100 Hz and B₁ inhomogeneity with a scaling range of 0.8–1.2. The slice profiles were degraded by off-resonance or B₁ variation but there was no significant difference between matched-phase RF and sinc RF pulses.

FIG. 4.

Simulated slice profiles using RF pulses designed based on a sinc waveform (a), RF pulses designed using SLR algorithm separately on 90° RF and 180° RF (b), and matched-phase RF pulses (c). Nominal slice thickness was 6 mm for all RF pulse types. Using SLR-designed RF, M_xy slice profile was sharpened but M_z slice profile was similar to sinc-based RF pulses. M_z slice profile was improved with matched-phase RF pulses such that the perturbation of magnetization in the adjacent slices would be minimized.

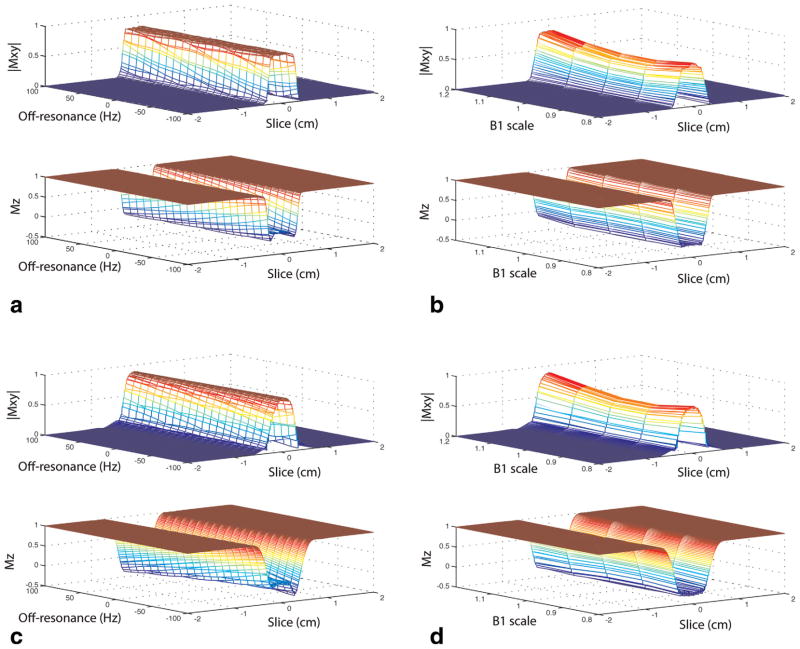
FIG. 5.

Simulated slice profiles of M_xy and M_z using matched-phase RF pulses (a and b) and sinc-based RF pulses (c and d) in the presence of off-resonance and B₁ inhomogeneity. Degradation of slice profiles due to off-resonance or B₁ variation was comparable between matched-phase and sinc-based RF pulses. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Slice Profile Measurements

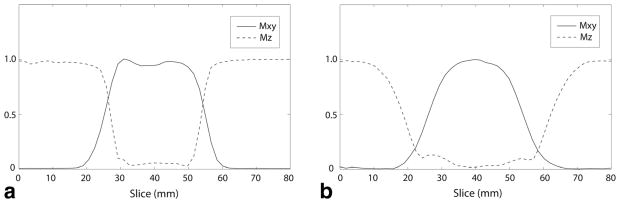
Figure 6 demonstrates the slice profiles measured using matched-phase RF and sinc-based RF pulses. Nominal slice thickness of 30 mm was used for both RF pulses, to better depict the profile without the need to increase the resolution of the spiral. The full width at half maximum of the measured M_xy profile was 29.7 mm with the matched-phase RF and 28.1 mm with the sinc-based RF. M_xy profile was slightly sharper with matched-phase RF than sinc-based RF pulse as expected from profile simulation but there was a small dip observed in the middle of profile with matched-phase RF. On the other hand, M_z profile indicates that the sinc-based RF pulse generates a much larger perturbation of magnetization beyond the prescribed slice thickness compared to matched-phase RF. The full width at half maximum of M_z profile was 26.9 mm with the matched-phase RF and 43.6 mm with the sinc-based RF.

FIG. 6.

M_xy and M_z slice profiles measured in a phantom using the matched-phase RF (a) and the sinc-based RF (b) with a nominal slice thickness of 30 mm. Full width at half maximum of M_xy profiles were similar for both RF types. However, the full width at half maximum of M_z profile was 26.9 mm for matched-phase RF and 43.6 mm for sinc-based RF, indicating a much larger perturbation of adjacent slices with the sinc-based RF pulses.

VSASL Perfusion Imaging

The temporal SD of CBF time series for four different combinations of RF types and slice spacing are summarized in Figure 7. When slice spacing was reduced from 6 to 2 mm, the temporal SD in the whole brain increased from 37 ± 11 mL/100 g/min to 48 ± 12 mL/100 g/min using sinc-based RF, but was maintained at 32 ± 6 mL/ 100 g/min using matched-phase RF. For 6-skip-2, mean CBF in the whole brain was 31.4 mL/100 g/min for sincbased RF and 28.9 mL/100 g/min for matched-phase RF, and SNR gain with matched-phase RF was 7.5%, which is consistent with the result from Figure 3b. Figure 8 shows CBF maps and temporal SD maps acquired in a representative healthy volunteer using the 6-skip-2 slice configuration. With sinc-based RF pulses, the temporal SD was higher in the second to sixth slices than the first slice (as expected). With matched-phase RF, however, temporal SD was rather consistent across the slices, showing a similar temporal SD level to that of the first slice with sinc-based RF. As can be predicted from SD maps, CBF maps acquired using sinc-based RF showed erroneous CBF values for a normal volunteer where temporal SD is high.

FIG. 7.

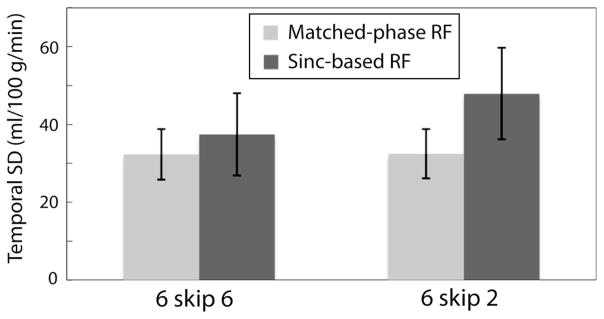
Temporal SD of CBF time series measured in normal volunteers using VSASL. Error bars correspond to the ± 1 SD across five subjects. When slice spacing was reduced from 6 to 2 mm, temporal SD increased from 37 mL/100 g/min to 48 mL/100 g/min using sinc-based RF pulses but was preserved at 32 mL/100 g/ min using matched-phase RF. Larger crosstalk is suspected to generate higher temporal SD in the presence of brain motion during image acquisition.

FIG. 8.

Temporal SD maps (a) and corresponding average CBF maps (b) acquired in a healthy volunteer using VSASL with sinc-based RF and matched-phase RF (in mL/100 g/min). All images were acquired with 6-mm slice thickness and 2-mm slice spacing. Using matched-phase RF, temporal SD of CBF of all slices was reduced in slice 2–6, and the hyperintensity in CBF maps (arrows) was reduced as a result of improved ASL signal stability.

DISCUSSION

In this study, we demonstrated that matched-phase RF pulses could be used to reduce the crosstalk between imaging slices without SNR loss when using smaller slice spacing that is necessary for near-contiguous multislice acquisition. We showed that the simulated and measured slice profiles had good agreement, and verified that the M_z component of slice profile produced a slice thickness closer to the nominal slice thickness using matched-phase RF than sinc-based RF. A narrow M_z profile with matched-phase RF is expected to reduce the perturbation of magnetization in the adjacent slices. We applied our designed matched-phased RF in VSASL perfusion imaging, and found that the SD of CBF time series was preserved using matched-phase RF when slice spacing was reduced to one third of slice thickness.

The reason that the crosstalk presented here may not be always observed in other applications with spin-echo imaging is that (1) ASL is very sensitive to small changes in the imaging volume and (2) the 180° refocusing slab is often reduced in other sequences to avoid interslice perturbation at the cost of reduced SNR. For example, sincbased RF pulses with the same slab thickness for 90° RF and 180° RF may enable a slice gap as small as 10% of the imaging slice thickness, but SNR loss will be about 25% compared to the case of slab ratio of 1.6 as shown in Figure 3a. Matched-phase RF pulses achieve SNR gain (43% compared to sinc RF with slab ratio of 1) without significant crosstalk in 6-skip-2 slice configuration.

Improvement in M_z profile with matched-phase RF is mostly attributed to the sharp profile of 180° refocusing pulse. Because the small-tip approximation in RF design based on Fourier transform breaks down with a 180° flip-angle, an increase in TBW product of sinc-based 180° RF does not linearly sharpen the slice profile but prolongs the pulse duration. Using SLR algorithm and removing restriction on linearity of the individual 90° and 180° pulse phases, matched-phase RF pulses achieve a sharper slice profile of the 180° pulse with a minimal increase in total pulse duration (2.5 ms in our design).

Matched-phase RF pulses produce slight signal reduction in slices subsequent to the first slice, and with smaller slice spacing, this signal inhomogeneity will increase and may cause non-negligible errors in quantitative imaging. In the example of ASL perfusion imaging, the difference images (with and without tagging) are normalized by MR signal of cerebrospinal fluid for quantification. Because cerebrospinal fluid signal is typically acquired from the middle slices of the same multislice configuration, the normalization process can compensate for the effect of signal reduction except for a few initial slices. In many applications as well as ASL, it may be desirable to at least maintain consistent signal attenuation across all slices. To this end, two or three extra slices next to the first slice may be excited with the same slice spacing immediately before the first slice imaging, and without data readout. Because, in ASL imaging, these extra imaging pulses can be placed in an inflow time of tagged blood, there will be no increase in total scan time due to the extra-slice imaging.

One limitation of the matched-phase RF pulses is that this RF design can only be applied to spin-echo sequences with a single echo but not with multiple echoes as in fast spin-echo (FSE) sequences. 90°–180° matched-phase RF pulses for a linear phase spin-echo are not suited for FSE sequences for two reasons. First, unlike spin-echo, FSE sequences must satisfy the Carr Purcell Meiboom Gil condition where the phases of the 90° excitation pulse and the subsequent refocusing RF pulses are offset by 90° with respect to each other (19,20). Our matched-phase pulses do not satisfy this condition because the 90° excitation has arbitrary phase that is compensated by the refocusing pulse, which essentially has half the phase variation of the 90° excitation. Therefore a constant phase offset is only possible if the excitation profile has a constant phase. Alternatively, a 90°–180° RF pulse pair in FSE was designed previously to deliberately achieve a nonlinear phase spin-echo in an attempt to reduce the dynamic range of signals in 3D imaging (17). Second, even if there was negligible B₁ inhomogeneity and the Carr Purcell Meiboom Gil condition was not required, only the odd echoes are usable because the even echoes would have nonlinear phase. One compromised method to incorporate matched-phase RF pulses into FSE would be to employ a series of conventional (linear-phase) 180° RF pulses after our 90°–180° matched-phase RF pulses. Although this approach may achieve some of the advantages of the matched-phase RF pair, especially when reduced flip angles are used, it may not improve the longitudinal slice profile and may not reduce the interslice crosstalk. We would also like to point out that the matched-phase approach is not applicable to sequences that do not incorporate spin echoes (such as spoiled gradient echo or gradient echo EPI). Finally, while we demonstrated the slice profile effects using a spiral readout, we anticipate that there would be similar performance improvement for spin-echo EPI. This is because the matched-phase approach only affects the excitation but not the readout portions of the imaging sequence.

Finally, we suspect that the larger temporal SD of the CBF measurements with VSASL that occur under the poor slice profile condition is because of the typical brain motion during image acquisition. In our measurements using navigators (21), the average velocity of bulk motion along superior-inferior direction is a few mm per second in healthy volunteers. This amount of motion can cause superior-inferior-directional translation on the order of 0.1 mm between each slice excitation. Large signal reduction using conventional RF, coupled with the time-varying slice offset, may be responsible for the increases the temporal SD of CBF.

CONCLUSIONS

We have demonstrated that near-contiguous multislice spin-echo imaging can be achieved by reducing substantial inter-slice crosstalk using matched-phase RF pulse design. We have applied matched-phase RF in VSASL perfusion imaging and shown that stability of ASL signal can be preserved with reduced slice spacing. Based on this, matched-phase RF pulses may have value for many spin-echo imaging applications in which near-contiguous or volumetric coverage is required.