Assessing the Dosimetric Impact of Real-Time Prostate Motion During Volumetric Modulated Arc Therapy

Abstract

Purpose

To develop a method for dose reconstruction by incorporating the interplay effect between aperture modulation and target motion, and to assess the dosimetric impact of real-time prostate motion during volumetric modulated arc therapy (VMAT).

Methods and Materials

Clinical VMAT plans were delivered with the TrueBeam linac for 8 patients with prostate cancer. The real-time target motion during dose delivery was determined based on the 2-dimensional fiducial localization using an onboard electronic portal imaging device. The target shift in each image was correlated with the control point with the same gantry angle in the VMAT plan. An in-house–developed Monte Carlo simulation tool was used to calculate the 3-dimensional dose distribution for each control point individually, taking into account the corresponding real-time target motion (assuming a nondeform-able target with no rotation). The delivered target dose was then estimated by accumulating the dose from all control points in the plan. On the basis of this information, dose-volume histograms and 3-dimensional dose distributions were calculated to assess their degradation from the planned dose caused by target motion. Thirty-two prostate motion trajectories were analyzed.

Results

The minimum dose to 0.03 cm³ of the gross tumor volume (D_0.03cc) was only slightly degraded after taking motion into account, with a minimum value of 94.1% of the planned dose among all patients and fractions. However, the gross tumor volume receiving prescription dose (V_100%) could be largely affected by motion, dropping below 60% in 1 trajectory. We did not observe a correlation between motion magnitude and dose degradation.

Conclusions

Prostate motion degrades the delivered dose to the target in an unpredictable way, although its effect is reduced over multiple fractions, and for most patients the degradation is small. Patients with greater prostate motion or those treated with stereotactic body radiation therapy would benefit from real-time prostate tracking to reduce the margin.

Introduction

Patient motion during radiation therapy can have a significant impact on the absorbed dose in the target (1). Random motion creates a blurring of the dose distribution. Furthermore, if the treatment modality involves fluence modulation, like intensity-modulated radiation therapy or volumetric modulated arc therapy (VMAT), an interplay effect between motion of the patient and motion of the multileaf collimator (MLC) leaves motion also exists. The combined motion of both can lead to an increased deviation in the absorbed dose.

Different strategies for dose reconstruction that take organ motion into account have been proposed and tested in phantoms (2–6). Clinically, dose reconstruction with target motion has been investigated with respect to patients with lung (7, 8), prostate (9–13), and liver (14) tumors. Concerning treatment of the prostate, the basic finding from those studies is that its motion during radiation therapy is unpredictable (15), suggesting that the interplay effect needs to be fully accounted for to achieve accurate dose reconstruction.

In this report we propose a new strategy for reconstructing the delivered prostate dose during VMAT treatment. There are 2 main novel aspects compared with previous work. First, we accurately model the interplay effect by establishing the temporal correspondence between the MLC leaf motion and real-time target motion measured with the onboard electronic portal imaging device. Second, we calculated the aperture-specific 3-dimensional (3D) dose distribution for each control point individually, using an in-house—developed Monte Carlo simulation tool and accumulated the dose from all control points in the plan to estimate the delivered target dose. The method was applied to assess the dosimetric impact of prostate motion during VMAT.

Methods and Materials

Patient treatment

Clinical volumetric modulated dose plans were optimized with Eclipse (Varian Medical Systems, Palo Alto, CA) and used for radiation therapy with curative intent of 8 patients with locally advanced prostate cancer. The gross tumor volume (GTV) was the prostate. The planning target volume (PTV) was constructed by expanding the GTV with a margin of 5 mm except at the posterior face of the rectum, where it was 2 mm. In some cases, the 5-mm margin was also modified to spare other organs at risk. Patients were treated with 2 modulated arcs, with a prescribed dose of 78 Gy delivered in 39 fractions, except for 2 patients who were prescribed 76 Gy and 50 Gy (2 Gy in each of 38 and 25 fractions, respectively). To characterize the degree of modulation in each arc, we used the definition introduced by Li and Xing (16) for VMATarcs, modified slightly to measure the distance traveled by all of the leaves between control points, and divided it by the dimension of the field that encompasses all the control points in the direction of leaves motion and by the number of control points in the arc. Table 1 contains the data for the modulation index of the arcs used in this study.

Table 1.

Detectability of the fiducials, number of subarcs with all fiducials occluded, maximum and mean angle of these subarcs, modulation index, and number of tracked fractions

	% of images with at least 1 fiducial detectable		#osa	Max. angle	Mean angle	#osa	Max. angle	Mean angle	Modulation index		No. of tracked fractions
Patient no.	Arc_1	Arc_2	Arc_1			Arc_2			Arc_1	Arc_2
1	87.1	62.8	18	37	7	12	11	4	1.38	1.41	8
2	49.0	90.2	14	27	4	21	52	9	1.33	1.41	7
3	60.7	10.9	6	249	64	24	53	7	1.84	1.84	7
4	65.5	44.9	12	59	15	9	50	14	1.59	1.48	2
5	85.4	41.7	15	45	14	12	12	4	1.81	1.60	4
6	77.5	24.4	10	147	24	16	20	5	2.25	2.28	1
7	82.4	13.7	10	164	36	15	18	4	1.53	1.22	2
8	39.9	64.3	18	45	8	16	54	14	2.16	2.01	1

Prostate tracking and trajectory determination

All patients were treated with 2 VMAT arcs (18). Four of the patients had weekly cine megavoltage (MV) imaging during the whole treatment, and the remaining patients had between 1 and 4 sets of images taken on different days (Table 1). The images were acquired at a rate of approximately 5 frames/s during the whole treatment fraction. We determined the trajectories followed from the prostate using an automatic fiducial detection algorithm for tracking and motion assessment (17, 18), calculating the 3D displacements from 2-dimensional (2D) measurements according to (19).

Thirty-two different prostate motion trajectories were tracked. The number of fiducials implanted in the patient for tracking was 3 in all cases. Patients were positioned by the acquisition of 2 orthogonal kilovoltage images followed by 2D/2D matching. The delay between positioning and the start of treatment was around 60 seconds. Because VMAT used dynamic leaves motion, fiducials were occluded during part of the treatment time (18), which could be a limitation in the application of this technique in certain patients. Table 1 contains data on the fiducial visibility and the number and extension (maximum and mean), measured in number of frames, of the subarcs with all fiducials invisible in the plans used. Our approach was to use, whenever possible, measured data to characterize the displacements. For the time of treatment at which each image was taken, the displacement was calculated as the average of the displacements of all the fiducials localized in that frame. When no measured information was available (all fiducials were blocked), we interpolated linearly the target position between the closest measured positions.

Several motion shifts measured in subsequent images can correspond to the same control point. Whenever this situation occurred, the average value of the displacements corresponding to the same control point was taken as the motion shift with which that control point was calculated.

Dose reconstruction

The VIMC-Arc (20) system was used for the Monte Carlo simulation of VMAT plans in the selected patient dataset. The dosimetric accuracy of the VIMC-Arc system, with respect to measurement, has been previously verified (20). Briefly, the VIMC-Arc system is a front-end to the VMC++ (21) software packages, allowing the streamlined Monte Carlo simulation of radiation therapy plans that have been exported from a treatment planning system in digital imaging in communications and medicine (DICOM) format. The VIMC-Arc tool was used to provide access to the separated dose matrices for each individual arc control point.

Each patient’s dose-volume histogram (DVH) for the GTV was compared as calculated with the Eclipse treatment planning system and the Monte Carlo software to ensure good agreement of their dose calculations. The original dose matrices in both Eclipse and Monte Carlo were calculated at 2.5-mm spatial resolution in the 3 spatial directions for compromising calculation accuracy with speed. Because all the dosimetric data in this work are given for the GTV, we first cropped the dose matrices to completely encompass the target, disregarding the rest of the dose matrices. Subsequently, we increased the dose resolution to 1 mm by linear interpolation in the 3 spatial directions.

To take the real-time target motion into account, we calculated with the VIMC-Arc a 3D dose distribution separately for each of the control points (~177) in each arc. The dose resolution was increased to 1 mm to resolve very small motion of the GTV and to characterize accurately the changes in the DVH. The correspondence between the target motion and the beam aperture of a control point in which it took place was accurately established by use of the gantry angle information.

To accumulate the 3D dose distributions in the prostate resulting from all control points, the voxels in the dose matrices that lay inside the GTV contour were labeled. The dose the GTV received with no motion was available from the VIMC-Arc calculated dose matrices for the whole treatment with 1-mm resolution. When motion was considered, the target contours were projected to the dose matrices for each of the individual control points, and shifted by their corresponding displacement obtained from the fiducial tracking procedure. The dose distribution was assumed to be invariant under prostate motion. Total dose was accumulated at each of the voxels inside the GTV, and the DVH was calculated. In-house software was developed in MATLAB (Mathworks, Inc, Natick, MA) to handle DICOM objects, correlate spatially the positions of the computed tomographic images, dose matrices, and structure contours, and to calculate the DVHs.

Interplay effect over multiple fractions

To assess the practical impact of the interplay effect, we summed up the absorbed dose for the 3 patients with weekly cine MV imaging. On that basis, we calculated the DVH and the V_100% and D_0.03cc. In addition, we simulated the dosimetric effect of random prostate motion by breaking the exact synchronization between the motion track and the plan delivery in a trajectory with relevant motion. We shifted the motion trajectory every 4 seconds to obtain 31 simulated fractions and calculated the maximum, minimum, mean, and standard deviation for V_100% and D_0.03cc. We also calculated the DVH for the average dose over these tracks.

We studied the correlation between the mean absolute displacement when motion exceeded the prostate-to-PTV expansion (5 mm) (the mean value and also multiplied by its duration) and V_100% and D_0.03cc.

Results

Dose reconstruction in single fractions

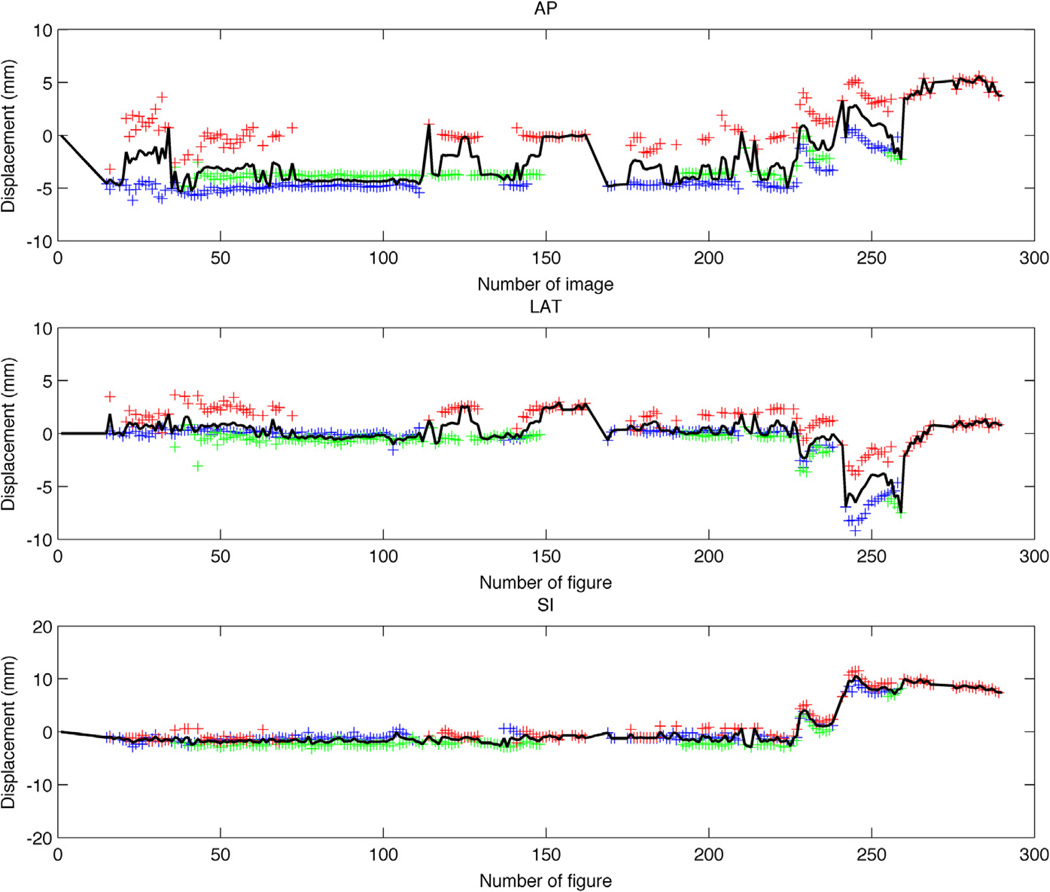
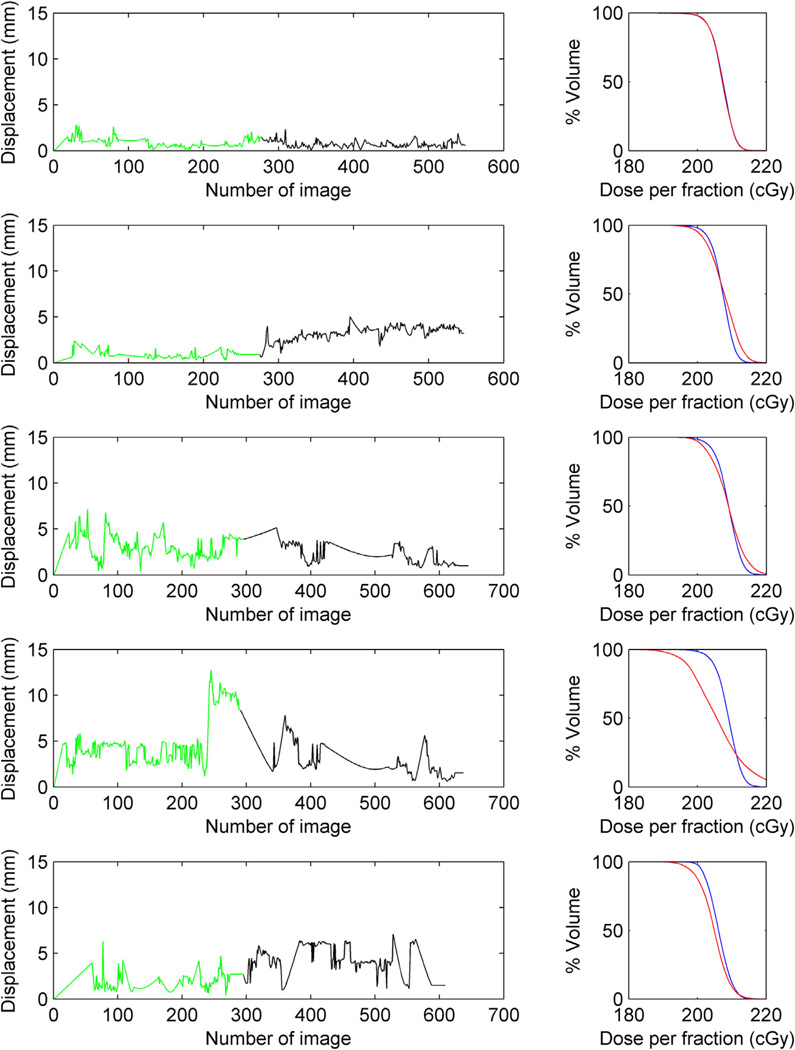
Good agreement was found between dose calculations with Eclipse and VIMC-Arc. Figure 1 displays the 3D prostate motion trajectory determined from the MV localizations of the 3 fiducials for 1 arc. The deviations in the motion tracked by the 3 fiducials could be attributed to different causes: uncertainty in fiducial localization resulting from its dimensions (length is 5 mm), prostate rotation, or prostate deformation. Figure 2 presents 5 different trajectories of 3 patients. They correspond to single fractions, and the DVHs are displayed to compare the situations with and without motion. The trajectories were characterized by the mean absolute displacement when it was larger than the prostate-to-PTV expansion. The DVH degradation was calculated and compared for each trajectory with the calculated DVH with no motion. Figure 2 presents the determined target trajectory for those 5 fractions, with the GTV DVH, compared in the case of no motion and taking into account the measured motion. It can be clearly seen that motion produced DVH degradation for the GTV.

Figure 1.

Trajectory determination from 2-dimensional (2D) fiducial positions measured with electronic portal imaging device cine MV imaging. The blue, green, and red crosses represent the positions of the 3 fiducials as derived from their 2D localization. The black solid line corresponds to the determined prostate displacement. AP = anteroposterior; LAT = lateral.

Figure 2.

Gross tumor volume dose-volume histogram (DVH) degradation for 5 different prostate trajectories measured in 3 different patient treatments. The green and black lines represent the trajectories for the 2 volumetric modulated arc therapy arcs. If the beam targeting is good (row 1), no significant degradation is seen in the DVH (planned DVH depicted in blue and delivery DVH depicted in red in the right column). In all the other trajectories, motion has an impact on the absorbed dose in the GTV (prostate).

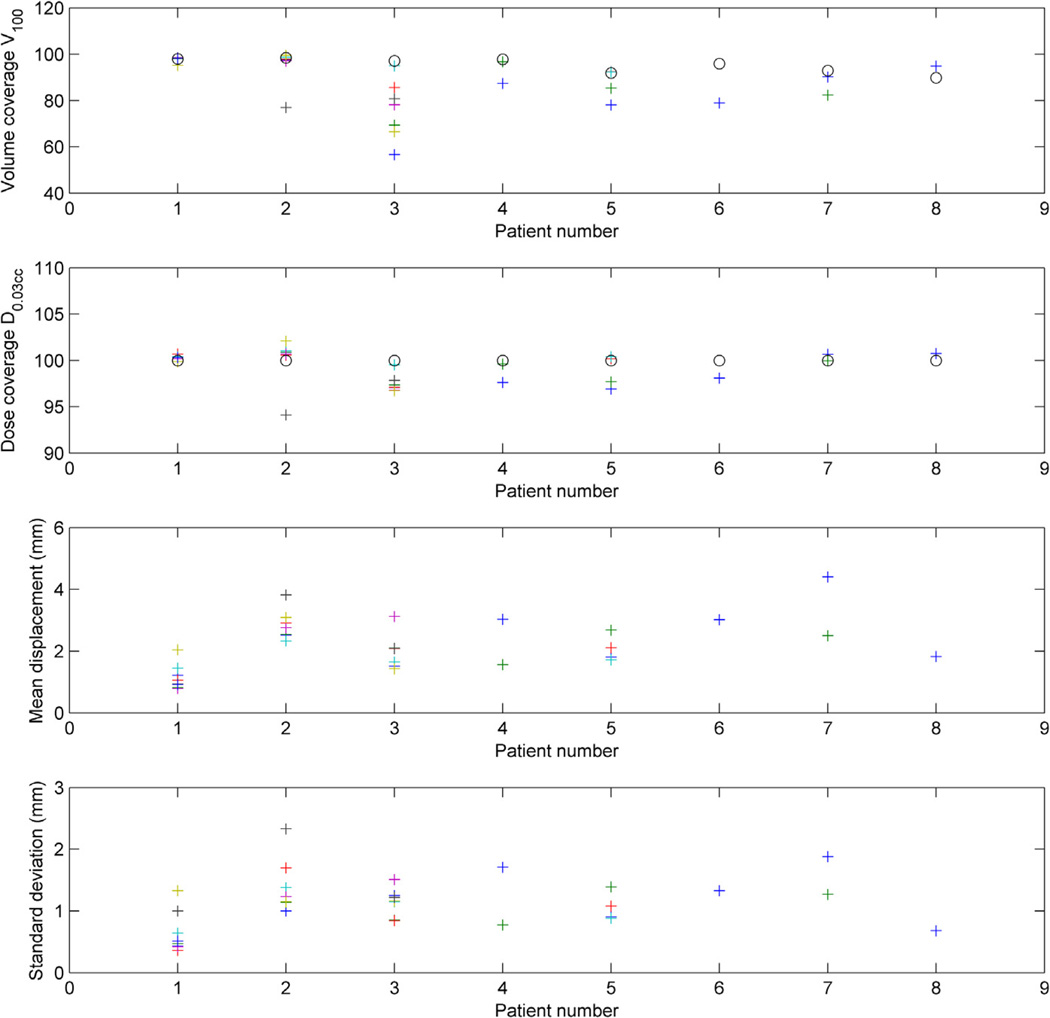
For each of all the patient trajectories, we reported the volume covered by the prescription dose (V_100%), the minimum dose that irradiates 0.03 cm³ of the target volume (D_0.03cc), and the mean shift displacement data with its standard deviation. This data are shown in Figure 3.We found no correlation between all patients and fractions mean absolute motion and dose degradation (V_100% and D_0.03cc). When we took into account motion when it was bigger than the prostate-to-PTV expansion, the correlation coefficients r were −0.47 and −0.46, respectively. We found no correlation between dosimetric outcome and mean absolute displacement exceeding prostate-to-PTV margin times its duration.

Figure 3.

Volume covered by the prescription dose (V_100%, first row), minimum dose that irradiates 0.03 cm³ of the volume (D_0.03cc, second row) normalized to the planned D_0.03cc as 100% reference, and mean displacement along the treatment fraction for each fraction (third row) with its standard deviation. The circles in the 2 upper rows represent the planned values, and the crosses the actual values for each of the fractions, for the 8 patients.

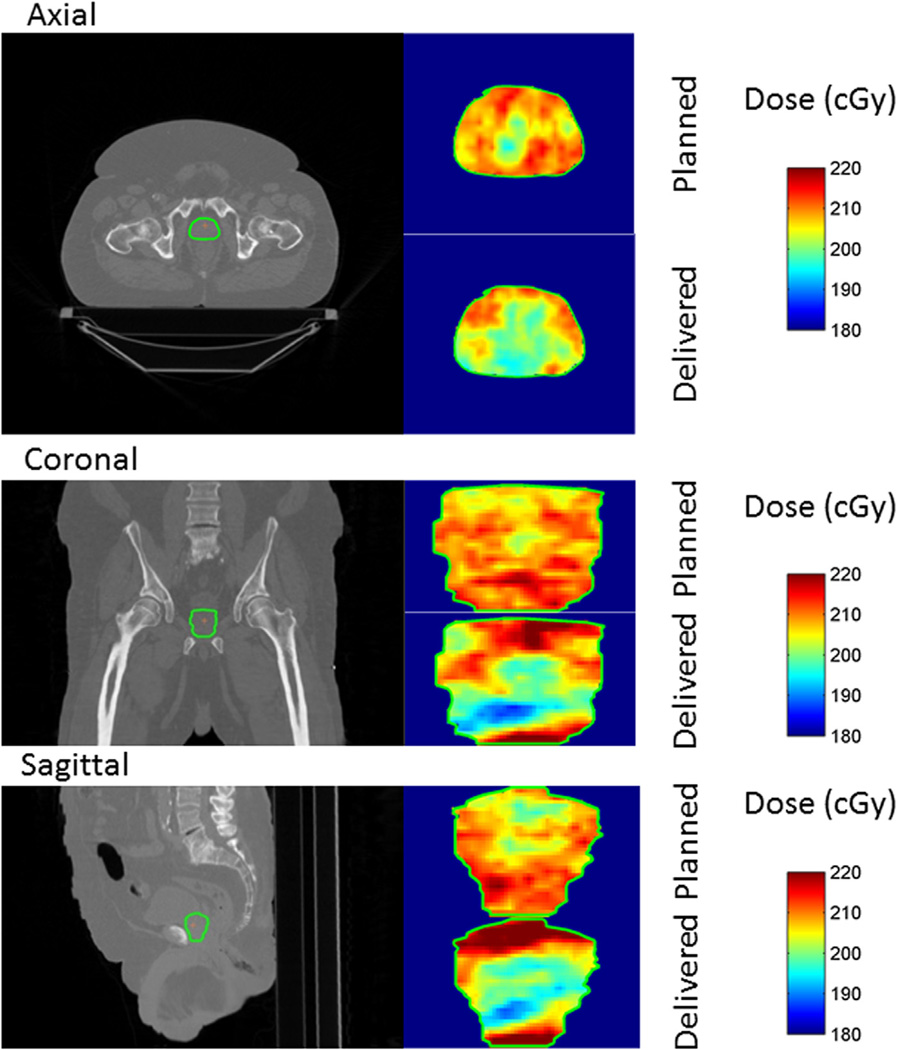
We also present in Figure 4 the dose distribution changes caused by motion in the GTVin only 1 fraction, for the case represented in Figure 2, row 4. In this case the interplay between the motion of the tumor and the leaves can be seen in the degradation of the dose distribution, where the cold spots lay in the inner part of the tumor. The percentage differences in the delivered dose with respect to the planned dose were within (−15.7; 13.2). Interplay effect can affect the absorbed dose in a counterintuitive way, as shown in Figure 4, where the minimum dosage is in the inner part of the tumor.

Figure 4.

Dose distribution reconstructed in the target by accumulating the dose due to each control point in each voxel. The axial, coronal, and sagittal slices are taken through the isocenter, depicted by the orange cross. The interplay effect can be seen, affecting the absorbed dose received in the inner part of the tumor. This dose reconstruction corresponds to the treatment fraction with the trajectory seen in Figure 2, row 4. The underdosage of the tumor in this fraction is significant, with some points receiving close to 10% less of the prescribed dose in the target.

Interplay effect over multiple fractions

Table 2 displays the interplay effect with the delivered dose averaged over multiple fractions as compared with the planned dose. In patients 1 and 2, the averaged DVH was essentially the same as the planned DVH, and patient 3 had a slight degradation in the averaged DVH.

Table 2.

V_100% and D_0.03cc averaged over 8 (patient 1) or 7 (patients 2 and 3) fractions

Patient no.	V100% (delivered/planned)	D0.03cc, Gy (delivered/planned)
1	98.4/98.0	75.3/74.8
2	99.7/98.5	77.5/75.8
3	88.7/97.2	75.4/76.2

For the trajectory depicted in Figure 3, row 4, we calculated the V_100% and D_0.03cc for the averaged dose distribution over the trajectory shifted 31 times. The values are basically the same with respect to the planned values. Among all the shifts, the standard deviation for V_100% was 6.8%; for D_0.03cc it was 1.6%.

Discussion

The unpredictable prostate motion and complex motion of MLC leaves in VMAT demands an accurate temporal correlation between the 2 factors to take into account the interplay effect. This effect is accurately modeled with our method by accumulating the dose for each control point, improving the accuracy of conventional convolution-based approaches (13, 22, 23). Whereas the use of PDF for estimation of motion effect could be useful to statistically estimate the effect of the interplay effect, our method provides a way to perform its effect based on actual interplay, and it paves the way for the clinical introduction of treatment adaptation. The method proposed in this work is general and could be extended to other modalities such as kilovoltage (kV) fluoroscopy tracking (24, 25) or intensity-modulated radiatin therapy delivery technique.

Interplay may be the reason for degradation in the GTV, even though the PTV encompasses the GTV with motion margin. Limiting the patient motion would limit the dose delivery uncertainty, as can be seen in Figure 3, where the patient with better beam targeting (patient 1) has the less spread in V_100% and D_0.03cc values. In our analysis, it can be seen that for most of the patients and fractions, the dose degradation is small. The parameter D_0.03cc assessed after motion is, in general, very close to its planned value. Furthermore, the effect of using a large number of fractions would average this effect (10, 12). Our study on the average interplay effect showed that within a few (7 of 8) fractions, the effect is reduced. The average of a track with significant motion shifted 31 times also shows that random motion is not expected to degrade the planned dose, when the treatment takes several fractions. However, interplay effect may be of concern when stereotactic body radiation therapy (SBRT) is used to treat prostate cancers with hypofractionation. SBRT is a promising technique for improving the treatment of patients with prostate cancer (26–28).

Our results show that motion increases the dose delivery uncertainty. A somewhat unexpected result appears for some fractions, for which a small amount of motion (within margins) seem to improve the DVH slightly. This can be attributed to a consequence of inverse planning, for which a higher fluence is a result of demanding good coverage in the tumor boundaries (area affected by the beam penumbra). With larger motion, the consequence is, in general, that dose degradation appears.

Patient 3 has a relatively large spread of V_100% values, although the D_0.03cc values are quite close to their planned values. This could be explained by a very homogeneous dose distribution in the GTV.

Fiducial occlusion has an impact on the suitability of patients for cine MV tracking. It hinders the accuracy of the tracking and the validity of the linear approximation for estimating the tumor position where no fiducial is visible. In treatment planning it is possible to foster the appearance of at least 1 fiducial (17, 29). In addition to this, MV detection can be combined with on-board kilovoltage to improve tracking (30). Nevertheless, the appropriateness of the VMAT plans in individual patients should be determined to use cine MV tracking.

The dose reconstruction scheme was based on the assumption of translation motion without rotation and no GTV deformation. This assumption was expected to be valid in the absence of severe inhomogeneities and for relative small displacements (of the order of several millimeters), which are fulfilled in most patients with prostate cancer. If large rotation or deformation of the tumor occurs, their effects need to be accounted for in the dose reconstruction procedure. Another extension would be to include in the analysis the actual parameters of the delivered treatment as recorded in Varian Dynalog files. This technique for dose reconstruction was proposed by Qian et al (31) to evaluate the impact of the actual treatment delivery on the planned dose. The combined procedure for dose reconstruction including motion and delivery parameters would be a useful tool for adaptive radiation therapy.

Conclusions

A method has been developed for accurate dose reconstruction of moving targets during VMAT treatments. The interplay effect affects the delivered dose in an unpredictable way. Fractionation reduces the amount of interplay effect, but it could become a concern for SBRT treatment with very few fractions. Patients with greater prostate motion or those treated with SBRT would benefit from real-time prostate tracking.

Summary.

We propose a strategy for accurate dose reconstruction in patients with prostate cancer with real-time tumor tracking during volumetric modulated arc therapy. By establishing the temporal correspondence between target motion and beam aperture shape, we are able to fully take into account the interplay effect between the 2 factors. We applied the strategy to assess the impact of target motion on dose coverage for multiple patients and fractions, calculating the dose-volume histograms and dose distribution degradation, and the V_100% and D_0.03cc changes.