Modeling Social Dimensions of Oral Health Among Older Adults in Urban Environments

Abstract

In both developed and developing countries, population aging has attained unprecedented levels. Public health strategies to deliver services in community-based settings are key to enhancing the utilization of preventive care and reducing costs for this segment of the population. Motivated by concerns of inadequate access to oral health care by older adults in urban environments, this article presents a portfolio of systems science models that have been developed on the basis of observations from the ElderSmile preventive screening program operated in northern Manhattan, New York City, by the Columbia University College of Dental Medicine. Using the methodology of system dynamics, models are developed to explore how interpersonal relationships influence older adults’ participation in oral health promotion. Feedback mechanisms involving word of mouth about preventive screening opportunities are represented in relation to stocks that change continuously via flows, as well as agents whose states of health care utilization change discretely using stochastic transitions. Agent-based implementations illustrate how social networks and geographic information systems are integrated into dynamic models to reflect heterogeneous and proximity-based patterns of communication and participation in the ElderSmile program. The systems science approach builds shared knowledge among an interdisciplinary research team about the dynamics of access to opportunities for oral health promotion. Using “what if” scenarios to model the effects of program enhancements and policy changes, resources may be effectively leveraged to improve access to preventive and treatment services. Furthermore, since oral health and general health are inextricably linked, the integration of services may improve outcomes and lower costs.

The aging of the U.S. population exacerbates the need for geographically coordinated allocation and cost-effective utilization of health resources, particularly in poor urban environments. Oral health outcomes among older adults reflect a complex set of causal pathways and time delays that compound inequities over the life course (U.S. Department of Health and Human Services, 2000). These inequities manifest at multiple scales: at the neighborhood scale in access to medical and dental health care, at the interpersonal scale in normative health behaviors such as oral hygiene practices, and at the individual scale in terms of related health outcomes such as diabetes, cardiovascular disease, and cognitive impairment. At the community level, oral health promotion such as the preventive screening services offered by the ElderSmile program operated by the Columbia University College of Dental Medicine can help older adults obtain treatment to mitigate or avoid oral conditions that cause discomfort, reduce the ability to chew, and impede social interaction (Marshall et al., 2009). ElderSmile participants are now being screened for diabetes and hypertension as well as for oral health conditions such as coronal and root caries, periodontitis, and oral cancer.

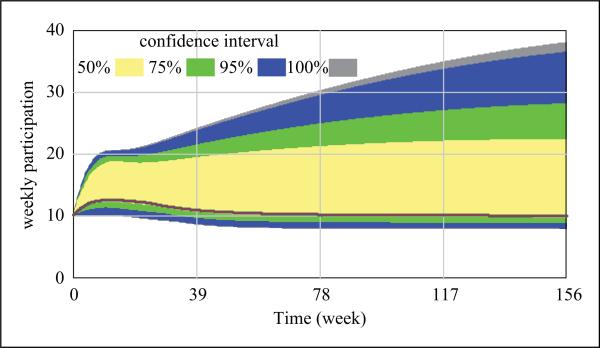
A detailed causal hypothesis was developed to express the reinforcing feedback loops that are likely to be induced with age at both the individual and interpersonal scales (Metcalf, Northridge, & Lamster, 2011). In this conceptual model, availability of social support is implicated in oral health along with individual-level considerations such as chronic illness and nutrition-related dynamics. The central hypothesis of this study is that social engagement positively affects oral health outcomes among older adults in urban environments. In particular, those who participate in preventive screening events are socially active by virtue of their presence at senior centers. The sociality of participating seniors helps explain why their oral health outperforms the U.S. national average, despite the persistence of inequities and unmet need for medical and dental care (Northridge et al., 2011). Issues of access are key to understanding oral health outcomes, as recent utilization of dental care correlates with improved self-rated oral health among ElderSmile participants (Northridge et al., 2012). Because ElderSmile observations reflect social behavior and exclude the experiences of more socially isolated adults, a simulation methodology provides a complementary way to consider a wider range of social behavior in communicating about preventive screenings, including extreme conditions of social isolation. In this way, models that simulate communication are more generalizable than the specific empirical context they are designed to represent. The degree of communication, or contact rate, is varied to produce different participation scenarios (see Figure 7 below) and can be extended to include changes in social support among older adults over time.

Figure 7.

Sensitivity testing of Model B produces a wide range of simulated participation outcomes from variation in contact rate (see text for full description).

Methodology

This simulation study is informed by spatial analysis of peer-group density integrating U.S. Census (hereafter Census) data and participant data from the ElderSmile preventive screening program in northern Manhattan. The significance of interpersonal relationships on individual oral health outcomes is revealed in distinct empirical patterns. These patterns serve both to guide model development and to test model utility (Grimm & Railsback, 2005). Recent research indicates that participants who reside in places with a higher spatial density of older adults report better self-rated oral health than those who are more isolated from their peer age group (Widener et al., 2012). The correlation between concentrations of older adults and positive self-reported oral health corroborates our hypothesis of positive social effects on individual oral health outcomes.

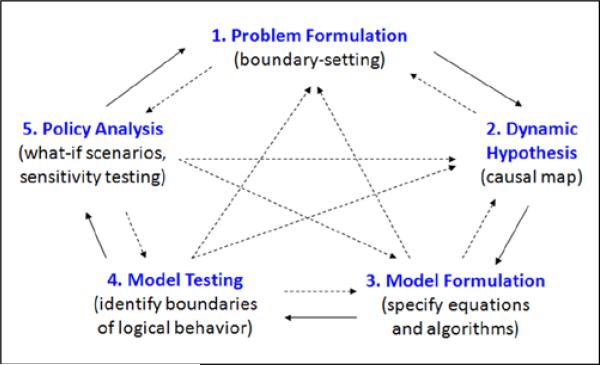
This study employs systems science to facilitate knowledge sharing among members of the research team (Mabry, Olster, Morgan, & Abrams, 2008). Because the process of modeling in the tradition of system dynamics is iterative (Figure 1), the construction of a set of models to address different aspects of a problem may be a useful strategy for handling system complexity (Ford, 2009; Sterman, 2000). The major steps in this process are the following: (1) problem formulation and boundary setting, (2) drawing a dynamic hypothesis in the form of a causal map, (3) building a computer model with equations and/or algorithms, (4) testing the logic and limitations of the model, and (5) exploring alternative assumptions and policies. As shown in Figure 1, the progression is often recursive in that each step can lead forward or backward to other steps during the modeling process.

Figure 1.

The iterative process of dynamic modeling.

A portfolio approach provides multiple entry points and checkpoints to the modeling process, facilitating input from different team members. As a collaborative effort, the team collectively determines which aspects of the ElderSmile operation provide interesting simulation experiments. A further benefit of the portfolio approach for a collaborative research context is that team members can work in parallel to develop models in different ways, exploring the simulated consequences of alternative assumptions.

Modeling Word of Mouth

This section introduces a set of three model structures, describes their behavior, and discusses insights and challenges associated with their implementation. All the models presented in this portfolio include balancing feedback effects, although the conceptual model that launched this study identified only reinforcing feedback effects likely to be triggered with age (Metcalf, Northridge, et al., 2011). Both the conceptual and computational models function as “boundary objects” in that they provide starting points for discussion about the problem and thereby facilitate team communication about project scope and underlying assumptions (Star & Griesemer, 1989). In this case, the boundary is the juxtaposition between distinct disciplines and institutions of team members, and the boundary object is an idea being passed between team members from these different disciplinary and institutional backgrounds. Using model representations and results as seeds for communication among members of the research team enables development of experiments relevant to the operation of ElderSmile.

As depicted in Figure 1, this research uses the system dynamics modeling process to hypothesize and simulate feedback relationships that link structure with behavior over time. According to the system dynamics principle of accumulation, all dynamic behavior occurs when flows accumulate in stocks that indicate the state of the system. Mathematically, stocks represent integrals that increase or decrease according to their respective in- and out-flow rates. Stock and flow models thus signify systems of ordinary differential equations connected via reinforcing or balancing feedback mechanisms.

In other modeling approaches, assumptions about social structure may be encoded with discrete agents and events. While stocks often represent aggregate or average characteristics of a population, simulation of individual agents enables consideration of heterogeneous attributes. To incorporate heterogeneous geographies and social networks, the portfolio developed in this study includes agent-based models (ABMs) as well as the stock and flow models characteristic of traditional system dynamics (SD). These models simulate dynamics at distinct spatial and temporal scales: Model A-SD and Model A-ABM both represent health-seeking behavior of older adults across New York City and operate at the scale of a day; Model B (SD) is aggregated for northern Manhattan and simulates ElderSmile participation on a weekly basis; and Model C (ABM) simulates each of the screening centers and Census blocks of northern Manhattan and operates on an hourly scale. Pattern-oriented modeling provides a strategy for aligning detail-rich ABMs with diverse data sources. Where empirical data are available at the individual level, a 1:1 correspondence enables precise parameterization of ABMs, as in the case of Model A-ABM for participants and in the case of Model C for screening centers.

The use of these multiple model structures and distinct (SD and ABM) paradigms enables triangulation among different ways of considering the problem of oral health among older adults. This triangulation expands the possibility space of virtual experiments that can be conducted and facilitates the collaborative modeling process, providing multiple opportunities to improve the behavioral assumptions implicit to a particular implementation. The models in this portfolio are all in active use and are presented below in chronological order of their development.

Model A-ABM and Model A-SD: Diffusion of Oral Health Care–Seeking Behavior Through Word of Mouth

The first modeling platform includes Model A-ABM and Model A-SD, which implement a basic diffusion process involving three states: without health care, seeking health care, and receiving health care. As word of mouth about opportunities to receive health care spreads among the population, more people enter the states of seeking and receiving health care. Transitions from the states of receiving and seeking health care back to the state of being without health care are also included. As with the classic Bass (1969) model of S-shaped diffusion over time, an outreach/advertising effect as well as a word of mouth effect is included.

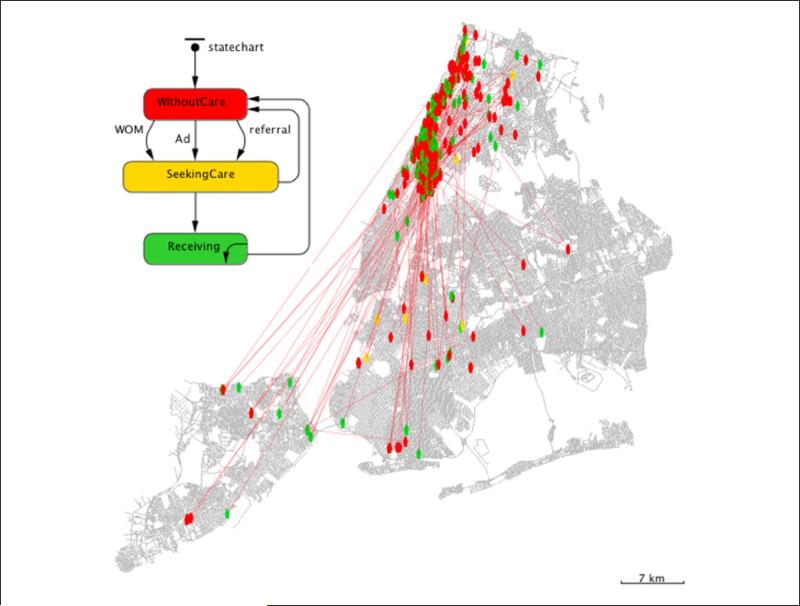
Model A-ABM (Figure 2) and Model A-SD (Figure 3) are formulated separately and respectively as ABM and SD models for comparative purposes. Model A-ABM includes a geographic dimension defined by the assignment of agent locations on the basis of ElderSmile participant residences. The inclusion of geographic context enables consideration of distance between agents as an influence on social behavior. To enable communication through word of mouth, the simulated agents are wired with a social network (Figure 2) that utilizes both proximity effects and small-world (Watts, 1999) algorithms to determine whether a connection between agents exists. Furthermore, since a 1:1 correspondence exists between simulated agents and empirical observations for participants, each agent contains a set of teeth parameterized by the dental caries status of the participant, as measured by the DMFT (decayed, missing, filled teeth) evaluation from the ElderSmile screening. Although such a micro-level of empirical resolution creates a platform from which the dynamics of tooth decay could be directly simulated, the research team agreed to center the focus of experimentation on the social dynamics relevant to oral health outcomes.

Figure 2.

Agent states and social networks of simulated ElderSmile participants in Model A-ABM (see text for full description).

Figure 3.

Model A-SD stock and flow structure for social diffusion of oral health care–seeking behavior (see text for full description).

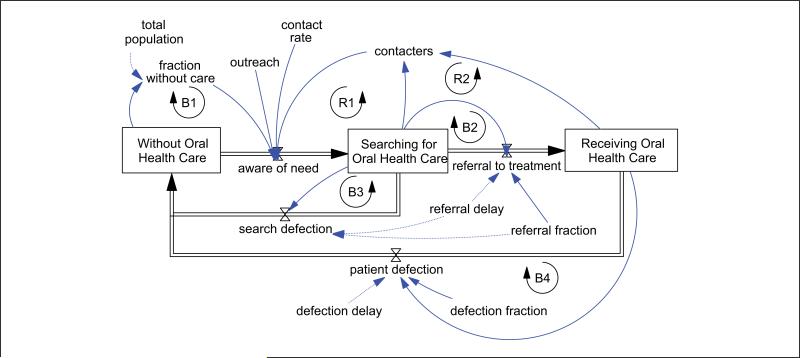
The stock and flow implementation of Model A-SD is outlined in Figure 3, in which reinforcing feedback (R1 and R2) from word of mouth encourages care-seeking behavior, whereas balancing feedback (B1) arises from saturation of the population of older adults in the community. Inverse relationships are depicted with a dotted arrow, while direct relationships are depicted with a solid arrow in Figure 3. Parameters such as outreach and contact rate also modulate the “aware of need” flow of a potential population to the state of searching for oral health care. Once members of the population are searching for oral health care, a referral fraction and delay is applied to determine the flow to a state of receiving health care. The referral to treatment flow is governed by changes in the population searching for health care, as evidenced through balancing loop B2. The extent of diffusion is limited by flows back to the state of being without care, which are based on exogenous fractions and delays applied to the population searching for and receiving health care, via the balancing loops B3 and B4.

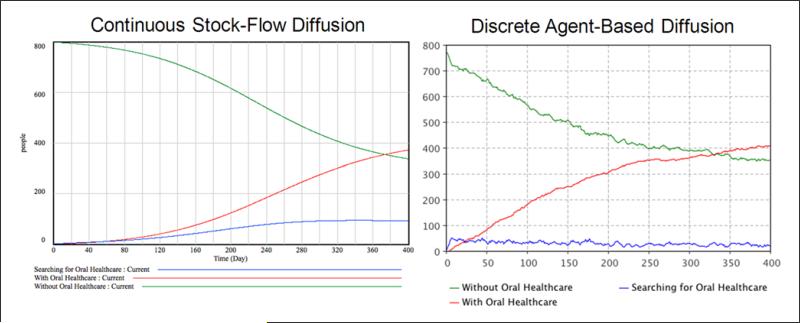
As illustrated in Figure 4, broad similarities exist for Model A-SD and Model A-ABM in both extent and timing of diffusion. A slight but noticeable difference appears in the nature of the curves, namely, a smooth S-shaped curve for the stock-flow model versus the noisier saturation curve associated with the agent-based model. In simulation, both continuous (stock and flow) and discrete (agent-based) diffusion patterns show an increase in patients receiving oral health care as referrals and word of mouth are transmitted to the population without care. The pattern of those receiving care is smooth in the continuous case, whereas simulation of a small-world network of discrete agents produces discontinuous shifts, such as the initial adjustment in the population searching for oral health care. In both Model A-SD and Model A-ABM, the population without access decreases over time as the number of adults receiving care increases.

Figure 4.

Simulation outcomes from stock-flow Model A-SD and agent-based Model A-ABM (see text for full description).

Model B: Word of Mouth About Preventive Screening Opportunities

To further develop the complexity of the feedback structure articulated in Model A-SD, Model B was introduced in Metcalf, Widener, et al. (2011) as a dynamic stock and flow model of preventive screening that includes the deterrent effect of long wait times on participation, as well as the reinforcing effect of positive word of mouth among older adults. This model emphasizes the particular preventive screening structure embodied by ElderSmile as a form of oral health promotion. In addition to the reinforcing dynamic of word of mouth and the balancing dynamic of saturation among the potential population, Model B includes additional balancing feedback with delays from the effects of perceived and actual availability.

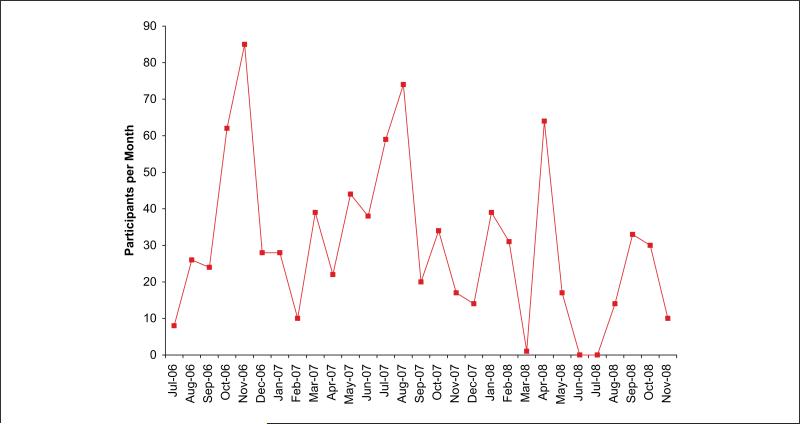
Under the system dynamics method, temporal reference modes for key variables are defined as a part of problem formulation (Step 1 in Figure 1). Such a temporal pattern of participation is plotted in Figure 5 at the monthly scale for ElderSmile workshops held from July 2006 through November 2008 at any of the 27 senior centers involved during that time (there are now 49 senior centers participating in the ElderSmile network). The dynamic reference mode presented in Figure 5 was constructed as part of an analysis demonstrating that the extent of ElderSmile participation depends on the number of workshops offered in a given month (Metcalf, Widener, et al., 2011). Nonetheless, a wide variation in ElderSmile participation exists, even when normalized by the number of workshops held by the program.

Figure 5.

Oscillatory dynamics of participation in ElderSmile preventive screening workshops.

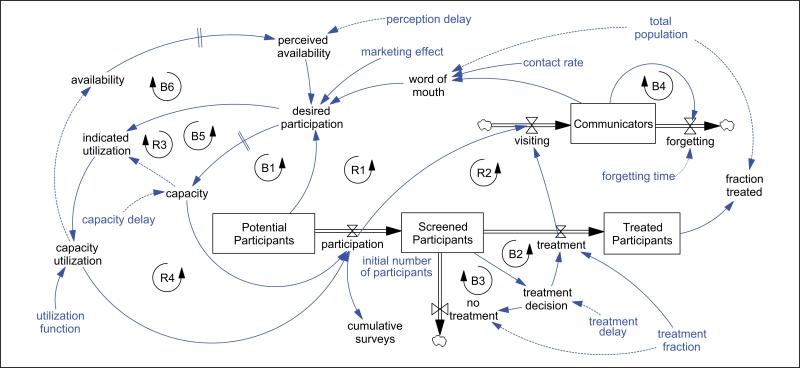
Because of the oscillatory nature of the reference mode for participation in ElderSmile workshops, delayed perception effects were included in Model B to explore whether the ElderSmile program might be characterized with an El Farol dynamic (Arthur, 1999). The El Farol problem is named for a bar in Santa Fe, New Mexico, that has a weekly Irish night. Arthur (1999) posed a thought experiment: if a potential Irish bar-goer (such as himself) wished to avoid a crowd and anticipated the likelihood of a crowd based on recent experience, oscillatory behavior would result from commonly held expectations about the system. The El Farol logic is encoded with balancing loop B6 in Figure 6: a delay (indicated with a double hatch mark) between actual and perceived availability modulates desired participation in ElderSmile screenings. Balancing feedback with delays is capable of inducing oscillatory El Farol behavior. Desired participation is diminished with lingering perceptions of unavailability, as with the bargoer intent on avoiding a crowd at El Farol's Irish night.

Figure 6.

Model B includes balancing feedback for adjustment of ElderSmile resource capacity and perceived availability (see text for full description).

Figure 6 shows additional feedback loops included in Model B (as compared to Model A-SD in Figure 3) to account for forgetting (B4) and endogenous capacity adjustments in response to desired participation (R3 and R4). Balancing loops B1 and B5 provide a saturating effect from increased participation of the potential population of older adults in northern Manhattan. As with the notation in Figure 3, dotted arrows in Figure 6 indicate inverse relationships, whereas solid arrows denote direct relationships between elements. As indicated in Figure 6, the transition from screening to treatment in Model B is modulated by an exogenous parameter for treatment delay. However, this delay could be represented as an endogenous function of treatment capacity, much as screening capacity affects participation in the program. This study deliberately emphasizes screening rather than treatment in accordance with the emphasis of the ElderSmile operation. Most ElderSmile participants are referred to treatment at their own dentists rather than one of the three ElderSmile treatment centers. Including the balancing effect of limited treatment capacity on longer delay times would pertain to scenarios in which screening is so successful that the new referrals overload treatment capacity downstream and as such is one of several potential model extensions.

Sensitivity testing of the contact rate parameter in Model B is illustrated in Figure 7, with the shading indicating the confidence intervals for the range of outcomes shown. These tests reveal the wide range of participation induced by variations in the contact rate, which provides the basis for communication about oral health services. The significance of contact rate on simulated ElderSmile participation provides impetus to represent different levels of sociability for different people, as enabled by the agent-based forms of Model A-ABM and Model C. Although the initial transient in Figure 7 shows slight oscillation, the degree of oscillation indicated by the reference mode in Figure 5 has not been replicated for Model B. While a preliminary version of Model B did produce oscillation, this behavior was attributed to an error in defining the time interval, an issue that has since been resolved as part of model boundary testing (Step 4 in Figure 1).

While the El Farol problem could be analogous to the ElderSmile program, the capacity for Arthur's El Farol dynamic is fixed, based on the size of the bar and the constant (weekly) frequency of the Irish night. Although Model B also simulates at a weekly frequency, the actual ElderSmile workshops are not evenly distributed throughout the year and are held at diverse geographic locations among a growing number of participating senior centers in northern Manhattan. Although the number of workshops per month varies, the endogenous screening capacity adjustment mechanism in Model B is more flexible than warranted on the basis of the ElderSmile program operation. Further considerations such as the level of external funding, the cost of program resources, and the effect of treatment capacity would more realistically constrain the range of simulations feasible under Model B.

Model C: Multiscalar Agent-Based Model With Empirical Preventive Screening Availability

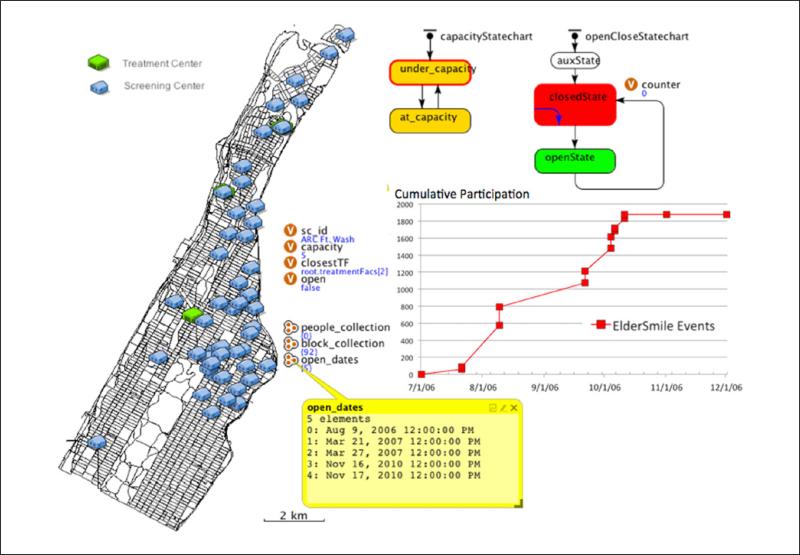
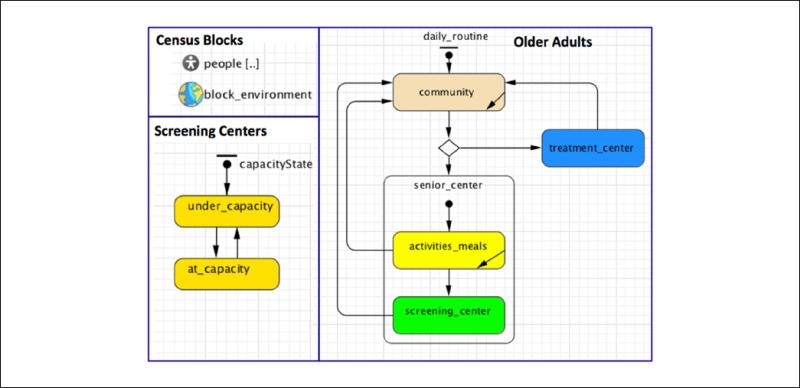
A third model was developed to explore some of the mechanisms simulated in Model B around ElderSmile capacity and utilization at a finer scale. In Model C, agents are simulated in four classes: older adults (potential ElderSmile participants), screening centers, treatment facilities, and Census blocks. All agents have a geographic context. Figure 8 illustrates the Census blocks, screening centers, and treatment facilities (two of which are partially obscured by screening centers) as visualized in the AnyLogic simulation of Model C. Because the simulated older adults officially reside at the centroid of their Census block, and because so many adults are simulated, the locations of agents representing older adults are not visualized during simulation of Model C (Figure 8). Structures for the Census blocks, screening centers, and older adults in Model C are depicted in Figure 9. The Census blocks encapsulate the set of older adults who reside therein. Simulated older adults visit screening centers and treatment facilities on the basis of proximity, daily routines, word of mouth, and referrals. ElderSmile workshops are scheduled as discrete events on the basis of the actual schedule for each screening center (e.g., the list of dates highlighted in Figure 8). As indicated in Figures 8 and 9, the relevant states of a screening center are whether or not it is open to host the ElderSmile program and whether it is operating at or under capacity.

Figure 8.

Model C simulates ElderSmile participation among 49 prevention, that is screening, centers (see text for full description). Note that the ElderSmile workshop schedule for one center is highlighted here.

Figure 9.

Multiscalar agent structures in Model C: Census blocks, screening centers, and older adults (see text for full description).

In contrast to Model A-ABM where the agents were defined directly from ElderSmile participation records (Figure 2), Model C simulates older adults on the basis of Census demographics and locates them at the centroid of the block in which they reside. Specifically, the number of adults 65 years and older is extracted from Census data to simulate potential participants in the ElderSmile program. Each block is equipped with a small-world network environment used to connect the resident agents. These connections facilitate word of mouth about preventive screenings. Each of the simulated older adults behaves according to the state chart outlined in Figure 9. Stochastic decision rules govern whether nearby agents visit a senior center during an ElderSmile workshop and whether they communicate to their peers about the program.

The resolution of Model C at the scale of the screening center enables comparison of simulated with actual participation in ElderSmile workshops. The hourly time scale is furthermore consistent with ElderSmile operation and enables simulation of deterrent effects on participation from factors such as long wait times, as well as amplifying effects from communication about the program. Alternative scenarios include workshops scheduled close in time or at regular intervals, as well as effects of screening at different locations in the ElderSmile network.

Discussion

The portfolio approach to system dynamics modeling enables the research team to interpret and triangulate between different scenarios at diverse geographic and temporal scales. The construction of a portfolio of models confers flexibility to the modeling process and is especially conducive to collaboration, allowing for multiple opportunities for input and adjustment of models by different members of the research team. In addition to the three models presented in this article, several other versions exist in various states of development. Nonetheless, the portfolio described above contains the models that have proven most useful as boundary objects, or talking points, among members of the research team to date. Building models iteratively enables time to assimilate the implications and limitations of each implementation. Furthermore, the process of translating stock and flow structures into agents with probabilistic and conditional state transitions compels a review of model assumptions and a consideration of adjustments that should be made for simulation at the individual level.

The results from this portfolio of models underscore the value of representing heterogeneity of agent attributes such as contact rate that significantly affect simulated levels of participation in oral health outreach programs. Advantages of agent-based modeling include the ability to represent heterogeneous attributes and behaviors of individuals, such as contact rate and social network structures. On the other hand, causal maps and stock-flow diagrams enable clearer representation of feedback loops through visualization of relationships between elements. To benefit from the advantages of both forms of representation, the feedback structure of Model A is implemented in both agent-based (Model A-ABM) and stock-flow (Model A-SD) forms, while certain stock-flow feedback mechanisms in Model B are encoded in the discrete agent-based framework of Model C.

Although the demographics informing this study are particular to northern Manhattan, the models can be adapted to other community health contexts. Furthermore, the diffusion structures employed in all the three models are broadly based on the word of mouth mechanism of the Bass (1969) diffusion model that has been widely applied to represent the adoption of technology and ideas over time. In Model A-SD and Model A-ABM, the population shifts from a situation of lacking dental health care, to seeking care, and then to receiving care. In contrast, Model B centers on the shift from potential to actual participants in the ElderSmile program and includes feedback structures designed to create the potential for the El Farol problem of capacity and perception delays. Using a multiscalar framework, Model C simulates individual-level activities that include living in the community, attending a senior center, participating in a preventive screening program, or receiving treatment (Figure 9). Although it has the advantage of greater resolution, the hierarchy embedded in Model C also makes it slow to simulate, so it is in the process of being streamlined to enable a thorough exploration of parameter space and calibration to observed ElderSmile participation.

In shifting from the more general framework of Model A-SD and Model A-ABM, Models B and C were designed to better inform the ElderSmile operation in particular. In Model B, the decision structure of the ElderSmile program is rendered endogenous through the feedback loops that adjust screening capacity in response to increased demand. In Model C, the actual ElderSmile workshop schedule is encoded as a basis for simulating potential participation. This enables a comparison of simulated to actual ElderSmile participation for each senior center. In both Models B and C, the screening capacity levels can be adjusted in accordance with ElderSmile resources.

While the models presented in this study implement variations on a basic word of mouth diffusion structure, more nuanced considerations of social influence are feasible. For example, a number of participants in the ElderSmile program become active hubs in getting the word out during events to peers in the community via mobile phones. One such active participant illustrated how social support extends into the physical domain as she brought wheelchair-bound friends into the screening center during a recent workshop. Social dimensions include household and community support from family, friends, and caretakers. Experiences such as the loss of a spouse or partner significantly disrupt the social fabric for older adults and negatively affect the extent of their access to community-based services such as oral health promotion.

Increasing computational power and software developments have enabled a flexible range of model representations, from discrete agents to continuous stocks embedded in diverse social networks and geographic contexts. Integrating different forms of representation creates multiple opportunities for input from the research team. Exploring alternative scenarios using internally consistent assumptions enables examination of social mechanisms that contribute to observed inequities in oral health among older adults in urban environments (Institute of Medicine, 2011). For example, the wide range of participation scenarios that result from variations in contact rate for Model B (Figure 7) demonstrates the importance of considering different levels of sociability for different people as feasible for the agent-based networks of Model A-ABM and Model C. Whereas a deeper examination of social influences on oral health outcomes is ongoing, the modeling to date has captured the capacity of social networks of older adults in disadvantaged communities to leverage the resources available through health screenings.

Because all three models are in active use by the research team, this portfolio of computational platforms enables further experimentation as well as modification to reflect insights that emerge from the ongoing research. Extensions of this work involve systematic exploration of parameter space to discover parameters that factor significantly in some scenarios but not in others. When the models are sufficiently calibrated relative to observed ElderSmile participation dynamics, they will be used to assess the effectiveness and systemic cost savings of alternative, geographically explicit oral health promotion strategies (such as screening center workshop schedules, marketing, and service coordination). Potential impacts of particular program interventions are then tested by adjusting parameters that modulate accessibility to oral health care (such as dental insurance coverage and transportation options).

The specification of alternative scenarios is guided by an ongoing group model building process (Andersen & Richardson, 1997; Vennix, 1996), which in turn is informed by insights from empirical research and experience of practitioners in the ElderSmile program. A particularly relevant policy scenario (see also Milstein, Homer, & Hirsch, 2010) to explore is the impact of the Patient Protection and Affordable Care Act (2010) on Medicaid expansion in New York State (which includes adult oral health care services). This is expected to especially affect adults aged 50 to 64 years, a group now suffering from extended unemployment and loss of employer health benefits (Collins, Doty, & Garber, 2010). Moreover, further modeling research will simulate the health advantages, cost savings, and associated community benefits of aging-in-place scenarios in urban environments (Hunt & Gunter-Hunt, 1986). As such, the portfolio of models presented in this study is not an end onto itself but rather a reflection of how collaborative modeling advances dialogue for broader changes in community health.