Signal and noise of Fourier reconstructed fMRI data

Abstract

In magnetic resonance imaging, complex-valued measurements are acquired in time corresponding to spatial frequency measurements in space generally placed on a Cartesian rectangular grid. These complex-valued measurements are transformed into a measured complex-valued image by an image reconstruction method. The most common image reconstruction method is the inverse Fourier transform. It is known that image voxels are spatially correlated. A property of the inverse Fourier transformation is that uncorrelated spatial frequency measurements yield spatially uncorrelated voxel measurements and vice versa. Spatially correlated voxel measurements result from correlated spatial frequency measurements. This paper describes the resulting correlation structure between voxel measurements when inverse Fourier reconstructing correlated spatial frequency measurements. A real-valued representation for the complex-valued measurements is introduced along with an associated multivariate normal distribution. One potential application of this methodology is that there may be a correlation structure introduced by the measurement process or adjustments made to the spatial frequencies. This would produce spatially correlated voxel measurements after inverse Fourier transform reconstruction that have artificially inflated spatial correlation. One implication of these results is that one source of spatial correlation between voxels termed connectivity may be attributed to correlated spatial frequencies. The true voxel connectivity may be less than previously thought. This methodology could be utilized to characterize noise correlation in its original form and adjust for it. The exact statistical relationship between spatial frequency measurements and voxel measurements has now been established.

1. Introduction

In functional magnetic resonance imaging (fMRI), we apply magnetic field gradients to encode then measure the complex-valued Fourier transformation (FT) of the effective proton spin density (PSD) in a real-valued physical object. In fMRI, complex-valued measurements are acquired in spatial frequency space (usually two-dimensional), also called k-space from the use of the k variables for its axes (k_x, k_y). These measurements are transformed into a complex-valued image by an image reconstruction method. The most common image reconstruction method is the inverse Fourier transform. These discrete complex-valued measurements, when placed at their proper spatial frequency location, are ideally the discrete FT of the PSD. A dis crete inverse Fourier transform (IFT) is applied to the discretely measured signal to reconstruct a discretely measured PSD or image. The original object or PSD is real-valued, but due to imperfections in the imaging process, a complex-valued image of PSDs is produced (Haacke et al., 1999). These complex-valued measurements are collected to yield a complex-valued time course in each voxel. Traditional methods to detect brain activation utilize magnitude-only voxel time courses (Bandettini et al., 1993; Friston et al., 1994). Work by Menon (2002) and others indicate that the generally discarded phase portion of the fMRI voxel time courses may contain information regarding the brain's vasculature and that the entire voxel time series either in the form of real–imaginary or magnitude-phase should be used. Recently complex-valued methods to detect brain activation have been introduced (Nan and Nowak, 1999; Rowe, 2005a,b; Rowe and Logan, 2004, 2005). Preliminary work with these methods indicate that they can be used in fMRI to postacquistion suppress venous BOLD (Nencka and Rowe, 2005, 2006; Rowe, 2005c; Rowe and Nencka, 2006). These complex-valued detection methods could be combined with the current methods that connect spatial frequency measurements to voxel measurements and a more natural representation of the noise utilized.

After Fourier (or non-Fourier) image reconstruction, images are complex-valued containing a matrix of real and imaginary components of the measured effective PSD. The real part of the complex-valued measurements in each image will be stacked on top of the imaginary part of the measurements to form a single real-valued vector of measurements. A one-to-one relationship will be described between the vector of complex-valued measurements in an image and the real-valued vector with twice the dimension of stacked measurements. This one-to-one relationship or correspondence is often called an isomorphism in the mathematical literature. It is known that image voxel measurements are spatially correlated, in measured fMRI data. A property of the inverse Fourier transformation is that uncorrelated spatial frequency measurements yield spatially uncorrelated voxel measurements and vice versa. Additionally, correlated voxel measurements result from correlated spatial frequency measurements. The thrust of this paper is to relate the signal and noise characteristics of spatial frequency measurements and Fourier reconstructed image measurements. It will be shown that the true spatial correlation between voxel measurements could be inflated by correlated noise of spatial frequency measurements and that this correlated noise between spatial frequency measurements could be adjusted to yield an estimate of the true spatial correlation between voxel measurements. This has many implications for fMRI including connectivity results and activation thresholding (Logan and Rowe, 2004). There has been much work on the physiological basis for temporal autocorrelations between spatially separated voxels. It has been reported that there are spontaneous fluctuations in regional cerebral blood flow (rCBF) from spatially distinct regions (Biswal et al., 1995). Further, time-dependent changes in effective connectivity during learning have been observed (Buchel et al., 1999).

2. Statistical theory

In this section, the statistical properties of the complex-valued spatial frequency measurements are described for a single time point image. The statistical properties of the complex-valued image measurements from a complex-valued inverse Fourier transformation of the complex-valued spatial frequency measurements are described. This is done for a one-dimensional image where the characteristics of the transformation in terms of mean and covariance are easier to understand then generalized for a two-dimensional image.

2.1. One dimension

Consider a one-dimensional horizontal complex-valued magnetic resonance image with p_x complex-valued voxels. To obtain this image, we must measure p_x spatial frequencies corresponding to the k_y = 0 center line. In this one-dimensional magnetic resonance image, complex-valued k-space measurements are taken in time but correspond to specific spatial frequencies. We will assume that the k-space measurements are acquired from left to right.

Let s_C = (s_C1, . . ., s_Cpx)^T be these p_x measured complex-valued spatial frequencies stacked into a p_x × 1 complex-valued vector s_C that is the sum of s_0C, a vector of true noiseless complex-valued spatial frequencies and ∈_C, a vector of complex-valued measurement error as in Appendix A where “T” denotes transposition. As shown in Appendix A, the measurements can be represented as a single real-valued vector by stacking the p_x real measurements upon the p_x imaginary measurements to yield the vector s, that is the sum of a vector of true noiseless complex-valued spatial frequencies s₀, and a vector of complex-valued measurement error ∈. Since the vector s is what is measured with error, it is assumed to be characterized as having a multivariate normal distribution with mean s₀ and covariance matrix Λ as described in Appendix A.

The Fourier image reconstruction process to generate a complex-valued measured image ρ_C consists of pre-multiplying the measured spatial frequencies s_C by the Fourier matrix Ω_Cx in Eq. (A.2). As shown in Appendix A, this is equivalently represented as the pre-multiplication if the real-valued vector of measured spatial frequencies s by the real-valued matrix Ω_x to arrive at the real-valued representation of the measured image ρ. The real-valued representation of the measured image ρ is a linear transformation of the real-valued representation of the measured spatial frequencies and thus normally distributed with mean ρ₀ = Ω_xs₀ and covariance matrix $\Delta ={\Omega }_x\Lambda {\Omega }_x^{\mathrm{T}}$.

An example of this methodology might be useful. Although explicit analytic expressions exist for the mean and covariance of the complex-valued transformed one-dimensional images measurements given the mean and covariance of the one-dimensional spatial frequency measurements, simulations were carried out to verify the analytic results in addition to determining those for magnitude-only image measurements where closed form analytic solutions do not exist due to the nonlinear and non one-to-one mapping. The simulations were performed under known conditions. These can be used to precisely characterize the signal and noise of the transformed measurements. All computations utilized Matlab (The Mathworks, Natick, MA, USA). Data was generated to mimic a one-dimensional magnetic resonance imaging experiment. Although this simulation is a mathematical ideal and possibly unrealistic, its results are useful in understanding the properties of the described methodology. Random complex-valued error vectors of dimension p_x were generated in the form of the real-valued representation. A large number, L, of random vectors of dimension 2p_x for the p_x real measurements stacked upon the p_x imaginary measurements denoted by s₁, . . ., s_L were generated from a normal distribution with mean s₀ and covariance ${\Lambda }_1\otimes {\Lambda }_2$. Without loss of generality, s₀ = 0 while Λ₁ and Λ₂ are taken to be unit variance correlation matrices. The 2 × 2 correlation matrix Λ₁ is taken to have an off diagonal correlation of ϱ₁ = 0.5 while the p_x × p_x correlation matrix Λ₂ is taken to be an AR(1) correlation matrix with (i, j)th element ${\varrho }_2^{\mid i-j\mid }$ where ϱ₂ = 0.25. The number of randomly generated vectors was selected to be L = 10⁶.

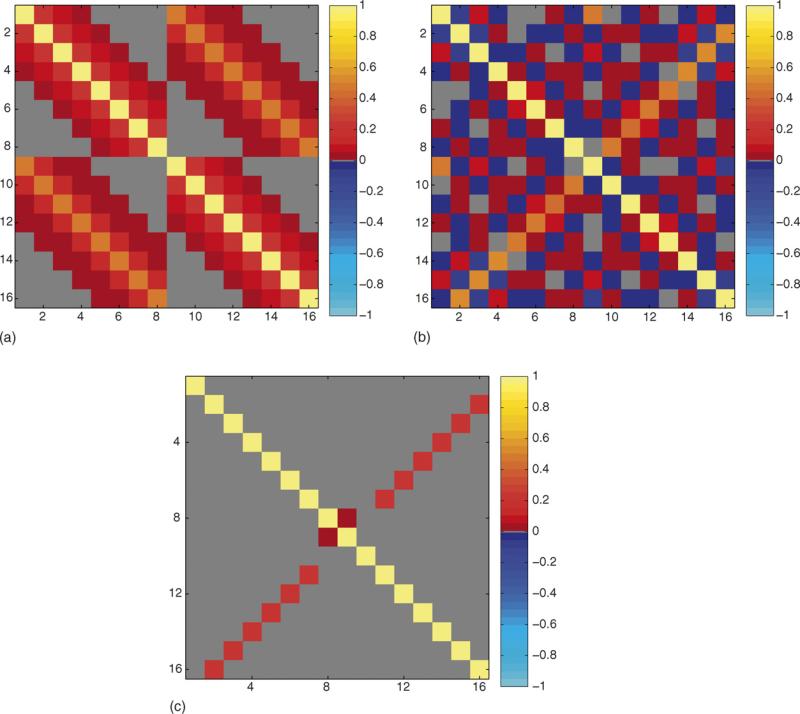
A value of p_x was chosen to be 8. Although the methodology equally applies to larger values, they are not shown to maintain the clarity of presentation. The sample correlation matrix from the L randomly generated one-dimensional spatial frequency vectors was computed as displayed in Fig. 1a. Further, each random one-dimensional spatial frequency vector was pre-multiplied by the appropriate inverse Fourier transform matrix Ω_x given in Eq. (A.3) to produce random one-dimensional images. The sample correlation matrix of the real-valued representation ρ of the complex-valued one-dimensional image measurements ρ_C was computed as displayed in Fig. 1b. The sample spatial frequency correlation matrix matched its theoretical population correlation matrix in Eq. (A.4) and the sample image correlation matrix matched the population value in Eq. (A.5) utilizing the previously described theory. Further, since an analytic expression for the theoretical covariance or correlation matrix for magnitude-only image quantities can not be found, the L vectors containing real and imaginary image measurements of dimension 2p_x were converted to L vectors of dimension p_x con taining magnitude-only image quantities. The sample correlation matrix of the magnitude-only image vectors was computed for the as displayed in Fig. 1c. Note that both complex-valued voxels and real-valued magnitude-only voxels are correlated.

Fig. 1.

Correlation maps, p_x = 8, L = 10⁶. (a) Correlation between complex spatial frequency measurements, Corr(s, s). (b) Correlation between complex image voxel measurements, Corr(r, r). (c) Correlation between magnitude image voxel measurements, Corr(m, m).

2.2. Two dimensions

In a two-dimensional echo planar magnetic resonance image, complex-valued measurements are taken in time but correspond to specific spatial frequencies on a Cartesian (k_x, k_y) grid. In a standard echo planar imaging (EPI) experiment, the measurements are taken in a “zig-zag” pattern. For example, with positive phase encode steps, the pattern starts at the bottom left of the grid with negative (k_x, k_y) values and moves from left to right, then right to left and so on, while going from bottom to top. The left–right direction is called the frequency encode direction while the top–bottom direction is called the phase encode direction.

We will assume that the data is collected according to this standard EPI trajectory.

Let S_C be a p_y × p_x complex-valued matrix of two-dimensional measured spatial frequencies that is the sum of S_0C, a matrix of true noiseless complex-valued spatial frequencies and E_C, a matrix of complex-valued measurement error as in Appendix B. As shown in Appendix B, the matrix of spatial frequency measurements can be represented as a single real-valued vector by stacking the rows to form:

$$s=\mathrm{vec}(\mathrm{Re}\left(S_C^{\mathrm{T}}\right),\mathrm{Im}\left(S_c^{\mathrm{T}}\right))$$

where Re( ) and Im( ) denote the operators that return the real and imaginary parts of their arguments and vec( ) denotes the the vectorization operator that stacks the columns of its matrix argument. This vector s, is the sum of a vector of true noiseless complex-valued spatial frequencies, s₀, and a vector of complex-valued measurement error, ∈. Since the vector s is what is measured with error, it is assumed to be characterized as having a multivariate normal distribution with mean s₀ and covariance matrix Φ as described in Appendix B.

The Fourier image reconstruction process to generate a complex-valued measured image R_C consists of pre-multiplying the measured spatial frequencies S_C by the Fourier matrix Ω_Cy in Eq. (B.1) and post-multiplying it by ${\Omega }_{Cx}^{\mathrm{T}}$ in Eq. (B.1). As shown in Appendix B, this is equivalently represented as the pre-multiplication of the real-valued vector of measured spatial frequencies s by the real-valued matrix Ω as in Eq. (B.6) to arrive at the real-valued representation of the measured image ρ. The real-valued representation of the measured image ρ is a linear transformation of the real-valued representation of the measured spatial frequencies and thus normally distributed with mean ρ₀ = Ω_s0 and covariance matrix Γ = ΩΦΩ^T. The measured p_y × p_x complex-valued image R_C can be found by sequentially putting every p_x elements of the vector ρ_R + iρ_I into a matrix then taking the transpose.

An example of this methodology might be useful. Although explicit analytic expressions exist for the mean and covariance of the complex-valued transformed two-dimensional images measurements given the mean and covariance of the two-dimensional spatial frequency measurements, simulations were carried out to verify the analytic results in addition to determining those for magnitude-only image measurements where closed form analytic solutions do not exist due to the nonlinear and non one-to-one mapping. The simulations were performed under known conditions. These can be used to precisely characterize the signal and noise of the transformed measurements. All computations utilized Matlab (The Mathworks, Natick, MA, USA). Data was generated to mimic a two-dimensional magnetic resonance imaging experiment. Although this simulation is a mathematical ideal and possibly unrealistic, its results are useful in understanding the properties of the described methodology. A large number, L of random matrices of dimension p_y × p_x were generated for the p_yp_x real spatial frequency measurements stacked upon the p_yp_x imaginary spatial frequency measurements denoted by s₁, . . ., s_L that were generated from a normal distribution with mean s0 and covariance ${\Lambda }_1\otimes {\Lambda }_2\otimes {\Lambda }_3$. Without loss of generality, s₀ = 0 while Λ₁, Λ₂, and Λ₃ are taken to be unit variance correlation matrices. The p_y × p_y correlation matrix Λ₁ is taken to be an AR(1) correlation matrix with (i, j)th element ${\varrho }_1^{\mid i-j\mid }$ where ϱ₁ = 0.25, the 2 × 2 correlation matrix Λ₂ is taken to have an off diagonal correlation ϱ = 0.5 while the p_x × p_x correlation matrix Λ₃ is taken to be an AR(1) correlation matrix with (i, j)th element ${\varrho }_3^{\mid i-j\mid }$ where ϱ₃ = 0.5. The number of randomly generated vectors was selected to be L = 10⁶.

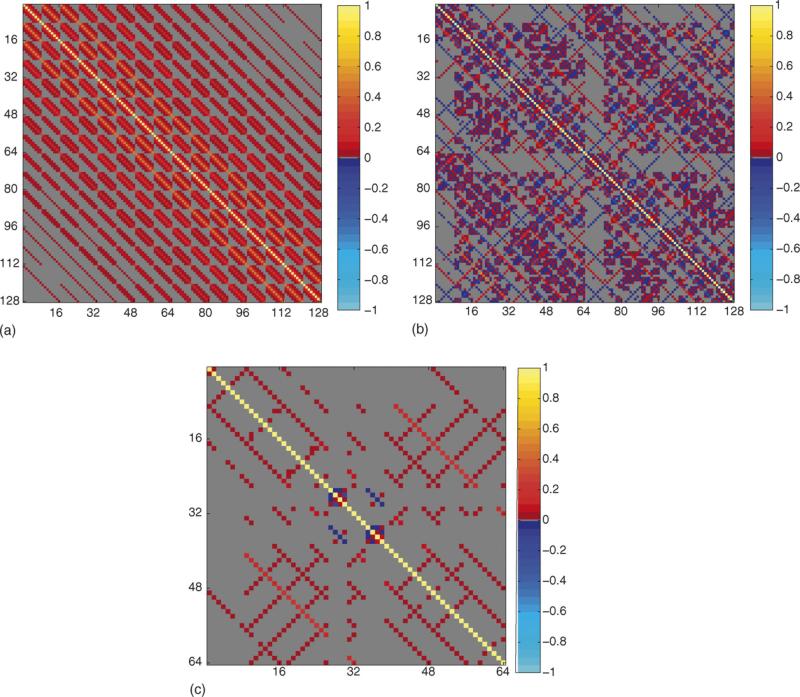
A value of p_y = p_x = 8 was chosen. Although the methodology equally applies to larger values, they are not shown to maintain the clarity of presentation. The corresponding sample correlation matrix from the L randomly generated noisy spatial frequency matrices in vector form was computed as displayed in Fig. 2a. Further, each random complex-valued spatial frequency matrix in vector form was pre-multiplied by Ω in Eq. (B.6) equilavent to pre- and post-multiplying in matrix form by the appropriate inverse Fourier transform matrices Ω_Cy and ${\Omega }_{Cx}^{\mathrm{T}}$ given in Eq. (B.1). The sample correlation matrix of the real-valued representation ρ of the complex-valued image measurements R was computed as displayed in Fig. 2b. The sample spatial frequency correlation matrix matched its theoretical population correlation matrix in Eq. (B.8) and the sample image correlation matrix matched the population value in Eq. (B.9) utilizing the previously described theory.

Fig. 2.

Correlation maps, p_x = p_y = 8, L = 10⁶. (a) Correlation between complex spatial frequency measurements, Corr(s, s). (b) Correlation between complex image voxel measurements, Corr(r, r). (c) Correlation between magnitude image voxel measurements, Corr(m, m).

Further, since a simple closed form analytic expression for the theoretical covariance matrix for magnitude-only image quantities cannot be found, the L matrices of dimension p_y = p_x containing real and imaginary measurements were converted to L matrices of dimension p_y × p_x containing magnitude-only image quantities. The sample correlation matrix of the magnitude-only image matrices was computed using the real-valued representation as displayed in Fig. 2c. Note that both complex-valued voxels and real-valued magnitude-only voxels are correlated.

3. Conclusions

This paper presented the resulting spatial correlation between voxels when Fourier reconstructing correlated spatial frequency measurements. However, the current methodology is applicable to any linear transformation. This includes non-Fourier reconstruction of Fourier encoded data (Cox and McCall, 2004) or non-Fourier reconstruction of non-Fourier encoded data (Panych et al., 1996). Additionally, the previously described Fourier Ω matrices can easily be adjusted to include phase terms as done when adjusting for magnetic field inhomogenieties with a field map (Jezzard and Balaban, 1995).

Spatially correlated voxels result from correlated spatial frequency measurements. These correlation results may have implications for functional magnetic resonance imaging. In particular, temporally autocorrelated spatial frequency measurements produce spatially correlated voxels. This may have specific implications for functional connectivity. The true voxel connectivity may be less than previously thought. This methodology could be utilized to characterize noise correlation in its original form and adjust for it. The baseline spatial correlation needs to be considered and accounted for when making statements regarding connectivity between voxels in fMRI. Although the normal distribution has been utilized in the present work, other statistical distributions could be used. Regardless of the chosen statistical distribution to model the noise, the mean and covariance results are still applicable. Additionally, some voxel correlation may be lost by the magnitude-only procedure. Making statistical inferences, interpreting analysis results, and drawing conclusions should be done in light of the current research.

Appendix A. One-dimensional image

The p_x × 1 dimensional complex-valued spatial frequency measurements s_C consisting of p_x × 1 dimensional true underlying noiseless complex-valued spatial frequencies s_0C and p_x × 1 dimensional complex-valued measurement error ∈_C can be represented as

$$\begin{array}{cc}\hfill s_C=& s_{0C}+{∊}_C=(s_{0\mathrm{R}}+\mathrm{i}{s}_{0\mathrm{I}})+({∊}_{\mathrm{R}}+\mathrm{i}{∊}_{\mathrm{I}})\hfill \\ \hfill =& (s_{0\mathrm{R}}+{∊}_{\mathrm{R}})+\mathrm{i}(s_{0\mathrm{I}}+{∊}_{\mathrm{I}})\hfill \end{array}$$ (A.1)

where i is the imaginary unit while s_0R, s_0I, ∈_R and ∈_I are p_x × 1 dimensional real and imaginary vector valued parts of the true signal and measurement noise. Let Ω_Cx be a p_x × p_x complex-valued matrix such as a Fourier type matrix such that

$${\Omega }_{Cx}={\Omega }_{\mathrm{R}x}+i{\Omega }_{\mathrm{i}x}$$ (A.2)

where Ω_Rx and Ω_Ix are real and imaginary matrix valued parts. Then, the p_x × 1 dimensional complex-valued inverse Fourier transformation ρ_C of s_C can be written (Strang, 1988) as the pre-multiplication by the complex-valued Fourier matrix as

$$\begin{array}{cc}\hfill {\rho }_C=& {\Omega }_{Cx}\times s_C=({\Omega }_{\mathrm{R}x}+\mathrm{i}{\Omega }_{\mathrm{I}x})\times [(s_{0\mathrm{R}}+{∊}_{\mathrm{R}})+\mathrm{i}(s_{0\mathrm{I}}+{∊}_{\mathrm{I}})]\hfill \\ \hfill =& [{\Omega }_{\mathrm{R}x}\times (s_{0\mathrm{R}}+{∊}_{\mathrm{R}})-{\Omega }_{\mathrm{I}x}\times (s_{0\mathrm{I}}+{∊}_{\mathrm{I}})]+\mathrm{i}[{\Omega }_{\mathrm{R}x}\times (s_{0\mathrm{I}}+{∊}_{\mathrm{I}})+{\Omega }_{\mathrm{I}x}\times (s_0\mathrm{R}+{∊}_{\mathrm{R}})]\hfill \\ \hfill =& [({\Omega }_{\mathrm{R}x}{s}_{0\mathrm{R}}-{\Omega }_{\mathrm{I}x}{s}_{0\mathrm{I}})+({\Omega }_{\mathrm{R}x}{∊}_{\mathrm{R}x}-{\Omega }_{\mathrm{I}x}{∊}_{\mathrm{I}})]+\mathrm{i}[({\Omega }_{\mathrm{R}x}{s}_{0\mathrm{I}}+{\Omega }_{\mathrm{I}x}{s}_{0\mathrm{R}})+({\Omega }_{\mathrm{R}x}{∊}_{\mathrm{I}}+{\Omega }_{\mathrm{I}x}{∊}_{\mathrm{R}})]\hfill \\ \hfill =& ({\rho }_{0\mathrm{R}}+{\eta }_{\mathrm{R}})+\mathrm{i}({\rho }_{0\mathrm{I}}+{\eta }_{\mathrm{I}})={\rho }_{\mathrm{R}}+\mathrm{i}{\rho }_{\mathrm{I}}\hfill \end{array}$$

where ρ_0R, ρ_0I, η_R, and η_I are real and imaginary vector valued parts of the Fourier transformed true signal (image) and transformed measurement noise. If Ω_Cx were a Fourier matrix, it is [Ω_Cx]_jk = κ (ω^JK) where κ = 1 and ω = exp[–i2π(j–1)(k – 1)/p_x] for the forward transformation while κ = 1/p_x and ω = exp[+i2π(j – 1)(k – 1)/p_x] for the inverse transformation, where j, k = 1, . . ., p_x.

This pre-multiplication of a complex-valued vector by a complex-valued matrix can be equivalently represented with the 2p_x dimensional real-valued representation:

$$\rho ={\Omega }_{x}s,\left(\begin{array}{c}\hfill {\rho }_{\mathrm{R}}\hfill \\ \hfill {\rho }_{\mathrm{I}}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill {\Omega }_{\mathrm{R}x}\hfill & \hfill -{\Omega }_{\mathrm{I}x}\hfill \\ \hfill {\Omega }_{\mathrm{I}x}\hfill & \hfill {\Omega }_{\mathrm{R}x}\hfill \end{array}\right)\left(\begin{array}{c}\hfill s_{0\mathrm{R}}+{∊}_{\mathrm{R}}\hfill \\ \hfill s_{0\mathrm{I}}+{∊}_{\mathrm{I}}\hfill \end{array}\right)$$ (A.3)

As previously described, data collected from a scientific experiment is never precisely known and thus contains both true signal and measurement error. Scientific measurement error is quantified with statistical distributions and inferences drawn. In most instances, real-valued measurements are taken and real-valued statistical distributions utilized. However, in MRI complex-valued measurements are taken and thus a complex-valued statistical distribution needs to be utilized. The data can be represented using a real-valued representation and a multivariate normal distribution (Rowe, 2003). The real-valued representation used here is very general and within this framework contains the particular representation used to represent the complex-valued multivariate normal distribution (Anderson et al., 1995; Wooding, 1956). The transformation from complex-valued spatial frequency space to image space modifies properties of both the true noiseless signal and the measurement noise. The relationship between correlated complex-valued measurements made in spatial frequency space and the modified correlation between inverse Fourier transformed or reconstructed complex-valued measurements in image space is examined.

Using the real-valued representation in Eq. (A.3), let the 2p_x dimensional vector $s={(s_{\mathrm{R}}^{\mathrm{T}},s_{\mathrm{I}}^{\mathrm{T}})}^{\mathrm{T}}$ be multivariate normally distributed (Rowe, 2003) with mean and covariance matrix:

$$s_0=\left(\begin{array}{c}\hfill s_{0\mathrm{R}}\hfill \\ \hfill s_{0\mathrm{I}}\hfill \end{array}\right)\text{and}\Lambda =\left(\begin{array}{cc}\hfill {\Lambda }_{11}\hfill & \hfill {\Lambda }_{12}\hfill \\ \hfill {\Lambda }_{12}^{\mathrm{T}}\hfill & \hfill {\Lambda }_{22}\hfill \end{array}\right)$$ (A.4)

Complex multivariate normal structure occurs when Λ₁₁ = Λ₂₂ = Ψ, –Λ₁₂ = Υ, and ${\Lambda }_{12}^{\mathrm{T}}={\rm Y}$ . That is, when the covariance matrix is of a skew-symmetric form as (Wooding, 1956; Anderson et al., 1995). The current representation is more general and less restrictive than multivariate complex normal structure. By carrying out a multivariate transformation of variable with the real-valued representation from s to ρ through ρ = Ω_xs, the statistical distribution of ρ is also multivariate normally distributed but with mean ρ₀ given by

$$\left(\begin{array}{c}\hfill {\rho }_{0\mathrm{R}}\hfill \\ \hfill {\rho }_{0\mathrm{I}}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill {\Omega }_{\mathrm{R}x}\hfill & \hfill -{\Omega }_{\mathrm{I}x}\hfill \\ \hfill {\Omega }_{\mathrm{I}x}\hfill & \hfill {\Omega }_{\mathrm{R}x}\hfill \end{array}\right)\left(\begin{array}{c}\hfill s_{0\mathrm{R}}\hfill \\ \hfill s_{0\mathrm{I}}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\Omega }_{\mathrm{R}x}{s}_{0\mathrm{R}}-{\Omega }_{\mathrm{I}x}{s}_{0\mathrm{I}}\hfill \\ \hfill {\Omega }_{\mathrm{R}x}{s}_{0\mathrm{I}}+{\Omega }_{\mathrm{I}x}{s}_{0\mathrm{R}}\hfill \end{array}\right)$$

and covariance matrix $\Delta ={\Omega }_x\Lambda {\Omega }_x^{\prime }$, given by

$$\begin{array}{cc}\hfill \Delta =& \left(\begin{array}{cc}\hfill {\Omega }_{\mathrm{R}x}\hfill & \hfill {\Omega }_{\mathrm{I}x}\hfill \\ \hfill {\Omega }_{\mathrm{I}x}\hfill & \hfill {\Omega }_{\mathrm{R}x}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill {\Lambda }_{11}\hfill & \hfill {\Lambda }_{12}\hfill \\ \hfill {\Lambda }_{12}^{\mathrm{T}}\hfill & \hfill {\Lambda }_{22}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill {\Omega }_{\mathrm{R}x}^{\mathrm{T}}\hfill & \hfill {\Omega }_{\mathrm{I}x}^{\mathrm{T}}\hfill \\ \hfill -{\Omega }_{\mathrm{I}x}^{\mathrm{T}}\hfill & \hfill {\Omega }_{\mathrm{R}x}^{\mathrm{T}}\hfill \end{array}\right).\hfill \\ \hfill {\Delta }_{11}=& {\Omega }_{\mathrm{R}x}{\Lambda }_{11}{\Omega }_{\mathrm{R}x}^{\mathrm{T}}-{\Omega }_{\mathrm{I}x}{\Lambda }_{12}^{\mathrm{T}}{\Omega }_{\mathrm{R}x}^{\mathrm{T}}+{\Omega }_{\mathrm{R}x}(-{\Lambda }_{12}){\Omega }_{\mathrm{I}x}^{\mathrm{T}}+{\Omega }_{\mathrm{I}x}{\Lambda }_{22}{\Omega }_{\mathrm{I}x}^{\mathrm{T}},\hfill \\ \hfill {\Delta }_{22}=& {\Omega }_{\mathrm{I}x}{\Lambda }_{11}{\Omega }_{\mathrm{I}x}^{\mathrm{T}}-{\Omega }_{\mathrm{R}x}{\Lambda }_{12}^{\mathrm{T}}{\Omega }_{\mathrm{I}x}^{\mathrm{T}}-{\Omega }_{\mathrm{I}x}(-{\Lambda }_{12}){\Omega }_{\mathrm{R}x}^{\mathrm{T}}+{\Omega }_{\mathrm{R}x}{\Lambda }_{22}{\Omega }_{\mathrm{R}x}^{\mathrm{T}},\hfill \\ \hfill {\Delta }_{12}=& {\Omega }_{\mathrm{R}x}{\Lambda }_{11}{\Omega }_{\mathrm{I}x}^{\mathrm{T}}-{\Omega }_{\mathrm{I}x}{\Lambda }_{12}^{\mathrm{T}}{\Omega }_{\mathrm{I}x}^{\mathrm{T}}-{\Omega }_{\mathrm{R}x}(-{\Lambda }_{12}){\Omega }_{\mathrm{R}x}^{\mathrm{T}}+{\Omega }_{\mathrm{I}x}{\Lambda }_{22}{\Omega }_{\mathrm{R}x}^{\mathrm{T}},\hfill \\ \hfill {\Delta }_{21}=& {\Delta }_{12}^{\mathrm{T}}\hfill \end{array}$$ (A.5)

where Ω_x is of full rank if it is a Fourier matrix. Again, this representation is more general and less restrictive than multivariate complex normal structure (Anderson et al., 1995; Wooding, 1956). In the multivariate complex normal case (Anderson et al., 1995; Wooding, 1956) where Λ₁₁ = Λ₂₂ = Ψ, –Λ₁₂ = Υ , and ${\Lambda }_{12}^{\mathrm{T}}={\rm Y}$, the covariance matrix Δ is

$$\begin{array}{cc}\hfill {\Delta }_{11}=& {\Omega }_{\mathrm{R}x}\Psi {\Omega }_{\mathrm{R}x}^{\mathrm{T}}-{\Omega }_{\mathrm{I}x}{\rm Y}{\Omega }_{\mathrm{R}x}^{\mathrm{T}}+{\Omega }_{\mathrm{R}x}{\rm Y}{\Omega }_{\mathrm{I}x}^{\mathrm{T}}+{\Omega }_{\mathrm{I}x}\Psi {\Omega }_{\mathrm{I}x}^{\mathrm{T}},\hfill \\ \hfill {\Delta }_{12}=& {\Omega }_{\mathrm{R}x}\Psi {\Omega }_{\mathrm{I}x}^{\mathrm{T}}-{\Omega }_{\mathrm{I}x}{\rm Y}{\Omega }_{\mathrm{I}x}^{\mathrm{T}}+{\Omega }_{\mathrm{R}x}{\rm Y}{\Omega }_{\mathrm{R}x}^{\mathrm{T}}+{\Omega }_{\mathrm{I}x}\Psi {\Omega }_{\mathrm{R}x}^{\mathrm{T}},\hfill \\ \hfill {\Delta }_{21}=& -{\Delta }_{12},{\Delta }_{22}={\Delta }_{11}\hfill \end{array}$$ (A.6)

where Υ is a skew symmetric matrix, Υ^T = –Υ .

It can readily be seen that if the measurement process that generates the data produces uncorrelated real and imaginary channels, that is, ${\Lambda }_{12}={\Lambda }_{12}^{\mathrm{T}}=0$ but correlated within the real imaginary channels, then after transformation the real and imaginary channels are correlated both between and within. It should be noted that if Υ = 0 and Ψ = ψ²I_px, then $\Delta ={\delta }^2{\mathrm{I}}_2\otimes {\mathrm{I}}_{px}$ where δ = ψ²/p_x for the inverse transformation and δ = ψ²p_x for the forward transformation. The Kronecker product ⊗ was utilized which multiplies every element of its first matrix argument by its entire second matrix argument.

The above specific multivariate complex normal structure could alternatively be developed utilizing the complex multivariate normal distribution (Anderson et al., 1995; Wooding, 1956). A property of the complex multivariate normal distribution is that if s_C ~ N_C (s_0C, Λ_C), then ρ_C = Ω_Cxs_C is also complex normal distributed, ρ_C ~ N_C (Ω_Cxs_0C, ${\rho }_C\sim N_C({\Omega }_{Cx}{s}_{0C},{\Omega }_{Cx}{\Lambda }_C{\Omega }_{Cx}^{\mathrm{H}})$) where Λ_C = Ψ + iΥ and “H” denotes the Hermitian or complex conjugate transpose.

After image reconstruction, the usual procedure is to convert from real and imaginary images to magnitude and phase images. The phase is generally discarded in fMRI and magnitude-only time course data are analyzed. The conversion from real and imaginary images to magnitude and phase images is a nonlinear transformation and thus the joint distribution of the magnitude image measurements is not straightforward. On an individual basis, the measured magnitude quantity in voxel j in each magnitude image is

$$m_j=\sqrt{{({\rho }_{0\mathrm{R}j}+{\eta }_{\mathrm{R}j})}^2+{({\rho }_{0\mathrm{I}j}+{\eta }_{\mathrm{I}j})}^2}$$

where ρ_0Rj and ρ_0Ij are the means in the real and imaginary parts while η_Rj and η_Ij are the zero mean real and imaginary Gaussian error terms with variances Δ_jj and Δ_{px+j, px+j}, j = 1, . . ., p_x, generally assumed to be the same. It is well known (Gudbjartsson and Patz, 1995; Rice, 1954; Rowe and Logan, 2004) that the measured magnitude voxel intensity m_j is Ricean distributed with parameters ${\rho }_{0j}=\sqrt{{\rho }_{0{\mathrm{R}}_j}^2+{\rho }_{0{\mathrm{I}}_j}^2}$, being the pixel magnitude intensity in the absence of noise, and Δ_j = Δ_jj = Δ_px+j,px+j, being the equal variances of the real and imaginary parts. The population correlation between Ricean distributed magnitude image measurements will be examined through simulation.

Appendix B. Two-dimensional image

The p_y × p_x dimensional complex-valued spatial frequency measurements S_C consisting of p_y × p_x dimensional true under lying noiseless complex-valued spatial frequencies S_0C and p_y × p_x dimensional complex-valued measurement error E_C can be represented as

$$S_C=(S_{0\mathrm{R}}+\mathrm{i}{S}_{0\mathrm{I}})+(E_{\mathrm{R}}+\mathrm{i}{E}_{\mathrm{I}})=(S_{0\mathrm{R}}+E_{\mathrm{R}})+\mathrm{i}(S_{0\mathrm{I}}+E_{\mathrm{I}})$$

where i is the imaginary unit while S_0R, S_0I, E_R and E_I are real and imaginary matrix valued parts of the true spatial frequencies signal and measurement noise. Let Ω_Cx and Ω_Cy be p_x × p_x and p_y × p_y Fourier matrices such that

$${\Omega }_{Cy}={\Omega }_{\mathrm{R}y}+\mathrm{i}{\Omega }_{\mathrm{I}y}\text{and}{\Omega }_{Cx}={\Omega }_{\mathrm{R}x}+\mathrm{i}{\Omega }_{\mathrm{i}x}$$ (B.1)

where Ω_Ry and Ω_Rx are real while Ω_Iy and Ω_Ix are imaginary matrix valued parts.

Then, the p_y × p_x complex-valued inverse Fourier transformation R_C of S_C can be written as

$$\begin{array}{cc}\hfill R_C=& {\Omega }_{Cy}\times S_C\times {\Omega }_{Cx}^{\mathrm{T}}=({\Omega }_y+\mathrm{i}{\Omega }_{\mathrm{I}y})\times [(S_{0\mathrm{R}}+E_{\mathrm{R}})+\mathrm{i}(S_{0\mathrm{I}}+E_{\mathrm{I}})]\times ({\Omega }_{\mathrm{R}x}^{\mathrm{T}}+{\Omega }_{\mathrm{I}x}^{\mathrm{T}})\hfill \\ \hfill =& ({\Omega }_{\mathrm{R}y}+\mathrm{i}{\Omega }_{\mathrm{I}y})\times \{[(S_{0\mathrm{R}}+E_{\mathrm{R}})\times {\Omega }_{\mathrm{R}x}^{\mathrm{T}}-(s_{0\mathrm{I}}+E_{\mathrm{I}})\times {\Omega }_{\mathrm{I}x}^{\mathrm{T}}]+\mathrm{i}[(S_{0\mathrm{R}}+E_{\mathrm{R}})\times {\Omega }_{\mathrm{I}x}^{\mathrm{T}}+(S_{0\mathrm{I}}+E_{\mathrm{I}})\times {\Omega }_{\mathrm{R}x}^{\mathrm{T}}]\}\hfill \\ \hfill =& (R_{0\mathrm{R}}+N_{\mathrm{R}})+\mathrm{i}(R_{0\mathrm{I}}+N_{\mathrm{I}})=R_{\mathrm{R}}+\mathrm{i}{R}_{\mathrm{I}}\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill R_{0\mathrm{R}}=& ({\Omega }_{\mathrm{R}y}{S}_{0\mathrm{R}}{\Omega }_{\mathrm{R}x}^{\mathrm{T}}-{\Omega }_{\mathrm{R}y}{S}_{0\mathrm{I}}{\Omega }_{\mathrm{I}x}^{\mathrm{T}}-{\Omega }_{\mathrm{I}y}{S}_{0\mathrm{R}}{\Omega }_{\mathrm{I}x}^{\mathrm{T}}-{\Omega }_{\mathrm{I}y}{S}_{0\mathrm{I}}{\Omega }_{\mathrm{R}x}^{\mathrm{T}}),\hfill \\ \hfill N_{\mathrm{R}}=& ({\Omega }_{\mathrm{R}y}{E}_{\mathrm{R}}{\Omega }_{\mathrm{R}x}^{\mathrm{T}}-{\Omega }_{\mathrm{R}y}{E}_{\mathrm{I}}{\Omega }_{\mathrm{I}x}^{\mathrm{T}}-{\Omega }_{\mathrm{I}y}{E}_{\mathrm{R}}{\Omega }_{\mathrm{I}x}^{\mathrm{T}}-{\Omega }_{\mathrm{I}y}{E}_{\mathrm{I}}{\Omega }_{\mathrm{R}x}^{\mathrm{T}}),\hfill \\ \hfill R_{0\mathrm{I}}=& ({\Omega }_{\mathrm{R}y}{S}_{0\mathrm{R}}{\Omega }_{\mathrm{I}y}^{\mathrm{T}}-{\Omega }_{\mathrm{R}x}{S}_{0\mathrm{I}}{\Omega }_{\mathrm{R}x}^{\mathrm{T}}-{\Omega }_{\mathrm{I}y}{S}_{0\mathrm{R}}{\Omega }_{\mathrm{R}x}^{\mathrm{T}}-{\Omega }_{\mathrm{I}y}{S}_{0\mathrm{I}}{\Omega }_{\mathrm{I}x}^{\mathrm{T}}),\hfill \\ \hfill N_{\mathrm{I}}=& ({\Omega }_{\mathrm{R}y}{E}_{\mathrm{R}}{\Omega }_{\mathrm{I}x}^{\mathrm{T}}-{\Omega }_{\mathrm{R}y}{E}_{\mathrm{I}}{\Omega }_{\mathrm{R}x}^{\mathrm{T}}-{\Omega }_{\mathrm{I}y}{E}_{\mathrm{R}}{\Omega }_{\mathrm{R}x}^{\mathrm{T}}-{\Omega }_{\mathrm{I}y}{E}_{\mathrm{I}}{\Omega }_{\mathrm{I}x}^{\mathrm{T}})\hfill \end{array}$$

are real and imaginary matrix valued parts of the inverse Fourier transformed true signal (image) and measurement noise. Each row in the curled bracket part of the expression for R_C is a one-dimensional complex-valued transformation:

$$S_C{\Omega }_{Cx}^{\mathrm{T}}=\left(\begin{array}{c}\hfill {\left({\Omega }_{Cx}{s}_{C1}\right)}^{\mathrm{T}}\hfill \\ \hfill ⋮\hfill \\ \hfill {\left({\Omega }_{Cx}{s}_{C{p}_y}\right)}^{\mathrm{T}}\hfill \end{array}\right)$$ (B.2)

as in the previous one-dimensional case where $s_{Cj}^{\mathrm{T}}$ represents the jth row in S_C that is p_x dimensional, j = 1, . . ., p_y. The complex matrices Ω_Cy and Ω_Cx can be Fourier matrices. This preand post-multiplication of a complex-valued matrix by complex-valued matrices could be equivalently represented with a similar real-valued representation. This could be accomplished by forming a p_y × 2p_x dimensional matrix where a given row j, is (${(s_{j\mathrm{R}}^{\mathrm{T}},s_{j\mathrm{I}}^{\mathrm{T}})}^{\mathrm{T}}$) a real-valued representation of the rows of S_C. This real-valued matrix is then post-multiplied by ${\Omega }_x^{\mathrm{T}}$. The resultant real-valued matrix is then reformed into a complex-valued matrix and another real-valued representation made from the columns to form a 2p_y × p_x matrix. This new real-valued representation is then pre-multiplied by Ω_y and the resultant real-valued matrix is then reformed into a complex-valued matrix being the measured two-dimensional image. In the procedure just described, it is difficult to keep track of individual measurements and the correlations between other measurements within the array.

A simple representation from matrix algebra can be utilized to assist with this endeavor. It is known (Harville, 1999) that the vectorization of the triple product of conformable matrices A, B, and C can be written as

$$\mathrm{vec}\left(ABC\right)=(C^{\mathrm{T}}\otimes A)\mathrm{vec}\left(B\right)$$

which translates to our application as

$${\rho }_C=({\Omega }_{Cy}\otimes {\Omega }_{Cx})\mathrm{vec}\left(S_C^{\mathrm{T}}\right)$$

where vec is the vectorization operator that stacks the columns of its matrix argument and ${\rho }_C=\mathrm{vec}\left(R_C^{\mathrm{T}}\right)$.

As previously noted, the matrix of spatial frequency measurements can be described with a real-valued representation. The large Kronecker product can be represented as

$${\Omega }_C={\Omega }_{Cy}\otimes {\Omega }_{Cx}$$ (B.3)

$${\Omega }_C=({\Omega }_{y\mathrm{R}}+\mathrm{i}{\Omega }_{y\mathrm{I}})\otimes \left({\Omega }_{x\mathrm{R}}\mathrm{i}{\Omega }_{x\mathrm{I}}\right)$$ (B.4)

$${\Omega }_C=[({\Omega }_{y\mathrm{R}}\otimes {\Omega }_{x\mathrm{R}})-({\Omega }_{y\mathrm{I}}\otimes {\Omega }_{x\mathrm{I}})]+\mathrm{i}[({\Omega }_{y\mathrm{R}}\otimes {\Omega }_{x\mathrm{I}})+({\Omega }_{y\mathrm{I}}\otimes {\Omega }_{x\mathrm{R}})]$$ (B.5)

$${\Omega }_C={\Omega }_{\mathrm{R}}+\mathrm{i}{\Omega }_{\mathrm{I}}$$ (B.6)

The complex-valued image vector can be represented as ρ_C = Ω_Cs_C. We can pre-multiply the complex-valued spatial frequency vector by this complex-valued matrix as in the one dimensional image case, or equivalently with a similar real-valued representation:

$$\rho =\Omega s,\left(\begin{array}{c}\hfill \rho \mathrm{R}\hfill \\ \hfill {\rho }_{\mathrm{I}}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill {\Omega }_{\mathrm{R}}\hfill & \hfill -{\Omega }_{\mathrm{I}}\hfill \\ \hfill {\Omega }_{\mathrm{I}}\hfill & \hfill {\Omega }_{\mathrm{R}}\hfill \end{array}\right)\left(\begin{array}{c}\hfill s_{0\mathrm{R}}+{∊}_{\mathrm{R}}\hfill \\ \hfill s_{0\mathrm{I}}+{∊}_{\mathrm{I}}\hfill \end{array}\right)$$ (B.7)

where the real-valued vector of spatial frequencies is formed by

$$s=\mathrm{vec}(\mathrm{Re}\left(S_C^{\mathrm{T}}\right),\mathrm{Im}\left(S_C^{\mathrm{T}}\right))$$

while Re( ) and Im( ) denote the operators that return the real and imaginary parts of their arguments and vec( ) denotes the vectorization operator that stacks the columns of its matrix argument.

The Fourier image reconstruction process to generate a complex-valued measured image R_C consists of pre-multiplying the measured spatial frequencies S_C by the Fourier matrix Ω_Cy in Eq. (B.1) and post-multiplying it by Ω^T_Cx in Eq. (B.1). As shown above, this is equivalently represented as the pre-multiplication of the real-valued vector of measured spatial frequencies s by the real-valued matrix Ω in Eq. (B.6) to arrive at the real-valued representation of the measured image ρ. The vector s is assumed to be characterized as having a multivariate normal distribution with mean s0 and covariance matrix Φ denoted as

$$s\sim \mathcal{N}(s_0,\Phi )$$ (B.8)

The real-valued representation of the measured image ρ is a linear transformation of the real-valued representation of the measured spatial frequencies and thus normally distributed with mean ρ₀ = Ω_s0 and covariance matrix Γ = ΩΦΩ^T denoted as

$$\rho \sim \mathcal{N}({\rho }_0,\Gamma )$$ (B.9)

The measured p_y × p_x complex-valued image R_C can be found by sequentially putting every p_x elements of the vector ρ_R + iρ_I into a matrix then taking the transpose.

In terms of complex-valued matrices, the mean of the transformed variables can be written as

$$\begin{array}{cc}\hfill R_{0C}=& {\Omega }_y{S}_{0C}{\Omega }_x^{\mathrm{T}}=({\Omega }_{y\mathrm{R}}+\mathrm{i}{\Omega }_{y\mathrm{I}})(S_{0\mathrm{R}}+S_{0\mathrm{I}})({\Omega }_{x\mathrm{R}}^{\mathrm{T}}+\mathrm{i}{\Omega }_{x\mathrm{I}}^{\mathrm{T}})\hfill \\ \hfill =& R_{0\mathrm{R}}+\mathrm{i}{R}_{0\mathrm{I}}\hfill \end{array}$$

as previously defined but the covariance of the transformed measurements is not easily represented with complex numbers and requires the larger real-valued representation.

Again, after image reconstruction, the usual procedure is to convert from real and imaginary images to magnitude and phase images. The phase is generally discarded in fMRI and magnitude-only time course data is analyzed. The conversion from real and imaginary images to magnitude and phase images is a nonlinear not one-to-one transformation and thus the joint distribution of the magnitude-only image quantities is not straightforward. However an approximation to the correlation of the square of the magnitudes, or in general any quadratic form exists. Further, the correlation of squared magnitudes is a good approximation to the correlation of magnitudes. If any pair of random variables is transformed by the same function (here the square root), their correlation remains roughly the same, by a Taylor series expansion argument.

On an individual basis, the measured magnitude quantity in voxel (i, j) in each magnitude image is

$$M_{jk}=\sqrt{{(R_{0\mathrm{R}jk}+M_{\mathrm{R}jk})}^2+{(R_{0\mathrm{I}jk}+M_{\mathrm{I}jk})}^2}$$

where R_0Rjk and R_0Ijk are the means in the real and imaginary parts, N_RjK and N_Ijk are the zero mean real and imaginary Gaussian error terms with variances Γ_jpx+k,jpx+k and Γ_{pxpy+jpx+k,pxpy+jpx+k}, j = 1, . . ., p_x = 1, . . ., p_y, generally assumed to be the same.

It is well known (Gudbjartsson and Patz, 1995; Rice, 1954; Rowe and Logan, 2004) that the measured magnitude voxel intensity m_j is Ricean distributed with parameters ${\rho }_{0j}=\sqrt{{\rho }_{0{\mathrm{R}}_j}^2+{\rho }_{0\mathrm{I}j}^2}$, being the pixel magnitude intensity in the absence of noise, and Γ_{pxpy+jpx+k,pxpy+jpx+k}, being the equal variances of the real and imaginary parts. The population correlation between Ricean distributed magnitude image measurements will be examined through simulation.