Evaluation of polygenic risk scores for predicting breast and prostate cancer risk

Abstract

Recently, polygenic risk scores have been shown to be associated with certain complex diseases. The approach has been based on the contribution of counting multiple alleles associated with disease across independent loci, without requiring compelling evidence that every locus had already achieved definitive genome-wide statistical significance. Whether polygenic risk scores assist in the prediction of risk of common cancers is unknown. We built polygenic risk scores from lists of genetic markers prioritized by their association with breast or prostate cancer in a training data set and evaluated whether these scores could improve current genetic prediction of these specific cancers in independent test samples. We used genome-wide association data on 1,145 breast cancer cases and 1,142 controls from the Nurses’ Health Study and 1,164 prostate cancer cases and 1,113 controls from the Prostate Lung Colorectal and Ovarian Cancer Screening Trial. Ten-fold cross validation was used to build and evaluate polygenic risk scores with 10 to 60,000 independent single nucleotide polymorphisms (SNPs). For both breast and prostate cancer, the models that included only published risk alleles maximized the cross-validation estimate of the area under the ROC curve (0.53 for breast and 0.57 for prostate). We found no significant evidence that polygenic risk scores using common variants improved risk prediction for breast and prostate cancer over replicated SNP scores.

Introduction

Since 2007, a wealth of genomic data investigating the germline contribution to cancer risk has been collected from genome-wide association studies (GWAS)[Ioannidis, Castaldi and Evangelou, 2010]. While this rapidly expanding repository of germline genetic information has been instrumental in discovering disease-associated loci not previously identified by linkage nor candidate gene approaches, it is remarkable that nearly all variants discovered so far confer relatively low risk (e.g., estimated odds ratios less than 1.3 per risk allele). This observation coupled with the small sample sizes in first generation GWAS has resulted in underpowered studies with limited ability to detect low risk variants at stringent significance levels required to compensate for multiple testing. The current state of dissecting the underlying genetic factors that contribute to most complex diseases is far from complete with a substantial portion of heritability remaining to be explained.

Although other forms of genetic variation not tagged by single nucleotide polymorphisms (SNPs) are expected to explain the proportion not explained by GWAS with common variants, [Manolio et al., 2009], the possibility remains there is unutilized information in GWAS data. In fact, a multitude of loci may be awaiting discovery, which current studies are underpowered to detect[Park et al., 2010]. Refined methods for exploring the available genomic information are needed to maximize the information that can be gleaned from GWAS.

Evans[Evans, Visscher and Wray, 2009] and Purcell[International Schizophrenia Consortium et al., 2009] have proposed methods of aggregating information on a large number of SNP alleles associated with a trait that do not achieve stringent genome-wide statistical significance or even nominal statistical significance of p<0.05. These models create polygenic risk scores by summing risk alleles from thousands or tens of thousands of loci spanning the genome to predict an individual's genetic risk of developing disease. Moreover, these scores could be used to predict an individual's outcome even without knowing which of the SNPs in the score are conclusively associated with disease.

Evans et al. have shown that the discriminatory ability of risk models using both known variants and a polygenic score is higher than a model using known variants only for bipolar disorder, coronary heart disease, hypertension, Crohn's disease, rheumatoid arthritis, and type I and II diabetes. Purcell et al. have demonstrated that polygenic scores for schizophrenia and bipolar disorder can explain up to 3% of disease variance, and that these scores are specific to those diseases, since they do not explain variance in other non-psychiatric disorders. Recently, a multiple sclerosis consortium also showed evidence they could explain up to 3% of the variance in multiple sclerosis with a polygenic risk score[International Multiple Sclerosis Genetics Consortium (IMSGC) et al., 2010]. For these phenotypes, the variance explained by a polygenic risk score adds to that already accounted for by known genetic variants. This suggests there are additional risk loci beyond those that have achieved genome-wide significance. Moreover, the variance explained by not-yet-known markers may be underestimated by these analyses due to the noise associated with including potentially non-associated markers into the polygenic risk score.

Although an array of complex chronic diseases have been investigated using polygenic techniques, to our knowledge, only one study applied polygenic methods to existing GWAS studies of cancer[Witte and Hoffmann, 2011]. While that study found a modestly significant association for polygenic risk scores at liberal SNP inclusion thresholds for PCa (p<0.01), the authors did not fully investigate the added variance that can be explained by polygenic risk scores that is independent of established genome-wide significant SNPs.

Our goal is to investigate currently available GWAS to examine genetic models for improving risk prediction for breast cancer (BCa) and prostate cancer (PCa) and also to investigate whether additional undiscovered disease susceptibility loci may be awaiting discovery. So far, the largest number of risk variants identified through GWAS have been for PCa and then BCa. To date, at least 13 independent loci have been associated with BCa[Thomas et al., 2009, Stacey et al., 2007, Ahmed et al., 2009, Stacey et al., 2008, Gold et al., 2008, Zheng et al., 2009b, Hunter et al., 2007, Easton et al., 2007, Turnbull et al., 2010] and over 30 independent genetic loci have been associated with PCa risk[Duggan et al., 2007, Eeles et al., 2009, Eeles et al., 2008, Thomas et al., 2008, Gudmundsson et al., 2007b, Gudmundsson et al., 2008, Sun et al., 2008, Gudmundsson et al., 2009, Yeager et al., 2009, Zheng et al., 2009a, Gudmundsson et al., 2007a]. Our first aim is to investigate the discrimination of models using established SNPs for prediction. Next, we aim to employ polygenic methods to compile prioritized lists of variants to be used in constructing polygenic risk scores. We further explore the added discriminative ability of the polygenic scores and assess whether there is significant information added to the overall prediction of BCa and PCa by these scores.

Methods

Data for this study are based upon the Cancer Genetic Markers of Susceptibility (CGEMS) initiative. Breast cancer genetic data originated from the Nurses’ Health Study (NHS) and prostate cancer data came from the Prostate, Lung, Colorectal, and Ovarian (PLCO) study[Hunter et al., 2007, Yeager et al., 2007].

Briefly, the NHS is a prospective cohort study established in 1976 with a total of 121,700 women recruited at baseline. During 1989 to 1990, 32,826 participants without previous BCa diagnosis provided a blood sample and were followed until June 1, 2004 for incident BCa. These participants were genotyped using the Illumina HumanHap500 array. Breast cancer cases were identified through personal mailings and searches of the National Death Index. Over 98% of BCa cases were ascertained in this cohort[Tworoger et al., 2007]. Controls were individually matched with cases on age at diagnosis, timing of blood collection, use of postmenopausal hormones, ethnicity, and menopausal status. All cases and controls were self-reported Caucasian and postmenopausal at diagnosis. After quality control, 1,145 BCa cases and 1,142 controls were used in the following analyses[Hunter et al., 2007]. All study participants provided informed consent and the study was reviewed by the Institutional Review Board of the Brigham and Women's Hospital, Boston, MA.

The PLCO Cancer Screening Trial, is a large randomized control trial designed to investigate the efficacy of cancer screening on early mortality from prostate, lung, colorectal, or ovarian cancer[Gohagan et al., 2000, Prorok et al., 2000]. Blood samples were collected from participants at screening visits and DNA extracted according to standard protocols. Incident PCa cases were identified by screening exams, self or physician report, or link with the state cancer registries or the National Death Index. All cases of PCa were pathologically confirmed by a trained pathologist. Genotypes for non-Hispanic white men randomized to the PCa screening arm of the PLCO were obtained using Illumina HumanHap300 and HumanHap240 genotyping platforms at separate times as explained elsewhere[Yeager et al., 2007]. A total of 1,164 PCa cases oversampled for aggressive disease and 1,113 PCa free incidence-density sampled controls were eligible for inclusion into the study. Written informed consent was required for participation in the study and all protocols were reviewed by the Institutional Review Boards of both the National Cancer Institute and each of the 10 participating study centers.

A total of 528,173 SNPs were genotyped and passed quality control for BCa and 546,593 SNPs were genotyped on the combined platforms for PCa[Hunter et al., 2007, Yeager et al., 2007].

Previously replicated genome-wide significant SNPs for BCa and PCa were extracted from the literature (Table I). These SNPs were moved to the top of a minor allele frequency ordered SNP list for each cancer, which was further thinned by using linkage disequilibrium filtration to remove redundant SNPs with correlation of an R² greater than 0.20. The thinning program was an in-house Python script that referenced the HapMap Rel.23a (NCBI B36) database. The result was a list of 161,702 LD thinned SNPs for BCa and 165,508 LD thinned SNPs for PCa.

Table I.

Genomic positions and nearby genes of replicated SNPs associated with BCa and PCa. Correlated and proxy SNPs with an R2 greater than 0.20 are not included. RA denotes the risk allele for the SNP. P-values are for BCa and PCa association in CGEMS and PLCO, respectively.

	Locus	Reported Genes	SNP	RA	P-Value	Reference	PMID
BreastCancer	lpll	Intergenic	rsl 1249433	G	4.20E-04	Thomas et al. NG 2009	19330030
	2q35	Intergenic	rsl3387042	A	3.02E-03	Stacey et al. NG 2007	17529974
	3p24	SLC4A7/NEK10	rs4973768	T	1.29E-01	Ahmed et al. NG 2009	19330027
	5pl2	MRPS30	rsl0941679	G	1.20E-03	Stacey et al. NG 2008	18438407
	5qll	MAP3K1	rsl6886165	G	1.23E-02	Thomas et al. NG 2009	19330030
	6q22	ECHDC1	rs2180341	G	3.49E-01	Gold et al. 2008	18326623
	6q25	Intergenic	rs2046210	A	7.77E-02	Zheng et al. NG 2009	19219042
	8q24	Intergenic	rsl562430	T	1.19E-02	Turnball et al. NG 2010	20453838
	10q26	FGFR2	rs2981579	A	4.87E-06	Hunter et al. NG 2007	17529973
	llpl5	LSP1	rs3817198	C	3.89E-01	Easton et al. Nature 2007	17529967
	14q24	RAD 51 LI	rs999737	C	1.51E-02	Thomas et al. NG 2009	19330030
	16ql2	TNRC9	rs3803662	A	6.41E-02	Easton et al. Nature 2007	17529967
	17q23	COX 11	rs6504950	G	8.98E-02	Ahmed et al. NG 2009	19330027
	Locus	Reported Genes	SNP	RA	P-Value	Reference	PMID
Prostate Cancer	2pl5	EHBP1	rs2710647	C	3.56E-02	Eeles et al. NG 2009	19767753
	2pl5	EHBP1	rs721048	A	8.84E-04	Gudmundsson et al. NG 2008	18264098
	2p21	THADA	rs 1465618	T	8.51E-01	Eeles et al. NG 2009	19767753
	2q31.1	ITGA6	rsl2621278	A	6.18E-01	Eeles et al. NG 2009	19767753
	3pl2.1	LOC285232	rs2660753	T	4.88E-01	Eeles et al. NG 2008	18264097
	3q21.3	EEFSEC	rs4857841	A	3.30E-03	Gudmundsson et al. NG 2009	19767754
	4q22.3	PDLIM5	rsl 2500426	A	7.30E-02	Eeles et al. NG 2009	19767753
	4q24	TET2	rs7679673	A	1.19E-02	Eeles et al. NG 2009	19767753
	6q25.3	SLC22A3	rs9364554	T	8.19E-01	Eeles et al. NG 2008	18264097
	7pl5.2	JAZF1	rsl0486567	G	7.87E-02	Thomas et al. NG 2008	18264096
	7q21.3	LMTK2	rs6465657	C	4.42E-01	Eeles et al. NG 2008	18264097
	8p21.2	NKX3-1	rsl512268	T	2.92E-01	Eeles et al. NG 2009	19767753
	8p21.2	SLC25A37	rs2928679	A	2.64E-01	Eeles et al. NG 2009	19767753
	8q21.3	CPNE3,CNGB3	rs4961199	A	2.79E-02	Thomas et al. NG 2008	18264096
	8q24.21	Intergenic	rsl6901979	A	1.40E-01	Gudmundsson et al. NG 2007	17401366
	8q24.21	Intergenic	rs4242382	A	1.47E-06	Thomas et al. NG 2008	18264096
	8q24.21	POU5F1B	rs6983267	G	7.50E-06	Thomas et al. NG 2008	18264096
	8q24.21	Intergenic	rs7841060	G	1.15E-01	Yeager et al. NG 2009	19767755
	9q33.2	DAB2IP	rsl571801	T	1.46E-03	Duggan et al. JNCI 2007	18073375
	10qll.23	MSMB	rsl0993994	T	2.25E-03	Thomas et al. NG 2008	18264096
	10q26.13	CTBP2	rs4962416	C	2.67E-05	Thomas et al. NG 2008	18264096
	llpl5.5	IGF2, IGF2A, INS, TH	rs7127900	A	3.06E-01	Eeles et al. NG 2009	19767753
	llql3.2	Intergenic	rs10896449	G	2.30E-03	Thomas et al. NG 2008	18264096
	llql3.2	Intergenic	rsl2418451	A	1.38E-02	Zheng et al. CEBP 2009	19505914
	17ql2	HNF1B	rs4430796	A	1.47E-02	Gudmundsson et al. NG 2007	17603485
	17ql2	HNF1B	rsl 1649743	G	2.58E-02	Sun et al. NG 2008	18758462
	17q24.3	Intergenic	rsl 859962	G	3.80E-03	Gudmundsson et al. NG 2007	17603485
	19ql3.33	KLK15,KLK3	rs266849	A	8.04E-01	Eeles et al. NG 2008	18264097
	22ql3.2	TTLL1,BIK	rs5759167	T	3.01E-03	Eeles et al. NG 2009	19767753
	Xpll	NUDT10,NUDT11	rs5945619	C	1.89E-04	Eeles et al. NG 2008	18264097

For purposes of cross-validation, cases and controls for each respective disease were randomly divided into 10 approximately equal subgroups. Cross validation was performed by setting aside one subgroup for the purpose of testing, while using the remaining 9 subgroups (training set) to construct a model to test in the testing subset. This procedure was repeated 9 additional times with a different subgroup set aside for testing.

Models were constructed using the list of LD filtered SNPs. The list was divided into a list of previously replicated SNPs and a list of non-replicated SNPs. Associations were calculated for each non-replicated SNP on disease outcome in the training set using an allelic association analysis in PLINK[Purcell et al., 2007]. Risk alleles for each non-replicated SNP were determined from the association test. These non-replicated SNPs were then ordered by increasing association p-value and broken into lists of the top k=10 to the top k=60,000 SNPs with increasing interval size as k increases for inclusion into the polygenic risk score. Replicated SNP scores (RSS) and polygenic risk scores (PRS) were constructed separately. Risk scores were calculated as the sum of the number of risk alleles an individual carried at each locus summed across all loci included in the list. This assumes an additive model for each known SNP with equal weight applied to each locus and ignores any interactions that may exist between SNPs. For each cross validation set, PLINK was used to calculate one risk score for the replicated SNPs and a separate risk scores for the polygenic SNPs. This procedure was continued repeatedly for increasing k until the top 60,000 SNPs showing the strongest evidence for association with cancer were included into the PRS.

Unconditional logistic regression models were fit to the data in the training set with case status as the outcome and two predictor variables, normalized RSS and normalized PRS. Scores were normalized by subtracting the mean and dividing by the standard error. Models were fit for each cross-validation training set for each k. The same models and parameter estimates from the training sets were used to define predicted disease probability in the testing set. Estimates of the area under the receiver-operating characteristic curve (AUC) were obtained for training and testing sets from each of the 10 cross-validation sets. Results were averaged over the 10 cross-validation sets to determine a final estimated average AUC for the testing sets. Data manipulation and statistical analyses were carried out using R 2.8.0 (R Foundation for Statistical Computing, Vienna, Austria) and SAS 9.1 (SAS Institute Inc., Cary, NC) on a UNIX platform.

Results

Breast Cancer

Thirteen SNPs that were found to be robustly associated with breast cancer in previous studies were used to construct the RSS here. Background information regarding the replicated SNPs is in Table I. For the entire dataset, the RSS ranged from 4 to 19 with an average of 11.6 for the cases and 10.8 for the controls (p=5.83×10^-17). Logistic regression estimated an OR of 1.16 (95% CI: 1.12-1.20) for each additional risk allele in the RSS with an AUC of 0.59 and a Nagelkerke pseudo-R² of 0.039.

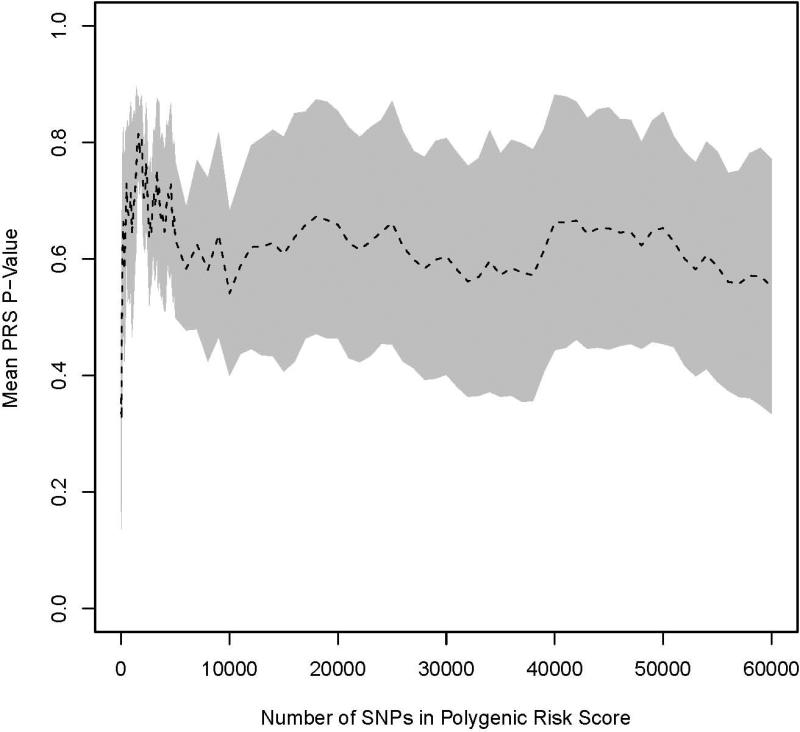
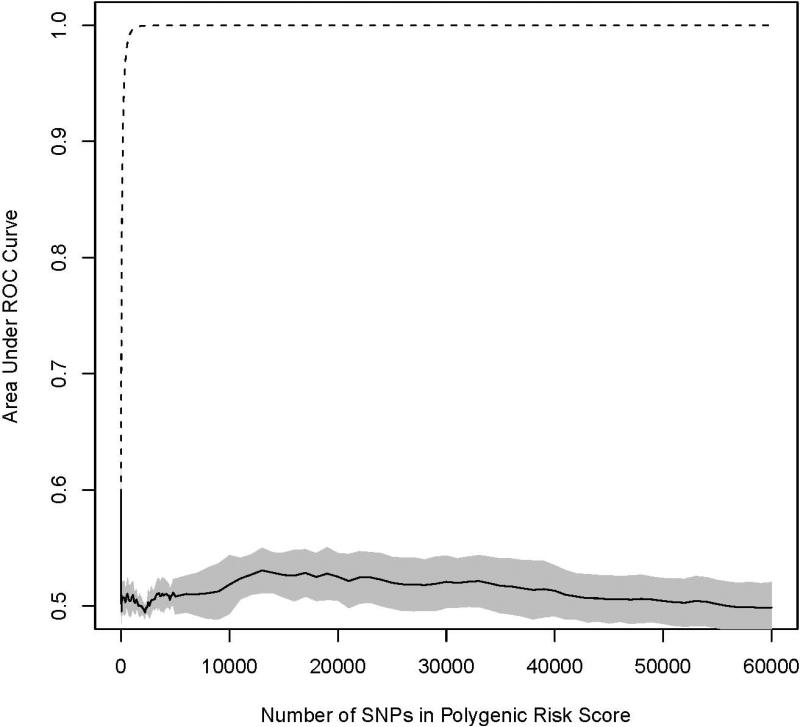
For each of the 10 cross validation sets, PRSs were constructed with increasing number of previously non-replicated SNPs added to predict the risk of BCa. We observed no statistically significant BCa association (p>0.05) between any PRS in any test set (Figure 1). Additionally, the mean AUC from the 10 cross validation sets were calculated for both the training and testing sets (Figure 2). For the training sets, average AUCs increased rapidly when the number of SNPs included in the score increased and approached 1.0 when 1,000 SNPs were included in the polygenic score. This phenomenon reflects overfitting in the training set and is used by algorithms to query whether a particular individual is in a genome-wide association study [Jacobs et al., 2009]. For testing sets, average AUCs initially dropped when the PRS was added to the RSS model and then remained relatively stable as the number of SNPs in the risk score increased. The average AUCs in the testing set ranged between 0.50 and 0.53 when both the RSS and GRS were in the model.

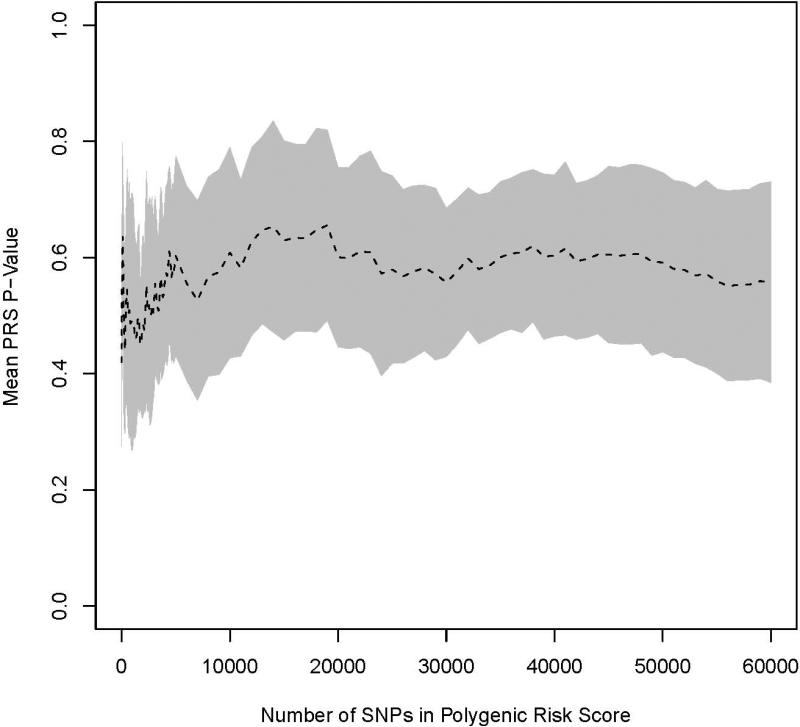
Figure 1.

Average p-values for PRS in the testing set as k increases from 10 to 60,000. Results for BCa are shown in (A) and PCa in (B). The shaded region denotes a 95% confidence interval around the mean.

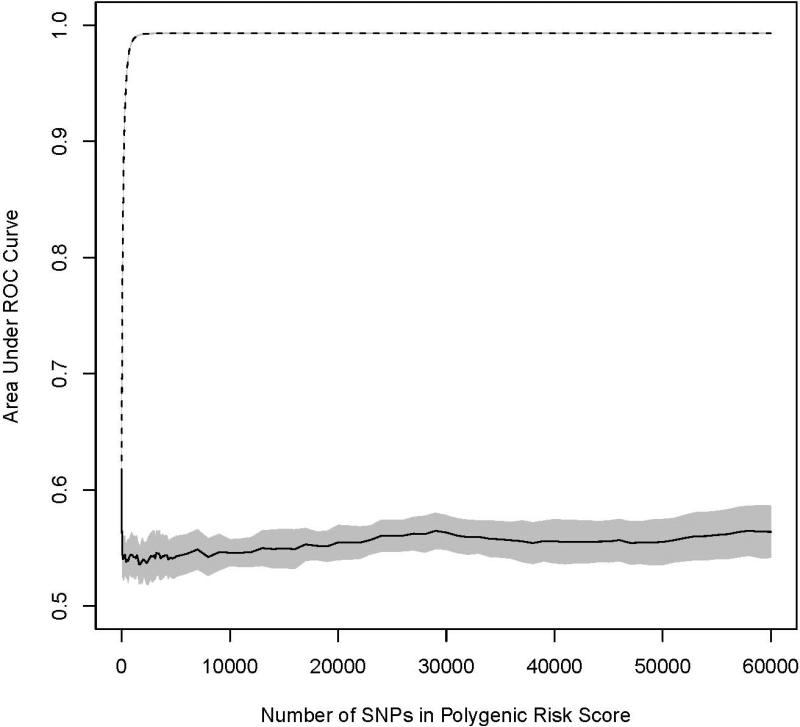
Figure 2.

Graphical trace of the average area under the receiver operator characteristic curve (AUC) across the ten cross-validation datasets for prediction of incident BCa (A) and PCa (B). The dashed line is the AUC as additional prioritized SNPs are added to the PRS in the training set (90%) and the solid line is the AUC for the same model in the testing set (10%). The shaded regions denote a 95% confidence interval around the mean.

Prostate Cancer

A total of 30 independent SNPs associated with PCa were extracted from the literature. The SNPs, their genetic location, and risk alleles are in Table I. Individual PCa RSS ranged between 12 and 38. On average, cases carried 25.0 risk alleles and controls carried 23.5 (p=2.51x10^-20). A logistic regression model fit to the entire dataset with the RSS as a predictor and PCa status as outcome indicated the RSS is a significant predictor of PCa status with every one unit in risk score associated with a 1.12 increase in the odds of incident PCa (95% CI: 1.09-1.14). The resulting model had an AUC of 0.614 and a Nagelkerke pseudo-R² of 0.051.

Ten cross validation datasets were produced to observe the effect of including additional nominally significant SNPs to a PRS, adjusting for the known associated SNPs in the RSS. None of the PRS was statistically significantly associated with prostate cancer in the testing sets (Figure 1). For AUC, the overarching pattern observed in the training sets was that of a sharp increase as additional SNPs were added to the PRS, which leveled off near an AUC of 1.0 at 1,500 SNPs. In the test sets, the primary pattern observed was a notable decrease in discrimination followed by minimal change as additional loci were included (Figure 2). The maximum AUC in the testing set of 0.569 was obtained at the first iteration when 10 loci were included into the PRS. After the inclusion of 60,000 SNPs into the PRS (approximately 35% of the SNPs in the thinned dataset) the testing set had an AUC of 0.564.

Discussion

Our results did not demonstrate that the approach of polygenic risk scores provides a more robust discrimination of risk for either breast or prostate cancer using common SNPs in a current single GWAS. The shift of the AUC was limited (less than 0.60) even when common SNPs not achieving genome-wide association were added to the score. Moreover, we did not find any evidence that polygenic risk scores were significantly associated with breast or prostate cancer risk in our sample sets. This suggests that the polygenic contributions to breast and prostate cancer beyond the known loci are subtle, and will require larger sample sizes or more sophisticated analytic approaches to discover.

In our study, it is not surprising the replicated SNPs performed better than the polygenic SNPs. The replicated SNPs are a cleaner set of signals that has been robustly replicated across several independent sample sets. These SNPs likely represent surrogates in high linkage disequilibrium with the variants that biologically contribute to specific cancer risk. Conversely, the genetic signal from the polygenic SNPs includes considerable noise, as a result of including genetic variants that are false positive markers in the PRS. While prioritizing SNPs by association p-value favors inclusion of genetic loci that are more likely to have true associations with disease causing loci, chance distribution of SNPs across the association p-value distribution allows for SNPs to be included in the PRS that are not associated with disease in the specific studies being tested. In this regard, the PRS is limited by the problem of a low signal-to-noise ratio in which, with the inclusion of each additional set of SNPs into the polygenic score, there is a possibility that additional disease-associated signal can overcome the high background, non-associated noise. The signal-to-noise ratio may be particularly problematic when the training sets are small (due to low power), or when the overall number of associated markers is small: e.g. several score instead of hundreds or thousands. Notably, using nonparametric modeling on existing GWAS data Park and colleagues [Park et al., 2010] estimate that the total number of breast, prostate, and colorectal cancer risk loci with effect sizes similar to those already discovered is 67 (95% CI 31, 173).

Our study avoided design artifact—a particular concern for these polygenic analyses[Evans, Visscher and Wray, 2009, International Schizophrenia Consortium et al., 2009]—by carrying out analyses on a homogenous population with European ancestry. Cases and controls were randomly distributed across genotyping plates, guarding our study from spurious genotyping artifacts between cases and controls. We included only high quality genotyped SNPs that passed a rigorous quality control assessment when constructing the PRSs, thus eliminating misclassification due to cross platform differences in performance. In addition, by using only genotyped SNPs, we avoided the uncertainty and error implicit in analyzing imputed genotypes into a PRS. We LD filtered the genotyped SNPs to remove an increase or decrease in discriminative ability that may be due to adding highly correlated redundant markers. Such an addition of an area of high LD to a PRS could result in substantial changes in the PRS. Furthermore, ten-fold cross validation was implemented in our dataset to minimize any potential chance findings or overtraining and improve external validity of these findings to other data sets. As evidenced by Figure 2, overtraining is a major concern when a large number of SNPs are compiled into a risk score.

The method implemented to compile risk scores in our dataset consisted of summing the number of risk alleles an individual carries. This method gives equal weight to all loci included in the risk score, regardless of the locus’ respective strength of association. Other methods of weighting the loci such as using the log of the odds ratio are possible, but produced little differences in our dataset (results not included) as well as in others[Evans, Visscher and Wray, 2009]. Such a weighting method would require large sample sizes to obtain more refined odds ratio estimates used as weights and ignores uncertainty in the estimated odds ratio. Because most odds ratio estimates are near one, we chose to present the risk allele counting method.

The AUC was the primary metric used to assess the discriminative ability of the resulting polygenic models because it can be used to assess the probability that a model can correctly distinguish a case from a control in a pair of individuals. The measure is also a summary estimate for the entire model and gives a quantitative estimate of how well the included parameters of a model are separating out cases from controls. By averaging estimates of AUC over the cross-validation testing sets, an informative metric was obtained in which to track the change in discriminative ability of each addition to the PRS. Other metrics such as R² or net reclassification indexes could have been used. We chose the AUC primarily for ease of interpretation—AUC values can directly compare samples with different case to control ratios, where R² and reclassification indexes cannot—and its close relationship to the sensitivity and specificity of a test.

In general, the results were similar for both BCa and PCa when the pool of SNPs was expanded in the PRS. Overall, in the testing sets as additional common variants (not achieving genome-wide significance) were included in the PRS there was a pattern of a noticeable drop in mean AUC initially followed by little change thereafter. Even at early intervals for the PRS, it appears more noise than signal is added to the model as evidenced by the noticeable decrease in discriminative ability of the overall model and insignificant PRS p-values in the testing set. After the initial decline, there seems to be little change in discriminative ability and PRS p-values remain insignificant. This indicates the model is saturated with noise from the PRS and any additional inclusion of SNPs into the risk score has little effect on the overall prediction ability of the model. Here, any discrimination of the model is primarily being driven by the RSS. It is noteworthy that some of the BCa and PCa loci used in the RSS were discovered in the sample sets we used. This may result in an artificial inflation of the AUC estimate for the RSS.

Although our study used the same CGEMS dataset accessed by Witte et al.[Witte and Hoffmann, 2011], our analysis produced slightly different conclusions for prostate cancer. Qualitative differences in analytic parameter settings within the polygenic risk score framework may be responsible for the observed differences. For example, Witte et al. chose not to remove known PCa SNPs from the polygenic risk score, whereas in our approach known PCa SNPs were removed and adjusted for as a separate parameter (RSS). Failing to adjust for known loci may result in known signal being detected in the PRS and, therefore, differences in overall conclusions surrounding the added significance of the PRS. The technique used to split the data into training and testing sets also differed. Witte et al. employed a 50:50 training to testing set split, while our analysis used a 90:10 split. The 50:50 split method is less powered to select SNPs for inclusion in the PRS, while the 90:10 method loses power to detect a PRS-trait association. However, when we repeated our analyses using a 50:50 split we did not see evidence for an association between GRS and either BCa or PCa (p>0.05 for all thresholds, detailed results not shown). Additionally, we pruned for linkage disequilibrium at an R² threshold of 0.20 and Witte et al. used a threshold of 0.50. Our conservative method for pruning may lose power by removing modestly tagging SNPs from the PRS, while less stringent LD pruning may lose power by upweighting large regions of high LD in the PRS that are not associated with disease. The above mentioned differences are all analytic settings for which there are currently no theoretical guidelines. The resulting slight differences in analytical conclusions suggest polygenic signals for PCa are likely weak since minor differences in analytic preferences produce conflicting qualitative results.

Our study had potential limitations related to power and the lack of a comprehensive set of common variants. The sample size of our analysis consisted of 1,145 cases and 1,142 controls for BCa, and 1,164 cases and 1,113 controls for PCa. In comparison to other studies that found significant associations of PRS with complex diseases, our total sample sizes were smaller. The Evans et al. study investigated the contribution of polygenic risk scores to several diseases with sample sizes ranging from 1,748 to 1,963 cases and a set of 1,480 common controls[Evans, Visscher and Wray, 2009]. Purcell et al. used a schizophrenia sample of 3,322 cases and 3,587 controls[International Schizophrenia Consortium et al., 2009]. The International Multiple Sclerosis Genetics Consortium used a training sample of 931 cases and 2,431 controls and a test sample of 806 cases and 1,720 controls[International Multiple Sclerosis Genetics Consortium (IMSGC) et al., 2010]. All of these studies found significant associations between PRS and disease. With a reduced sample size, our study had limited power to detect true signals and prioritize these signals for inclusion into the PRS. Furthermore, splitting the dataset into 10 equally-sized cross validation sets leaves a restricted number of cases and controls for our testing set and may explain some of the differences in the PCa results between our study and the study by Witte and Hoffman[Witte and Hoffmann, 2011]. Other, more sophisticated analytic approaches to estimating the polygenic contribution to traits may be better powered than the polygenic risk score approach. The linear mixed model approach implemented by Yang et al. [Yang et al., 2011], for example, uses all markers to estimate the additive genetic contribution to a trait (not just those below a significance threshold) and does not require the available data be split into training and test sets. Finally, our data sets included cases unselected for family history of these cancers; it is possible that it may be easier to detect a polygenic signal in data from cases with a higher proportion of affected relatives.

We conducted additional simulations to see what range of polygenic models our study was powered to detect (detailed results not shown). We had over 50% and over 90% power to detect two of the models consistent with the polygenic score results for schizophrenia (Models M1 and M2 in Purcell et al.[International Schizophrenia Consortium et al., 2009], respectively). While our results indicate there is no significant evidence for a strong polygenic effect for BCa and PCa, we cannot rule out the possibility of a weak polygenic effect. Results from our study suggests that if there is a polygenic component to breast and prostate cancer the effect is subtle and therefore the utility of using such polygenic models for genetic risk prediction may be limited.

In conclusion, our analysis found no strong evidence that polygenic risk scores improve risk prediction of breast or prostate cancer over current replicated SNP scores. With increases in sample sizes and formation of consortia, it will be possible to revisit this approach in expectation of improving risk prediction of complex diseases such as breast and prostate cancer. Innovative analytical techniques will be needed to extract genetic predictors of disease from GWAS.