Abstract
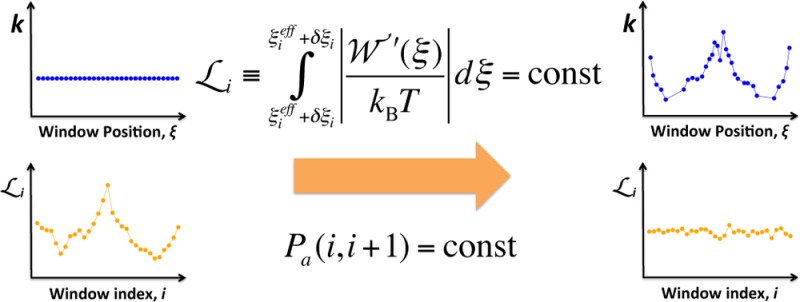
We present a theory of adaptive optimization for umbrella sampling. With the analytical bias force constant obtained from the constrained thermodynamic length along the reaction coordinate, the windows are distributed to optimize the overlap between neighbors. Combining with the replica exchange method, we propose a method of adaptive window exchange umbrella sampling. The efficiency gain in sampling by the present method originates from the optimal window distribution, in which windows are concentrated to the region where the free energy is steep, as well as consequently improved random walk.
Introduction
The potential of mean force (PMF), 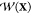 , as a function of a set of collective
variables
(CVs), X, can be formally written as
, as a function of a set of collective
variables
(CVs), X, can be formally written as
| 1 |
where kB is the Boltzmann constant, T is the temperature, β = (kBT)−1, δ(z) is a delta function of z, U is the potential energy, and R is a particular configuration of the system. Clearly, the quality of the calculated PMF relies on sampling in the configuration space, {R}. Extensive sampling to obtain the PMF of a complex system is generally difficult even by long molecular dynamics (MD) or Monte Calro (MC) simulations. To better sample along the CVs, especially in steep-PMF regions, the umbrella sampling (US) method1 has been extensively employed.
There have been many excellent US methods such as the adaptive US,2 self-healing US,3 Gaussian mixture adaptive US,4 and self-learning adaptive US5 to name a few. Except the last one, all the mentioned methods aim to achieve uniform sampling along the CVs by applying an adaptively estimated umbrella potential, which would eventually allow diffusive sampling along the CVs. The last method aims to efficiently determine (multidimensional) free energy landscape around the transition (minimum free energy) pathway by gradually adding windows over low free energy regions.
A typical system for (regular) US simulations consists of a set of windows with umbrella potentials that restrain the CVs near the center of each window, and the simulation data are postanalyzed to calculate the PMF by the weighted histogram analysis method6 or the mean force integration.7,8 For meaningful and efficient US simulations, the overlap between neighboring windows should be sufficient and well controlled. However, there has been no general theory to control the fine overlap because the window centers are system-dependently shifted to the nearest PMF minimum. In order to control the overlap systematically, there should be a quantitative measure of the overlap between a pair of windows. The average acceptance probability Pa is such a measure, which has been originally derived in the theory of replica exchange (REX) methods.9−13Pa describes the overlap between two replicas quantitatively and thus can be directly applied to control the overlap between neighboring windows in US as well.
Recently, there have been efforts in the systematic control of the overlap between windows for the US REX method.9,14 The first approach in this direction is our previous work,9 where we derived a simple relationship between the window force constant k and the window spacing d based on an analytical expression for Pa,
| 2 |
where zopt = 0.8643, which provides the optimal window overlap (i.e., Pa ≈ 0.39) based on the first passage time optimization of REX methods.9−11 Equation 2 assumes that the PMF has minimal effects on shifts of the window centers. However, when the effect of the PMF becomes significant, the window parameters based on eq 2 are no longer optimal, although it still provides a good initial guess. In addition, the optimal number of windows for efficient US simulations still needs to be determined in an empirical (and system-dependent) manner.
More recently, Dashti and Roitberg14 proposed a protocol for the optimization of US REX by realizing uniform Pa between replicas, which provides a way to determine where to put windows and how many windows are needed. However, the bias force constant were kept constant and there were only the examples with the fixed number of windows. Without optimization of the bias force constant, the statistical uncertainty in the calculated PMF from US would not be minimized15,16 and thus its convergence would be slow.
The concept of the thermodynamic length15−18 provides a rigorous way to minimize the statistical uncertainty by finding a pathway that minimizes the dissipation,15,16,18 which have been applied in optimization of thermodynamic processes.19−21 Using the information theory, the connection between the thermodynamic length and the statistical uncertainty in the free energy calculation has been studied.15,22−24 In these studies, it has been shown that the statistical uncertainty is minimized when intermediate states are spaced along a minimum distance pathway connecting these states,15,16,18 which lies on the geodesic connecting the end states.15,16
In this work, to resolve these general issues in US simulations (efficient sampling with minimal statistical uncertainty), we present a theory of adaptive optimization for umbrella sampling, which is based on equidistant window distribution along the thermodynamic length. Here, we consider one-dimensional US (X = ξ), which can be readily combined with REX methods.25,26 In the following, the theoretical background for the present method is described. Then, we derive an analytical expression for the optimal (PMF-dependent) bias force constant for US and describe an adaptive optimization that distributes the windows with the optimal bias force constant by constraining Pa. We validate the method and explore its sampling efficiency along the hidden (or orthogonal) degrees of freedom (DOF) by using a toy-model. We then examine the efficacy and the limitation of the present method by applying it to a more realistic (and complicated) example, the assembly of the transmembrane domain of glycophorin A (GpA-TM).
Theoretical Background
Let us consider a system whose canonical distribution of ξ
is given by 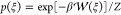 , where
, where 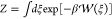 . The corresponding (regular) US system
consists of N windows and each window i is under the effective potential, Ueff(R) = U(R) + wi(ξ|ξi), where wi(ξ|ξi) is the window potential to restrain sampling
of ξ near ξi (i = 0, 1,...,N – 1). We assume that the sampling
range Λ is continuous (i.e., Λ = [ξmin, ξmax]). The sampling range at window i, Λi, can be conveniently described
by the variance of sampled ξ, σξi2, and then,
their average for the entire windows becomes σξ = ∑iσξi2/N. For
the uniform sampling along ξ, σξi = σξ2 should hold,
which is equivalent to the minimization of the total variance, ∑iσξi (see Figure 1A for schematic description). Note that the adaptive
bias force and potential methods27−30 aim to achieve this criterion
by flattening the effective potential along ξ.
. The corresponding (regular) US system
consists of N windows and each window i is under the effective potential, Ueff(R) = U(R) + wi(ξ|ξi), where wi(ξ|ξi) is the window potential to restrain sampling
of ξ near ξi (i = 0, 1,...,N – 1). We assume that the sampling
range Λ is continuous (i.e., Λ = [ξmin, ξmax]). The sampling range at window i, Λi, can be conveniently described
by the variance of sampled ξ, σξi2, and then,
their average for the entire windows becomes σξ = ∑iσξi2/N. For
the uniform sampling along ξ, σξi = σξ2 should hold,
which is equivalent to the minimization of the total variance, ∑iσξi (see Figure 1A for schematic description). Note that the adaptive
bias force and potential methods27−30 aim to achieve this criterion
by flattening the effective potential along ξ.
Figure 1.
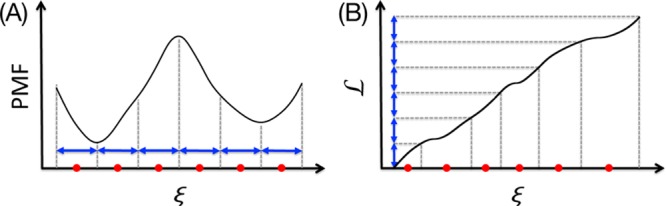
Schematic
description of the equidistant window distribution with
respect to (A) the sampling range Λ and (B) the thermodynamic
length 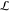 calculated
from the PMF in (A) by eq 3. By equipartitioning
Λ or
calculated
from the PMF in (A) by eq 3. By equipartitioning
Λ or 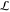 (blue arrows),
the boundaries for each
window can be easily determined (vertical gray dashed lines) and the
midpoint can be assigned to the center of each window (red circles).
Note that the windows are not equally distributed along ξ in
(B).
(blue arrows),
the boundaries for each
window can be easily determined (vertical gray dashed lines) and the
midpoint can be assigned to the center of each window (red circles).
Note that the windows are not equally distributed along ξ in
(B).
However,
in the framework of US, this criterion does not imply
the optimal sampling for efficient PMF calculations because the variance
of the estimated PMF at each window, 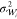 , is larger where the PMF changes faster
and is smaller near the PMF minima, which increases the statistical
errors and thus results in slow convergence of the calculated PMF.
It has been known that the minimization of the statistical errors
in the calculated free energy is equivalent to that of the total variance
of the PMF estimated from intermediate states (i.e., windows in US)
connecting two end states.15,16,23,24 In the context of US, the equidistant
window distribution along the thermodynamic length corresponds to
the window distribution that minimizes
, is larger where the PMF changes faster
and is smaller near the PMF minima, which increases the statistical
errors and thus results in slow convergence of the calculated PMF.
It has been known that the minimization of the statistical errors
in the calculated free energy is equivalent to that of the total variance
of the PMF estimated from intermediate states (i.e., windows in US)
connecting two end states.15,16,23,24 In the context of US, the equidistant
window distribution along the thermodynamic length corresponds to
the window distribution that minimizes 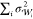 , which would result
in the maximized PMF
convergence (with the least statistical errors). Therefore, we consider
the thermodynamic length as an alternative metric rather than ξ.
, which would result
in the maximized PMF
convergence (with the least statistical errors). Therefore, we consider
the thermodynamic length as an alternative metric rather than ξ.
The thermodynamic length 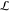 along a given
path connecting two states
can be defined as the length traveled along the free energy coordinate.15−18 Assuming that the PMF is known (or can be estimated from the data
of the previous US simulations),
along a given
path connecting two states
can be defined as the length traveled along the free energy coordinate.15−18 Assuming that the PMF is known (or can be estimated from the data
of the previous US simulations), 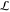 can
be written as
can
be written as
| 3 |
where z̅ ≡ βz. Similarly,
we define the thermodynamic length for a given
window i, 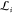 , as the length between two states,
ξieff – δξi and
ξi + δξi, where ξieff is the center of the window and δξi is its half-range, which is defined by δξi ≡ ασξi. Then, we define the range Λi = [ξi – δξ, ξieff + ξi] as the thermally accessible
range of ξ at window i, that is, 2kBT range of ξ with respect to the
effective PMF,9 which is the sum of the
PMF and the window potential. The above definition is reasonable because
the majority of sampled ξ is within this range. With the Gaussian
approximation of the sampled ξ-distribution31 (i.e., the harmonic approximation of the effective PMF),
one can determine α = 2 (see below). Note that Λi is wider than that from the equipartition of
, as the length between two states,
ξieff – δξi and
ξi + δξi, where ξieff is the center of the window and δξi is its half-range, which is defined by δξi ≡ ασξi. Then, we define the range Λi = [ξi – δξ, ξieff + ξi] as the thermally accessible
range of ξ at window i, that is, 2kBT range of ξ with respect to the
effective PMF,9 which is the sum of the
PMF and the window potential. The above definition is reasonable because
the majority of sampled ξ is within this range. With the Gaussian
approximation of the sampled ξ-distribution31 (i.e., the harmonic approximation of the effective PMF),
one can determine α = 2 (see below). Note that Λi is wider than that from the equipartition of 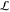 for optimal
overlap between neighboring
windows. The sampling along the free energy coordinate (PMF) would
be optimal when
for optimal
overlap between neighboring
windows. The sampling along the free energy coordinate (PMF) would
be optimal when 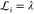 (constant) for all the windows16 (schematically
shown in Figure 1B), which results in the following
constraint:
(constant) for all the windows16 (schematically
shown in Figure 1B), which results in the following
constraint:
| 4 |
A naturally arising question is how to determine the optimal bias force constant (eq 12) for each window that satisfies eq 4.
Optimal Bias Force Constant
To address this question, let us consider a typical harmonic window potential, wi(ξ|ξi) = ki(ξ – ξi)2/2. We start with the assumption that the distribution of sampled ξ, pb(ξ|ki,ξi), can be well approximated by a Gaussian distribution pG(ξ|kieff, ξi), that is, pb(ξ|ki, ξi) ≈ pG(ξ|kieff, ξi), where kieff is the effective bias force constant and ξi is a shifted center from the (original or input) window center ξi due to the PMF effect:31
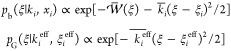 |
5 |
where k̅ieff = 1/σξi. The effective PMF, 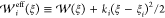 , is then approximated to
, is then approximated to 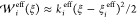 . Near ξieff,
. Near ξieff, 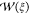 can be approximated to
can be approximated to
| 6 |
where Δξi = ξ – ξieff. By substituting eq 6 into eq 5 and comparing the exponents between pb(ξ|ki,ξi) and pG(ξ|ki, ξieff), one can obtain the relations between the window parameters and the effective ones:
| 7 |
It should be noted that, without properly chosen kieff, eq 4 is not satisfied in general. Therefore, for an optimal US, one needs to find a set of {ki, ξieff} that satisfies eq 4 for all the windows. The corresponding set of window parameters ({ki,ξi}) for the subsequent US simulations are then determined by eq 7.
An analytic solution of eq 4 can be obtained as follows. We start from rewriting eq 4 as
| 8 |
By noting that 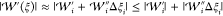 for ξ near ξieff, we obtain
for ξ near ξieff, we obtain
| 9 |
where 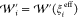 and
and 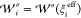 . Then, by assuming the equality in eq 9 and solving it, we obtain
. Then, by assuming the equality in eq 9 and solving it, we obtain
| 10 |
The (unknown) parameters α and λ
in eq 10 can be determined as follows. By noting
that the effective PMF can be approximated to a harmonic function,
the thermodynamic length with respect to 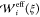 for Λi can be written as
for Λi can be written as
| 11 |
Because we
defined Λi as the thermally accessible
range, 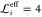 , we obtain α = 2. Hereafter,
we omit
the window index unless it is necessary, and consider k and keff as a function of ξ. One
can show that λ ≤ α2 for US, which implies
that the maximum
, we obtain α = 2. Hereafter,
we omit
the window index unless it is necessary, and consider k and keff as a function of ξ. One
can show that λ ≤ α2 for US, which implies
that the maximum 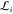 cannot exceed
cannot exceed 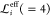 . By matching
. By matching 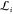 and
and 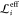 (λ = α2 = 4), we
obtain an analytical expression for the optimal effective bias force
constant keff(ξ)
(λ = α2 = 4), we
obtain an analytical expression for the optimal effective bias force
constant keff(ξ)
| 12 |
Adapative Optimization for Umbrella Sampling
With the effective bias force constant (eq 12) that satisfies eq 4 (i.e., the equidistant constraint along the thermodynamic length), the next question for optimal US is how to distribute windows with well controlled overlap between neighbors. To achieve this, we make use of Pa (the average acceptance probability) as a quantitative measure of the overlap between a pair of windows, which can be formally written for US as
| 13 |
where subscripts 1 and 2 are indices for a pair of windows i and j, Pex = min{1,exp(−βΔ)} is the metropolis criterion for the exchange between the pair with Δ being the difference between the effective potential before and after the exchange of the windows. In the theories of the optimization of REX methods10−13 and in our previous work,9 the optimal performance of window exchange umbrella sampling (WEUS) is achieved when Pa between neighboring windows is a constant whose value is in 0.28–0.4, depending on the exchange schemes. In this work, we set Pa to 0.4, which is optimal for the so-called “even-odd” exchange scheme.9,10 For efficient evaluation of eq 13, we obtained an accurate analytic expression for Pa (see Appendix for details).
With eqs 7, 12, and 13, for a given 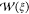 calculated after a (short) US simulation,
the windows can be optimally redistributed over Λ as follows.
Let us consider a window at one fixed end-point, ξ0 = ξmin. The effective window parameters, ξ0eff and k0 = keff(ξ0eff), and the (updated)
bias force constant k0 are determined
from eqs 7 and 12. The
ξ1 and k1eff of the next window 1 are then determined by satisfying the constraint, Pa = 0.4, and the corresponding ξ1 and k1 are obtained by eq 7. This procedure is repeated until Λ is covered by the
windows. It should be noted that the extensive evaluation of Pa can be efficiently performed by using the
analytic expression for eq 13. After the redistribution,
an estimate of the optimal number of windows, Nopt, is obtained as an outcome, which may be different from N for the previous simulation.
calculated after a (short) US simulation,
the windows can be optimally redistributed over Λ as follows.
Let us consider a window at one fixed end-point, ξ0 = ξmin. The effective window parameters, ξ0eff and k0 = keff(ξ0eff), and the (updated)
bias force constant k0 are determined
from eqs 7 and 12. The
ξ1 and k1eff of the next window 1 are then determined by satisfying the constraint, Pa = 0.4, and the corresponding ξ1 and k1 are obtained by eq 7. This procedure is repeated until Λ is covered by the
windows. It should be noted that the extensive evaluation of Pa can be efficiently performed by using the
analytic expression for eq 13. After the redistribution,
an estimate of the optimal number of windows, Nopt, is obtained as an outcome, which may be different from N for the previous simulation.
In a typical US simulation,
however, N is not
changed. By a simple modification of eq 12 and
the window distribution procedure, one can still optimize US with
a fixed N. First, let us consider keff(ξ) when N > Nopt (ρ < 1 where ρ = Nopt/N). In this case, one can naturally
scale λ by ρ (λ → ρλ) in eq 4. Then, keff(ξ)
for optimal US with N windows can be obtained by
substituting 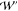 and
and 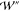 with
with 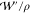 and
and 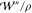 in eq 12 as
in eq 12 as
| 14 |
When N < Nopt (ρ > 1), the above scaling cannot be applied because k(ξ) could be negative around the PMF minima. By decreasing the target value of Pa for the distribution of windows, keff(ξ) for ρ = 1 can still be used in the optimization procedure. However, lowering Pa implies localized sampling around the window centers. Therefore, to maintain Pa, we sacrifice the optimal sampling by adding a bias force constant
| 15 |
so that the same scaling can be applied for ρ > 1 as well. Therefore, the optimization of the distribution of N windows can be performed with the adjustable parameter ρ. This modified optimization procedure can be readily combined with the WEUSMD method, which is termed adaptive WEUSMD (aWEUSMD).
Simulation Details
To validate and explore the sampling efficiency of aWEUSMD along the hidden (or orthogonal) DOF, we considered two systems: (1) a toy model and (2) the assembly of the GpA-TM.
The toy model is designed to examine not only the sampling along an explicit CV but also an efficiency gain in sampling along the orthogonal DOF if any. In the model, a particle (whose mass is the same as phosphorus) is moving under the potential U(x,y) = U0(x,y) + UR(x,y) (in kcal/mol). As shown in Figure 2A, it has four Gaussian wells and barriers along x- and y-directions, which are described by U0(x,y):
| 16 |
where r = (x,y), r1 = (4,4), r2 = (−4,4), r3 = (−4,–4), r4 = (4,–4), Hx = 5, and Hy is the adjustable barrier along y-direction. The particle is restrained in a bounded area by UR(x,y):
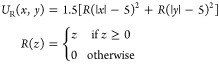 |
17 |
Figure 2.
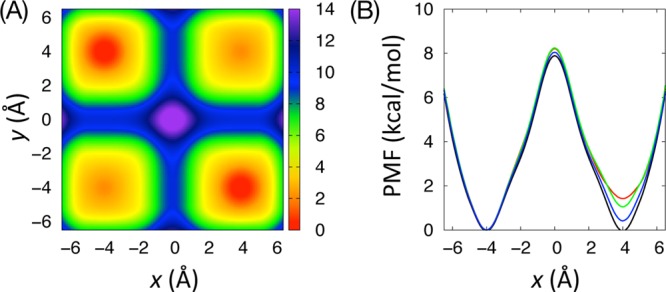
(A) Potential energy, U(x,y), of the model system
with Hy = 6 in eq 16. (B) The one-dimensional
PMF, 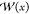 , calculated from U(x,y) (black) and the results of 120-ns
simulation data from USMD (red), WEUSMD (green), and aWEUSMD (blue)
with N = 31 windows.
, calculated from U(x,y) (black) and the results of 120-ns
simulation data from USMD (red), WEUSMD (green), and aWEUSMD (blue)
with N = 31 windows. 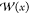 from U(x,y) is calculated by eq 1 and
those from simulations are calculated by WHAM.
from U(x,y) is calculated by eq 1 and
those from simulations are calculated by WHAM.
By varying Hy from 5 to 6.5 with the increment of 0.5, we performed 120-ns Langevin dynamics MD simulations of USMD, WEUSMD, and aWEUSMD for a set of the number of windows, N ∈ {21,31,41,51,61}, with two fixed end points at xmin = −6 Å and xmax = 6 Å. Initially, the windows were equally distributed along x with d = (xmax – xmin)/(N – 1) and k was obtained from eq 2. We have performed nine simulations for each set of Hy and N, where the initial x-coordinate was set to each window center. The initial y-coordinate y0 was set to y0 = 3.8 + 0.05r, where r ∈ {0,1,···,8}.
For a more realistic (and complicated) example, we considered the assembly of the right-handed GpA-TM dimer because it has been extensively studied for transmembrane (TM) helix assembly32−35 and represents one of the tightest interfacial packing (with the well-known GxxxG motif) among all the known TM helix interfaces. Such tight packing makes it challenging to sample the conformational space (e.g., right-handed to left-handed dimer at short helix−helix distance rHH) and thus makes the GpA-TM to be a valuable target to assess the sampling power.35 We defined the GpA-TM as 72EITLI IFGVM AGVIG TILLI SYGIR96, in which we have chosen Cα atoms of residues 76–92 to define the helix principal axis for rHH and the crossing angle Ω.36,37 For the NMR structure (PDB: 1AFO),38 the calculated rHH and Ω are 6.59 Å and −39.2°, respectively.39 To test and compare the sampling power of WEUSMD and aWEUSMD, we prepared three sets of initial configurations of GpA-TM: left-handed (IS1, Ω < 0), right-handed (IS2, Ω > 0), and parallel (IS3, Ω ≈ 0) helix–dimer interfaces.
The initial configurations were generated from the NMR structure by translating each helix along rHH and then by rotating the helices along the helix–helix distance vector for a desired Ω. A total of 80 windows were generated for each initial configuration set in a rHH range 5.2–21 Å with d = ΔrHH = 0.2 Å and the restraint force constant k obtained from eq 2 for WEUSMD (initial k for aWEUSMD). Then, we have performed 200-ns WEUSMD and aWEUSMD for IS1, IS2, and IS3. For computational efficiency, the IMM1 implicit membrane model40 was used with the hydrophobic thickness of 23 Å to mimic a dimyristoylphosphatidylcholine (DMPC) lipid bilayer.
All the simulations were performed using
CHARMM.41 For GpA-TM simulations, we used
the SHAKE algorithm and
default IMM1 options. We used a time step of 2 fs and the collision
frequency γ = 5 ps–1, which is a typical value
for Langevin dynamics with proteins. Window exchanges were attempted
every 1 ps and controlled by the REPDSTR module42 in CHARMM. In aWEUSMD, the window parameters were updated
every 0.2 ns. The adaptive update were controlled by in-house Python
scripts, which take the window parameters and the time series of ξ
(x or rHH) for all the
windows from the previous simulation as input. The derivatives of
the PMF (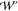 and
and 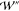 ) were calculated, for the numerical stability,
using the cubic spline interpolation of
) were calculated, for the numerical stability,
using the cubic spline interpolation of 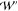 obtained by the umbrella integration method.31 The resulting derivatives were used to obtain
the updated window parameters for the next simulation by eqs 7 and 12–15. We limited the maximum shift of ξi in one update cycle by d/4 for its smooth
evolution.
obtained by the umbrella integration method.31 The resulting derivatives were used to obtain
the updated window parameters for the next simulation by eqs 7 and 12–15. We limited the maximum shift of ξi in one update cycle by d/4 for its smooth
evolution.
Results and Discussion
Toy Model
In this section, we show
the results from
a representative parameter set, Hy = 6 and N = 31 (see Supporting
Information section S1 for the results from all the tested
parameter sets). The one-dimensional (1D) PMF, 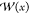 , calculated from the results of USMD, WEUSMD,
and aWEUSMD for y0 = 4.1 are shown in
Figure 2B. The accuracy of the aWEUSMD-PMF
is the best among the three methods, while the WEUSMD-PMF is marginally
better than the USMD-PMF. The most obvious reason
for the improved accuracy of the PMFs from WEUSMD and aWEUSMD over
USMD is the regular window exchange attempts, which facilitates the
sampling of configurations. This improvement is clearly shown in Figure 3 by comparing the conditional probability, P(y|x) ≡ P(x,y)/P(x), where P(x) and P(x,y) are
the populations sampled by simulations.
, calculated from the results of USMD, WEUSMD,
and aWEUSMD for y0 = 4.1 are shown in
Figure 2B. The accuracy of the aWEUSMD-PMF
is the best among the three methods, while the WEUSMD-PMF is marginally
better than the USMD-PMF. The most obvious reason
for the improved accuracy of the PMFs from WEUSMD and aWEUSMD over
USMD is the regular window exchange attempts, which facilitates the
sampling of configurations. This improvement is clearly shown in Figure 3 by comparing the conditional probability, P(y|x) ≡ P(x,y)/P(x), where P(x) and P(x,y) are
the populations sampled by simulations.
Figure 3.
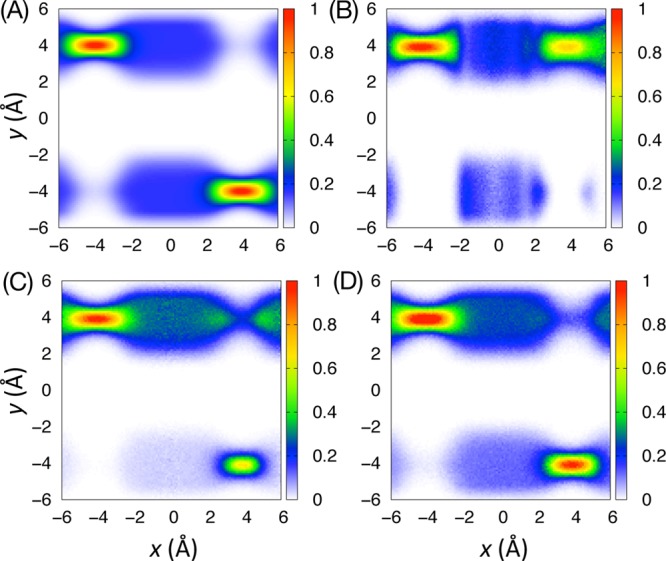
Conditional probability, P(y|x), calculated from (A) U(x,y), (B) USMD, (C) WEUSMD, and (D) aWEUSMD for Hy = 6 and N = 31. P(y|x) is normalized by max{P(y|x)|| x| ≤ 6 and |y| ≤ 6} and the binwidth is 0.1 Å for both x- and y-directions.
The sampling power (i.e., the accuracy of the sampling compared to the reference) can be quantitively estimated by the Kullback–Leibler divergence43
| 18 |
where Pr(y|x) is calculated from U(x,y), Nbin,x is the number of bin size along x, and xi and yj are the i- and j-th bins along x and y, respectively. Smaller values of DKL indicate better agreement of P(y|x) with Pr(y|x), and DKL vanishes when they are identical. In addition, the relaxation time of DKL, τ, can be a measure of the efficiency, estimated by fitting DKL(t) to an exponential function: DKL(t) = a+b exp (−t/τ). As shown in Figure 4A, the WEUSMD-DKL (τ = 18.6 ± 1.1 ns) decays much faster than USMD-DKL (τ = 68.5 ± 14.4 ns), and aWEUSMD-DKL (τ = 8.91 ± 0.47 ns) relaxes even faster; similar results are obtained for most parameter sets examined (Supporting Information Figure S1 and Table S1).
Figure 4.
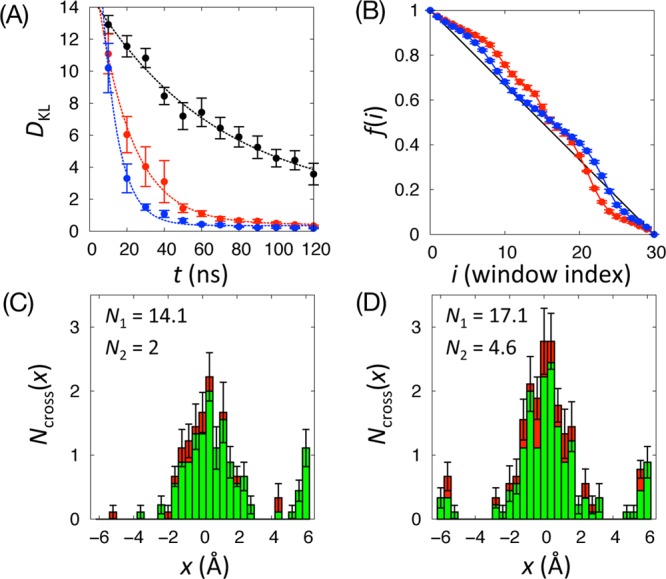
(A) Kullback–Leibler divergence DKL calculated from 10-ns blocks of P(y|x) from USMD (black), WEUSMD (red), and aWEUSMD (blue) by eq 18. Shown together are the exponential fits of DKL (dashed lines). (B) The fraction of replicas that have visited the lowest-index window, f(i), in eq 19, from WEUSMD (red) and aWEUSMD (blue) simulations. Shown together is f(i) for the ideal random walk of replicas (black line). (C–D) The histogram of the number of y-barrier crossing, Ncross(x), from (C) WEUSMD and (D) aWEUSMD simulations. Ncross(x) is the sum of the number of crossing from y > 0 to y < 0, N1(x) (green), and that in the opposite direction, N2(x) (red). The total number of y-barrier crossing is denoted by Ncross and similarly by N1 and N2. In all the figures, the data are averaged over nine independent simulations and the error bars represent the standard errors.
The efficiency gain in aWEUSMD over WEUSMD can be attributed
to
the optimal window distribution (Pa =
0.4) with keff(x), where
the windows are concentrated in steep PMF (high 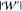 ) regions. In these regions, the y-barrier is lower than those around 1D-PMF minima (x = 4 or −4 in Figure 2B),
which results in better sampling along y-direction
in aWEUSMD, that is, the increased number of y-barrier
crossing Ncross (Figures 4C and D). As expected, there is no meaningful increase in Ncross from WEUSMD compared to that from USMD
(Supporting Information Figure S2 and Table S2). Considering the fact that aWEUSMD optimizes WEUSMD only along
the explicit CV (i.e., the x axis), the increase
in Ncross (along the y axis) is noteworthy.
) regions. In these regions, the y-barrier is lower than those around 1D-PMF minima (x = 4 or −4 in Figure 2B),
which results in better sampling along y-direction
in aWEUSMD, that is, the increased number of y-barrier
crossing Ncross (Figures 4C and D). As expected, there is no meaningful increase in Ncross from WEUSMD compared to that from USMD
(Supporting Information Figure S2 and Table S2). Considering the fact that aWEUSMD optimizes WEUSMD only along
the explicit CV (i.e., the x axis), the increase
in Ncross (along the y axis) is noteworthy.
In addition, there is an efficiency gain from the improved random walk of replicas, which can be quantified as the fraction of replicas that have visited the lowest-index window most recently,11,44
| 19 |
where n0(i) is the accumulated number of replicas with traveling state “0” monitored at window i during the course of simulation and nN–1(i) is similarly defined. The traveling state of a given replica is assigned (or updated) to “0” or “N – 1” only when it reaches at the lowest- or the highest-index window, 0 or N – 1, respectively. For the ideal random walk of replicas, f(i) should be linear.11,44 By comparing eq 3 with eq 25 in ref (45) (a work for the optimization of replica’s random walk), it is clear that aWEUSMD indeed improves the random walk as well, as shown in Figure 4B; similar results are obtained for most parameter sets examined (Supporting Information Figure S3).
GpA-TM Assembly
In this section, we show the results
from the WEUSMD and aWEUSMD for the assembly of the GpA-TM starting
with the initial configurations with left-handed (IS1) and right helix–dimer
interfaces (IS2) (see Supporting Information section S2.2 for the results from the parallel TM dimer initial
configurations, IS3). Figure 5 shows the 1D-PMF
as a function of rHH, 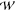 (rHH), for IS1
and IS2. There is significant difference between the IS1-PMF and the
IS2-PMF from WEUSMD, which is originated from incomplete sampling
(see Figures 6A and C). The agreement between
the IS1-PMF and the IS2-PMF from aWEUSMD is significantly improved,
which we attribute to the improved sampling power of aWEUSMD over
WEUSMD.
(rHH), for IS1
and IS2. There is significant difference between the IS1-PMF and the
IS2-PMF from WEUSMD, which is originated from incomplete sampling
(see Figures 6A and C). The agreement between
the IS1-PMF and the IS2-PMF from aWEUSMD is significantly improved,
which we attribute to the improved sampling power of aWEUSMD over
WEUSMD.
Figure 5.
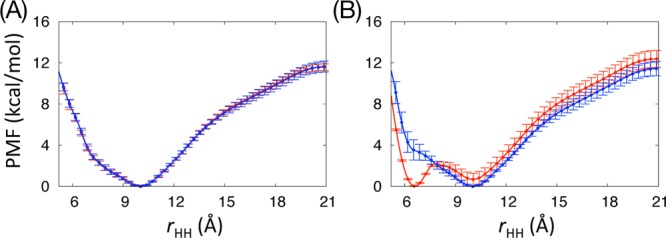
PMF as a function of rHH, 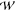 (rHH), calculated
from WEUSMD (red) and aWEUSMD (blue) starting from the initial configurations
of (A) left-handed (IS1) and (B) right-hand (IS2) helix-dimer interfaces.
For the PMF calculation, we used trajectories from 40 ns to 200 ns.
The error bars represent the standard deviations calculated from 16
10-ns block average PMFs.
(rHH), calculated
from WEUSMD (red) and aWEUSMD (blue) starting from the initial configurations
of (A) left-handed (IS1) and (B) right-hand (IS2) helix-dimer interfaces.
For the PMF calculation, we used trajectories from 40 ns to 200 ns.
The error bars represent the standard deviations calculated from 16
10-ns block average PMFs.
Figure 6.
Conditional probability, P(Ω|rHH), calculated from the results of (A) WEUSMD and (B) aWEUSMD for IS1. P(Ω|rHH) calculated from the results of (C) WEUSMD and (D) aWEUSMD for IS2. P(Ω|rHH) is normalized by max{P(Ω|rHH)} and the binwidth is ΔrHH = 0.05 Å and ΔΩ = 6°.
The improved sampling efficiency of aWEUSMD over WEUSMD is supported by the conditional probability P(Ω|rHH), as shown in Figure 6. The agreement between P(Ω|rHH) calculated from aWEUSMD for IS1 and IS2 is improved up to shorter rHH ≈ 7 Å (Figures 6B and 6D) compared to the results from WEUSMD, which show good agreement for rHH > 9 Å. This improvement allows the sampling of the right-handed NMR structure-like conformations in aWEUSMD with IS1 (Figure 6B and Supporting Information Figure S4B), indicating that aWEUSMD indeed promotes the sampling along Ω, where no restraint potential was applied.
The sampling power of aWEUSMD and WEUSMD for the GpA-TM assembly are quantitatively compared by DKL of Pt(Ω|rHH) with respect to Pr(Ω|rHH) from the results of 2D-WEUSMD in our previous work,35 where Pt(Ω|rHH) is calculated from the trajectories up to time t. As shown in Figure 7, the aWEUSMD-DKL relaxes faster to its estimated steady-state value, DKLss, compared to the WEUSMD-DKL. For IS1, the estimates of (DKL,τ) from aWEUSMD and WEUSMD are (0.515 ± 0.004,10.27 ± 0.53 ns) and (1.538 ± 0.002,14.20 ± 0.76 ns), respectively. For IS2, these estimates are (0.185 ± 0.003,12.84 ± 0.89 ns) and (0.541 ± 0.021,37.89 ± 3.59 ns) for aWEUSMD and WEUSMD, respectively. Although DKL is a quantity that dictates both the accuracy and the efficiency of the sampling, it should be noted that this quantity is not always available in general because the probability distribution of the reference state needs to be known a prior.
Figure 7.
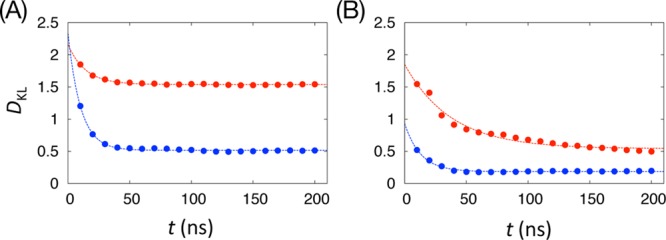
Kullback–Leibler divergence DKL calculated using Pt(Ω|rHH) from WEUSMD (red) and aWEUSMD (blue) for (A) IS1 and (B) IS2 by eq 18 with respect to Pr(Ω|rHH) calculated from 2D-PMF in ref (35). Pt(Ω|rHH) is calculated from trajectories up to time t. Shown together are the exponential fits of DKL (dashed lines).
In aWEUSMD, as shown in Figure 8, the window parameters relax to their limiting values once the PMF is converged (albeit with fluctuations). The relaxation time of the window centers (including the effective ones) was estimated to be about 4 ns (20 update cycles). The estimated τ of the bias force constants (including the effective ones) are about 20 ns and 26.5 ns for IS1 and IS2, respectively. Interestingly, τ for the bias force constants are well correlated to that of DKL. This good correlation enables us to estimate the efficiency by τ of window parameters without the need of DKL. However, it should be noted that the converged window parameters does not guarantee the convergence of the PMF to the true one because aWEUSMD does not actively sample along the hidden DOF.
Figure 8.
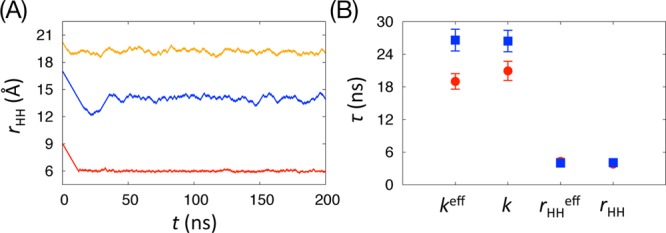
(A) Time-series of windows center (rHH,i) for three windows (i = 19,59, and 75). (B) The average relaxation time τ of window parameters for IS1 (red) and IS2 (blue). The error bars are the standard errors of the average τ over the entire windows.
Discussion
Such an overlap problem can be alleviated in the present optimization method because of (1) the minimization of the shift in the windows center by the adaptively optimized (PMF-dependent) bias force constants and (2) the concentrated window distribution in the steep PMF regions with well-controlled overlap between neighboring windows by constraining Pa. However, it should be noted that, when N ≪ Nopt (ρ ≫ 1), aWEUSMD with fixed N cannot overcome this problem although it performs better than WEUSMD and USMD (data not shown). By relaxing the fixed N condition, aWEUSMD would be free of the overlap problem along ξ.
In this work, the efficiency of all the tested methods (USMD, WEUSMD, and aWEUSMD) was estimated by the relaxation time (τ) of DKL. We observed that τ of DKL is well correlated with that of window parameters which would be stable once the PMF is converged. Therefore, even in a situation in which one cannot calculate DKL because of unknown reference state, the sampling efficiency (especially, convergence rate) can be estimated by τ of the window parameters (see Figure 8).
As shown in Figure 4A, the efficiency and sampling power of aWEUSMD and WEUSMD are significantly better than those of USMD due to the REX. The quality of REX is improved by aWEUSMD compared to that in WEUSMD, which is more clearly shown for smaller N but becomes less obvious as N increases (Figure S3). In Figure 9, we plotted f(i) obtained from the results of WEUSMD and aWEUSMD for the GpA-TM assembly. Although the quality of REX was improved by aWEUSMD, the significant nonlinearity in f(i) indicates that aWEUSMD has limited power in optimization of the flux of replicas, which we attribute to the incomplete sampling along the hidden DOF due to high barriers (>6 kcal/mol).
Figure 9.
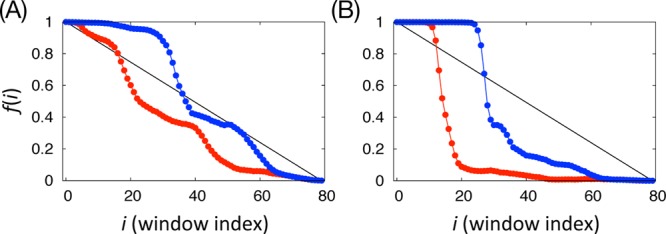
Fraction of replicas that have visited the lowest-index window, f(i), in eq 19, from WEUSMD (red) and aWEUSMD (blue) simulations for (A) IS1 and (B) IS2. Shown together is f(i) for the ideal random walk of replicas (black line).
The REX itself does not improve the barrier crossing along the hidden DOF for a given replica (see Supporting Information Figure S2). However, in aWEUSMD, where the windows are more densely distributed in the steep PMF regions (with optimal bias force constants), there are more barrier crossing events than WEUSMD and USMD. This implies that the present adaptive optimization method indeed improves the sampling efficiency of US along the hidden DOF. However, it should be noted that aWEUSMD does not actively sample the hidden DOF, as attempted in some recent efforts.28,29 Therefore, the efficiency gain in aWEUSMD over WEUSMD is limited by the barrier height along the hidden DOF. The results from the toy-model suggests that aWEUSMD can overcome the barriers along the hidden DOF, whose height is up to about 6 kcal/mol. It is consistent with the results from the GpA-TM assembly in that the sampling along Ω is improved up to rHH ≈ 7 Å, at which the barrier height along Ω is about 6 kcal/mol.35
Concluding Remarks
In this work,
we present a theory of adaptive optimization for
umbrella sampling for optimal PMF calculations based on two constraints:
(1) the uniform thermodynamic length for all the windows (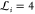 ) and
(2) the uniform average acceptance
probability between neighboring windows (Pa = 0.4). From the first constraint, we obtained an analytic expression
for the effective bias force constant keff(ξ). Then, the windows are distributed by constraining Pa = 0.4, which is known to be optimal for the
exchange scheme chosen for the present work.
) and
(2) the uniform average acceptance
probability between neighboring windows (Pa = 0.4). From the first constraint, we obtained an analytic expression
for the effective bias force constant keff(ξ). Then, the windows are distributed by constraining Pa = 0.4, which is known to be optimal for the
exchange scheme chosen for the present work.
As an immediate consequence of the present theory, an estimate of the optimal number of windows Nopt and a parameter ρ (=Nopt/N) are obtained. The latter provides a criterion from which one can judge whether the given number of windows N is sufficient or not: when ρ ≈ 1, N is close to Nopt. Sampling along ξ by aWEUSMD would be proper as long as ρ ≤ 1, whose efficiency can be conveniently estimated by the relaxation time (τ) of the window parameters. However, when N ≪ Nopt, aWEUSMD with fixed N cannot overcome the overlap problem, which is an intrinsic limitation of any US-type methods. By relaxing the fixed N condition, aWEUSMD would be free of the overlap problem along ξ.
The efficiency gain in aWEUSMD over WEUSMD originates from the optimal window distribution concentrated in the steep PMF regions, where more barrier crossing along the hidden (or orthogonal) DOF are feasible, and also from the consequently improved random walk of replicas. As a result, the synergetic improvements in the sampling along both explicit and hidden DOF by aWEUSMD make the PMF converge faster than WEUSMD. However, it should be noted that the advantage of aWEUSMD over WEUSMD is limited by the barrier height along the hidden DOF. The results from the two test cases suggest that aWEUSMD can help sampling along the hidden DOF, whose barrier height is up to about 6 kcal/mol.
In this work, we fixed N in aWEUSMD for comparison with USMD and WEUSMD with the same N. If we relax this condition, a better performance of aWEUSMD would be achieved by employing self-learning scheme, analogous to that in the self-learning adaptive US.5 In this scheme, windows are added gradually until N reaches Nopt starting from aWEUSMD with small N. Then, aWEUSMD would be free of the overlap problem and would exploit its other advantages over WEUSMD (improved random walk of windows and sampling along the hidden DOF) simultaneously. This version of aWEUSMD (self-learning aWEUSMD) would be more useful in one-dimensional US simulations for efficient sampling and PMF calculations.
Acknowledgments
This work was supported by NIH R01-GM092950 and XSEDE MCB070009.
Glossary
Abbreviations
- PMF
potential of mean force
- CV
collective variable
- MD
molecular dynamics
- MC
Monte Carlo
- US
umbrella sampling
- REX
replica exchange
- DOF
degrees of freedom
- WEUS
window exchange US
- aWEUSMD
adaptive WEUSMD
Appendix: An Accurate Analytic Expression for Pa
Here, we derive an accurate analytical approximate expression for Pa between a pair of windows i and j for arbitrary window parameters (ξi,ki) and (ξj,kj), whose corresponding effective window parameters, (ξieff, ki) and (ξjeff, kj). Formally, Pa between the pair of windows is given by the integral,
| 20 |
where subscripts 1 and 2 are indices for a pair of windows i and j, Pex = min{1,exp(−βΔ)} is the metropolis criterion for the exchange between the pair, and Δ is
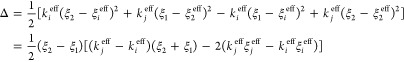 |
21 |
It can be shown easily that
| 22 |
Simply, one can evaluate Pa by the numerical integration of eq 13 (or eq 22). However, its analytical expression can provide deeper understanding and insights, which is helpful in further applications. For example, when kieff = kj, the exact analytical expression of eq 13 is available,9 which is utilized to obtain eq 2 for the relationship between the window force constant and the window spacing for WEUSMD. In general cases (when kieff ≠ kj), there has been no such analytical expression for Pa, which we are in need of, for fast and accurate evaluation of eq 13 in order to redistribute windows in our adaptive optimization for US method.
The starting point is rewriting eq 13 in a symmetric form as
| 23 |
where, for m ∈ {i,j}, the kernels in eq 23 are defined as
| 24 |
and erf(x) is the error function of x, fm = zm2/(zi – zj2), zm ≡ |Δξj,i|/(√2σm), Δξj,ieff ≡ |ξj – ξieff|, and σm = (βkm)−1/2. Hereafter, we assume that kjeff > ki (zi > zj). When kjeff < ki, one can use the result after exchanging indices i and j.
To make eq 23 be integrable, we introduced a Gaussian approximation of the error function,
| 25 |
where sign(x) is the sign function of x. With 100 000 equally distributed supporting points along x in a range of [1.0 × 10–20,5.0], the coefficients c1 and c2 are determined from the numerical fit to log[1–erf(x)] = 2c1x + c2x2 as c1 = −0.425672 and c2 = −0.913347, respectively. After substitution of eqs 24 and 25 into eq 23, the integrals become those of Gaussian, whose analytic solution is available46
| 26 |
Using eq 26, we obtained an analytic approximate expression for Pa as a function of z1 and z2,
| 27 |
where
| 28a |
| 28b |
| 28c |
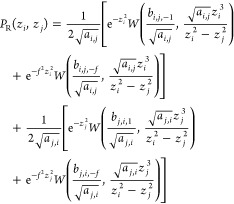 |
28d |
Here, erfc(x) = 1–erf(x) is the complementary error function, Ω(x) = exp(x2)erfc(x), W(x,y) = exp(x2)erfc(x + y), f = fi + fj, and am,n = 1 – c2(zm/zn)2 and bm,n,r = rzm – c1(zn/zm) for m ∈ {i, j} and n ∈ {i,j} (m ≠ n).
We compared the exact expression for Pa for kieff = kj (zi = zj ≡ z), eq 4 in ref (9), with the equal z limit of eq 27 obtained by taking limit zi → z and zj → z,
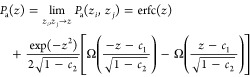 |
29 |
As shown in Figure 10A, eq 29 agrees excellently with the exact solution. The absolute error is less than 1.48% (at z = 0.856) for any z ≥ 0 and the relative error is less than 8.94% (at z = 2.459) for z ∈ [0,6], which verified the accuracy of eq 27. In Figure 10B, eq 27 as a function of z1 and z2, Pa(z1,z2), is shown, in which the green area is the region of the interest (Pa ∼ 0.4) for the optimal overlap between neighboring windows.
Figure 10.
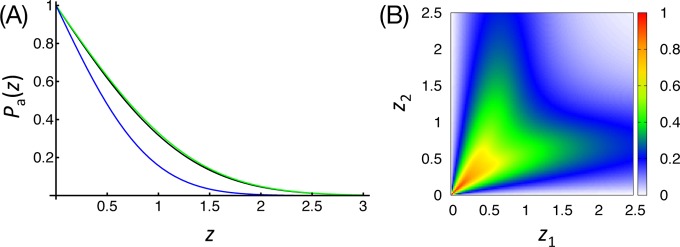
(A) The average acceptance probability, Pa(z), calculated from the exact solution, eq 4 in ref (9). (black), and the equal z limit of eq 27, eq 29 (green). Shown together is erfc(z) (blue), which is the first term of the approximate expression of Pa given by eq 29. (B) The average acceptance probability as a function of z1 and z2, Pa(z1,z2), given by eq 27.
Supporting Information Available
S1: Data for the toy model from all the tested parameter sets. S2: Additional data for the GpA-TM assembly. This material is available free of charge via the Internet at http://pubs.acs.org/.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Torrie G. M.; Valleau J. P. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar]
- Mezei M. J. Comput. Phys. 1987, 68, 237–248. [Google Scholar]
- Marsili S.; Barducci A.; Chelli R.; Procacci P.; Schettino V. J. Phys. Chem. B 2006, 110, 14011–14013. [DOI] [PubMed] [Google Scholar]
- Maragakis P.; van der Vaart A.; Karplus M. J. Phys. Chem. B 2009, 113, 4664–4673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wojtas-Niziurski W.; Meng Y.; Roux B.; Berneche S. J. Chem. Theory Comput. 2013, 9, 1885–1895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar S.; Bouzida D.; Swendsen R. H.; Kollman P. A.; Rosenberg J. M. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar]
- Vaneerden J.; Briels W. J.; Harkema S.; Feil D. Chem. Phys. Lett. 1989, 164, 370–376. [Google Scholar]
- Lee J.; Im W. Phys. Rev. Lett. 2008, 100, 018103. [DOI] [PubMed] [Google Scholar]
- Park S.; Kim T.; Im W. Phys. Rev. Lett. 2012, 108, 108102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lingenheil M.; Denschlag R.; Mathias G.; Tavan P. Chem. Phys. Lett. 2009, 478, 80–84. [DOI] [PubMed] [Google Scholar]
- Nadler W.; Hansmann U. H. E. Phys. Rev. E 2007, 75, 026109. [DOI] [PubMed] [Google Scholar]
- Kofke D. J. Chem. Phys. 2002, 117, 6911–6914. [Google Scholar]
- Predescu C.; Predescu M.; Ciobanu C. J. Phys. Chem. B 2005, 109, 4189–4196. [DOI] [PubMed] [Google Scholar]
- Dashti D. S.; Roitberg A. E. J. Chem. Theory Comput. 2013, 9, 4692–4699. [DOI] [PubMed] [Google Scholar]
- Crooks G. E. Phys. Rev. Lett. 2007, 99, 100602. [DOI] [PubMed] [Google Scholar]
- Shenfeld D. K.; Xu H.; Eastwood M. P.; Dror R. O.; Shaw D. E. Phys. Rev. E 2009, 80, 046705. [DOI] [PubMed] [Google Scholar]
- Weinhold F. J. Chem. Phys. 1975, 63, 2479–2483. [Google Scholar]
- Salamon P.; Berry R. S. Phys. Rev. Lett. 1983, 51, 1127–1130. [Google Scholar]
- Salamon P.; Nulton J. Europhys. Lett. 1998, 42, 571–576. [Google Scholar]
- Schaller M.; Hoffmann K.; Siragusa G.; Salamon P.; Andresen B. Comput. Chem. Eng. 2001, 25, 1537–1548. [Google Scholar]
- Nulton J.; Salamon P. J. Non-Equilib. Thermodyn. 2002, 27, 271–288. [Google Scholar]
- Bennett C. J. Comput. Phys. 1976, 22, 245–268. [Google Scholar]
- Shirts M.; Bair E.; Hooker G.; Pande V. Phys. Rev. Lett. 2003, 91, 140601. [DOI] [PubMed] [Google Scholar]
- Maragakis P.; Spichty M.; Karplus M. Phys. Rev. Lett. 2006, 96, 100602. [DOI] [PubMed] [Google Scholar]
- Sugita Y.; Okamoto Y. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar]
- Sugita Y.; Kitao A.; Okamoto Y. J. Chem. Phys. 2000, 113, 6042–6051. [Google Scholar]
- Darve E.; Rodriguez-Gomez D.; Pohorille A. J. Chem. Phys. 2008, 128, 144120. [DOI] [PubMed] [Google Scholar]
- Zheng L.; Chen M.; Yang W. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 20227–20232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng L.; Chen M.; Yang W. J. Chem. Phys. 2009, 130, 234105. [DOI] [PubMed] [Google Scholar]
- Laio A.; Parrinello M. Proc. Natl. Acad. Sci. U.S.A. 2002, 99, 12562–12566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kästner J.; Thiel W. J. Chem. Phys. 2005, 123, 144104. [DOI] [PubMed] [Google Scholar]
- Hènin J.; Pohorille A.; Chipot C. J. Am. Chem. Soc. 2005, 127, 8478–8484. [DOI] [PubMed] [Google Scholar]
- Zhang J.; Lazaridis T. Biophys. J. 2006, 91, 1710–1723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li P.-C.; Miyashita N.; Im W.; Ishido S.; Sugita Y. J. Comput. Chem. 2014, 35, 300–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S.; Im W. J. Chem. Theory Comput. 2013, 9, 13–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Im W.; Lee J.; Kim T.; Rui H. J. Comput. Chem. 2009, 30, 1622–1633. [DOI] [PubMed] [Google Scholar]
- Lee J.; Im W. J. Comput. Chem. 2007, 28, 669–680. [DOI] [PubMed] [Google Scholar]
- MacKenzie K.; Prestegard J.; Engelman D. Science 1997, 276, 131–133. [DOI] [PubMed] [Google Scholar]
- Chothia C.; Levitt M.; Richardson D. J. Mol. Biol. 1981, 145, 215–250. [DOI] [PubMed] [Google Scholar]
- Lazaridis T. Proteins 2003, 52, 176–192. [DOI] [PubMed] [Google Scholar]
- Brooks B. R.; Brooks C. L. III; Mackerell A. D. Jr.; Nilsson L.; Petrella R. J.; Roux B.; Won Y.; Archontis G.; Bartels C.; Boresch S.; Caflisch A.; Caves L.; Cui Q.; Dinner A. R.; Feig M.; Fischer S.; Gao J.; Hodoscek M.; Im W.; Kuczera K.; Lazaridis T.; Ma J.; Ovchinnikov V.; Paci E.; Pastor R. W.; Post C. B.; Pu J. Z.; Schaefer M.; Tidor B.; Venable R. M.; Woodcock H. L.; Wu X.; Yang W.; York D. M.; Karplus M. J. Comput. Chem. 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodcock H. L. III; Hodoscek M.; Gilbert A. T. B.; Gill P. M. W.; Schaefer H. F. III; Brooks B. R. J. Comput. Chem. 2007, 28, 1485–1502. [DOI] [PubMed] [Google Scholar]
- Kullback S.; Leibler R. A. Ann. Math. Statist. 1951, 22, 79–86. [Google Scholar]
- Trebst S.; Huse D. A.; Troyer M. Phys. Rev. E 2004, 70, 046701. [DOI] [PubMed] [Google Scholar]
- Escobedo F. A.; Martinez-Veracoechea F. J. J. Chem. Phys. 2007, 127, 174103. [DOI] [PubMed] [Google Scholar]
- Handbook of Mathematical Functioins With Formulas, Graphs, and Mathematical Tables; Abromowitz M., Stegun I. A., Eds.; Dover:: New York, 1972. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


