Active Relearning for Robust Supervised Training of Emphysema Patterns

Abstract

Radiologists are adept at recognizing the character and extent of lung parenchymal abnormalities in computed tomography (CT) scans. However, the inconsistent differential diagnosis due to subjective aggregation necessitates the exploration of automated classification based on supervised or unsupervised learning. The robustness of supervised learning depends on the training samples. Towards optimizing emphysema classification, we introduce a physician-in-the-loop feedback approach to minimize ambiguity in the selected training samples. An experienced thoracic radiologist selected 412 regions of interest (ROIs) across 15 datasets to represent 124, 129, 139 and 20 training samples of mild, moderate, severe emphysema and normal appearance, respectively. Using multi-view (multiple metrics to capture complementary features) inductive learning, an ensemble of seven un-optimized support vector models (SVM) each based on a specific metric was constructed in less than 6 s. The training samples were classified using seven SVM models and consensus labels were created using majority voting. In the active relearning phase, the ensemble-expert label conflicts were resolved by the expert. The efficacy and generality of active relearning feedback was assessed in the optimized parameter space of six general purpose classifiers across the seven dissimilarity metrics. The proposed just-in-time active relearning feedback with un-optimized SVMs yielded 15 % increase in classification accuracy and 25 % reduction in the number of support vectors. The average improvement in accuracy of six classifiers in their optimized parameter space was 21 %. The proposed cooperative feedback method enhances the quality of training samples used to construct automated classification of emphysematous CT scans. Such an approach could lead to substantial improvement in quantification of emphysema.

Introduction

Pulmonary emphysema is characterized by irreversible destruction of lung parenchyma and is one of the major causes of morbidity and mortality in chronic obstructive pulmonary disease (COPD) patients [1]. The contrast and spatial resolution of High Resolution Computed Tomography (HRCT) reveals the complex architecture of the emphysematous lung [2]. The destroyed lung parenchyma and resulting air pockets in lung result in low attenuations areas on CT scans. Nevertheless, these abnormalities pose a visual quagmire for accurate and reproducible classification since the radiologist mentally maps and aggregates the findings while wading back and forth through the lung. Additionally, the increasing incidence of emphysema [3], the exponential use of CT scans [4] and the increasing spatial resolution of CT images reduces throughput efficiency — the number of unambiguous radiological reads per minute. This scenario requires a reinvention of current radiological approaches for robust diagnosis, staging and assessment in response to treatment for emphysema.

An initial effort to objectively evaluate the extent of emphysema based on a density threshold was proposed in 1988 [5]. Subsequently, several density thresholds have been proposed ranging from −910 to −1,000 HU based on statistically significant correlation of quantified extent to physiologic indices such as the pulmonary function tests or visual radiology emphysema index [6]. Despite its success, the density based threshold quantification is not a stable measure of low attenuation areas across patients, scans and protocols [7–9]. This has led to the exploration of robust and reproducible supervised quantitative techniques for classification of discernible emphysematous patterns in chest CT scans [10–15]. However, supervised classification of emphysema has found few clinical champions. This can be partly attributed to the inaccurate classification due to noisy training samples arising from subjective, tedious and error prone processes. Fundamentally, the faithful adoption and implementation of the supervised training by a classifier is contingent upon the quality of acquired training samples and their discriminability across classes. In this paper, we are interested in addressing the problem of efficient development of classification models using expert chosen training samples.

Clean classification models are achieved through elimination of outlier samples [16] or through active learning processes where the learner actively chooses the most informative training samples from a pool of previously labeled samples and hence steers the choice of expert labels. Active learning methods have demonstrated value where large training datasets are available, such as in remote sensing [17], text classification [18, 19] and object recognition applications. However, medical image classification models are typically constructed from a limited pool of expert-chosen regions of interest (ROIs). Our experience within a clinical setting suggests that physician apathy and related sub-optimal performance in clinically relevant pattern classification is predominantly due to lack of real time feedback on the effect the chosen samples have on the classifier. In this paper, we propose a feedback mechanism — active relearning — that engages the expert to reduce uncertainty in the training samples through initial inductive learning and subsequent active relearning to steer the classifier towards optimal performance in one exercise. Unlike the active learning process, the proposed methodology resolves the conflicting labels through a physician-in-the-loop feedback mechanism.

Support Vector Machine (SVM) [20–22] models are the state-of-the-art learning models with firm theoretical foundations and proven performance in wide range of applications. In the training phase, SVM models are trained to discriminate the features of the data. The training samples are projected on to the feature space and SVM constructs hyper-planes in feature space by maximizing the margins. The meta-parameters such as penalty term and kernel parameters are used to construct feature space and define hyper-plane boundaries between training classes. Support vectors lie on the maximum margin hyperplanes. In this paper, pairwise dissimilarity between training samples is generated using seven different metrics and seven corresponding SVM models are constructed. Radial basis functions (RBF) kernel is used to model the individual SVMs. The ensemble of one-against-one SVMs based on these seven metrics is used in the inductive learning process, wherein, the predictions made by the ensemble of SVMs are voted through a simple majority and compared with the expert's original labeling. In the active relearning phase, the expert resolves the conflict, if any, in one of three ways: retaining the original label; relabeling; or removing the sample from the training set. Since the SVMs were implemented with default parameters in active relearning phase, to assess the true efficacy of expert-assisted sample cleaning across other commonly used general-purpose six classifiers (SVM, Random Forest, Nearest Neighbor, Naïve Bayes, One-R and Decision Tree) with their respective optimized parameters were assessed with the original and cleaned training samples. The optimal values of the individual classifiers' meta-parameters were chosen through a detailed design of experiments (DOE) study. The results of our investigation provides evidence that with physician-in-the-loop feedback and a flexible and trainable algorithm, better accuracy in supervised training and thus eventually efficient classification method can be achieved towards confident quantitative diagnosis of emphysema patients.

Materials: Data and ROI Selection

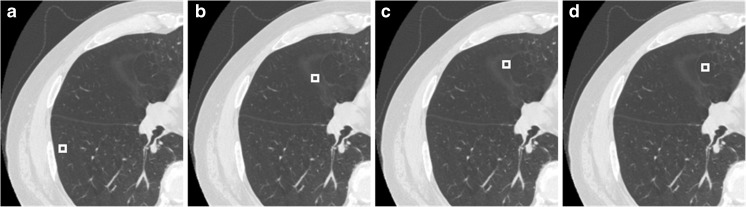
CT scans from 86 patients with different stages of emphysema were used for this study. Scans were performed with a HiSpeed CT/i GE scanner (120 kVp, BONE kernel recon, 512×512 axial matrix with 0.7422×0.7422×1 mm³). The experienced thoracic chest radiologist selected multiple 9×9 voxel ROIs from any of the 86 scans. In contrast to the traditional approach of binning emphysema severity based on the relative area of voxels below a certain threshold, the expert used clinically compliant binning by assessing the visual texture, location and context of the ROI based on the attenuation characteristics that best captures the severity of parenchymal destruction. The texture based approach enables more consistent characterization of disease compared to threshold based emphysema assessment which is prone to variations with noise, different CT acquisition and reconstruction protocols [6, 23, 24]. Accordingly, four classes of ROIs were selected to represent normal parenchyma; mild, moderate and severe emphysema (Fig. 1). Under this protocol, the radiologist selected 412 ROIs across 15 datasets with good CT scan quality and no artifacts to represent 124, 129, 139 and 20 training samples of mild, moderate, severe and normal appearance, respectively. The low count of normal samples is due to the strong emphysematous criterion used in the initial enrollment of patients in the study. The locations and the cases corresponding to the individual ROIs were tagged to facilitate review during the relearning phase.

Fig. 1.

Representative ROIs selected by the expert as training samples to represent normal parenchyma (a), mild (b), moderate (c) and severe (d) emphysema

Methods

Dissimilarity Metrics

Histogram-based distance measures were used to compute the dissimilarity among the samples to the supervised learning models. Probability density functions (PDFs) of the individual ROIs were computed as their respective normalized histograms and pairwise dissimilarities among them were computed using seven metrics: Manhattan, Sorensen, Tanimoto, Jaccard, Squared Chord, Pearson χ² and Kullback–Leibler (summarized in Table 1). The metrics were drawn from different metric families to reflect the multi-view perspective.

Table 1.

PDF based pairwise dissimilarity metrics used in the SVM models

Metric ID	Metric	Metric family	Equation
M1	Manhattan	L p Minkowski
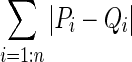
M2	Sorensen	L 1
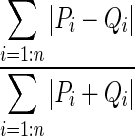
M3	Tanimoto	Intersection
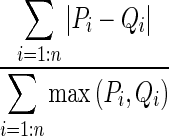
M4	Jaccard	Inner Product
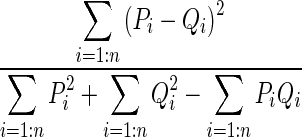
M5	Squared Chord	Fidelity
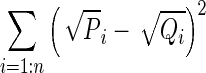
M6	Pearson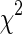
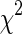
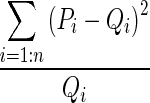
M7	Kullback–Leibler	Shannon Entropy

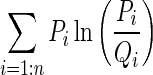
P and Q represent the PDFs of the two ROIs with n bins

Feedback Mechanism

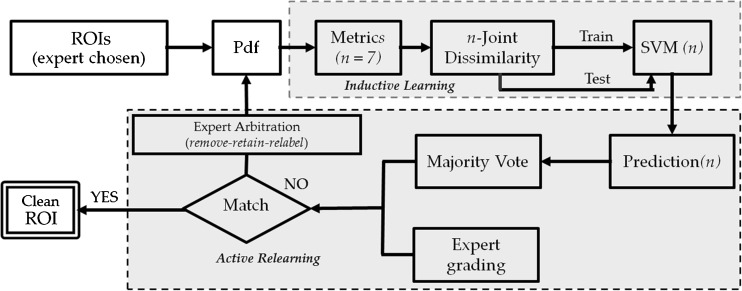
The proposed physician-in-the-loop feedback mechanism has two phases: passive inductive learning and expert-in-the-loop active relearning. Figure 2 outlines the workflow of the proposed feedback mechanism. After the ROIs are selected and labeled by the expert, the inductive learning phase is initiated and followed by active relearning.

Fig. 2.

The workflow of feedback mechanism paradigm which outlines the two stages: inductive learning and active relearning

Inductive Learning

SVM model was used for the passive inductive learning process. As mentioned before, SVMs learn hyperplanes in a feature space based on the training data mapped to a high dimensional feature space by means of a kernel function and applied to future test data for classification. SVM model is constructed based on training with 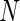instances of data vector x and class label y by minimizing the following error function:

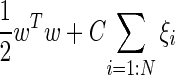Subject to constraints y_i(w^T ϕ (x_i) + b) ≥ 1 − ξ_i,ξ_i > 0: where 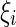is a non-negative regularization variable, introduced to reduce model complexity and achieve convergence. 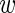is the function of linear combination of support vectors defining the hyper-planes in the feature space and 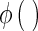is the kernel function. The performance of SVM models depends on penalty term (C), part of the regularization term in quadratic optimization and kernel function, applied to the training data to improve discriminability in feature space. The RBF kernel for one-against-one classification used in this paper for a pair of support vectors i and j is defined by [20, 25]:

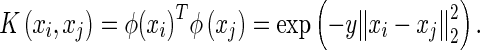The other tunable meta-parameter is the kernel parameter, γ, which tunes the RBF kernel to map the training samples nonlinearly into multi-dimensional space.

In the inductive learning stage, pairwise dissimilarity among the expert-labeled samples is computed with seven metrics (Table 1). An ensemble of SVM models based on these seven independent dissimilarity metrics is constructed. The pairwise dissimilarity matrix derived from each metric is the input to the respective SVM model. Default meta-parameter values of 1 and 1/#ROIs, respectively, for C and γ were used for all the SVM models. Note that the SVM models are not optimized for the optimal parameters at this point. This was in consideration of the following combined effects of (a) the computational complexity of parameter optimization, (b) the need to engage the expert without interruption, (c) the assumption that naturally clean samples can be labeled confidently by the vanilla classifier and (d) the premise that gross inaccuracies can be corrected easily in the relearning phase. The predictions for 412 ROI samples for each of the seven classifiers are made using one-against-one multiclass classification. The accuracy of SVM models using original and clean training was evaluated using 10-fold stratified sampling strategy (random subsets with class distribution kept constant) for cross-validation.

Active Relearning

The consensus of the ROI labels is derived based on simple majority of the predictions obtained from the seven individual SVM models. ROI samples for which the consensus label differed from that of the expert are flagged for expert review without revealing the exact consensus label to the expert. The conflict represents the machine confusion to reproduce expert’s label for the sample. For each of the conflicts, the expert had the option of (a) retaining the original label, (b) relabeling to another appropriate class or (c) removing the sample from the training set.

Generality of Relearning Efficacy

As mentioned before, SVM models used in the relearning phase were based on default parameter settings. Consequently, the accuracy improvements do not reflect the true efficacy of sample cleaning. To augment the value of the on-line expert feedback, a detailed off-line DOE study is required to train the model by exhaustively sampling its parameter space. Moreover, the effect of true sample cleaning should transcend across classifiers in their respective optimized parameter space. This was assessed using the grid parameter optimization in RapidMiner [26], an open source data mining software that allows analysis of data for standard processes and tools such as classification algorithms and parameter optimization methods. Six commonly used classifiers — LibSVM, Random Forest, Nearest Neighbors, Naive Bayes, One R and Decision Tree — were used to conduct the DOE study where the parameter space of the respective classifiers were sampled along a linear grid and model validation was performed at each of the grid points using 10-fold cross-validation and stratified sampling of original and cleaned samples. The grid based approach to parameter optimization ensures the choice of optimal parameter for the classifier given the training samples. Performance was characterized by the mean accuracy of the validation process.

Experimental Results

Figure 3 shows the pairwise dissimilarity matrices for original samples using the Manhattan (left) and Tanimoto (right) metric. The matrix elements were permuted such that the mild, moderate, severe and normal samples are grouped together (black partitions). The diagonal blocks show the inter-class dissimilarity variation. Off-diagonal blocks capture the intra class variation; the lighter the shade the stronger the dissimilarity. Lack of an adequate number of samples for the normal class hinders its discriminability. Both dissimilarities reveal the separability of mild and severe classes, and the strong overlap that moderate samples have with both mild and severe. The inter- and intra-observer variation to grade emphysema based on these subtle but pathologically significant attenuation variations explains the conventional practice (and limitation) of lumping abnormalities together based on a single threshold. The overlapping nature of features as observed in the matrices justifies our selection of non-linear RBF kernels to learn the feature space.

Fig. 3.

Pairwise dissimilarity matrix of Manhattan (left) and Tanimoto (right) metrics. The thick line partitions along the diagonal show the mild, moderate, severe and normal classes of 412 ROI expert chosen. The darker shade represents the similarity among pairs of ROIs

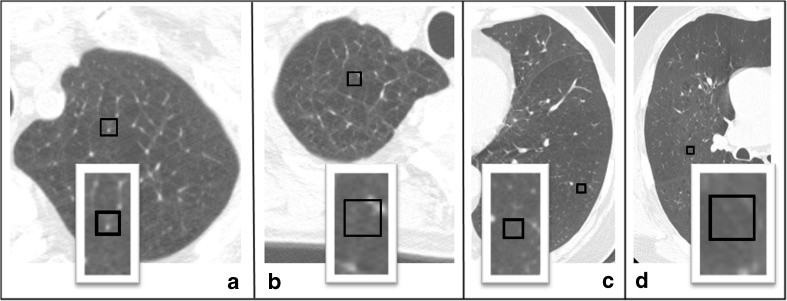
SVM models based on the aforementioned metrics were constructed and their respective predictions were collated to form the consensus predictions. It took less than 6 s on a standard PC (single core, 3.1GHZ processor) to complete the inductive learning and consensus building, highlighting the just-in-time computation to engage the expert without diminishing his interest. Table 2 shows the results of a single iteration of relearning. A total of 87 conflicts from 412 training samples were found based on the consensus predictions of seven SVM models. The conflicts were resolved by the expert using remove–relabel–retain options with no knowledge of the consensus labels. The expert's decision to remove some of the ROI samples was based on the presence of confounding vessels or due to mixed attenuation types within the ROIs. The training sets were refined depending on the expert's decision. Figure 4 shows the representative options exercised in the resolution process. Samples were removed either due to vessel intrusion (Fig. 4a) or mixed types (Fig. 4b) within ROIs. Panels c and d respectively highlight scenarios where the original label (normal) was retained and relabeled (from moderate to severe). At the end of the 5-min-long relearning session, 87 conflicts were resolved through 35 removes, 15 relabels, and 37 retains.

Table 2.

Distribution of labels across inductive learning and active relearning processes

	Mild	Moderate	Severe	Normal	Total
Label distribution
Original	124	129	139	20	412
Consensus	106	92	127	0	325
Conflicts	18	37	12	20	87
Expert resolution
Removed	7	17	8	3	35
Relabeled	8	5	1	1	15
Retained	3	15	3	16	37
Final distribution	113	116	132	16	377

Fig. 4.

Representative remove–retain–relabel resolution. Panels highlight ROI (a) removed due to confounding vessel, (b) removed due to mixed tissue type, (c) retained as normal and (d) moderate relabeled as severe

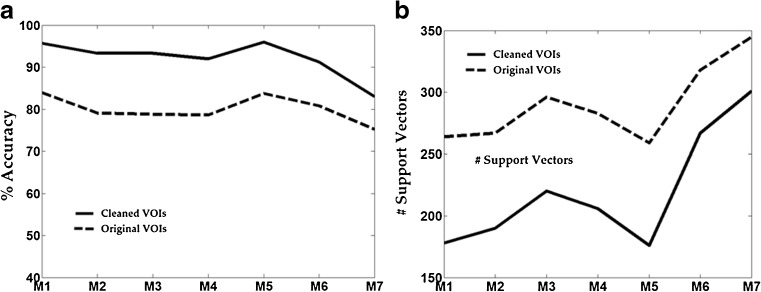
Figure 5 illustrates the improvement in accuracy in SVM for each of the seven metrics and corresponding reduction in the number of support vectors with original and clean training samples. Due to the reduction in label uncertainty, all the models showed significant improvement in the accuracy with concomitant reduction in the number of support vectors. The average percentage improvement in accuracy was 15 %; mean reduction in number of support vectors was 25 %. Co-occurrence of reduced support vectors and increased accuracy is in contrast to prevalent accuracy compromising methods for reducing support vectors [27]. It is also worth reiterating that the SVM models herein used default parameter settings and no exhaustive search was conducted to optimize parameters. Nevertheless, the relative gain in performance suggests that the power of relearning would be further highlighted in the optimized parameter space.

Fig. 5.

a Improvement in percentage accuracy in the un-optimized SVM model for the seven metrics after relearning. b The reduction in support vectors in the SVM model for the seven metrics after relearning

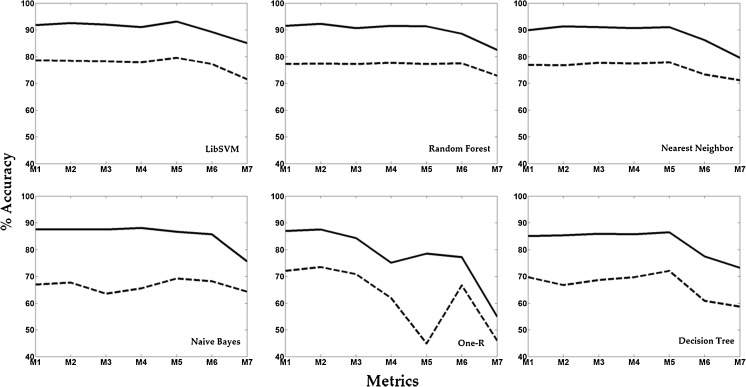
Figure 6 shows the results in the optimized parameter space obtained through the DOE study which illustrates the corresponding improvement in accuracy for all the six classifiers for the seven metrics. With clean samples, accuracy increased across all the classifier–metric combinations. The maximum and minimum changes of 33.6 and 8.5 were observed, respectively, for the OneR-SquaredChord and Nearest Neighbors–Kullback Leibler combinations. Mean percentage change over all combinations was 21.

Fig. 6.

The improvement in the percentage accuracy due to sample cleaning through active relearning across the six classifiers and seven metrics in their optimized parameter space

Discussion

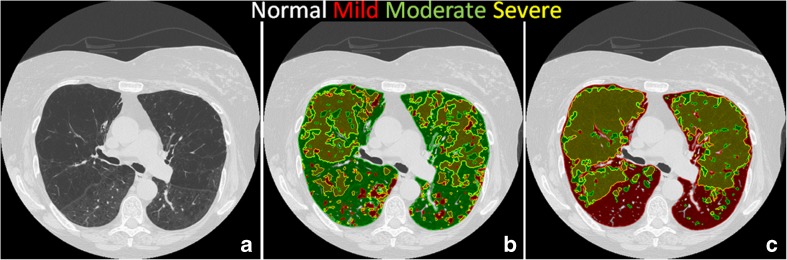
The grades of severity of parenchymal distortion in patients with emphysema characterized by low attenuation areas on CT have significant prognostic and therapeutic consequences [28]. The density based thresholds tend to quantify severe emphysema and thus has limitation in quantification of mild and moderate emphysema. Although, desired pattern classification can be achieved through supervised classification methods, identification of subtle grades of emphysema is not easily mastered even by experts. Since the discriminability of the training samples is crucial, efforts to maximize the supervised learning is necessary. Active learning methods attempt to minimize the manual effort by selecting the most appropriate data to label and this produces the best possible classifier within a reasonable number of expert engagements. It is typically accomplished using divide-and-conquer strategies like multi-view partitions of samples [29] or through hierarchical cascades of classifiers [11, 30]. In this paper, we have proposed simpler relearning strategy wherein an ensemble of naïve learners collaborate and collectively resolve their differences through expert guidance in a single exercise. SVM models are constructed within 6 s and the conflicts were resolved in about 5 min. We have shown that just-in-time physician-in-the-loop feedback demonstrates promising performance. The classifier, once trained, is available for general use without the need for further physician-in-the-loop intervention. Figure 7 shows representative classification results with the original (panel b) and clean (c) samples on a randomly chosen test dataset. The original conflicts in the moderate class between the mild and severe classes have been correctly resolved with clean samples. The less clutter in panel c illustrates the improvement in classification achieved solely due to clean training samples. This strategy can be incorporated effectively in improving the validity of samples by obtaining multiple expert consensuses on labels. We would like to point that this paper demonstrates the need and value of obtaining clean samples for more efficient algorithm with lesser errors due to sampling process itself. Nevertheless, there are other contributors to classification models such as most optimal metric or metric combinations and classifier parameters to achieve efficacy in classification of emphysema per se is not evaluated in this paper. Future study would be to incorporate active relearning and optimize classification algorithms to classify dataset from emphysema population towards establishing the clinical significance.

Fig. 7.

A representative axial cross section of a CT volume scan (a) with classification results obtained using original (b) and clean (c) training samples

The SVMs are deemed state-of-the-art supervised classification models with proven efficacy in wide areas of application. The classification speed of SVMs is governed by number of support vectors used to define the decision boundaries. Several support vector reduction methods [31] are incorporated with a trade-off in classification performance to overcome the limitation of classification time. Active relearning process, originally designed to ensure the selected training samples have discriminatory power, resulted in reduction of support vectors of about 25 % and increase in classification accuracy of about 21 % across seven SVM models assessed by 10-fold cross-validation. In addition to obtaining clean training samples, the efficiency of the classification system is improved.

There is room for further improvement of the proposed work. We have used dissimilarity metrics derived from pairwise comparisons of the PDFs. Such appearance based metrics in combination with active shape metrics such as local binary patterns [32], could provide complementary multi-view optimization of the data. A critical measure of expert acceptance and system learnability is the number of label conflicts that the expert prefers to repeatedly retain. This can be minimized using sampling of critical patterns based on local measures in feature space [33]. The effect of sample cleaning on the ultimate classification must be further assessed for clinical significance and relevance.

Conclusion

The automated classification of severity grades of emphysema is valuable in clinical management of patients. The efficacy of supervised classification methods are limited by noise in the expert-chosen training samples characteristic of pathological patterns. We have proposed a simple physician-in-the-loop feedback based active relearning to ensure selection of most discriminative training samples reproducible by the classification system. This leads to considerable improvement in quantitative assessment of emphysema thereby improving the throughput efficiency in chest radiology practices and their confidence in quantitative imaging methods towards providing optimal patient care.