Supervised Segmentation of Polycystic Kidneys: a New Application for Stereology Data

Abstract

Stereology is a volume estimation method, typically applied to diagnostic imaging examinations in population studies where planimetry is too time-consuming (Chapman et al. Kidney Int 64:1035–1045, 2003), to obtain quantitative measurements (Nyengaard J Am Soc Nephrol 10:1100–1123, 1999, Michel and Cruz-Orive J Microsc 150:117–136, 1988) of certain structures or organs. However, true segmentation is required in order to perform advanced analysis of the tissues. This paper describes a novel method for segmentation of region(s) of interest using stereology data as prior information. The result is an efficient segmentation method for structures that cannot be easily segmented using other methods.

Introduction

Stereology is commonly used in medical imaging to estimate volumetric information about organs or other three-dimensional objects from a series of two-dimensional sections [2–4]. Stereology is relatively quick to acquire compared to planimetry; a typical image volume can be analyzed in 10–20 min instead of 45–90 min for planimetry [5]. Stereology yields unbiased, robust results [2, 3, 6, 7]. The main limitation of stereology is that it only estimates information, like volume or surface area, from labeled objects [2]. Stereology does not segment these objects. Thus, traditional stereology cannot be used for advanced image analysis.

In this report, we used data from imaging studies of patients with autosomal dominant polycystic kidney disease (ADPKD). ADPKD is a genetic disorder with prevalence of approximately 1 in 1,000 representing a major cause of renal failure [8, 9]. Clinical trials for ADPKD therapies began after the NIH-sponsored Consortium for Radiologic Imaging Studies of Polycystic Kidney Disease (CRISP) showed total kidney volume (TKV) correlates with disease progression, detects change in individuals with normal lab values, and can do so after as little as 12 months [10]. The current standard for TKV measurements in ADPKD studies and clinical trials is stereology [11]. The labeled stereology data consist of an undersampled grid of points overlaid on each image in an exam series, labeled by a trained user. The Cavalieri principle [7, 12] allows calculation of the volume of labeled objects from the stereology grid.

The purpose of this study is to evaluate the possibility of obtaining fully segmented images from undersampled stereology grid data. The method we developed aims to utilize labeled stereology grids, routinely obtained in ADPKD imaging studies like CRISP [11] and used to obtain the primary volume outcome metric in clinical trials [13–15], to segment volumes of interest. We hypothesize these stereology data will provide a rich source of a priori information to supervise and constrain soft tissue segmentations and will test this using magnetic resonance imaging (MRI) series from polycystic kidneys.

Methods

MRI Data

Institutional Review Board approval was obtained for this study. Twenty (20) MRI exams from patients with ADPKD prior to renal failure were studied. The MR imaging series used consisted of coronal T2-weighted single-shot fast spin echo (SSFSE) fat-suppressed breath hold images, with matrix size 256 × 256 × Z with Z sufficient to contain the enlarged polycystic kidneys in the field of view.

Planimetry

Manual segmentations of the right and left kidneys via planimetry were obtained for each series from two separate experts, to examine interobserver variability. The planimetry experts were instructed to trace kidney parenchyma, including cysts, but to exclude the renal pelvis and other hilar vascular structures. One expert traced the set a second time, after a delay of several months to eliminate potential memory, in order to evaluate intraobserver variability. Thus, for each imaging series, three sets of planimetry data were available. These three data sets were combined using a simple voting scheme into a consensus segmentation for each series. All planimetry data was collected using the Analyze© 11 software package [16, 17].

Stereology Volume Estimates

Expert stereology data was acquired, independently of the planimetry tracings, for each image in each MRI series. Instructions for acquiring this experimental stereology data were the same as for planimetry, and the left and right kidneys were labeled. Comparing the expert stereology data to expert planimetry data revealed small mismatches, averaging approximately 5 % of stereology grid points, due to partial volume effects or reconstruction artifacts. Thus, the expert stereology data were only used as independent volume estimates to define a threshold in our algorithm. Experimental stereology data was acquired and volume estimates obtained using the Analyze© 11 software package [16, 17].

Simulated Stereology Data

While one would hope that the stereology points are 100 % consistent with planimetry tracings, this was not generally true. We observed cases where the stereology sample is near the edge and might be “in” in the gold standard planimetry set but “out” in the stereology set or vice versa. Such inconsistencies are misleading to the algorithm. Therefore, we created simulated stereology data that would be correct with respect to the planimetry data as follows. Simulated stereology data was generated from the planimetry consensus as the intersection of an unlabeled stereology grid with the consensus planimetry left or right kidney regions. The evaluation of our algorithm used this simulated stereology data to approximate the consensus planimetry segmentation as closely as possible.

Semiautomated Algorithm

The purpose of our algorithm is to segment volumes of interest given stereology data. We note that we assume polycystic kidneys represent solid, if irregular, volumes. The input to our algorithm is the stereology data and the image data; no other human input is passed.

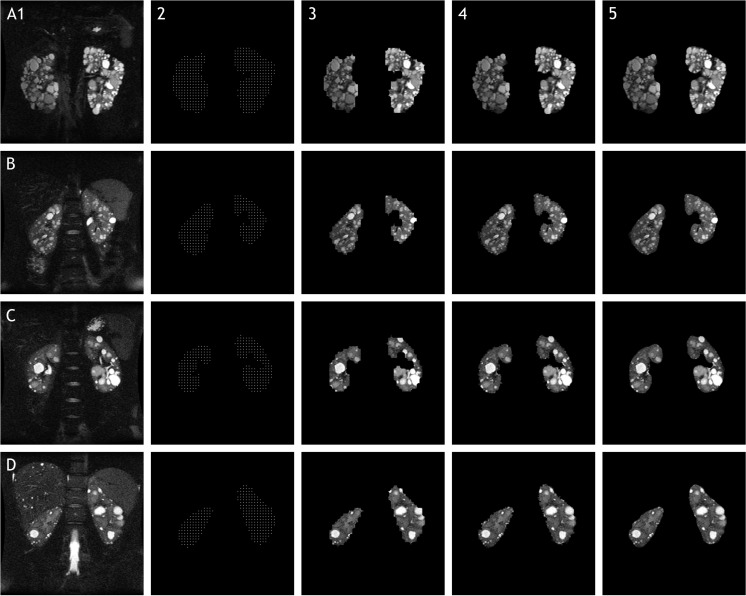
Our algorithm begins by preprocessing the stereology grid with mathematical morphology. Two sequential mathematical morphology operations are performed: dilation and erosion, also known together as morphological closing [18]. A 2D circular structuring element was chosen for these operations, because stereology data is available for every slice and the voxel spacing is larger in the “Z” dimension. The radius of the disk was the minimum necessary to fill between diagonally adjacent stereology grid points in homogeneous regions. The morphological preprocessing reduces the problem’s complexity to a band containing the kidney border, or a shell in three-dimensional space (see Fig. 1).

Fig. 1.

Representative slices of coronal T2-weighted SSFSE fat-suppressed MRI data from four different individuals (rows). Columns show original image (1), simulated stereology data (2), morphological preprocessing (3), raw segmentation (4), and final cleanup (5). Note that magnetic field heterogeneity in row A did not affect the result, and left kidney parenchyma was correctly segmented from adjacent spleen in rows B and D

This band region is passed with the image volume to a minimal spanning forest watershed algorithm for semiautomated segmentation [19]. After this step, rough edges may remain in regions with low intensity contrast due to image noise (Fig. 1).

The final step is to execute a postprocessing cleanup on the segmented data using fuzzy logic. The cleanup step was applied separately to each labeled object, in this case the right and left kidneys. The cleanup step fuzzified (converted a binary input into a floating point output with degrees of truth as gray levels) each segmented object by applying a fuzzy membership function to every labeled point in image space and summing the result. In this work, the fuzzy membership function chosen was a spherical Gaussian with sigma half the in-plane stereology grid spacing. The fuzzy array is then defuzzified (returned to binary form from floating point gray levels) using a threshold chosen to minimize aggregate volume error, as measured by the independent expert stereology volume estimates. The defuzzified output is the final result of our algorithm (Fig. 1).

Evaluation Methods

The segmentation results from our algorithm were compared to the consensus planimetry tracings by the Dice coefficient and the Jaccard coefficient, which are set similarity measurements [20, 21]. Previous semiautomated ADPKD segmentation efforts have focused on volume error alone [22]. While it is important to minimize this quantity to eliminate systematic error, volume is insufficient to evaluate the accuracy of a segmented set. Dice and Jaccard coefficients provide a proper comparison to evaluate our calculated segmentation.

In addition, we evaluated Dice and Jaccard coefficients comparing intraobserver and interobserver variability. These comparisons also had N = 20. Metrics used were volume error, Dice coefficient, Jaccard coefficient, sensitivity, and specificity.

Results

Comparing our computed segmentations with the consensus planimetry tracings, we observed a volume error of −0.27 ± 1.9 %, which was not significantly different from 0 % by two-tailed t test (p = 0.54). For this comparison, we also obtained Dice coefficients of 0.969 ± 0.007 ranging from 0.954 to 0.980 and Jaccard coefficients of 0.940 ± 0.014 ranging from 0.912 to 0.961 (perfect match = 1.0 for both coefficients). The sensitivity was 97.0 ± 0.9 % ranging from 95.1 to 98.5 %. The specificity was 96.8 ± 0.8 % ranging from 95.0 to 98.2 %. All reported uncertainties are standard deviations.

We also calculated these metrics from two intermediate steps in the algorithm: morphological preprocessing and raw minimal forest watershed. These data quantify the relative contributions of each step to the final result (see Fig. 2).

Fig. 2.

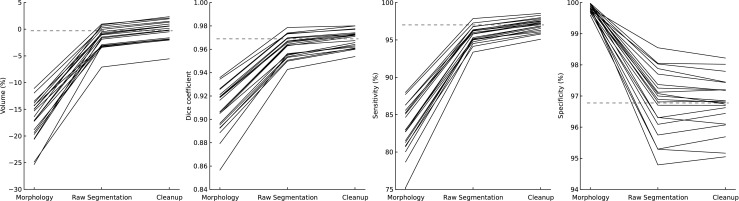
Comparison of individual algorithm steps for all 20 data sets. The gray dashed lines represent the mean of the final result. Within each metric, each stage is a significant improvement (p < 0.001) except for specificity. A decrease in specificity from morphology to raw segmentation was expected

Finally, we evaluated the difference between our segmentations and the consensus planimetry data. The salient comparison was against the expected intraobserver and interobserver variability from human experts. The intraobserver variability was found by comparing planimetry data from two different experts, while the interobserver variability was obtained from comparing two sets of planimetry data from the same individual after a delay. For all comparisons, we computed the volume error, Dice coefficient, sensitivity, and specificity. These comparisons are shown in Fig. 3. For these comparisons, Jaccard coefficient tracked with the Dice coefficient and was not included in Fig. 3 for compactness. Our segmentation was significantly superior to interobserver variability for all metrics (p < 0.01) except volume error (p = 0.88), and our segmentation was not significantly different from intraobserver variability for any metric (p > 0.2).

Fig. 3.

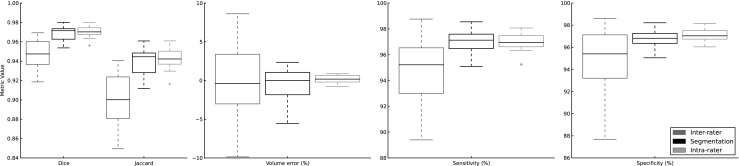
Metrics comparing interobserver variability (left, dark gray), our algorithm (middle, black), and intraobserver variability (right, light gray). For each metric except volume, the performance of our segmentation is significantly better than interobserver variability (p < 0.01) and not significantly different from intraobserver variability (p > 0.2). Considering volume, our segmentation was not significantly different from either intraobserver (p = 0.39) or interobserver (p = 0.88) variability by paired t tests

Our algorithm was implemented in Python 2.7.5 [23] using NumPy 1.6.3 [24], SciPy 0.12 [25], and Scikit-Image 0.8.2. As currently implemented, it requires less than 7 seconds on an Intel Xeon E5345 processor to fully segment both kidneys in an image volume.

Discussion

Semiautomated kidney segmentation efforts using MR data, particularly in ADPKD, have met with little success [22]. Atlas-based or automated methods fail because polycystic kidneys vary widely in shape and size, or due to similar intensity in the adjacent tissues (liver, spleen, gallbladder, adrenal glands, or collecting system [22]). Magnetic field heterogeneity also produces variations in signal intensity that further increase the difficulty of segmentation, even for semiautomated methods. We know of no prior efforts using stereology data as a priori information for supervised segmentation.

Our results are quantitatively very good for all metrics calculated. As shown in Fig. 3, our segmentation is superior to planimetry interobserver variation but not significantly different from planimetry intraobserver variation. However, large population-based studies employ many people for analysis, often spread across multiple sites, so the most realistic comparison is interobserver variability. Our results indicate that semiautomated segmentation using stereology data increases accuracy over interobserver planimetry variation. The relatively large volume uncertainty for interobserver variation is likely due to disagreements between observers about partial volumes and collecting system structures in the hilar region. In addition, a workflow using stereology and then semiautomated segmentation can be completed in a fraction of the time required for planimetry: 10–20 min plus 7 s for stereology followed by segmentation vs. 45–90 min for planimetry.

Limitations and Challenges

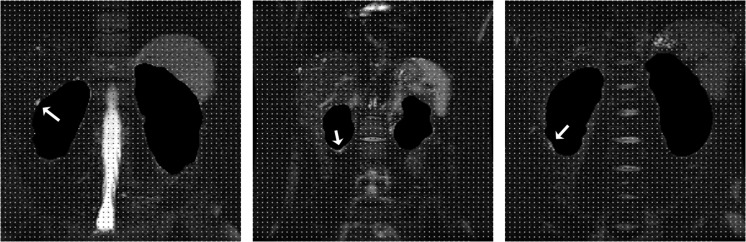
Like any algorithm accepting human input, our algorithm is vulnerable to the “garbage in, garbage out” principle. The result is highly dependent on the quality of the input baseline stereology data. Also, even if the user is perfect, the stereology grid may not sample features finer than the grid spacing. This is a higher dimensional analog to the Nyquist frequency. Choosing a denser grid spacing or operating on more regular objects can minimize this undersampling effect. Figure 4 shows examples of this in our study, where occasionally small exophytic cysts were not correctly segmented because the simulated stereology grid missed them.

Fig. 4.

Examples where our algorithm missed small exophytic cysts (arrows). The stereology grid did not sample these small regions

Fluid in cysts, vessels, and the collecting system appears bright on T2-weighted images, but fat suppression can result in minimal intensity contrast between normal kidney parenchyma and surrounding perirenal fatty tissue. This is of greater concern in patients with a lower cyst burden, where large portions of the kidney-tissue interface consist of similar-intensity tissue. In these cases, intensity-based supervised segmentation algorithms typically output rough borders due to image noise. This is the reason for the fuzzy cleanup postprocessing step. The cleanup step results in smoothed edges, so discontinuities in object surfaces will be subtly smoothed. However, the error introduced is only a few voxels, the quantitative benefits outweigh them (Fig. 2), and smooth regions of the segmented objects are unchanged. Choosing objects with minimal discontinuities can mitigate this effect. Despite their lobulated contours, polycystic kidneys exhibit few mathematical discontinuities at borders, so this smoothing was not a large concern for ADPKD. The subtle effects of this step are shown in Fig. 1, best observed comparing columns 4 vs. 5 for individuals B–D.

Finally, the current supervised segmentation algorithm step [19] is primarily intensity-based, so borders must be visible and defined. Infiltrating tumors or excessive partial volumes, for example, would be poor choices for both stereology and this algorithm. Edge contrast need not be global; the T2-weighted scans of ADPKD kidneys in this study include borders defined both by parenchyma (relatively dark) and cysts (bright fluid) from which good results were obtained.

These limitations are acceptable for the problem of ADPKD segmentation, but may be a challenge for readers wishing to apply our technique to other problems. We expect that this approach will return good results for any visually defined object with local contrast between its border and surrounding tissue, which the chosen stereology data samples adequately.

Conclusion

Our algorithm delivered consistently excellent quantitative results without any need for manual postprocessing or editing. The only requirement is baseline stereology data, routinely collected and retained in ADPKD imaging studies and other clinical trials. We wish to note that the algorithm described herein is not specific to ADPKD and could be applied to any imaging study collecting stereology data for a solid object of interest.

This work presents a novel algorithm to segment solid objects from stereology data. It opens the door for new, advanced biomarkers or textural feature analyses, which require segmentations to define volume(s) of interest, in large population studies. In many large studies, planimetry is too time-consuming and expensive to be feasible. Future studies could acquire stereology data instead of planimetry, use our algorithm to calculate segmentations, and realize significant cost savings. Alternatively, this workflow would allow a fixed-cost study to enroll more patients. We expect this algorithm to enable the extraction of advanced image features in future studies and also may be retrospectively applied to past imaging studies, like CRISP, which retained stereology data. This novel application of stereology data permits time-efficient segmentation of solid objects in large population studies where planimetry was previously infeasible, enabling advanced image analyses that may better predict individual clinical prognosis and therapy requirements in ADPKD or other disorders.