The body-size dependence of mutual interference

Abstract

The parameters that drive population dynamics typically show a relationship with body size. By contrast, there is no theoretical or empirical support for a body-size dependence of mutual interference, which links foraging rates to consumer density. Here, I develop a model to predict that interference may be positively or negatively related to body size depending on how resource body size scales with consumer body size. Over a wide range of body sizes, however, the model predicts that interference will be body-size independent. This prediction was supported by a new dataset on interference and consumer body size. The stabilizing effect of intermediate interference therefore appears to be roughly constant across size, while the effect of body size on population dynamics is mediated through other parameters.

1. Introduction

The abundance and dynamics of populations depend on the parameters that set species interactions, growth rates and death rates [1–4]. Documenting patterns in these parameters is therefore crucial to understanding ecological communities and predicting changes in their structure in space and time. One common pattern is that the parameters are strongly tied to body size. For example, intrinsic rates of growth and mortality rates both show −¼ power scalings with body size [5,6].

Foraging interactions between consumers (C) and their resources (R) are also body-size dependent [7]. These interactions are generally modelled with a functional response that relates prey density to per capita foraging rate (f) [8]. A typical functional response is

1.1

where a is the area of capture, which sets how fast a consumer clears its environment of resources, and h is the pause in searching upon prey capture during which organisms ‘handle’ their prey. Both a and h have power-law-like relationships with body size for a wide array of taxonomic groups [2–4,9].

To account for the negative effect of increasing consumer density on foraging rates (mutual interference), equation (1.1) has been modified in several ways [10,11]. One common way to account for interference is with the Hassel–Varley–Holling (HVH) model, which reduces the a parameter by linking it to consumer density with a power-law function [12,13]:

1.2

where m is ‘mutual’ interference, and α is the value of a when C = 1 or m = 0. Because interference has a strong effect on population stability [14,15], any body-size dependence of this parameter would indicate systematic dependence of stability on body size [16,17]. Here, I assess the body-size dependence of mutual interference using a new mechanistic model and an empirical analysis of a new dataset assembled from the literature.

2. Model

Although originally phenomenological, the HVH model can be mechanistically generated by incorporating the effect of predator density on the average predator velocity [15]. Area of capture (a) can be decomposed into an area of detection A_d and the encounters between consumer and resource individuals: 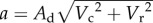, where V_c and V_r are the velocities of the consumer and the resource, respectively [18]. By rescaling the consumer velocity by C², to represent mass–action encounters among consumers, the rescaled area of capture ã declines as C increases:

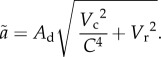2.1

This change causes the effective searching velocity of the consumer to decline as consumer density increases, lowering encounters and thus foraging rates. Equation (2.1) does not, however, produce m analytically. Instead, the value of m must be determined from a linear regression of ã against C [15]. Nonetheless, equation (2.1) clearly demarcates the typical range of mutual interference values found in the literature (0 to −2) [11,15]. It produces a dependence of ã on C that ranges from the power of −2 when the prey are stationary (when 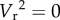, ã is a function of C⁻²) to the power of 0 when predators are sit-and-wait (when 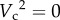, ã is independent of C). It also collapses to the original expression when C = 1, when there are no other individuals with which to interfere.

To make m dependent on body size, I first define the scaling of velocity V with body mass M as V = v₀M^γ, where γ is a scaling exponent, and ν₀ is the value of V when M = 1. Assuming that γ does not vary between consumer and resource, because it usually falls in a narrow range of about 0.1–0.25 [19], I substitute to get

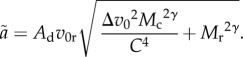2.2

Here, I have specified the mass for the consumer, M_c, and the resource, M_r, separately. For convenience, I have defined the relative velocity as Δv₀ = v_0c/v_0r (following the notation of [20], again with subscripts c and r for consumer and resource, respectively) which allows us to have only one parameter in the radical indicating mass-specific velocity differences. When predators travel much faster than their prey, Δv₀ is large, but Δv₀ ≈ 0 for sit-and-wait predators. Finally, I define the consumer–resource body size scaling as 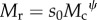, where s₀ is the value of M_r when M_c = 1, and ψ is a scaling exponent, and substituting this yields

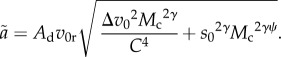2.3

Because interference is more severe when V_c² is large relative to V_r² (see equation (2.1)), equation (2.3) shows that the magnitude of interference depends on the relative velocity (Δv₀) and the scaling of resource body size with consumer body size (s₀ and ψ). In other words, a relatively fast-moving consumer makes the 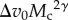term relatively large, magnifying the effect of C on ã and making interference stronger (closer to m = −2). An important special case in equation (2.3) is when the scaling of resource to consumer body size (ψ) is one, which is approximately true across a large body-size range [21]. In this case, 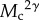can be factored out, showing that interference is independent of body size. Otherwise, for any given set of parameters corresponding to specific consumer–resource groups, ψ will determine whether interference increases (when ψ < 1) or decreases (when ψ > 1) with body size.

3. Material and methods

I assessed the model's predictions for the body-size dependence of interference in two ways. In both cases, I estimated m by regressing ã on C across a broad range of body sizes (10⁻⁷ to 10⁵ g). In the first case, I varied only the level of ψ to show its effect. In the second case, I randomly sampled all parameters in equation (2.3) from an empirically observed range and again estimated m across the same range of body sizes. This time I drew 500 sets of parameter values from a uniform distribution set by the typical ranges for each parameter reported in the literature: γ (0.1–0.3 [19]), ψ (0.5–1.5 [22]) and s₀ (0.001–1000 [21]). The value of Δv₀ could range from that for a sit-and-wait predator that never moves (Δv₀ = 0) to that for a consumer that moves considerably faster than its prey, such as predatory birds eating small mammals. From the velocity–mass relationships in [19], this could be as much as 10-fold, so I varied Δv₀ from 0 to 10. These parameter sets reflect a behaviourally and taxonomically diverse range of possible consumer–resource interactions across body sizes. For the 500 parameter sets, I plotted the resulting m against body size with a grey line in figure 1b.

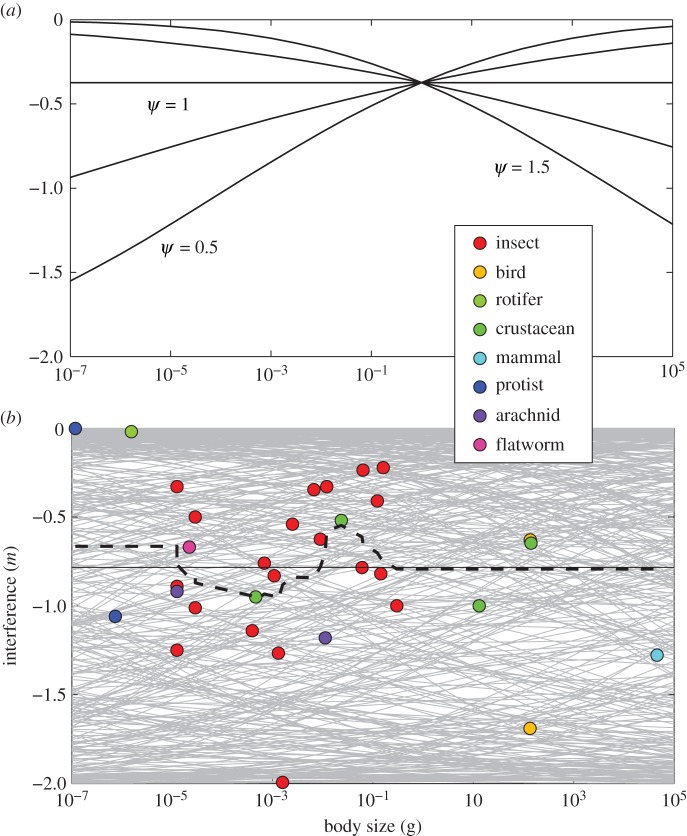
Figure 1.

(a) The body-size dependence of mutual interference driven by the scaling exponent relating resource body size to consumer body size (ψ, see text). The other parameters in this simulation were γ = 0.25, s₀ = 10 and Δv₀ = 10. Similar results were obtained with other parameter combinations. (b) The body-size dependence of mutual interference across a wide range of taxa, with parameters for equation (2.3) drawn randomly from typical ranges (grey lines, see Material and methods). Both model and data indicate no systematic effect of mass on interference. The overall (thin horizontal line) and running mean (heavy dashed line) of the observed levels of interference are shown.

I then assembled a dataset on body size and mutual interference from the literature (see the electronic supplementary material and data in [23]). These data came from studies where foraging or parasitism rates were measured under a range of resource and consumer densities, as required by equation (1.2). The estimates of m came from either the original source or were recalculated from data presented in the figures following the approaches in [11,13]. For this study, I added new data from [17,24–28] to the datasets in [11,15] and then searched the original papers and the literature for estimates of body size for each of the focal consumers. I averaged multiple observations for the same consumer. The final dataset included observations for 33 consumers of a variety of taxa including insects (20), arachnids (2), crustaceans (4), birds (2), protists (2), mammal (1), flatworm (1) and rotifer (1).

3. Results

The value of ψ strongly influenced the relationship between interference and body size and controlled whether there was a positive or negative nonlinear relationship or no relationship at all (figure 1a). Randomly sampling parameters indicates that the model does not predict a systematic variation of interference across a wide range of body sizes (figure 1b). In other words, any level of interference is possible for any body size given the underlying parameters. The empirical data support this observation. A linear regression of m on body size has a non-significant slope of −0.02 (95% CI: −0.04 to 0.01), and the running mean of m (window length of 10; heavy dashed line in figure 1b) followed the overall mean (thin horizontal line) very closely.

4. Discussion

By setting growth and mortality, body-size-dependent parameters determine the abundance, stability and dynamical properties of populations [3,29,30]. The results presented here indicate that unlike all other population parameters, mutual interference appears broadly independent of body size (figure 1b). Under certain conditions, there may be a small effect; for example, four orders of magnitude variation in terrestrial mammalian predator body size would change interference from about −0.75 to −1.25, assuming ψ = 1.5 [3]. By contrast, this change produces three orders of magnitude of change in area of capture [3].

Interference is generally a stabilizing force in populations because it decreases interaction strengths [14]. If interference were tied to body size, then population stability would be as well. Instead, most species show intermediate levels of interference, with a mean of approximately −0.7. Thus, the effect of body size on populations is more pronounced through parameters other than interference, while interference applies to about the same degree across a wide size range. There appears to be a benefit to these intermediate levels, as no interference allows large swings in population sizes, while severe interference, because of its association with high levels of consumer–resource engagement, tends to push populations deterministically towards extinction [15].

Equation (2.2) can make testable predictions about interference from knowledge of consumer and resource velocities. Such predictions may apply to any given system as well as the broad effects of environmental factors such as temperature [17,20]. For example, if warming accelerates the velocities of the consumers more than their resources, interference should increase, and vice versa. Indeed, in the case of two ground beetles, interference levels went up for one species and down for another species with temperature [17]. Such effects could be predicted from equation (2.2), although in the case of the beetles it is not known whether velocity changes could account for the observations.

With a mechanistic model linking body mass and temperature to a functional response with interference in hand, we can more thoroughly investigate how population properties respond to environmental change. Yet the vast majority of functional response studies have measured foraging rates of only one individual consumer, and as a result levels of interference are mostly unknown. More work is needed to understand how factors like body mass, predation mode and temperature influence interference, as independent of body mass, it has potent effects on populations and the communities in which they reside.