Abstract
Through combined three-dimensional electromagnetic and particle tracking simulations we demonstrate a THz driven electron streak camera featuring a temporal resolution on the order of a femtosecond. The ultrafast streaking field is generated in a resonant THz sub-wavelength antenna which is illuminated by an intense single-cycle THz pulse. Since electron bunches and THz pulses are generated with parts of the same laser system, synchronization between the two is inherently guaranteed.
Ultrafast generation of electrons and ultrafast manipulation of their trajectories is a rapidly developing field and is, in most cases, tightly intertwined with ultrafast laser technology. Ultrafast lasers illuminate metallic plane photocathodes or nanotips to produce correspondingly short electron bunches through photo- or field emission. One major driving force behind ultrashort electron pulse generation and measurement developments has been the field of ultrafast electron diffraction in the femtosecond time domain, which has recently been reviewed by Miller1,2. Notable work in this field includes studies on chemical reactions in the gas phase3, ultrafast melting dynamics of metals4,5, ultrafast dynamics in charge density wave materials6,7, and insulator to metal phase transitions in organic salts8, to name but a few. The success of these experiments has depended heavily on advances in ultrafast electron source technology. In the 10–100 kV electron energy regime, pulsed electron guns based on planar photocathodes are capable of producing electron bunches with pulse durations in the few hundred femtosecond regime4,9,10,11,12 while nanotip sources13,14,15,16,17 and bunch re-compression based systems8,18,19,20 are, at least in principle, capable of reaching the 10–100 fs time domain. Pulsed electron sources in the MeV are expected to have a similar performance in terms of electron pulse duration21,22. Full temporal characterization of ultrashort electron wavepackets is a prerequisite for their use not only in ultrafast electron diffraction experiments, but also electron rescattering in atoms, as well as seeding of femtosecond x-ray free electron lasers (XFEL)23. This issue is especially acute for systems with non-negligible pulse-to-pulse fluctuations, in which single-shot characterization techniques are required. While temporal characterisation of ultrashort light pulses in the visible and near-visible regime with sub-100 fs precision is routine, measurements of similar precision on ultrashort electron pulses are currently considered a technical challenge. The literature therefore abounds with reports of both conceptual and experimental realizations of temporal electron pulse characterisation in the femtosecond regime. Streak cameras have been applied in the field of ultrafast electron diffraction (UED), initially in single-shot mode, to obtain sub-picosecond pulse duration measurements5,10. Subsequently, Kassier et al. demonstrated a low-jitter streak camera suitable for accumulation mode measurements of electron pulses with a temporal resolution of 150 fs12. Large improvements to the temporal resolution obtained by this streak camera may be difficult due to limitations of the maximum voltage that can be applied to the GaAs photo switches. In addition, it is not clear how large the jitter is on a sub-100 fs timescale. Streak cameras based on deflection mode RF cavities with sub-100 fs resolution have been demonstrated in the keV and MeV electron energy regimes16,24, yet the issue of phase jitter in RF cavities is currently a problem, typically limiting temporal resolutions in accumulation mode to >100 fs25. Cross correlation techniques of electron pulses with laser pulses have also yielded temporal resolutions of order 100 fs in the sub-relativistic regime11. The main factor limiting the temporal resolution here is the transit time of the electrons through the laser focus, which is about 30 fs assuming a minimal laser focal spot size of 10 microns. Recently, optical cycle modulation of electron energy has been demonstrated by cross correlation of a laser pulse with an electron pulse at the interface of a thin metal film, showing promise as a technique for femtosecond and even attosecond resolution of high energy electron pulses26. The temporal resolution would, however, be severely hampered in the case of electron pulses with a moderate to large energy bandwidth, essentially limiting the technique to single- or few-electron pulses. In the relativistic regime, techniques based on autocorrelation of coherent transition radiation have been demonstrated for sub-picosecond resolution27. While obtaining temporal resolutions in the 10–100 fs regime is conceivable with current proven technologies, few-femtosecond resolution seems out of reach for both relativistic and sub-relativistic electron energy regimes.
Here, we propose a route to accomplish temporal electron bunch characterization with the potential capability of achieving few-femtosecond temporal resolution for high-energy electron pulses (10–100 kV range) as well as relativistic electrons in the MeV range. This is to be achieved by combining resonant THz sub-wavelength structures with intense single-cycle THz pulse generation. Very recent experiments proof that it is indeed feasible to manipulate electron trajectories through nanostructures illuminated by THz pulses28. Essentially, the design is reminiscent of a streak camera with the streaking field being replaced by the THz pulse illuminating a so-called split-ring resonator. Since electron bunches and THz pulses are generated with the same laser system, synchronization between the two is inherently guaranteed under ideal conditions (e.g. no intensity fluctuations of the laser system, temperature, and humidity etc.). The THz split-ring resonator is designed to feature a resonant response and a moderate field enhancement in order to alleviate the demands on the driving laser. Its resonance frequency can be varied between 100 GHz and several THz simply by changing the ring's geometry, allowing for THz streak field rise times between hundreds of femtoseconds to several picoseconds29. Combined with a sensitive electron detector, THz-driven streaking is therefore well adapted to measure ultrashort electron bunches, even on a single-shot basis.
Figure 1 shows a schematic of the proposed THz streak camera. While part of the driving laser system or a second synchronized laser system produces the electron bunches, the other part is used to generate intense single-cycle THz pulses which are subsequently focused to the split-ring resonator. Electron bunches are commonly generated through photo-effect at flat cathodes using UV pulses with photon energies above the work function of the metal30 or through field ionization with NIR pulses at isolated nanotips13 and arrays thereof14. The electron bunch length can be tuned between about 50 fs and tens of picoseconds depending on the application by changing the pulse duration of the driving laser. The intense single-cycle THz pulses can be produced through optical rectification in suitable inorganic or organic crystals, such as LiNbO329,31 or DAST32. Field strengths on the order of tens of MV/m have been reported at diffraction-limited THz focal spots33,34. If a split-ring resonator is positioned at the focal spot, the resonantly absorbed THz radiation induces a current flow in the ring that results in an accumulation of charge carriers across the gap region. The capacitive charging leads to an in-gap enhancement of the electric field whose magnitude depends on the gap geometry and leads to field enhancement factors as high as several orders of magnitude. A simulated electric field distribution is shown in Figure 2. The in-gap field distribution is very close to that of a parallel-plate capacitor. Effectively, the split ring shaped sub-wavelength structure serves as an efficient resonant antenna absorbing the incident THz radiation and concentrating it in the gap volume thereby increasing the field strength by a factor that is roughly given by the ratio of the structure size and the gap area. For a gap area of 10 μm by 10 μm and a resonance frequency of 0.3 THz the field enhancement is approximately 100, boosting the maximum attainable electric fields of today's THz sources to the GV/m level35. While typical electron pulses in ultrafast electron diffraction guns have a diameter of order 100 μm, such beams can be apertured for purposes of temporal characterisation; this is also necessary for other temporal characterisation techniques such as the ponderomotive cross correlation method, or the compact streak camera implemented by Kassier et al. The electron pulses pass through this gap region approximately at the zero-crossing of the in-gap electric field and are deflected by the time varying electric field distribution. For a judicious choice of the split ring's resonance frequency the longitudinal charge distribution of the passing electron bunch is mapped onto the transverse momentum axis. That is, electrons from different longitudinal positions within the electron bunch propagate in different directions after passing through the split ring's gap region. Finally, the electrons are detected by a spatially resolving detector, e.g. a micro channel plate (MCP), with the x-axis now being directly proportional to the time axis.
Figure 1. Schematic of the experimental setup (details see text).
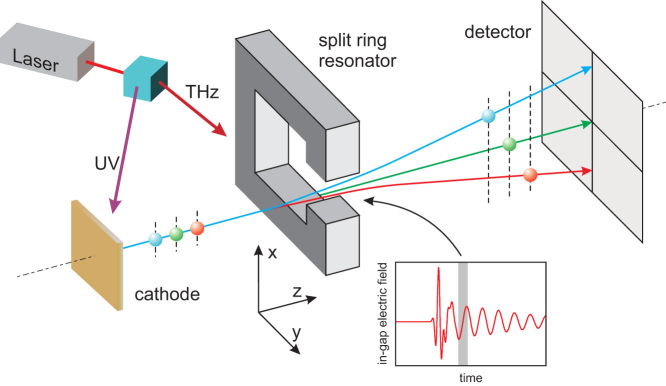
Figure 2. Simulated electric field distribution.
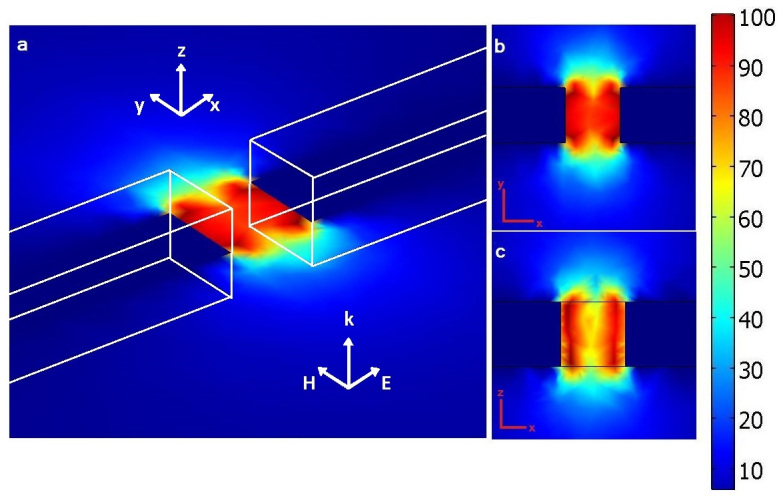
(a) Ex component normalized to the incident field in a plane through the middle of the gap of the split-ring resonator (SRR) at 300 GHz, (b) horizontal and (c) vertical field distributions across the gap.
The use of a split-ring resonator is essential for several reasons. First, it generates a field distribution close to that of a plane capacitor which is beneficial for the streaking process. Second, the interaction volume is determined by the gap volume rather than the focused THz spot size and can, thus, be adapted to the electron pulse energy. Finally and most importantly, a focused free space electromagnetic pulse does not transfer net energy to free electrons (Woodward-Lawson-Palmer theorem), other than via the ponderomotive force which is rather small for the electron energies considered here. The metallic split-ring resonator introduces boundary conditions which render energy and momentum transfer possible.
Results
Through combined three-dimensional electromagnetic and particle tracking simulations we analyse the performance of such a THz-driven streak camera with respect to angular streak velocity, time resolution, and intrinsic time smearing due to, for example, electric field inhomogeneities. Initially, we assume the actual electron bunches to consist of 1000 quasi-randomly distributed electrons with a square transverse distribution of 4 μm × 4 μm and a zero transverse emittance, and without considering space charge forces. The electron energy is fixed to 30 keV and the temporal duration of the initial bunch length is varied in the 0–100 fs range in order to properly evaluate the potential performance of this device for sub-100 fs electron pulse characterisation. After passing through the split-ring's gap the electron bunches propagate for 20 mm before their transverse spatial distribution is measured. While a propagation distance of 20 mm is not realistic from an experimental point of view due to the resultant small electron spot size on the detector, it is used here for convenience in the rather time consuming simulations. In the absence of space charge, the parameters of importance such as angular streak velocity and temporal resolution are invariant with respect to the chosen detector distance. We assume more realistic camera lengths in the subsequent section with simulations that take account of space charge.
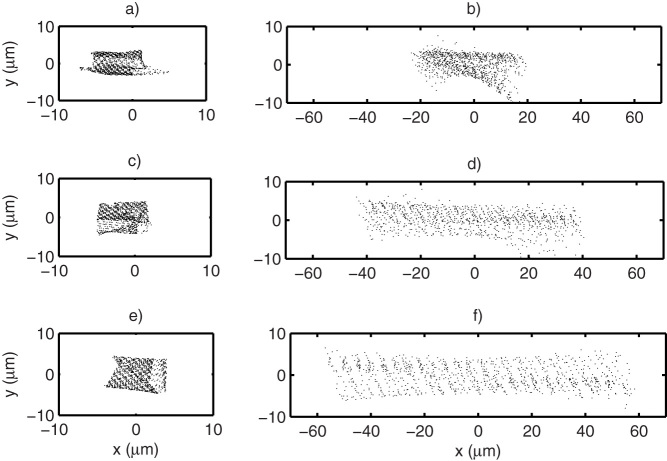
Figure 3 depicts the simulated transverse electron distributions for a peak electric field Ex set to 100 MV/m. Subfigures a) and b) correspond to the fr = 0.3 THz split ring resonance frequency and electron pulse durations of 0 fs and 50 fs, respectively. Similarly, subfigures c) and d) represent the fr = 0.6 THz case and e) and f) the fr = 0.9 THz case with the same initial electron bunch length. The value of 50 fs was chosen here since this is comparable to the current state of the art for bunched highly charged electron pulses18. Showing for comparison the 0-fs pulse duration case allows one to distinguish between effects of the streak field on the one hand and distortion effects due to transverse beam size on the other. It should be noted that not only the arrival time of electrons, but also their transverse position in the bunch, affects their net deflection. It must be concluded that a small but not vanishing lensing effect must be attributed to the streaking field, which inherently limits the achievable temporal resolution. From figure 3 it is already apparent that at a fixed peak electric field, here Ex = 100 MV/m, the streak velocity increases with the resonance frequency.
Figure 3. Simulated transverse electron distributions captured at 20 mm propagation distance downstream from the split ring for different THz frequencies and initial electron pulse durations.
For graphs a), c), and e), the initial temporal duration was set to zero, while graphs b), d) and f) correspond to 50 fs initial temporal duration (top hat profile). Graphs a) and b), c and d), and e) and f) correspond to THz frequencies of 0.3 THz, 0.6 THz, and 0.9 THz, respectively. The peak transverse electric field in the gap was 100 MV/m in all cases.
Figure 4a) shows the behaviour of the streak angle as a function of pulse duration for different THz frequencies at a value of Ex = 100 MV/m. As indicated by the good linear fits, the streak angle is linear with pulse duration, yielding a constant angular streak velocity vs,θ of 10 mrad/ps, 23 mrad/ps, and 33 mrad/ps for gapped ring oscillator frequencies of 0.3 THz, 0.6 THz, and 0.9 THz, respectively. The achievable temporal resolution corresponding to these streak velocities depends on the “background” angular spread of the beam σ0, which in the best case (zero emittance electron beam in the absence of post- streaking space charge effects) is dependent on the distortions introduced by the streak field on an electron pulse with zero temporal duration. As already seen in Figure 3, such distortions are small but not vanishing. For Ex = 100 MV/m, we find σ0 = 0.026 mrad, 0.035 mrad, and 0.028 mrad for the 0.3 THz, 0.6 THz, and 0.9 THz cases, respectively. The achievable temporal resolution is given by Δt = σ0/vs,θ, yielding 2.6 fs, 1.5 fs, and 0.9 fs in the 0.3 THz, 0.6 THz, and 0.9 THz cases. In Figure 4b), the angular streak velocity is plotted as a function of the split ring's resonance frequency for different values of Ex. Clearly, the angular streak velocity increases linearly with both frequency and field amplitude, culminating in a very large streak velocity of 330 mrad/ps at 0.9 THz and 1 GV/m peak electric field. Since the “background” angular spread varies in the same proportion as the streak velocity with changing Ex, the maximal achievable temporal resolution is still only about 0.9 fs for this case. However, a larger streak field has the advantage of yielding a higher temporal resolution with realistic electron beams that do not have a vanishing emittance. For example, assuming an electron pulse angular spread of σ0 = 0.5 mrad for split-ring oscillator parameters of 0.9 THz and Ex = 1 GV/m yields a temporal resolution of 1.5 fs, while the corresponding temporal resolution for the 100 MV/m case is only 15 fs.
Figure 4.
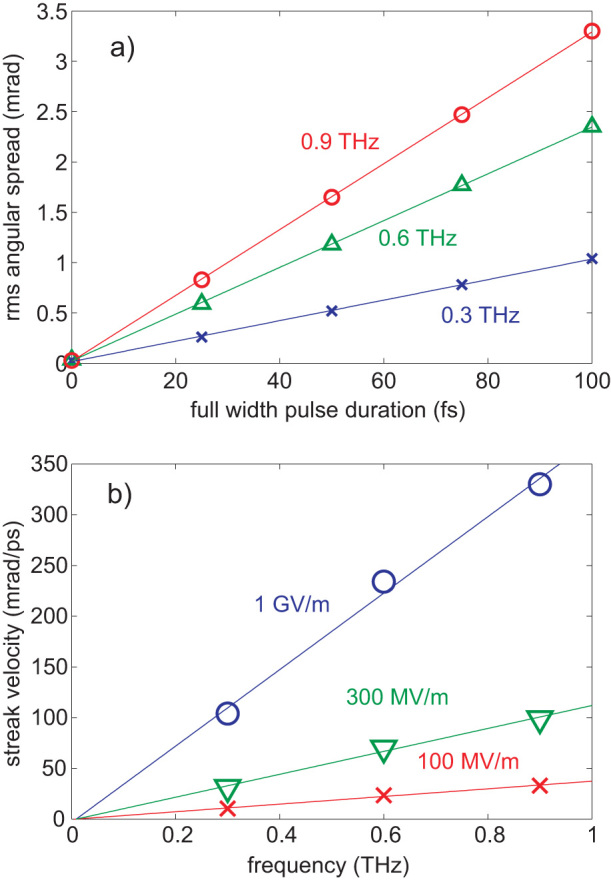
a) Simulated rms angular spread versus full width initial temporal pulse duration of 30 kV electron pulses for 0.3 THz (crosses), 0.6 THz (triangles) and 0.9 THz (circles). The gradients of the linear fits shown in the figure yield angular streak velocities of vs,θ = 10 mrad/ps, 23 mrad/ps and 33 mrad/ps respectively. The peak transverse electric field was 100 MV/m for all cases. b) Angular streak velocity versus resonance frequency for different peak streak electric fields. Crosses represent a peak field of 100 MV/m while triangles and circles correspond to 300 MV/m and 1 GV/m, respectively.
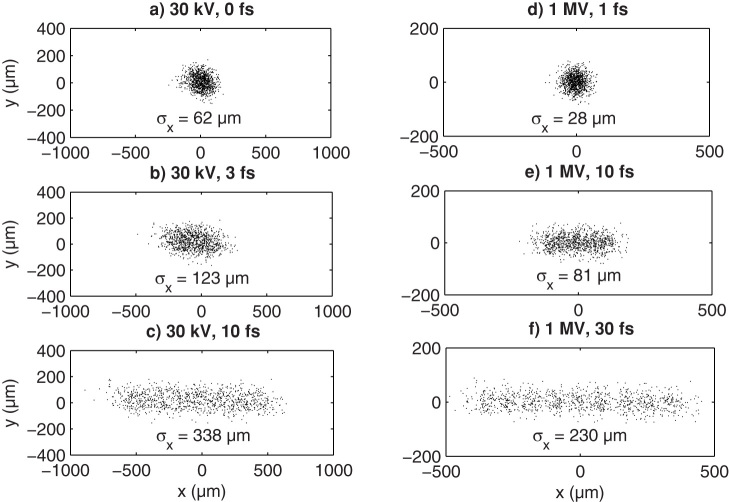
For a more realistic evaluation of the streak camera performance, space charge forces were included for 4 μm × 4 μm sized electron bunches with a transverse normalized emittance of εn = 1 nm, a bunch charge of Q = 6.4 × 10−9 nC (40 electrons), and a relative rms energy spread of ΔEr = 0.1% (1%) in case of 30 keV (1 MeV) electron bunch centre energy. The simulations were performed using the 0.9 THz resonance frequency with a peak transverse electric field of 1 GV/m. For the two cases considered (30 kV and 1 MV electron energy), the gapped ring oscillator to detector distances were 10 cm and 50 cm, respectively. The results of these simulations, depicting the streaking pattern at the detector plane, are given in Figure 5. For the 30 keV case, it is clear that a pulse duration of 3 fs (Figure 5b) already results in significant broadening relative to a “zero length” pulse duration (Figure 5a). Using the result of Figure 5c, a streak velocity vs = 33.8 μm/fs at the detector plane can be calculated (corresponding to an angular streak velocity of vs,θ = 0.338 mrad/fs), from which the temporal resolution Δt = σ0/vs = 1.8 fs with the un-streaked pulse width σ0 equal to 62 μm, the result of Figure 5a. Similarly for the 1 MeV case, the temporal resolution is 3.7 fs. Thus, the proposed streak camera is expected to be capable of few femtosecond resolution for the measurement of realistic electron bunches in the high energy and in the relativistic energy regimes. It should also be highlighted that the recorded streaking pattern depends negligibly on the chosen relative electron energy bandwidth in the 0–1% range, making the split ring resonator an ideal tool for electron bunch measurements in UED experiments and femtosecond RF guns such as injectors for FELs or relativistic UED setups.
Figure 5. Simulated transverse electron distributions for a 0.9 THz split ring resonator with a peak gap field of 1 GV/m.
Electron bunches with an rms size σx and σy = 2 μm, transverse normalized emittance εn = 1 nm and aerial space charge density σQ = 107 electrons/mm2 were propagated through the split ring resonator towards the detector which was located 10 cm and 50 cm further along the beam line for the 30 keV (sub-figures a) through c)) and 1 MeV (sub-figures d) through f)) respectively. Space charge effects are taken into account in this simulation, and the rms bunch size in the x- direction σx are indicated in the figure. The relative rms energy spread was assumed to be 0.1% and 1% for the 30 keV and 1 MeV cases, respectively.
Discussion
The proposed THz-driven streak camera is a very promising device for temporal electron pulse measurements in the few femtosecond up to few hundred femtosecond time domain. While the temporal resolution, as shown above, depends on a variety of parameters, the total streaking window is determined by the resonance frequency of the split-ring resonator alone. If we allow for a 5% deviation from the linear time-to-space mapping the total streaking window is approximately given by T = 0.11/fr. Table 1 summarizes the performance parameters of the THz driven streak camera for a hypothetical electron bunch with vanishing emittance and energy bandwidth. Clearly, a temporal resolution close to 1 fs is achievable for suitable parameters such as electron beam energy, THz frequency and peak THz field, with increasing THz frequency and field and decreasing electron energy leading to better temporal resolution. The presence of transverse pulse distortions also for zero temporal duration pulses suggests that the THz streak camera exhibits lensing effects due to the spatial curvature of the electric field. These distortions seem to confine the achievable temporal resolution to the 0.1–1 fs range. While optical cycle streaking techniques show promise of temporal resolutions deep in the attosecond range, the present streak camera would be more ideal for measuring temporal durations in the 1 fs to 100 fs range. In addition, we find no discernable effect of the energy bandwidth of the measured electron bunches on the streak pattern up to relative bandwidths of 1%, thereby making our THz streak camera an ideal tool for electron bunch diagnostics in beam lines with highly charged bunches and compressor elements, as found in UED setups, synchrotrons, and XFEL's.
Table 1. The total streaking window and the rms time resolution for different split ring resonator frequencies and field strengths. A bunch centre electron energy of 30 keV and an rms angular spread of 0.5 mrad imminently prior to streaking are assumed.
| Temporal resolution [fs] | ||||
|---|---|---|---|---|
| Resonance frequency [THz] | Total streaking window [fs] | 100 MV/m | 300 MV/m | 1000 MV/m |
| 0.3 | 717 | 48 | 16 | 4.8 |
| 0.6 | 358 | 21 | 7.1 | 2.1 |
| 0.9 | 239 | 15 | 5.1 | 1.5 |
Methods
Three-dimensional electromagnetic simulation
The numerical simulations are based on the finite element method (FEM)36 and are performed with a commercial software package (COMSOL Multiphysics). The three-dimensional simulations are carried out in the frequency-domain which allows including the frequency-dependent THz properties of the metal structures through a complex conductivity, as obtained from the Drude model37. The plasma frequency and damping constant of gold are taken from reference38. The split ring resonator is positioned at the centre of a cubic simulation domain and the refractive index of the surrounding dielectric is set to unity (vacuum). The incident THz field is approximated by a plane electromagnetic wave, which is justified because the width and the height of a split ring resonator are typically given by the fundamental resonance wavelength over 8, i.e. λres/8, and the focal spot size of a THz pulse centred at λres is approximately 4 F# λres/π, with the f-number F#. That is, even for an f-number of 1 the focal spot of the THz pulse is about 10 times larger than the size of the split ring resonator and a plane wave excitation is a reasonable approximation. The plane wave is launched from one of the boundaries and the frequency is chosen as a scanned parameter. For the other boundaries scattering boundary conditions are applied to avoid unwanted reflections. The simulation domain is discretized using a tetrahedral mesh and additional mesh layers at all metal vacuum interfaces are added in order to account for the different length scales of the free-space THz wavelength (~1 mm) and the interaction length in the metal (~100 nm). The size of the split ring resonator is chosen to 370 μm, 200 μm, and 140 μm to obtain fundamental resonances at 0.3 THz, 0.6 THz, and 0.9 THz, respectively. The structure width and thickness are set to 10 μm and the gap width is 10 μm. Resonances occur whenever the length of the unfolded split ring resonator corresponds to integer multiples of half the wavelength. Due to the symmetry of the modes relative to the linearly polarized incident THz pulse odd-numbered resonances are excited when the electric field of the THz pulse is parallel and even numbered when it is polarized perpendicular to the gap38,39. Here, we consider electric field coupling, that is, the electric field is parallel to the side containing the gap and the E, H, and k triad of the incoming field is oriented along the x, y and z axes (see Figure 2). We focus on the fundamental resonance of the split ring resonator which we refer to as the C mode, since it is characterized by a circulating current flow leading to a build-up of charge across the gap40. The next higher order resonances would appear at 0.9 THz, 1.8 THz, and 2.7 THz. In all three cases discussed we assume that the spectrum of the incident THz pulse is centred approximately at the respective resonance frequencies. Moreover, higher order resonances show a lower field enhancement since the charge distribution on the split ring resonator is no longer localized solely around the gap. Therefore, the spectral amplitude at the third order resonances and their contribution to the streak field may safely be neglected. Finally, the three-dimensional electric and magnetic field distributions in a volume around the gap region are exported for further use in the ASTRA particle tracking simulations. The dimensions of the volume were chosen large enough to capture the enhanced electromagnetic fields.
Electron tracking simulation
The electron optical behaviour of the THz split ring resonators is evaluated via particle trajectory simulations using the ASTRA particle tracking code41. In order to assess the potential streaking performance of the split ring resonators, an initial particle distribution consisting of 1000 quasi-randomly distributed electrons is generated. The root mean square transverse (x and y) size of the square initial distribution is 4 μm, and a zero angular spread, and consequently zero transverse emittance, is assumed. The bunch momentum in the z-direction corresponds to an electron energy of 30 keV. The temporal duration of the initial bunch length is set to various values in the 0–100 fs range. The ASTRA code is capable of full three dimensional space charge tracking, but space charge effects are ignored initially so as not to obscure the effect of the split ring resonator's electromagnetic field. Subsequently, simulations of electron pulses with more practically realistic bunch parameters, along with the inclusion of space charge forces and considering the case of relativistic electrons, have been performed. The same initial rms bunch size was assumed, but a finite transverse normalized emittance of 1 nm, as well as a space charge density of 107 electrons/mm2, corresponding to 40 electrons per bunch, was assumed. In addition, a relative rms energy spread of 0.1% and 1% was imparted on the initial electron pulse for the 30 keV and 1 MeV cases respectively, which are realistic values for bunched electron beams. Space charge tracking was implemented by approximating the electron bunch as a 12 × 12 × 12 three-dimensional grid of line charges with the “3D-FFT” algorithm in the ASTRA code41 and particle tracking with a 4th order Runge-Kutta integration. The simulated electromagnetic field distributions are incorporated into ASTRA by defining two overlapping RF cavities with a three-dimensional electromagnetic field input (Ex, Ey, Ez, Bx, By, Bz). The phase difference of the two cavities is set to 90 degrees such that one cavity represents the real part of the electromagnetic field, while the other corresponds to the imaginary. Electromagnetic fields of three different centre frequencies (0.3 THz, 0.6 THz, and 0.9 THz) are considered in these simulations. The magnitudes of the electromagnetic field components are scaled such that the peak electric field amplitude in the x-direction corresponded to 100 MV/m, 300 MV/m, and 1 GV/m, respectively. The position of the cavities is set such that the initial electron distribution passes exactly through the centre of the cavities in the x-y plane. To visualise the electron optical effect of the THz field, the electron pulses are allowed to travel some distance beyond the position of the split ring resonator before their spatial distribution is analysed.
Author Contributions
J.F. performed the electromagnetic simulations and G.K. the electron trajectory simulations. J.F., G.K. and T.F. contributed to the conceptual design and the writing of the paper. All authors reviewed the manuscript.
Acknowledgments
J.F. and T.F. acknowledge funding from the SNF grant 200020-140943 and the NCCR MUST. G.K. gratefully acknowledges support from the Max Planck Society, and would also like to thank Klaus Floettmann (DESY) for his valuable advice on the use of the ASTRA code.
References
- Miller R. J. D. Mapping Atomic Motions with Ultrabright Electrons: The Chemists' Gedanken Experiment Enters the Lab Frame. Phys. Chem. 65, 583 (2014). [DOI] [PubMed] [Google Scholar]
- Miller R. J. D. Femtosecond Crystallography with Ultrabright Electrons and X-rays: Capturing Chemistry in Action. Science 343, 1108 (2014). [DOI] [PubMed] [Google Scholar]
- Ihee H. et al. Direct imaging of transient molecular structures with ultrafast diffraction. Science 291, 458 (2001). [DOI] [PubMed] [Google Scholar]
- Siwick B. J. & Miller R. J. D. An atomic-level view of melting using femtosecond electron diffraction. Science 302, 1382 (2003). [DOI] [PubMed] [Google Scholar]
- Siwick B. J., Dwyer J. R., Jordan R. E. & Miller R. J. D. Femtosecond electron diffraction studies of strongly driven structural phase transitions. Chem. Phys. 299, 285 (2004). [Google Scholar]
- Eichberger M. et al. Snapshots of cooperative atomic motions in the optical suppression of charge density waves. Nature 468, 799–802 (2010). [DOI] [PubMed] [Google Scholar]
- Erasmus N. et al. Ultrafast dynamics of charge density waves in 4H(b)-TaSe2 probed by femtosecond electron diffraction. Phys. Rev. Lett. 109, 167402 (2012). [DOI] [PubMed] [Google Scholar]
- Gao M. et al. Mapping molecular motions leading to charge delocalization with ultrabright electrons. Nature 496, 343–346 (2013). [DOI] [PubMed] [Google Scholar]
- Hebeisen C. T. et al. Femtosecond electron pulse characterization using laser ponderomotive scattering. Opt. Lett. 31, 3517–3519 (2006). [DOI] [PubMed] [Google Scholar]
- Wang X. et al. Measurement of femtosecond electron pulse length and the temporal broadening due to space charge. Rev. Sci. Instrum. 80, 13902 (2009). [DOI] [PubMed] [Google Scholar]
- Hebeisen C. T. et al. Grating enhanced ponderomotive scattering for visualization and full characterization of femtosecond electron pulses. Opt. Express 16, 3335 (2008). [DOI] [PubMed] [Google Scholar]
- Kassier G. H. et al. A compact streak camera for 150 fs time resolved measurement of bright pulses in ultrafast electron diffraction. Rev. Sci. Instrum. 81, 105103 (2010). [DOI] [PubMed] [Google Scholar]
- Krüger M. et al. Interaction of ultrashort laser pulses with metal nanotips: a model system for strong-field phenomena. New J. Phys. 14, 085019 (2012). [Google Scholar]
- Mustonen A., Beaud P., Kirk E., Feurer T. & Tsujino S. Efficient light coupling for optically excited high-density metallic nanotip arrays. Nature Sci. Rep. 2, 915 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffrogge J. et al. A tip-based source of femtosecond electron pulses at 30 keV. J Appl. Phys. 115, 094506 (2014). [Google Scholar]
- Krüger M., Schenk M., Förster M. & Hommelhoff P. Attosecond physics in photoemission from a metal nanotip. J. Phys. B: At. Mol. Opt. Phys. 45, 074006 (2012). [Google Scholar]
- Wachter G. et al. Electron rescattering at metal nanotips induced by ultrashort laser pulses. Phys. Rev. B 86, 035402 (2012). [Google Scholar]
- van Oudheusden T. et al. Compression of subrelativistic space-charge-dominated electron bunches for singleshot femtosecond electron diffraction. Phys. Rev. Lett. 105, 264801 (2010). [DOI] [PubMed] [Google Scholar]
- Veisz L. et al. Hybrid dc–ac electron gun for fs-electron pulse generation. New J. Phys. 9, 451 (2007). [Google Scholar]
- Kassier G. H. et al. Photo-triggered pulsed cavity compressor for bright electron bunches in ultrafast electron diffraction. Appl. Phys. B 109, 249 (2012). [Google Scholar]
- Murooka Y. et al. Transmission-electron diffraction by MeV electron pulses. Appl. Phys. Lett. 98, 251903 (2011). [Google Scholar]
- Reckenthaeler P. et al. Proposed method for measuring the duration of electron pulses by attosecond streaking. Phys. Rev. A 77, 042902 (2008). [Google Scholar]
- Grguras I. et al. Ultrafast X-ray pulse characterization at free-electron lasers. Nature Photon. 6, 852–857 (2012). [Google Scholar]
- Musumeci P. et al. Capturing ultrafast structural evolutions with a single pulse of MeV electrons: Radio frequency streak camera based electron diffraction. J. Appl. Phys. 108, 114513 (2010). [Google Scholar]
- Gao M., Jiang Y., Kassier G. H. & Miller R. J. D. Single shot time stamping of ultrabright radio frequency compressed electron pulses. Appl. Phys. Lett. 103, 33503 (2013). [Google Scholar]
- Kirchner F. O., Gliserin A., Krausz F. & Baum P. Laser streaking of free electrons at 25 keV. Nature Photon. 8, 52 (2013). [Google Scholar]
- Lihn H., Kung P., Settakorn C. & Wiedermann H. Measurement of subpicosecond electron pulses. Phys. Rev. E 53, 6413 (1996). [DOI] [PubMed] [Google Scholar]
- Wimmer L. et al. Controlling and streaking nanotips photoemission by enhanced single-cycle terahertz pulses. arXiv:1307.2581. Date of access, 09/07/2013 (2013).
- Aydin K. et al. Investigation of magnetic resonances for different split-ring resonator parameters and designs. New J. Phys. 7, 168 (2005). [Google Scholar]
- Piot P. et al. Formation and acceleration of uniformly filled ellipsoidal electron bunches obtained via space-charge-driven expansion from a cesium-telluride photocathode. Phys. Rev. ST – Accel. Beams 16, 010102 (2013). [Google Scholar]
- Hirori H., Doi A., Blanchard F. & Tanaka K. Single-cycle terahertz pulses with amplitudes exceeding 1 MV/cm generated by optical rectification in LiNbO3. Appl. Phys. Lett. 98, 091106 (2011). [Google Scholar]
- Hauri C. P., Ruchert C., Vicario C. & Ardana F. Strong field single cycle THz pulses generated in an organic crystal. Appl. Phys. Lett. 99, 161116 (2011). [Google Scholar]
- Ruchert C., Vicario C. & Hauri C. P. Scaling Sub-mm single-cycle transients towards MV/cm fields via optical rectification in organic crystal OH1. Opt. Lett. 37, 899 (2012). [DOI] [PubMed] [Google Scholar]
- Sell A., Leitenstorfer A. & Huber R. Phase-locked generation and field-resolved detection of widely tuneable terahertz pulses with amplitudes exceeding 100 MV/cm. Opt. Lett. 33, 2767 (2008). [DOI] [PubMed] [Google Scholar]
- Merbold H., Brunner F., Cannizzo A. & Feurer T. Near Field Enhancement for THz Switching and THz Nonlinear Spectroscopy Applications. Chimia 65, 316 (2011). [DOI] [PubMed] [Google Scholar]
- Jin J. The Finite Element Method in Electromagnetics. Willey-IEEE Press, Second ed. (2002). [Google Scholar]
- Ordal M. A., Bell R. J., Alexander Jr R. W., Long L. L. & Querry M. R. Optical properties of fourteen metals in the infrared and far infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W. Appl. Opt. 24, 4493 (1985). [DOI] [PubMed] [Google Scholar]
- Gay-Balmaz P. & Martin O. Electromagnetic resonances in individual and coupled split-ring resonators. J. Appl. Phys. 92(5), 2929 (2002). [Google Scholar]
- Katsarakis N., Koschny T., Kafesaki M., Economou E. & Soukoulis C. Electric coupling to the magnetic resonance of split ring resonators. Appl. Phys. Lett. 84(15), 2943 (2004). [Google Scholar]
- Rockstuhl C. et al. On the reinterpretation of resonances in split-ring-resonators at normal incidence. Opt. Express 14(19), 88278836 (2006). [DOI] [PubMed] [Google Scholar]
- Floettmann K. Astra – A space charge tracking algorithm, DESY. (2014).