Morphing structures of the Dionaea muscipula Ellis during the trap opening and closing

Abstract

The Venus flytrap is a marvelous plant that has intrigued scientists since the times of Charles Darwin. This carnivorous plant is capable of very fast movements to catch a prey. We found that the maximal speed of the trap closing in the Dionaea muscipula Ellis is about 130 000 times faster than the maximal speed of the trap opening. The mechanism and kinetics of this movement was debated for a long time. Here, the most recent Hydroelastic Curvature Model is applied to the analysis of this movement during closing and opening of the trap with or without a prey. Equations describing the trap movement were derived and verified with experimental data. Chloroform and ether, both anesthetic agents, induce action potentials and close the trap without the mechanical stimulation of trigger hairs. We tested this by dropping 10 μL of ether on the midrib inside the trap without touching any of the mechanosensitive trigger hairs. The trap closed slowly in 10 s. This is at least 20 times slower than the closing of the trap mechanically or electrically. The similar effect can be induced by placing 10 μL of chloroform on the midrib inside the trap, however, the lobes closing time in this case is as fast as closing after mechanical stimulation of the trigger hairs.

Introduction

Many plants react to mechanical stimuli, but only certain plants with rapid and highly noticeable touch-stimulus response mechanisms, such as the Venus flytrap, have received much attention.^1-11 The trap closure has been investigated by the mechanical stimulation of the trigger hairs by a cotton thread,^1,2,12-14 by fingers of researchers,¹⁵ by electrical stimulation between the lobes and midrib of the Venus flytrap,^5-9,14-16 by 7.35 μm laser with 50 μW power,¹⁶ and by various chemicals.^1,17

Touching the trigger hairs protruding from the upper epidermal layer of the Venus flytrap’s leaves (Fig. 1) activates mechanosensitive ion channels. As a result, receptor potentials are generated which in turn induce a propagating action potential throughout the upper leaf of the Venus flytrap.^6,10,18,19 A receptor potential always precedes an action potential and couples the mechanical stimulation step to the action potential step of the preying sequence.¹⁹ A possible pathway of action potential propagation to the midrib includes vascular bundles and plasmodesmata in the upper leaf.^13,20-23

Figure 1. The open trap (A) and a triggering hair (B) of the Venus flytrap.

Upon closure, the cilia protruding from the edge of each lobe form an interlocking wall that is impenetrable to all except the smallest prey. The trap uses the double-trigger mechanism and shuts when the prey touches its trigger hairs twice in succession within a 25 s window of time. Partial closure allows the cilia to overlap, while the lobes are still held slightly ajar. This partial closure occurs in a fraction of a second, and several minutes may be required for the lobes to completely join together. When a prey is caught, the lobes seal tightly and remain closed for 5–7 d, allowing digestion to take place.^10,24 The stalk and basal cells containing lipid globules and the common wall between these 2 cells are traversed by numerous plasmodesmata.²⁵ Electron micrographs of the trigger hairs reveal 3 regions where the cells differ in size, shape, and cytoplasmic content. Plasmodesmata found in anticlinal and podium cells pass through constricted zones in the cell wall; there are numerous plasmodesmata in the peripheral podium cells.²⁶

The lobes of the Venus flytrap move because of changes in shape, curvature, and volume of cells. In the case of the osmotic motor, water flux and ion flux are linked to one another. If water follows H⁺ or K⁺ flux by osmosis, then the rate of flux will determine the rate of volume change in the lobes. Rapid movement of each lobe requires water co-transporters. Water flux across biological membranes occurs as a passive diffusion across the lipid bilayer;²⁷ it is also facilitated by aquaporins, which may play a pivotal role in osmoregulation in plants. The rate of cellular movement is determined by the water flux. This flux is induced by a rapid change in osmotic pressure, which is monitored by a fast and transient opening of aquaporins.

Kinetics of the lobes closing can be calculated from the Hydroelastic Curvature Model of the Venus flytrap developed by Markin et al.^14,28 The trap possesses curvature elasticity and consists of outer and inner hydraulic layers where different hydrostatic pressures can build up. The open state of the trap contains elastic energy accumulated due to the hydrostatic pressure differences between the outer and inner layers of the lobe. Applied stimuli open water channels connecting the 2 layers, water rushes from one hydraulic layer to another, and the trap relaxes to the equilibrium configuration, its closed state. The change of curvature results in the movement of the peripheral parts of the leaf so that the rims of lobes approach each other and close the trap.

The hydroelastic curvature model describes the closing process by the change of distance between the rims of the lobes X(t).^14,28 Initially this distance is equal to X₁. It is well known that the closing of the trap in not tight, because a small gap between the rims remains. So in the end, the distance between the rims X does not come to zero but rather to a certain small value X₂. The variation of the distance X(t) during the trap closing was found to proceed according to the equation:

$$X(t)=\left(X_1-X_2\right)\exp \left\{\frac{{\tau }_a}{{\tau }_r}\left[1-\exp \left(-\frac{t-t_s}{{\tau }_a}\right)\right]-\frac{\left(t-t_s\right)}{{\tau }_r}\right\}+X_2$$ (1)

This equation describes a complex process with 3 distinct stages of trap closing. Right after the electrical stimulation there is a silent period – nothing happens during this time$t_s$. In this period the plant processes the electrical signal in a mechanically silent manner: nothing can be seen from outside – the leaf does not move. Then the channels between 2 hydraulic layers start to open; they open randomly and the characteristic time of this process was designated${\tau }_a$. This is the main hunting stage in which the movement of the leaf is quickly accelerated. So, characteristic time ${\tau }_a$is the main parameter that tells us how fast and efficient the hunting abilities of the Venus fly trap are. Finally the third phase of elastic relaxation of the leaf to the new equilibrium state occurs with the characteristic time${\tau }_r$.

The speed of the trap movement $v(t)$ can be found from this equation:

$$v(t)=\frac{dX}{dt}=\frac{\left(X_1-X_2\right)}{{\tau }_r}\exp \left\{\frac{{\tau }_a}{{\tau }_r}\left[1-\exp \left(-\frac{t-t_s}{{\tau }_a}\right)\right]-\frac{\left(t-t_s\right)}{{\tau }_r}\right\}\left[\exp \left(-\frac{t-t_s}{{\tau }_a}\right)-1\right]$$ (2)

The curvature of the lobe, according to Hydroelastic Curvature Model,^14,28 changes with time as:

$$C_M(t)=\left(C_1-C_2\right)\exp \left\{\frac{{\tau }_a}{{\tau }_r}\left[1-\exp \left(-\frac{t-t_s}{{\tau }_a}\right)\right]-\frac{\left(t-t_s\right)}{{\tau }_r}\right\}+C_2$$ (3)

Trap closure is believed to represent non-muscular movement based on hydraulics and mechanics. The nastic movement in various plants involves a large internal pressure (turgor). It is quite likely that these movements are driven by differential turgor that is actively regulated by the plants. Trap closure occurs via quick changes in the curvature of each lobe rather than by movement of the leaf as a whole. The cell walls of the upper and lower epidermis and adjacent mesophyll feature a preferential microfibril orientation in the direction of the applied stress. These anatomical features are selected as the basis of the Hydroelastic Curvature Model presented above. It is well known that the trap closes very fast but its opening is very slow.¹ Kinetics of mechanically stimulated the trap closing was investigated in detail by Stuhlman,²⁹ Forterre et al.,¹⁵ Markin et al.,¹⁴ and Volkov et al.^6,28 Stuhlman²⁹ recorded kinetics of the lobes separation distance during the trap opening after a mechanical stimulation of trigger hairs.

The goal of this study is the analysis of morphing kinetics in the Venus flytrap during the trap closing and opening in the presence or absence of a prey.

Results

Closing and opening the empty trap

In the open state the trap has a convex shape. During the trap closing, after mechanical stimulation of the trigger hairs, the trap changes its curvature from the convex to the concave shape (Fig. 2). In the closed state the curvature of the trap was found about -0.6 cm⁻¹. In the open state the curvature of the trap in different plants varies from 0.37 to 0.45 cm⁻¹. Curvature was measured in frames obtained from video recording. In this measurement we assumed that the shape of the leaf was described by a part of a sphere. Having equation (3) we can plot curvature variation with time (Fig. 3, curve 1). By fitting this curve to the experimental points the following parameters were found: C₁ = 0.454 cm⁻¹, C₂ = -0.593 cm⁻¹, τ_a = 0.05 s, τ_r = 0.07 s, t_s = 0.07 s. So, the curvature of the leaf monotonously changes from positive value of 0.454 cm⁻¹ in the open state to the negative -0.593 cm⁻¹ in the closed state.

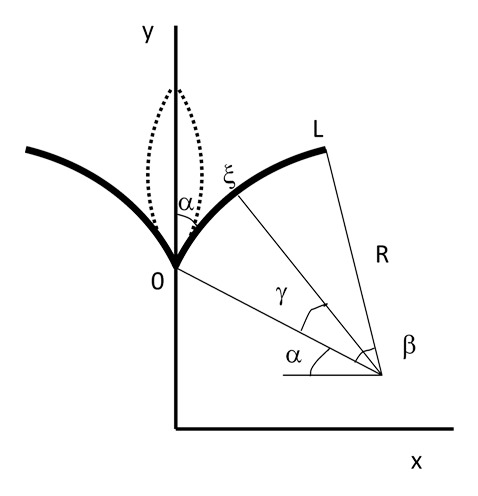
Figure 2. Description of the model: transition from open (solid lines) to closed state (dashed lines). The system has cylindrical symmetry and the leaf (from 0 to L) is modeled as a circle. L – the length of the leaf; β – angle at the center of this circle; R – radius of curvature; α – initial angle at the midrib (does not change); ξ – an arbitrary point at the leaf; and γ - the angle at the center of curvature corresponding to this point ξ.

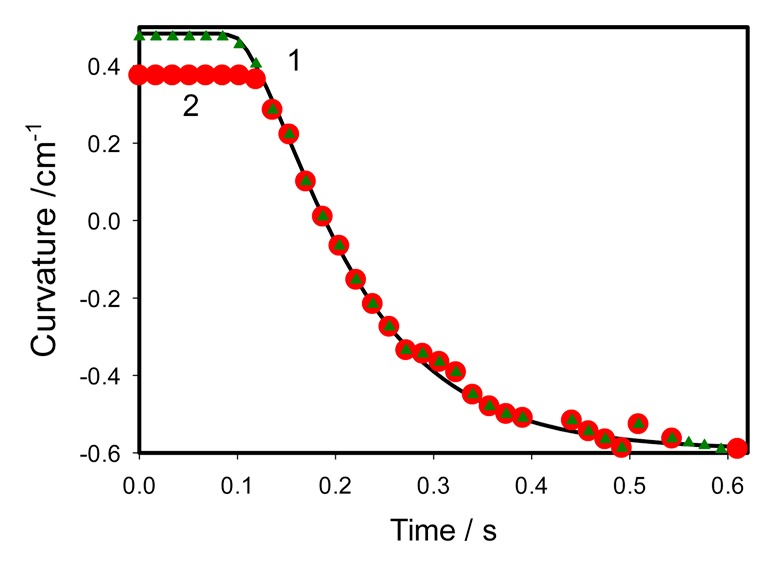
Figure 3. Closing of the empty trap induced by mechanical stimulation. Experimental points are taken from experiments on 2 different plants. 2 mechanosensitive hairs were touched by a cotton thread for 0.2 s before fast removing from the trap at time equal to 0 in this Figure. Solid line was estimated using equation (3) with the following parameters found in the experiment: C₁ = 0.454 cm⁻¹, C₂ = - 0.593 cm⁻¹, τ_a = 0.05 s, τ_r = 0.07 s, t_s = 0.07 s.

The closing process is preceded by a silent period $t_s$. After silent period, the movement quickly accelerates and at the moment $t_{\max }$ the rate of curvature change reaches maximum${\frac{dC}{dt}|}_{\max }$. After standard analysis of the second derivative of function (3) one can find that:

$$t_{\max }=t_s-2{\tau }_a\log \left(\sqrt{\frac{{\tau }_r}{4{\tau }_a}+1}-\frac{1}{2}\sqrt{\frac{{\tau }_r}{{\tau }_a}}\right)$$ (4)

and:

$${\frac{dC}{dt}|}_{\max }=\frac{\left(C_1-C_2\right)}{{\tau }_r}\exp \left\{\frac{{\tau }_a}{{\tau }_r}\left[1-\exp \left(-\frac{t_{\max }-t_s}{{\tau }_a}\right)\right]-\frac{\left(t_{\max }-t_s\right)}{{\tau }_r}\right\}\left[\exp \left(-\frac{t_{\max }-t_s}{{\tau }_a}\right)-1\right]$$ (5)

The maximal speed of curvature change during closing can be calculated from equations (4) and (5). It was found equal to 5 cm⁻¹s⁻¹ (Fig. 3, curves 1 and 2). We selected 2 cases of the trap closing kinetics with maximum deviations (Fig. 3) from video recordings on 14 different plants. Although starting curvature can be between 0.37 and 0.45 cm⁻¹, the kinetics of closing follows to the same equation (3). After gentle touch of 2 trigger hairs by cotton thread the trap closes in less than a second and stays in a closed state for a few hours without additional tightening.

After closing, the trap starts to open after 5 to 15 h. This period under continuous illumination is less than the period in “night” darkness. Seemingly, the process of the trap opening requires a source of energy. The closing of the trap is about 130 000 faster than the trap opening. During the trap closing ATP concentration in the midrib decreases and light is required for the ATP synthesis during photosynthetic process and for mitochondrial respiration.³⁰ The fact that the trap opens faster under continuous illumination is probably caused by production of a substrate for a dark respiration.³⁰ The variation of curvature with time has a sigmoid shape (Fig. 4) and has 2 regions. The shape of the trap is concave in the beginning of opening and starts to change to convex shape after 13 h. Transformation from concave to convex shape is a slow process (Fig. 4). Kinetics of the trap opening can be parameterized by the equation:

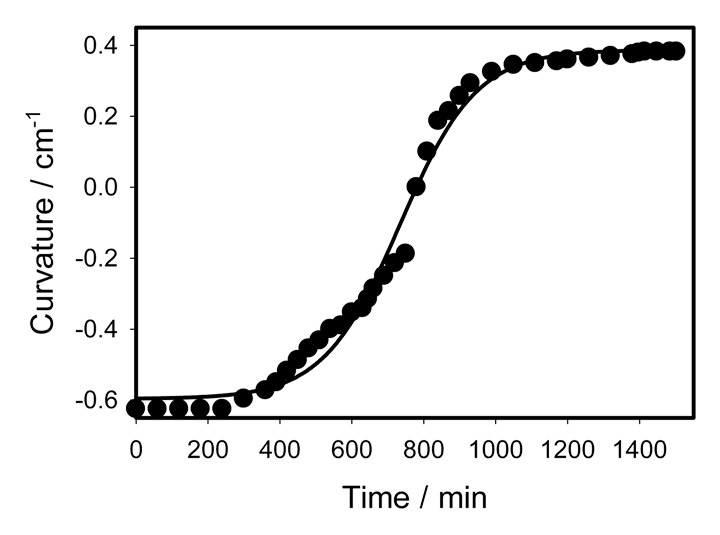
Figure 4. Time variation of a curvature during the trap opening after mechanical stimulation during continuous illumination. Dots are experimental points; solid line was estimated from equation (4).

$$C=C_0+\frac{a}{1+\exp \left[-\left(t-t_m\right)/b\right]}$$ (6)

with parameters a = 0.9836 cm⁻¹, b = 106.3909 min, t_m = 733.9818 min, and C₀ = -0.5965 cm⁻¹. The maximum rate of curvature change is:

$${\frac{dC}{dt}|}_{\max }==\frac{a}{4b}$$ (7)

With parameters given above this rate amounts to 0.0023 cm⁻¹min⁻¹ = 3.85x10⁻⁵ cm⁻¹s⁻¹. It means that maximal speed of curvature change during closing is 5 cm⁻¹s⁻¹/3.85x10⁻⁵ cm⁻¹s⁻¹ = 129870 times faster than opening.

Kinetics of the trap closing after catching the prey and opening after that

We selected a piece of gelatin as a model prey for the stimulation of the trap closing. Figure 5 shows kinetics of the trap closing induced by 0.1 cm³ of gelatin. Kinetics of the trap closing can be parameterized by equation (3) with parameters C₁ = 0.41167 cm⁻¹, C₂ = -0.7159 cm⁻¹, τ_a = 0.02747 s, τ_r = 0.2556 s, t_s = 0.306 s. The trap closes in a half of a second. Kinetics of the trap opening after gelatin digestion is shown in Figure 6. Kinetics of the trap opening can be parameterized by equation (6) with parameters a = 0.9843 cm⁻¹, b = 8.2473 h, t₀ = 164.1573 h, and C₀ = -0.6018 cm⁻¹.

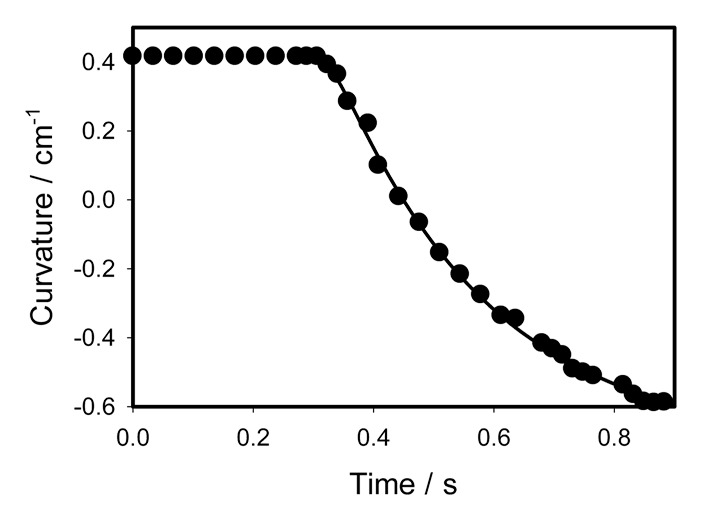
Figure 5. Closing of the trap with a “prey” induced by 0.1 cm³ of gelatin. Dots are experimental points, solid line was estimated from equation (3).

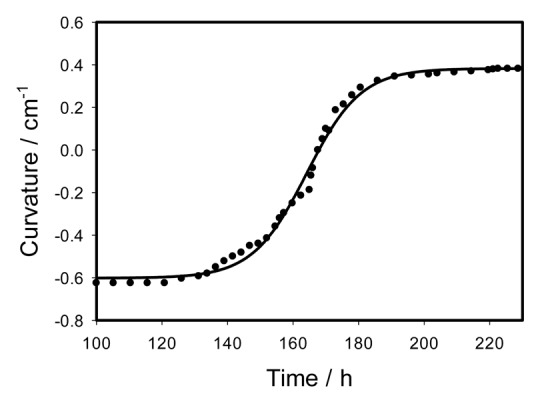
Figure 6. Time variation of a curvature during the trap opening after digestion of 0.1 cm³ of gelatin during 100 h. Dots are experimental points, solid line was estimated from equation (4).

Why are the characteristic times of the closing and opening of the Venus flytrap so much different? These differences occur because the hunting process in the Venus flytrap is similar to a loaded and cocked gun ready to shoot. All elastic energy stored in the trap is ready to be released momentarily. After closing the trap, the plant needs to “charge the gun,” meaning the plant has to pump energy into the trap spring. It is achieved by pumping water from one surface layer of the trap to another at the expense of photosynthesis and ATP stored in the leaf. It is a slow process which takes a considerable amount of time.

Effects of anesthetics

We have studied the effect of anesthetics on the morphing process in the Venus flytrap. If the Venus flytrap with a petri dish containing 5 mL of chloroform or diethyl ether is covered by a 12 L glass jar (Figs. 7and8), anesthetic agents chloroform or ether induce lobes movement and closes the trap without a mechanical stimulation of trigger hairs (Figs. 7 and8). Long incubation with chloroform or ether is destructive and can irreversible kill the Venus flytrap plant.¹ Short incubation with anesthetics is reversible: when the anesthetic is removed, the trap recovers in a week and can be closed again. Time dependence of the trap curvature after the deposition of 10 μL of chloroform to the midrib is shown in Figure 9. Kinetics of the trap closing can be parameterized by equation (3) with parameters C₁ = 0.3728 cm⁻¹, C₂ = -0.55451 cm⁻¹, τ_a = 0.069964 s, τ_r = 0.1232 s, t_s = 0.0989 s.

Figure 7. Effect of incubation of the Venus flytrap with a Petry dish containing 5 mL of chloroform covered by a 12 L glass jar on kinetics of the trap closing.

Figure 8. Effect of incubation of the Venus flytrap with a Petry dish containing 5 mL of ether covered by a 12 L glass jar on kinetics of the trap closing.

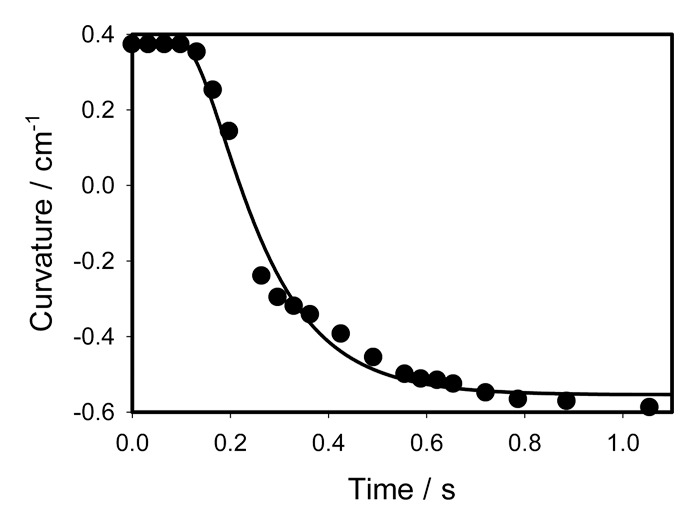
Figure 9. Time variation of a curvature during the trap closing induced by deposition of 10 μL of chloroform on the surface of a midrib inside the trap without touching the mechanosensitive hairs. Dots are experimental points; solid line was estimated from equation (3).

Kinetics of the trap closing induced by chloroform is fast and similar to kinetics of mechanical closing of the trap (Fig. 3). One possible mechanism of action for chloroform is that it increases movement of potassium ions through certain types of potassium channels.³¹ The deposition of 10 μL of water to the midrib does not close the trap.

Anesthetics such as ether or chloroform can be used as chemical agents, which can close the trap without mechanical stimulation. To check this hypothesis, we drop 10 μL from a micropipette of ether on the midrib inside the trap without touching of lobes of mechanosensitive trigger hairs and the trap slowly closes in 10 s. This is at least 10–20 times slower than with mechanical or electrical stimulation of the Venus flytrap. The similar effect can be induced by placing 10 μL of chloroform to the midrib inside the trap, but the lobes closing time is less than 1 s (Fig. 10). Chloroform induces action potentials and close the trap without the mechanical stimulation of trigger hairs (Fig. 10). We tested this by dropping 10 μL of chloroform on the midrib inside the trap without touching any of the mechanosensitive trigger hairs (Fig. 10). The amplitude of action potentials is equal to 40 mV (mean 40.2 mV, median 40.0 mV, std. dev. 1.22 mV, std. err. 0.24 mV, n = 25).

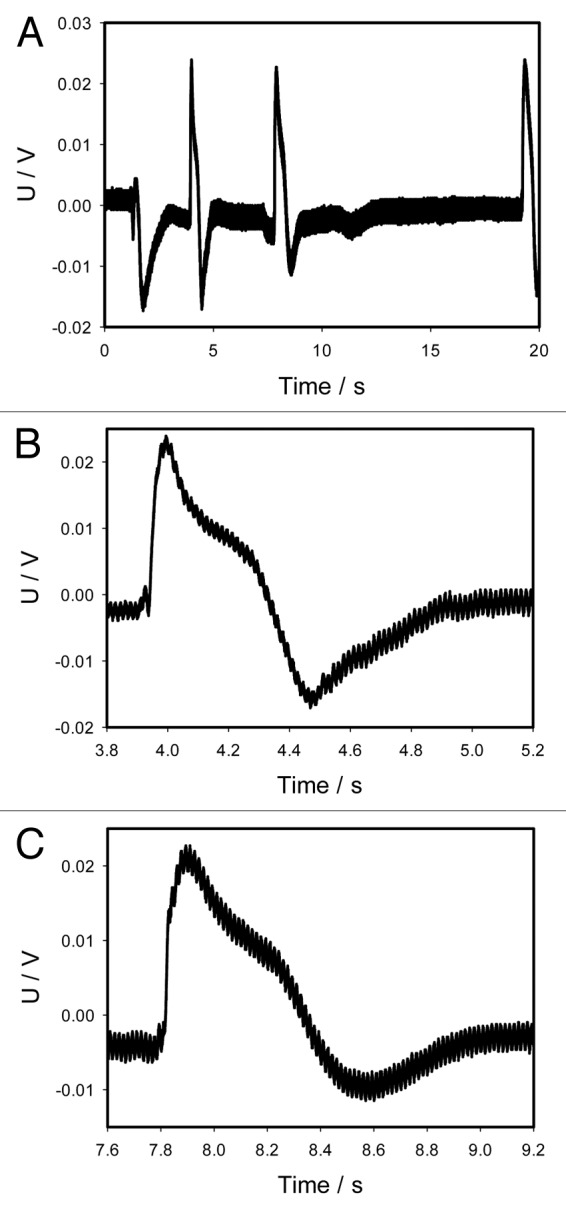
Figure 10. Electrical signaling in the Venus flytrap induced by deposition of 10 μL of chloroform on the surface of a midrib inside the trap without touching the mechanosensitive hairs (A). Panels (B) and (C) were taken from the panel (A). Both show action potentials in higher resolution and shorter intervals of time in comparison to panel (A). One Ag/AgCl electrode was located in the midrib and a reference Ag/AgCl electrode was in the center of a lobe. The frequency of scanning was 50 000 samples per second.

The effect of anesthetics on the Venus flytrap is quite different from the effect on the sensitive plant Mimosa pudica, which we studied earlier.³² If M. pudica with a petri dish containing 5 μL of chloroform or ether are covered by a 12 L glass jar for 10 min, anesthetic agent chloroform inhibits pinnule closing and leaflets movement after mechanical stimulation or by brief flaming. The effect of anesthetics is reversible: when the anesthetic is removed, the leaves of Mimosa pudica recover and pinnules can close again. The effects of anesthetics on mechanical stimulation and responses in the M. pudica were first described by Bose.^33,34 The disappearance of thigmonastic mobility of M. pudica caused by volatile or local anesthetic agents was observed by Bernard,³⁵ Milne and Beamish,³⁶ Okazaki et al.,³⁷ Paes and De Luccia,³⁸ and Wallace.³⁹

Discussion

The mechanism of the trap closing has been a subject for intensive debates since the 19th century and numerous models have been proposed.^{1-3,6,12-15,40-44} Darwin was the first to observe that the lobes of traps are convex when held open and concave when held shut.^1,2 Brown³ noted that the area of the underside of the lobes expands during closure, whereas the area of the inner sides of the lobes increases upon reopening. This model helps explain the flipping action “of the most wonderful plant” mentioned by Darwin.¹ By painting the surface with dots, Darwin¹ was able to prove that during the process of closing, the superficial layer of cells of the leaf contracted over the whole upper surface. Forterre et al.¹⁵ and Bobji⁴² suggested that the leaf’s geometry plays a crucial role in a buckling instability and considered Venus flytrap as a bistable vibrator, which can open and close simultaneously. This model contradicts with well known experimental facts: 1) ion and water channels blockers as well as uncouplers are inhibitors of the trap closing, but neither ion channels nor aquaporins are necessary during a buckling instability,⁸ 2) 2 mechanical stimuli in interval of up to 35 s are required for the closing of the trap, 3) the trap does not close during rain or after blasts of air,^1,40,41 4) the trap is stable and does not close spontaneously without stimuli, 5) opening of the trap is a slow process and lobes change their shapes from flat to concave and finally to convex, 6) Forterre et al.¹⁵ observed no ringing in the process of closing, and 7) closing of the trap requires ATP hydrolysis in the midrib.²⁴ Forterre et al.¹⁵ suggested that the measured speed at which the leaves closed depended on a dimensionless geometric parameter:

$$\alpha =\frac{L^4{K}^2}{h^2}$$ (8)

and the characteristic time for the trap movement:

$$\tau \sim \mu L^2/\kappa E$$ (9)

where L is the size of leaf, K its mean curvature, μ is viscosity in the porous plant tissue with κ hydraulic permeability, E is the elastic module of the tissue, and h the thickness of the leaf. Our experiments and literature data do not show the dependence of the closing time on size of the leaf L. This contradicts with equation (9), which predicts a dramatic increase in the closing time for large Venus flytrap plants.

The rapid trap closure of Dionaea muscipula Ellis has been explained by either a loss of turgor pressure of the upper epidermis or by a sudden acid-induced wall loosening of the motor cells.⁴² According to Hodick and Sievers⁴⁴ experiments, both explanations are doubtful. Another explanation is an expansion of the cell wall through acid growth.

Parameters of equation (3) for the trap closing induced by mechanical stimulation of trigger hairs (Fig. 3) or by deposition of 10 μL of chloroform on the surface of a midrib inside the trap (Fig. 9) are very similar. If the trap is simulated by a piece of gelatin or by gently touching the mechanosensitive hairs, there is a difference in time constants. Characteristic time τ_a tells us how fast and efficient is the movement of lobes when water channels between 2 layers in the lobes are open and τ_a is 2 times longer for mechanical stimulation of trigger hairs than for stimulation by a piece of gelatin. The elastic relaxation of the leaf to the new equilibrium state occurs with the characteristic time τ_r, which is 3.7 longer for stimulation by a piece of gelatin than for mechanical stimulation of mechanosensitive hairs. Ultra fast and slow video recording permits the study of different steps in biomechanics of plants and could lead to the development of new materials with unsuspected applications in science and engineering.

Materials and Methods

Plants

Fifty bulbs of D. muscipula (Venus flytrap) were purchased for this experimental work from Fly-Trap Farm (Supply, North Carolina) and grown in a well drained peat moss in plastic pots at 22 °C with a 12:12 h light:dark photoperiod. The soil was treated with distilled water. Irradiance was 700 μE/m²s. All experiments were performed on healthy adult specimens.

Chemicals

Chloroform and gelatin were obtained from Sigma-Aldrich (New York, NY). Diethyl ether was obtained from Acros Organics (Pittsburgh, PA).

Images

Digital high speed video camera system Olympus i-Speed 3 (Houston, TX) was used to collect digital images during the trap closing, which were analyzed frame by frame. Olympus i-Speed 3 video camera system has maximum sampling frequency of 150 000 frames per second. Basler ACE camera AC2000–340KC interfaced to PC using NI PCle-1435 high-performance camera link (National Instruments, Austin, TX) was used to collect images with maximum speed of 330 frames per second and with minimum speed of 1 frame per minute to collect images during the trap closing and opening (Fig. 11).

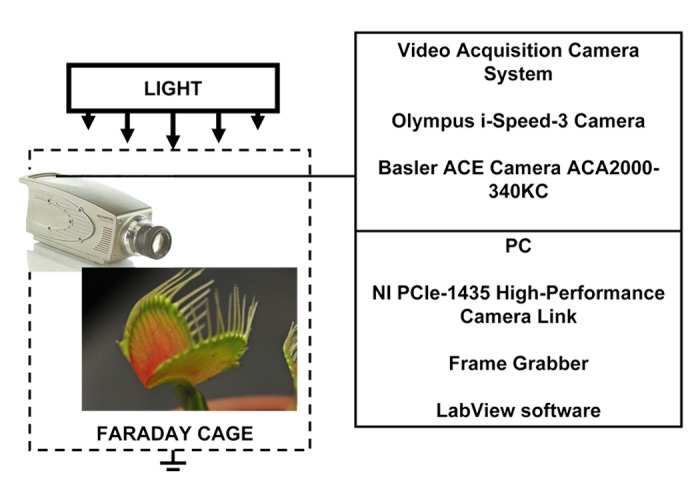
Figure 11. Experimental setup.

Data acquisition

All measurements were conducted in the laboratory at a 21 °C and some experiments at 30 °C inside a Faraday cage mounted on a vibration-stabilized table. Data acquisition boards NI-PXI-6115 or NI-PCI-6115 (National Instruments) interfaced through a NI SCB-68 shielded connector block to 0.1 mm thick nonpolarizable reversible Ag/AgCl electrodes were used to record the digital data (Fig. 10). The results were reproduced on a workstation with data acquisition board NI 6052E DAQ with input impedance of 100 GΩ interfaced through a NI SC-2040 Simultaneous Sample and Hold. The system integrates standard low-pass anti-aliasing filters at one-half of the sampling frequency. Measuring signals were recorded as ASCII files using LabView (National Instruments) software with low pass filters. Ag/AgCl electrodes were prepared from Teflon coated silver wires. Following insertion of the electrodes into lobes and a midrib, the traps closed. We allowed plants to rest until the traps were completely open.

Statistics

All experimental results were reproduced 25 times on different Venus flytrap plants. Software SigmaPlot 12 (Systat Software, Inc.) was used for statistical analysis of experimental data.

A photo camera Nikon D3x with AF-S Micro Nikkor 105 mm 1:2.8 G ED VR lens (Nikon, Melville, NY) was used for the photography of the Venus flytrap.