Effects of Crowding on the Stability of a Surface-Tethered Biopolymer: An Experimental Study of Folding in a Highly Crowded Regime

Abstract

The high packing densities and fixed geometries with which biomolecules can be attached to macroscopic surfaces suggest that crowding effects may be particularly significant under these often densely packed conditions. Exploring this question experimentally, we report here the effects of crowding on the stability of a simple, surface-attached DNA stem-loop. We find that crowding by densely packed, folded biomolecules destabilizes our test-bed biomolecule by ∼2 kJ/mol relative to the dilute (noninteracting) regime, an effect that presumably occurs due to steric and electrostatic repulsion arising from compact neighbors. Crowding by a dense brush of unfolded biomolecules, in contrast, enhances its stability by ∼6 kJ/mol, presumably due to excluded volume and electrostatic effects that reduce the entropy of the unfolded state. Finally, crowding by like copies of the same biomolecule produces a significantly broader unfolding transition, likely because, under these circumstances, the stabilizing effects of crowding by unfolded molecules increase (and the destabilizing effects of neighboring folded molecules decrease) as more and more neighbors unfold. The crowding of surface-attached biomolecules may thus be a richer, more complex phenomenon than that seen in homogeneous solution.

Introduction

The behavior of surface-tethered biomolecules, which play key roles throughout biology and in an increasing number of biotechnologies, can differ dramatically from the behavior of the same biomolecules free in solution. The relevant differences arise, in part, due to stabilizing or destabilizing interactions between the biopolymer and the surface, including excluded volume effects,^1,2 electrostatic effects,^1,3 and the formation of chemo-specific surface–biomolecule interactions.⁴ Surface attachment can also affect biomolecules, however, via interactions between neighboring molecules.⁵ Previously, we explored the former effects by experimentally determining the extent to which surface–biopolymer interactions alter the folding free energy of a simple biomolecule when it is attached to a set of well-defined, macroscopic surfaces.¹ Here, in contrast, we use the same system to explore the latter effect: crowding.

Several effects alter the folding thermodynamics of biomolecules that are crowded in solution (see ref (6) for a recent review). The excluded volume associated with crowding agents, for example, reduces the entropy of the unfolded molecule, thus stabilizing the native state.⁷⁻¹¹ Conversely, the formation of specific chemical interactions between the crowding agent and the biomolecule¹² can occur, which can preferentially stabilize the unfolded state.^13,14 Finally, many crowding agents are also chaotropes or kosmotropes, which alter the interaction between solvent and solute and thus modulate, for example, the hydrophobic effect.¹⁵ Given, however, that the effects of crowding in solution are generally small (typically less than 2–3 kJ/mol) and, more often than not, are stabilizing,¹⁶⁻¹⁸ it appears that the excluded volume usually dominates, but that its magnitude is limited by the relatively low solubility of most crowding agents.

The crowding agent concentrations that can be achieved in the surface-tethered regime are often significantly higher than those seen in bulk solution, suggesting that surface-crowding effects may be more significant than those seen in solution. DNA, for example, can be packed onto surfaces at such high grafting densities that the effective concentration of molecules within one contour length of the surface reaches a few tens of percent (w/v),^19,20 which is more than an order of magnitude greater than the solubility limit of DNA in bulk solution.^20,21 Crowding on surfaces may also differ from crowding in bulk solution due to immobilization, which limits the extent to which neighboring molecules can diffuse away from one another to relax unfavorable interactions. While reasonably well-explored theoretically,^9,22,23 however, and shown empirically to affect the performance of some technologies reliant on surface-attached biomolecules,^5,19,24 surface-crowding effects have not seen any significant experimental examination. In response, we demonstrate here the extent to which crowding alters the folding free energy of a model biopolymer attached to a well-defined macroscopic surface.

Results and Discussion

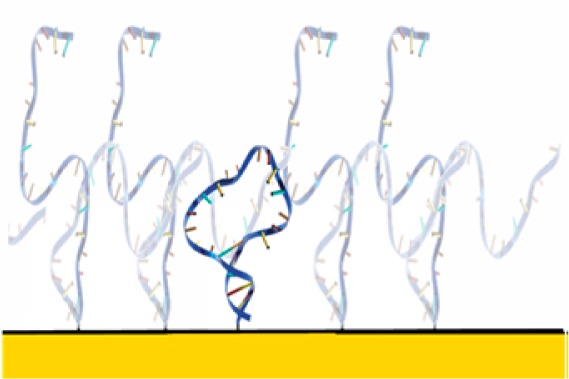
As our model system, we have employed a 25-base DNA with self-complementary ends. This sequence adopts a simple stem-loop structure in the absence of denaturant that unfolds as the concentration of the denaturant urea rises (Figure 1). We have measured the folding free energy of this stem-loop in four crowding regimes: (1) the “dilute regime” (i.e., largely uncrowded), in which neighboring molecules are, on average, separated by a distance greater than the contour length of the unfolded DNA; (2) the “folded crowding regime”, in which the stem-loop under investigation is crowded by a dense brush of similar, but much more stable, stem-loops that remain folded even at the highest urea concentrations we have employed; (3) the “unfolded crowding regime”, in which the stem-loop is crowded by a dense brush of a 25-base polythymine sequence that remains unstructured at all denaturant concentrations; or (4) the “homogeneous crowding regime”, in which crowding is driven by identical copies of the same stem-loop. We tethered both the test-bed stem-loop and the two crowding agents via their 5′-termini to a hydroxyl-terminated, six-carbon self-assembled monolayer deposited on a gold electrode. For the case of homogeneous crowding, we can reliably control the density with which the stem-loops are packed on the surface. More specifically, by varying the concentration of these various DNA constructs during surface deposition over the range of 50 nM to 2 μM, we achieved surface densities from 4.7 × 10¹⁰ to 3.3 × 10¹² molecules/cm² (Supporting Information Figure S1), which correspond to mean nearest-neighbor separations ranging from 46 to 6.1 nm, respectively. Given the 15.5 nm contour length of the unfolded stem-loop and assuming that, due to electrostatic repulsion and excluded volume effects, the DNA molecules achieve near maximal separation (a supposition supported experimentally²⁵), these packing densities range from highly crowded to the dilute regime in which interpolymer interactions are effectively abolished. Indeed, at the highest packing densities we have explored, the concentration of DNA molecules within one contour length (of the folded stem-loop) of the surface reaches ∼100 mg/mL (∼13 mM for oligonucleotides of the length employed here), which is significantly higher than the solubility limit of short DNA oligonucleotides in solution.^20,21 For the case of the unfolded crowding agent, the reproducible control of packing density at intermediate values is more difficult, presumably due to repulsion between unfolded molecules; for this system, we have only explored a single, relatively high packing density regime (mean nearest-neighbor separation of 9.1 nm achieved at a deposition concentration of 2 μM). Because the effects of a folded crowding agent are relatively small even under highly crowding conditions (mean nearest-neighbor separation of 6 nm), for these studies, we likewise only explored the most highly packed regime.

Figure 1.

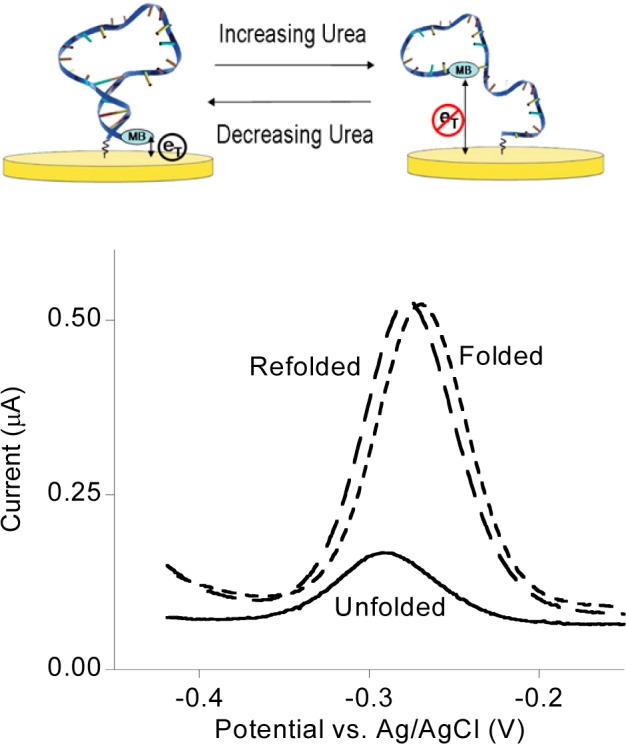
To explore the thermodynamic consequences of crowding for surface-tethered biomolecules, we have measured the folding free energy of (top) a simple DNA stem-loop attached by one terminus to a hydroxyl-terminated, six-carbon thiol-on-gold self-assembled monolayer (SAM). A redox-active methylene blue reporter on its distal terminus provides a means of monitoring the unfolding of the stem-loop using (bottom) square-wave voltammetry. Recovery of the original peak height after urea-induced unfolding and subsequent refolding illustrates the reversibility of folding under the experimental conditions we have employed.

To measure folding free energy, we modify our stem-loop with a terminal methylene blue redox reporter and use square-wave voltammetry to monitor the fraction of these molecules remaining in the stem-loop configuration as we titrate in urea. Such urea-melt data are traditionally fitted by assuming a linear relationship between free energy and denaturant concentration:

1

where [urea] is the concentration of the denaturant, i, i_f, and i_u are the experimentally observed signal (here the observed peak current) and the (fitted) signals arising from the fully folded (i_f) and fully unfolded states (i_u), respectively, ΔG°′ is the standard free energy of folding in the absence of denaturant, and m is the denaturant strength and describes the relative change in folding free energy per 1 M change in denaturant concentration. (Of note, as is also true when the urea-induced unfolding of biomolecules is measured optically via circular dichroism or intrinsic fluorescence,²⁶i_f and i_u are linearly dependent on urea concentration in our experiments; see Figure S1 for examples of raw urea unfolding data.) Using this approach, we have previously¹ shown that, in the absence of crowding (i.e., in the dilute regime), the folding free energy of the stem-loop is −6.7 ± 0.8 kJ/mol (all reported error bars reflect 95% confidence intervals derived from multiple, independent replicates). This represents slightly lower stability than that observed in solution under these same conditions, an effect that we attribute to electrostatic repulsion from the gold surface,¹ which is negatively charged at the redox potential of the methylene blue reporter.

Being in the folding crowded regime destabilizes our stem-loop (Figure 2). To show this, we co-deposited the stem-loop (in the dilute regime) with a 20-fold excess (in the deposition solution) of a more stable stem-loop (which remains folded at even the highest urea concentrations we employ)²⁷ to ensure that, while each stem-loop is surrounded by a dense brush of always-folded molecules, neighboring test-bed stem-loops are generally too far apart to interact with one another. At a total packing density of 3(±1) × 10¹² molecules/cm², which corresponds to a mean nearest-neighbor separation of 6 ± 1 nm, the stability of our stem-loop is −4.7 ± 0.8 kJ/mol, which is 2 kJ/mol less stable than the same stem-loop in the “dilute regime”. We presume this destabilization arises because the charge density within one (folded) contour length of the surface is extremely high under these conditions. If a single chain unfolds and expands such that much of its length is well above this highly charged brush of folded neighbors, this will reduce the charge density at the surface leading, in turn, to (enthalpic) stabilization of the unfolded state. Conversely, crowding by neighboring chains reduces the extent to which this unfolded chain can expand (relative to the dilute regime), an effect that should, in contrast, (entropically) destabilize the unfolded state. Given the observed destabilization, it appears that the former effect (enthalpic, charge-density-linked stabilization of the unfolded state) dominates over the latter effect (entropic destabilization of the unfolded state) for the system we have studied.

Figure 2.

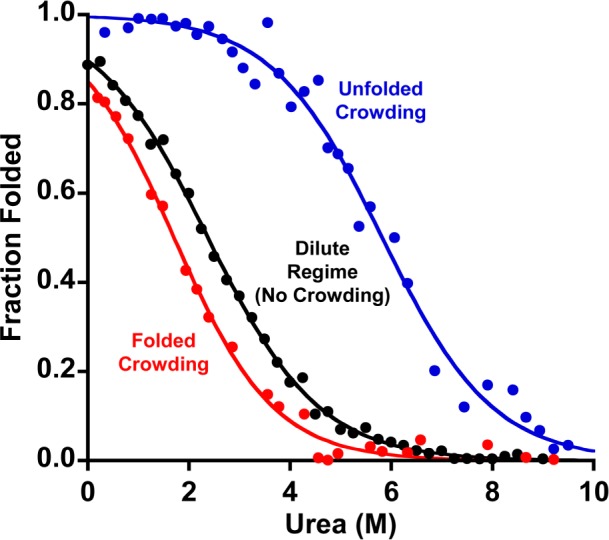
In bulk solution, crowding generally stabilizes the more compact native state.^9,16,17 On a surface, in contrast, crowding is more complex. Shown is the urea-induced unfolding of a methylene-blue-modified stem-loop (in the dilute regime, i.e., with each too far, on average, from its like neighbors to interact) when (red) crowded with a highly stable stem-loop that remains folded throughout the experiment, (black) in the dilute regime (no crowding), or (blue) when crowded with a polythymine construct that remains unfolded throughout the experiment. Whereas crowding by other folded stem-loops is destabilizing (by ∼2 kJ/mol), crowding by unfolded chains strongly stabilizes the folded stem-loop (by ∼6 kJ/mol). Of note, neither of these crowding regimes alters the width of the unfolding transition, which is a measure of the m value (i.e., denaturant strength): the best-fit m values in all three regimes are within error of the 2.1 kJ/mol/M value seen in (dilute) bulk solution.¹

In contrast to crowding by folded neighbors, being in the unfolding crowding regime increases the stability of our test-bed stem-loop (Figure 2). To see this, we co-deposited the stem-loop (again, being deposited at conditions that would render it in the dilute regime) with a 20-fold (solution phase) excess of inert, unfolded polythymine constructs of the same length. Under these conditions, the stability of the stem-loop is enhanced. Specifically, at a (total) packing density of 9(±3) × 10¹¹ molecules/cm² (corresponding to a mean nearest-neighbor separation of just ∼11 ± 2 nm between adjacent DNA molecules), the stability of the stem-loop reaches −12 ± 4 kJ/mol. While this increase in stability presumably arises due to the same electrostatically and sterically driven excluded volume effects postulated to underlie solution-phase crowding,¹⁷ its magnitude is rather greater than the effects typically seen in solution.^18,28 This difference may arise in part due the high local concentrations of DNA that can be achieved in the surface-bound state, which approach 100 mg/mL within one contour length (the 15 nm length of the unfolded DNA chain) of the surface. This said, the stability of proteins (in the dilute regime) typically increases by only ∼1 kJ/mol with the addition of ∼100 mg/mL of highly soluble, nonbiomolecular crowding agents, such as polyvinylpyrrolidone²⁹ or dextran,^30,31 suggesting that additional mechanisms may be playing a role in our results. Because the polythymines we employ here as our crowding agent are, like the stem-loop, negatively charged, electrostatic repulsion may account for this discrepancy, as electrostatic repulsion between unfolded chains would reduce their entropy beyond the reductions produced by steric-excluded volume effects alone.¹⁶ Theory suggests, however, that the fixed relative positions (and perhaps common orientations) of the surface-bound DNA strands could also enhance the entropic effects of crowding on the surface relative to those seen in bulk solution.²²

The “homogeneous crowding” regime (crowding by other foldable stem-loops) differs from “heterogeneous crowding” (crowding by always-folded stem-loops or always-unfolded polythymine) in producing a broader unfolding transition (Figure 3). This may arise because the extent of crowding in this regime is dependent on urea concentration. Specifically, at low denaturant, the test-bed stem-loops are crowded by adjacent, folded stem-loops, which, as shown above, is destabilizing. As the urea concentration rises, however, any stem-loop that remains folded will be crowded by unfolded neighbors, which, as shown above, is stabilizing. Thus, as each additional stem-loop unfolds, the next becomes more stable, an “anti-cooperative” behavior that should broaden the unfolding transition. Unfortunately, such anti-cooperative behavior invalidates the linear (in urea concentration) free-energy relationship assumed in eq 1, preventing us from accurately determining the stability of the surface-bound stem-loop under these homogeneous crowding conditions.

Figure 3.

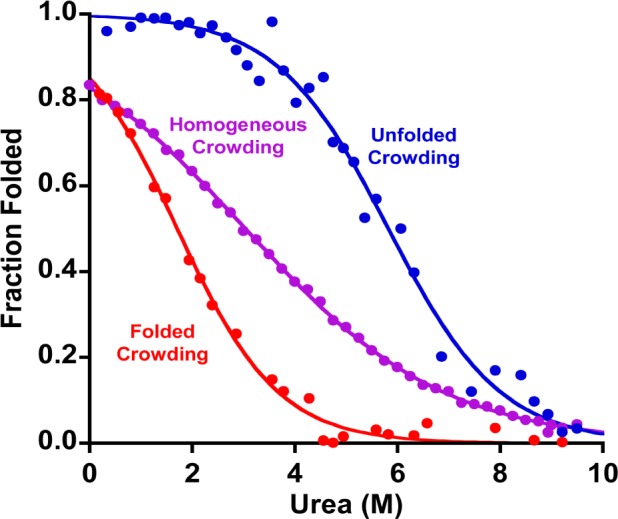
Homogeneous crowding (purple), i.e., crowding by other copies of the same, relatively unstable stem-loop, broadens the unfolding transition relative to that seen when the stem-loop is crowded by either always-folded (red) or always-unfolded (blue) molecules (the latter curves taken from Figure 2). This presumably occurs because the stabilizing effect of crowding by unfolded neighbors increases and the destabilization caused by folded neighbors decreases as more and more of the chains unfold. Shown are unfolding data collected at a mean separation of 6 nm between adjacent chains. See Figure S1 for more homogeneous crowding denaturation curves.

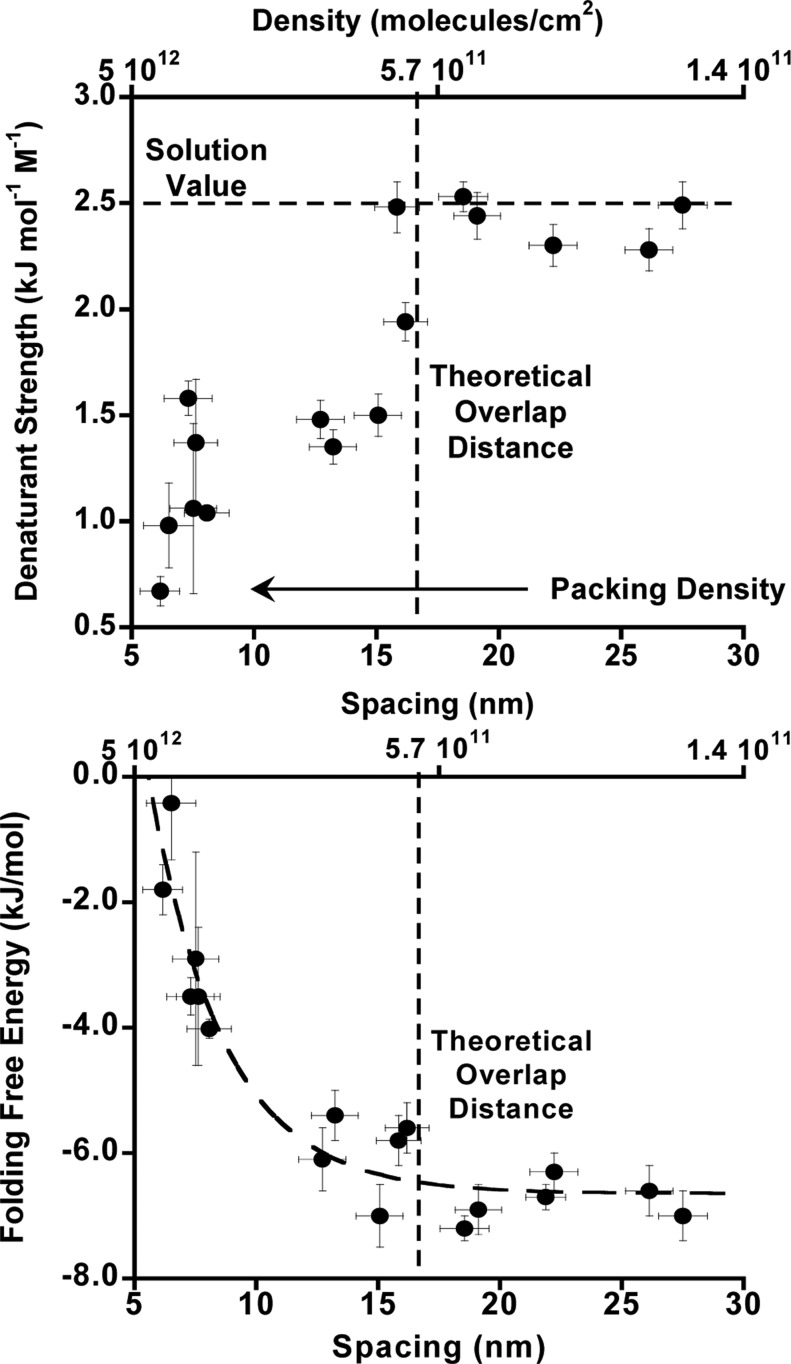
The broader transition seen for homogeneous crowding by our test-bed stem-loop is reflected in its effect on the observed m value, a measure of the strength of the denaturant. In solution, m values are strongly correlated with the solvent-accessible surface area liberated in the folding transition.³² Given this, and given that even our most densely packed surfaces are likely too sparsely packed to affect the solvent-accessible surface area of the unfolded stem-loop, we would expect crowding effects to leave m unchanged. Consistent with this, the m values we observe upon crowding with both folded and unfolded crowding agents are both within error of the value seen in the dilute regime (2.6 ± 0.6, 2.4 ± 0.3, and 2.4 ± 0.2 kJ/mol/M). All of these m values are likewise within error of the 2.1 ± 0.2 kJ/mol/M m value seen in bulk solution.¹ In contrast, however, the best-fit m value we observe under the most highly homogeneously crowded regime is just 1.1 ± 0.3 kJ/mol/M, reflecting the much broader transition we observe under these conditions (Figure 3).

Given that m values are, generally, inversely proportional to the change in solvent-accessible surface area upon unfolding,³² the reduced m value we observe under these conditions could be indicative of an unfolded state that is less unfolded (i.e., less solvent-accessible surface area is exposed). This could arise, for example, due to the formation of intermolecular base pairing at low urea, which could produce heterogeneity of the folded state. We believe this scenario unlikely, however, because, even at the highest packing densities we have explored, the chain would have to be rather extended in order for the complementary regions of adjacent chains to interact. Interchain hybridization would thus be both entropically (because the chain is highly extended) and enthalpically (because the chain is forced closer to the negatively charged surface) unfavorable. We believe instead that the reduction in the apparent m value arises due to broadening of the unfolding transition caused by the anti-cooperative unfolding behavior described above. Consistent with this, when the packing density is low enough that neighboring chains no longer interact, the observed m value approaches the value seen in bulk solution (Figure 4, top).

Figure 4.

(Top) Naively assuming a linear relationship between folding free energy and urea concentration (eq 1) suggests that the m value (a measure of denaturant strength) for unfolding is strongly dependent on packing density under these crowding conditions. The fitted m value approaches that seen in solution (and in the case of crowding by either always-folded or always-unfolded neighbors, Figure 2); however, the packing density falls low enough that neighboring molecules no longer interact. (Bottom) Similarly, the calculated folding free energy approaches the value seen for dilute surface coverage when the packing density falls below this interaction distance.

Conclusions

The crowding effects we have observed for surface-tethered biomolecules are larger and somewhat more complex than those generally seen in bulk solution. It appears, for example, that crowding on a surface can flip from stabilizing to destabilizing depending on the structure of the crowding agent even when its chemistry is effectively held fixed, with the effects reaching several kilojoules per mole as the effective concentration of the crowding agent increases from the dilute limit to ∼100 mg/mL. This is in contrast to crowding effects in solution, which generally affect stability by less than ∼1 kJ/mol.^29−31,33 The effects seen in the surface-bound regime thus offer new insight into the consequences of crowding. It likewise illustrates, once again, the significant and often complex effects that surface attachment can have on the physical properties of biopolymers.

Methods and Materials

The DNA oligonucleotides employed were synthesized by Bio-Search Technologies (Novato, CA) and purified by anion exchange HPLC followed by reverse-phase HPLC. The model stem-loop sequence employed is 5′-ACT CTC GAT CGG CGT TTT AGA GAG G-3′. The polythymine sequence used to produce heterogeneous crowding is 25 bases. The sequence of the highly stable stem-loop used in the semi-homogeneous crowding regime is 5′-ACG CGC GAT CGG CGT TTT AGC GCG G-3′. All three sequences were modified with a six-carbon thiol on their 5′-termini. The model stem-loop sequence was also modified with a methylene blue attached via amide bond formation to a six-carbon amine on its 3′-terminus.

As the gold surface, we employed polycrystalline gold disk electrodes (2 mm diameter; BAS, West Lafayette, IN). These were electrochemically cleaned as previously described.¹ In brief, the cleaning consists of a series of oxidation and reduction cycling in (1) 0.5 M NaOH (−0.4 to −1.35 V), (2) 0.5 M H₂SO₄ (0–2 V), (3) 0.5 M H₂SO₄ (0 to −0.35 V), (4) 0.5 M H₂SO₄ (−0.35 to +1.5 V), and finally (4) 0.01 M KCl/0.1 M H₂SO₄ (−0.2 to +1.25 V). The clean gold electrode surface was modified with the relevant oligonucleotide(s) by incubation for 5 min at room temperature in a solution of the thiol-terminated DNA. For homogeneous packing, the relevant oligonucleotide was used at concentrations ranging from 50 nM to 2 μM (depending on the desired packing density) in 20 μM tris(2-carboxyethyl)phosphine hydrochloride to reduce any disulfide bonds and 30 mM NaCl in 20 mM phosphate buffer pH 7. For heterogeneous and semihomogenous packing, the model stem-loop sequence was used at 50 nM in 30 mM NaCl in 20 mM phosphate buffer pH 7 for 5 min, then the polythymine sequence or the highly stable stem-loop sequence was used at 2 μM in 150 mM NaCl in 50 mM phosphate buffer pH 7 for 2 h, increasing salt concentration to increase screening interactions and thus the possible packing density. The resulting DNA-modified surface was washed with deionized water before being treated with 2 mM 6-mercapto-1-hexanol overnight to complete the formation of the SAM. Packing density was measured using the RuHex method described elsewhere.³⁴ Reported packing densities are means and standard errors determined by making multiple independent measurements on each surface.

We determined folding free energies using urea melts generated either with a Hamilton 500C titrator or by manual titrations starting at 10 M urea in buffer (20 mM sodium phosphate pH 7, 30 mM sodium chloride) and titrating in the same buffer lacking urea. At each urea concentration, the system was allowed to equilibrate for 30 s after mixing prior to measurement. Electrochemical measurements were conducted using square-wave voltammetry from 0 to −0.5 V at a frequency of 60 Hz on either a CHI 630 potentiostat (CH Instruments, Austin, TX) or a PalmSens (PalmSens BV, The Netherlands) in a standard cell with a platinum counter electrode and a Ag/AgCl (saturated with 3 M NaCl) reference electrode. Prior to use, each electrode was washed with 10 M urea in buffer, washed again with buffer, and then incubated in 10 M urea for at least 1 h prior to the start of the titration. To determine the folding free energy, a plot of peak current (at the −260 mV potential of methylene blue) versus urea concentration was fitted to a standard two-state unfolding curve with linear, sloping baselines.²⁶ Error bars reflect estimated standard errors based on the goodness of fit.

Supporting Information Available

An additional plot illustrating the unfolding transition of a surface-tethered stem-loop in the homogeneous crowded regime. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^∥ Department of Applied Physics, 348 Via Pueblo Mall, Stanford University, Stanford, CA 94305-4090.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States