DYNAMICS OF SI MODELS WITH BOTH HORIZONTAL AND VERTICAL TRANSMISSIONS AS WELL AS ALLEE EFFECTS

Abstract

A general SI (Susceptible-Infected) epidemic system of host-parasite interactions operating under Allee effects, horizontal and/or vertical transmission, and where infected individuals experience pathogen-induced reductions in reproductive ability, is introduced. The initial focus of this study is on the analyses of the dynamics of Density-Dependent and Frequency-Dependent effects on SI models (SI-DD and SI-FD). The analyses identify conditions involving horizontal and vertical transmitted reproductive numbers, namely those used to characterize and contrast SI-FD and SI-DD dynamics. Conditions that lead to disease-driven extinction, or disease-free dynamics, or susceptible-free dynamics, or endemic disease patterns are identified. The SI-DD system supports richer dynamics including limit cycles while the SI-FD model only supports equilibrium dynamics. SI models under “small” horizontal transmission rates may result in disease-free dynamics. SI models under with and inefficient reproductive infectious class may lead to disease-driven extinction scenarios. The SI-DD model supports stable periodic solutions that emerge from an unstable equilibrium provided that either the Allee threshold and/or the disease transmission rate is large; or when the disease has limited influence on the infectives growth rate; and/or when disease-induced mortality is low. Host-parasite systems where diffusion or migration of local populations manage to destabilize them are examples of what is known as diffusive instability. The exploration of SI-dynamics in the presence of dispersal brings up the question of whether or not diffusive instability is a possible outcome. Here, we briefly look at such possibility within two-patch coupled SI-DD and SI-FD systems. It is shown that relative high levels of asymmetry, two modes of transmission, frequency dependence, and Allee effects are capable of supporting diffusive instability.

1. Introduction

Parasitism contributes to the selection of future generations of hosts through their impact on factors that lead to reductions in fitness (Hudson et al. 2002) and as a result, wildlife managers must account for emerging and/or re-emerging diseases. Competition for space and resources (finding mates or food) also impact the reproductive ability and likelihood of survival of individuals, particularly those housing pathogens or parasites. Hosts’ dynamics (survival in particular) often depends on the ability of a population to maintain a critical mass (Kang and Castillo-Chavez 2012).The impact of heterogenous transmission factors including multiple transmission modes by altering a population’s dynamics may lessen the plausibility of conservation goals or the economic viability of selected management policies (Potapov et al 2012). Hence, it is not surprising that the pressure which parasites or pathogens place on their hosts and the relation of such interactions to community and/or ecosystem structure has been the subject of continuous empirical and theoretical studies. Some of the theoretical consequences associated to host-pathogen dynamics with factors like: i) multiple modes of disease transmission; (ii) host population density; and (iii) the presence or absence of critical host population thresholds, are addressed in this manuscript.

Modes of disease transmission, like horizontal and vertical, differentially facilitate the colonization of host populations by bacteria, fungi, or viruses. Colonization (horizontal transmission) is sometimes seen as the result of close interactions (contacts) between disease-free host and infected individuals. A contact process that implicitly assumes the sharing of a common, local habitat. The passage of a disease-causing agent from a mother to offspring during the “ birth” process is also sometimes possible (vertical transmission). Feline leukemia (FeLV) and feline immunodeficiency (FIV) viruses are transmitted horizontally and vertically. Leishmaniasis, a disease caused by the protozoan parasite Leishmania infantum, is transmitted horizontally and vertically. Domesticated dog populations are presumed to be a reservoir for Leishmania infantum; a reservoir maintained by the differential contributions of multiple modes of transmission (Santaella et al. 2011). The deadly septicaemia, which manages to kill 80% of septicaemia-infected birds, gets lodged in the ovary of surviving birds; passed later to the birds eggs (vertical transmission); spreading horizontally within the hatcher and brooder.

Traditionally, density-dependent transmission (DDT) and frequency-dependent transmission (FDT) are two extreme forms of disease transmission. DDT refers to parasite transmission in which the rate of contact between susceptible hosts and the source of new infections increases with host density while FDT refers to the rate of contact between susceptible hosts and the source of new infections is independent of host density. Teasing out the roles of density- and frequency-dependent transmission (DDT versus FDT) on the dynamics of host-parasite systems is carried out for theoretical and policy reasons. FDT is the result of density-independent contact rates between susceptible and infected individuals. DDT assumes that infection risks increase with host density. Density-dependent transmission (DDT) may require a minimal number of available susceptible hosts, that is, a threshold density, for transmission to occur. Density-dependent parasitic disease transmission plays a role in regulating host population size (Anderson and May 1978&1991) while frequency-dependent parasitic transmission does not require host density thresholds or regulatory host population constraints on the birth or death rates to ”work” (Getz and Pickering 1983).

In population biology we often lack absolutes. And so, vector- and sexually-transmitted diseases have been seen to thrive in frequency-dependent transmission settings while density-dependent infections that lead to pathogens being shed by infected hosts into common environments may sometimes need a critical mass of susceptible individuals to thrive (Anderson and May 1991; Antonovics et al. 1995). Pathogens can be spread via “direct” contacts (kissing can spread herpes viruses), aerosol (sneezing can spread influenza viruses), or via indirect contacts (ingesting water contaminated with fecal material can cause result in cholera infections), or through vectors (ticks and mosquitoes often spread viruses and bacteria to their hosts), or via some combination of direct and indirect modes, sometimes mediated by a vector. Empirical work on mice, voles, lady bird beetles, frogs, and plants has shown that pathogen transmission often involve DD and FD transmission modes, with one predominant mode (Hudson et al. 2002). The negative impact of deliberate releases of pathogens via aerosol or in water systems tends to increase with host density. On the other hand, sexually transmitted pathogens seem to thrive equally well or bad in small or large population settings while some vector-borne diseases have been shown to support frequency-dependent transmission patterns (Anderson and May 1991; Antonovics and Alexander 1992; Ferrari et al 2011). Antonovics and Alexander (1992) manipulated the density and frequency of infected hosts Silene latifolia and in the process they found out that deposition of the anther smut fungus Microbotryum violaceum by pollinating insects managed to increase with the frequency of infection.

A pathogen may or may not be deleterious enough to regulate the dynamics of host populations and so it is not surprising that the impact of pathogens on hosts is tied in to virulence. Pathogen’s levels of virulence differentially impacts host’s fitness. Often, increases in virulence result in a reduced probability survival or a diminished ability of a host to reproduce successfully, or both (Anderson and May 1978; Hudson et al. 2001; Hilker et al. 2009). Pathogens whose transmission successes increases with host density seem to have managed to select for variants capable of regulating a host population. Dwyer et al (1990) studied a host-pathogen system where a detailed account of virus titer on infected hosts could be estimated. Their study focused on studying the ability of the Myxoma virus to control an exploding rabbit populations over a long window in time. Empirical evidence from systems involving conjunctivitis in house finches or parasitic nematodes in red grouse and feral Soay sheep provide an example of a system where disease regulates population size (Gulland 1992; Hudson et al. 1998; Hochachka and Dhondt 2000). Pathogen infections are contributors to the decline or the extinction of some species (Dwyer et al 1990; Daszak et al. 1999; Smith et al. 2006; Thieme et al. 2009). The deleterious role of chytridiomycosis in amphibians, chestnut blight in American chestnuts, avian malaria in Hawaiian birds, devil facial tumour disease in Tasmanian devils, or sudden oak death in Californian trees provide classical examples of the role of disease in regulating a population. Theory suggests that density-dependent specialist pathogens (i.e., those infecting a single host) alone rarely drive their hosts’ extinction but can lead to extinction of the pathogen while frequency-dependent transmission may be capable of supporting significant decreases, including the potential extinction of host and parasite populations in the presence of moderately lethal pathogens (de Castro and Bolker 2005; Ferrari et al 2011; Kilpatrick and Altizer 2012).

The impact of disease outbreaks can be devastating and their dynamics must be particularly monitored within populations near extinction; that is, those with population levels near established Allee effects thresholds (Allee 1938; Stephens and Sutherland 1999; Stephens et al 1999; Courchamp et al 2009; Kang and Lanchier 2011). The relevance of threshold effects has been identified within a wide array of taxa (Courchamp et al. 2008; Kramer et al. 2009). Populations under Allee effects or facing extinction or both must be effectively managed (Drake 2004; Hilker 2009). The fragility of these populations means that limiting the transmission of highly deleterious diseases is critical (Deredec and Courchamp 2007; Hilker 2009). Recurrent infectious disease outbreaks tend to enhance the deleterious role of Allee effects within diseases capable of inducing reductions in host fitness (Hilker et al. 2005; Deredec and Courchamp 2006; Yakubu 2007; Hilker et al. 2009; Thieme et al. 2009; Hilker 2010; Friedman and Yakubu 2011; Kang and Castillo-Chavez 2013 a&b). The results of this manuscript seem to be in sync with the overall conclusions reached the study of predator-prey systems (e.g., Cushing 1994; Emmert and Allen 2004; Drew et al 2006; Jang and Diamond 2007; Berezovskaya et al. 2010; Kang and Armbruster 2011; Kang and Castillo-Chavez 2012).

Parasites and hosts co-evolve in response to environmental clues and/or selective pressures (Kilpatrick and Altizer 2012). Mammals, birds, fish, and insects generate mobility patterns as they track resources and as it is well known movement and/or dispersal can impact disease dynamics (Altizer et al 2011). In short, mobility has been a key player in the evolution of host-parasite systems. Studies that in addition to disease and mobility (dispersal) also include the impact of Allee effects are not well understood (Rios-Soto et al. 2006; Hilker et al. 2007; Kang and Castillo-Chavez 2013 a&b). Hilker et al. (2007) used a reaction-diffusion SI model within a frequency-dependent transmission framework in their explorations of the impact of disease and mobility on the spatiotemporal patterns of disease transmission. SI models that incorporate disease-reduced fertility have been explored by a number of researchers (see Diekmann and Kretzshmar (1991) and Berezovskaya et al. (2004)). In Kang and Castillo-Chavez (2013b) a two-patch SI model with density-dependent transmission is used to show that the differential movement of susceptible and infected individuals can enhance or suppress the spread of a disease. A SI model that incorporates a horizontally and vertically transmitted disease; infectives giving birth to infectives; susceptibles giving birth to susceptibles; Allee effects within the net reproduction term; disease-induced death rate; and disease reduced reproductive ability, is used in this manuscript to begin to address questions that include: What is the role of multiple modes of transmission? Will density-dependent and frequency-dependent vertical transmission affect host-parasite dynamics differentially? Under what conditions would Allee effects alter disease-free dynamics or facilitate disease-driven extinction? Would Allee thresholds on reproductive fitness become altered (reduced) by disease? What is the role of DDT or FDT in support of diffusive instability?

In Section 2, a general SI (Susceptible-Infected) model with Allee effects built in the reproduction that incorporates horizontal and vertical transmission modes, is formulated. The basic dynamic properties of the model are characterized, in particular, sufficient conditions in support of disease-free and persistence of species results are identified (Theorem 2.1 and its corollary 2.2). In Section 3, the dynamics of SI models under frequency-dependent or density-dependent horizontal transmission are contrasted. Boundary dynamics are characterized (Proposition 3.1) and sufficient conditions for disease- and susceptible-population persistence are provided in Theorem 3.2. A classification of interior dynamics comes in Theorem 3.3. In Section 4, disease-driven extinction, disease-free or susceptible-free dynamics, and endemic persistent dynamics are characterized. The nature of bifurcations supported by SI models is studied with the aid of the reproduction numbers linked to horizontal and vertical transmission modes. In Section 5, sufficient conditions leading to diffusive instability (Theorem 5.1) are identified. The nature of mechanisms potentially capable of supporting diffusive instability in SI-models and prey-predator models, is briefly discussed. The implications of the results in this manuscript are discussed in the Conclusion.

2. An SI model with Allee effects and vertical transmission

The model outlined in this section deals with a population facing a disease that can be effectively captured within a SI framework under assumptions that include the possibility of multiple modes of transmission, that is, horizontal and vertical. It is therefore assumed that infected individuals can give birth to infected hosts; that Allee effects alter the net reproduction term (possibly due to mating limitations or predator saturation); the presence of increases in mortality due to disease-induced deaths; and the fact that infected individuals may experience reductions in reproductive ability.

We let S and I denote the susceptible and infective populations, respectively, with N = S + I denoting the total host population. The approach followed from Deredec and Courchamp (2006) leads to the following set of nonlinear equations after the incorporation of the above assumptions:

$$\frac{dS}{dt}=\underset{\text{Growth with Allee effects}}{\underbrace{rSf(N)}}-\underset{\text{Horizontal transmission}}{\underbrace{\varphi (N)\frac{I}{N}S}}\frac{dI}{dt}=\varphi (N)\frac{I}{N}S+\underset{\text{Vertical transmission}}{\underbrace{\rho rIf(N)}}-\underset{\text{Additional death due to infections}}{\underbrace{dI}}$$ (2.1)

where r > 0, ρ ∈ [0, 1], d > 0 are respectively the intrinsic growth rate, the reduction of growth rate due to disease, and the excess death rate from the disease. The horizontal transmission term ϕ(N) includes density-dependent transmission, ϕ(N) = βN (the law of mass action) or frequency-dependent transmission, ϕ(N) = β (proportionate mixing or standard incidence). In the absence of disease, the SI Model (2.1) reduces to the following single species growth model:

$$\frac{dN}{dt}=rNf(N)$$ (2.2)

where the per capita growth function rf(N) is subject to strong Allee effects, i.e., there exists an Allee threshold K⁻ and a carrying capacity K⁺ such that

$$f(N)<0\text{if}0<N<K^{-}\text{or}N>K^{+};f(N)>0\text{if}{K}^{-}<N<K^{+};f(K^{-})=f(K^{+})=0.$$ (2.3)

Thus, the population model described by Equation (2.2) converges to 0 if initial conditions are below K⁻ or converges to its carrying capacity K⁺ whenever the initial conditions are above K⁻.

Note: The formulation of this SI model (2.1) is similar in approach to that found in Boukal and Berec (2002), Deredec and Chourchamp (2006), Courchamp et al (2009), Hilker et al (2009), Thieme et al (2009), and Kang and Chavez-Castillo (2012), particularly in the way we model the effects of Allee effects and disease. Our models allow for infectives to give birth to infectives with the caveat that their reproductive ability may be reduced; a feat that being captured with the parameter ρ.

The need for biological consistency (well posed model) is addressed with the help of the state-space naturally associated with Model (2.1), namely, $X=\{(S,I)\in {ℝ}_{+}^2\}$ with its interior defined as $\mathrm{X̊}=\{(S,I)\in {ℝ}_{+}^2:S>0\text{and}I>0\}$. The state space when ϕ(N) = β is $X=\{(S,I)\in R_{+}^2:S+I>0\}$. The assumption that f(N) is differentiable leads to the following theorem for Model (2.1):

Theorem 2.1 (Basic dynamical features of (2.1)). Assume that r > 0, d > 0, ρ ∈ [0, 1] and both f, ϕ are continuous in X with f satisfying Condition (2.3), then the system (2.1) is positively invariant and bounded in X with the following property

$$\underset{t\to \infty }{\text{lim sup}}N(t)=\underset{t\to \infty }{\text{lim sup}}(S(t)+I(t))\le K^{+}.$$

In addition, we have the following:

1. If N(0) ∈ (0, K⁻), then lim_t→∞ N(t) = 0.

2. If there exists a positive number α > K⁻ such that rρf(α) > d, then

   $$\underset{t\to \infty }{\text{lim inf}}N(t)=\underset{t\to \infty }{\text{lim inf}}(S(t)+I(t))\ge \alpha \mathit{\text{for any}}N(0)>\alpha .$$

3. If ${\text{max}}_{K^{-}\le N\le K^{+}}\{\frac{K^{+}\varphi (N)}{N}+r\rho f(N)\}<d$, then lim sup_t→∞ I(t) = 0.

Proof. Since both S = 0 and I = 0 are invariant manifold for the system (2.1), then according to the continuity of the system, we can easily show that (2.1) is positively invariant in X. In addition, the system (2.1) gives the following equation:

$$\frac{dN}{dt}=r(S+\rho I)f(N)-dI$$ (2.4)

where N = S + I. We have the following three cases

1. If K⁻ ≤ N ≤ K⁺, we have the following inequalities

   $$r\rho Nf(N)-dN=N(r\rho f(N)-d)\le \frac{dN}{dt}=r(S+\rho I)f(N)-dI\le rNf(N)$$ (2.5)

   which indicates that lim_t→∞ N(t) = 0 if N(0) < K⁻ since f(N) satisfies the condition (2.3), i.e., f(N) > 0 when K⁻ ≤ N ≤ K⁺. Similarly, if N < K⁻ or N > K⁺, then we have the following inequalities

   $$rNf(N)-dN=N(rf(N)-d)\le \frac{dN}{dt}=r(S+\rho I)f(N)-dI\le r\rho Nf(N)$$ (2.6)

   which indicates that lim sup_t→∞ N(t) ≤ K⁺ if N(0) > K⁻ since f(N) satisfies the condition (2.3), i.e., f(N) < 0 when N < K⁻ or N > K⁺.

   The discussion above also implies that lim sup_t→∞ N(t) ≤ K⁺.

2. If there exists a positive number α > K⁻ such that rρf(α) > d, then according to (2.5), we have

   $${\frac{dN}{Ndt}|}_{N=\alpha }\ge {r\rho f(N)-d|}_{N=\alpha }>0.$$

   Therefore, lim inf_t→∞ N(t) ≤ α for any N(0) > α.

3. If ${\text{max}}_{K^{-}<N<K^{+}}\{\frac{K^{+}\varphi (N)}{N}+r\rho f(N)\}<d$, then from (2.1) and the fact that lim sup_t→∞ N(t) ≤ K⁺, we have

   $$\frac{dI}{dt}=\varphi (N)\frac{I}{N}S+\rho rIf(N)-dI=I(\frac{S\varphi (N)}{N}+r\rho f(N)-d)<I(\frac{K^{+}\varphi (N)}{N}+r\rho f(N)-d)<0$$

   which indicates that lim sup_t→∞ I(t) = 0.

Notes: Some of the consequences that follow from Theorem 2.1 are:

1. The size of the initial population is extremely important for persistence regardless of the disease due to Allee effects.

2. The total population will not be above its carrying capacity K⁺ in the long run.

3. Species persistence requires that the initial population α is above the Allee threshold K⁻, and excess deaths $\frac{d}{r\rho }$ are small enough, smaller than the per capita growth function evaluated at the total population α, i.e., $f(\alpha )>\frac{d}{r\rho }$.

4. In the absence of vertical transmission, disease free dynamics requires that

   $$\underset{K^{-}\le N\le K^{+}}{\text{max}}\{\frac{\varphi (N)}{N}\}<\frac{d}{K^{+}}.$$
   In the presence of vertical transmission, disease free dynamics requires that

   $$\underset{K^{-}\le N\le K^{+}}{\text{max}}\{\frac{\varphi (N)}{N}+\frac{r\rho f(N)}{K^{+}}\}<\frac{d}{K^{+}}.$$

For convenience, we can consider that f(N) has a generic form of (N − K⁻)(K⁺−N) and ϕ(N) = β (i.e., frequency-dependent) or βN (i.e., the law of mass action) then scaling and setting

$$S\to \frac{S}{K^{+}},I\to \frac{I}{K^{+}},K^{-}\to \frac{K^{-}}{K^{+}},t\to rt,\rho \to \frac{\rho }{r},\beta \to \frac{\beta }{r},d\to \frac{d}{r}$$

leads to the following two SI models with both horizontal and vertical transmission and Allee effects:

$$\frac{dS}{dt}=S(N-\theta )(1-N)-\frac{\beta SI}{N}$$ (2.7)

$$\frac{dI}{dt}=\frac{\beta SI}{N}-dI+\rho I(N-\theta )(1-N)$$ (2.8)

and

$$\frac{dS}{dt}=S(N-\theta )(1-N)-\beta SI$$ (2.9)

$$\frac{dI}{dt}=\beta SI-dI+\rho I(N-\theta )(1-N)$$ (2.10)

where f(N) = (N − θ) (1 − N) is the per capita growth in the absence of disease; the parameter $\theta =\frac{K^{-}}{K^{+}}$ represents the Allee threshold; ρ ∈ [0, 1] represents the reduce reproductive ability due to the disease; β represents the disease transmission rate while d denotes the additional death rate coming from infections. The direct application of Theorem 2.1 to the systems (2.7)–(2.8) and (2.9)–(2.10) gives the following corollary:

Corollary 2.2 (Basic dynamic features of (2.7)–(2.8) and (2.9)–(2.10)). The systems (2.7)–(2.8) and (2.9)–(2.10) are positively invariant and bounded in their state space X with the following property

$$\underset{t\to \infty }{\text{lim sup}}N(t)\le 1.$$

In addition, we have the following:

1. If N(0) ∈ (0, θ), then lim_t→∞ N(t) = 0.

2. If there exists a positive number α > θ such that ρf(α) > d, then

   $$\underset{t\to \infty }{\text{lim inf}}N(t)\ge \alpha \mathit{\text{for any}}N(0)>\alpha .$$

3. If $\beta +\frac{\rho {(1-\theta )}^2}{4}<d$, we have lim sup_t→∞ I(t) = 0.

Proof. The application of Theorem 2.1 is direct by letting r = 1, f(N) = (N − θ)(1 − N) and ϕ(N) = β or βN. We only show the item 3. Since we have

$$N=S+I\ge S\text{and}\underset{t\to \infty }{\text{lim sup}}N(t)\le 1,$$

therefore, the system (2.7)–(2.8) has the following property

$$\frac{S\varphi (N)}{N}+r\rho f(N)=\frac{\beta S}{N}+\rho (N-\theta )(1-\theta )\le \beta +\rho (N-\theta )(1-\theta )\le \beta +\frac{\rho {(1-\theta )}^2}{4}.$$

For the system (2.9)–(2.10), we also have

$$\frac{S\varphi (N)}{N}+r\rho f(N)=\beta S+\rho (N-\theta )(1-\theta )\le \beta +\rho (N-\theta )(1-\theta )\le \beta +\frac{\rho {(1-\theta )}^2}{4}.$$

Therefore, if $\beta +\frac{\rho {(1-\theta )}^2}{4}<d$, we have lim sup_t→∞ I(t) = 0 for the system (2.7)–(2.8) and the system (2.9)–(2.10).

Notes: The traditional basic reproduction number for SI- Allee effects free- and vertical transmission free-models, namely $R_0=\frac{\beta }{d}$ is naturally no longer relevant. The item 3 of Corollary 2.2 indicates that the additional condition is needed for disease-free dynamics. Since our systems (2.7)–(2.8) and (2.9)–(2.10) involve both horizontal and vertical disease transmissions, their dynamics can be governed by the vertical transmission reproduction number, i.e., $R_0^{\upsilon }=\frac{\rho }{d}$ and the horizontal transmission reproduction number, i.e., $R_0^h=\frac{\beta }{d}$. The remainder of this article focuses on the dynamics of the systems (2.7)–(2.8) and (2.9)–(2.10).

3. Mathematical analysis

Notice that the system (2.7)–(2.8) is not defined at (S, I) = (0, 0) but from Corollary 2.2, we know that

$$\underset{t\to \infty }{\text{lim}}(S(t),I(t))=(0,0)\text{whenever}S(0)+I(0)<\theta .$$

Thus, we artificially define (0, 0) as the extinction equilibrium. Hence, the systems (2.7)–(2.8) and (2.9)–(2.10) have the same boundary dynamics since both of them can be reduced to the system given by

$$\frac{dS}{dt}=S(S-\theta )(1-S)\text{if}I=0$$

and

$$\frac{dI}{dt}=\rho I(I-\theta )(1-I)-dI\text{if}S=0.$$

Therefore, the systems (2.7)–(2.8) and (2.9)–(2.10) have the following three boundary equilibria

$$E_{0,0}=(0,0),E_{\theta ,0}=(\theta ,0),E_{1,0}=(1,0).$$

If, in addition, $R_0^{\upsilon }=\frac{\rho }{d}>\frac{4}{{(1-\theta )}^2}$ holds, then systems (2.7)–(2.8) and (2.9)–(2.10) support the following additional boundary equilibria on the I-axis:

$$E_{0,\theta }=(0,\frac{1+\theta }{2}-\frac{\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}),E_{0,1}=(0,\frac{1+\theta }{2}+\frac{\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}).$$

We have arrived at the following proposition regarding the boundary equilibria of the systems (2.7)–(2.8) and (2.9)–(2.10):

Proposition 3.1 (Boundary equilibria of the systems (2.7)–(2.8) and (2.9)–(2.10)). The systems (2.7)–(2.8) and (2.9)–(2.10) always have boundary equilibria E_0,0 = (0, 0), E_θ,0 = (θ,0), E_1,0 = (1, 0). If in addition Condition $R_0^{\upsilon }=\frac{\rho }{d}>\frac{4}{{(1-\theta )}^2}$ holds then both systems will support two additional boundary equilibria E_0,θ = (0, θ₂) and E_0,1 = (0, K₂) where

$$\theta <{\theta }_2=\frac{1+\theta }{2}-\frac{\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}<K_2=\frac{1+\theta }{2}+\frac{\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}<1.$$

The nature of the stability of these boundary equilibria is listed in Table 3.1.

Table 3.1.

The local stability of boundary equilibria for the systems (2.7)–(2.8) and (2.9)–(2.10) where ${\theta }_2=\frac{1+\theta -\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2},K_2=\frac{1+\theta +\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2},R_0^{\upsilon }=\frac{\rho }{d}$, and $R_0^h=\frac{\beta }{d}$.

Boundary Equilibria	Stability Condition
E0,0	Always locally asymptotically stable
Eθ,0	For Model (2.7)–(2.8)- Saddle if $R_0^h<1$; Source if $R_0^h>1$. For Model (2.9)–(2.10)-Saddle if $R_0^h<1/\theta$; Source if $R_0^h>1/\theta$
E1,0	Saddle if $R_0^h>1$; Locally asymptotically stable if $R_0^h\le 1$
E0,θ	For Model (2.7)–(2.8)- Saddle if $R_0^h>1/\rho$; Source if $R_0^h<1/\rho$ For Model (2.9)–(2.10)-Saddle if $\frac{1+\theta -\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}>\frac{d}{\rho \beta }$ (i.e., $R_0^h>\frac{1}{\rho {\theta }_2}$); Source if $\frac{1+\theta -\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}<\frac{d}{\rho \beta }$ (i.e., $R_0^h<\frac{1}{\rho {\theta }_2}$)
E0,1	For Model (2.7)–(2.8)- Saddle if ${ℝ}_0^h<1/\rho$; Locally asymptotically stable if $R_0^h>1/\rho$; For Model (2.9)–(2.10)-Saddle if $\frac{1+\theta +\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}<\frac{d}{\rho \beta }$ (i.e., $R_0^h<\frac{1}{\rho K_2}$); Locally asymptotically stable if $\frac{1+\theta +\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}>\frac{d}{\rho \beta }$ (i.e., $R_0^h>\frac{1}{\rho K_2}$)

Proof. If S = 0, the systems (2.7)–(2.8) and (2.9)–(2.10) are reduced to the following equation:

$$\frac{dI}{dt}=I(\rho (I-\theta )(1-I)-d)=0\Rightarrow \rho (I-\theta )(1-I)-d=0.$$

Therefore, if ${(1-\theta )}^2>4d/\rho =4/R_0^{\upsilon }$, we have

$$E_{0,\theta }=(0,{\theta }_2)=(0,\frac{1+\theta }{2}-\frac{\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}),E_{0,1}=(0,K_2)=(0,\frac{1+\theta }{2}+\frac{\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}).$$

Notice that $\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}/2<\frac{1-\theta }{2}$, therefore,

$${\theta }_2=\frac{1+\theta }{2}-\frac{\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}>\frac{1+\theta }{2}-\frac{1-\theta }{2}>\theta$$

and

$$K_2=\frac{1+\theta }{2}+\frac{\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}<\frac{1+\theta }{2}-\frac{1-\theta }{2}=1.$$

Thus, we have

$$\theta <{\theta }_2=\frac{1+\theta }{2}-\frac{\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}<\frac{1+\theta }{2}<K_2=\frac{1+\theta }{2}+\frac{\sqrt{{(1-\theta )}^2-4/R_0^{\upsilon }}}{2}<1.$$

The stability of the boundary equilibria is obtained from the signs of eigenvalues of the corresponding Jacobian matrices. We omit the details but collect the results in Table 3.1.

Notes: The results in Proposition 3.1 are used to determine the global dynamics in the absence of interior equilibrium (see the proof of Theorem 3.3 for details).

Theorem 3.2 (Persistence of disease or susceptibles). Assume that $R_0^{\upsilon }>\frac{4}{{(1-\theta )}^2}$ and the initial condition N(0) ∈ (θ₂, K₂) then the following statements follow:

1. For the systems (2.7)–(2.8) and (2.9)–(2.10), a sufficient condition for the persistence of disease is $R_0^{\upsilon }>1$.

2. For the system (2.7)–(2.8), a sufficient condition for the persistence of susceptibles is $R_0^h<\frac{1}{\rho }$ while for the system (2.9)–(2.10) is $R_0^h<\frac{1}{\rho K_2}$.

The persistence of disease (or susceptibles) means that there exists a positive number ε such that

$$\underset{t\to \infty }{\text{lim inf}}I(t)[\mathit{\text{or}}S(t)]\ge \epsilon \mathit{\text{for any}}N(0)\in ({\theta }_2,K_2).$$

Proof. Define $h(N)=\rho (N-\theta )(1-N)-d=R_0^{\upsilon }[(N-\theta )(1-N)-1/R_0^{\upsilon }]$. Notice that θ₂ and K₂ are roots of the equation $(N-\theta )(1-N)=1/R_0^{\upsilon }$ if the condition $\frac{{(1-\theta )}^2}{4}>1/R_0^{\upsilon }$ holds, thus we have

$$h(N)=\rho (N-\theta )(1-N)-d=\frac{\rho }{d}(N-{\theta }_2)(K_2-N).$$

This indicates that h(α) > 0 for any α ∈ (θ₂, K₂).

Since h(N) = ρf(N) − d then Theorem 2.1 and (its) Corollary 2.2 imply that

$$\underset{t\to \infty }{\text{lim inf}}N(t)=\underset{t\to \infty }{\text{lim inf}}(S(t)+I(t))\ge \alpha \text{for any}N(0)=\alpha \in ({\theta }_2,K_2).$$

The use of Theorem 2.1 and (its) Corollary 2.2 again allows to conclude that the systems (2.7)–(2.8) and (2.9)–(2.10) attract to the compact set 0 ≤ N ≤ 1 and are positively invariant within α ≤ N ≤ 1 for any α ∈ (θ₂,K₂).

Letting B_S = {(S, I) ∈ X : α ≤ S+I ≤ 1}∩{I = 0} and B_I = {(S, I) ∈ X : α ≤ S+I ≤ 1}∩{S = 0} leads to the facts that (i) B_S and B_I are positively invariant and that (ii) the omega limit set of B_S is E_1,0 while the omega limit set of B_I is E_0,1.

The results (Theorem 2.5 and its corollary) in Hutson (1984) guarantee that the persistence of disease is determined by the sign of ${\frac{dI}{Idt}|}_{B_S}={\frac{dI}{Idt}|}_{E_{1,0}}$ while the persistence of susceptibles is determined by the sign of ${\frac{dS}{Sdt}|}_{B_I}={\frac{dI}{Idt}|}_{E_{0,1}}$.

Letting ϕ(N) = β or βN means that the dynamics of I-class are governed by

$$\frac{dI}{dt}=\varphi (N)\frac{I}{N}S+\rho If(N)-dI=I(\frac{S\varphi (N)}{N}+\rho f(N)-d),$$

which gives

$${\frac{dI}{Idt}|}_{B_S}={(\beta +\rho f(N)-d)|}_{B_S}={(\beta +\rho f(S)-d)|}_{E_{1,0}}=\beta -d>0\text{if}\varphi (N)=\beta \text{and}\frac{d}{\beta }=1/R_0^h<1$$

and

$${\frac{dI}{Idt}|}_{B_S}={(\beta S+\rho f(N)-d)|}_{B_S}={(\beta S+\rho f(S)-d)|}_{E_{1,0}}=\beta -d>0\text{if}\varphi (N)=\beta N\text{and}\frac{d}{\beta }=1/R_0^h<1.$$

The results (Theorem 2.5 and its corollary) in Hutson (1984) guarantee that the persistence of disease for the systems (2.7)–(2.8) and (2.9)–(2.10) as long as $1<\text{min}\{\frac{R_0^{\upsilon }{(1-\theta )}^2}{4},R_0^h\}$ and the initial condition N(0) ∈ (θ₂, K₂).

The dynamics of the S-class are governed by

$$\frac{dS}{dt}=Sf(N)-\varphi (N)\frac{I}{N}S=S(f(N)-\frac{I\varphi (N)}{N}),$$

which gives

$${\frac{dS}{Sdt}|}_{B_I}={f(N)-\frac{I\varphi (N)}{N}|}_{B_I}={f(I)-\beta |}_{E_{0,1}}=f(K_2)-\beta =\frac{d}{\rho }-\beta >0\text{if}\varphi (N)=\beta \text{and}\frac{d}{\beta \rho }>1$$

and

$${\frac{dS}{Sdt}|}_{B_I}=f(N)-{\frac{I\varphi (N)}{N}|}_{B_I}={f(I)-\beta I|}_{E_{0,1}}=\frac{d}{\rho }-\beta K_2>0\text{if}\varphi (N)=\beta N\text{and}\frac{d}{\beta \rho }>K_2.$$

Therefore, applications of the results in Hutson ((Theorem 2.5 and its corollary, 1984) allows us to conclude that:

1. A sufficient condition for the persistence of susceptibles in the system (2.7)–(2.8) is that $\frac{{(1-\theta )}^2}{4d}>\frac{1}{\rho }>\beta /d=R_0^h$ as long initial condition are such that N(0) ∈ (θ₂, K₂).

2. A sufficient condition for the persistence of susceptibles in the system (2.9)–(2.10) is that $\frac{{(1-\theta )}^2}{4d}>\frac{1}{\rho }>\beta K_2/d=R_0^h{K}_2$ as long initial condition are such that N(0) ∈ (θ₂, K₂).

Note: The system (2.7)–(2.8) or the system (2.9)–(2.10) satisfies the definition of permanence provided that there exists a positive number ε such that for any N(0) ∈ (θ₂, K₂)

$$\underset{t\to \infty }{\text{lim inf}}\text{min}\{I(t),S(t)\}\ge \epsilon$$

An application of Theorem 3.2 leads to the following permanency results:

1. A sufficient condition for the permanence of the system (2.7)–(2.8) is that the initial condition N(0) ∈ (θ₂, K₂) and

   $$\rho <\frac{d}{\beta }=1/R_0^h<\text{min}\{1,\frac{\rho {(1-\theta )}^2}{4\beta }\}\iff \text{max}\{1,\frac{4\beta }{\rho {(1-\theta )}^2}\}<R_0^h<\frac{1}{\rho }.$$
2. A sufficient condition for the permanence of the system (2.9)–(2.10) is that the initial condition N(0) ∈ (θ₂, K₂) and

   $$\rho K_2<\frac{d}{\beta }=1/R_0^h<\text{min}\{1,\frac{\rho {(1-\theta )}^2}{4\beta }\}\iff \text{max}\{1,\frac{4\beta }{\rho {(1-\theta )}^2}\}<R_0^h<\frac{1}{\rho K_2}.$$

We postulate (throughout the rest of this manuscript) that the system (2.7)–(2.8) or the system (2.9)–(2.10) have disease-free dynamics if its attractor is E_0,0 ∪ E_1,0; or the system (2.7)–(2.8) or (2.9)–(2.10) has susceptibles-free dynamics if its attractor is E_0,0 ∪ E_0,1; or the system (2.7)–(2.8) or (2.9)–(2.10) has disease-driven extinction if its attractor is E_0,0.

3.1. Interior equilibrium

Notice that the equilibria of the system (2.7)–(2.8) satisfy the following equations:

$$S\prime =S[(N-\theta )(1-N)-\frac{\beta I}{N}]=0\Rightarrow S=0\text{or}I=\frac{N(N-\theta )(1-N)}{\beta },I\prime =I[\frac{\beta S}{N}+\rho (N-\theta )(1-N)-d]=0\Rightarrow I=0\text{or}S=\frac{N[d-\rho (N-\theta )(1-N)]}{\beta }.$$

The equilibria of the system (2.9)–(2.10) satisfy the following equations

$$S\prime =S[(N-\theta )(1-N)-\beta I]=0\Rightarrow S=0\text{or}I=\frac{(N-\theta )(1-N)}{\beta },I\prime =I[\beta S+\rho (N-\theta )(1-N)-d]=0\Rightarrow I=0\text{or}S-\frac{d}{\beta }=-\frac{\rho (N-\theta )(1-N)}{\beta }.$$

If we let (S*, I*) be an interior equilibrium of the system (2.7)–(2.8) or the system (2.9)–(2.10) then we have that:

1. The following equation

   $$N^{*}=S^{*}+I^{*}=\frac{N^{*}[d+(1-\rho )(N^{*}-\theta )(1-N^{*})]}{\beta }\Rightarrow \frac{\beta -d}{1-\rho }=(N^{*}-\theta )(1-N^{*})$$ (3.1)

   for the system (2.7)–(2.8) must be satisfied, and so, we see that the system (2.7)–(2.8) has no interior equilibrium if d ≥ β (i.e., $R_0^h\ge 1$) and

   $$N^{*}=\frac{1+\theta }{2}\pm \frac{\sqrt{{(1-\theta )}^2-\frac{4(\beta -d)}{1-\rho }}}{2}\text{if}\frac{{(1-\theta )}^2}{4}>\frac{(\beta -d)}{1-\rho }>0I^{*}=\frac{N^{*}(N^{*}-\theta )(1-N^{*})}{\beta },S^{*}=N^{*}\frac{d-\rho (N^{*}-\theta )(1-N^{*})}{\beta }[=\rho N^{*}\frac{(N^{*}-{\theta }_2)(N^{*}-K_2)}{\beta }\text{if}\frac{{(1-\theta )}^2}{4}>\frac{d}{\rho }].$$
   The system (2.7)–(2.8) may have the following two interior equilibria $N_i^{*}$, i = 1, 2, i.e.,

   $$\theta <S_1^{*}+I_1^{*}=N_1^{*}=\frac{1+\theta }{2}-\frac{\sqrt{{(1-\theta )}^2-\frac{4(\beta -d)}{1-\rho }}}{2}<\frac{1+\theta }{2}$$

   and

   $$\frac{1+\theta }{2}<S_2^{*}+I_2^{*}=N_2^{*}=\frac{1+\theta }{2}+\frac{\sqrt{{(1-\theta )}^2-\frac{4(\beta -d)}{1-\rho }}}{2}<1.$$
   The Jacobian matrix of Model (2.7)–(2.8) evaluated at the interior equilibrium (S*, I*) can be represented as follows

   $$J_{(S^{*},I^{*})}=\left(\begin{array}{cc}\hfill S^{*}[1+\theta -2N^{*}+\frac{\beta I^{*}}{{(N^{*})}^2}]\hfill & \hfill S^{*}[1+\theta -2N^{*}-\frac{\beta S^{*}}{{(N^{*})}^2}]\hfill \\ \hfill I^{*}[\rho (1+\theta )-2\rho N^{*}+\frac{\beta I^{*}}{{(N^{*})}^2}]\hfill & \hfill I^{*}[\rho (1+\theta -2N^{*})-\frac{\beta S^{*}}{{(N^{*})}^2}]\hfill \end{array}\right)$$ (3.2)

   where N* = S* + I*. Its two eigenvalues λ_i, i = 1, 2 satisfy the following equalities:

   $${\lambda }_1+{\lambda }_2=(S^{*}+\rho I^{*})(1+\theta -2N^{*})\text{and}{\lambda }_1{\lambda }_2=\frac{\beta S^{*}{I}^{*}(1-\rho )(2N^{*}-1-\theta )}{N^{*}}.$$ (3.3)

   Thus, if an interior equilibrium (S*, I*) exists, it would be locally asymptotically stable provided that $N^{*}>\frac{1+\theta }{2}$, or a saddle if $N^{*}<\frac{1+\theta }{2}$. We conclude that the system (2.7)–(2.8) has either no interior or two interior equilibria $N_i^{*}$, i = 1, 2 and if we happen to have two interior equilibria then we must have that $N_1^{*}$ is always a saddle and $N_2^{*}$ is always a source.

2. The following equation

   $$N^{*}=S^{*}+I^{*}=\frac{d}{\beta }+(1-\rho )\frac{(N^{*}-\theta )(1-N^{*})}{\beta }\Rightarrow \frac{\beta }{1-\rho }(N^{*}-\frac{d}{\beta })=(N^{*}-\theta )(1-N^{*})$$ (3.4)

   for the system (2.9)–(2.10). According to Corollary 2.2, we have N* < 1, thus (3.4) implies that the system (2.9)–(2.10) has no interior equilibrium if $R_0^h\le 1$ and

   $$N^{*}=\frac{1+\theta }{2}-\frac{\beta }{2(1-\rho )}\pm \frac{\sqrt{{(1+\theta -\frac{\beta }{1-\rho })}^2+4(\frac{d}{1-\rho }-\theta )}}{2}\text{if}\frac{{(1+\theta -\frac{\beta }{1-\rho })}^2}{4}>\theta -\frac{d}{1-\rho }=\frac{1+\theta }{2}-\frac{\beta }{2(1-\rho )}\pm \frac{\sqrt{{(1-\theta -\frac{\beta }{1-\rho })}^2-4\frac{d-\theta \beta }{1-\rho }}}{2}\text{if}\frac{{(1+\theta -\frac{\beta }{1-\rho })}^2}{4}>\theta -\frac{d}{1-\rho }{I}^{*}=\frac{(N^{*}-\theta )(1-N^{*})}{\beta },S^{*}=\frac{d-\rho (N^{*}-\theta )(1-N^{*})}{\beta }[=\rho \frac{(N^{*}-{\theta }_2)(N^{*}-K_2)}{\beta }\text{if}\frac{{(1-\theta )}^2}{4}>1/R_0^{\upsilon }].$$
   The system (2.9)–(2.10) may have the following two interior equilibria:

   $$S_1^{*}+I_1^{*}=N_1^{*}=\frac{1+\theta }{2}-\frac{\beta }{2(1-\rho )}-\frac{\sqrt{{(1+\theta -\frac{\beta }{1-\rho })}^2+4(\frac{d}{1-\rho }-\theta )}}{2}<\frac{1+\theta }{2}-\frac{\beta }{2(1-\rho )}$$

   and

   $$\frac{1+\theta }{2}-\frac{\beta }{2(1-\rho )}<S_2^{*}+I_2^{*}=N_2^{*}=\frac{1+\theta }{2}-\frac{\beta }{2(1-\rho )}+\frac{\sqrt{{(1+\theta -\frac{\beta }{1-\rho })}^2+4(\frac{d}{1-\rho }-\theta )}}{2}<1+\theta -\frac{\beta }{(1-\rho )}$$

   if

   $$\frac{1+\theta }{2}>\frac{\beta }{2(1-\rho )},{(1+\theta -\frac{\theta }{1-\rho })}^2>4(\theta -\frac{d}{1-\rho })\text{and}\theta >\frac{d}{1-\rho }.$$
   On the other hand if $\theta <\frac{d}{1-\rho }$ then the system (2.9)–(2.10) may have at most one interior equilibrium, namely,

   $$S_2^{*}+I_2^{*}=N_2^{*}=\frac{1+\theta }{2}-\frac{\beta }{2(1-\rho )}+\frac{\sqrt{{(1+\theta -\frac{\beta }{1-\rho })}^2+4(\frac{d}{1-\rho }-\theta )}}{2}.$$
   The Jacobian matrix of the system (2.9)–(2.10) evaluated at the interior equilibrium (S*, I*) is represented as

   $$J_{(S^{*},I^{*})}=\left(\begin{array}{cc}\hfill S^{*}(1+\theta -2N^{*})\hfill & \hfill S^{*}(1+\theta -\beta -2N^{*})\hfill \\ \hfill I^{*}(\beta +\rho (1+\theta )-2\rho N^{*})\hfill & \hfill \rho I^{*}(1+\theta -2N^{*})\hfill \end{array}\right)$$ (3.5)

   where N* = S* + I*. Its two eigenvalues λ_i, i = 1, 2 satisfy the following equalities:

   $${\lambda }_1+{\lambda }_2=(S^{*}+\rho I^{*})(1+\theta -2N^{*})\text{and}{\lambda }_1{\lambda }_2=\beta S^{*}{I}^{*}[(1-\rho )(2N^{*}-1-\theta )+\beta ].$$ (3.6)

   Thus, when the interior (S*, I*) exists, it is locally asymptotically stable as long as $N^{*}>\frac{1+\theta }{2}$ while a saddle whenever $N^{*}<\frac{1+\theta }{2}-\frac{\beta }{2(1-\rho )}$. It is a source if

   $$\frac{1+\theta }{2}-\frac{\beta }{2(1-\rho )}<N^{*}<\frac{1+\theta }{2}.$$

   If the system (2.9)–(2.10) has two interior equilibria $N_i^{*}$, i = 1, 2 then using their expressions and the criteria for interior stability allow us to conclude that $N_1^{*}$ is always a saddle while $N_2^{*}$ can be a sink or source. If, on the other hand, the system (2.9)–(2.10) has only one interior equilibrium, namely $N_2^{*}$, then we see that it can be a sink or source depending on parameter values.

The above discussion can be summarized in the following theorem:

Theorem 3.3 (Interior equilibria of Models). Let $E_{i1}=(S_1^{*},I_1^{*})$ and $E_{i2}=(S_2^{*},I_2^{*})$ then existence and stability conditions for the interior equilibria of the system (2.7)–(2.8) are listed in Table 3.2. Existence and stability conditions for the interior equilibria of the system (2.9)–(2.10) are listed in Table 3.3.

Table 3.2.

The local stability of interior equilibrium for the system (2.7)–(2.8)

Interior Equilibrium	Condition for existence	Condition for local asymptotically stable
Ei1	$R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}<\frac{1-\rho }{\beta -d}$ or $\frac{4}{{(1-\theta )}^2}<R_0^{\upsilon }<\frac{1-\rho }{\beta -d}$	Always a saddle
Ei2	$R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}<\frac{1-\rho }{\beta -d}$ or $\frac{4}{{(1-\theta )}^2}<R_0^{\upsilon }<\frac{1-\rho }{\beta -d}$	Always locally asymptotically stable.

Table 3.3.

The local stability of interior equilibrium for the system (2.9)–(2.10)

Interior Equilibrium	Condition for existence	Condition for stability
Ei1	$\text{max}\{\frac{1-\rho }{d},R_0^h,\frac{1-\rho }{\beta +\rho -1}\}>1/\theta$ and (a) $R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}$ or (b) $R_0^{\upsilon }>\frac{4}{{(1-\theta )}^2}$ & N1 < θ2	Always a saddle
Ei2	Case (1):$\text{max}\{\frac{1-\rho }{d},R_0^h,\frac{1-\rho }{\beta +\rho -1}\}>1/\theta$ and (a) $R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}$ or (b) $R_0^{\upsilon }>\frac{4}{{(1-\theta )}^2}$ & N2 < θ2 or (c) $R_0^{\upsilon }>\frac{4}{{(1-\theta )}^2}$, N2 > K2; Case (2): $1<R_0^h<1/\theta$ and (a) $R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}$ or (b) $R_0^{\upsilon }>\frac{4}{{(1-\theta )}^2}$, N2 < θ2 or (c) $R_0^{\upsilon }>\frac{4}{{(1-\theta )}^2}$, N2 > K2	Locally asymptotically stable if $N_2^{*}>\frac{1+\theta }{2}$ while it’s a source if $\frac{1+\theta }{2}-\frac{\beta }{2(1-\rho )}<N_2^{*}<\frac{1+\theta }{2}$

Sufficient conditions leading to no interior equilibrium and the related global dynamics of the systems (2.7)–(2.8) and (2.9)–(2.10) are listed in Table 3.4.

Table 3.4.

No interior equilibrium and the related global dynamics for the systems (2.7)–(2.8) and (2.9)–(2.10)

Cases	The system (2.7)–(2.8)	The system (2.9)–(2.10)
No interior equilibrium	Case (1): $R_0^h\le 1$; Case (2): $\frac{1-\rho }{\beta -d}<\frac{4}{{(1-\theta )}^2}$; Case (3): $\frac{4}{{(1-\theta )}^2}<\frac{1-\rho }{\beta -d}<R_0^{\upsilon }$.	Case (1): $R_0^h\le 1$; Case (2): $\frac{1-\rho }{\beta \theta -d}<\frac{4}{{(1-\theta -\frac{\beta }{1-\rho })}^2}$; Case (3): $\text{max}\{\frac{1-\rho }{d},R_0^h,\frac{1-\rho }{\beta +\rho -1}\}>1/\theta ,R_0^{\upsilon }>\frac{4}{{(1-\theta )}^2},{\theta }_2<N_i^{*}<K_2$, i = 1, 2; Case (4): $R_0^h<1/\theta ,R_0^{\upsilon }>\frac{4}{{(1-\theta )}^2}$, θ2 < N2 < K2
Disease-free dynamics	$R_0^h\le 1$	$R_0^h\le 1$
Susceptible-free dynamics	$\text{min}\{R_0^h,\frac{{(1-\theta )}^2}{4d}\}>\frac{1}{\rho }$.	$R_0^{\upsilon }>\text{max}\{\frac{1}{\beta K_2},\frac{4}{{(1-\theta )}^2}\}$ and Conditions of Case (2) or Case (3) or Case (4)
Disease-driven extinction	$\frac{4}{{(1-\theta )}^2}>\text{max}\{\frac{1-\rho }{\beta -d},R_0^{\upsilon }\}$	$R_0^{\upsilon }>\frac{4}{{(1-\theta )}^2}$ and $\frac{1-\rho }{\beta \theta -d}<\frac{4}{{(1-\theta -\frac{\beta }{1-\rho })}^2}$.
Permanence	N(0) ∈ (θ2, K2) and $R_0^h<\frac{1}{\rho }<\text{min}\{\frac{R_0^h}{\rho },\frac{{(1-\theta )}^2}{4d}\}$.	N(0) ∈ (θ2, K2) and $R_0^h<\frac{1}{\rho K_2}<\text{min}\{\frac{R_0^h}{\rho K_2},\frac{{(1-\theta )}^2}{4d{K}_2}\}$.

Proof. The above discussion shows that a necessary condition for the systems (2.7)–(2.8) and (2.9)–(2.10) to a have interior equilibrium is that $R_0^h>1$ while the existence of interior equilibrium for the systems (2.7)–(2.8) and (2.9)–(2.10) can be classified with the conditions $R_0^{\upsilon }>\frac{4}{{(1-\theta )}^2}$ and $R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}$.

If $R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}$ then the systems (2.7)–(2.8) and (2.9)–(2.10) have no boundary equilibria E_0,θ and E_0,1 on I-axis and therefore

$$h(N)=\rho (N-\theta )(1-N)-d<0\text{for all}N>0.$$

Necessary conditions for the existence of interior equilibrium for the systems (2.7)–(2.8) and (2.9)–(2.10) are tied in to the existence of solutions of the following equations:

$$\frac{\beta -d}{1-\rho }=(N-\theta )(1-N),0<\frac{\beta -d}{1-\rho }<\frac{{(1-\theta )}^2}{4}<\frac{d}{\rho }(i.e.,R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}<\frac{1-\rho }{\beta -d})$$ (3.7)

and

$$\frac{\beta }{1-\rho }(N-\frac{d}{\beta })=(N-\theta )(1-N),\frac{d}{\beta }>\theta ,\text{or}\frac{\beta }{1-\rho }(N-\frac{d}{\beta })=(N-\theta )(1-N),\frac{1+\theta }{2}>\frac{\beta }{2(1-\rho )},{(1-\theta -\frac{\beta }{1-\rho })}^2>\frac{4(\beta \theta -d)}{1-\rho }>0.$$ (3.8)

Therefore, if $R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}$ then the systems (2.7)–(2.8) and (2.9)–(2.10) have no interior if $R_0^h\le 1$ or if the following conditions

$$\frac{1-\rho }{\beta -d}<\frac{4}{{(1-\theta )}^2}\text{for the system}(2.7)–(2.8)$$

and

$$\frac{4}{{(1-\theta -\frac{\beta }{1-\rho })}^2}<\frac{1-\rho }{(\beta \theta -d)}\text{for the system}(2.9)–(2.10).$$

If $R_0^{\upsilon }>\frac{4}{{(1-\theta )}^2}$, then the systems (2.7)–(2.8) and (2.9)–(2.10) have boundary equilibria E_0,θ and E_0,1 on the I-axis. Additional conditions are needed to guarantee the existence of interior equilibrium for the systems (2.7)–(2.8) and (2.9)–(2.10). The systems (2.7)–(2.8) and (2.9)–(2.10) are discussed separately.

1. For the system (2.7)–(2.8), if $\frac{1-\rho }{\beta -d}<\frac{4}{{(1-\theta )}^2}$ Equation (3.7) should have solutions in the interval (0, θ₂) or (K₂, 1) since

   $$S^{*}=N^{*}\frac{d-\rho (N^{*}-\theta )(1-N^{*})}{\beta }=\rho N^{*}\frac{(N^{*}-{\theta }_2)(N^{*}-K_2)}{\beta }>0.$$

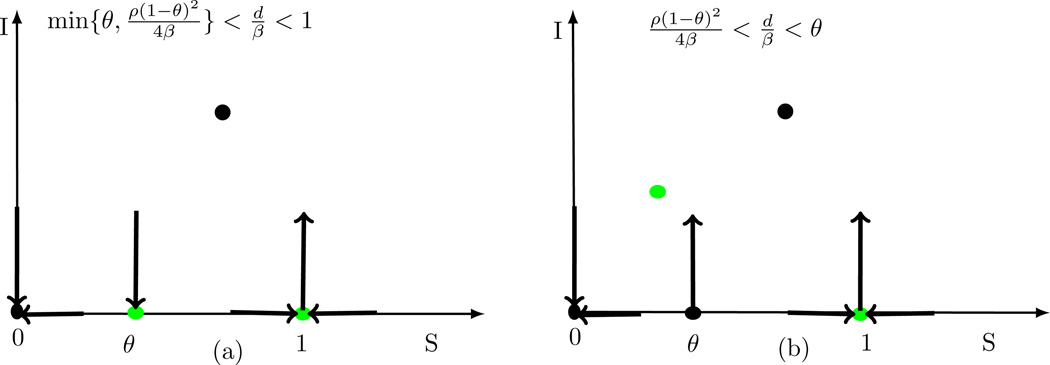
   The schematic nullclines for the system (2.7)–(2.8) when $\frac{1-\rho }{\beta -d}<\frac{4}{{(1-\theta )}^2}$ are illustrated in Figure 3.1. Two interior equilibria occur whenever $\frac{4}{{(1-\theta )}^2}<R_0^{\upsilon }<\frac{1-\rho }{\beta -d}$ with one interior a saddle (i.e., the horizontal line intercepts in the green region of (N − θ)(1 − N)) and the other a sink (i.e., the horizontal line intercepts in the blue region of (N − θ)(1 − N)). There is no interior equilibrium when the horizontal line intercepts (crosses) the black region of (N − θ)(1 − N), i.e., $\frac{4}{{(1-\theta )}^2}<\frac{1-\rho }{\beta -d}<R_0^{\upsilon }$.

2. For the system (2.9)–(2.10), whenever $\frac{1-\rho }{\beta \theta -d}>\frac{4}{{(1-\theta -\frac{\beta }{1-\rho })}^2}$ Equation (3.8) should have solutions in the interval (0, θ₂) or (K₂, 1) since

   $$S^{*}=\frac{d-\rho (N^{*}-\theta )(1-N^{*})}{\beta }=\rho \frac{(N^{*}-{\theta }_2)(N^{*}-K_2)}{\beta }>0.$$
   The schematic nullclines for the system (2.9)–(2.10) when $\frac{1-\rho }{\beta \theta -d}>\frac{4}{{(1-\theta -\frac{\beta }{1-\rho })}^2}$ are found in Figure 3.2. There are two cases depending on the sign of $\frac{d}{\beta }-\theta$: (1) $\frac{d}{\beta }>\theta \iff R_0^h<1/\theta$ (see Figure 3.2(a)), two interior equilibria occur whenever

   $$\frac{1+\theta }{2}>\frac{\beta }{2(1-\rho )},\frac{4}{{(1-\theta -\frac{\beta }{1-\rho })}^2}<\frac{1-\rho }{(\beta \theta -d)}$$

   and

   $$N_1^{*}<{\theta }_2,N_2^{*}<{\theta }_2\text{or}{N}_2^{*}<K_2$$

   where $N_1^{*}$ is always a saddle (i.e., the line $\frac{\beta }{1-\rho }(N-\frac{d}{\beta })=\frac{\beta }{1-\rho }(N-\frac{1}{R_0^h})$) intercepts the green region of (N − θ)(1 − N)) and $N_2^{*}$ can be sink (i.e., the line intercepts the red region of (N − θ)(1 − N)) or source (i.e., the line intercepts the blue region of (N − θ)(1 − N)). If Condition $N_2^{*}<{\theta }_2$ or $N_2^{*}<K_2$ does not hold, i.e., ${\theta }_2<N_2^{*}<K_2$ then the system (2.9)–(2.10) has only one interior equilibrium $N_1^{*}$, a saddle. (2) If $\frac{d}{\beta }<\theta$ (see Figure 3.2(b)) then only one interior equilibria occurs whenever

   $$1<R_0^h<1/\theta ,\theta <\frac{d}{1-\rho }\text{and}[N_2^{*}<{\theta }_2\text{or}{N}_2^{*}<K_2]$$

   and this interior equilibrium $N_2^{*}$ can be a sink or a source, depending on parameters’ values. There is no interior if the line intercepts the black region of (N − θ)(1 − N) when

   $$R_0^h>1/\theta ,{\theta }_2<N_2^{*}<K_2$$

   or

   $$\frac{4}{{(1-\theta -\frac{\beta }{1-\rho })}^2}>\frac{1-\rho }{(\beta \theta -d)}.$$

Fig. 3.1.

Schematic nullclines for the system (2.7)–(2.8) when $\frac{\beta -d}{1-\rho }<\frac{{(1-\theta )}^2}{4}$ (i.e., $\frac{\beta -d}{1-\rho }<\frac{4}{{(1-\theta )}^2}$). Potential (two) interior equilibria are the intercepts of the horizontal line $\frac{\beta }{1-\rho }$ and the curve (N − θ)(1 − N) with their stability determined by the location of the intercept. The green region of (N − θ)(1 − N) is a saddle and the blue region is a sink. Two interior equilibria (see the purple horizontal line) occur whenever $\frac{\beta -d}{1-\rho }<\frac{d}{\rho }<\frac{{(1-\theta )}^2}{4}$ (i.e., $\frac{4}{{(1-\theta )}^2}<R_0^{\upsilon }<\frac{1-\rho }{\beta -d}$) where one interior is saddle and the other one a sink.

Fig. 3.2.

Schematic nullclines for the system (2.9)–(2.10) when $\frac{1-\rho }{\beta \theta -d}>\frac{4}{{(1-\theta -\frac{\beta }{1-\rho })}^2}$ Potential interior equilibria are intercepts of the line $\frac{\beta }{1-\rho }(N-\frac{d}{\beta })$ and the curve (N − θ)(1 − N) with their stability determined by the location of the intercept. The green region of (N − θ)(1 − N) is a saddle; the red region is a source and the blue region is a sink. The left graph corresponds to the case when $R_0^h>1/\theta$: one (see the black line $\frac{\beta }{1-\rho }(N-\frac{d}{\beta })$) or two interior equilibria (see the purple or dark green line $\frac{\beta }{1-\rho }(N-\frac{d}{\beta })$) are possible. The right graph corresponds to the case when $1<R_0^h<1/\theta$, potentially one interior equilibria (see the dark green or purple line $\frac{\beta }{1-\rho }(N-\frac{d}{\beta })$).

In short, sufficient conditions for the existence of interior equilibria and their stability have been identified and listed in Table 3.2 for the system (2.7)–(2.8) and in Table 3.3 for the system (2.9)–(2.10).

The above analysis has identified conditions (sufficient) that guarantee the absence of interior equilibria for the systems (2.7)–(2.8) and (2.9)–(2.10); listed in Table 3.4. In the absence of interior equilibrium, we can conclude thanks to the Poincaré-Bendixson Theorem (Guckenheimer & Holmes 1983), that a trajectory starting with arbitrary initial conditions in X converge to its locally asymptotically stable boundary equilibria since the systems (2.7)–(2.8) and (2.9)–(2.10) support each a global compact attractor {(S, I) ∈ X : 0 ≤ S + I ≤ 1} in X. The fact that E_0,0 is always an attractor results according to Proposition 3.1 in the following three cases:

1. Disease-free dynamics that corresponds to the case where E_0,0 and E_1,0 are the only locally asymptotically stable boundary equilibria while other existing boundary equilibria are unstable. This implies that β ≤ d (i.e., $R_0^h\le 1$) is a sufficient condition in support of disease-free dynamics within the systems (2.7)–(2.8) and (2.9)–(2.10).

2. Susceptible-free dynamics that corresponds to the case where E_0,0 and E_0,1 are the only locally asymptotically stable boundary equilibria while other existing boundary equilibria (including those on the I-axis) are unstable. This implies that $R_0^h>\frac{1}{\rho K_2}$ and $R_0^{\upsilon }>\frac{4}{{(1-\theta )}^2}$ for the systems (2.7)–(2.8) and (2.9)–(2.10), in addition to the conditions of non-existence of interior equilibrium. Our results imply that large value of $R_0^h$ and $R_0^{\upsilon }$ may lead to the susceptible-free dynamics

3. Disease-driven extinction that corresponds to the case where E_0,0 is the only locally asymptotically stable boundary equilibria provided that there is no boundary equilibria on the I-axis a result based on Theorem 3.2. This implies that $1<R_0^h<\frac{1}{\rho K_2}$ and $R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}$ for the systems (2.7)–(2.8) and (2.9)–(2.10) in conjunction to the conditions that there are no interior equilibrium.

Detailed conditions on the three cases discussed above are listed in Table 3.4.

Notes: Theorem 3.3 implies the following:

1. Small values of ρ make the systems (2.7)–(2.8) and (2.9)–(2.10) prone to disease-driven extinction since one necessary condition for disease-driven extinction requires that $R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}$ according to Theorem 3.2. This also suggests that vertical transmission may save a species from extinction provided that the reproductive ability of infectives is large enough (some additional conditions must be met).

2. The system (2.7)–(2.8) has simpler dynamics than the system (2.9)–(2.10). In fact, the system (2.7)–(2.8) has no interior equilibria or two interior equilibria (a saddle and a sink) while the system (2.9)–(2.10) may have one or two interior equilibria.

4. Classifications on dynamics and related bifurcation diagrams

This section focuses on the classification of the dynamics and related bifurcations of the systems (2.7)–(2.8) and (2.9)–(2.10) by using the horizontal transmission reproduction number $R_0^h=\frac{\beta }{d}$ and the vertical transmission reproduction number $R_0^{\upsilon }=\frac{\rho }{d}$.

4.1. The SI model with frequency-dependent horizontal transmission

For the system (2.7)–(2.8), notice that

$$\frac{\beta -d}{1-\rho }<\frac{d}{\rho }\iff R_0^{\upsilon }=\frac{\rho }{d}>\frac{1}{\beta }.$$

Thus, if the system (2.7)–(2.8) has boundary equilibria on the I-axis, i.e., $R_0^{\upsilon }>\frac{4}{{(1-\theta )}^2}$, then the no interior equilibria condition $\frac{1-\rho }{\beta -d}<\frac{4}{{(1-\theta )}^2}$ says that the boundary equilibrium E_0,θ is a source while E_0,1 is locally asymptotically stable according to Proposition 3.1 and the fact that

$$\frac{\beta -d}{1-\rho }>\frac{d}{\rho }\Rightarrow R_0^{\upsilon }=\frac{\rho }{d}<\frac{1}{\beta }.$$

Therefore, the system (2.7)–(2.8) have two interior equilibria provided that

$$0<\frac{\beta -d}{1-\rho }<\frac{{(1-\theta )}^2}{4}<\frac{d}{\rho }\iff R_0^{\upsilon }=\frac{\rho }{d}<\text{min}\{\frac{1}{\beta },\frac{4}{{(1-\theta )}^2}\}$$

or

$$0<\frac{\beta -d}{1-\rho }<\frac{d}{\rho }<\frac{{(1-\theta )}^2}{4}\iff \frac{4}{{(1-\theta )}^2}<R_0^{\upsilon }=\frac{\rho }{d}<\frac{1}{\beta }.$$

Corollary 2.2, Proposition 3.1, and Theorem 3.2–3.3 lead to the study of three cases for the system (2.7)–(2.8):

1. The disease-driven extinction occurs in the situation depicted in Figure 4.1. First, no interior equilibrium, which requires $\frac{\beta -d}{1-\rho }>\frac{{(1-\theta )}^2}{4}$. Within Figure 4.1, we see that the existence and the stability of boundary equilibria requires $R_0^{\upsilon }=\frac{\rho }{d}<\frac{4}{{(1-\theta )}^2}$ and $R_0^h=\frac{\beta }{d}>1$. Thus, a sufficient condition that makes Figure 4.1 possible is

   $$\text{max}\{\frac{\rho }{d},\frac{1-\rho }{\beta -d}\}<\frac{4}{{(1-\theta )}^2}\text{and}{R}_0^h=\frac{\beta }{d}>1.$$

   The system (2.7)–(2.8) may also support disease-driven extinction whenever it supports an interior equilibrium. In such a case, disease-driven extinction occurs as a result of catastrophic events, that is, when a stable limit cycles merges with the adjacent saddle, leading to the annihilation of the susceptible and infected sub-populations.

2. An endemic situation occurs whenever the system (2.7)–(2.8) supports the interior equilibria shown in Figure 4.2. A necessary condition is that $\frac{1-\rho }{\beta -d}>\frac{4}{{(1-\theta )}^2}$ and thus we can conclude that the sufficient condition leading to Figure 4.2(a) is

   $$R_0^h=\frac{\rho }{d}<\frac{4}{{(1-\theta )}^2}<\frac{1-\rho }{\beta -d}\text{and}\rho <\frac{d}{\beta }<1(\text{or}1<R_0^h<\frac{1}{\rho })$$

   while the sufficient condition leading to Figure 4.2(b) is

   $$\frac{4}{{(1-\theta )}^2}<\frac{1-\rho }{\beta -d}<R_0^h=\frac{\rho }{d}\text{and}\rho <\frac{d}{\beta }<1(\text{or}1<R_0^h<\frac{1}{\rho }).$$
3. Disease-free or susceptible-free dynamics occur when the system (2.7)–(2.8) has no interior equilibrium with either E_1,0 or E_0,1 locally asymptotically stable, as shown in Figure 4.3. Figure 4.3(a) highlights a disease-free situation for which the condition

   $$R_0^h\le 1\text{and}\frac{4}{{(1-\theta )}^2}<R_0^{\upsilon }=\frac{\rho }{d}$$

   is sufficient. Figure 4.3(b) highlights a susceptible-free state for which sufficient the condition is

   $$R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}<\frac{1-\rho }{\beta -d}\text{and}\frac{d}{\beta }<\rho (\text{or}{R}_0^h>\frac{1}{\rho }>1).$$

Fig. 4.1.

Schematic phase plane for the system (2.7)–(2.8) when it experiences the possibility of disease-driven extinction.

Fig. 4.2.

Schematic phase plane for the system (2.7)–(2.8) when it has the endemic occurs.

Fig. 4.3.

Schematic phase plane for the system (2.7)–(2.8) when it has no coexistence of susceptibles and infectives.

The vertical transmission reproduction number, $R_0^{\upsilon }=\frac{\rho }{d}$, and the horizontal transmission reproduction number, $R_0^h=\frac{\beta }{d}$ help, using the above discussions and the analytical results in previous sections, understand the effects of parameters ρ, d, β, θ on the dynamics of the system (2.7)–(2.8). The results can briefly summarized as follows:

1. A horizontal transmission reproduction number $R_0^h$ less than 1 supports disease-free dynamics for the system (2.7)–(2.8) (see Theorem 3.3 when combined with the relevant results in Table 3.4).

2. Both initial condition N(0) = S(0)+I(0) and the value of the vertical transmission reproduction number, $R_0^{\upsilon }$, are important in determining global dynamics (see Corollary 2.2 and Theorem 3.3). We can conclude that large values of $R_0^{\upsilon }$ tend to lead to susceptible-free dynamics; while intermediate values of $R_0^{\upsilon }$ tends lead to the coexistence of susceptibles and infectives; and small values of $R_0^{\upsilon }$ tends to lead to disease-driven extinction.

3. The SI model with frequency-dependent transmissions or the system (2.7)–(2.8) supports relatively simple equilibrium dynamics. It can support no interior or two interior equilibria, with one of the interior equilibrium always stable (see Theorem 3.3, Table 3.3–3.4 and Figure 3.1).

4.2. The SI model with density-dependent horizontal transmissions

In this subsection, the dynamics and potential bifurcations of the SI model, with density-dependent horizontal transmission, given by the system (2.9)–(2.10), are classified. The classification of stability of boundary equilibria for the system (2.9)–(2.10) on the I-axis E_0,θ and E_0,1 when $\frac{{(1-\theta )}^2}{4}>\frac{d}{\rho }$ can be determined from the signs of ${\theta }_2-\frac{d}{\rho \beta }$ and $K_2-\frac{d}{\rho \beta }$. Since

$$\theta <{\theta }_2=\frac{1+\theta }{2}-\frac{\sqrt{{(1-\theta )}^2-4d/\rho }}{2}<K_2=\frac{1+\theta }{2}+\frac{\sqrt{{(1-\theta )}^2-4d/\rho }}{2}<1.$$

Hence, the signs can be determined by solving $R_0^{\upsilon }=\frac{\rho }{d}$ from the equations ${\theta }_2=\frac{d}{\rho \beta }$ and $K_2=\frac{d}{\rho \beta }$, i.e.,

$$\frac{1+\theta }{2}-\frac{\sqrt{{(1-\theta )}^2-4d/\rho }}{2}=\frac{d}{\rho \beta }\Rightarrow R_0^{\upsilon }=\frac{\rho }{d}=\frac{1+\theta -4\beta \pm \sqrt{{(4\beta -1)}^2+{(1-\theta )}^2-1-8\beta \theta }}{2\beta \theta }$$

and

$$\frac{1+\theta }{2}+\frac{\sqrt{{(1-\theta )}^2-4d/\rho }}{2}=\frac{d}{\rho \beta }\Rightarrow \frac{\rho }{d}=\frac{1+\theta -4\beta \pm \sqrt{{(4\beta -1)}^2+{(1-\theta )}^2-1-8\beta \theta }}{2\beta \theta }.$$

Letting $c_1=\frac{1+\theta -4\beta -\sqrt{{(4\beta -1)}^2+{(1-\theta )}^2-1-8\beta \theta }}{2\beta \theta }$ and $c_2=\frac{1+\theta -4\beta +\sqrt{{(4\beta -1)}^2+{(1-\theta )}^2-1-8\beta \theta }}{2\beta \theta }$ leads, making use of Proposition 3.1, to the following (a two dimensional bifurcation diagram example is shown in Figure 4.4 when β = 0.1 and θ = 0.15) results:

1. Black area in Figure 4.4: E_0,θ is a saddle and E_0,1 is locally asymptotically stable if

   $$R_0^{\upsilon }=\frac{\rho }{d}>\text{max}\{\frac{4}{{(1-\theta )}^2},c_2\}.$$
2. Cyan area in Figure 4.4: E_0,θ is a source and E_0,1 is locally asymptotically stable if

   $$\text{max}\{\frac{4}{{(1-\theta )}^2},c_1\}<R_0^{\upsilon }=\frac{\rho }{d}<c_2.$$
3. Green area in Figure 4.4: E_0,θ is a source and E_0,1 is a saddle if

   $$\frac{4}{{(1-\theta )}^2}<R_0^{\upsilon }=\frac{\rho }{d}<c_1.$$
4. White area in Figure 4.4: there is no boundary equilibrium on I-axis, i.e.,

   $$R_0^{\upsilon }=\frac{\rho }{d}<\frac{4}{{(1-\theta )}^2}.$$

Fig. 4.4.

An example of two dimensional bifurcation diagram (d − ρ) of the system (2.9)–(2.10) when β = 0.1 and θ = 0.15. The black area indicates that the reproduction number of vertical transmission $R_0^{\upsilon }=\frac{\rho }{d}$ is large, i.e., $R_0^{\upsilon }>\text{max}\{\frac{4}{{(1-\theta )}^2},c_2\}$; the cyan area indicates that $R_0^{\upsilon }$ has intermediate values, i.e., $\text{max}\{\frac{4}{{(1-\theta )}^2},c_1\}<R_0^{\upsilon }<c_2$; the green area indicates that $R_0^{\upsilon }$ has small values, i.e., $\frac{4}{{(1-\theta )}^2}<R_0^{\upsilon }<c_1$ and the white area indicates that $R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}$. The green dots indicate that the system (2.9)–(2.10) has only one interior equilibrium which can be a source, saddle or sink while the red dots indicate that the system (2.9)–(2.10) has two interior equilibria where one is a saddle and the other one can be a sink or source.

We therefore identify only four cases for the system (2.9)–(2.10):

1. Case one: There is no boundary equilibrium E_0,θ and E_0,1 when the reproduction number of vertical transmission $R_0^{\upsilon }=\frac{\rho }{d}$ is small enough, i.e., $R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}$. For a certain range of parameter values, the system (2.9)–(2.10) can have a unique interior attractor, which can be an interior equilibrium (see Figure 4.5; where within the the sub-figure (a) corresponds to the white area with blue dots, i.e., $R_0^h=\frac{\beta }{d}>\frac{1}{\theta }$, and (b) corresponds to the white area with red dots, i.e., $1>R_0^h>\frac{1}{\theta }$, below the green area of Figure 4.4) or a stable limit cycle through Hopf-Bifurcation. This is the case when the system (2.9)–(2.10) can support disease-driven extinction as it was the case for the system (2.7)–(2.8).

2. Case two: There are boundary equilibria E_0,θ and E_0,1 when the reproduction number of vertical transmission $R_0^{\upsilon }=\frac{\rho }{d}$ is large enough, i.e., $\frac{4}{{(1-\theta )}^2}<R_0^{\upsilon }$ and the reproduction number of horizontal transmission has a large value, i.e., $R_0^h>\frac{1}{\theta }$. An example of this case is shown in the black area [whose dynamics is corresponding to the sub-figure (a) of Figure 4.6] and the green area [whose dynamics is corresponding to the sub-figure (b) of Figure 4.6] on the right of the purple vertical line d = 0.015 of Figure 4.4.

3. Case three: There are boundary equilibria E_0,θ and E_0,1 and the reproduction number of horizontal transmission has intermediate values, i.e., $1<R_0^h<\frac{1}{\theta }$. An example of this case is shown in the green area [whose dynamics corresponds to the sub-figure (a) of Figure 4.7] and the black area [whose dynamics is corresponding to the sub-figure (b) of Figure 4.7] on the left of the purple vertical line d = 0.015 of Figure 4.4.

4. Case four: There are boundary equilibria E_0,θ and E_0,1 and the reproduction number of vertical transmission has intermediate values, i.e., $\text{max}\{\frac{4}{{(1-\theta )}^2},c_1\}<R_0^h<c_2$. An example of this case is shown in the cyan area of Figure 4.4 whose dynamics on the right side of the purple vertical line d = 0.015, i.e., the reproduction number of horizontal transmission has large values, i.e., $R_0^h>\frac{1}{\theta }$. Dynamics represented by the sub-figure (a) of Figure 4.8 and the dynamics on the left side of the purple vertical line d = 0.015, i.e., $1<R_0^h<\frac{1}{\theta }$, represented by the sub-figure (b) of Figure 4.8.

Fig. 4.5.

Schematic phase plane of the system (2.9)–(2.10) when I-class is not able to persist in the absence of S-class, i.e., $R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}$.

Fig. 4.6.

Schematic phase plane of the system (2.9)–(2.10) when I-class is able to persist in the absence of S-class, i.e., $\frac{\rho {(1-\theta )}^2}{4\beta }>\frac{d}{\beta }$.

Fig. 4.7.

Schematic phase plane of the system (2.9)–(2.10) when I-class is able to persist in the absence of S-class, i.e., $\frac{4\beta }{\rho {(1-\theta )}^2}<R_0^h$.

Fig. 4.8.

Schematic phase plane of the system (2.9)–(2.10) when I-class is able to persist in the absence of S-class, i.e., $\frac{4\beta }{\rho {(1-\theta )}^2}<R_0^h$.

The above discussion and the associated analytical results, including Proposition 3.1, Theorem 2.1, 3.2, 3.3 lead us to conclude that the effects of parameters ρ, d, β, θ on the dynamics of the system (2.9)–(2.10) can be summarized as follows:

1. The values of the reproduction number of horizontal transmission $R_0^h=\frac{\beta }{d}$ and the reproduction number of vertical transmission $R_0^{\upsilon }=\frac{\rho }{d}$ determine the dynamics of the system (2.9)–(2.10):

   • If $1<R_0^h<\frac{1}{\beta }$ and $R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}$, then the system (2.9)–(2.10) has no boundary equilibrium on the I-axis and it may have the disease-driven extinction in certain range of parameter values.
   • If the system (2.9)–(2.10) has the intermediate values of $R_0^{\upsilon }$, i.e., $\text{max}\{\frac{4}{{(1-\theta )}^2},c_1\}<R_0^{\upsilon }<c_2$, then the system tends to have susceptible-free dynamics.
   • The values of $R_0^h$ determines whether the system (2.9)–(2.10) can have unique interior equilibrium $(R_0^h>\frac{1}{\beta })$ or two interior equilibria $(1<R_0^h<\frac{1}{\beta })$.

2. The large values of ρ, θ, β and the small values of d can destabilize the system (2.9)–(2.10) (see Figure 4.9).

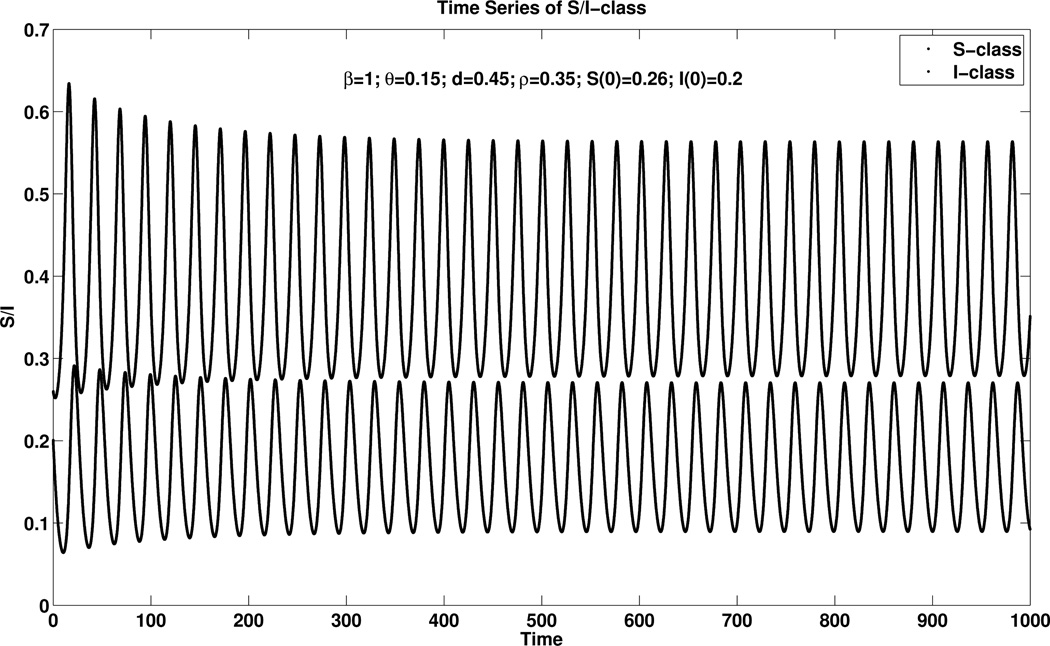
3. The system (2.9)–(2.10) can have a stable limit cycle; an example is included in Figure 4.10.

Fig. 4.9.

Bifurcation Diagrams of ρ, β, d, θ for the system (2.9)–(2.10) where the blue dots in the left figure means the interior equilibrium is locally asymptotically stable while the red dots means source.

Fig. 4.10.

An example of a stable limit cycle when β = 1, θ = 0.15, d = 0.45, ρ = 0.35, S(0) = 0.26, I(0) = 0.2 where the blue dots in the right figure means the population of I-class while the red dots means the population of S-class.

5. Diffusive instability

The ecological and evolutionary dynamics of host-pathogen or host-parasite systems are theoretically challenging for factors that include the impact of recurrent disease invasion, the ability of a parasite or pathogen to modify a host’s mobility-tied fitness, or reducing life span, or limiting/eliminating reproductive ability. Dispersal is capable of shaping the boundaries of habitats through increases or reductions on the size of the sphere-of-influence of infectious hosts, a cumulative process possibly altering infection rates (reductions or increases in effective contact rates), or its ability to generate clusters, or disease-driven selection of particular behavioral types (Altizer et al 2011; Diaz 2010; Levin 1974; Murray 2003).

Diffusive instability arises when diffusion or migration destabilizes stable situations (Segel and Jackson 1972; Levin 1974; Segel and Levin 1976). It may emerge as a result of the dynamics of metapopulation systems when coupled by dispersal or reaction-diffusion (Diaz 2010; Levin 1974; Murray 2003). The possible emergence of diffusive instability from two-patch systems, coupled by dispersal, when the local dynamics are governed by variants of the general SI-FD or SI-DD systems, is briefly addressed in this section.

Segel and Jackson (1972) using a simple predator-prey model studied the possibility of diffusive instability in predator-prey systems. Hence, first, some classical results addressing the emergence of diffusive instability in predator-prey systems, are revisited. Segel and Jackson (1972) showed that the addition of random dispersal was enough to generate instability from an otherwise initially stable uniform steady-state distribution. Diffusive instability, as shown by Levin (1974), also arises from the effects of dispersal on predator-prey interactions under the pressure of Allee effects. Segel and Levin (1976) used approximate methods and a multiple-time scale theoretical approach in their development of a small amplitude nonlinear theory of prey-predator interactions under random dispersal; a process modeled via diffusion-like terms in discrete and continuous settings. Segel and Levin (1976) showed that dispersal can destabilize spatially uniform states; diffusive instability moving the system to new nonuniform steady states. Levin and Segel (1976 & 1985) noted that the emergence of diffusive instabilities may explain some of the spatial irregularities observed in nature. The possibility of diffusive instability in general SI models is briefly discussed since identifying conditions that lead to diffusive instability on systems where disease and dispersal play a non-independent role are explored. The discussion below, we hope, will instigate further research on the study of diffusive instability in the settings introduced in this manuscript.

A general SI-model can be represented abstractly via the following set of equations

$$\frac{dS}{dt}=f(S,I)\frac{dI}{dt}=g(S,I),$$ (5.1)

operating under the assumption that the system (5.1) has a local asymptotically stable interior equilibrium (S*, I*), an assumption formulated using the inequalities

$$f_S+g_I<0\text{and}{f}_S{g}_I-f_I{g}_S>0$$ (5.2)

where $f_S=\frac{\partial f}{\partial S}(S^{*},I^{*}),f_I=\frac{\partial f}{\partial I}(S^{*},I^{*}),g_S=\frac{\partial g}{\partial S}(S^{*},I^{*}),g_I=\frac{\partial g}{\partial I}(S^{*},I^{*})$.

The inclusion of dispersal leads, for example, to the study of symmetric two-patch models. An example of such a system is given by the following set of equations:

$$\frac{d{S}_1}{dt}=f(S_1,I_1)+l_S(S_2-S_1)\frac{d{I}_1}{dt}=g(S_1,I_1)+l_I(I_2-I_1)\frac{d{S}_2}{dt}=f(S_2,I_2)+l_S(S_1-S_2)\frac{d{I}_2}{dt}=g(S_2,I_2)+l_I(I_1-I_2)$$ (5.3)

where l_S is the dispersal rate of the S-class and l_I is the dispersal rate of I-class. A typical pseudo diffusion model analog, involving constant diffusion coefficients, is given by the following system:

$$\frac{\partial S}{dt}=D_S\mathrm{\Delta }S+f(S,I)\frac{\partial I}{dt}=D_I\mathrm{\Delta }I+g(S,I)$$ (5.4)

where Δ is the Laplacian; D_S, D_I are the constant diffusion coefficients for susceptibles and infectives, respectively. We say the SI Model (5.1) supports diffusive instability (or Turing Effects) if (S*, I*) is a locally asymptotically stable interior equilibrium of the system (5.1) but (S*, I*, S*, I*) becomes unstable when embedded in the symmetric two-patch model given by the system (5.3) for certain values of l_I, l_S. We can achieve similar results as long as the (S*, I*) equilibrium is unstable for the Diffusion the system (5.4) at least for some values of D_S, D_I. The following theorem provides conditions that support the diffusive instability of the systems (2.7)–(2.8) and (2.9)–(2.10):

Theorem 5.1 (Diffusive instability). The general SI model (5.1) can have diffusive instability only if f_Sg_I < 0. In particular, the system (2.7)–(2.8) can support diffusive instability provided that the following inequalities hold

$$\frac{\beta -d}{1-\rho }<\text{min}\{\frac{d}{\rho },\frac{{(1-\theta )}^2}{4}\}\mathit{\text{and}}\frac{1+\theta }{2}+\frac{\sqrt{{(1-\theta )}^2-\frac{4(\beta -d)}{1-\rho }}}{2}<\frac{(1+\theta )+\sqrt{{(1+\theta )}^2-3\theta }}{3}.$$

The system (2.9)–(2.10) does not support diffusive instability.

Proof. Recall that the general SI model (5.1) has locally asymptotically stable interior equilibrium (S*, I*) if

$$f_S+g_I<0\text{and}{f}_S{g}_I-f_I{g}_S>0.$$

Since the two-patch model (5.3) is symmetric, thus, (S*, I*, S*, I*) is its interior equilibrium. The Jacobian matrix of two-patch model (5.3) evaluated at (S*, I*, S*, I*) can be represented as follows:

$$J_{(S^{*},I^{*},S^{*},I^{*})}=\left[\begin{array}{cccc}\hfill f_S-l_S\hfill & \hfill f_I\hfill & \hfill l_S\hfill & \hfill 0\hfill \\ \hfill g_S\hfill & \hfill g_I-I_I\hfill & \hfill 0\hfill & \hfill l_I\hfill \\ \hfill l_S\hfill & \hfill 0\hfill & \hfill f_S-l_S\hfill & \hfill f_I\hfill \\ \hfill 0\hfill & \hfill l_I\hfill & \hfill g_S\hfill & \hfill g_I-l_I\hfill \end{array}\right]$$

which has four eigenvalues λ_i, i = 1, 2, 3, 4. These four eigenvalues satisfy the following two conditions:

1. λ₁ and λ₂ are eigenvalues of the Jacobian matrix of the SI model (5.1) evaluated at (S*, I*), thus they are both negatives.

2. λ₃ and λ₄ have the following properties:

   $${\lambda }_3+{\lambda }_4=2(f_S+g_I-l_S-l_I)<0$$

   and

   $${\lambda }_3{\lambda }_4=\mathrm{\Lambda }=f_S{g}_I-f_I{g}_S-2(f_S{l}_I+g_I{l}_S)+4l_S{l}_I.$$

This implies that (S*, I*, S*, I*) is an interior equilibrium of its two-patch model (5.3) with its stability being determined by the sign of Λ. Thus, diffusive instability can occur only if Λ < 0 which indicates that f_Sg_I < 0, that is, if either f_S or g_I, is positive then (f_Sl_I + g_Il_S) > 0 can be made positive and large enough with the right combination of l_S, l_I; in other words, we conclude that for these parameter values, we have that Λ < 0. For example, if f_S > 0 then we can select the dispersal rate of the I-class l_I large enough and the dispersal rate of S-class l_S small so that the condition Λ < 0 is met. Now, under g_I > 0 diffusive instability may be possible as long as l_S is large and l_I is small.

Relying on the discussion in Section 8.9 of Brauer and Castillo-Chavez (2012), we conclude that (S*, I*) is a steady state of its reaction-diffusion model, namely Model (5.4), where the necessary and sufficient conditions for diffusive instability are given by

$$f_S+g_I<0,f_S{g}_I-f_I{g}_S>0\text{and}{f}_S{D}_I+g_I{D}_S>\sqrt{D_S{D}_I(f_S{g}_I-f_I{g}_S)}$$

which also implies that f_Sg_I < 0.

From Theorem 3.3, we know that if an interior equilibrium (S*, I*) is locally asymptotically stable then for the system (2.7)–(2.8) or the system (2.9)–(2.10).

$$N^{*}=S^{*}+I^{*}>\frac{1+\theta }{2}.$$

Thus, for the system (2.7)–(2.8), its Jacobian matrix (3.2) evaluated at the interior equilibrium (S*, I*) gives

$$f_S=S^{*}[1+\theta -2N^{*}+\frac{\beta I^{*}}{{(N^{*})}^2}]\text{and}{g}_I=I^{*}[\rho (1+\theta -2N^{*})-\frac{\beta S^{*}}{{(N^{*})}^2}]$$

which implies that g_I < 0 since $N^{*}>\frac{1+\theta }{2}$. Therefore the possibility of diffusive instability in the system (2.7)–(2.8) requires that f_S > 0. Since

$$I^{*}=\frac{N^{*}(N^{*}-\theta )(1-N^{*})}{\beta }\text{and}{N}^{*}=\frac{1+\theta }{2}+\frac{\sqrt{{(1-\theta )}^2-\frac{4(\beta -d)}{1-\rho }}}{2}>\frac{1+\theta }{2},$$

we have

$$f_S>0\Rightarrow 1+\theta -2N^{*}+\frac{\beta I^{*}}{{(N^{*})}^2}=1+\theta -2N^{*}+\frac{(N^{*}-\theta )(1-N^{*})}{N^{*}}=\frac{-3{(N^{*})}^2+2(1+\theta )N^{*}-\theta }{N^{*}}>0.$$

Since

$$-3{(N^{*})}^2+2(1+\theta )N^{*}-\theta =0\Rightarrow N^{*}=\frac{(1+\theta )\pm \sqrt{{(1+\theta )}^2-3\theta }}{3},$$

therefore f_S > 0 requires that $\frac{\beta -d}{1-\rho }<\text{min}\{\frac{d}{\rho },\frac{{(1-\theta )}^2}{4}\}$ for the existence of N* based on Theorem 3.3 and

$$N^{*}=\frac{1+\theta }{2}+\frac{\sqrt{{(1-\theta )}^2-\frac{4(\beta -d)}{1-\rho }}}{2}<\frac{(1+\theta )+\sqrt{{(1+\theta )}^2-3\theta }}{3}.$$

For the system (2.9)–(2.10), its Jacobian matrix (3.5) evaluated at (S*, I*) gives

$$f_S=S^{*}(1+\theta -2N^{*})\text{and}{g}_I=\rho I^{*}(1+\theta -2N^{*})$$

which implies that f_S < 0 and g_I < 0 since $N^{*}>\frac{1+\theta }{2}$. Therefore, we conclude that the system (2.9)–(2.10) does not support diffusive instability.

Remark: A direct application of the proof for Theorem 5.1 leads to the following statements:

1. If f_S > 0 and g_I < 0, then diffusive instability for the patchy model (5.3) requires that $\frac{l_I}{l_S}$ is large enough and $l_S<\frac{f_S}{2}$ while diffusive instability for the reaction-diffusion model (5.4) requires that $\frac{D_I}{D_S}$ is large enough.

2. If f_S < 0 and g_I > 0, then diffusive instability for the patchy model (5.3) requires $\frac{l_S}{l_I}$ to be large enough and $l_I<\frac{g_I}{2}$ while diffusive instability for the reaction-diffusion model (5.4) requires $\frac{D_S}{D_I}$ to be large enough.

In addition, Theorem 5.1 indicates that the SI system (2.7)–(2.8) with frequency-dependent horizontal transmission can support diffusive instability under certain conditions. For example, when the system (2.7)–(2.8) has β = 1, d = 0.85, ρ = 0.05, θ = 0.2, then it has two interior equilibria

$$E_{i1}=(S_1^{*},I_1^{*})=(0.4666247185,0.08749213472)\text{and}{E}_{i2}=(S_2^{*},I_2^{*})=(0.5439015973,0.1019815495)$$

where E_i1 is a saddle and E_i2 is locally asymptotically stable with

$$f_S=0.0830521552>0,f_I=-0.7590531079,g_S=0.02446282446\text{and}{g}_I=-0.1334319123<0.$$

Thus if we choose $\frac{l_I}{l_S}(\text{or}\frac{D_I}{D_S})$ large enough and $l_S<\frac{f_S}{2}$ then diffusive instability occurs.

These results agree with the study of predator-prey systems by Timm and Okubo (1992), which suggest that the existence of diffusive instability in such systems may require density effects on intra-specific coefficients and on a predator’s diffusivity that must be sufficiently larger when compared to the prey’s. There is a critical value involving the ratio of the prey/predator diffusivities that must be crossed before diffusive instability sets in. An alternative SI model (5.5)–(5.6) with Allee effects and horizontal and vertical transmission disease that can also support diffusive instability is given by the system

$$\frac{dS}{dt}=S(S-\theta )(1-S-I)-\beta SI$$ (5.5)

$$\frac{dI}{dt}=\beta SI-dI+\rho I(I-\theta )(1-S-I)$$ (5.6)

with a locally asymptotically stable interior equilibrium (S*, I*) given by

$$\begin{array}{cc}{f}_S=S^{*}(1-N^{*}-S^{*}+\theta ),\hfill & f_I=-S^{*}(S^{*}+\beta -\theta ),\hfill \\ g_S=I^{*}(-\rho I^{*}+\beta +\rho \theta ),\hfill & g_I=\rho I^{*}(1-N^{*}-I^{*}+\theta )\hfill \end{array}.$$ (5.7)

For example, when β = .1, θ = .2, d = 0.095, ρ = 0.001, the system (5.5)–(5.6) has a unique locally asymptotically stable interior equilibrium (S*, I*) = (0.95, 0.044) with

$$f_S=-0.70680<0,f_I=-0.8075,g_S=0.004406864\text{and}{g}_I=0.000006864>0.$$

Thus, if we choose $\frac{l_S}{l_I}(\text{or}\frac{D_S}{D_I})$ large enough and $l_I<\frac{g_I}{2}$, then diffusive instability occurs. This suggests that the existence of diffusive instability in (5.5)–(5.6) requires that susceptible’s diffusivity is sufficiently larger than that of infectives with a critical value involving the ratio of the susceptible/infectives diffusivities moving beyond a threshold after which diffusive instability sets in.

The SI system (5.8)–(5.9) with Allee effects and disease modified fitness studied by Kang and Castillo-Chavez (2013a) is given by

$$\frac{dS}{dt}=f(S,I)=\{\begin{array}{c}(S+\rho I)(S+{\alpha }_{1}I-\theta )(1-S-{\alpha }_{2}I)-\beta SI\hfill \\ 0,\text{if}S=0\text{and}({\alpha }_{1}I-\theta )(1-{\alpha }_{2}I)\le 0\hfill \end{array},$$ (5.8)

$$\frac{dI}{dt}=g(S,I)=\beta SI-dI,$$ (5.9)

where the assumptions of the model and the detailed biological meaning of parameters can be found in Kang and Castillo-Chavez (2013a), cannot support diffusive instability. The model can have a locally asymptotically stable interior equilibrium (S*, I*) with

$$f_S=[2S^{*}+({\alpha }_1+\rho )I^{*}-\theta ](1-S^{*}-{\alpha }_2{I}^{*})-(S^{*}+\rho I^{*})(S^{*}+{\alpha }_1{I}^{*}-\theta )-\beta I^{*},f_I=[(\rho +{\alpha }_1)S^{*}+2\rho {\alpha }_1{I}^{*}-\theta ](1-S^{*}-{\alpha }_2{I}^{*})-{\alpha }_2(S^{*}+\rho I^{*})(S^{*}+{\alpha }_1{I}^{*}-\theta )-\beta S^{*},g_S=\beta I^{*},g_I=0.$$ (5.10)

However, if we replace density-dependent transmission with frequency-dependent transmission in the SI the system (5.8)–(5.9) then we obtain the following SI the system (5.11)–(5.12) by letting ρ = 0, α₁ = α₂ = 1:

$$\frac{dS}{dt}=f(S,I)=S(N-\theta )(1-N)-\frac{\beta SI}{N}$$ (5.11)

$$\frac{dI}{dt}=g(S,I)=\frac{\beta SI}{N}-dI,$$ (5.12)

who supports the unique locally asymptotically stable interior equilibrium

$$(S^{*},I^{*})=(\frac{d{N}^{*}}{\beta },\frac{N^{*}(N^{*}-\theta )(1-N)}{\beta })\text{where}\frac{d}{\beta }<1,N^{*}=\frac{1+\theta +\sqrt{{(1-\theta )}^2-4(\beta -d)}}{2}$$

and

$$\begin{array}{cc}{f}_S=\frac{\partial f}{\partial S}(S^{*},I^{*})=S^{*}(1+\theta -2N^{*}+\frac{\beta I^{*}}{{(N^{*})}^2}),\hfill & f_I=\frac{\partial f}{\partial I}(S^{*},I^{*})=S^{*}(1+\theta -2N^{*}-\frac{\beta S^{*}}{{(N^{*})}^2})<0\hfill \\ g_S=\frac{\partial g}{\partial S}(S^{*},I^{*})=\frac{\beta {(I^{*})}^2}{{(N^{*})}^2}>0,\hfill & g_I=\frac{\partial g}{\partial I}(S^{*},I^{*})=-\frac{\beta S^{*}{I}^{*}}{{(N^{*})}^2}<0\hfill \end{array}.$$ (5.13)

Thus, the system (5.11)–(5.12) can have diffusive instability if

$$f_S>0\Rightarrow 1+\theta -2N^{*}+\frac{\beta I^{*}}{{(N^{*})}^2}=1+\theta -2N^{*}+\frac{\beta I^{*}}{{(N^{*})}^2}=\frac{-3{(N^{*})}^2+2(1+\theta )N^{*}-\theta }{N}>0.$$

Therefore, according to the proof of Theorem 5.1 and the discussion on the system (2.7)–(2.8), we can conclude that sufficient conditions leading to diffusive instability are that $\frac{l_I}{l_S}(\text{or}\frac{D_I}{D_S})$ is large enough and the following inequalities hold

$$l_S<\frac{f_S}{2},\frac{d}{\beta }<1,\frac{1+\theta +\sqrt{{(1-\theta )}^2-4(\beta -d)}}{2}<\frac{(1+\theta )+\sqrt{{(1+\theta )}^2-3\theta }}{3}.$$

Since SI-disease and prey-predator interaction models share structural similarities, we first look at the following two patch prey-predator model (5.14) with differential migration coefficients μ, ν introduced by Levin (1974):

$$\frac{d{x}_i}{dt}=x_i(K-a{x}_i-b{y}_i)+\mu (x_j-x_i)=f(x_i,y_i)+\mu (x_j-x_i)\frac{d{y}_i}{dt}=y_i(-L+c{x}_i+d{y}_i)+\nu (y_j-y_i)=g(x_i,y_i)+\nu (y_j-y_i)$$ (5.14)

which supports the equilibrium:

$$x^{*}={\mathrm{x̄}}_1={\mathrm{x̄}}_2=\frac{Lb-Kd}{bc-ad},y^{*}={ȳ}_1={ȳ}_2=\frac{Kc-La}{bc-ad}$$

and

$$\begin{array}{cc}{f}_S=\frac{\partial f}{\partial x_i}(x^{*},y^{*})=-a{x}^{*}<0,\hfill & f_I=\frac{\partial f}{\partial y_i}(x^{*},y^{*})=-b{x}^{*}<0\hfill \\ g_S=\frac{\partial g}{\partial x_i}(x^{*},y^{*})=c{y}^{*}>0,\hfill & g_I=\frac{\partial g}{\partial y_i}(x^{*},y^{*})=d{y}^{*}>0\hfill \end{array}.$$ (5.15)

According to Theorem 5.1, we conclude that diffusive instability arises if $\nu <\frac{g_I}{2}\frac{\mu }{\nu }$ is large enough and the following equalities hold

$$\frac{a}{c}<\frac{K}{L}<\text{min}\{\frac{b}{d},\frac{a(b+d)}{d(a+c)}\},bc>ad.$$

Notice that the positivity of g_I comes from the assumption that y_i is able to survive without x_i, i.e., y_i → ∞ if y_i(0) > L/d. If there is no Allee effects, i.e., d = 0, then the prey-predator Model (5.14) does not have diffusive instability. However, if we replace a Holling-Type I functional response with a Beddington-DeAngelis type functional response in the Prey-predator Model (5.14) with d = 0, then we obtain the following two-patch prey predator model that can have diffusive instability:

$$\frac{d{x}_i}{dt}=x_i(K-a{x}_i-\frac{b{y}_i}{1+h_1{x}_i+h_2{y}_i})+\mu (x_j-x_i)=f(x_i,y_i)+\mu (x_j-x_i)\frac{d{y}_i}{dt}=y_i(-L+\frac{c{x}_i}{1+h_1{x}_i+h_2{y}_i})+\nu (y_j-y_i)=g(x_i,y_i)+\nu (y_j-y_i)$$ (5.16)

which supports a unique locally asymptotically stable interior equilibrium (x*, y*) whenever

$$c{h}_2>b{h}_1,\frac{cK}{a+h_{1}K}>L,\mu =\nu =0$$

and

$$\begin{array}{cc}{f}_S=\frac{\partial f}{\partial x_i}(x^{*},y^{*})=x^{*}(-a+\frac{b{h}_1{y}^{*}}{{(1+h_1{x}^{*}+h_2{y}^{*})}^2}),\hfill & f_I=\frac{\partial f}{\partial y_i}(x^{*},y^{*})=-\frac{b{x}^{*}(1+h_1{x}^{*})}{{(1+h_1{x}^{*}+h_2{y}^{*})}^2}<0\hfill \\ g_S=\frac{\partial g}{\partial x_i}(x^{*},y^{*})=\frac{c{y}^{*}(1+h_2{y}^{*})}{{(1+h_1{x}^{*}+h_2{y}^{*})}^2}>0,\hfill & g_I=\frac{\partial g}{\partial y_i}(x^{*},y^{*})=-\frac{c{h}_2{x}^{*}{y}^{*}(1+h_1{x}^{*})}{{(1+h_1{x}^{*}+h_2{y}^{*})}^2}<0\hfill \end{array}.$$ (5.17)

For example, if K = .5, L = 0.01, c = 2.5, a = .1, h₁ = 1.5, h₂ = 1., b = 1, μ = ν = 0, then Prey-predator Model (5.14) has a unique locally asymptotically stable interior equilibrium (x*, y*, x*, y*) = (0.008084, 1.008, 0.008084, 1.008) with f_S = 0.0022 > 0, g_I = −0.005.

In this section, we have discussed diffusive instability in the context of five different SI-models and three different Prey-predator models. So, what are the criterions and mechanisms leading to diffusive instabilities? Comparisons between models supporting diffusive instability [SI-Models (2.7)–(2.8), (5.5)–(5.6), (5.11)–(5.12); Prey-predator models (5.14), (5.16)] and models not supporting diffusive instability [SI-models (2.9)–(2.10), (5.8)–(5.9); the prey-predator model (5.14) with d = 0] are summarized in Table 5.1.

6. Conclusion

Parasites and pathogens are sometimes effective “regulators of natural populations” (Anderson and May 1978; Dwyer et al 1990). Hence, it is of theoretical and empirical interest to study when multiple transmission modes are preferred; or whether pathogen/disease transmission depends on either host population density or its frequency; or the role of small populations (Allee effects) on populations living under the selection pressures placed by pathogens or parasites. Answers to such questions are needed to assess the role and impact of selection on populations, communities and ecosystems. In this manuscript, we explore the contributions of some of these factors on the dynamics of host-parasite interactions within a controlled setting, namely a general SI model that includes: (a) Horizontally and vertically-transmitted disease modes, (b) Net reproduction terms that account for the limitations posed by Allee effects, (c) Disease induced death rates, and (d) Disease-driven reductions in reproduction ability. The analyses carried out in the prior sections leads to the following conclusions and observations:

• Density- versus frequency-dependent horizontal transmission: From Theorem 3.3, we know that the system (2.7)–(2.8) can have two interior equilibria, one a saddle and one a locally asymptotically stable equilibrium. the system (2.9)–(2.10) can support stable limit cycles that emerge via Hopf-Bifurcation (see Figure 4.4 and 4.10). In other words, the SI model with density-dependent horizontal transmission turns out to support more complicated outcomes than its frequency-dependent counterpart.

• Effects of ρ, β, d and θ: $R_0^h=\frac{\beta }{d}$ is identified as the horizontal-transmission reproduction number and $R_0^{\upsilon }=\frac{\rho }{d}$ as the vertical-transmission reproduction number.

  1. Theorem 2.1 and its Corollary 2.2 assert that for the SI systems (2.7)–(2.8) and (2.9)–(2.10), sufficiently large initial conditions (N(0) = S(0) + I(0)) and $R_0^{\upsilon }$ can prevent extinction.
  2. Proposition 3.1, Theorem 3.2 and Theorem 3.3 imply that whenever $R_0^h\le 1$ we can expect disease-free dynamics in the systems (2.7)–(2.8) and (2.9)–(2.10).
  3. The SI-FD given by the system (2.7)–(2.8) tends to support susceptible-free dynamics under large values of $R_0^{\upsilon }$; coexistence of susceptibles and infectives under intermediate values of $R_0^{\upsilon }$; and disease-driven extinction for small values of $R_0^{\upsilon }$.
  4. The SI-DD system (2.9)–(2.10) supports the following outcomes: (i) No boundary equilibrium on the I-axis and possibly disease-driven extinction for a range of parameter values whenever $1<R_0^h<\frac{1}{\beta }$ and $R_0^{\upsilon }<\frac{4}{{(1-\theta )}^2}$. (ii) Susceptible-free dynamics for $R_0^{\upsilon }$-intermediate values; values that satisfy the inequality $\text{max}\{\frac{4}{{(1-\theta )}^2},c_1\}<R_0^{\upsilon }<c_2$. (iii) An unique interior equilibrium whenever $R_0^h>\frac{1}{\beta }$ and possibly two interior equilibria if $1<R_0^h<\frac{1}{\beta }$. (iv) Large values of ρ, θ, β and small values of d can destabilize the system (bifurcation diagrams; Figure 4.9).

• Horizontal versus vertical modes of transmission in the SI systems: Small values of the horizontal transmission rate can lead to the disease-free dynamics for both the systems (2.7)–(2.8) and (2.9)–(2.10)) with low reproductive rates for infectives leading, under certain conditions, to disease-driven extinction.

  The systems (2.7)–(2.8) and (2.9)–(2.10) have similar dynamics to those of the SI-model

  $$\frac{dS}{dt}=S(N-\theta )(1-N)\frac{dI}{dt}=\rho I(N-\theta )(1-N)-dI$$ (6.1)

  whenever the horizontal-transmission reproductive number is not greater than 1 $(R_0^h\le 1)$ and the vertical-transmission reproduction number is dominant. In this case, the system (6.1) has E_0,0 ∪ E_1,0 as its global attractor (disease-free dynamics).
  If horizontal transmission is dominant, that is, the vertical transmission rate is small due to the low reproductive ability (ρ) of those infected $(R_0^{\upsilon }\ge \frac{4}{{(1-\theta )}^2})$ then the systems (2.7)–(2.8) and (2.9)–(2.10) have similar dynamics to those supported by the SI-Models (6.2) and (6.3), respectively:

  $$\frac{dS}{dt}=S(N-\theta )(1-N)-\frac{\beta SI}{N}\frac{dI}{dt}=\frac{\beta SI}{N}-dI$$ (6.2)

  and

  $$\frac{dS}{dt}=S(N-\theta )(1-N)-\beta SI\frac{dI}{dt}=\beta SI-dI.$$ (6.3)

  Model (6.2) and (6.3) can in fact have the disease-driven extinction, under some conditions.

• Diffusive instability: Sufficient conditions leading to diffusive instability (Theorem 5.1 in Section 5) require that SI/Prey-Predator models support a locally asymptotically stable interior equilibrium with the product of the diagonal entries of the Jacobian matrix (evaluated at this interior equilibrium) being negative. In this manuscript, we have investigated possible ways for diffusive instability to emerge in five different SI-models while contrasting their behavior with those of three different prey-predator models. The results of these comparisons have been summarized (Table 5.1). From Table 5.1 we conclude that:

  1. In the context of our SI models, asymmetricity and nonlinearity that emerge as a result of frequency-dependent horizontal transmission or some forms of vertical transmission in populations under Allee effects, can generate diffusive instability.
  2. In the context of Prey-Predator models, asymmetricity and nonlinearity arising from certain forms of functional responses such as Beddington-DeAngelis type functional response or Allee effects in the predator population, can generate diffusive instability.
     In conclusion, the presence of asymmetricity and nonlinearity such as nonlinear density dependent factors including Allee effects, could be critical for the generation of diffusive instabilities in both SI models and Prey-Predator models.

Table 5.1.

Summary of diffusive instability for SI models and Prey-Predator models

Models	fS	fI	Diffusive Instability	Potential Mechanisms
SI-Model (2.7)–(2.8)	$f_S=S^{*}[1+\theta -2N^{*}+\frac{\beta I^{*}}{{(N^{*})}^2}]>0$	$g_I=I^{*}[\rho (1+\theta -2N^{*})-\frac{\beta S^{*}}{{(N^{*})}^2}]<0$	Yes	Asymmetricity and nonlinearity arise from frequency-dependent horizontal transmission
SI-Model (2.9)–(2.10)	fS = S* (1 + θ − 2N*) < 0	gI = ρI* (1 + θ − 2N*) < 0	No	Symmetricity arises from certain forms of vertical transmission with Allee effects; Linearity arises from density-dependent vertical transmission
SI-Model (5.5)–(5.6)	fS = S* (1 − N* − S* + θ) < 0	gI = ρI* (1 − N* − I* + θ) > 0	Yes	Asymmetricity and nonlinearity of arise from certain forms of vertical transmission with Allee effects
SI-Model (5.8)–(5.9)	fS = [2S* + (α1 + ρ)I* − θ] (1 − S* − α2I*) − (S* + ρI*)(S* + α1I* − θ) − βI* < 0	gI = 0	No	Linearity arises from density-dependent horizontal transmission
SI-Model (5.11)–(5.12)	$f_S=S^{*}(1+\theta -2N^{*}+\frac{\beta I^{*}}{{(N^{*})}^2})>0$	$g_I=\frac{\beta S^{*}{I}^{*}}{{(N^{*})}^2}<0$	Yes	Asymmetricity and nonlinearity arise from frequency-dependent horizontal transmission
PP-Model (5.14)	fS = −ax* < 0	gI = dy* > 0	Yes	Nonlinearity arises from Allee effects in predator
PP-Model (5.14) with d = 0	fS = −ax* < 0	gI = 0	No	Linearity arises from a Holling Type I functional response
PP-Model (5.16)	$f_S=x^{*}[-a+\frac{b{h}_1{y}^{*}}{{(1+h_1{x}^{*}+h_2{y}^{*})}^2}]>0$	$g_I=-\frac{c{h}_2{x}^{*}{y}^{*}(1+h_1{x}^{*})}{{(1+h_1{x}^{*}+h_2{y}^{*})}^2}<0$	Yes	Asymmetricity and nonlinearity arise from a Beddington-DeAngelis type functional response

We study SI models with Allee effects and different modes of disease transmissions.

We identify sufficient conditions of disease-free and endemic disease patterns.

The SI Density-Dependent system can support rich dynamics such as limit cycles.

The SI Frequency-Dependent model can only support equilibrium dynamics.

High levels of asymmetry and Allee effects can generate diffusive instability.