Importance of Protein Dynamics during Enzymatic C–H Bond Cleavage Catalysis

Abstract

Quantum tunneling and protein dynamics have emerged as important components of enzyme function. This review focuses on soybean lipoxygenase-1, to illustrate how the properties of enzymatic C–H bond activation link protein motions to the fundamental bond making–breaking processes.

The principle of “enhanced transition-state binding” sufficed for many decades as a basis for the study and interpretation of the huge rate accelerations catalyzed by enzymes.¹ However, the need for a revised conceptual framework is now apparent. An inability to design and prepare de novo catalysts, either proteins or small molecules, with rates approximating those of highly active enzymes has persisted,^2–5 as has the frequent failure to observe changes in enzyme structure following the introduction of site-specific mutants that greatly alter enzymatic rate constants. The large size and inherent flexibility of proteins have long been recognized as being important for the formation of the enzyme–substrate Michaelis complex and for the manifestation of allostery.^6–9 The link of protein motions, designated protein dynamics herein, to the bond making–bond cleavage step of catalysis is another matter altogether. This subject has generated much interest and controversy over the past decade, with a consensus beginning to emerge regarding the relationship of a hierarchy of protein motions to the effectiveness of chemical transformations at enzyme active sites.^10–13 Of particular note in this field are, first, single-molecule studies that demonstrate a second scale interconversion of proteins among a range of conformers with different kinetic properties^14,15 and, second, ensemble studies of mutant versus native enzymes that allow correlations to be made between altered catalytic capability and altered dynamics within the protein backbone and side chains.^16,17 While correlations do not constitute proof, a convergent picture is emerging from studies of a large number of divergent enzyme systems, characterized by different active site structures and mechanisms.

Electron and hydrogen transfer processes dominate the chemistry of life, and in recent years, it has become clear that quantum effects contribute to both processes at room temperature.^18,19 As originally shown in the formulation of a rate theory for electron tunneling, the motions of the heavy atoms of the environment play the central role in determining the electron flux from reactant(s) to product(s).²⁰ A similar theory for hydrogen tunneling focuses attention on the need to adjust active site electrostatics and internuclear distances via heavy atom motions, either within the substrate or in the surrounding protein matrix.^21,22

For the purposes of this perspective, the focus will be on a soybean lipoxygenase (SLO-1), a paradigmatic enzymatic system that displays some of the largest primary deuterium kinetic isotope effects (KIEs ≳ 100) seen at room temperature in either an enzymatic or solution C–H bond abstraction reaction.^23,24 Because of the inflated size of the KIEs, SLO-1 played an important and early role in convincing the research community that tunneling could be a dominant feature of room temperature C–H bond activation. In subsequent years, exceedingly large KIEs have also been reported for a range of fatty acid oxidizing enzymes (e.g., refs 25–27) as well as lipoxygenases that use Mn(III)-OH as the active site oxidant.^28,29 As will be discussed in the section Temperature Dependence Parameters, E_a, A_H, E_a(D)–E_a(H), and A_H/A_D, mutant forms of SLO-1 have played a key role in developing models for the link between the H-tunneling event and protein motions.

ESTABLISHING CONDITIONS UNDER WHICH THE PRIMARY KINETIC HYDROGEN ISOTOPE EFFECT IN SLO-1 REFLECTS A SINGLE STEP

The original studies of deuterium isotope effects with SLO-1 used a form of substrate that was, by ease of synthesis, dideuterated at the C-11 position of the substrate (cf. Scheme 1). This raised the potential contribution of an inflated and anomalous secondary KIE. Synthesis of the 13(R) and (S)-monodeuterio species made it possible to show that the secondary KIE was, in fact, small (~1.1–1.2) and that the hugely inflated experimental KIE was due to the primary, 13(S) position.³⁰ A notable oddity of these studies with a stereo-specifically labeled substrate was that insertion of a single deuterium into the 13(S) position led to abstraction of the alternate 13(R) protium, revealing a loss of stereochemistry that had been induced by the huge primary deuterium KIE at the normally reactive position.³⁰

Scheme 1. Reaction Mechanism for Soybean Lipoxygenase-1³¹.

At the outset of the studies of SLO-1, it was also essential to prove that the large KIEs were intrinsic to a single chemical step, and not due to experimental artifacts that could have arisen from either the partitioning of an enzyme-bound, chemical intermediate or the presence of multiple, isotopically sensitive steps. A central feature of the SLO-1 steady-state reaction mechanism (Scheme 1) is that it occurs via a “ping-pong” process, in which the transfer of a proton and electron from the substrate to the active site Fe(III)-OH is followed by a trapping of the substrate-derived free radical by molecular oxygen.³¹ Studies of lipoxygenases from a number of species have shown that the substrate-derived radical intermediate can be released from enzyme at low O₂ concentrations, leading to alternate reaction products.³² However, in the case of SLO-1, the K_m for O₂, using either protio- or deuterio-labeled substrates, lies far below the O₂ concentration in air. Characterization of kinetic parameters and their isotope effects in air (~20% O₂) and 100% O₂ leads to virtually unchanged parameters.³¹ Importantly, these conditions ensure complete trapping of the substrate-derived free radical to the expected product, making the reaction a simple 1:1 conversion of linoleic acid to its 13-hydroperoxy product. There is, additionally, no evidence that the C–H bond abstraction in SLO-1 is reversible at saturating O₂ levels, eliminating the possible contribution of a second isotopically sensitive step to measured KIEs.³¹ The magnitude of ^Dk_cat/K_m for linoleic acid (LA) moves toward ^Dk_cat at low pH and high temperature, supporting the conclusion that a single C–H bond cleavage step dominates k_cat.³³ Finally, single-turnover experiments with SLO-1, which directly monitor the time dependence for the reduction of the iron center by substrate, confirm the presence of a very large deuterium KIE on this step.³⁴

TEMPERATURE DEPENDENCE PARAMETERS, E_A, A_H, E_A(D)–E_A(H), AND A_H/A_D

The earliest experimental evidence of H-tunneling in enzyme reactions came from the magnitude of secondary KIEs, either in relation to limits set by equilibrium isotope effects³⁵ or from the comparison of pairs of molecules with different labeling schemes, e.g., k_H/k_T versus k_D/k_T.¹⁹ In hydride transfer reactions, the pattern of deviations of secondary KIEs from semiclassical expectations was shown fairly early to be accompanied by anomalies in the temperature dependence of the KIE, with both types of probes leading to similar conclusions regarding the nature of enzyme active site tunneling and its relation to protein motions.³⁶ Over time, the temperature dependence of the KIE has emerged as the more general and useful probe among a wide range of enzyme reactions,^13,37 with SLO-1 playing an important conceptual and experimental role in this regard. As will be described below, the properties of remote secondary KIEs in SLO-1 have also expanded the phenomenon of tunneling beyond the transferred hydrogen and to the backbone of the substrate itself.³⁸

The temperature dependence parameters for the reaction of protio- and deuterio-labeled LA with native SLO-1 include a remarkably low value for the energy of activation (Table 1), together with a small difference in this energy of activation for H versus D abstraction from substrate that leads to a very large deuterium isotope effect on the Arrhenius prefactor (A_H/A_T ≫ 1). Almost all of the KIE for SLO-1 and most of the reaction barrier reside in the entropy of activation.²² These unprecedented experimental observations have sparked considerable interest among theoreticians, who have differed in their views with regard to the degree of tunneling from within deep wells (ground-state tunneling) (Figure 1C vs at or near the top of the reaction barrier, Figure 1A, B).^{21,22,39–,41} One of the primary issues to be addressed is the near temperature independence of the KIE seen not only in SLO-1 but also for a large number of divergent enzyme systems.^12,13 This has focused attention on models that invoke “deep tunneling” from ground-state vibronic modes of the substrate and/or product, with the energetic barrier for the reaction coming from motion of the heavy atoms of the enzyme and substrate^21,22 (Figure 2).

Table 1.

Kinetic Parameters of SLO-1 and Mutants in 0.1 M Borate (pH 9) at 30 °C

enzyme	kcat (s−1)	kcat/Km (μM−1 s−1)	Ea(H)c (kcal/mol)	Dkcat	r0d	ωxd
SLO-1 WTa	297 (12)	11 (1)	2.1 (0.2)	81 (5)	2.7 (2.7)	292 (174)
553Aa	280 (10)	12 (1)	1.9 (0.2)	93 (4)	3.8 (2.8)	47 (140)
546Aa	4.8 (0.6)	0.33 (0.1)	4.1 (0.4)	93 (9)
754Aa	0.31 (0.02)	0.07 (0.02)	4.1 (0.3)	112 (3)
546A/754Ab	0.021 (0.001)	0.0023 (0.0004)	9.9 (0.2)	≫81

^aFrom ref 42.

^bFrom ref 55.

^cDetermined from the temperature dependence of k_cat.

^dThese computed values for the initial DAD (r₀) and the DAD sampling frequency (ω_x) are from ref 44, and the numbers in parentheses are from ref 49.

Figure 1.

Illustrative free energy profiles and Arrhenius plots for the cleavage of a C–L bond, where L is H, D, or T. (A) Semiclassical KIEs predict extrapolation at high temperatures to Arrhenius prefactors that are close to being independent of isotopic labeling. (B) Tunneling correction models predict a larger value for both E_a and A_L in the case of the heavier isotope(s). (C) Full tunneling models are able to reproduce data where there is no or little difference in the magnitude of E_a among the isotopes and values of A_L that are greatly elevated for H in relation to D and T.

Figure 2.

Rate constant for tunneling, as formulated in ref 42, comprised of three exponential terms. (a) Heavy atom motions that lead to degeneracy of reactant and product wells, a prerequisite for hydrogen tunneling between the donor and acceptor. The rate of reaching this state depends on the reaction driving force (ΔG°) and the reorganization energy (λ). (b) Resulting wave function overlap that is dependent on mass (m_H), frequency (ω_H), and distance (r_H). The wave function overlap is shown as being greater for protium than for deuterium. (c) Energy dependence (E_x) for sampling of different donor–acceptor distances (r_x). The increased energy at shorter donor–acceptor distances is offset by a more efficient wave function overlap. Adapted from ref 65.

The essential feature of the tunneling mechanism of Figure 2 is its multidimensionality, with separate coordinates controlling heavy atom motion versus wave function overlap. The latter, which is dependent on the mass of the transferred particle but is independent of temperature, occurs only after the heavy atom environment has been properly tuned with regard to ground-state energetics and donor–acceptor distance (DAD). These heavy atom motions are activated by increasing temperature in a manner that is (i) largely independent of the isotope at the reactive C–H bond (the adjustment of ground-state energetics to obtain transient degeneracy between the donor and acceptor) or (ii) dependent on the mass of the transferred hydrogen (the sampling of multiple donor–acceptor distances). The mass dependence of the DAD sampling coordinate may not be immediately apparent, but arises from the smaller wavelength for the heavy isotopes of hydrogen and the attendant need for shorter donor–acceptor distances. The model shown incorporates both weakly temperature-dependent and temperature-independent KIEs (when the H-donor and -acceptor are initially very close in space) and highly dependent KIEs (when the initial donor–acceptor distances are too long for effective tunneling).

Mathematical derivations for a nonadiabatic Franck–Condon hydrogen wave function overlap (Figure 2B) were able to reproduce very well the KIEs and their temperature dependences in wild-type (WT) and single-site mutant forms of SLO-1⁴² (cf. Table 1 for a comparison of WT to the Ile553Ala variant). The formal hydrogen atom transfer in SLO-1, with its expectation of weak coupling between the H-donor and -acceptor, contrasts with reactions in which hydrogen moves as a charged particle. Fitting of data for the more adiabatic hydride and proton transfer enzyme-catalyzed reactions is generally difficult,^13,43 in large part, because of the need to accommodate a greater electronic coupling between the H-donor and -acceptor and the smaller KIEs in these reaction types. Nonetheless, the fundamental physics that underlies a C–H bond activation process via tunneling is captured in Figure 2.

For SLO-1, the mechanistic picture that emerges from the data in Table 1 is as follows.^42,44 In the WT enzyme, the H-donor and -acceptor can approach one another at a distance that is tunneling appropriate, ca. 2.7–3.0 Å, reduced from an expected C–H···O van der Waals distance of 3.2–3.5 Å. This eliminates the need for significant DAD sampling, thereby generating the small experimental temperature dependence of the KIEs. A close donor–acceptor distance can arise, in principle, from either a compacted or compressed ground state or from a sampling among possible protein conformers to find those appropriate for tunneling. With regard to ground-state effects, it has not yet been possible to obtain an X-ray structure of SLO-1 in complex with a substrate or substrate analogue, and the product hydroperoxide binds in a noncatalytic mode. However, a recent, 1.9 Å structure for a substrate-like inhibitor complex of a mammalian 12-lipoxygenase shows an ~2.9 Å distance from the carbon at position 10 of the inhibitor to the oxygen of the iron-bound hydroxide.⁴⁵ This implication of a noncanonical H-bond from substrate to the active site ferric hydroxide is in need of further study and validation, with X-ray structures for enzymes catalyzing C–H bond abstraction by tunneling generally showing the expected van der Waals distances between the H-donor and -acceptor (cf. ref 46). The currently accepted view for H-tunneling in WT SLO-1, as well as other optimized enzyme systems,^13,17 is the achievement of the protein substates that are tunneling-ready via a statistical search of a large protein conformational landscape.

The transition from weakly temperature-dependent or temperature-independent KIEs to temperature-dependent KIEs is a second signature observation for SLO-1 variants that have undergone site-specific mutagenesis.^42,44 Similar behavior has been seen in a large number of other enzyme systems after perturbation from their native or optimal structures and dynamics.^12,13,17 According to the model in Figure 2, temperature-dependent KIEs arise when a protein is no longer able to bring the H-donor and -acceptor atoms into precise alignment. The simplest situation for visualizing this behavior is in the context of a key active site hydrophobic side chain that normally constrains the position of the H-donor and -acceptor atoms with respect to one another; a reduction in the size of this side chain via site-specific mutagenesis will then lead to the donor and acceptor groups moving apart.^42,44,47,48 The barrier for restoration of the tunneling-ready distance will be a function of the force constant for the distance sampling mode, which is expected to decrease, concomitant with the increase in the amount of space within the active site that results from mutagenesis.¹⁷ The increasing distance and decreasing force constant for internuclear sampling that reproduce the SLO-1 single-site mutant Ile553Ala kinetic data are listed in Table 1. The differences in the numbers in the last two columns reflect the manner in which the data were fit, with the values in parentheses resulting from all-atom molecular dynamics simulations of the fully solvated WT and mutant enzymes.⁴⁹ For this comparison, the trends in r_o and ω_x are considered important, rather than the absolute values of the parameters. As shown in refs 44 and 49 for an extended series of mutations at position 553, the more temperature-dependent the KIE, the longer the initial DAD and the weaker the force constant for the distance sampling mode. The motion that restores the tunneling-ready distance, via the DAD sampling coordinate, is estimated to be on the nanosecond to picosecond time scale and separate from the actual movement of hydrogen via its wave function overlap between the donor and acceptor. Once again, there was no expectation of any direct coupling of protein motions to the actual tunneling coordinate.

It is important to question whether alternate models are able to accommodate the onset of temperature-dependent KIEs. In particular, it has recently been proposed that temperature-dependent KIEs may reflect the introduction of an increasing number of reactive conformers upon protein mutation that are characterized by very different donor–acceptor distances and KIEs.^43,50 According to this model, it is the change in the temperature-dependent distribution of reactive conformers that gives rise to the temperature dependence of the KIE. While on the surface this model is attractive, the one instance in which it has been analyzed in an in-depth manner requires the presence of extreme protein conformers in which the transferred hydrogen either tunnels through the H-transfer barrier (with a large intrinsic KIE) or undergoes transfer above the top of the H-transfer barrier (with no apparent KIE).⁴³ This model further requires that the protein conformer lacking a KIE increases its occupancy at elevated temperatures, a feature that is unlikely to be generally applicable to the wide range of enzymes exhibiting highly temperature-dependent KIEs (cf. ref 12). In any case, behavior of this extreme type appears to be unlikely for the formal hydrogen atom transfer reaction catalyzed by SLO-1, with the high bond dissociation energy (estimated to be 80 kcal/mol⁴²) and poor hydrogen bonding ability of the C–H bond at position 11 of substrate.

Evidence against a model that depends on a temperature-dependent distribution of protein conformers with different intrinsic KIEs also comes from recent studies of the hydride transfer reaction catalyzed by a thermophilic alcohol dehydrogenase.⁴⁸ For this system, decreasing the size of an active site residue by mutation increases the temperature dependence of the KIE in the physiologically relevant temperature regime, >30 °C. Independent experiments have indicated that mutation of a homologous alcohol dehydrogenase elongates the donor–acceptor distance,⁴⁶ as anticipated for a greater dependence on DAD sampling for effective tunneling. At a reduced temperature, <30 °C, where the ht-ADH undergoes an abrupt rigidification in the substrate-binding domain,⁵¹ the KIEs for the mutant proteins revert to the temperature-independent regime.⁴⁸ The latter, which is accompanied by reduced activity and elevated KIEs, almost certainly reflects a restricted ability of the mutants at the reduced temperature to recover the optimal tunneling configuration via a donor–acceptor distance sampling coordinate (cf. Figure 3 for a cartoon of this behavior).

Figure 3.

Model to illustrate the impact of active site mutations in ht-ADH above and below the transition temperature at 30 °C. State 1 is the ideal state and represents the WT protein above 30 °C. The protein is optimally flexible (in the black region), and this generates active site compression that is accompanied by a close approach of the H-donor and H-acceptor. State 2 represents the situation following active site mutation above 30 °C. The white region, representing the active site, is shown in an artificially enlarged manner to allow a depiction of the resulting increased distance between the H-donor and H-acceptor that is accompanied by a decrease in the force constant for DAD sampling. State 3 is the situation that results from the combination of active site mutation and low temperature. Once again, the region representing the active site (white) is enlarged, to allow depiction of the increase in the donor–acceptor distance. Under the conditions of state 3, the increased rigidity of the protein below 30 °C prevents any “recovery” via DAD sampling and the KIE once again becomes temperature-independent.⁴⁸

DETECTING THE ROLE OF CONFORMATIONAL LANDSCAPES IN THE C–H BOND CLEAVAGE STEP OF SLO-1

One of the major challenges in enzymology is to link changes in the protein conformational landscape to the promotion of chemical step(s) in enzymatic reactions. While it is expected that enzymes will change shape as they move along the reaction coordinate, this is best considered an accommodation of a protein to new active site intermediates (cf. ref 52). What we and others wish to address is whether there has been an evolutionary selection toward conformational landscapes that enhance the rates for bond cleavage step(s) of enzyme reactions. Hydrogen tunneling offers an excellent experimental opportunity to examine this question. We have already introduced a role for protein motions in the distance-sampling mode that produces temperature-dependent KIEs. In what may appear to be initially contradictory, the observation of temperature-independent KIEs also offers one of the important insights into a second category of protein motions in catalysis. The requirement for short, tunneling-ready donor–acceptor distances, which follows from temperature-independent KIEs, implicates active site structures that have become compacted or compressed. In the absence of data for a compressive feature in the dominant ground-state structures for enzymes acting on C–H bonds, the capacity to create active site compaction must occur via a transient sampling of specific protein substates.

The role of multiple ground-state protein conformational substates was initially introduced in the context of the protein folding mechanism and later incorporated into ideas regarding enzyme catalysis. A pictorial representation of this phenomenon is presented in Figure 4. As illustrated, the protein moves quickly from one conformational substate to another, implying relatively small energetic barriers for these interconversions under optimal conditions. Each protein substate is characterized by a unique rate constant for the chemical conversion step(s), with the most rapid rates occurring when the alignment of active site residues in relation to substrate(s) provides a precise tuning of electrostatic potentials and internuclear distances.¹⁷ While computational studies have proposed a direct coupling of protein motions to the chemical step(s),⁵³ more experimental data are needed to support such a view. Thus far, the motions that influence catalysis are assumed to be sampled in a statistical manner that precedes the bond cleavage process.

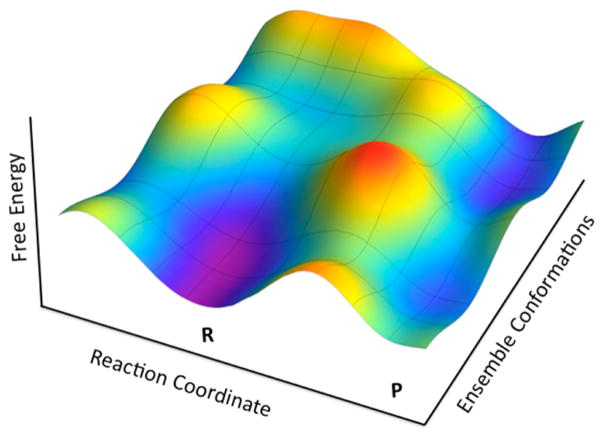
Figure 4.

Dependence of the chemical coordinate (Reaction Coordinate) on the conformational substates (Ensemble Conformations). As illustrated, each conformational substate converts substrate to product with a distinctive rate constant (provided by R. Larsen and A. Kohen¹³). A similar picture has been introduced by Benkovic et al.⁶⁴ to illustrate the role of a conformational landscape in enzyme catalysis.

The introduction of mutations anywhere throughout a protein has the potential to perturb the conformational landscape and is certainly one of the reasons why remote mutations are frequently found to alter catalytic turnover numbers. In the context of H-tunneling during C–H bond activation reactions, remote mutations affect not only the rate but also the ability to bring about precise alignment between the H-donor and -acceptor atoms, leading most generally to temperature-dependent KIEs.^12,17 In general, the impact of mutations can be considered in two contexts. In the first case, a mutation may directly alter the catalytic properties within each conformational substate, and this may be the default situation when mutagenesis is conducted at highly conserved active site residues that play a direct role in chemical catalysis. A second and more general scenario of the impact of a mutation involves a shift in the conformational landscape toward low-activity or inactive conformers. This shift is distinct from the creation of a subpopulation of denatured protein and implies an ongoing equilibration between less active and more active regions of the conformational subspaces.

Evidence in support of a reversible shift of the protein conformational space toward a less active region has come from studies of the ht-ADH in a low-temperature regime where the protein undergoes a cooperative transformation at 30 °C into a more rigid and less active form^48,51 [introduced in the section Temperature Dependence Parameters, E_a, A_H, E_a(D)–E_a(H), and A_H/A_D]. The creation of active site mutations in ht-ADH, when combined with low temperatures, was found to lead to enormously elevated values for the Arrhenius prefactor, with an A_H(obs) as large as 10²⁵ s^{−1 54} and more than 10 orders of magnitude greater than the expected semiclassical A_H(obs) of ≅10¹³ s⁻¹. An energy-dependent equilibration of the protein among active and inactive substates was able to explain the enormously inflated Arrhenius prefactors according to eq 1:

$$ln{A}_{\mathrm{H}(\text{obs})}=ln{A}_{\mathrm{H}(int)}+\frac{\mathrm{\Delta }S{°}_{\mathrm{c}}}{R}$$ (1)

where A_H(int) arises from the chemical coordinate and ΔS°_c represents the entropic barrier for moving from low-energy, inactive states to the catalytically productive region of the conformational landscape. The observed enthalpy of activation was found to be similarly elevated by the enthalpic barriers for moving between inactive and active states, ΔH°_c:

$$\mathrm{\Delta }{H^{‡}}_{(\mathit{obs})}=\mathrm{\Delta }{H^{‡}}_{(int)}+\mathrm{\Delta }H{°}_{\mathrm{c}}$$ (2)

Recent investigations with SLO-1 have pursued the generation of double-active site mutants, in an effort to detect a similar trapping of the protein into low-energy, low-activity conformational substates.⁵⁵ The active site of SLO-1 (Figure 5) illustrates the three hydrophobic residues that were the initial focus of studies with single-site mutations, Leu546Ala, Leu754Ala, and Ile553Ala (Table 1). These studies have been extended to double mutants, Ile553Ala/Leu546Ala, Ile553Ala/Leu754Ala, and Leu546Ala/Leu754Ala. The measurement of kinetic parameters as a function of temperature with perprotio-LA indicates that double mutants generated with Ile553Ala are similar to the parent, single mutants. This result is not surprising, given that Ile553Ala alone has a very modest impact on k_cat using the protio substrate. By contrast, the mutant in which the two proximal hydrophobic residues have undergone a reduction in size, Leu546Ala/Leu754Ala, causes the rate to be reduced by ~4 orders of magnitude relative to that of the WT enzyme. The enthalpy of activation for this mutant is also seen to increase by almost 8 kcal/mol (Table 1).

Figure 5.

X-ray structure of SLO-1, with LA modeled into the active site.²²

Considerable mechanistic insight into the behavior described above became possible once reliable KIEs were available for the second-order and unimolecular rate constants, ^Dk_cat/K_m(LA) and ^Dk_cat, respectively. In contrast to the successful measurement of noncompetitive KIEs via a continuous spectrophotometric method with the more active variants of SLO-1, we found it was difficult or impossible to obtain similarly reproducible KIEs on ^Dk_cat/K_m(LA) (with all double mutants, because of the need to monitor the reaction at very low substrate concentrations) and on ^Dk_cat for Leu546Ala/Leu754Ala (because of its extremely slow rate). It was, however, possible to overcome these limitations using discontinuous HPLC methods. In the case of ^Dk_cat/K_m(LA), the reaction was conducted with a mixture of perprotio- and perdeuterio-LA, with the latter allowing baseline HPLC separation of the 13(S)-hydroperoxy-9(Z),11(E)-octadecanoic acid (HPOD) derived from unlabeled and uniformly deuterated substrate (cf. ref 25). Previous kinetic studies had established that perdeuterio-LA and substrate dideuterated at the reactive C-11 position of LA behave in a similar fashion. At a variety of pH values and temperatures, ^Dk_cat/K_m(LA) is always seen to be reduced by a factor of ≥2 in relation to ^Dk_cat.⁵⁵ Further, under each of the conditions studied, the magnitude of ^Dk_cat/K_m(LA) for the double mutants remains strikingly similar to that of the WT, a very surprising result given the reduction in the second-order rate constants that approximates 10⁴-fold for Leu546Ala/Leu754Ala (Table 1). A selective, negative impact of the double mutation on steps that lead to the productive enzyme–substrate complex would have generated smaller values for ^Dk_cat/K_m(LA) in relation to that of the WT (dashed black line in Scheme 2). Alternatively, if the double active site mutant had exerted its primary impact on the H-tunneling step, the value of ^Dk_cat/K_m(LA) would have increased toward ^Dk_cat (dashed red line in Scheme 2).

Scheme 2. Diagram To Illustrate the Expected Consequences for k_cat/K_m(LA) in the Event of a Decrease in the Rate Constant To Reach the Reactive Enzyme–Substrate Complex (E–S) via TS-1 (dashed line) versus a Decrease in the Rate Constant for C–H Bond Cleavage via TS-2 (dashed red line)^a.

^aThe standard state for the binding of substrate has been arbitrarily set at the K_d for substrate, resulting in equal energies for E+S and E·S.

In the absence of any evidence of a change in the rate-limiting step, the SLO-1 data necessitate an alternate explanation for the lack of trends in isotope effects on k_cat/K_m(LA) that accompany the large reductions in rate. At the simplest, phenomenological level, the data implicate a reduction in “concentration” of the catalytically active forms of the enzyme. High-resolution X-ray data for a series of single mutants at position 553 have already shown superimposable structures.⁴⁴ While X-ray data are not yet available for the double mutants of SLO-1, circular dichroism measurements indicate identical behavior among the WT and double variants,⁵⁵ ruling out any significant protein denaturation that would alter the proteins’ secondary structure (the N-terminus of SLO-1 is predominantly β sheet, and the catalytic domain is almost exclusively α helix). In no instance were the double active site mutants shown to induce enzyme instability, either during kinetic assays or during enzyme purification.

The most plausible explanation for the impact of double active site mutations in SLO-1 on k_cat/K_m(LA) is an increasing shift in population among interconverting protein substates toward those that are inactive or of low catalytic viability, with the remaining active states behaving in a manner similar to that of the WT. Because the rate parameter k_cat/K_m(LA) measures differences in free energy between the free enzyme and downstream activated complexes, the shift in the protein population detected from the comparison of ^Dk_cat/K_m(LA) to k_cat/K_m(LA) values must be occurring at the level of the unbound enzyme state. Insight into the role of conformational sampling at the level of the enzyme–substrate complex comes from two directions with SLO-1. First, there are the markedly increased enthalpies of activation on k_cat for two of the double mutants relative to that of the WT (cf. Table 1 for Leu546Ala/Leu754Ala). This behavior is accompanied by an increase in A_H(obs).⁵⁵ Analogous to the behavior of mutant forms of ht-ADH at low temperature, the increase in active site packing defects caused by the double mutations in SLO-1 is likely giving rise to “low-energy traps”, from which the protein must exit in its search for the catalytically efficient region of the protein conformational landscape. Although a single such trap is shown for the sake of simplicity in Figure 6, this property is expected to be distributed across an ensemble of protein substates in the mutant proteins. Further exploration of the structures of the double mutants of SLO-1 is underway and will include X-ray studies under conditions that, we are hopeful, will allow detection of alternate protein conformers (cf. ref 11).

Figure 6.

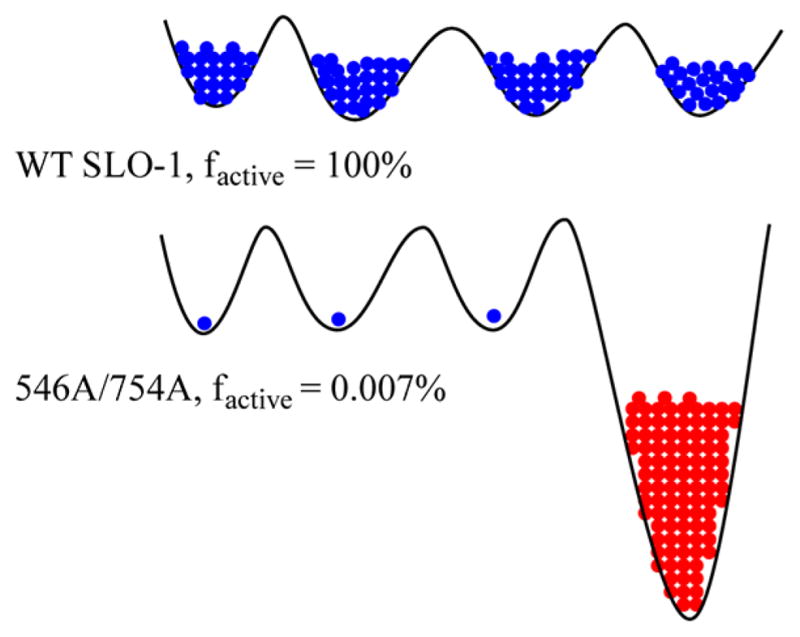
Schematic impact of deleterious mutation on the conformational landscape of SLO-1. The conformational landscape of the enzyme is shown by solid black lines with energy increasing along the vertical axis. Blue indicates active conformers and red inactive conformer(s). In the case of WT SLO-1, the enzyme molecules are fully populated in the catalytically active regions of the conformational spaces. In the double mutant, Leu546Ala/Leu754Ala, only a small proportion of the enzyme is populated in the catalytically active region of the conformational space and a significant proportion of enzyme occupies deep local minima of catalytically very slow and/or inactive conformations. For the sake of simplicity, only one deep local minimum is shown. Different conformational landscapes are expected for the free enzyme (controlling k_cat/K_m(LA)) and the E·S′ complex (controlling k_cat). In the example shown, the fraction of active enzyme is obtained from the relative k_cat numbers.

A second indicator of the impact of the double mutation on the conformational landscape of SLO-1 comes from the magnitude of the ^Dk_cat with Leu546Ala/Leu754Ala. In initial studies of this variant, it became clear that a combination of an extremely low rate and an extremely large KIE was precluding meaningful rate measurements. Even with an HPLC method developed specifically for measuring ^Dk_cat with Leu546Ala/Leu754Ala, a huge lag in the appearance of product was observed when the activity of [11-²H₂]LA was assayed, such that no product could be detected until the samples had been incubated for hours. In general, kinetic traces for SLO-1 show small lags, generally in the range of seconds to minutes, as a small amount of substrate undergoes oxidation to the product hydroperoxide, which is needed to activate the protein by oxidation of the as-isolated ferrous form to the catalytically functional ferric hydroxide (cf. Scheme 1). The analysis of the behavior of Leu546Ala/Leu754Ala with its 11-²H₂-labeled substrate indicates a ^Dk_cat that is significantly elevated above the value for the WT and is distinct from the ^Dk_cat for the other mutants.⁵⁵ The simultaneous observation of very large reductions in k_cat/K_m(LA) and k_cat, together with a differential impact of this double mutation on ^Dk_cat/K_m(LA) and ^Dk_cat in relation to those of the WT, is difficult to interpret without invoking distinct families of conformational landscapes for free enzyme versus the E·S complex. The role of conformational selection, upon binding of a ligand to its cognate enzyme, has been elegantly formulated and demonstrated by Kern and coworkers.^56,57

DETECTION OF TUNNELING IN THE REORGANIZATION OF THE SUBSTRATE BACKBONE DURING C–H BOND CLEAVAGE

Once the C–H bond cleavage step of SLO-1 had been isolated and characterized, it became of considerable interest to consider the role of the nontransferred atoms within the backbone of the substrate. To this end, an NMR assay of both ¹³C KIEs and remote secondary ²H KIEs was pursued.³⁸ In both instances, these studies involved competitive studies, between the reaction of either ¹²C and natural abundance ¹³C, or using substrate that had been modestly (4%) deuterated at vinylic positions 9 and 10 and positions 12 and 13 of the substrate (Scheme 3). The fact that competitive KIE measurements can only access effects on k_cat/K_m(LA), when coupled with the observation that this parameter is complex and only partially limited by C–H bond cleavage in SLO-1 made it necessary to “extract” the magnitude of the intrinsic carbon and remote secondary KIEs (KIE_int). In the case of the reaction of the protio substrate with SLO-1, this was achieved following correction of measured KIEs (KIE_obs) for the contribution of kinetic complexity⁵⁸ according to eq 3 and a previously determined value for C_f:³⁸

Scheme 3. Summary of Experimental and Computational Secondary Deuterium KIEs at Positions 9, 10, 12, and 13 of LA.^38a.

^a(A) Reaction of [11-H₂]LA, corrected for kinetic complexity. (B) Reaction of [11-²H₂]LA. (C) Computed KIEs using an optimized structure for LA bound to SLO-1 and the assumption of a freely equilibrated pentadienyl radical intermediate (cf. Scheme 1).

$${\text{KIE}}_{\text{obs}}=\frac{{\text{KIE}}_{int}+C_{\mathrm{f}}}{1+C_{\mathrm{f}}}$$ (3)

$$C_{\mathrm{f}}=\frac{{{}^{\mathrm{D}}k}_{\text{cat}}-{{}^{\mathrm{D}}k}_{\text{cat}}/K_{\mathrm{m}(\text{LA})}}{{{}^{\mathrm{D}}k}_{\text{cat}}/K_{\mathrm{m}(\text{LA})}-1}$$ (4)

It was also possible to obtain values for KIE_int much more directly by using a substrate that was dideuterated in the position undergoing loss of hydrogen. In this instance, the large, almost 100-fold rate reduction for deuterium transfer reduces the commitment for catalysis from ~2.5 to 0.03, a value smaller than the experimental error of the measured numbers.

Scheme 3 shows the resulting secondary deuterium KIEs, in comparison to computed values that depend solely on changes in force constant as LA is converted to the pentadienyl radical intermediate upon hydrogen atom abstraction from position 11 (cf. Scheme 1). These calculations assume a symmetrical distribution of the intermediate free radical over positions 9–13, with the additional imposition of a restriction in the electronic distribution only bringing the computed KIEs closer toward unity. While the manipulations needed to extract the intrinsic KIEs from the experimental values for reaction of the protio substrate inflate the errors, the final values for reaction of either [11-H₂]- or [11-²H₂]LA are remarkably similar to one another. The only experimental value that is within error of the computed KIEs is at position 13, which is where the enzyme directs the insertion of molecular oxygen (Scheme 1). In the original publication of these results, a number of mechanistic possibilities were considered for the significantly inflated secondary KIEs at positions 9, 10, and 12 (average KIE = 1.24). Quite significantly, only when the secondary KIE was treated in a fully quantum mechanical manner, as initially proposed by Jortner and co-workers for electron transfer⁵⁹ and extended to an enzymatic reaction by Roth et al.,⁶⁰ was it possible to reproduce the experimental findings. The following model has emerged for SLO-1. First, the substrate is strongly anchored at position 13 for its subsequent stereo- and regioselective reaction with O₂, and second, the atoms at positions 9, 10, and 12 undergo a collective tunneling motion that converts substrate to the free radical intermediate. The magnitudes of the measured carbon KIEs, though smaller and with larger errors, fully support this conclusion of tunneling within the substrate backbone.³⁸

CONCLUSIONS

The studies summarized here illustrate how the stepwise analysis of each facet of the SLO-1 reaction mechanism has altered our thinking about enzyme catalysis. Although large primary KIEs had intermittently been reported for solution reactions, these were often attributed to experimental artifact and, hence, generally disregarded. The relative simplicity of enzyme reactions, defined environments and, most often, single reaction paths, made it possible to establish the phenomenon of “deviant” KIEs, i.e., values that greatly exceed semiclassical predictions at room temperature. A second major insight for SLO-1 came from the finding of a small temperature dependence of the KIE, which could not be interpreted in the context of ground-state differences in zero-point energy or tunneling corrections (Figure 1A, B). This was a fortuitous turn of events, as very small temperature dependences of KIEs have turned out to be signature features of enzyme-catalyzed C–H bond cleavage reactions.¹³ It has, thus, been possible to extend the interpretations of the behavior seen in SLO-1 to enzymes that exhibit much smaller, “semi-classical appearing” KIEs.^12,13,17

The importance of protein dynamics subsequently emerged from attempted mathematical modeling of the kinetic properties of SLO-1 and its mutants. Initially, the focus was on the impact of active site mutants with regard to the placement between the H-donor and -acceptor for optimal wave function overlap. The most robust model to emerge from this behavior, both in SLO-1 and in mutants of other C–H bond activating enzymes, is the introduction of a temperature-dependent distance sampling coordinate that is also sensitive to the isotope labeling at the C–L bond and transiently restores the tunneling-ready donor–acceptor distances within perturbed active sites^21,22 (Figure 2C). A caveat of this phenomenon is the ability of native enzymes to achieve, in a manner independent of the C–L bond labeling pattern, very short donor–acceptor distances (the origin of temperature-independent KIEs). This requires a second class of motion, termed conformational sampling (Figure 4), which has, more generally, been discussed in the context of all classes of enzyme reactions.¹⁰ Though conformational sampling is increasingly accepted as a critical aspect of enzyme function, the direct experimental link of such behavior to bond-breaking and -making steps has been difficult. Once again, the pursuit of KIEs, both in native SLO-1 and via the introduction of double mutants, provides experimental support for the contribution of protein conformational landscapes at the stage of substrate binding and during the subsequent C–H bond activation step.

At this juncture, it is valuable to step back and to inquire how the models that describe SLO-1 and other C–H bond activating enzymes relate to the earlier theories of enzyme catalysis originally advanced by Pauling¹ and greatly elaborated by Jencks.⁶¹ The models of Pauling and Jencks noted the importance of achieving active site configurations with a large number of potential interactions between the protein and substrate, with these interactions becoming optimal at the position of the transition state. The presence of a constellation of active site residues was subsequently related to a very large reduction in the entropy of activation for the enzyme reaction in relation to a comparable model reaction.⁶² The presence of remote interactions, in particular between the substrate and enzyme, has also played a central role in understanding the generation of very large rate accelerations.⁶¹ All of these properties can be understood in the context of a family of interconverting protein conformers that differ in the extent to which the enzyme–substrate active site interactions (hydrophobic, H-bonding, dipole–dipole, point charges, DADs, etc.) are optimized.¹⁷ It is expected that there will be a subset of protein conformers for which the majority (or all) of the potential interactions can be realized simultaneously. These states are reached via a thermal excitation of the heavy atoms within the protein backbone and side chains and are distinct from the dominant ground state that is generally visualized by X-ray crystallography. It is these alternate and transient ground-state structures that provide an environment suitable for very rapid bond cleavage events. The strength of binding of the substrate to the enzyme within the reactive substates will be enhanced relative to that of the dominant E·S complex, but these substates have stable chemical bonds and thus are still considered ground states (cf. ref 63). The fact that enzymes are generally very large, in relation to the size of their active sites and substrate-binding pockets, may be an evolutionary consequence of their need to sample, on a wide range of submillisecond time scales, a family of protein substates, only some fraction of which will permit bond cleavage to proceed rapidly. From these considerations, it can be seen that there are many similarities between the older and more recent theories, though there remains the fundamental difference that the earlier models were focused on the reactivity of “static” E·S complexes. There are additional concepts, however, that appear to be significantly different between tunneling and classical transition-state stabilization models. These include the importance of barrier width, not just a reduced barrier height, as well as the ability of enzymes to achieve highly compacted active sites as a result of their dynamical excursions.

This is an exciting time for enzymology. Contrary to comments made several decades ago, the origin of enzyme catalysis is hardly a closed book. As in any scientific endeavor, new data require a revision of entrenched concepts, while methodological advances allow probing at increasingly sensitive levels of understanding. While a period of disagreement and “deconstruction” may have appeared to dominate this field in recent years, the possibility of a revised consensus has begun to emerge.

ABBREVIATIONS

SLO-1

soybean lipoxygenase-1

KIE

kinetic isotope effect

LA

linoleic acid

DAD

donor–acceptor distance

WT

wild-type

ht-ADH

high-temperature alcohol dehydrogenase

HPOD

13(S)-hydroperoxy-9(Z),11(E)-octadecanoic acid