Identifying Regions Based on Flexible User Defined Constraints

Abstract

The identification of regions is both a computational and conceptual challenge. Even with growing computational power, regionalization algorithms must rely on heuristic approaches in order to find solutions. Therefore, the constraints and evaluation criteria that define a region must be translated into an algorithm that can efficiently and effectively navigate the solution space to find the best solution. One limitation of many existing regionalization algorithms is a requirement that the number of regions be selected a priori. The max-p algorithm, introduced in Duque et al. (2012), does not have this requirement, and thus the number of regions is an output of, not an input to, the algorithm. In this paper we extend the max-p algorithm to allow for greater flexibility in the constraints available to define a feasible region, placing the focus squarely on the multidimensional characteristics of region. We also modify technical aspects of the algorithm to provide greater flexibility in its ability to search the solution space. Using synthetic spatial and attribute data we are able to show the algorithm's broad ability to identify regions in maps of varying complexity. We also conduct a large scale computational experiment to identify parameter settings that result in the greatest solution accuracy under various scenarios. The rules of thumb identified from the experiment produce maps that correctly assign areas to their “true” region with 94% average accuracy, with nearly 50 percent of the simulations reaching 100 percent accuracy.

1 Introduction

Regions are a fundamental geographic concept. A region is a categorization of space such that entities within one region are in some way distinguished from other entities that lie outside the region (or in a different region) (Montello, 2003). Typically, entities within a region share one or more properties and these are delimited through the setting of physical boundaries, a process called regionalization. Regions are widely used in both the physical and social sciences—if one is speaking of a river delta or an urban neighborhood, one is implicitly invoking the concept of region.

While the definition of a region is straightforward, the process of regionalization is not. Regionalization is a computationally intensive technique because of its combinatorial nature—other than for trivially small problems, a brute force assessment of all possible spatial partitions is computationally intractable. Moreover, while the properties that define regions are often clear, these criteria can be difficult to translate into an operational form (Spielman and Logan, 2013). It is relatively easy to list the socioeconomic characteristics of a neighborhood, but it is difficult to develop an algorithm that given multiple inputs can precisely and accurately identify the spatial extent of any particular neighborhood. Galster (2001) called a method to “unambiguously, meaningfully bound urban neighborhoods” a “holy grail” of social science (p. 2113).

Part of the difficulty in identifying regions is that they are fundamentally a human concept; while regions unequivocally exist, their existence is a product of the human mind. Few would argue that the Mississippi River Delta is a region with unique social and ecological properties. However, even experts on the Mississippi River Delta might disagree on the exact geographic boundaries which include the socio-ecological elements that define the region. One cannot touch a region as one can touch a tree, and this ambiguity has led to efforts in philosophy to understand the ontology of regions (Smith and Mark, 2003; Bittner and Smith, 2003; Casati and Varzi, 1996). As Smith and Mark (2003) suggest, while traversing space it can be difficult to identify the precise point at which one leaves one region and enters another.

This paper uses the term ‘regionalization’ to refer to a computational process through which a user provides input data to an algorithm that categorizes this data subject to a spatial constraint and returns a map of regions. Given this definition there are many algorithms and resulting computer programs that partition space into regions (e.g. Openshaw, 1977; Murtagh, 1992; Martin, 2002; Guo, 2008; Logan et al., 2011; Duque et al., 2012; Spielman and Logan, 2013; Duque et al., 2013b). While these algorithms have different properties and strengths, few have been evaluated on their ability to correctly identify “real” or “true” regions. Ontological questions about the nature of regions make it difficult to evaluate regionalization output (Gordon, 1996). If the truth is not known, or is simply not knowable it is hard to say if an algorithm's partition of space into regions is “right” or “wrong.” Of course if a researcher knows the boundaries of the regions he/she would not need a computer to preform the regionalization. However, it is important to know if, and under what conditions, computational regionalization algorithms return the optimal map from a large list of possible maps. Validating the efficacy of computational regionalization is one of the key contributions of this paper.

Regionalization is complicated by the fact that most computer routines require a user to identify the number of regions a priori. For example, one must specify the number of groups (k) prior to identifying the groups using the k-means clustering algorithm or the AZP regionalization algorithm (Openshaw 1995). Similarly, in a hierarchical clustering algorithm such as REDCAP (Guo 2008), the user must choose the level for cutting to get a final solution. When k is a key part of the solution, say in a political (re)districting problem where the number of seats is fixed, then there exist a wealth of regionalization options (Ricca and Simeone, 2008). However, when the criteria that define a region are clear, it can be entirely unclear how many regions exist within a study area.

This paper extends and generalizes the max-p algorithm (Duque et al., 2012), an algorithm that treats the number of regions endogenously. That is, the number of regions is not directly selected by the user, rather the user specifies criteria that define a region, and regions that optimally satisfy the user's criteria are returned. This approach has the advantage of being rooted in substantive characterizations of regions instead of an a priori selection of the number of regions. Subject to these criteria the algorithm maximizes the total number of regions in order to preserve as much geographic detail from the input data as possible. Our extensions to the max-p algorithm include broadening the types of possible constraints on region feasibility and implementing additional stopping criteria during the heuristic improvement phase. We evaluate the algorithm's ability to correctly identify the spatial extent of regions using synthetic datasets and maps of varying size and complexity. In these synthetic datasets there is no uncertainty about the boundaries of regions; because the boundaries of regions are known it is possible to evaluate the modified max-p algorithm's ability to correctly identify regions under varying conditions. We find that the modified max-p algorithm returns regions that over a large parameter space are 84 percent accurate on average, with many parameter settings reaching 100 percent accuracy.

2 Background

Regionalization algorithms fit within the much broader field of clustering algorithms. Regionalization covers the subset of clustering algorithms designed specifically for two-dimensional spatial data. As such, a contiguity constraint restricts the possible partitions of the data to those in which each observation within a cluster is a neighbor to at least one other observation in the cluster. The contiguity relationships can be codified as a graph where nodes are observations and links signify that the two endpoints are neighbors, or as an n × n array where non-zero cells indicate a neighbor relationship between the associated row and column observations. The graph conceptualization may be more intuitive since every partition of the observations can be viewed as resulting from removing links from the graph. In this sense, the number of possible solutions depends on the density of the neighbor relationships between observations. Keane (1975) compares the unconstrained case¹ to the opposite extreme in which all observations are arranged in a chain, meaning that each observation has two neighbors, except the ends, which have one. For example, there are 15 ways to partition six observations into five clusters for the unconstrained case, but only five for chain case. But this difference explodes as the number of observations increases—for ten observations partitioned into five clusters there are 42,525 possibilities for the unconstrained case, but only 126 for the chain spatial arrangement. Real world regionalization problems will lie somewhere between these extremes, but Keane (1975) hints at the importance of the configuration of input areas to the size of the solution space. Detailed reviews of the regionalization literature can be found in Fischer (1980), Murtagh (1985), Gordon (1996) and Duque et al. (2007).

One of the key challenges facing empirical researchers interested in clustering algorithms in general and regionalization algorithms in particular is the choice of the number of clusters, k. This requirement raises one of the central problems in cluster analysis. Openshaw et al. (1980) (p. 421) observes that arbitrary decisions about k can shape results, and decisions about k are often framed in terms of a desired level of generalization. Nearly all existing clustering and regionalization methods require k as part of the starting conditions for the algorithm. For substantive problems where k is fixed, there are myriad options for the assignment of observations to groups. When k is not fixed, post-processing approaches can be applied to any of these algorithms to compare the solutions resulting from different values of k. Nearly 30 years ago, Milligan and Cooper (1985) compared 30 procedures for determining the number of clusters, a study if undertaken today would require an even larger set (e.g. Kaufman and Rousseeuw, 1990; Yan and Ye, 2007).² However, these a posteriori approaches to finding k compare final solutions on the observations as opposed to the original units themselves—they involve comparisons of solutions, but do not include information on the intrinsic nature of the regions based on the problem domain.

The max-p-regions problem introduced in Duque et al. (2012) is a specific case within the broader class of p-regions problems (Duque et al., 2011). The p-regions problem is concerned with finding the optimal partitioning of n small areas into p spatially contiguous regions according to some objective function, where p is analogous to k in the broader clustering literature. The max-p-regions problem imposes the additional goal of maximizing p, given a constraint. By endogenizing the magnitude of p, the user must put substantive constraints on the characteristics of a region in lieu of arbitrarily choosing the number of output regions a priori.

Some of the classic p-regions problems such as political districting do not fit the max-p domain. In redistricting the number of congressional or city council districts is fixed. Similarly, redefining fire service coverage areas in light of population growth when no new stations are budgeted is not a max-p-regions problem. In contrast, the max-p approach is ideally suited to developing optimal geographic supports for spatially varying statistical estimates. For example, disease incidence rates are notoriously volatile. Even when 100 percent of the disease cases are known, in areas with a small population these rates are susceptible to misinterpretation due to spikes in the rate when a small area increases from say one to two cases of disease (Anselin, 2006). In this case max-p, as described by Duque et al. (2012), can be used to construct regions that are demographically coherent and sufficiently large that small increases in disease prevalence do not cause large spikes in disease rates. Similarly, data from population surveys that employ random or quasi-random sampling strategies are often used to produce demographic and economic estimates for geographic tabulation areas, such as census tracts. The size of these tabulation areas affects data quality, the spreading of a sample across a large number of tabulation areas increases the margin of error on the resulting estimate bringing into question how well estimates reflect the areas they are supposed to represent. In the U.S. context this is why census tracts are used more often for applied social-science and policy than census block groups. Again, in this case aggregating areas into regions would help stabilize the results, and make inferences based on these regions more reliable.

The Duque et al. (2012) solution to the max-p problem relies on each region exceeding some threshold on a spatially extensive variable such as number of persons or number of housing units. For example, each “market area” must have at least 20,000 households to meet minimum demand requirements. When this threshold is combined with a spatial contiguity constraint, the algorithm is able to endogenously partition the physical space into regions that all meet or exceed the user defined threshold. In this paper we extend the max-p algorithm to a wider set of optimization challenges—to challenges where regions must meet multiple constraints and where an ideal region can be evaluated on multiple criteria. We further offer additional rules for identifying when the algorithm should stop seeking further improvements.

3 General Framework

At its core, the solution to the max-p problem is a two phase approach. The first phase makes repeated attempts, from different random starting points, to find the maximum number of feasible regions, where a feasible region must meet a set of user defined constraints. These constraints can come in the form of a minimum or maximum population threshold for each region, or other thresholds that capture key benchmarks that a feasible region much achieve. As we discuss below, constraints should be selected to not result in trivial solutions. The solution from the first phase is then passed to an improvement phase that swaps areas, one at a time, between neighboring regions. In this phase all possible single swaps that maintain an overall feasible solution are enumerated and the best swap, as determined by user defined evaluation criteria, is selected. Evaluation criteria could include maximizing compactness or attribute homogeneity of each region. This process continues until a stopping criterion is met. In this section we first define the three parts of the problem domain: spatial constraints on the system, constraints on the set of possible spatial partitions and criteria for evaluating feasible partitions. We follow this with a detailed exposition of the two phase solution.

3.1 Generalized max-p-regions Problem

The Duque et al. (2012) solution to the max-p problem is both innovative and elegant. While this solution is flexible, it is only applicable to a certain subset of spatial problems. We follow much of their notation and description in this formal expansion of the problem.

Organization of Space

Let A = {A₁, A₂, …, A_n} define a set of n areas, each of which is a polygon with positive area, and |A| = n.

Let W define the unweighted undirected contiguity graph associated with A such that an edge exists between nodes A_i and A_j if A_i and A_j are spatially contiguous. The edges of W can be defined based on A_i and A_j sharing at least a single point, i.e. queen criterion, or sharing at least a non-zero length border, i.e. rook criterion. If W is disconnected, let D = {D₁, D₂,…, D_u} define its u subgraphs.

Let P_p = {R₁, R₂,…, R_p} define a partition of A into p regions, where |D| ≤ p ≤ n, and:

$$\begin{array}{c}|R_k|>0\text{for}k=1,2,\dots ,p;\\ R_k\cap R_{k^{\prime }}=\varnothing \text{for}k,k^{\prime }=1,2,\dots ,p,\text{where}k\ne k^{\prime };\\ \underset{k=1}{\overset{p}{\cup }}{R}_k=A\\ W(R_k)\text{is connected for}k=1,2,\dots ,p.\end{array}$$

The above definitions state that a partition must contain regions of at least one area each, regions must be non-overlapping, regions must fill the entire space, areas within each region must be connected and regions cannot span disconnected subgraphs.

Constraints

Let C = {C₁, C₂,…, C_t} define a set of t constraints on the feasibility of each R_k, where t ≥ 1. Therefore, a feasible partition of A is any P_p where R_k satisfies C_s for k = 1, 2, …, p and s = 1, 2, …, t. This implies that a feasible partition can occur if and only if each C_s in C cannot result in a violation of |D| ≤ p ≤ n. Later we will discuss constraints that violate |D| ≤ p ≤ n, and also those that result in feasible yet trivial partitions of A. Let Π define the set of all feasible partitions of A.

Evaluation Criteria

Let G = {G₁, G₂, …, G_e} define a set of e criteria to evaluate any P_p in Π. Let G̃(P_p) define the realization of G(P_p), where G̃(P_p) combines the e criteria in G such that $\stackrel{\sim }{G}(P_p^{\prime })<\stackrel{\sim }{G}(P_p)$ indicates that $P_p^{\prime }$ is a better solution than P_p.

Solution

A solution to the max-p regions problem can then be defined as a partition of A that maximizes the number of regions, |P_p|, subject to the constraints, C, and that minimizes the evaluation criteria, G. Stated formally: find $P_p^{\ast }$ such that $|P_p^{\ast }|=max[|P_p||P_p\in \mathrm{\Pi }],$ and $\nexists P_p\in \mathrm{\Pi }:[|P_p|=|P_p^{\ast }|\text{and}\stackrel{\sim }{G}(P_p)<\stackrel{\sim }{G}(P_p^{\ast })]$.

3.2 Solving the max-p-regions Problem

The broader p-regions problem, of which the max-p-regions problem is a member, is a non-deterministic polynomial-time hard (NP-hard) problem, which is prohibitively large for an evaluation of all possible partitions (Duque et al., 2011). We extend the Duque et al. (2012) approach, which resolves the size problem by proposing a two phase heuristic solution composed of an initialization phase that searches for the maximum number of regions and an improvement phase that improves the best solution from the first phase. Both approaches generally follow the high level outline put forward in Fischer (1980).

3.2.1 Initialization Phase

In the initialization phase, areas are joined together to form regions. Regions are built one at a time by joining connected areas until the region meets all the criteria. This means that a region can be made up of one or more areas. The phase begins by selecting one area from the set of all areas. This area forms the seed of the region; if the region satisfies all constraints in C, then this region is finalized. If the region fails any constraint, then a contiguous area is added to the region, where the added area cannot already be assigned to a region. The revised region is again tested against C, with the process repeating until the region is feasible, i.e. satisfies C. Once a feasible region is found, a new seed is drawn from the set of areas not already assigned to a region, and the region building process repeats. Once no additional regions can be formed, the remaining unassigned areas are joined to existing regions to which they are contiguous, with the expanded regions tested against C as each new area is added.

The initialization phase is repeated many times in an attempt to find a partition with the highest number of regions (p). To speed up the initialization phase, region seeds and contiguous areas to join to them are chosen randomly. This allows for completing say 100 repetitions in a relatively short time. A new partition $P_p^{\prime }$ would only be retained if $|P_p^{\prime }|>p^{\ast }$, where p* is the largest p seen to that point. In the case of $|P_p^{\prime }|=p^{\ast },$ one could either retain all partitions with the maximum number of regions or select that partition with the lowest G̃. The initialization phase is defined formally in Figure 1.

Figure 1. Generalized max-p Initialization Phase.

The constraints play the key roll during the initialization phase by determining which areas can be feasibly joined together into a region. A minimum threshold on a spatially extensive variable, e.g. number of persons or number of households, is the most straightforward constraint to apply. The strictly additive nature of the initialization phase meshes well with a lower bound constraint—adding an additional area to a region will always result in a count greater than or equal to the count prior to the addition. A feasible solution can always be found if the threshold is set to any value less than or equal to the total in the smallest component. It should be noted that a very low threshold, say zero, would always result in the trivial solution of |P_p| = n.

An alternative constraint would be to set a maximum threshold on a spatially extensive variable. As should be clear from the initialization phase as described above, any constraint of this type that would allow for |D| ≤ |P_p| ≤ n would necessary result in |P_p| = n.³ However, if this constraint is used in combination with the minimum count constraint, say to create a population window through which all regions must fit, then a trivial solution will not necessarily be the result. As one considers more exotic constraints, the ability to find feasible partitions of the space may become more difficult. Say Π₁ represents those P_p feasible under C₁ and Π₂ those feasible under C₂, it is entirely possible that Π₁ ∩ Π₂ = ∅. If the constraint was instead that the region's average income had to be above (or below) some threshold, then each additional area could either increase or decrease the average for the region. Again, too many or too restrictive constraints could result in no possible feasible partitions or so few that a heuristic algorithm would have a difficult time finding them.

3.2.2 Improvement Phase

The result of the initialization phase is then passed to the improvement phase.⁴ In this phase, each area's region assignment can be swapped to improve the evaluation criteria. The first step is to identify the set Π^max, which contains all feasible partitions of A that can be reached by moving a single area from one region to another, while maintaining p^max regions. This is a highly constrained subset of Π since 1) only the A_i on the edges of regions can be reassigned, and 2) each reassignment must not result in the violation of any constraint or a change in p. Each partition in Π^max is then evaluated against the set of criteria in G, and the best partition is chosen. This process is repeated so as to find the lowest G̃.

This second phase is largely driven by the evaluation criteria, of which there could be many. The concept of within region “similarity” (Tversky, 1977) is immediately appealing as a criterion. Minimizing the global sum of squared deviations (SSD) on various attributes on the areas within each region can capture internal homogeneity. This could be augmented or replaced by maximizing the SSD between regions to maximize the heterogeneity between regions. Martin (2002) implements the intra-area correlation statistic in an effort to combine the within and between region criteria. Another option could focus on maximizing the compactness of the regions (Li et al., 2013). A challenge in any multi-objective environment is the allocation of importance between the various criteria, usually manifest in some weighting of the criteria. Equal weighting is the most straightforward, but may not reflect the problem domain. This is further compounded by the sensitivity of the final solution to the various evaluation criteria.

The improvement phase is like many other optimization problems that attempt to min­imize some evaluation criterion subject to a set of constraints. As such it is susceptible to becoming trapped in a local minima, as measured by G̃. If a simple steepest decent type approach is taken, the algorithm would stop if there were no partition in Π^max with a lower G̃ than that from the previous iteration. Duque et al. (2012) test a number of common strategies for escaping from local minima. In general these strategies allow the partition to temporarily become “worse,” as measured by G̃, in the hope of finding a path to a partition with an even lower G̃. They find that the tabu search performs the best for the max-p-regions problem (see Openshaw and Rao, 1995; Ricca and Simeone, 2008, for other evalutions of local search approaches in the regionalization context). A tabu search maintains a memory, a simple list, of partitions that are ineligible. After each iteration the tabu list is extended to reflect the best feasible partition in Π^max, whether or not the partition is an improvement on the current best G̃. Once the list has reached its maximum length, T*, each new element added to the end of the list pushes the first element off the list. Partitions on the tabu list are ineligible for consideration.

Glover (1990) outlines a number of approaches for implementing a tabu search. We implement a two stage tabu search—the first is a diversification stage intended to explore a wide range of the search space, and the second is an intensification stage aimed at finding the best solution in the general vicinity of the best result from the wide search.

At each iteration, one area (A_i) is moved from its current region (R_orig) to a neighboring region (R_neig). During the diversification stage the tabu list is extend to disallow any partition that includes A_i being situated in R_orig—in effect saying that A_i cannot return to R_orig until after T* other moves have occurred. This is one element added to the tabu list, but it excludes many possible partitions of A. This stage prevents the algorithm from back tracking for the duration of T* in a relatively aggressive way, and thus encourages the algorithm to explore partitions quite different from its starting point. Since this approach could be overly aggressive, we add an aspirational criterion (Glover, 1990) that will override the tabu list. If a partition is found that improves the best G̃ seen so far, the partition is accepted whether or not it is in the tabu list.

The improvement phase has three stopping criteria. The first is a maximum number of moves that improve G̃. The improvement phase can continue to iterate in search of a better partition until it has reached this fixed value. This simply acts as a constraint on time allowed to run the algorithm since it implies that further improvements could be found by continuing down this path. The second criterion is the maximum number of consecutive moves that do not improve G̃. At each iteration of the tabu search the best available partition is accepted, but this may not improve G̃. A long chain of non-improving moves could imply that the global minimum has been found or that the current path has found some local minimum from which it cannot escape—in either case it is futile to continue searching for better partitions of the space. In the examples presented later using simulated data we are able to distinguish between these two scenarios, however in empirical situations one will not know if they have found a global or local minima. The third criterion considers the marginal benefit of continuing the search. If the algorithm is finding improving solutions, but the gain from each improvement is negligible, then this marginal improvement criterion will stop the algorithm. In the experiment presented later we compare the current G̃ to that from ten iterations previous to avoid being misled by a single very small improvement.

If the second or third criterion is reached in the diversification stage, the algorithm shifts to the intensification stage of the tabu search. The intensification stage builds a tabu list containing single partitions. When A_i is moved from R_orig to R_neig, the entire originating partition is added to the tabu list. This restricts the return to an entire partition, but could allow A_i to return to R_orig as long as there is at least one intervening move. This is an intensification because it targets individual partitions, and allows areas to swap in and out of regions more rapidly. The aspirational criterion is irrelevant in this stage since each partition in the tabu list will be greater than (i.e. worse than) G̃*. The second phase is detailed in Figure 2.

Figure 2. Generalized max-p Improvement Phase.

4 Experiment: Accuracy and Parameter Space

In applied settings neither the number of regions nor their boundaries are known. Furthermore, the regions themselves are likely to be domain dependent. Park (1925) noted that neighborhoods in Chicago could be drawn based on political affiliation, culture or the physical environment each of which might yield different sets of neighborhood boundaries. This implies that for empirical data there is no single partition that is correct for all applications (Openshaw, 1983).

While computationally intensive, it is relatively easy to automatically partition a study area, but it is difficult to evaluate the veracity of any particular partition. A regionalization is “correct” or “accurate” if each constituent area is assigned to the appropriate region. In practice, however, the correct region may not be known or only identifiable subjectively. Thus, we create a series of synthetic datasets (scenarios) of varying complexity, with “true” regions that can be objectively identified. For any given scenario the intra-region variance is minimized by the correct assignment of areas to regions. We then conduct a large scale computational experiment in which we examine the ability of the algorithm to identify the “true” regions under various parameter settings and input data complexity. A five dimensional parameter space is explored and for each scenario the “accuracy rate” is recorded. These experiments demonstrate the utility of the proposed approach and its sensitivity to parameters across a wide set of study areas with varying complexity.

4.1 Input Data Scenarios

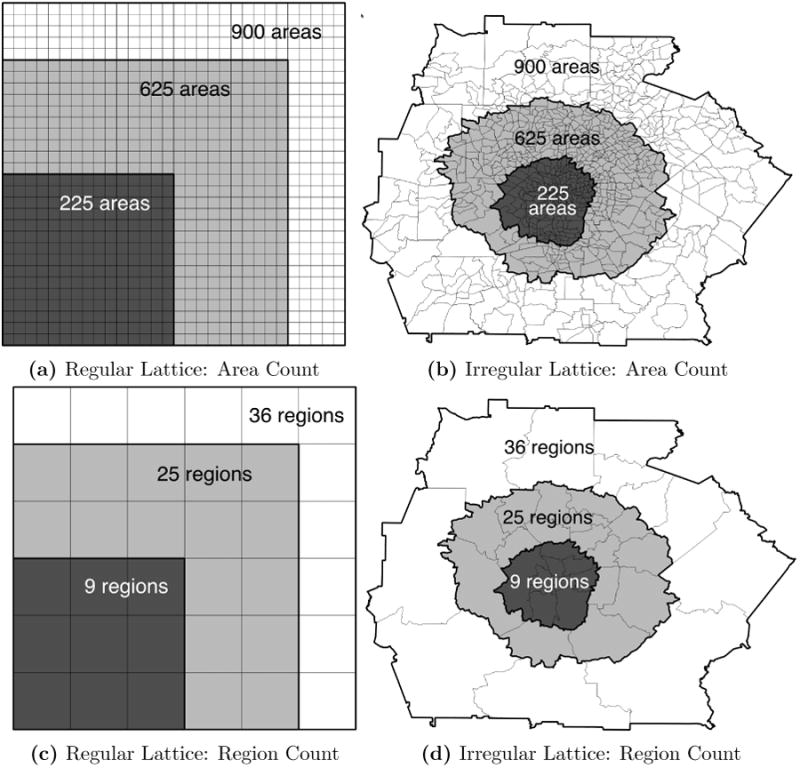
In the synthetic datasets we vary five dimensions, two relating to the spatial aspects of the problem and three relating to the attribute data. The input data scenarios range from a stylized representation of the problem to something more closely resembling actual empirical data. The first spatial dimension is the size of the input map in terms of the number of areas being partitioned. We use three study area sizes: 225, 625 and 900 areas. In the context of metropolitan statistical areas (MSAs) and census tracts these three regions roughly correspond to MSAs such as Salt Lake City, Utah, St. Louis, Missouri and Atlanta, Georgia respectively. The second spatial dimension considers the spatial relationships between areas. We do this by constructing “regular” and “irregular” lattices (see Duque et al., 2013a, for background on this approach). The regular lattices are square with dimensions 15 × 15, 25 × 25 and 30 × 30, and the irregular lattices are subsets of tract boundaries from the Atlanta MSA.⁵ These two dimensions result in six unique spatial arrangements, or maps (see Figures 3a and 3b). In both cases we use the rook criterion for defining relationships between areas, meaning that for the regular lattice all areas on the interior of the map have exactly four neighbors. In contrast, the 900 area irregular lattice has an average of 5.5 neighbors per area, with a minimum of two and a maximum of 12 neighbors. For each map we define true regions of 25 areas each, which translates to 9, 25 and 36 regions for the respective input maps. For the regular lattice these are simply 5 × 5 square regions equally distributed in the space; in the irregular case we partition the map into regions. As can be seen in Figure 3d the irregular regions are relatively compact, but most regions have some areas with only a single linkage to other members of their “true” regions.

Figure 3. Simulated Study Areas and Regions.

The remaining three dimensions relate to the attributes for each area. The first attribute dimension controls the total population variable on each area. The simple case assumes all areas have a population of exactly 2000. The varying case randomly assigns a count of 1000, 1500, 2000, 2500 or 3000 to each area within a region, constraining each count to five areas. This means that each region has a total count of 50,000 under either case. We refer to these as the “constant” and “varying” population scenarios. The second attribute dimension tests the cases of one, three and nine attributes on each area. The final attribute dimension assigns values to each attribute. Each attribute's values range from 1000 to (p + 1) × 500 at increments of 500. The values are assigned to areas so that all areas in the same region get the same value. This process is repeated for each attribute, which results in homogeneous regions with one, three or nine attributes. To introduce more realistic cases, we jitter the data. The magnitude of the jitter is drawn from a uniform distribution of ±50 or ±100 around the raw attribute value (labeled 10 or 20 percent in the graphics that follow). The magnitude of the jitter creates some intra-region heterogeneity, while ensuring that the true regions are the most homogeneous solutions of all possible combinations of areas. Combining all five dimensions results in 108 different input data scenarios.

4.2 Algorithm Parameters

The algorithm has two sets of user defined parameters: the constraints that each feasible region must meet (C) and the controls on the tabu search. We use a single constraint algorithm that requires choosing a minimum population size, which we set at 46,000. In an empirical setting users could presumably choose these constraints based on the research question at hand. In contrast, the tabu parameters could be perceived as nuisance parameters—artifacts of the algorithm that are somewhat separated from the substantive research objectives. A user would simply want to set these tabu parameter to get the best possible results in a reasonable time. For this reason we fix the constraint that defines feasible regions for all scenarios in the experiment, and explore possible settings for the four tabu parameters.

For the tabu list length, maximum number of improvements and maximum number of consecutive non-improvements, we generate random draws from a uniform distribution ranging from one to two times the number of areas in the study area, i.e. from 1 to 450, 1250 or 1800. The marginal improvement threshold is drawn from a uniform distribution on the range [0.0000001, 0.001].

The algorithm has two phases, the initial solution phase and the improvement phase. For each of the 108 map and attribute scenarios we use the best partition resulting from 100 iterations of the initialization phase. We then run the improvement phase 1000 times on each scenario, where each iteration is based on random draws of the tabu parameters.

In all cases, the evaluation criterion (G) is the global sum of squared deviations (SSD), which is used to measure intra-region homogeneity. Specifically, for each variable in each input area we compute the squared deviation from the region mean, we sum the variable specific SSD for each region and then sum all of the area-level SSD values to a single global value.

4.3 Accuracy Rate

For each scenario we know the true partition (P^true) and the solution partition resulting from the algorithm (P*). With this information we can compute an accuracy rate for P* as follows:

$$\text{accuracy rate}=\frac{\sum _k\underset{l}{max}[|R_k^{P^{\ast }}\cap R_l^{\mathit{\text{true}}}|]}{|A|}\forall k\text{in}{P}^{\ast },\text{and}\forall l\text{in}{P}^{\mathit{\text{true}}},$$ (1)

where k and l index regions in P* and P^true respectively. Each region in P*, $R_k^{P^{\ast }}$, is compared to each region in P^true to find its best match, where “best” is defined as the true region with the greatest overlap. In this experiment P^true = p*, therefore the minimum accuracy rate is p*/|A| = 0.04, and the maximum is 1.0. Using Equation 1 we can also compute the gain in accuracy from the improvement phase by differencing the accuracy rates from the base solution (P^base) and final solution and then dividing by the maximum possible improvement:

$$\text{accuracy improvement}=\frac{\text{accuracy rate}(P^{\ast })-\text{accurac rate}(P^{\mathit{\text{base}}})}{1-\text{accuracy rate}(P^{\mathit{\text{base}}})}.$$ (2)

The 108 scenarios provide a diverse set of conditions for exploring the robustness of the algorithm. The initialization phase itself is relatively good at partitioning the space given that it is a mostly random approach that chooses the best solution from 100 random starting points. As can be seen in the first row of Table 1, on average this random approach achieves an accuracy rate of over 60 percent. The subsequent rows in the table show that this initial average accuracy rate is relatively stable across different subsets of the 108,000 simulations. The middle columns of the table present the accuracy improvement over the initial base solution. The minimum and maximum columns show a wide range in the results from the improvement phase. All subsets have a maximum value of 1.0 indicating the algorithm is able to find the true partitioning of the space, however most have a negative minimum value meaning the solution actually got worse in terms of accuracy as a result of the “improvement” phase. In all cases the solution improved in terms of SSD in the second phase, the metric being evaluated by the algorithm during the improvement phase. However, reduction in SSD does not necessarily imply improved accuracy. For a small number of runs the second phase hit stopping criteria that yielded an improvement in SSD over the base case but a worse map in terms of accuracy. This happened very rarely, 22 out of 108,000 simulations (0.02 percent of runs), and only in the one attribute scenario. This small subset of solutions highlight the reality that in an empirical setting the algorithm must often use an often inferior metric, which in some cases can lead the algorithm astray.

Table 1. Accuracy Rate and Improvement.

	Base Accuracy		Acc Improvement Over Base				Final Accuracy		Number of Sims
	Mean	Med	Min	Mean	Med	Max	Mean	Med
overall	0.629	0.598	-0.100	0.687	0.731	1.0	0.872	0.892	108000
225 areas	0.727	0.747	-0.100	0.861	1.000	1.0	0.953	1.000	36000
625 areas	0.590	0.592	0.004	0.643	0.707	1.0	0.853	0.874	36000
900 areas	0.570	0.571	0.002	0.556	0.590	1.0	0.810	0.830	36000
regular lat	0.664	0.614	0.003	0.729	0.753	1.0	0.892	0.902	54000
irregular lat	0.594	0.592	-0.100	0.645	0.675	1.0	0.852	0.862	54000
1 attributes	0.628	0.602	-0.100	0.520	0.441	1.0	0.804	0.778	36000
3 attributes	0.630	0.597	0.000	0.737	0.747	1.0	0.892	0.899	36000
9 attributes	0.630	0.603	0.002	0.803	0.820	1.0	0.920	0.924	36000
0% jitter	0.629	0.598	-0.050	0.685	0.743	1.0	0.872	0.894	36000
20% jitter	0.629	0.598	-0.100	0.688	0.732	1.0	0.873	0.892	36000
40% jitter	0.629	0.598	-0.074	0.687	0.720	1.0	0.872	0.887	36000
constant pop	0.640	0.615	-0.100	0.700	0.747	1.0	0.879	0.901	54000
varying pop	0.619	0.594	-0.074	0.673	0.698	1.0	0.865	0.868	54000

Looking more closely at the five scenario dimensions, we see that the most important dimension is the number of attributes. The median improvement when only one attribute is used is 44.1 percent, and this rises to 82.0 percent in the nine attribute case. In the experiment there is no explicit correlation between the attributes, this means that each attribute generally provides unique information on why particular areas should be grouped together to form a region. If there is only one attribute, then it would be expected that every map would have some cases where two adjacent regions would, for example, both have relatively low values for the attribute. In contrast, it is unlikely that two adjacent regions would have similar values for all nine attributes. The greater number of attributes provides more information on each area, and thus more information on which areas should be grouped together to form homogeneous regions. In an empirical setting this lack of correlation between attributes is unlikely, a practical issue that we address in the discussion section.

In contrast, the three data jitter rates tested show far less variation in their mean or median values meaning that the algorithm's improvement capability is not greatly affected if their descriptors are not perfectly homogeneous. Combined, these are generally positive results as empirical data will certainly have variation from area to area, and multivariate analyses are more the norm than the exception. The algorithm performs better on study areas with fewer areas. For the 225 area case, the median base solution achieves nearly 75 percent accuracy, while the 900 area case starts on average at only 57.1 percent accuracy. This wide range in the initial partition accuracy to some extent masks the improvement measures in the middle columns of the table. The smallest study area has both the highest median base solution and the highest median improvement on this base. The final two dimensions, the lattice type and constant versus varying population, show the algorithm has higher success in the more stylized scenarios.

4.4 Tabu Parameter Analysis

We use a response surface approach to summarize the impact the four tabu parameters have on the accuracy rate. The logic of this approach is to fit a model as closely as possible to a set of experimental results, and then use the resulting model to examine the main parameter effects and their interactions. We code the variables following the approach laid out in Kutner et al. (2005) (chapter 30). The five dimensions describing the spatial and attribute design for each scenario enter the model as indicator variables, which are coded as -1 or 1. Lattice type (regular versus irregular) and population per area (constant versus varying) are binary variables, which result in two dummy variables. Study area size (225, 625 or 900), number of attributes (1, 3 or 9) and maximum attribute jitter (0, 10 or 20 percent) are three level indicators, resulting in six additional dummy variables.

The magnitudes of the four tabu parameters are scaled to fit on the continuous range [-1, 1] using the following coding scheme:

$$\text{coded parameter}=\frac{\text{actual parameter}-\frac{\text{high level}+\text{low level}}{2}}{\frac{\text{high level}-\text{low level}}{2}}.$$ (3)

While the coded parameters are on a fixed range, the actual parameters for maximum number of improvements, maximum number of consecutive non-improvements and tabu list length are set relative to the number of areas in the scenario. Taking the scenarios with 225 areas as an example, a coded parameter of -1 corresponds to an actual parameter of 1, 0 corresponds to 225 and 1 corresponds to 450. For the 625 and 900 scenarios the corresponding values are 1, 625 and 1250, and 1, 900 and 1800 respectively. For the marginal improvement threshold, the zero corresponds to 0.0005.

Using these input data, we fit a high order multivariate regression model, where the dependent variable is the accuracy improvement described above.⁶ The independent variables consist of the eight dummy variables and four continuous variables along with their two-way interactions. We further add the second through fifth powers of the continuous variables, resulting in a total of 95 independent variables including the constant. The pseudo R² for the model based on 108,000 simulations is 0.842. In the results that follow we use the fitted model to predict the impact of one or two tabu parameters. This is done by systematically varying the tabu parameter(s) of interest, while setting the remaining independent variables to their midpoints. Note that the dummy and continuous variable coding schemes result in each independent variable having a midpoint of zero.

The four tabu parameters can be divided into three stopping criteria and the tabu list length. Nearly three-fourths (74.4 percent) of the simulations stopped due to reaching the maximum number of non-improving moves, meaning that the algorithm found either the global minimum or a local minima from which it could not escape. For the remaining quarter, 19.1 percent stopped due to reaching the maximum number of allowed improvements, with the remainder stopping by hitting the marginal improvement threshold (6.5 percent). These latter two stopping criteria imply that more improvement was potentially available but not explored.

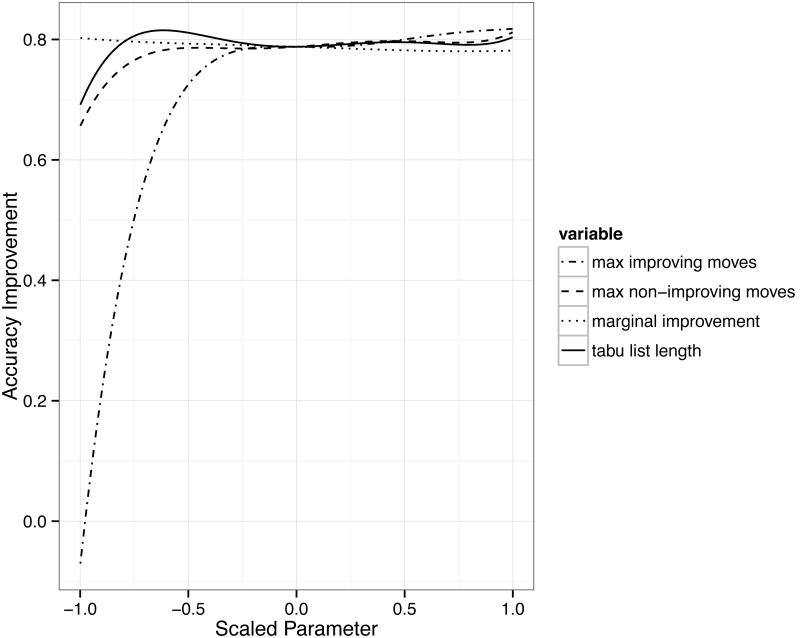
The model describes the impact the parameter settings have on the accuracy rate. Figure 4 summarizes the main effects of the four tabu parameters on accuracy rate. In contrast to what might be expected from the previous result, the parameter that provides the largest gain in accuracy rate is the maximum number of total improving moves allowed. Figure 4 shows that holding all other variables constant at their midpoints, variation in this parameter provides improvements ranging from approximately -7 to 82 percent over the base partition. This can be contrasted with the improvement gains provided by the maximum number of consecutive non-improvements, which corresponds to a range of approximately 66–81 percent improvement in accuracy (Figure 4). The interpretation of this result is that setting the maximum number of improvements too low will essentially render moot the other tabu parameters—the algorithm needs to be given a reasonable opportunity to explore the solution space in order for the other tabu parameters to influence the final result (we present interactions directly in Figure 6). The marginal improvement threshold shows even less effect on the accuracy rate, ranging from approximately 78–80 percent improvement over the range 0.0000001 to 0.001. The tabu list length, although not a stopping criterion, also influences the accuracy rate improvement. Variation in this parameter corresponds to a range of approximately 69 to 82 percent improvement. Of note here is that the maximum is not at an extrema of the parameter space, but at an intermediate point.

Figure 4. Tabu Parameters, Accuracy Rate Main Effects.

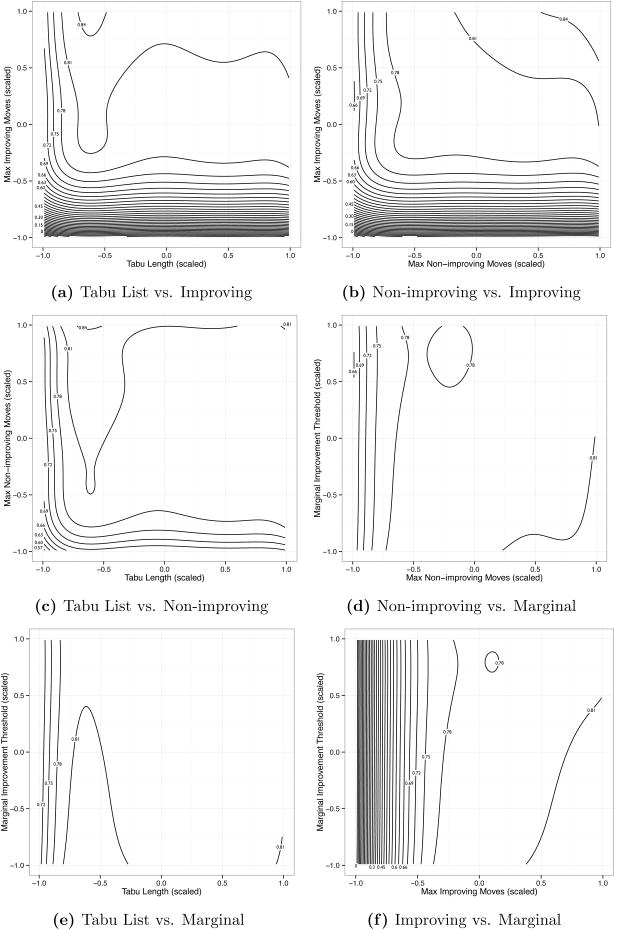
Figure 6. Accuracy Rate by Tabu Parameter Interaction.

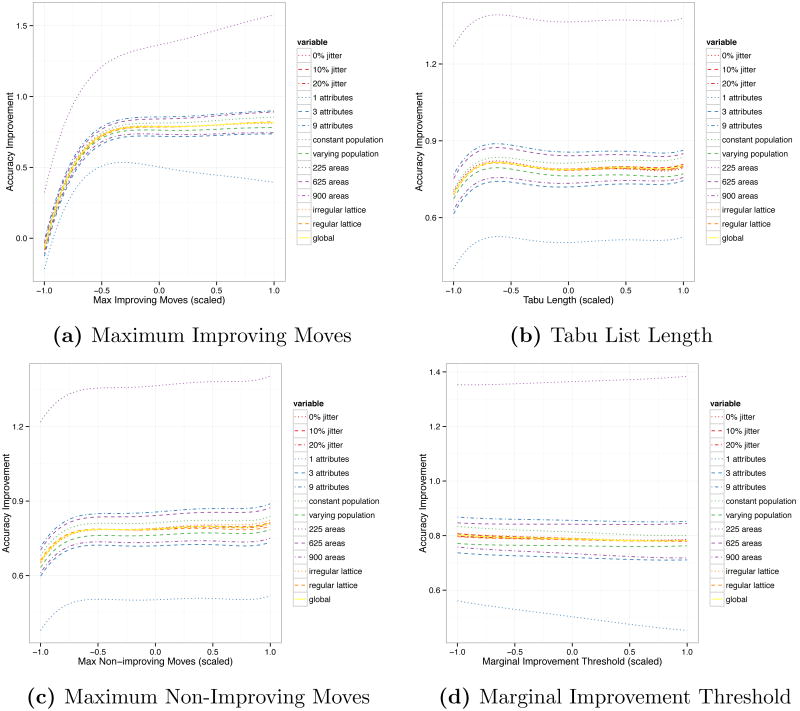
Figure 5 splits the results from Figure 4 by the 13 rows in Table 1. The most dramatic scenario is the one attribute case, which consistently shows the lowest magnitude of accuracy rate improvement. Similarly the smallest study area, 225 areas, is consistently the highest performer. The ordering of the lines is generally constant across the four plots, with crosses highlighting where the tabu parameter settings manifest themselves differently in different scenarios.

Figure 5. Tabu Parameters, Accuracy Rate Main Effects Split by Scenarios.

Figure 6 explores the pairwise interactions between the parameters. A high-level view of Figure 6 shows that tabu list length is the most challenging of the four parameters to explain. The contour plots for the interaction between the other parameters (Figures 6b, 6d and 6f) show the highest accuracy rate improvement in a particular corner of the plot. This indicates that even when the parameters are interacting, the path to choosing the level of those other three parameters is relatively clear: maximize (or minimize) them. The results in Figures 6a, 6c and 6e in contrast show that the accuracy rate improvement is maximized not at an extreme, but at an intermediate point for the tabu list length. The tabu list length should not be set too high or too low. This is clearest when comparing to the maximum number of improving moves (Figure 6a) and the maximum number of consecutive non-improvements (Figure 6c). The shapes of the contours indicate that by getting the tabu setting right, fewer improving and non-improving moves are needed to get the same results in terms of accuracy; this implies a reduction computational time and resources.

5 Discussion

The experiment systematically modeled a number of characteristics applicable to the use of the generalized max-p approach to regionalization. In this section we summarize those results and provide rules of thumb for applying max-p to empirical problems.

Regionalization, and other computationally intensive algorithms, try to codify a parsimonious set of rules and then let the data drive the final solution. This is sometimes characterised as an “objective” approach to finding a solution to the problem at hand. This is not the case however, as user intervention is critical to arriving at the solution. The previous section explored a number of the user level choices in an effort to provide guidance on the performance of the algorithm under different spatial and data arrangements, and under different parameter settings. In an applied analysis a user may not be able to control any of the scenario characteristics we tested. In this case the experiment gives guidance on parameter settings and variable selection under a fixed scenario faced by a researcher. If flexibility is available, then a slightly redesigned problem could result in much greater success.

In terms of attributes describing each area, more is better. Higher dimensionality allows the algorithm to more effectively discriminate between the areas. In the one attribute case, two distinct regions located near one another, but with similar magnitudes of the attribute are difficult to distinguish. However, adding a second, and hopefully uncorrelated attribute, could help differentiate the members of the two regions. In an empirical setting we would need to contend with correlation between the attributes and spatial autocorrelation between observations on each attribute. Attribute correlation can be addressed using a principle components type transformation to disentangle redundant information. Spatial autocorrelation however is particularly challenging in a regionalization context as it can blur the lines between regions. A multivariate approach is one avenue out of this problem, under the assumption that each attribute has a different spatial pattern.

When considering the number of input areas to regionalize, fewer areas tend to result in better solutions. Oftentimes the extent of the study area cannot be varied. However, if a researcher has knowledge that regions do not cross some barrier, the metaphorical or actual “railroad tracks” for example, then it could be possible to subdivide the study area into parts in advance. This is of course a slippery slope as one strength of automated algorithms of the type presented here is to reduce, but clearly not eliminate, biases introduced by the researcher; and in some cases uncover patterns previously outside the researcher's vision of possible outcomes.

In terms of the tabu settings, the three stopping criteria not only affect the accuracy rate, but also time, and in turn resources, devoted to the solving the problem. While in principle extreme values of these criteria result in better solutions, Figure 5 shows that beyond some point there are diminishing returns. For example, the maximum number of consecutive non-improvements reaches a near maximum at approximately 0.5 × study area size. The accuracy improvement gains for the maximum number of improvements is greatly reduced after approximately 0.75 × study area size. The marginal improvement threshold shows little impact on accuracy rate improvement. In the simulations we applied a lag of ten iterations, meaning that the current solution is tested against the solution from ten iterations previous, further exploration of this lag parameter may be warranted. The tabu list length emerges as the trickiest parameter to set. It provides the greatest impact on accuracy rate improvement at approximately 0.33 × study area size, but deviations in either direction from this peak potentially lessen the improvement from this parameter. Figure 5b indicates that erring on the shorter list length side of this peak is more detrimental than choosing too long of a list.

For all spatial and attribute scenarios and all tabu parameter settings, we find an overall median accuracy rate of 89.2 percent (mean of 87.2 percent). If we subset the results based on these rules of thumb (adding a 0.20 range around each, and ignoring the marginal improvement threshold since it had little effect): maximum improving moves between 0.75×study area size and 0.95×study area size, maximum non-improving moves between 0.40×study area size and 0.60×study area size, tabu list length between 0.33×study area size and 0.53×study area size and scenarios with more than one attribute, we find an overall median accuracy rate of 99.6 percent (mean of 94.1 percent).

6 Conclusion

We are currently in an era of unprecedented data availability and computational resources. That being said, heuristic algorithms are still necessary for solving all but the smallest regionalization problems. This means that in an empirical setting we never know if the results of our algorithms reflect the best possible result.

In this paper we use synthetic maps and data, where the true regions are known, to identify the validity and applicability of the max-p algorithm. We show that when the true regions are known, the algorithm is able to find these true regions under a number of complicating scenarios. However, its ability to find these accurate solutions depends on a number of parameters that must be set by the user. In the initialization phase of the algorithm, which requires little user intervention, the algorithm finds solutions that are on average approximately 63 percent accurate. Through a series of simulations, we identify parameter settings that can greatly improve this initial accuracy using a tabu search. Overall, the final average accuracy rate was 87 percent; and over 30 percent of simulations had 100 percent accuracy. Using the rules of thumb identified from the simulation experiment, the average accuracy rate increased to 94 percent, and 50 percent of simulations achieved 100 percent accuracy.

In the generalized version of the algorithm presented here we emphasize the strength of the approach, which is that the researcher is able to define the characteristics of a region as opposed to the number of regions. In this sense we see this as an approach well suited for discovering true regions, as opposed to approaches designed to find the best regions given a constraint on the required number of regions, e.g. in the political redistricting scenario. The max-p approach allows a researcher to identify the best regions for a particular problem domain, by varying constraints and evaluation criteria. We see this approach to region identification as one with great flexibility and broad applicability.