Airflow and Particle Deposition Simulations in Health and Emphysema: From In-Vivo to In-Silico Animal Experiments

Abstract

Image-based in-silico modeling tools provide detailed velocity and particle deposition data. However, care must be taken when prescribing boundary conditions to model lung physiology in health or disease, such as in emphysema. In this study, the respiratory resistance and compliance were obtained by solving an inverse problem; a 0D global model based on healthy and emphysematous rat experimental data. Multi-scale CFD simulations were performed by solving the 3D Navier Stokes equations in an MRI-derived rat geometry coupled to a 0D model. Particles with 0.95 μm diameter were tracked and their distribution in the lung was assessed. Seven 3D-0D simulations were performed: healthy, homogeneous, and five heterogeneous emphysema cases. Compliance (C) was significantly higher (p = 0.04) in the emphysematous rats $(\mathrm{C}=0.37\pm 0.14\frac{c{m}^3}{cm{H}_{2}O})$ compared to the healthy rats $(\mathrm{C}=0.25\pm 0.04\frac{c{m}^3}{cm{H}_{2}O})$, while the resistance remained unchanged (p=0.83). There were increases in airflow, particle deposition in the 3D model, and particle delivery to the diseased regions for the heterogeneous cases compared to the homogeneous cases. The results highlight the importance of multi-scale numerical simulations to study airflow and particle distribution in healthy and diseased lungs. The effect of particle size and gravity were studied. Once available, these in-silico predictions may be compared to experimental deposition data.

Introduction

Simulations of airflow in the lung can augment experimental knowledge and physiologic understanding only if they can accurately model in vivo respiratory conditions and anatomy. Computational fluid dynamics (CFD) can complement experimental efforts by providing information that cannot be easily measured, or by motivating new targeted experiments. Due to the vast range of length scales in the lung, complex geometry, computational cost and complex pulmonary tissue mechanics, it is currently impossible to model the lung in full. Therefore, multi-scale methods must be employed that couple realistic 3D CFD geometry of the upper structures to lower-dimensional models of the rest of the respiratory system.

Deposition in emphysematous lungs has been previously studied in human patients,⁷ animal models,⁴⁸ in vitro models,³⁶ and empirical models,⁴⁷ however several questions remain unanswered. For example compared to healthy controls, Sweeney et al.⁴⁸ found decreased particle deposition in an emphysematous hamster model, while Brand et al.⁷ found no changes in deposition in emphysematous human patients. Empirical^44,47 and experimental in-vitro models³⁶ have supported decreased deposition in emphysema. Deposition was found to increase 50 percent in COPD patients compared to healthy subjects,⁵ however the authors hypothesized that this was due to increased airway resistance in bronchitis, rather than in changes that occur in emphysema.

While prior numerical studies have investigated airflow,^3,26,33 particle deposition^12,29,35,51 and distribution¹⁶ in the lung, few have incorporated patient or animal specific geometry and breathing parameters. Airflow^17,18,32 and particle deposition^13,25,35 in the lung were shown to be highly dependent on geometry and flow asymmetry⁸. Boundary conditions that describe the upstream and downstream mechanics outside of the 3D domain must be defined on the inlets and outlets for all CFD simulations. Traditionally, constant pressure¹⁷ or flow rate^11,26 boundary conditions have been applied at the mouth or trachea. Constant pressure^17,26,46 or flow rate^11,32 boundary conditions are typically implemented at the distal airway outlets. However, as the flow patterns change in time, CFD simulations should model the breathing unsteadiness, to determine airflow³⁰ and particle¹³ deposition patterns in the lung. Thus, appropriate boundary conditions must be devised.

Multi-scale modeling techniques have been applied to numerous studies in the cardiovascular system.²⁴ However, not until recently have these methods been applied to the respiratory system.^3,27,28,30 Typically, a multi-scale numerical model includes a 3D CFD description of the large airways and a 1D³⁰ or 0D^3,28 lower-dimensional model representing the smaller airways and peripheral tissue. These models enable more realistic 3D unsteady flow simulations because they do not require direct description of time-dependent flow and pressure waveforms at the distal branches, which are typically unknown.²⁷ However proper care must be taken to accurately model lung physiology. For example, imposing constant flow or pressure boundary conditions may result in the flow and pressure being in phase and / in unrealistically low mean pressure values. Employing impedance boundary conditions in a ventilated healthy human 3D lung CFD model, Comerford et al.¹⁴ demonstrated that downstream impedance significantly influences the overall pressure field, but has little effect on the flow velocity. Additionally, while several groups^3,27,28,30 have made significant advances in multi-scale respiratory modeling, none of these works directly parameterized their lower dimensional models from animal or patient in-vivo specific data. In addition, the recent work of Wongviriyawong et al.⁵³ showed that their lumped parameter model of the human lung could only reproduce the ventilation measurements if it included the downstream resistances and compliances tuned from healthy and asthmatic measurements. These findings help motivate the usage of lumped parameter models that include resistance and compliance when solving for airflow in a 3D CFD model.

Despite their extensive use in toxicology⁵² and therapeutic studies¹ relatively few studies have simulated airflow³² and particle deposition in the rat lung. In a recent study, CFD and MRI steady flow measurements agreed well in the conducting airways.³² Empirical models can be predictive of particle deposition in the rat,² however there have been no prior 3D simulations of particle transport and deposition in the rat airways.

The goal of the current work was to develop a multi-scale respiratory model to simulate airflow and particle deposition to replicate animal aerosol exposure experiments³⁸ in both healthy and emphysematous rats. ³⁹ In the experimental study, pressure was measured over time at the trachea and the maximum pressure was significantly lower (p = 0.01) in the emphysematous rats compared to the healthy rats.³⁹ In this current study, the global respiratory resistance and compliance were inferred by solving a well-known two-component lumped parameter model (0D global model)⁴ from aerodynamics measurements taken during the exposure experiments. The multi-scale airflow simulations were then performed by coupling MRI-derived 3D rat conducting airways³⁷ to the 0D global model. Finally, particles were tracked in the 3D domain during inspiration to determine deposition sites within the 3D model and delivery distribution of particles into the five rat lobes. Simulations were performed for a healthy rat lung, one with homogeneously distributed emphysema, and five different cases of heterogeneous emphysema. Furthermore, the influence of particle size and rat position were investigated. This study presents a novel combination of a subject-specific multi-scale airflow model and its parameterization directly from in-vivo experimental data. The airflow and particle deposition in the rat airways were solved under unsteady breathing conditions, and the CFD model was used to predict the influence of emphysema on deposition and distribution of particles in the conducting airways of the lung.

Materials and Methods

The computational models developed herein were based on breathing parameters from aerosol exposure experiments previously performed on rats.^38,39 The global respiratory values, i.e. resistance and compliance, were estimated from the airway pressure and the breathing parameters measured during the experiments. Based on this 0D global respiratory model, a multi-scale 3D-0D airflow CFD scheme was then devised to simulate the experiments. Particle deposition was then simulated throughout inspiration, matching as closely as possible the experimental conditions. The influence of particle size and rat position on particle deposition was explored.

The rat aerosol exposure protocol is described in detail elsewhere.^38,39 Five healthy and five elastase induced emphysematous³⁹ anesthetized rats (body weight of 409 ± 26 grams and 432 ± 46 grams, respectively) were mechanically ventilated. During inhalation, the piston pump pushed 2.2 mL of particle-laden air into the lung at a breathing frequency (BF) of 80 $\frac{breaths}{min}$. The particles had a 0.95 μm geometric diameter and a density of 1.35 $\frac{g}{c{m}^3}$.³⁸ At the end of inhalation, the rat passively exhaled through a tube into a jar filled with water, subjecting the rat to a constant 1 cmH₂O end expiratory pressure (P_Peep).

Estimation of Global Respiratory Parameters from Experimental Data

Each rat's global respiratory parameters were estimated based on the available experimental data. The pressure at the trachea (P (t)), total inhaled volume, breathing frequency and the inhalation time were either measured or imposed by the pump. The time varying flow rate and volume curves were not measured during the experiments. Therefore, a two component lumped parameter model (linear compartment model) was chosen⁴ to model the overall resistance (R) and compliance (C) of the respiratory system:

$$R\frac{d{V}_{total}\left(t\right)}{dt}+\frac{V_{total}\left(t\right)}{C}=P\left(t\right)-P_0,$$ (1)

where V_total(t) is the total volume of air in the lungs, $\frac{d{V}_{total}\left(t\right)}{dt}$ is the flow rate, P(t) is the pressure at the trachea, and P₀ is the pleural pressure. As the rats were ventilated at a breathing frequency and tidal volume representative of normal breathing, it was appropriate to assume linear resistance and compliance.²⁰ At the end of expiration, the flow rate was zero and the volume and pressure satisfied V_min = (P_peep – P₀)C, and therefore by defining the tidal volume (inhaled volume) as V = V_total(t) – V_min, the global respiratory model can also be written as:

$$R\frac{dV}{dt}+\frac{V\left(t\right)}{C}=P\left(t\right)-P_{peep}.$$ (2)

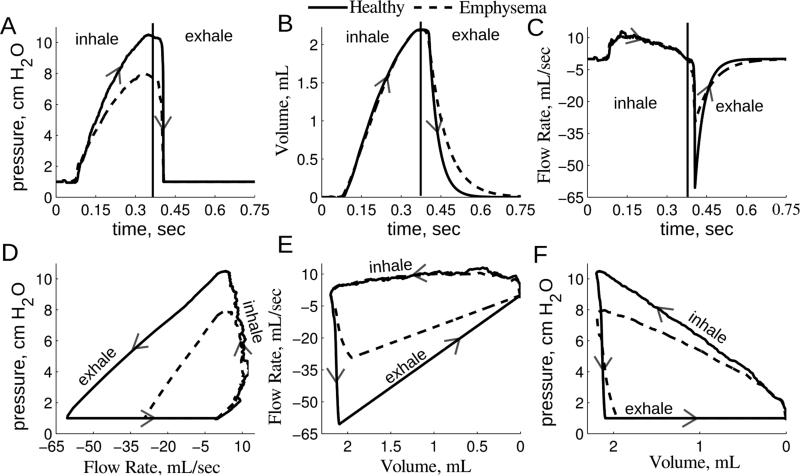
This equation was solved with an implicit Euler time stepping scheme. Pressure was imposed after filtering out the high frequency experimental noise. The pressure curves for representative healthy and emphysematous rats are shown in Figure 2A. As the R and C parameters were unknown, equation 2 was solved using a large range of values. A unique pair was found for each rat satisfying the following constraints from the experimental data: a) the maximum volume was the one imposed by the pump (i.e. 2.2 mL) and b) inspiration ended as set by the pump (i.e. time of maximum volume was $\frac{1}{2BF}$). Resistance during exhalation was set to 1.5 times the resistance during inhalation following previous work.⁴² Once the R and C parameters were found for each rat, the volume and flow rate throughout the full breathing cycle were numerically calculated by solving equation 2. The average and standard deviation in each rat category were calculated for the maximum pressure, resistance, compliance, maximum flow rates during inhalation and exhalation. A Mann Whitney two-tailed t-test was used to determine if the global respiratory parameters were significantly different between the healthy and emphysematous rats.

Figure 2.

Global 0D model solution for one healthy and emphysematous representative rat. Panel A: Experimental pressure tracing used to solve Eq. 2 and applied to the trachea face for the multiscale CFD simulations. Panels B and C: The 0D volume and flow rate solution. Panels D, E and F: The pressure and flow rate loops, flow rate and volume loops and pressure and volume loops. Arrows show the direction of the breathing cycle, beginning with inspiration.

Coupled Multi-scale Simulation and Analysis

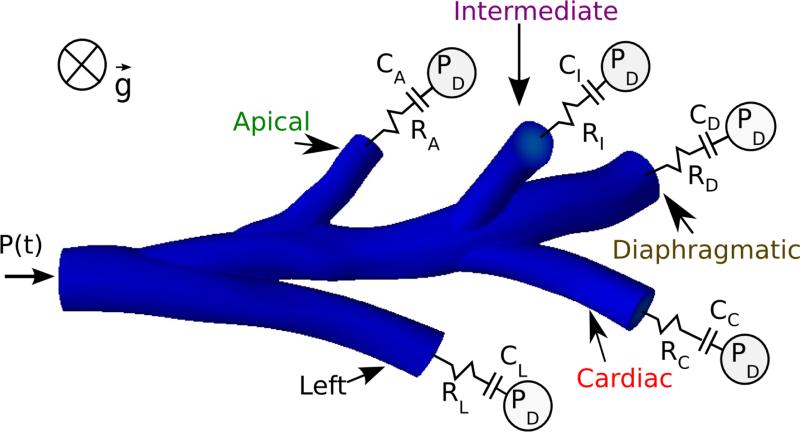
The 3D geometric model was created from MR images³⁷ with the open source software, Simvascular (simtk.org)⁴³ (Figure 1). The airway geometry did not include the upper respiratory passages as the animals were tracheotomized. The 3D model ended at the distal airways, each corresponding to one of the five rat lobes. As the conducting airways were not influenced by emphysema, as confirmed by measuring the airway diameter from the MR images,³⁹ the same geometric model was used for the healthy and emphysema simulations. A custom stabilized finite element Navier-Stokes solver was employed to simulate airflow in the 3D model, assuming rigid walls and Newtonian flow with a density of $1.2\ast {10}^{-6}\frac{g}{m{m}^3}$ and viscosity of $1.81\ast {10}^{-5}\frac{g}{mm-s}$. A custom linear solver was used with resistance based preconditioning and a combination of GMRES and conjugate gradient methods.²² Anisotropic mesh adaptation based on the Hessian of the velocity field was employed to ensure mesh convergence of the solution.³⁴ Mesh independence was determined by computing the root mean squared error of the flow rate at the trachea face. For each 3D simulation a time step of 10⁻⁴ seconds was employed, with 8 nonlinear iterations per time step. Simulations were run for 3 respiratory cycles to insure convergence to a periodic solution.

Figure 1.

Illustration of the 3D rat CFD airway geometry³⁷ connected to Neumann boundary conditions. Time varying pressure was imposed at the trachea and RC models were connected to the distal airways.

The 3D Navier-Stokes equations were solved with the following boundary conditions. The experimental pressure used to estimate the global parameters (Figure 2A) was applied at the trachea as a Neumann boundary condition. At the airway walls, the no-slip zero velocity boundary condition was set. At each distal face, the 3D Navier-Stokes equations were coupled to a 0D model, meaning that neither flow nor pressure was imposed as a boundary condition for the 3D domain but rather the relationship between pressure and flow that represents the 0D model. This was implemented with a modular yet robust implicit two-way coupling algorithm.²⁴ More specifically, at each nonlinear iteration of the Navier-Stokes solver, the flow rate of each distal face was sent to its 0D model, which outputs the pressure that was then applied homogeneously at this face at the next nonlinear iteration. The contribution of this 0D relationship between pressure and flow, which effectively couples all the 3D velocity nodes of each face, was part of the quasi-Newton tangent matrix for robustness. A time step of 10⁻³ seconds was used to solve the 0D model at each 3D nonlinear iteration. To prevent numerical divergence, convective stabilization²³ was imposed at the trachea and distal faces with β = 0.1. The distal 0D models were the two-component lumped parameter models described by equation 2. While a few recent studies have measured ventilation in rat lungs,²¹ none of these have measured the ventilation distribution to each lobe. However, Raabe et al.⁴¹ measured the lobar distribution of 0.52 μm particles in spontaneously breathing rat lungs and found the distribution of deposited particles to be proportional to lung volume. Particles of this size have minimal intrinsic properties and consequently they closely trace the convective flow in the lung. Therefore, for each lobe, the parameters R_distal,i and C_distal,i were computed assuming that the regional tidal volume to each lobe was proportional to its volume at total lung capacity, where α_i is the volume of each lobe divided by the total lung volume:³⁷

$$C_{distal,i}={\alpha }_{i}C;R_{distal,i}=\frac{R}{{\alpha }_i}$$ (3)

The global resistance is thus distributed among the resistances distal to the 3D domain, assuming that the resistance in the 3D domain is negligible. This assumption is justified in the Multi-scale CFD Simulations section of the discussion.

One healthy and one emphysematous rat were chosen for the simulations, and their global R and C values are given in Table 1 and their pressure curves are shown in Figure 2. Six cases of emphysema were simulated: one with homogeneous and five with heterogeneous distributions of emphysema. For the heterogenous emphysema cases the assumption was made that the emphysema was contained to a single lobe, with a different lobe for each case studied. In the heterogeneous cases the emphysematous pressure curve (Figure 2) was applied at the trachea and the healthy resistance values R_distal,i were applied at each distal face. The healthy compliance values C_distal,i were applied to the four healthy distal faces. The compliance at the remaining faces was defined such that the sum of all C_distal,i was equal to the total emphysema compliance. Post processing and particle tracking were performed on the last respiratory cycle. Resistance of the 3D model was calculated by dividing the pressure drop at maximum flow rate (inspiration or expiration) by the flow rate at the trachea, such that pressure drop was e.g. for inspiration P_{trachea, max. inspiration} - P_{distal, max. inspiration} (with P_distal chosen to give the maximum pressure drop). Lobar tidal volume was determined by normalizing the total volume of air delivered to each lobe by the total inhaled volume.

Table 1.

Global 0D model parameters. Simulation model parameters were used for the determination of the 0D distal parameters according to equations 3. Average values were between all healthy and emphysematous rats. Values are labeled based on whether they were measured during the experiment (black), estimated from solving Eq. 2 (bold), or predicted from model (gray)

		Maximum Pressure cm H2O	Inhale Resistance, Rin$\frac{cm{H}_{2}O\cdot s}{c{m}^3}$	Exhale Resistance Rex$\frac{cm{H}_{2}O\cdot s}{c{m}^3}$	Compliance $\frac{c{m}^3}{cm{H}_{2}O}$	Maximum Inhale Flow $\frac{mL}{sec}$	Maximum Exhale Flow $\frac{ml}{sec}$
healthy	Average For All Rats	10.60 ± 1.19	0.22 ± 0.12	0.33 ± 0.18	0.25 ± 0.04	11.3 ± 1.39	−31.5 ± 19.23
	Representative Case	10.50	0.098	0.147	0.236	12.63	−55.61
Emphysematic	Average For All Rats	7.90 ± 1.43	0.18 ± 0.05	0.27 ± 0.08	0.37 ± 0.14	11.2 ± 1.41	−22.8± 8.41
	Representative Case	8.00	0.135	0.167	0.330	10.47	−29.85

Lagrangian Particle Tracking

Once the airflow simulations were completed, rigid spherical particles were tracked in the 3D model by solving the Maxey-Riley equation.³¹ For small particles the Faxen correction and Basset/Boussinesq memory terms may be neglected.³¹ Therefore, the Maxey-Riley equation reduces to

$$\left({\rho }_p+\frac{1}{2}{\rho }_f\right)\frac{d\overrightarrow{v}\left(\overrightarrow{x}\left(t\right)\right)}{dt}=({\rho }_p-{\rho }_f)\overrightarrow{g}+\frac{3}{2}{\rho }_f\frac{D\overrightarrow{u}(\overrightarrow{x},t)}{Dt}-\frac{9}{2}\frac{\mu }{a^2}(\overrightarrow{v}\left(\overrightarrow{x}\left(t\right)\right)-\overrightarrow{u}(\overrightarrow{x},t)),$$ (4)

where $\overrightarrow{v}$ is the particle velocity, a is the particle radius, μ is the viscosity of air, ρ_p is the particle density, ρ_f is the fluid density, $\overrightarrow{u}$ is the air velocity, and $\overrightarrow{x}$ is the position of the particle. The derivative $d∕dt=\partial ∕\partial t+\overrightarrow{v}\cdot \nabla$ is evaluated along the particle path whereas the derivative $D∕Dt=\partial ∕\partial t+\overrightarrow{u}\cdot \nabla$ is evaluated following a fluid element. The aerosol particles were assumed to be inert and monodisperse with a diameter of 0.95 μm and density of 1.35 g cm⁻³, to match the exposure experiment.³⁹ Additional particles with diameters of 3 and 5 μm were simulated. Equation (4) was solved analytically for $\overrightarrow{v}\left(x_j\left(t\right)\right)$, the velocity of the particle j at arbitrary time t_i as a function of the other variables (namely $\overrightarrow{u}\left(t_i\right)$, obtained from linear space-time interpolation from the air velocity field mesh, and $\frac{D\overrightarrow{u}}{Dt}\left(t_i\right)$, obtained by linear interpolation of the air velocity field and a second order accurate central difference formula for the spatial and temporal derivatives). Once the velocity of the particle at time t_i was obtained, the position at time t_i+1 was updated with an explicit Euler discretization scheme with a time step of 10⁻⁵ sec.^10,45 Gravity, $\overrightarrow{g}$, was either positioned to represent a rat in the supine position as in the experiments,³⁹ or such that the rat was in the standing position. Particle seed locations were uniformly defined over the trachea face. As particle deposition is highly dependent on starting location,²⁹ the numbers of particles released was proportional to the local flow velocity such that more particles were released at the center of the model and at times of high flow velocity. The particles were seeded at the trachea face throughout inhalation. Particles that came in contact with the wall were assumed to be deposited. Particle distribution to each lobe was determined by counting the number of particles exiting from each distal face. To ensure independence from a particles's starting location, the spatial density of the particles was increased until there was no change in deposition or distribution. The number of particles deposited, suspended in the 3D domain, and delivered to each lobe were summed at the end of inhalation. In addition, massless particles were tracked by solving $\frac{d\overrightarrow{x}}{dt}=\overrightarrow{u}(\overrightarrow{x},t)$, with a fourth order Runge-Kutta scheme.

Results

Global 0D Parameters

Respiratory compliance was significantly higher (p = 0.04) in the emphysematous rats compared to the healthy rats (Table 1). The respiratory resistances were not significantly different (p = 0.83). As expected, the inhalation flow rates and volumes were the same among all rats, as this was uniformly controlled by the ventilator pump in all experiments (Figure 2). The maximum exhalation flow rate tended to be larger in the healthy rats than in the emphysematous rats (Table 1), but was not statistically significant (p = 0.4). The decay rate of the expiration volume was less for the emphysematous rats (Figure 2). The pressure versus flow curve and the flow versus volume curve were more restrictive for the emphysematous rat, compared to the healthy rat (Figure 2D and E). The pressure peaked slightly before the volume in both groups (Figure 2A, B and F).

Multi-Scale CFD Simulations

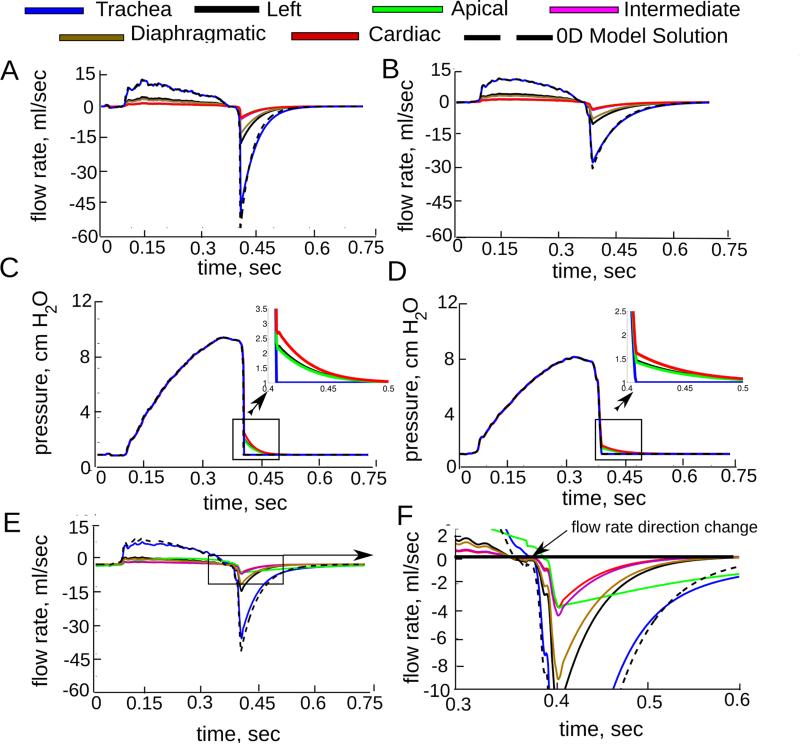
The finite element mesh of the 0D-3D CFD simulation was adapted until there was less than 2 % difference in the inlet flow rate between successive adaptation steps, resulting in a final mesh with ~ 3.5 × 10⁴ elements. In both the healthy and homogeneous emphysema cases the flow rate measured at the trachea was similar to that of the global 0D model, except at peak expiration, when it was slightly less than the global 0D prediction (Figure 3). This decrease was caused by the pressure drop between the trachea and the distal airways (Figure 3C and D) which slightly increased the resistance in the 3D domain. Indeed, the predicted pressure drop to each lobe (Table 2) was over 30 times greater during maximum exhalation than during maximum inhalation for the healthy rat. The same trend was found for the homogeneous emphysema case, as the pressure drop was very small for both. In the apical heterogeneous emphysema case (Figure 3E and F) the increased compliance in the apical lobe, due to the disease localization, caused the lobe to fill and empty more slowly than in the healthy lobes. The time for the flow to change from inspiration to expiration was the same for all the healthy lobes (Figure 3F). However the apical flow changed direction 0.014 seconds after the healthy lobes. Therefore during this short time, air was both exiting and entering from the lobes into the 3D model. Similar behavior was observed for the other four heterogeneous cases. As expected, the airflow delivery to each lobe for the healthy and homogeneous emphysema cases was the same as the applied regional tidal volume (Table 2). In each of the heterogeneous emphysema cases flow increased in the lobe that contained the disease and decreased in the healthy lobes. This resulted in a higher pressure drop for the diseased lobe and a lower pressure drop for the healthy lobes.

Figure 3.

Computed flow rate and average pressure at each face for healthy (panels A and C), homogeneous emphysema (panels B and D) and heterogeneous emphysema (apical lobe) (panels E and F). The simulated flow rate at the trachea was similar to the 0D model solution, except during maximum exhalation where the 3D pressure drop was the greatest (shown in panels C and D). Panel F shows the delay in the flow direction change and slower emptying in the diseased lobe.

Table 2.

Multi-scale CFD results for each of the seven simulations performed.

Airflow Delivery to Each Lobe Normalized by the Inhaled Volume, %
	Left	Apical	Intermediate	Diaphragmatic	Cardiac
Alpha37	0.359	0.110	0.135	0.280	0.116
Healthy	0.358	0.110	0.135	0.279	0.116
Homo. Emphysema	0.359	0.110	0.135	0.280	0.116
Left Diseased	0.529	0.0801	0.0983	0.204	0.0844
Apical Diseased	0.279	0.306	0.105	0.218	0.090
Inter. Diseased	0.274	0.0840	0.339	0.214	0.0884
Dia. Diseased	0.263	0.0806	0.0988	0.469	0.0848
Card. Diseased	0.278	0.0852	0.104	0.217	0.315

Pressure Drop From Trachea Face During Maximum Inhalation, cmH2O
	Left	Apical	Intermediate	Diaphragmatic	Cardiac
Healthy	0.037	0.048	0.052	0.016	0.034
Homo. Emphysema	0.036	0.043	0.044	0.022	0.034
Left Diseased	0.057	0.037	0.032	0.016	0.023
Apical Diseased	0.027	0.063	0.028	0.009	0.022
Inter. Diseased	0.029	0.038	0.069	0.019	0.036
Dia. Diseased	0.028	0.041	0.058	0.038	0.045
Card. Diseased	0.030	0.038	0.048	0.027	0.048

Pressure Drop From Trachea Face During Maximum Exhalation, cmH2O
	Left	Apical	Intermediate	Diaphragmatic	Cardiac
Healthy	1.38	1.25	1.87	1.82	1.86
Homo. Emphysema	0.464	0.431	0.626	0.616	0.627
Left Diseased	0.718	0.632	0.909	0.894	0.907
Apical Diseased	0.676	0.636	0.926	0.912	0.926
Inter. Diseased	0.682	0.654	0.944	0.927	0.939
Dia. Diseased	0.711	0.683	0.991	0.989	0.998
Card. Diseased	0.664	0.616	0.911	0.897	0.914

Flow Profiles in the 3D Model

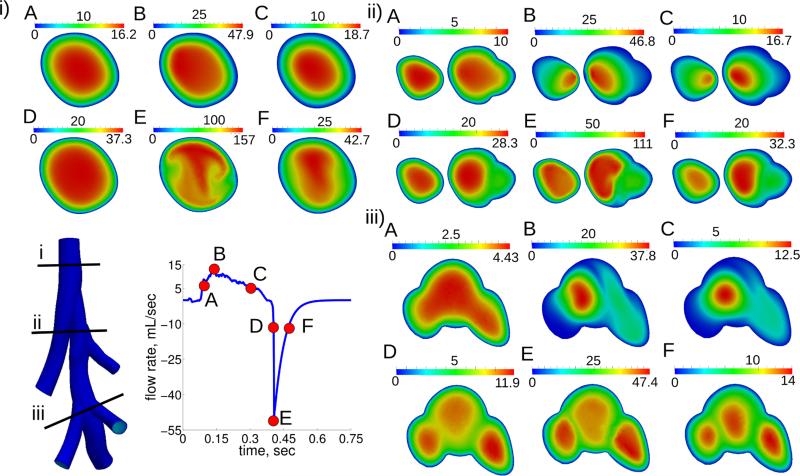
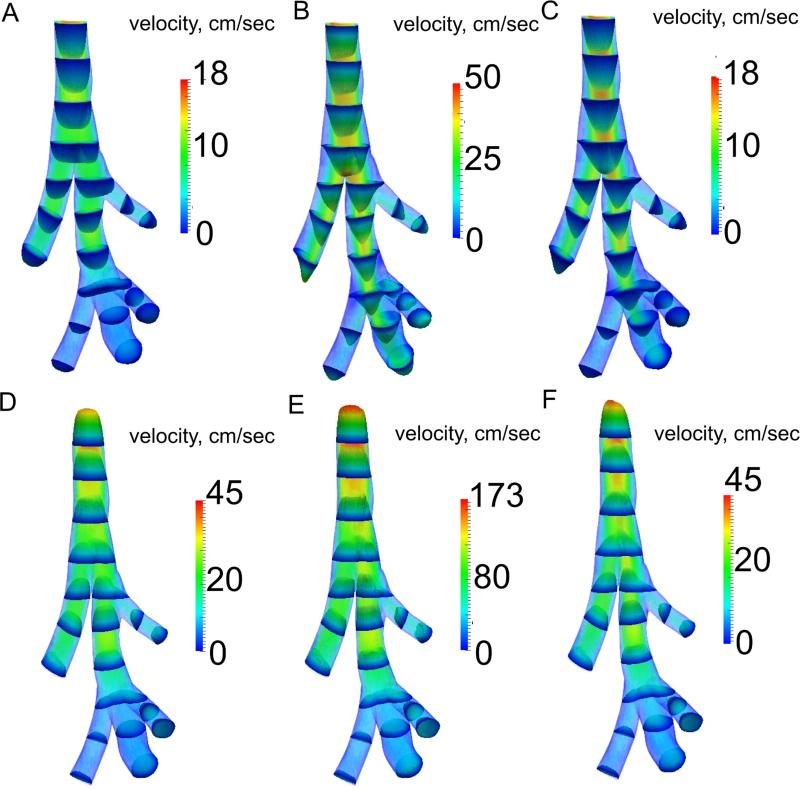
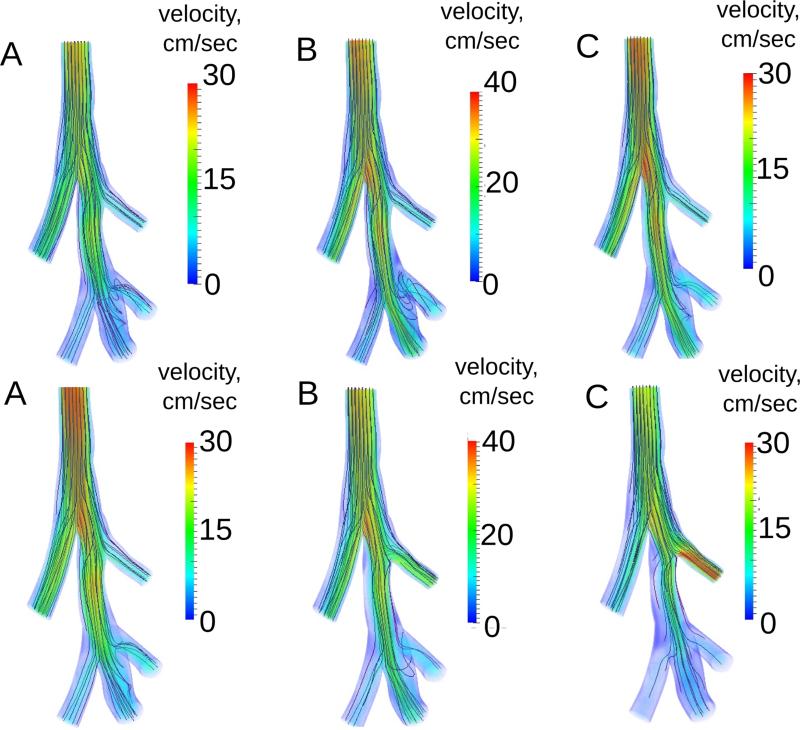
The flow patterns developed throughout the breathing cycle (Figure 4 and 5). For example, although the flow rate magnitude was the same at time points A and C (Figure 4 and 5), before and after maximum inhalation, respectively, the flow patterns were quite different. At maximum inhalation the flow changed from being nearly parabolic in every airway (Figure 5 A) to being skewed towards the inside of the bifurcations (Figure 5 B). These flow patterns remained during the deceleration phase of inspiration (Figure 5 C). At position iii, the flow began to recirculate from the diaphragmatic lobe to the intermediate lobe (Figure 4 iiiB). During expiration, although the flow magnitude varied much more than during inspiration, the flow patterns remained quite similar (Figure 4 and 5). Velocity profiles in the lobe airways were shaped by the airways’ curvature, where flow profiles were initially nearly flat but developed complex patterns at maximum expiration (Figure 4 iE). The velocity field was different between the homogeneous and apical heterogeneous emphysema cases at the same three time points during inspiration (Figure 6). This difference was not only observed in the diseased lobe airways, but also in other parts of the domain. For example, the transient flow rate was higher in the trachea at time point A for the apical diseased case. In the homogeneous emphysema case there were more recirculation patterns present between the diaphragmatic and intermediate lobes than in the apical diseased case (Figure 6). Figure 6 2A-2C also shows that the increased airflow delivery to the diseased lobe (apical lobe) occurred only after maximum inspiration (panel C).

Figure 4.

Velocity magnitude for three locations (1-3) at six time points (A-F) for the healthy case. Time points at A and C are at the same flow rate with A being before maximum inspiration (B), and C being after maximum inspiration. D and F are at the same flow rate, with D being before the maximum expiration (E), and F being after the maximum expiration.

Figure 5.

3D rendering of the velocity magnitude for the healthy simulation at six time points (A-F). Flow profiles’ shapes were normalized by the maximum velocity in the 3D domain at each time point.

Figure 6.

3D rendering of the velocity magnitude and massless fluid particle pathlines for homogeneous emphysema (panels 1A - 1C) and for heterogeneous emphysema (apical lobe diseased) (panels 2A - 2C). Time points are the same as shown in Figure 4. The color scale is the same for each time point.

Particle Deposition and Distribution

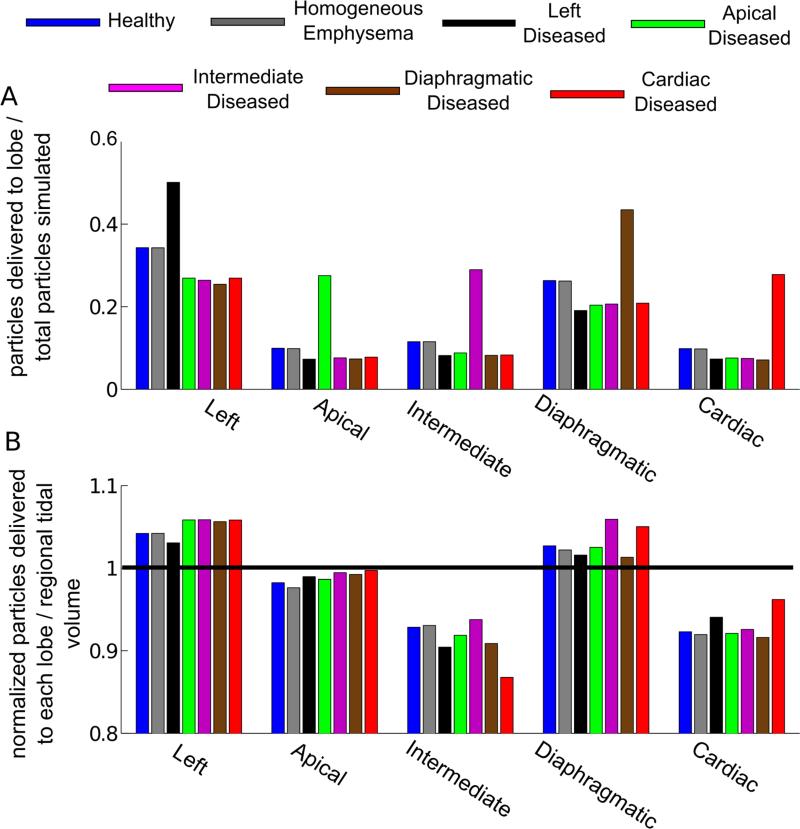
Convergence was reached when there was less than 1 % difference in particle deposition with increasing seeding densities, corresponding to a 2000 particle seed per release with ~ 1.7 10⁷ total particles released during inspiration. There was no difference in the normalized distribution of particles between the healthy and homogeneous emphysema cases (Figure 7A). However, there was an increase in delivery of particles to the diseased lobe and consequently a decrease in delivery of particles to the healthy lobes, for the heterogeneous emphysema cases. The increase in particles delivery to the diseased lobe was mainly due to the increased flow to this lobe (Figure 7B). Additionally, while the delivery of particles to the apical and diaphragmatic lobes was proportional to the regional tidal volume, this was not the case for the left, intermediate and cardiac lobes. For example, in the healthy case, the particle delivery to the left lobe was 4% higher than the flow delivered and 7 and 8 % less than the flow delivered for the intermediate and cardiac lobes, respectively.

Figure 7.

Panel A: Normalized number of particles exiting to each lobe. Panel B: Normalized number of particles delivered to each lobe (number of particles exiting to lobe divided by total number of particles exiting) divided by the flow split values given in Table 2.

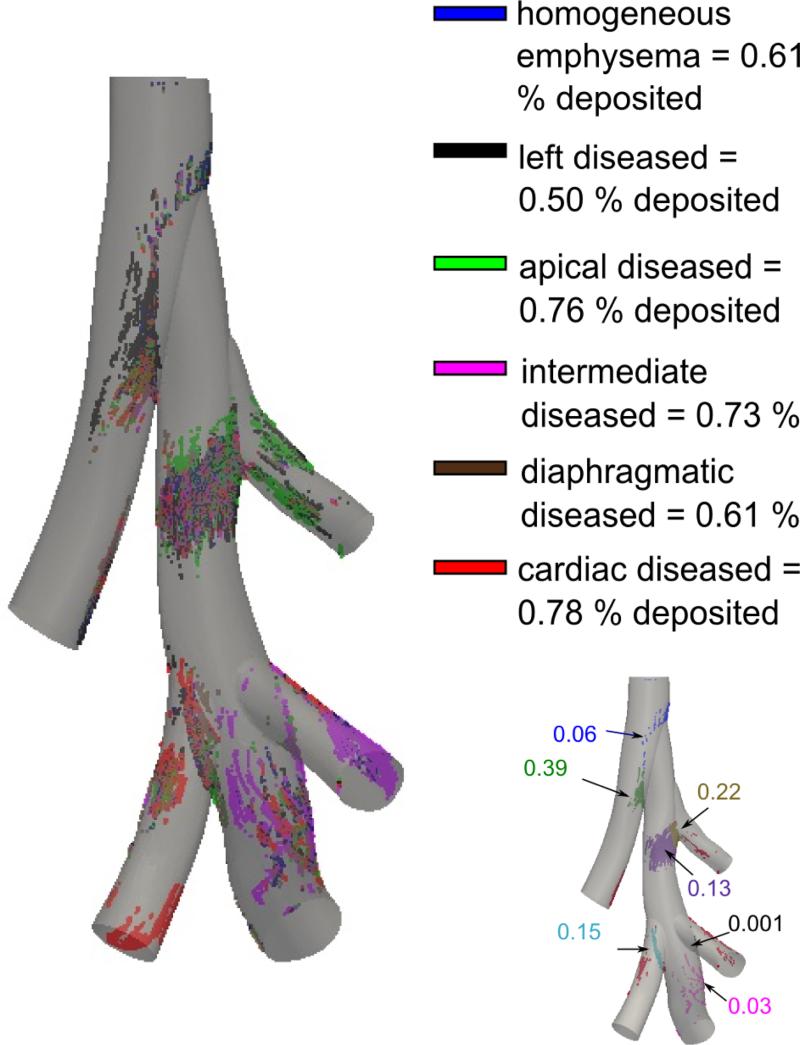
Only 0.64 and 0.61 % of particles were deposited in the 3D geometric model for the healthy and homogeneous emphysema cases, respectively. There was no difference in the particle deposition locations between the healthy and homogeneous emphysema cases. Approximately 76 % of the particles that deposited did so at the bifurcation areas (Figure 8). The rest of the particles deposited on the back face of the 3D model, in the direction of gravity. Particles deposited mainly at the first and second bifurcations for all emphysema cases simulated (Figure 8). Additionally, particles deposited on the airway back wall after the second bifurcation. In the apical, cardiac and intermediate heterogeneous emphysema cases, there was an increase in particle deposition on the wall of the airway leading to the diseased lobe.

Figure 8.

Particle deposition in the 3D model for 0.95 μm diameter particles with the different colors representing the 6 different cases of emphysema simulated. The percentage of total deposition in the 3D domain is also given for each emphysema case. Image in the bottom right corner shows the deposition pattern for the homogenous emphysema case, including the deposition fraction. Approximately 76 % of the particles that deposited did so at the bifurcation zones, while the rest of the particles deposited on the back face of the model, in the direction of gravity.

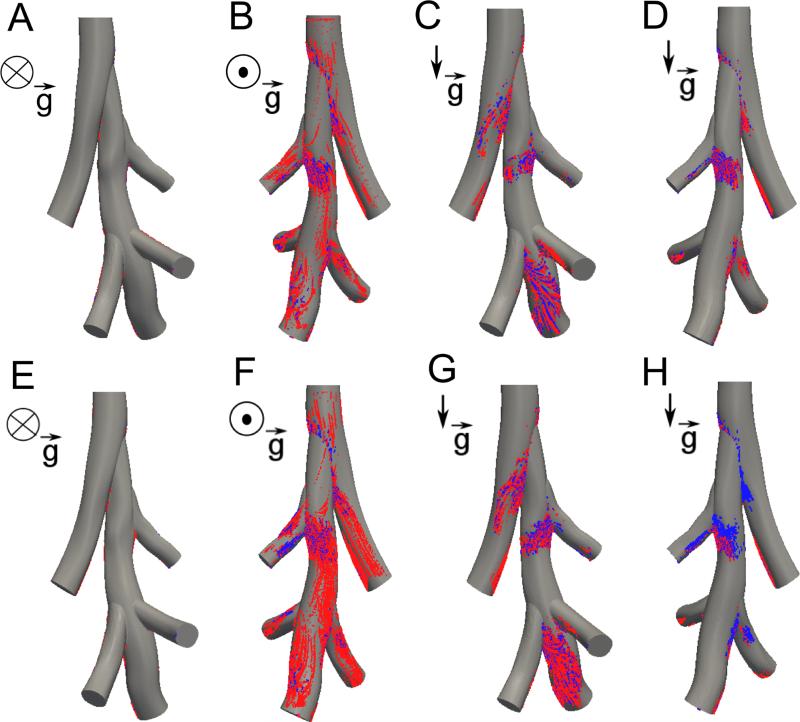
The influence of rat position and particle size was investigated by tracking 0.95, 3 and 5 μm diameter particles with the rat in both the supine and standing positions (Table 3, Figure 9). As expected, the number of deposited particles in the 3D model increased with particle size. Deposition mostly increased when the rat was in the standing position; there were more particles depositing on the front face of the diaphragmatic airway (Figure 9B and D). The deposition patterns for 3 μm diameter particles were remarkably different between the homogeneous emphysema and the apical diseased cases.

Table 3.

Percentage of particles deposited in the 3D geometry.

Position:	supine			standing
Particle Diameter:	1 μm	3 μm	5 μm	1 μm	3μm
Healthy	0.64	2.68	9.81	0.95	2.97
Homogeneous Emphysema	0.61	2.54	8.56	1.31	3.11
Apical Diseased	0.76	2.35	9.24	1.48	2.25

Figure 9.

Particle deposition in homogeneous emphysema (panels A-D) and for heterogeneous emphysema (apical diseased) (panels E-H) for the rat in the supine position (A-B, E-F) and in the standing position (C-D, G-H). Each position shows the front of the rat (A, C, E, G) and back of the rat (B, D, F, H). Blue particles are 1 microns in diameter and red particles are 3 microns in diameter.

Discussion

Global Respiratory Parameter Estimation

The global resistances and compliances identified in this study agreed well with previously published data,^21,42,49 despite the limited experimental data available in this current study (Table 4). While the previous studies reported higher compliance values, the relative increase in compliance between emphysematous and healthy rats was similar. Variances between these studies may be attributed to differences in strain, body weight, and functional test measurement techniques. No difference between the healthy and emphysematous resistance was found, which also agreed with the previous studies. This is likely due to a mild to moderate emphysema induction.⁶ If the resistance in emphysema was markedly different from the normal case during expiration only, then additional experimental measurements would be necessary to infer this information from the data. This would however not change the particle simulation results, as they were performed only during inspiration.

Table 4.

Lumped parameter values found in this current study compared to values found by previous studies for resistance⁴² and compliance.^21,49 Resistance values determined by Rubini et al.⁴² were for 300 gram healthy Wistar rats ventilated with a tidal volume of 1 ml and a constant flow rate of 4 $4\frac{ml}{s}$. The compliance values were determined from Sprague-Dawley rats with body weight of 470 grams⁴⁹ and 531 grams.²¹

	Resistance, $\frac{cm{H}_{2}O\cdot s}{c{m}^3}$				Compliance, $\frac{c{m}^3}{cm{H}_{2}O}$
	Inspiration		Expiration		Healthy			Emphysematous
	Current Study	Rubini42	Current Study	Rubini42	Current Study	Tolnai49	Emami21	Current Study	Tolnai49	Emami21
mean	0.22	0.25	0.33	0.33	0.25	0.46	0.61	0.37	0.74	0.92
std	0.12	0.05	0.18	0.15	0.04	N.A.	0.12	0.14	N.A.	0.16

To test the robustness of the parameter estimation method, the same procedure was repeated for two additional pressure curves collected for the same rat, and the intra-animal standard deviation normalized by the mean (RD) was less than the inter-animal RD for the healthy rats. A linear least squares fitting method was also employed to estimate the global parameters based on the inhaled volume approximated by video recording of the ventilator pump linear displacement. This method resulted in similar parameters as the original method for a single rat. It uses the entire volume curve to estimate the parameters, yet there was potential for experimental error in estimating the pump volume displacement. Additionally, there was sensitivity in matching the start time of the volume and pressure curves, resulting in the inability to estimate parameters for several rats. For such a method, the pressure and volume curves should be both measured simultaneously.

Multi-scale CFD Simulations

To further demonstrate the need for the multi scale framework introduced here, an additional simulation was performed. The healthy flow rate curve (see Figure 2) was applied at the trachea and a zero pressure boundary condition was applied at each of the distal faces. The pressure drop from the trachea to each distal airway was thus the same, and the air distributed according to the path of least resistance. This led to as much as 95% difference in the regional tidal volume compared to the multi-scale simulations (Table 2). This significant difference highlights the importance of realistic CFD boundary conditions if unsteadiness is simulated. Boundary condition choices would have less influence in steady flow simulations, as the primary difference was in the compliances between the healthy and emphysematous cases. The need to tune the downstream resistances⁵⁰ was mitigated by the fact that the resistance in the 3D airways was a small fraction of the global 0D resistance in both inspiration and expiration.

The airway resistance was estimated by assuming Poiseuille flow with geometric dimensions given by Oakes et al.³⁷ This resulted in an airway resistance of $9.93{10}^{-4}\frac{cm{H}_{2}O\cdot s}{c{m}^3}$, which was in-between the resistance found during inhalation and exhalation. Therefore the Poiseuille model is appropriate if the resistance in the first couple of airway generations of the rat is desired.

The velocity field in the 3D domain was qualitatively compared to results given in Minard et al.³² The group compared steady CFD flow profiles in a rat to those measured directly with MRI. The velocity fields from our current simulations were selected at the time points with similar flow rates. For the time point before maximum inspiration, the velocity field qualitatively compared well with their results, despite the fact that their 3D geometry was more extensive. However at the time point following maximum inspiration the velocity fields were different due to the unsteady effects of deceleration (see Figure 4). This comparison underlines the importance of performing unsteady simulations, as the flow dynamically changes throughout inspiration. In addition, the regional tidal volume to each lobe in this current study compared well to their MRI data.

It should be noted that in each of the heterogenous emphysema cases the diseased lobe had a larger regional tidal volume than it did in the homogenous emphysema case (Table 2). This was because the compliance was increased in the diseased lobe. This finding suggests that, while emphysema reduces area for gas exchange to occur, airflow may be increased to the diseased regions, resulting in reduction of airflow to the healthy regions.

Particle Deposition and Distribution

The results showed that the deposition and distribution of particles in the lung not only depend on the regional tidal volume between lobes, but also on the 3D geometry. In regions dominated by convective transport, the likelihood of a particle to follow the flow depends on the Stoke's number, ^{16, 19} defined as, $Stk=\frac{{\rho }_p{d}_p^{2}u}{18\mu d}$, where ρ_p is the particle density, d_p is the particle diameter, u is the mean flow velocity and d is the airway diameter. In a previous modeling study in an idealized human geometry and flow conditions, Darquenne et al.¹⁶ concluded that convective flow was the main determinant of particle distribution between the airways when Stk in the trachea was less than 0.01. At the trachea, Stk = 0.0028 for the current study. The particles did deviate from the flow (Figure 7B) however by no more than 8% which agreed with this prior work. In fact, the velocity profile at peak inspiration was slightly directed towards the left lobe (Figure 5). Hence, since the particle release density was proportional to the flow rate, more particles moved towards the left lobe. The decrease in particle delivery relative to the lobar flow in both the cardiac and intermediate lobes (Figure 7), compared to the other three lobes, was likely due to the triple bifurcation and its influence on the flow field (Figure 6). Indeed, the particle density was higher on the massless particle pathlines going towards the diaphragmatic lobe. The other main reason is that the diaphragmatic lobe is sloped in the direction of gravity, while the intermediate and cardiac lobes are sloped upwards, in the direction opposite to gravity. Therefore, particles traveling to the intermediate and cardiac lobes had to move against gravity. Besides, at the location where flow recirculated from the diaphragmatic lobe to the intermediate lobe (Figure 6B), particles may not have followed this change of flow direction. These three effects caused fewer particles to be advected into the cardiac and intermediate lobes compared to their regional tidal volume.

Less than 1 % of the 0.95 μm particles deposited in the 3D model for all healthy and diseased cases considered (Figure 8). Particles mainly deposited at the first and second bifurcations for all diseased cases considered. The model revealed an increase in delivery of air and particles to the diseased lobe. In addition to the increase in particle delivery to the diseased lobe, a greater number of particles deposited in the 3D domain in the localized diseased cases compared to the healthy or homogeneously distributed emphysema cases. This was mainly because there was more particle-laden air traveling through these airways. While this increase in deposition was small (0.76 % in apical diseased versus 0.61 % in homogeneous emphysema), the influence of disease on deposition may become more significant in a model that includes more airway generations.

The particle deposition on the main right bronchus, downstream of the apical bifurcation, was mainly due to the local high curvature of the airway and gravity, both promoting deposition in the same direction. Note that the number of particles depositing on the left bronchus was very small (blue particles) compared to the number of particles depositing at the bifurcation zone (green particles) (Figure 8). Some of the 3 micron particles deposited on the left bronchus (Figure 9B), gravity and particle momentum combined with the airway curvature playing a larger role. When the rat was in the standing position, particles deposited on both the back and front of the model (Figure 9 CDGH) at the curved areas of the right main bronchus. This was also seen in other areas where gravity was in the same direction as the bifurcation zones and the longitudinal curvature. Moreover, few particles deposited at the intermediate bifurcations, as the flow patterns near the intermediate bifurcation were not of a typical bifurcation (Figure 8): the fluid at this location (see Figure 6B) did not decelerate quickly (the flow upstream of the bifurcation was also slow so the particles going towards the bifurcation had low momentum). Most of the massless particle path lines did not go towards the bifurcation but continued downwards from the middle of the right airway towards the diaphragmatic lobe. On the other hand, for the cardiac lobe, the situation is closer to a typical bifurcation, as the fluid decelerated quickly on the massless particle pathlines that then split at this bifurcation. About 15 % of the particles that deposited in the 3D domain did so at the cardiac bifurcation for the homogenous emphysema case (Figure 8). Additionally, as was shown for the apical diseased case (Figure 9), the flow slowed down in the healthy airways (Figure 6), leading to increased particle deposition in these airways.

Deposition in the 3D airways was also predicted by solving analytical models for gravitational sedimentation⁹ and inertial impaction⁴⁰ using an average flow rate of $9\frac{c{m}^3}{s}$. With a 0.95 μm diameter, particles deposited 0.89 % due to impaction and 0.23 % due to gravitational sedimentation. Considering that these calculations did not take unsteadiness into account, the deposition prediction was close to that found with the numerical simulations. For 3 μm diameter particles, the analytical formulas however overestimated deposition (8.9 % due to impaction, 2.3 % due to sedimentation). The total deposition of 11.2 % was significantly higher than the 2.68 % found during the current unsteady numerical simulations. This is an example where numerical simulations may be used to study the hypotheses on which analytical formulas are based.

Furthermore, assuming the number of particles deposited in each lobe is proportional to the number delivered, our predictions are within 10 % of the previous measurements of Raabe et al.⁴¹ taken in healthy rats in the left, intermediate, diaphragmatic and cardiac lobes lobes, with a maximum of 12 % difference in the apical lobe. Sweeney et al.⁴⁸ found significantly less deposition in emphysematous hamsters than in age-matched healthy hamsters, with more heterogeneous distribution in the emphysematous hamsters compared to healthy. While the deposition downstream of the 3D model in the current study was not determined, the increased delivery of particles to the diseased lobe suggests that more particles would deposit in emphysematous regions of the lung, in disagreement with Sweeney et al's findings.⁴⁸ We note that while the diseased lobe in our model of heterogeneous emphysema had a larger compliance than the healthy lobes, resistance in the diseased and healthy lobes were similar. However, the loss of elastic recoil in the emphysematous lobe may increase the resistance of the small airways.¹⁵ Such increase in resistance may limit ventilation in the subtended parenchymal region, hence limiting the delivery and deposition of aerosols in the diseased lobe. Finally, while reasonable in a homogeneous lung, our assumption that deposition was proportional to aerosol delivery may not be as suitable in a lung with heterogeneous compliance. For example, if the air becomes trapped due to airway collapse, there may be an increase in deposition in emphysema due to gravitational sedimentation. These differences should be used to guide experimental design and model refinement in future studies.

Study Limitations and Future Work

As the flow or volume curves were not measured during the aerosol exposure experiments, it was impossible to determine a time varying resistance and compliance in the global model. However, as the rats were ventilated at tidal breathing, it was appropriate to assume constant values.²⁰ Moreover, dynamic data could be readily integrated in the current CFD framework.

Our multi-scale approach enabled realistic unsteady simulations, and more accurately modeled the regional tidal volume in each lobe compared to constant pressure boundary conditions. However, the distal resistance and compliance were partitioned based on the sub-tending lobar volume. Pulmonary ventilation may not be directly proportional to the lobe volume; only a few experimental studies^21,32 have investigated ventilation in the rat lung, which was well matched here. Additionally, in this work, emphysema was modeled as homogeneous or only contained in one lobe. However, it is likely that the disease affects the whole lung in a heterogeneous fashion rather than being restricted to one specific lobe. Nonetheless, our simulations, can be used to offer insights into the relationship between disease, airflow and particle delivery.

As most of the airways included in the simulations are covered in cartilaginous rings, all simulations were performed assuming rigid walls. If fluid structure interaction simulations were performed in future studies, the tissue wall properties must be known. As the Reynolds number was small (Re_mean = 380) and the upper airways were bypassed, turbulence is unexpected. Therefore, a turbulence model was not needed for these simulations.

While particle transport was simulated throughout unsteady inspiration, particles were not tracked once they left the 3D domain or during exhalation. Determining particle deposition downstream of the 3D model would require either a more extensive 3D model, a mean multiple path deposition model,² or a 1D description of airflow and particle deposition. In spite of this, the model matched both experimental⁴¹ and analytical models^9,40 reasonably well.

Conclusion

In this study, the airflow and particle distribution in healthy and emphysematous rat lungs were investigated by replicating an aerosol exposure study.³⁹ First, we identified the respiratory parameters from a whole-lung simple lumped model⁴ that best fit the available respiratory experimental data. The respiratory compliance was found to be statistically higher and the resistance unchanged in the emphysematous rats compared to the healthy rats. In conjunction with an MRI-generated airway geometric model, the whole-lung respiratory resistances and compliances were integrated into a multi-scale (3D-0D) unsteady simulation framework to study the airflow in the healthy, homogeneous and heterogeneous emphysematous rats. The regional tidal volume at each of the distal airways was found to match the expected flow distribution in these multi-scale simulations, unlike when a constant pressure boundary condition was applied at the distal airway faces. The unsteady simulations exhibited complex flow patterns, especially at the triple bifurcation area. These complex flow patterns influenced the particle deposition in the airways; fewer particles traveled to the cardiac and intermediate lobes compared to their corresponding fraction of regional tidal volume. There was an increase in airflow, particle deposition in the 3D model, and particle delivery to the diseased regions for the heterogeneous cases compared to the homogeneous cases. Moreover, a standing rat position and a larger particle size both increased deposition in the 3D model. Finally, in some cases the particle deposition analytical models studied here predicted a higher deposition compared to the 3D numerical simulations. This is likely because the analytical models do not account for the influence of unsteady flow and complex flow patterns.