Characterization of Complex Systems Using the Design of Experiments Approach: Transient Protein Expression in Tobacco as a Case Study

Abstract

Plants provide multiple benefits for the production of biopharmaceuticals including low costs, scalability, and safety. Transient expression offers the additional advantage of short development and production times, but expression levels can vary significantly between batches thus giving rise to regulatory concerns in the context of good manufacturing practice. We used a design of experiments (DoE) approach to determine the impact of major factors such as regulatory elements in the expression construct, plant growth and development parameters, and the incubation conditions during expression, on the variability of expression between batches. We tested plants expressing a model anti-HIV monoclonal antibody (2G12) and a fluorescent marker protein (DsRed). We discuss the rationale for selecting certain properties of the model and identify its potential limitations. The general approach can easily be transferred to other problems because the principles of the model are broadly applicable: knowledge-based parameter selection, complexity reduction by splitting the initial problem into smaller modules, software-guided setup of optimal experiment combinations and step-wise design augmentation. Therefore, the methodology is not only useful for characterizing protein expression in plants but also for the investigation of other complex systems lacking a mechanistic description. The predictive equations describing the interconnectivity between parameters can be used to establish mechanistic models for other complex systems.

Download video file ^{(37.5MB, mp4)}

Introduction

The production of biopharmaceutical proteins in plants is advantageous because plants are inexpensive to grow, the platform can be scaled up just by growing more plants, and human pathogens are unable to replicate ^1,2. Transient expression strategies based for example on the infiltration of leaves with Agrobacterium tumefaciens provides additional benefits because the time between the point of DNA delivery and the delivery of a purified product is reduced from years to less than 2 months ³. Transient expression is also used for functional analysis, e.g. to test genes for their ability to complement loss-of-function mutants or to investigate protein interactions ^4-6. However, transient expression levels tend to show greater batch-to-batch variation than expression levels in transgenic plants ^7-9. This reduces the likelihood that biopharmaceutical manufacturing processes based on transient expression will be approved in the context of good manufacturing practice (GMP) because reproducibility is a critical quality attribute and is subject to risk assessment ¹⁰. Such variation can also mask any interactions that researchers intend to investigate. Therefore, we set out to identify the major factors that affect transient expression levels in plants and to build a high-quality quantitative predictive model.

The one-factor-at-a-time (OFAT) approach is often used to characterize the impact (effect) of certain parameters (factors) on the outcome (response) of an experiment ¹¹. But this is suboptimal because the individual tests (runs) during an investigation (experiment) will be aligned like pearls on a string through the potential area spanned by the factors that are tested (design space). The coverage of the design space and hence the degree of information derived from the experiment is low, as shown in Figure 1A ¹². Furthermore, interdependencies among different factors (factor interactions) can remain concealed resulting in poor models and/or the prediction of false optima, as shown in Figure 1B ¹³.

The drawbacks described above can be avoided by using a design of experiments (DoE) approach in which the runs of an experiment are scattered more evenly throughout the design space, meaning that more than one factor is varied between two runs ¹⁴. There are specialized designs for mixtures, screening factors (factorial designs) and the quantitation of factor impacts on responses (response surface methods, RSMs) ¹⁵. Furthermore, RSMs can be realized as central-composite designs but can also be achieved effectively by using specialized software that can apply different criteria for the selection of runs. For example, the so called D-optimality criterion will select runs so to minimize the error in the coefficients of the resulting model, whereas the IV-optimality criterion selects runs that achieve the lowest prediction variance throughout the design space ^15,16. The RSM we describe here allows the precise quantitation of transient protein expression in plants, but it can easily be transferred to any system involving several (~5-8) numeric factors (e.g. temperature, time, concentration) and a few (~2-4) categoric factors (e.g. promoter, color) in which a mechanistic description is unavailable or too complex to model.

The DoE approach originated in the agricultural sciences but has spread to other areas because it is transferable to any situation where it is useful to reduce the number of runs necessary to obtain reliable data and generate descriptive models for complex processes. This in turn has led to the inclusion of DoE in the "Guidance for Industry, Q8(R2) Pharmaceutical Development" published by the International Conference on Harmonisation of Technical Requirements for Registration of Pharmaceuticals for Human Use (ICH) ¹⁷. DoE is now used widely in scientific research and industry ¹⁸. However, care must be taken during the planning and execution of the experiment because selecting an improper polynomial degree for the multiple-linear-regression model (base model) can introduce a need for additional runs to model all factor effects correctly. Furthermore, corrupted or missing data generate incorrect models and flawed predictions, and may even prevent any model building attempt as described in the protocol and discussion sections ¹⁸. In the protocol section, we will initially set out the most important planning steps for a RSM-based experiment and then explain the design based on the DoE software DesignExpert v8.1. But similar designs can be built with other software including JMP, Modde, and STATISTICA. The experimental procedures are followed by instructions for data analysis and evaluation.

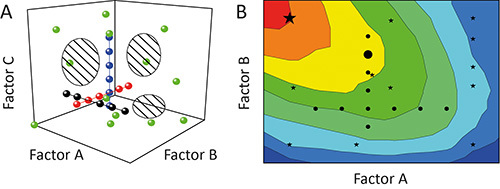Figure 1. Comparison of OFAT and DoE.A. Sequential variation of one factor at a time (OFAT) in an experiment (black, red and blue circles) achieves a low coverage of the design space (hatched regions). In contrast, the variation of more than one factor at a time using the design of experiments (DoE) strategy (green circles) enhances the coverage and thus the precision of the resulting models. B. The biased design space coverage means that OFAT experiments (black circles) can also fail to identify optimal operating regions (red) and predict sub-optimal solutions (large black circle), whereas DoE strategies (black stars) are more likely to identify preferable conditions (large black star).

Protocol

1. Planning a DoE Strategy

1. Identify relevant factors and responses for inclusion in the design.

   1. Define one or several responses for measurement. Here, 2G12 and DsRed expression levels were used (μg/ml), including the minimum detectable difference regarded as relevant (10 and 20 μg /ml, respectively) and an approximate value for the estimated standard deviation of the system (4 and 8 μg/ml, respectively) based on previous experiments.
   2. Use the available literature, data from previous experiments or specialized screening designs (e.g. a factorial design, see the introduction) to select significant factors whose impact on the responses will be quantified (Table 1) ^7,8,19,20.
   3. Allocate the factor types (numeric or categoric) and select ranges within which the numeric factors will be varied during the DoE investigation (Table 1).
   4. Identify numeric factors for which continuous variation is difficult to implement.

      1. Avoid using continuous variation for factors that cannot be adjusted precisely to a certain level. e.g. Incubation temperature can typically be controlled only within ±2 °C, therefore continuous variation using values such as 27.2 °C, 25.9 °C, and 29.3 °C must be avoided.
      2. Instead, select a number of discrete levels for these factors (Table 1). The number of levels should match the anticipated base model (step 1.2).This is only important for optimal designs, because central composite designs always have discrete factor levels.
   5. Assign whether a categoric factor is nominal, i.e. no implied order (e.g. different manufacturers), or ordinal and thus a discrete numeric parameter (e.g. different leaves on a plant).
   6. Select the levels for both types of categoric factors.
2. Select a useful base model.

   1. Based on the preliminary experiments and literature, anticipate the relation between each factor and the response as well as factor interactions and the response. For example, linear (the more the better), quadratic (single optimum or nonlinear increase/decrease) or cubic (skewed optimum).
   2. Make sure that the number of levels for discrete numeric factors is n + 1, with n being the polynomial degree of the relation between factor and response. For example, if temperature is expected to have a quadratic effect on the response, n = 2 and hence at least three temperature levels should be investigated to achieve a fit to the quadratic effect.

3. Define the fraction of design space (FDS) for which the prediction variance should be below a certain threshold (alpha level). The FDS should be >0.95 (cover more than 95% of the design space) to achieve models that yield robust predictions throughout the entire design space ^21-23 . Note: A threshold of 0.05 corresponds to a 5% significance level (type I error) and is a typical value. Increasing this value will reduce the number of experiments required for a DoE strategy but will simultaneously increase the likelihood that significant effects will be missed and that estimates of their impact on the response will be incorrect.

Table 1. Factors affecting transient protein expression in tobacco including the variation ranges during DoE. Factors in bold were only included in the design for the experiments described under "A descriptive model for DsRed accumulation during transient expression using different promoter/5'UTRs" whereas factors in italics were only included in the design for "Optimizing incubation conditions and harvest schemes for the production of monoclonal antibodies in plants using transient expression".

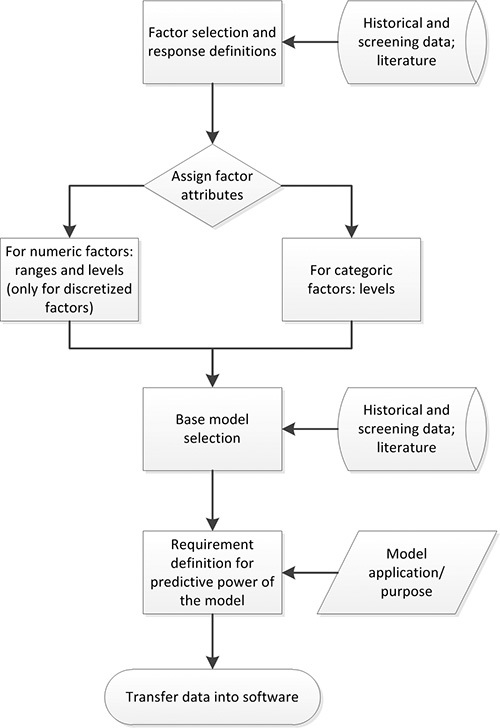Figure 2. DoE planning process. Factors with a significant impact on the response under investigation are selected based on available data. Then factor attributes (e.g. numeric), ranges and levels are assigned. Previous knowledge and experiments are used to define a suitable base model. The predictive power requirements are defined based on the application/purpose of the final model. The compiled data can then be transferred into appropriate DoE software.

2. Setting up a RSM in DesignExpert

1. Start DesignExpert and select "New Design". In the "Response Surface" window, choose "Optimal" and enter the number of numeric and categoric factors selected in section 1.1).

2. Enter factor names, units, types, sub-types, number of levels/level borders and values for the levels for all factors in the corresponding fields.

3. Continue to the next page and under "Search" options select "Best" as well as the desired "Optimality" criterion, here "D-optimal".

4. In the "Edit model…" menu, select the model that contains the factors and interactions anticipated in section 1.2). If uncertain, select a full model that covers all factors and interactions for a certain polynomial degree, here "Quadratic". Note that selecting a full model (containing all interactions) can increase the number of experiments required for the DoE.

5. Select the number of "Blocks". Here, a single block was used because all plants were from the same batch, all bacteria had been cultured simultaneously and all injections were carried out on the same day by the same operator. Use more than one block if more than one batch of plants is used or several operators handle the injections.

6. Balance the design

   1. Enable "Force categoric balance" in order to distribute the runs of the experiment evenly among the categoric factor levels, e.g. different promoters that are tested. Note: this can reduce the optimality of the design to a degree that DesignExpert will report as a % value depending on the points selected by the optimality algorithm.
   2. Recalculate the design several times using the implemented random seed algorithm to minimize the reduction in optimality. Note: losses in optimality can range from ~3-40% using the same input data, but changing the number of replicates can be used to maintain categoric balance.

7. The software will suggest a value for the number of "Model points" based on the base model, here 70 runs. Adjust the number of runs for "Replicates" and "To estimate the lack of fit" to ensure it is >5% of the number of "Model points" for each, here 10 runs each.

8. Continue to the next page, select the number of responses and enter their names and units. Additional responses can also be added at any time during data evaluation without any negative impact on the design.

9. Continue to start the algorithm, calculating the factor levels for the runs of the DoE. If the selected base model does not match the number of levels for a certain factor, a notification will be displayed and the calculation will not start. In this case either:

   1. Increase the number of levels for this factor; or
   2. Deselect the terms in the base model that cannot be calculated based on the current number of levels.
   3. For example, if there are two levels for the factor "Incubation time" t (i.e. 2 d and 5 d) in the current design and a quadratic base model including the term t² was selected, either add a third level for t (i.e. 8 d) or remove the factor t² from the model.

10. Save the spreadsheet containing the optimal factor combinations that is displayed once the calculation is complete.

11. In the "Design" node select the "Evaluation" sub-node and go to the "Graphs" tab.

    1. In the "Graphs tool" select "FDS" and in the "FDS Graph" box choose "Pred" as the error type. Then enter the minimum detectable difference as well as the approximate value for the estimated standard deviation of the system defined in section 1.1.1) as values for "d" and "s" respectively (here 20 and 8 μg/ml for DsRed). Also enter the alpha level (acceptable % missing a significant effect) suitable for the application, typically 0.05 (5%).
    2. Make sure that the calculated FDS matches the percentage defined in section 1.3) (typically >0.95 for predictive models). A flat curve in the FDS plot is preferable, indicating uniform prediction accuracy throughout the design space.

       1. If this is not the case (as found here, FDS was 1% as shown in Figure 3A), go back to the "Design" node and in the task bar select "Design Tools", then "Augment Design…" and choose "Augment".
       2. Select the same "Search" and "Optimality" criteria as before. Also chose the same "Edit model" and "Force categoric balance" settings. If the design augmentation is performed before any experiment (as done here), then change the "Put runs into block" setting to "Block1".
       3. In the "Runs" section enter the number of additional "Model points", maintaining at least 5% "Replicates" and "To estimate lack of fit" in the total design. Here, 100 additional runs were added and no "Replicates" and "To estimate lack of fit" were included.
       4. Once the calculation has finished, reexamine the FDS graph as described above. If the FDS is still not satisfactory, repeat the design augmentation as described above. Here the FDS was 100% after augmentation and thus no further augmentation was needed (Figure 3B).

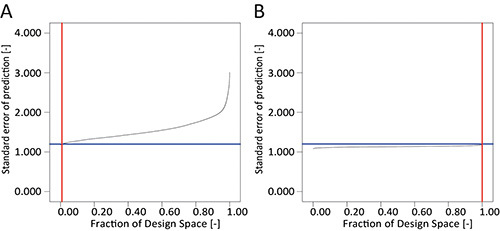Figure 3. Comparison of FDS plots. A. A DoE consisting of 90 runs produces an insufficient FDS of only 1% for the standard error of prediction, using a quadratic base model in combination with the values for the minimum detectable difference (20 μg/ml) and estimated standard deviation of the system (8 μg/ml). B. Augmentation of the DoE to a total of 210 runs achieved a 100% FDS and a flat curve indicating uniform precision of the model throughout the design space.

3. Cloning and Analysis of Expression Cassettes

1. Cultivate Escherichia coli in 5 ml LB medium (10 g/L tryptone, 5 g/L yeast extract, 170 mM NaCl, 50 mg/L ampicillin; for LB-agar plates include 15 g/L agar) at 37 °C for 6-8 hr or overnight on an orbital shaker at 160 rpm. CAUTION: ampicillin is a harmful substance. Inoculate the LB medium with either 50 μl of liquid culture or transfer cells from colonies grown on plates using a pipette tip.

2. For the purification of pSo plasmid DNA, and other derivatives of pPAM (GenBank AY027531), from E. coli K12 strain DH5a, follow the instructions in the DNA purification kit manual ²⁴ . CAUTION: the purification kit contains harmful chemicals (see above manual for details). The plasmid sequence is described in Figure 4 and by Buyer et al. ²⁰ .

3. Determine the DNA concentration in the purified eluate by measuring the absorbance of a 2 μl sample at 260 nm in a NanoDrop device.

4. Confirm the identity of the purified plasmid DNA by digestion with restriction endonucleases (REs).

   1. Select the REs according to the plasmid sequence so that unique and distinguishable fragment patterns are generated. Follow the manufacturer's recommendations for the digestion conditions such as reaction volume, time, temperature and concentration of the stabilizer bovine serum albumin. Depending on the sensitivity the analysis device, use 50-500 ng of plasmid DNA per digestion.
   2. Prepare 0.8-2.0% gels for the separation of DNA fragments by boiling agarose in Tris-borate-EDTA (TBE) buffer (90 mM Tris, 90 mM borate, 2 mM EDTA; pH 8.0). The larger the expected fragments, the less agarose should be used in the gel.
   3. Add 5 μl of five-fold sample buffer (5x SABU, 0.1% (w/v) bromophenol blue, 0.1% (w/v) xylene cyanol, 10% (w/v) glycerol dissolved in TBE) to 50 μl of the RE-treated DNA sample and separate the fragments by agarose gel electrophoresis at 100 V for ~40 min or until clear separation of the fragments is achieved. On each gel, include a lane containing DNA ladder size markers for comparison, e.g. 2-3 μl 1-kb ladder.
5. Replace the omega 5'UTR in pSo with one of the other three 5'UTRs.

   1. Release the omega 5'UTR sequence from ~4 μg purified pSo DNA by treatment with 20 units of EcoRI-HF and NcoI-HF REs in NEBuffer 4 at 37 °C for ~60 min. Then separate the fragments as described in sections 3.4.2 and 3.4.3.
   2. Isolate the larger fragment (pS, "backbone") from the agarose gel using a gel extraction kit according to the manufacturer's manual ²⁵ and determine the concentration of the purified DNA as described in section 3.3). CAUTION: the gel extraction kit contains harmful chemicals, see the manual for details.
   3. Isolate the CHS, CHS-LPH and TL 5'UTRs from suitable donor vectors by treating ~10 μg of each vector with 20 units of EcoRI-HF and NcoI-HF REs in NEBuffer 4 at 37 °C for ~60 min. Then separate the fragments as described in sections 3.4.2 and 3.4.3 and purify the smaller 5'UTR-containing fragment as described in section 3.5.2.
   4. Ligate the isolated purified 5'UTRs in separate aliquots to the isolated purified linear pS vector at 25 °C for 5 min according to the manufacturer's recommendations ²⁶. Use ~50 ng of vector DNA and a three-fold molar excess of 5'UTR DNA in a total volume of 20 μl.
6. Transformation E coli cells with the recombinant plasmids ^26,27.

   1. Add ~10 ng (~4-5 μl) of ligation mixture (see section 3.5.4) to 50 μl RbCl competent E. coli and mix gently, and then incubate for 30-60 min on ice. Heat shock for 1.5 min at 42 °C and chill on ice for 5-30 min.
   2. Add 950 μl of antibiotic-free LB medium and incubate for 1 hr at 37 °C and 160 rpm. For the selection of transformants, spread 50 and 100 μl of the culture on LB agar plates containing ampicillin and incubate for ~16-20 hr at 37 °C.
   3. Inoculate 5-10 separate colonies representing each promoter-5'UTR ligation described in section 3.1 into 5-ml aliquots of LB medium containing ampicillin. Then purify the plasmid DNA and confirm its identity as described in sections 3.2 to 3.4.

7. Replace the 35SS promoter with the nos promoter in each of the four 5'UTR plasmids using AscI and EcoRI REs in NEBuffer 4 at 37 °C for 1 hr as described in sections 3.5 and 3.6.

8. Introduce each of the eight resulting plasmids into A. tumefaciens strain GV3101:pMP90RK by electroporation ²⁸.

   1. Add ~500 ng of purified plasmid DNA to 50 μl competent A. tumefaciens cells on ice. Gently mix and transfer into a prechilled 0.2 cm electroporation cuvette. Make sure that the mixture is at the bottom of the cuvette and does not contain bubbles.
   2. Pulse cells at 2.5 kV for 5 msec and confirm the intensity and duration of the pulse.
   3. Avoid elevated salt concentrations in the DNA sample or incorrect preparation of the competent A. tumefaciens cells because these can result in high ion currents causing instant vaporization of the cell suspension, greatly reducing transformation efficacy.
   4. Add 950 μl of YEB medium without antibiotics (5 g/L beef extract, 1 g/L yeast extract, 5 g/L peptone, 5 g/L sucrose, 2 mM MgSO₄, pH 7.0), gently mix and transfer immediately into a sterile 1.5-ml reaction tube. Incubate for 2-4 hr at 26-28 °C and 160 rpm.
   5. Spread 1-2 μl onto YEB agar plates containing antibiotics (50 mg/L carbenicillin, 25 mg/L kanamycin, 25 mg/L rifampicin) for the selection of transformants. CAUTION: rifampicin is a toxic substance.
   6. Inoculate three 5-ml aliquots of YEB medium containing antibiotics with cells from separate colonies representing each promoter-5'UTR ligation and incubate for 48-72 hr at 26-28 °C and 160 rpm.
9. Confirm the success of A. tumefaciens transformation.

   1. Transfer 2 μl of each aliquot from section 3.8.6 to separate 48 μl aliquots of PCR mastermix (2 μl of each 10 μM primer stock (400 nM final concentration of each primer), 1 μl 10 mM dNTP mix (200 μM final concentration of each deoxynucleoside triphosphate), 5 μl 10-fold Expand High Fidelity buffer with 15 mM MgCl₂, 0.75 μl Expand High Fidelity enzyme mix, and 39.25 μl sterile distilled water).
   2. Amplify the expression cassette of each plasmid using appropriate primers (FWD: 5'-CCT CAG GAA GAG CAA TAC-3', binding 1026 nucleotides upstream of the promoter; REV: 5'-CCA AAG CGA GTA CAC AAC-3', binding within the 35S polyadenylation site) under appropriate PCR conditions. Here, 94 °C was used for initial denaturation followed by 30 cycles of 94 °C denaturation for 15 sec, 51 °C annealing for 30 sec and 72 °C elongation for 120 sec, and a final elongation step at 72 °C for 8 min.
   3. Determine the size of the PCR products by agarose gel electrophoresis as described in section 3.4.3.

10. Prepare A. tumefaciens glycerol stocks by mixing 500 μl 50% (v/v) sterile glycerol with 500 μl of A. tumefaciens cultures from section 3.8.6 for which transformation has been confirmed (section 3.9.3). Store the glycerol stocks at -80 °C until further use.

11. Calculate the folding energies of the different mRNAs using the RNAfold webserver ²⁹ and include the nucleotide sequence from the transcriptional start site through to the first 50 bp of the coding region.

    1. In the "Fold algorithms and basic options" section select the "minimum free energy (MFE) and partition function" and "avoid isolated base pairs" options.
    2. In the "Advanced folding options" choose "dangling energies on both sides of a helix in any case", "RNA parameters (Turner model, 2004)" and change "rescale energy parameters to given temperature (C)" to 25 °C.
    3. In the "Output options" section select all options.
    4. From the "Results for thermodynamic ensemble prediction" section of the output file, extract the "free energy of the thermodynamic ensemble" and the "frequency of the MFE structure in the ensemble" values for comparison.

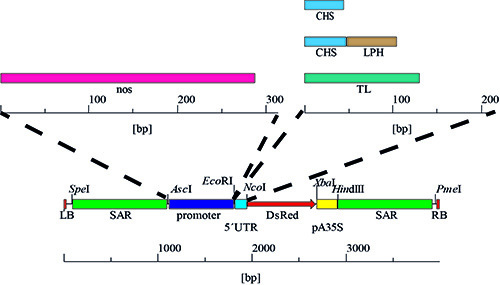Figure 4. Promoter and 5'UTR variants. The expression cassettes were generated by the stepwise exchange of the 5'UTR, resulting in four combinations with CaMV 35SS promoter, followed by the replacement of this promoter with the nos sequence yielding four additional variants and a total of eight different promoter/5'UTR combinations.

4. Plant Cultivation

1. Prepare a 0.1% solution of the fertilizer Ferty 2 Mega in de-ionized water at pH 5.9.

2. Prepare 10 x 10 x 8 cm rockwool blocks by extensive flushing with deionized water to remove residual chemicals and finally equilibrate with fertilizer.

3. Seed tobacco plants by placing 1-2 tobacco seeds on each rockwool block followed by a short flush with fertilizer being careful to avoid washing the seeds away.

4. Germinate and cultivate the tobacco plants for 42 days in a greenhouse at 25/22 °C day/night temperature, 70% relative humidity and a 16-hr photoperiod (180 mmol sec^-1 m^-2; λ = 400-700 nm). During this photoperiod, irrigate with fertilizer for 15 min every hour in hydroponic culture.

5. Transient Protein Expression

1. Prepare A. tumefaciens for injection into leaves.

   1. Inoculate 5-50 ml of YEB medium containing antibiotics with 1% A. tumefaciens cryo-stock culture and incubate at 27 °C until the OD_600nm reaches 5.0 (~48-72 hr depending on the volume and vessel type).
   2. Dilute the A. tumefaciens culture with water and 2-fold infiltration medium (4.3 g/L Murashige and Skoog salts (pH 5.6), 5 g/L sucrose, 1.8 g/L glucose, 100 mM acetosyringone) to match the OD_600nm required for injection. Confirm the OD_600nm just before injection. Note: An OD_600nm of 1.0 corresponds to ~1.43 ± 0.12 x 10⁹ colony forming units per ml.
2. Inject the A. tumefaciens suspension into leaves.

   1. Select and label the noncotyledon leaves and positions thereon to be treated (e.g. according to a DoE strategy).
   2. Do not inject different A. tumefaciens solutions into the same intercostal field. Instead, use opposing sections on each side of the mid-vein axis. If more than two different solutions need to be injected at the same position use an additional plant.
   3. Thoroughly shake A. tumefaciens solution to resuspend any cells that may have settled since preparing the dilution and aspirate into a 1-ml syringe.
   4. Gently scratch the epidermis at the position intended for injection with a pipette tip or similar to facilitate the influx of the A. tumefaciens solution. Avoid rupturing the leaf blade while doing so.
   5. Hold the syringe perpendicular to the leaf blade touching the barrel against the intercostal field to be treated and gently push the outlet (with no needle attached) onto the bottom side of the leaf. Press the top side of the leaf gently at the same time to prevent the leaf blade from shifting or rupturing.
   6. Gently push down the syringe piston. The A. tumefaciens solution will enter the intercellular spaces within the leaf blade as indicated by the treated areas appearing darker green and moist. Repeat this procedure at several positions until the whole intercostal field is infiltrated with A. tumefaciens. Then continue with the next intercostal field.
   7. Make sure the syringe remains perpendicular to the leaf. Tilting the syringe will cause the bacterial suspension to spurt out under high pressure.
   8. If different A. tumefaciens solutions are used (e.g. to test different promoters), remove any excess solution remaining on the underside of the leaf from the first injection using a paper towel or similar before applying the next solution.
3. Post-infiltration incubation of plants and sampling.

   1. Prepare a phytotron for the treated plants ~24 hr before injection to allow temperature and humidity equilibration at the levels required for the DoE.
   2. After injection, transfer plants into the phytotron and place them into trays large enough for irrigation with water until the end of the incubation period determined by the DoE.
   3. Establish a 16 hr photoperiod using six Osram cool white 36 W fluorescent tubes per 0.7 m² (75 mmol sec^-1 m^-2; λ = 400-700 nm). Prevent the plants from shading each other by limiting the number of plants to six per 0.7 m².
   4. Before sampling, make sure the correct intercostal field was selected by comparing the label added in section 5.2.1 and the DoE plan.
   5. Use a cork borer to remove 4-5 leaf discs from the treated intercostal fields at the positions and times indicated by the DoE. Do not remove the whole leaf from the plant during sampling. Stabilize the leaf with a hand-held paper towel while removing the discs to prevent rupture.
   6. Determine the mass of each sample and place it in a 1.5 ml plastic reaction tube labeled with sample name and mass. Store the samples at -20 °C or -80 °C before protein quantitation. The process may be paused at this stage for several months depending on sample stability and the storage temperature.

6. Protein Quantitation

1. Extract proteins from the leaf disc samples.

   1. Add 3 ml of extraction buffer (50 mM sodium phosphate, 500 mM sodium chloride; pH 8.0) per mg of sample mass and grind leaf discs in the reaction tube using an electric pestle until no large fragments remain. Avoid overheating of the sample.
   2. Remove dispersed solids by centrifuging the sample twice at 16,000 x g for 20 min at 4 °C. Transfer the supernatant into a clean 1.5 ml reaction tube after each step without disturbing the pellet.
   3. After centrifugation, the process may be paused by freezing the plant extracts at -20 °C or -80 °C for several months depending on the sample stability and storage temperature. Confirm that a freeze-thaw cycle does not affect the concentration of the target protein(s).
2. Measure the DsRed fluorescence.

   1. Prepare three technical replicates of each sample into black 96-well half-area plates (50 μl extract per well). Avoid the formation of bubbles during pipetting.
   2. Use a set of six dilutions (0, 25, 75, 125, 175 and 225 μg/ml) of a DsRed standard per 96-well plate to generate a liner reference curve. Prepare the dilutions in PBS and store them at 4 °C for use within 3 months.
   3. Measure the fluorescence twice, sequentially, in a 96-well plate reader fitted with 530/25 nm excitation and 590/35 nm emission filters.
   4. For each sample, average the fluorescence over the two reads and the three technical replicates and subtract the value recorded for the blank control containing 0 μg/ml DsRed. Also subtract this value from the reads of the standard dilutions and use these blank-corrected values for a linear regression yielding a reference curve (through the origin of ordinates).
   5. Use the slope of the reference curve to convert the fluorescence measured for the samples into DsRed concentrations. If necessary, dilute the samples so that the readout falls within the concentration interval of the standards and consider this dilution factor in subsequent calculations.
3. Determine the concentration of 2G12.

   1. Prepare a surface plasmon resonance (SPR) device for the measurement of antibody concentration by coupling Protein A to the activated surface of one flow cell. Use another flow cell as reference by inactivating the surface without coupling of Protein A ^30,31.
   2. Dilute plant extracts 1:20 in SPR running buffer (10 mM HEPES pH 7.4, 3 mM EDTA, 150 mM NaCl, 0.05% v/v Tween-20) and measure the response units (RU) of antibody binding to Protein A in three technical replicates of each sample at the end of a 90 μl injection (180 sec at 30 μl/min). Subtract the RU measured at the reference flow cell (no Protein A) from the RU measured in the experimental flow cell (Protein A surface).
   3. Measure a 585 ng/ml 2G12 standard after each 10-15 samples and subtract the value measured in the reference flow cells as described above. Use the average RU of these standards to calculate a linear reference curve through the origin of ordinates.
   4. Calculate the 2G12 concentrations in the samples based on the 1:20 dilution and the slope of the reference curve.
   5. Check for strong nonspecific binding to the reference cell, which can corrupt the measurement. Also check whether the 2G12 standards maintain approximately constant values (<5% variation) throughout analysis, as greater variation reflects aging of the Protein A surface.

7. Data Analysis and Evaluation

1. Manually analyze the responses observed in the expression experiments for (i) extreme values (high or low) indicating measurement errors; (ii) unusual results, e.g. factor combinations that generate unanticipated responses indicating data interchange; and (iii) missing values. Note: use these actions to prevent model building based on faulty data.

2. Transfer the analyzed response data (here the protein concentrations) into the "Design" node of DesignExpert. Make sure that response data are correctly assigned to the corresponding factor settings. There is an extensive help section available in the DesignExpert software that covers the aspects addressed below.

3. In the "Analysis" node, choose the response to be analyzed and initially select "none" in the transformation tab. Note: a transformation is recommended for min/max ratios of the response larger than 10. The most useful transformation can be obtained from the Box-Cox-plot in the "Diagnostics" tab in the "Diagnostics" section of the "Diagnostics tool" described below (section 7.8). A Log₁₀ transformation is often appropriate.

4. Continue to the "Fit summary" tab, which provides general information about factors that are important for the system under investigation (e.g. two-factor interactions, quadratic effects). The software will suggest an initial model based on its significance.

5. In the "Model" tab, an initial model is preselected based on the "Fit summary" results. Use the automated mode to edit this model:

   1. Select a "Process order" that is one order above the suggested model, e.g. if the suggested model is "2FI" (two factor interaction) then select "Quadratic".
   2. Choose "Backward" in the "Selection" field, which will iteratively remove nonsignificant terms from the model after proceeding to the "ANOVA" tab based on the "Alpha out" value which should initially be 0.100.
   3. If asked by the software, always automatically correct the model hierarchy because this is necessary to generate reliable models ^32,33.

6. In the "ANOVA" tab, investigate the suggested model and the included factors. If necessary, manually remove any factors with p-values above a predefined threshold (here 0.05, corresponding to a 5% significance level) or those that are unlikely based on mechanistic consideration by switching back to the "Model" tab, changing "Selection" to "Manual" and eliminating the appropriate factors from the model.

7. Back in the "ANOVA" tab, evaluate the refreshed model in terms of the p-value of the "Model" (a low value is desirable because this indicates significance) and the "Lack-of-fit" (a high value is desirable because this indicates lack of significance) as well as the values for "R-squared", "Adjusted R-squared" and "Predicted R-squared" (values > 0.80 are desirable for all three values).

   1. Compare these values for different models including/excluding factors at several significance levels. Note: it may be helpful to duplicate the response column in the "Design" node and perform each analysis individually, or to export the whole "ANOVA" table into another program such as a spreadsheet.
8. Continue to the "Diagnostics" tab to confirm the quality of the model and detect potential outliers in the dataset that have a strong influence on the model by examining all the tabs in the "Diagnostics Tool" ("Diagnostics" and "Influence" section).

   1. In the "Diagnostics" section of the "Diagnostics tool", perform the following actions:

      1. Ensure the points are randomly scattered within the limits in the "Residuals vs. Predicted" chart. Here, a chevron-shaped distribution indicates a need for data transformation.
      2. Ensure the points are randomly scattered within the limits in the "Residuals vs. Predicted" chart. Here, a chevron-shaped distribution indicates a need for data transformation.
      3. Investigate whether the points in the "Residuals vs. run" chart scatter randomly within the limits. A pattern (e.g. "stairway") indicates a trend in the data and block building can be used to counteract its influence on the model.
      4. Look for a straight diagonal line indicating the ideal model in the "Predicted vs. Actual" plot. The greater the scattering of data around the diagonal, the less accurate the model.
      5. Check for an overlap of the blue (best) and green (actual) vertical lines in the Box-Cox-plot indicating the data transformation. If the green line does not match the blue one (outside the interval indicated by the red vertical lines) go back to section 7.3 and improve the model building round by selecting the data transformation suggested by the Box-Cox-plot. Again the duplication of the response column can be useful to compare different models.
      6. Make sure that the points in the "Residuals vs. Factor" charts (there is one chart for each model factor) scatter randomly within the limits. Curvature in the data distribution may indicate a factor missing in the model.
   2. In the "Influence" section of the "Diagnostics tool", make sure there is random scattering of the data within the limits in the "Externally studentized residuals", "Leverage", "DFFITS" and "DFBETAS" plots and evenly low distribution without extreme values in the "Cook's Distance" plot.
9. In the "Model graphs" tab, visualize the evaluated model. For a limited number of numeric factors (e.g. 3) the response surface ("3D surface") representation is useful to assess optima/characteristics manually. Note: response surfaces only illustrate the impact of two factors on the response under investigation. The effect of any additional factor on the response is revealed by changing its value (numeric factors) or level (categoric factors) in the "Factors tool" window. Alternatively, factors can be assigned to the plot axis by right-clicking them in the "Factors tool" window and selecting the desired independent variable axis.

   1. Manipulate the factor levels and assign them to the graph ordinates using the "Factors tool".
   2. Export graphs using the "Export graph to file…" command in the "File" tab.
10. Use the "Numerical" sub-node in the "Optimization" node to optimize the response numerically (minimize, maximize, in range) depending on the model factors, to which in turn certain constraints can be applied (e.g. limits and weights) via the "Criteria" tab.

    1. Calculate and examine numerical solutions in the "Solutions" tab based on the input provided in the "Criteria" tab.
    2. Export these solutions to other software (e.g. spreadsheets) for further analysis (e.g. histograms) revealing the factor settings associated with high or low response values. Note: this is helpful if more than three numeric factors are investigated and 3D representation is difficult.
11. Use the "Point prediction" sub-node to predict the response for specific factor settings.

    1. Use this prediction for all settings to be evaluated (here, all promoter and 5'UTR combinations as well as all leaves and incubation times or leaf positions and incubation temperatures).
    2. Export the predicted values and compile them to a data array which can be used to describe transient expression in tobacco plants, e.g. by calculating the expression for a specific promoter-5'UTR combination at a certain time averaged over all leaf positions or across all leaves of a plant.
    3. Normalize the expression data based on the masses of the different leaves to yield the specific expression level (μg g^-1) or specific expression rate (μg g^-1 hr^-1).
    4. Alternatively, export the coefficients of the "Final equation" from the bottom of the "ANOVA" tab into a spreadsheet and multiply them with an array of factor settings to yield the same data array. Note: this array may only contain factor values from within the initial design space, because the fitted model equation is not suited for extrapolation.
12. Conduct a confirmation experiment for model points that are of major interest.

    1. Perform transient protein expression under conditions selected for "Point prediction" (section 7.11). E.g. use the same temperatures and leaves etc.
    2. Determine the protein concentrations for this transient expression experiment as describe above (section 6) and compare them with the values predicted by the model.
    3. Check whether the average protein concentration in the confirmation experiment falls within the response surface model's prediction interval obtained during point prediction. A match affirms the predictive power of the model. A mismatch indicates a low model quality and additional runs can be required.
    4. Note: plant batch-to-batch variability broadens the prediction interval and may devaluate confirmation experiments performed with a different batch of plants. However, samples that were not used to generate the model but that originated from the same plant batch as the samples contained in the model may serve as effective controls.

Representative Results

A descriptive model for DsRed accumulation during transient expression using different promoters and 5'UTRs

DsRed fluorescence in leaf extracts was used to indicate the expression level of the recombinant protein and thus was used as the response in the DoE strategy. The minimum detectable difference we considered relevant was 20 μg/ml and the estimated standard deviation of the system was 8 μg/ml based on initial experiments. Factors included in the transient expression model were selected based on literature data ^7,8 and our previous results ⁹. The investigated ranges were also chosen according to these data (Table 1). At least three levels were selected for all discrete numeric factors to allow the calculation of a quadratic base model. A D-optimal selection algorithm was chosen for the selection of the DoE runs to obtain the most accurate estimates for the coefficients of the regression model. The design initially suggested by DesignExpert consisted of 90 runs but the FDS was insufficient to achieve a 1% standard error of prediction (Figure 3A). D-optimal augmentation of the design to a total of 210 runs resolved this issue and resulted in a FDS of 100% with more uniform prediction accuracy across the design space indicated by the flat curve (Figure 3B).

The DsRed concentrations were determined for all 210 runs and the data were Log₁₀ transformed. Model factors were chosen by automated backward selection from a cubic model with an alpha level of 0.100. This resulted in a significant model (Table 2) with insignificant lack-of-fit and high values for the multiple correlation coefficients (Table 2). The p-value of all model factors was <0.05 and thus no further manual manipulation of the model was required. The model contained three-factor interactions that were not part of the initial quadratic base model (Table 2). Re-evaluation of the FDS graph using all factors included in the final prediction model revealed that the FDS for the standard error of prediction had not significantly diminished by including the additional three-factor interactions (FDS = 0.99).

The model quality diagnostic tools in DesignExpert indicated that the data transformation was useful and there were no missing factors in the model because the normal plot of residuals showed linear behavior and no specific pattern was observed in the residuals vs. predicted plot (Figures 5A and 5B). There was also no trend throughout the course of the experiment to indicate a hidden time-dependent variable (Figure 5C). Instead, the model predictions were in very good agreement with the observed DsRed fluorescence (Figure 5D). We therefore assumed that the selected model was useful to predict the transient expression of DsRed in non-cotyledon tobacco leaves driven by different promoter/5'UTR combinations during a post-infiltration incubation period lasting 8 days. We also selected an artificial linear regression model without data transformation to illustrate the consequences of wrong factor selection and transformation (Figure 6). Clearly, the normal plot of residuals deviates from the expected linear behavior (Figure 6A) and there is a "v"-shaped pattern in the residuals vs. predicted plot instead of a random scatter (Figure 6B). Additionally, the residuals vs. run plot highlights two extreme values (Figure 6C), while predictions are poor for both, small and high values, deviating from the optimal model (diagonal) (Figure 6D).

The 5'UTR combinations with the CaMV 35SS promoter resulted in stronger DsRed expression than combinations with the nos promoter (Figures 5A and 5B) as previously reported ³⁴ and the corresponding factors were found to be significant in the DoE model (Table 2). The model also predicted that leaf age was a significant factor (Table 2) with expression levels shown to be higher in young leaves (Figures 7B and 7D) which was in good agreement with our previous findings ¹⁹ and those of others ^7,8. The progression of DsRed accumulation in leaves was not linear or exponential but followed a sigmoidal curve during the 8 days of post-infiltration incubation according to the model. Interestingly, there was no fixed order of the 5'UTRs in terms of corresponding DsRed expression. Hence, the "strength" of a 5'UTR was dependent on the accompanying promoter. It is unlikely that this interdependence between the promoter and 5'UTR would have been revealed using an OFAT experiment. The predictive model also indicated that certain pairs of promoter/5'UTR combinations (e.g. CaMV 35SS/CHS and nos/CHS (Figures 7A and 7B), CaMV 35SS/omega and nos/CHS or CaMV 35SS/CHS and CaMV 35SS/TL) resulted in a balanced expression levels, differing by less than 30% from a defined ratio across all leaves and incubation times >2 days (e.g. for CaMV 35SS/omega and nos/CHS the ratio was ~8.0) ²⁰. Such balanced expression would be useful for the expression of multimeric proteins such as IgA with a defined stoichiometry ^35,36.

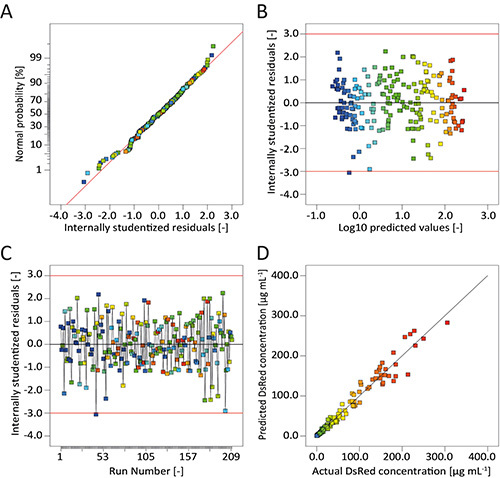Figure 5. Graphical evaluation of model quality. A. The normal probability plot of the internally studentized residuals indicates normal distribution because the residuals follow a line. B. Internally studentized residuals scatter around the value zero for all ranges of the predicted response (fluorescence) indicating an appropriate data transformation. C. Internally studentized residuals scatter around the value zero during the whole course of the experiment, showing the absence of hidden temporal effects. D. Predicted and actual values of the response are in good agreement as all points lie close to the diagonal (ideal model).

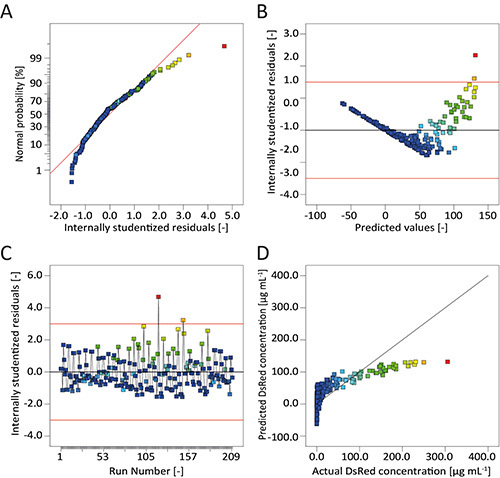Figure 6. Diagnostics indicating low model quality.A. The normal probability plot of the internally studentized residuals indicates non-normal distribution because the residuals deviate from a line. B. Internally studentized residuals show a "v"-shaped distribution indicating an inappropriate data transformation. C. Internally studentized residuals scatter not around the value zero during the whole course of the experiment, but exhibit a tendency towards positive values. Additionally, two extreme values can be found. D. Predicted and actual values of the response are in poor agreement as most points deviate from the diagonal (ideal model).

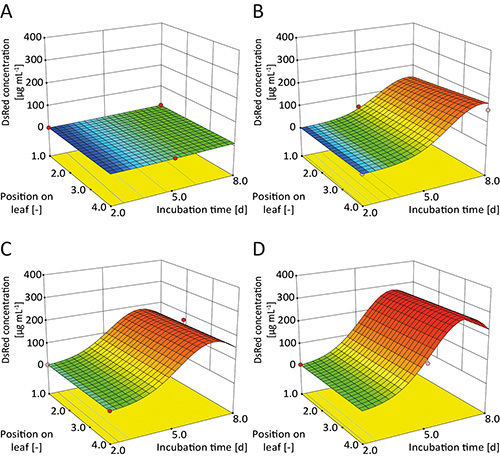Figure 7. Response surfaces for transient DsRed expression in tobacco leaves.A. nos/CHS in leaf 2; B. CaMV 35SS/CHS in leaf 2; C. CaMV 35SS/TL in leaf 6; D. CaMV 35SS/CHS in leaf 6. DsRed concentrations increased in a sigmoidal manner during the incubation period. Expression levels were lower in old leaves (e.g. leaf 2 in A and B) compared to young leaves (e.g. leaf 6 in C and D) and for nos (A) compared to the CaMV 35SS promoter (B). The 5'UTR also had a significant impact on DsRed expression (e.g. TL (C) vs. CHS (D)) but the expression strength was dependent on the accompanying promoter.

Source	Sum of squares	df	Mean square	F-value	p-value
Model	174.85	95	1.84	182.12	< 0.0001
Position on leaf (A)	0.16	1	0.16	16.06	0.0001
Incubation time (B)	112.46	1	112.46	11128.22	< 0.0001
Leaf age (C)	15.24	7	2.18	215.39	< 0.0001
Promoter (D)	23.49	1	23.49	2324.29	< 0.0001
5'UTR (E)	0.93	3	0.31	30.61	< 0.0001
AC	0.24	7	0.034	3.38	0.0026
BC	1.46	7	0.21	20.64	< 0.0001
BD	2.27	1	2.27	224.51	< 0.0001
BE	0.87	3	0.29	28.74	< 0.0001
CD	0.29	7	0.042	4.11	0.0005
CE	0.43	21	0.021	2.04	0.0093
DE	0.48	3	0.16	15.73	< 0.0001
B2	6.34	1	6.34	627.29	< 0.0001
BCD	0.95	7	0.14	13.42	< 0.0001
BCE	0.39	21	0.019	1.83	0.0230
BDE	0.16	3	0.054	5.37	0.0017
B2D	1.49	1	1.49	147.93	< 0.0001
Residual	1.15	114	0.010
Lack-of-fit	1.08	104	0.010	1.45	0.2669
Pure error	0.072	10	7.153E-003
Correlation total	176.01	209
Correlation coefficients	Value
R-Squared	0.9935
Adjusted R-Squared	0.9880
Predicted R-Squared	0.9770

Table 2. Factors included in the predictive model for transient DsRed expression in tobacco leaves using different promoter/5'UTR combinations. Three-factor interactions are highlighted in bold.

Optimizing incubation conditions and harvest schemes for the production of monoclonal antibodies in plants by transient expression

The DoE approach was also used to optimize the incubation temperature, bacterial OD600nm for leaf infiltration, plant age and harvest schemes, for the simultaneous production of the monoclonal HIV-neutralizing antibody 2G12 and DsRed in tobacco ¹⁹. The harvest scheme determined which leaves were used for protein extraction, e.g. the six uppermost leaves. We therefore established a predictive model for the expression of each protein (2G12 and DsRed) in plants at different ages (young = early bud stage = harvest at 40 days after seeding; old = mature bud stage = harvest at 47 days after seeding). These four models were then evaluated and a consensus model established that included each factor found to be significant in the individual models. We then confirmed that the consensus model was still a good representation of all initial data sets (Table 3). The consensus model was then used to identify optimal incubation temperatures (~22 °C for 2G12 and ~25 °C for DsRed) and bacterial OD_600nm (~1.0) for both proteins. These optimal conditions were then used to predict protein concentrations in all leaves (1-8) and leaf positions (1-4) in young and old plants. The concentration profiles were integrated with biomass data ¹⁹ to yield the absolute amount of target protein obtained from different leaves and plant ages (Figure 8A). Absolute protein amounts were then correlated with associated downstream costs allowing us to carry out a cost-benefit analysis for the processing of each leaf/plant age. This revealed that young plants were advantageous for transient expression because the proteins reached higher concentrations during shorter growth periods despite the lower overall biomass compared to old plants (Figures 8B and 8C). We also found that processing all the leaves from old plants was more expensive than discarding leaves 1-3 and increasing the number of plants per batch instead (Figure 8D). Hence, DoE-based models are suitable not only to mark the final step of an experiment, but also for combination with other data to facilitate more complex aspects of process analysis. A series of interconnected models covering the whole production process for a biopharmaceutical protein could be the ultimate goal.

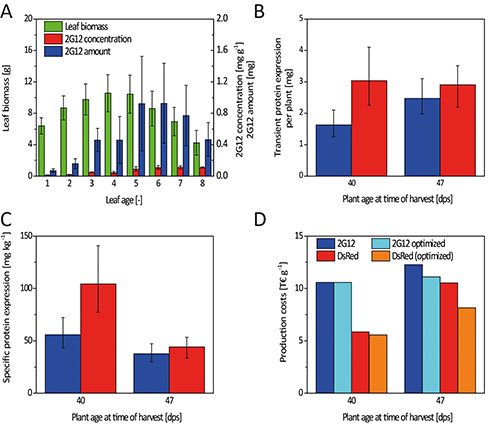Figure 8. Integration of biomass and protein concentration data resulting in absolute protein yield and process costs. A. Leaf biomass and target protein concentration did not develop in a collinear manner resulting in a biased accumulation of 2G12 in young leaves. B. The same amount of DsRed and ~65% of 2G12 was found in young plants compared to old ones despite a ~50% lower average biomass. C. This reflected the higher specific protein expression in young plants. D. The increased specific expression translated into reduced production costs for both proteins because less biomass needed to be processed requiring less greenhouse space, fewer consumables (e.g. filters), and less downstream equipment.

Plant age [dps]	40	47
Target protein [-]	DsRed	2G12	DsRed	2G12
Model [-]	Initial	Consensus	Initial	Consensus	Initial	Consensus	Initial	Consensus
R-squared [-]	0.9829	0.9577	0.9321	0.9099	0.9436	0.9403	0.8826	0.8782
Adjusted R-squared [-]	0.9711	0.9480	0.9059	0.8893	0.9362	0.9350	0.8716	0.8674
Predicted R-squared [-]	0.9510	0.9336	0.8272	0.8587	0.9254	0.9282	0.8554	0.8516

Table 3. Comparison of correlation coefficients for initial RSM models and the final consensus model of DsRed and 2G12 expression in tobacco plants.

Discussion

Every experiment requires careful planning because resources are often scarce and expensive. This is particularly true for DoE strategies because errors during the planning phase (e.g. selecting a base model that does not cover all significant factor interactions) can substantially diminish the predictive power of the resulting models and thus devalue the entire experiment. However, these errors can easily be avoided by following basic procedures.

Considerations during DoE planning

First, it is important to select a response that is suitable to evaluate the outcome (positive or negative) for each DoE run. For example: the concentration of a target protein determined by UV absorption ³⁷ is useful to assess the activity of a certain promoter/5'UTR combination. However, functional evaluation of a protein (e.g. by fluorescence in the case of DsRed or binding to Protein A in the case of 2G12) is even better because it also includes a protein quality aspect. Responses can also be values calculated from two or more separate parameters, such as the power number NP in fermentation experiments (calculated from power input, rotational speed and stirrer diameter). The response should yield values with high precision (i.e. low standard deviation) and accuracy (i.e. zero or few interfering parameters) to improve the model quality. Suitable detection devices and methods should therefore be optimized prior the experiment if necessary.

Factors affecting the response must be identified before the DoE is implemented because the RSM is used to determine the precise impact of the factors and not to select them. The selection of factors with a significant influence on the response can be achieved by studying literature data but full or fractional factorial DoE strategies are more effective. These screening experiments should also be used to determine a range for each factor within which meaningful results can be achieved, e.g. in biological systems the factor "temperature" is often restricted to the range 10-40 °C. Discrete levels should then be defined within these ranges for numeric factors that are technically difficult to control, e.g. phytotron temperatures have a tolerance of ±2.0 °C so it is inappropriate to investigate temperature differences of ±1.0 °C. Practical limitations may also come into play, e.g. using >25 different concentrations of a particular compound. However, the number of levels must be at least one greater than the anticipated polynomial order of that factor in the base model, e.g. if the polynomial order of temperature is n = 2, then at least three temperature levels must be investigated. Using base models of high polynomial order (cubic or above) is an option if the polynomial order of a factor is uncertain. However, this can significantly increase the number of runs required for the DoE.

For complex systems with many factors and high polynomial orders this can result in designs which cannot be calculated effectively. In such cases it may be advisable to split the problem into two or more designs investigating different subsets of factors. However, the significant factors omitted from such "split-designs" must be carefully adjusted to fixed values to prevent any distortion of the results. Each split-design should be repeated at different settings for the omitted factors to reveal interactions between them and the factors included in the design. It is beneficial to identify the factors with the greatest impact on the response and include them in all designs.

Critical aspects during DoE evaluation

The FDS should be the first parameter assessed in a newly-calculated DoE. The operator must confirm that the DoE provides the necessary coverage of the design space for the required minimal detectable difference and estimated standard deviation of the response. If this is not the case, the design should be augmented with a suitable number of runs and replicates until the requirements are met. The procedure to calculate DoE runs can be initialized several times to select designs with a minimal loss of optimality if the balance between categoric factors is enabled.

Data transformation should be carried out if response values span more than one order of magnitude. A Log₁₀ transformation is often appropriate but the Box-Cox plot will suggest the transformation that will yield the most stable model. The transformation suggested in this plot may change once the final model has been selected and should therefore be reevaluated. Only significant factors (p-value < 0.05) should be included in the response surface model in order to guarantee its predictive power. Exceptions can be made to maintain the model hierarchy ^32,33 or to include factors that are known to have an effect based on previous results. In the latter case, it is advisable to investigate why such important factors were not found to be significant in the current DoE. The lack-of-fit parameter can be used in combination with the R-squared value (Tables 2 and 3) for the rapid detection of poor models/fits, whereas the adjusted R-squared indicates whether too many/insignificant factors have been selected and the predicted R-squared is an indicator for the predictive power of the model. However, the residual plots provided in the diagnostics section of DesignExpert are even more important to assess the model quality because they allow the detection of trends in the dataset indicating the presence of hidden factors as well as the identification of extreme values. The latter have an above average impact on the fit and distort the model. Such values can originate from flawed data (e.g. permuted values) that must be corrected, or from failed experiments that must be repeated. If an extreme value is found to be "real" in such repetition experiments it is advisable to add several runs in the proximity of this value to improve the model quality within this region of the design space.

Corrections to designs which are imperfect or too small

Regardless of why additional runs may be required (e.g. missing data, failed runs, genuine extreme values and regions, unanticipated high order factor interactions), these runs should be added to the existing design in an ordered manner by using the "Design augmentation" tool to introduce the new runs in a separate block. Doing so will facilitate the use of the previous dataset while selecting the most meaningful additional runs. The result will be a model that fits to the data and allows the reliable prediction of future results.

Disclosures

The publication fee was partially sponsored by the companies Statease, Inc. (USA) and Statcon (Germany), which were not involved in the involved in the preparation of the manuscript or responsible for any of its contents.