Single-Cell Analysis Uncovers Extensive Biological Noise in Poliovirus Replication

ABSTRACT

Viral infections often begin with a very small number of initiating particles. Accordingly, the outcome of an infection is likely to be affected by variability in the initial molecular interactions between virus and host. In this study, we investigated the range of outcomes upon infection of single cells. We isolated individual cells infected with poliovirus at low or high multiplicities of infection (MOI) and measured viral genomic replication and infectious viral progeny in each cell. We first determined that at 7 h postinfection, the ratio of positive to negative strands in individual cells varies from 5:1 to more than 190:1, with and average of 20:1, suggesting a significant variability in RNA synthesis. We further found that while virus genome production is higher in cells infected at a high multiplicity, the production of infectious particles is largely independent of the number of viruses infecting each cell. Strikingly, by correlating RNA and particle production within individual infections, we uncovered a significant contribution of stochastic noise to the outcome of infection. At low MOI, stochastic influences appear as kinetic effects which are most critical at the initial steps in infection. At high MOI, stochastic influences appear to dictate the virus's ability to harness cellular resources. We conclude that biological noise is a critical determinant of the overall productivity of viral infections. The distinct nature of stochasticity in the outcome of infection by low and high numbers of viral particles may have important implications for our understanding of the determinants of successful viral infections.

IMPORTANCE By correlating genome and particle production in single-cell infections, we elucidated sources of noise in viral infections. When a cell was infected by only a single infectious particle, variation in the kinetics of the initial steps of replication contributed significantly to the overall productivity of the infection. Additionally, variation in the distribution of subcellular resources impacted infections initiated by one or many infectious particles. We also observed that when a cell was infected with multiple particles, more genomes were produced, while particle production was hindered by an apparent cellular resource limit. Understanding variations in viral infections may illuminate the dynamics of infection and pathogenesis and has implications for virus adaptation and evolution.

INTRODUCTION

When a virus infects a cell, it sets in motion a complex group of reactions. Some reactions, programmed by the viral genome, lead to virus replication and progeny production, while others, inherent to the host, act to restrict or limit viral replication. It is unclear how these contrasting forces shape the outcome of an infection. In principle, an infection is a seemingly deterministic series of processes—uncoating, translation, replication, and encapsidation. However, infections often begin with so few molecules that the progress of any given infection may occur in a more stochastic manner than is often appreciated (1). Indeed, individual cells in a population infected with the same virus at the same multiplicity of infection (MOI) have been observed to produce varied levels of viral progeny. The first rigorous observation of this variation during infection was made using single bacteriophage infections, where the large distribution in burst size (progeny per infected cell) could not be explained simply by the distribution in bacterial size (2). More recently, the effect of cell size on virus yield was also examined in a mammalian RNA virus (3). This study confirmed that while host cell size is a factor contributing to virus yield, it is insufficient to explain the variation in burst sizes. The source of variation remains unknown. We hypothesized that by removing cell size-dependent variation, we should be able to uncover the extent of stochasticity in viral infection and define the contribution of other factors to the overall productivity of single-cell infections. Understanding this issue may illuminate the dynamics of infection and pathogenesis and has implications for designing therapeutic and preventive strategies.

In this study, we examined if nondeterministic, stochastic processes play a role in the outcome of viral infections. We determined the contribution of noise to RNA synthesis and infectious particle production in single-cell infections from cell size-selected populations. From each infected cell we accurately measured the generation of positive-strand RNA genomes; of negative-strand RNA templates, which are used as templates of replication for the positive-strand genome; and of infectious particles. Our measurements defined the variation in genome and viral progeny production across a cell population and allowed us to determine the correlation between the synthesis of viral RNA and infectious virus particle production in individual cells. Surprisingly, we did not observe tight correlations between the distributions of genomes and viral progeny, suggesting that stochastic effects have a significant impact on the outcome of infection. Furthermore, by comparing variation and stochasticity in cells infected at low and high multiplicities of infection, we observed that the sources of biological noise are different when cells are infected with multiple viral particles. While at a low multiplicity of infection the kinetics of the early replication events is a significant source of variation, at a high multiplicity of infection access to cellular resources becomes a determining factor in the outcome of infection. Our findings have important implications for the evolution of viral strategies of transmission and pathogenesis and raise the question of how viruses balance the distinct dynamics in singly and multiply infected cells.

MATERIALS AND METHODS

Cells and viruses.

HeLaS3 cells (ATCC CCL-2.2), provided by R. Geller and J. Frydmann (Stanford University), were maintained in 50% Dulbecco modified Eagle medium (DMEM)–50% F-12 medium supplemented with 10% newborn calf serum, 100 U/ml of penicillin, 100 U/ml of streptomycin, and 2 mM glutamine (Invitrogen). Poliovirus Mahoney type I genomic RNA was generated from in vitro transcription of prib(+)XpAlong. To generate virus, 20 μg of RNA was electroporated into 4 × 10⁶ HeLaS3 cells in a 4-mm cuvette with the following pulse: 300 V, 24 Ω, and 1,000 μF. The resulting virus was passaged at high multiplicities of infection (∼1 to 10) three times and then subjected to ultracentrifugation through a 30% sucrose cushion.

Infections.

HeLasS3 cells in 12-well plates were rinsed twice with phosphate-buffered saline (PBS) to remove unattached cells and then infected in 100 μl at an MOI of 10 or 0.1 for 20 min at 37°C. The inoculum was removed and cells were washed twice with PBS to remove any unattached virus. Cells were given 2% serum medium for 7 h and then frozen at −70°C. All lysates were thawed once on ice and then refrozen. Lysates were homogenized at a final concentration of 0.06% NP-40, incubated on ice for 20 min, vortexed, and aliquoted.

For serum starvation experiments, cells were plated in serum medium overnight, rinsed twice with PBS, and then given serum-free medium for 48 h. After infection with virus-containing PBS, cells were given serum-free medium for 7 h and then frozen at −70°C.

For experiments with PIK93, a phosphatidylinositol 4-kinase III beta inhibitor, after infection, cells were given 2% serum medium containing 1.5 μM PIK93 in dimethyl sulfoxide (DMSO) or DMSO (mock treated) for 7 h and then frozen at −70°C.

Isolation of individual infected cells.

HeLaS3 cells in a 6-well plate (1.335 million cells per well) were rinsed twice with PBS to remove unattached cells and then infected in 100 μl at an MOI of 10 or 0.1 for 20 min at 37°C. The inoculum was removed and cells were washed twice with PBS to remove any unattached virus. The cells were detached with 200 μl of 0.05% trypsin with EDTA for 3 min at 37°C. Trypsin was inactivated with 3 ml of 10% serum medium, and cells were pelleted at 300 × g for 3 min at 4°C. Cells were resuspended in cold 2% serum medium and placed on ice. Cells were sorted via light scattering to 1 cell per well of a 96-well plate containing 200 μl of 2% serum medium per well using a FACSAriaIII flow cytometer (BD Biosciences) under biosafety level 2 (BSL2) conditions. Tight gating of both forward and side scatter was performed to restrict the size heterogeneity of the population as well as eliminate cell debris and cell aggregates. Gating removed greater than 60% of the cell population, resulting in forward scatter pulse width variance (seen to correlate well with cell volume [4]), with a coefficient of variation (CV) of 0.06. The same gating settings were used to isolate cells from both infections. Isolated individual cells in 96-well plates were incubated for 7 h at 37°C and then frozen at −70°C. Plates were thawed once on ice and then refrozen. Lysates were homogenized by adding 20 μl of 0.66% NP-40 per well. Plates were sealed with adhesive plate seals (Thermo Scientific) and vortexed on high for 20 s. Plates were incubated on ice for 30 min and vortexed again, and then samples were aliquoted into fourths.

Chromosomal copy number analysis.

Batch-collected samples of 50,000 cells were isolated with or without gating and immediately fixed in 4% formaldehyde and stored at 4°C. Cells were stained with 40 μg/ml of propidium iodide and analyzed by fluorescence-activated cell sorting (FACS).

“Infection find” assay.

After homogenization, 30 μl of cell lysate from cells infected at an MOI of 0.1 was added to 30,000 cells in 1.8 ml of 5% serum medium in a deep-well 96-well plate and incubated for 5 days at 37°C. According to Poisson statistics, 30 μl of lysate ensures a 99% chance of transferring at least 1 PFU to the fresh cells as long as the original lysate contained at least 34 PFU. Growth of HeLaS3 cells in wells which received lysate from uninfected cells acidified the medium, allowing for colorimetric distinction of lysates which did and did not contain infectious virus.

Determination of PFU.

For single-cell measurements, 50 μl of lysate was used in the first dilution of a 50% tissue culture infective dose (TCID₅₀) assay, resulting in a final concentration of 0.001% NP-40, which we found did not inhibit growth of HeLaS3 cells. For population measurements, 166 μl of lysate was used in the first dilution of a TCID₅₀ assay. Calculations were based on the Reed-Muench method. The PFU count was determined to be 3.3 times the TCID₅₀. Measurements above the limit of detection but below the limit of quantification were included in distribution histograms (see Fig. 2Aiii and 2Bii) but excluded from other calculations and figures.

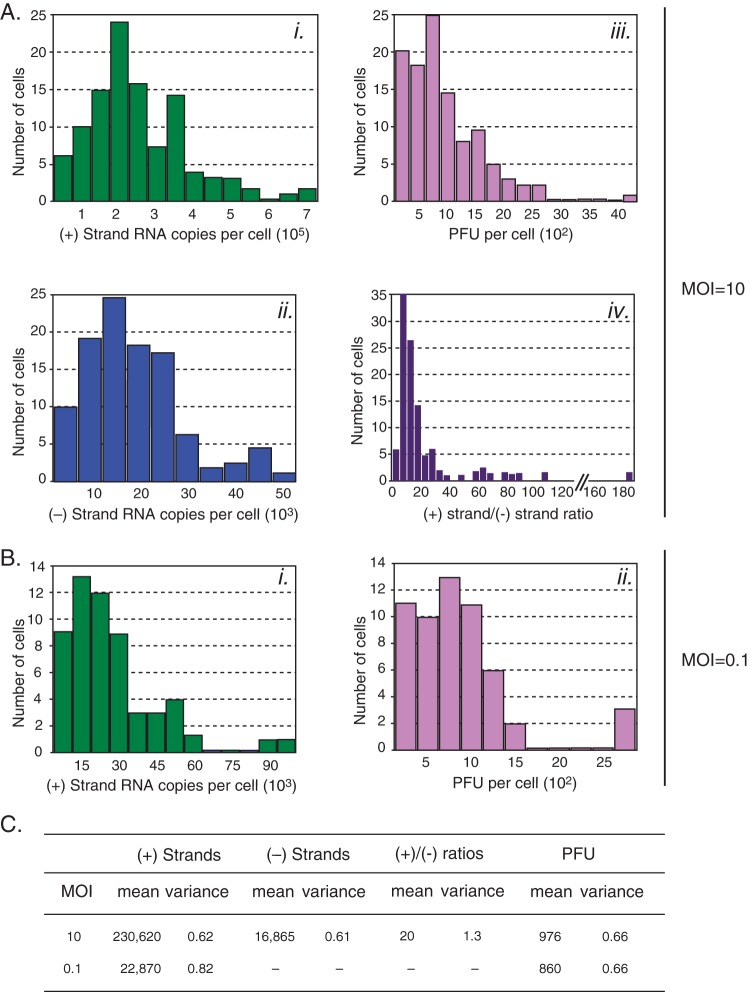
FIG 2.

Distributions of products from single-cell infections. (A) RNA and infectious virus distributions from cells infected at an MOI of 10; n = 106. (i) Positive-strand RNA; (ii) negative-strand RNA; (iii) infectious virus; (iv) ratio of positive-strand to negative-strand RNAs. (B) RNA and infectious virus distributions from cells infected at an MOI of 0.1; n = 56. (i) Positive-strand RNA; (ii) infectious virus. (C) Summary of means and variances from single-cell distributions. Mean variance is expressed as CV. Positive-strand RNA from infections at an MOI of 10 had a CV of 0.62 (95% confidence interval, 0.54 to 0.72). Positive-strand RNA from infections at an MOI of 0.1 had a CV of 0.82 (95% confidence interval, 0.67 to 1.01).

RNA extraction, RT, and qPCR.

RNA was extracted via the PureLink RNA microkit (Life Technologies) according to the manufacturer's instructions. cDNA was synthesized from total RNA using SuperScript III reverse transcriptase (Life Technologies) and 125 nM strand-specific reverse transcription (RT) primer (+strand_RT, 5′-GGCCGTCATGGTGGCGAATAATGTGATGGATCCGGGGGTAGCG-3′, and −strand_RT, 5′-GGCCGTCATGGTGGCGAATAACATGGCAGCCCCGGAACAGG-3′) in a 5-μl reaction volume. Separate RT reactions for positive- and negative-strand RNAs were performed for each sample. RT products were treated with 0.5 U of exonuclease I (Fermentas) to remove excess RT primer prior to quantitative PCR (qPCR). Strand-specific qPCR was based on a published protocol (5). cDNAs were analyzed by qPCR using 2× SYBR FAST master mix (Kapa Biosystems), 200 nM strand-specific qPCR primer (+strand_For, 5′-CATGGCAGCCCCGGAACAGG-3′, and −strand_Rev, 5′-TGTGATGGATCCGGGGGTAGCG-3′), and 200 nM Tag primer (5′-GGCCGTCATGGTGGCGAATAA-3′) in a 10-μl reaction volume. A 10× dilution series of in vitro-transcribed positive- and negative-strand RNA standards was run alongside experimental samples and used to construct a standard curve.

Bootstrapping for confidence intervals.

Confidence intervals were acquired in R (R Core Team, Vienna, Austria [http://www.R-project.org/]) using the bootstrapping package “boot” (R package version 1.3-9, Canty A, Ripley B). A total of 1,000 bootstrap replicates were performed for each statistic.

Sucrose gradients.

HeLaS3 cells were infected for 2, 4, or 6 h at an MOI of 10 in 15-cm dishes and simultaneously treated with 100 μg/ml of cycloheximide (CHX) for 2 min at 37°C. Cells were washed with PBS plus CHX and lysed with 0.5% NP-40 lysis buffer containing CHX on ice for 20 min. Cell debris was pelleted in a tabletop centrifuge at 2,000 rpm for 10 min at 4°C, and then nuclei were pelleted at 9,000 rpm for 10 min at 4°C. Cell lysates were loaded on a 10% to 50% sucrose gradient containing CHX and ultracentrifuged at 35,000 rpm for 3 h. Gradients were analyzed using a Biocomp gradient station with a Bio-Rad Econo UV monitor.

RESULTS

Estimating experimental noise.

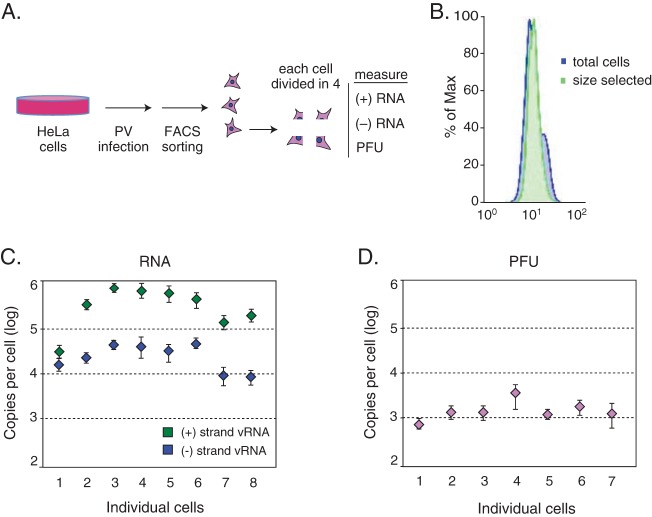
To determine the variance within infection of individual cells, we infected HeLaS3 cells with poliovirus Mahoney type 1 at two multiplicities of infection (MOIs): 10 and 0.1. Individual cells from each infection were isolated using a cell sorter with tight forward and side scatter gating to restrict cell size (4) (Fig. 1A). Chromosomal copy number analysis indicated that this cell sorter procedure enriched for cells in G₁ and S phases (Fig. 1B), which represent the most common cell cycle states (85% of a mixed-state population [6]) and have been shown to produce viral titers close to the average of a mixed-state population (3). Cell lysates were obtained and divided, allowing multiple measurements to be taken from each cell (Fig. 1A). We measured positive-strand viral RNA, negative-strand viral RNA, and PFU produced by each individual cell.

FIG 1.

Measurement error. (A) Schematic of single-cell isolation, division, and measurement. (B) Chromosomal copy number analysis shows enrichment of G₁/S-phase cells. (C) qRT-PCR measurements of positive-strand viral RNA and negative-strand viral RNA from 8 quartered control cells had average CVs of 0.21 and 0.23, respectively. (D) PFU measurements from 7 quartered control cells had an average CV of 0.31. Error bars indicate standard deviations.

To estimate experimental error of our measurements, we divided single cells into four fractions, and we measured either the viral RNA concentration or virus production in each of the four fractions separately. We utilized the coefficient of variation (CV), or relative standard deviation, for each set of measurements to normalize measurements with distinct mean values. Measurements of positive-strand RNA genomes and negative-strand RNA templates by qPCR from 8 control cells had average CVs of 0.21 and 0.23, respectively (Fig. 1C). Measurements of PFU from 7 control cells had a slightly higher average CV, 0.31 (Fig. 1D). The standard deviation measured in this experiment must result from experimental noise derived from cellular lysate fractionation into quarters, extraction, and/or all downstream analysis steps. Based on these measurements, we assumed that variance significantly greater than this experimental error represents the biological noise characteristic of the dynamic biological processes under study.

Fluctuations in virus replication revealed by measurements in single infected cells.

We first carried out an experiment in which cells were infected with a high multiplicity of infection. We isolated 106 cells infected at an MOI of 10. These cells had positive-strand RNA genome measurements ranging from 13,907 to 720,360 copies/cell (Fig. 2Ai). The mean value for positive-strand RNA genomes/cell was 230,620 copies, with a CV of 0.62 (Fig. 2C). Measurements of negative-strand RNA templates ranged from 2,157 to 45,990 copies/cell (Fig. 2Aii). The mean measurement of negative-strand RNA templates/cell was 16,865 copies, with a CV of 0.61 (Fig. 2C). Thus, the distribution of RNA accumulation from individual infected cells is highly dispersed, with some cells producing few copies of viral RNA and others extremely high concentrations. PFU measurements from these cells ranged from below our limit of detection of 269 to 4,225 PFU/cell (Fig. 2Aiii). Within the range we could detect PFU, the mean PFU per cell was 976, with a CV of 0.66 (Fig. 2C).

We first analyzed the ratio of positive- to negative-strand RNAs for poliovirus in individual infected cells. On average, the ratio of positive- to negative-strand RNAs was 20 to 1 at 7 h postinfection. Interestingly, individual infected cells displayed a wide range of ratios, from 2 to almost 200, resulting in a CV of 1.3. The average ratio of 20 we measured from within single cells is an accurate description of true strand ratio and is a statistically distinct measure from previously reported ratios of averages. Because average ratios and ratios of averages are incomparable, we use our data to compute a ratio of averages of 14 to compare to previous studies using different methodologies. Previously reported ratios of averages of 36 (7) and 30 (8) at 6 h postinfection along with observed decreases in the ratio between 4 and 6 h postinfection (7) suggest that our ratio of averages of 14 at 7 h postinfection is in line with previous studies.

We next determined whether initiating infection at a low MOI (0.1) further increased the biological noise in virus replication. Given that the majority of cells are expected to be uninfected at an MOI of 0.1 (9), it was necessary to identify infected cells from the population of cells before measuring RNA and infectious virus production. Accordingly, a small portion of isolated cell lysate was removed and used to infect fresh uninfected cells to determine the presence of infectious virus (see Materials and Methods). A total of 56 infected cells were then analyzed for RNA and virus production. These infected cell extracts contained between 1,580 and 91,897 copies/cell of the positive-strand RNA genome (Fig. 2Bi). This represents a mean count of positive-strand RNA genomes/cell of 22,870 copies, with a CV of 0.82 (Fig. 2C). While negative-strand RNA templates were detectable in these cells, the amount of copies accumulated was too low for confident quantification. PFU measurements from these cells ranged from below our limit of quantification to 2,713 PFU/cell (Fig. 2Bii). The mean value for PFU/cell was 860, with a CV of 0.66 (Fig. 2C).

Biological noise is greater in infections initiated at a low MOI.

To determine the contribution of the number of viruses initiating infection to the fluctuations observed in RNA and virus yield, we compared RNA and virus production distributions from an MOI of 0.1, where infections likely began with only a single infectious particle, with distributions from an MOI of 10, where infections began with a Poisson distribution around 10 infectious particles. We found that infections that began at an MOI of 10 produced, on average, 10 times more genomes than those initiated at an MOI of 0.1 (i.e., infections initiated by a single genome) (Fig. 2C). This is consistent with the idea that RNA replication is independently initiated by individual genomes, so more initiating genomes should, in principle, produce proportionally more viral RNA. Interestingly, we observed a significant difference in the fluctuations of genome productivity between the two infections, with a CV of 0.62 for an MOI of 10 and a significantly larger CV of 0.82 for an MOI of 0.1 (Fig. 2C). We argue that this difference in variance is likely to originate from the kinetic stochasticity of the early reactions that lead to productive infection. Infections beginning with multiple viral genomes (MOI of 10) average the effect on individual RNA replication reactions, are overall less susceptible to stochastic kinetics, and therefore produce a number of genomes closer to the mean than infections beginning with a single genome (MOI of 0.1).

The single infectious particles that initiate low-MOI infections are clearly more sensitive to effects on RNA replication. Low-MOI infections performed with subinhibitory concentrations of the RNA replication inhibitor PIK93 (10) produced significantly fewer genomes and PFU than high-MOI infections performed under the same conditions (Fig. 3). Low-MOI infections produced less than 75% as many genomes and less than 40% as many PFU as high-MOI infections relative to mock-treated cultures. Low-MOI poliovirus infections have previously been reported to produce a lower number of genomes than high-MOI infections in the presence of this inhibitor (10). We believe that longer delays in the initiation of the initial reactions, or increased kinetic stochasticity, caused by RNA replication inhibition dampen the productivity capacity of low-MOI infections.

FIG 3.

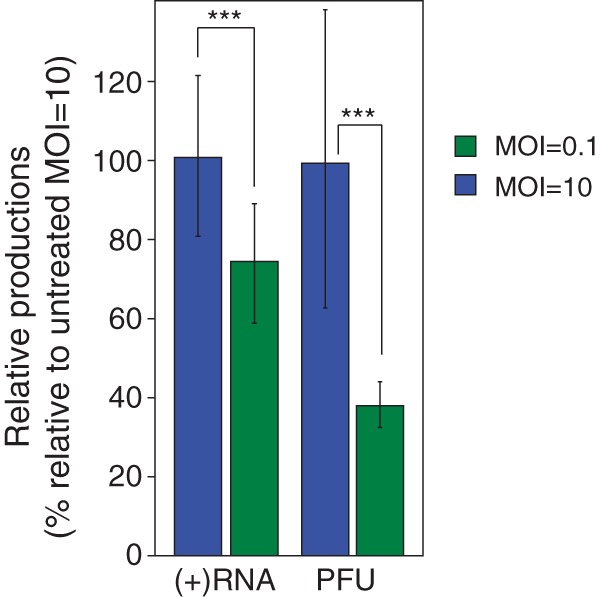
Low-MOI infections are more sensitive to RNA replication inhibition. In the presence of 1.5 μM PIK93, infections at an MOI of 0.1 produce less than 75% as many genomes and less than 40% as many PFU as infections at an MOI of 10 compared to mock-treated cultures; n = 6. ***, P < 0.05 by Student's t test. Error bars indicate standard deviations.

Infectious particle production is independent of MOI and RNA production.

Surprisingly, the effects of MOI and stochastic noise did not determine infectious particle production. The mean and variance of the distributions of PFU between the two infections were nearly equivalent (Fig. 2C). This observation suggests that infectious virus production is modulated by a limiting step in the infection that is not largely affected by the MOI-dependent stochastic noise. Furthermore, these observations were also confirmed at the population level, where genome production is proportional to MOI, but infectious virus production appeared to be independent of MOI and restricted by factors that do not depend on the initial kinetics of infection (Fig. 4A and B). We speculate that infectious virus production is limited by a global cellular resource required for virus particle formation. Consistent with this hypothesis, we observed a slightly higher mean PFU/cell in cell populations which had not been size restricted (population PFU measurements) (Fig. 4B). This global cellular resource limitation does not appear to be affected by serum starvation, which is expected to reduce the amount of cellular resources available for replication (Fig. 4C). Polysome profiling analysis on sucrose gradients indicates that free 40S and 60S ribosomal subunits are available throughout an infection, suggesting that ribosomal subunits are not limiting for virus production (Fig. 4D).

FIG 4.

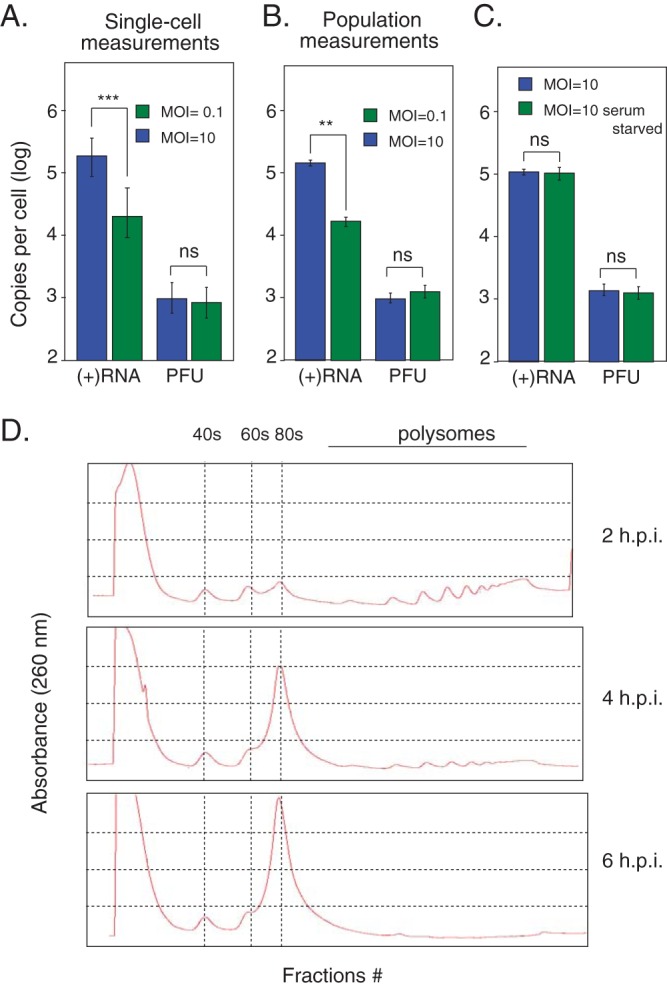
Genome production scales with MOI, but PFU production does not. Shown is a comparison of single-cell measurements and population measurements. (A) Single-cell measurements. For an MOI of 10, n = 106 for RNA and n = 86 for PFU. For an MOI of 0.1, n = 56 for RNA and n = 45 for PFU. (B) Population measurements; n = 6. (C) Serum starvation has no significant effect on RNA or PFU production of infections at an MOI of 10; n = 6. **, P < 0.001 by Student's t test; ***, P < 0.001 by the Kolmogorov-Smirnov test. ns, not significant. Error bars indicate standard deviations. (D) UV absorbance at 260 nm of sucrose gradient-fractionated lysates from a time course of poliovirus infections shows free 40S and 60S ribosomal subunits throughout infection.

Correlations between RNA and virus production at the single-cell level.

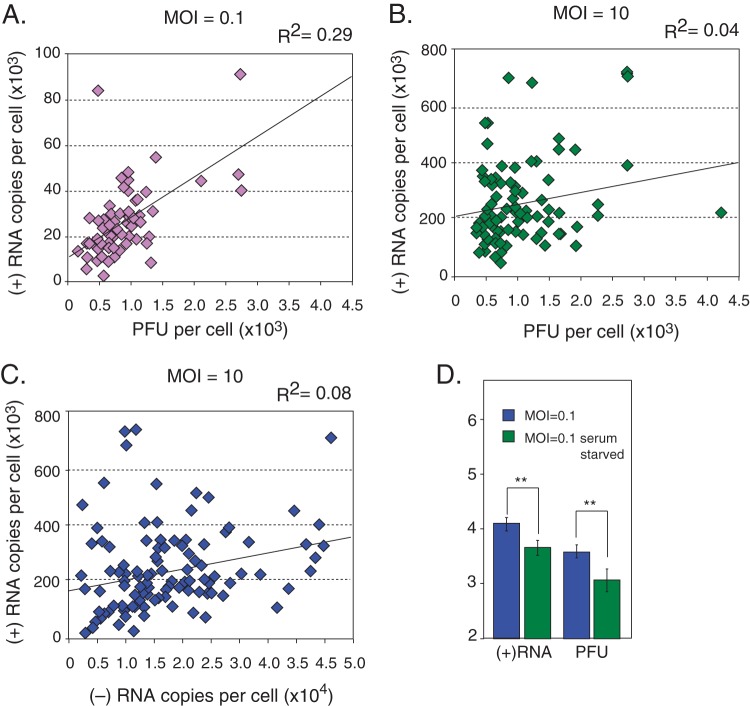
Next, we took advantage of our ability to take multiple measurements per individual cell to determine correlations between RNA synthesis and virus production. By comparing the quantity of multiple viral products from each cell, we were able to determine how biological noise affects early (RNA production) and late (particle production) steps in virus replication. At a low multiplicity of infection (0.1), we observed a relatively good correlation between genomes and infectious particles produced per cell (nearly 30%) (Fig. 5A). This suggests that although the initial reactions of low-MOI infections are highly susceptible to the effects of kinetic stochastic noise, once replication is established and viral translation and RNA synthesis are initiated, the infection progresses in a fairly deterministic manner. The variation in the initial steps of translation and RNA synthesis contribute significantly to the overall trajectory of the infection. This is consistent with the observation that reducing the kinetics of these initial reactions lowers the average productive trajectory (Fig. 3).

FIG 5.

Correlations between products of single-cell infections and effects of serum starvation on low-MOI infections. (A) Correlation between positive-strand RNA and PFU from infection at an MOI of 0.1 shows that a significant portion of the noise in one product can be explained by the noise in the other (R² = 0.29; 95% confidence interval, 0.05 to 0.76); n = 45. (B) Correlation between positive-strand RNA and PFU from infection at an MOI of 10 shows a poor correlation (R² = 0.04; 95% confidence interval, 0.00 to 0.19); n = 86. (C) Correlation between positive-strand RNA and negative-strand RNA from infection at an MOI of 10 also shows a poor correlation (R² = 0.08; 95% confidence interval, 0.00 to 0.25); n = 86. (D) Serum-starved infections at an MOI of 0.1 produce less than 40% as many genomes and less than 35% as many PFU as serum-fed infections at an MOI of 0.1; n = 6. **, P < 0.005 by Student's t test. Error bars indicate standard deviations.

Given that infections starting with a higher MOI are less susceptible to this initial kinetic noise (Fig. 2C), we expected a better correlation between the distributions of viral RNA and infectious particle production for the infection starting at an MOI of 10. Surprisingly, we observed very little correlation between the distributions of RNA and infectious virus from the infection at an MOI of 10: 4% between genomes and PFU and 8% between genomes and negative-strand RNA templates (Fig. 5B and C). Because these correlations were obtained from measurements of individual infections, we can exclude the Poisson distribution of initial infecting genomes as a factor contributing to this relationship. This lack of correlation reveals stochastic influences in multiply infected cells beyond the kinetic noise of the initial reactions and may be the result of local fluctuations within individual cells of critical factors involved in virus replication.

Low-MOI infections provide critical insights into this local resource stochasticity. When low-MOI infections initiate in serum-starved cells, significantly fewer genomes and PFU are produced. Low-MOI infections of serum-starved cells produced less than 40% as many genomes and less than 35% as many PFU as serum-fed cultures (Fig. 5D). Serum starvation does not affect the global productive capacity of high-MOI infections (Fig. 4C). Therefore, serum starvation appears to create local deficiencies in resources to which only low-MOI infections are sensitive. Accordingly, we propose that as a consequence of local variation in resources, hot spots and cold spots within the cell are created, which determine the efficiency of initiating infection. In serum-starved cells, fewer hot spots exist, and single infectious particles have a lower probability of establishing a productive infection.

DISCUSSION

The determinants of a successful viral infection are not well understood. In this study, we examined whether the outcomes of infection are deterministic or governed by stochastic events. We found considerable variability in the outcomes of infections. The sources of noise appear to be different for viral infections beginning with only one or many infectious particles. Infections initiated with only a single infectious particle have the highest degree of variability in viral replication, independent of cell size. In infections initiated by multiple infectious particles, we observed less variance in the distribution of RNA accumulation, suggesting that the initial steps of infection are particularly susceptible to stochastic kinetics. However, in multiply infected cells, the lack of correlation between RNA produced and number of infectious particles produced suggests that when viral RNA replication initiates in multiple locations, the infection suffers from access to host resources. Interestingly, particle production also demonstrates a high degree of fluctuation (Fig. 2C), indicating that additional sources of variation exist at later stages of the replication cycle.

Our data highlight the stochastic nature of the interaction between the infecting virus and the host cell and indicate that biological noise significantly impacts the distributions of viral RNA and particle production. The source of noise may be variations in the biochemical reactions that underlie virus replication which stem from resource limitations or simply variations in the kinetics of the initiation of an infection. Infections that begin quickly would be expected to transition to exponential growth more rapidly and be highly productive, while infections that falter or lag would, conversely, be less productive. In addition, cells have many mechanisms to block viral replication, whereas all viruses have mechanisms to evade them and hijack the cellular resources. Differences in the effectiveness of host innate immune responses at the earliest times of infection could have a significant impact on the initial kinetics of replication.

An important observation from this study was that despite the difference in production of genomes between singly infected and multiply infected cells, similar amounts of virus are produced. The observation of similar burst size distributions between singly infected and multiply infected cells was first made by Delbruck using phage (2). More recently, it was reported that virus yield of vesicular stomatitis virus, a mammalian RNA virus, does not correlate with multiplicity of infection (11), but it was unknown what limited virus production. Clearly, at least in the case of poliovirus, there are sufficient cellular resources for an order of magnitude increase in genome production with MOI, but a global cellular resource limits virus particle production. This is likely due to differences in the nature of these processes. Viral genome replication is dependent on the polymerase, which is an enzyme and can be utilized repeatedly, while virion production is dependent on capsid proteins, which are continuously consumed during virion synthesis. The synthetic requirements for viral capsid protein production exceed those for genome replication and the synthesis of other viral proteins for several additional reasons: (i) virions are comprised of a single genome and 60 copies of each of the viral capsid proteins, meaning that production of a virion requires only a single genome replication event but 60 translation events (12); (ii) the rate of genome replication within infected cells is estimated to be 5 times higher than the rate of translation (13); and (iii) because of the functional compartmentalization of viral nonstructural proteins (14, 15), cytosolic concentrations of capsid proteins are likely much lower than the compartmentalized concentrations of the nonstructural proteins, meaning that replication occurs with higher, localized concentrations of viral nonstructural proteins, while encapsidation occurs under more dilute, global concentrations of viral capsid proteins.

Strikingly, our study uncovers the importance of local resource variability within the cell architecture on the initiation of infection. Because infections initiated by multiple infectious particles are thought to proceed by generating multiple, compartmentalized replication foci that progress through the infection with limited cross talk (14–16), local differences in the subcellular availability of resources for replication, such as ribosomes, energy, nucleotides, membranes, etc., likely create variation in the productive capacity of each focus. In multiply infected cells, noise could arise from random fluctuations in the spatial organization of reactions, as these foci are subject to more limited and variable access to cellular resources. As a result of this variability, asynchronies or inefficiencies could be introduced to the overall replication cycle that could skew the productivity of each infection, thus generating “architectural” or spatial stochasticity. Similarly, local resource variation appears to create hot spots and cold spots of replication initiation, as evidenced by the differential effects of serum starvation on high- and low-MOI infections (Fig. 4C and 5D).

Similarities between the burst size distributions of singly infected and multiply infected cells were originally interpreted to stem from a self-interference phenomenon, whereas bacteria which were “simultaneously infected with several virus particles of the same kind” would “react as if only one of the virus particles was effective” (17). Our data suggest that, at least for poliovirus, self-interference at the level of genome synthesis does not occur. It is possible that a fundamental difference exists between bacteria and mammalian host cells, that, for example, restricts bacteriophages to only a single nucleation site for replication while allowing mammalian viruses many sites of replication. The observations that self-interference of genome synthesis does not occur and that the mammalian host cells restrict virion production create an intriguing question: what advantage does the virus gain by allowing multiple infecting genomes to replicate? Is it simply a kinetic issue, with the benefit coming from the virus making the maximum number of virions before the cell mounts a response or apoptosis (18)? Or is there a more complex answer, with the benefit coming from multiple infecting genotypes creating a more diverse population of progeny to gain adaptive advantage (19)? Future studies should define the particular cellular resource limitation imposed on virus production and elucidate the evolutionary advantage of the mechanisms of replication within multiply infected cells.

Our observation of how random events play a perhaps larger-than-envisioned role in infection is relevant to the understanding of the dynamics of virus infection and their consequences for adaptation. For example, cells experiencing low-productivity infection may be more likely to evade host immune responses, which may, in turn, extend the overall infection cycle time and increase the chances for the virus to spread from host to host (20). During infections, hosts are infected with a small number of viruses, which continuously face strong bottleneck events (21). In this scenario, variance in viral replication dynamics at the single-cell level can have a strong effect on the outcome of infection. Considerable attention has been given to the idea that organism survival and reproduction are subject to stochastic fluctuations and chance rather than fitness alone (22). Stochastic processes during replication lead to sampling errors over generations. These sampling errors, i.e., random genetic drift, can cause significant changes in the abundance of genetic variants. Such genetic drift can represent a significant hurdle for adaptation and therefore can play a large role in determining the fate of an infection. Newly arising beneficial mutations may often be lost by chance and may need to occur many times before they succeed in reaching fixation (23), thus reducing the chance of effective adaptation to a new host or switch in the environment. Stochasticity manifested as genetic drift can also serve to isolate neutral mutations, opening new evolutionary avenues for virus adaptation (24). Future work will be necessary to extend these observations and elucidate the precise relationship between biological noise and virus adaptation.