Opening and closing of a toroidal group II chaperonin revealed by a symmetry constrained elastic network model

Abstract

Recently, the atomic structures of both the closed and open forms of Group 2 chaperonin protein Mm-cpn were revealed through crystallography and cryo-electron microscopy. This toroidal-like chaperonin is composed of two eightfold rings that face back-to-back. To gain a computational advantage, we used a symmetry constrained elastic network model (SCENM), which requires only a repeated subunit structure and its symmetric connectivity to neighboring subunits to simulate the entire system. In the case of chaperonin, only six subunits (i.e., three from each ring) were used out of the eight subunits comprising each ring. A smooth and symmetric pathway between the open and closed conformations was generated by elastic network interpolation (ENI). To support this result, we also performed a symmetry-constrained normal mode analysis (NMA), which revealed the intrinsic vibration features of the given structures. The NMA and ENI results for the representative single subunit were duplicated according to the symmetry pattern to reconstruct the entire assembly. To test the feasibility of the symmetry model, its results were also compared with those obtained from the full model. This study allowed the folding mechanism of chaperonin Mm-cpn to be elucidated by SCENM in a timely manner.

Introduction

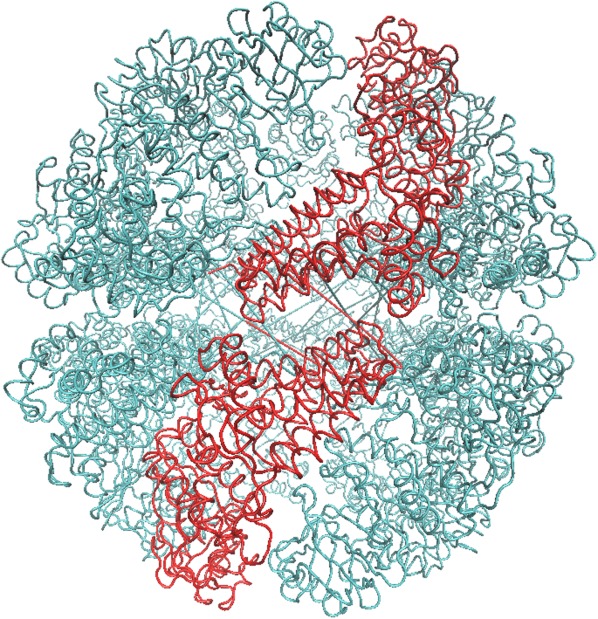
Group 2 chaperonins are essential proteins in eukaryotes and archaea that help thousands of different proteins fold into tertiary structures.¹ This process is induced by ATP hydrolysis.² If this process is disturbed, it can cause various diseases, including cancer, neurodegenerative disorders, and cardiovascular diseases.³ Group 2 chaperonins in eukaryotic cytosol are typically composed of 14–18 subunits that align back-to-back, making a sevenfold–ninefold ring with a central chamber.⁴ A single subunit has three taxonomic domains: apical, intermediate, and equatorial.⁵ The apical domain binds the substrate, the intermediate domain acts as a hinge, and the equatorial domain binds ATP.⁶ The opening and closing mechanism occurs through the enzymatic binding and hydrolysis of ATP, which is accompanied by a large conformational change.⁷ Recently, research has revealed the atomic structure of mesophilic archaea Methanococcus maripaludis chaperonin (Mm-cpn). Through crystallography and cryo-electron microscopy, both its in vitro nucleotide-induced (closed form, PDB ID: 3J03) and nucleotide-free (open form, PDB ID: 3IYF) forms as well as its closed in vivo form (PDB ID: 3LOS) were elucidated.⁸ These structures are composed of eight identical subunits that have an overall toroidal-like shape (Fig. 1). Although both the open and closed in vitro structures are well known, no clear understanding exists of Mm-cpn's transition between the two states. Many studies exist that simulate the dynamics of the GroEL-GroES complex mechanism using a coarse-grained model.^9–13 Such research typically uses a model that considers a single residue as a mass point that is connected to others by a linear spring, creating a mass-spring system. However, the GroEL-GroES complex has a very large molecular structure, which requires a long computation time. By considering its symmetric molecular structure, we will apply a symmetry constrained elastic network model (SCENM) to the protein to create a dynamic analysis on the atomic scale. Using this method, we expect a reasonably accurate simulation when compared with the full-scale model that also achieves a significant reduction in computation time.

Figure 1.

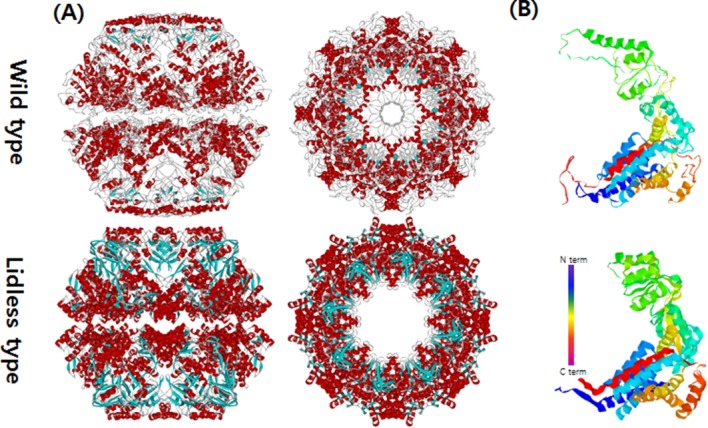
The closed conformations of Mm-cpn in both the wild and lidless types. (A) Top and side views of Mm-cpn (upper: wild type, lower: lidless type). (B) A single subunit of each type is shown.

Results

SCNMA evaluation

To validate the SCNMA results, we applied two different simulation methods to the same Mm-cpn protein structure. The first method was a full-scale NMA, which considered the entire atomic structure (eight subunits per ring), and the second was SCNMA, which focused on only three subunits. We then compared the two simulation results using the combinatorial extension algorithm to calculate the root mean square distance (RMSD) between the atoms.¹⁴ We also compared the computation times of the two methods to emphasize the strength of SCNMA. Because the majority of the computation time of either method is used to solve the eigenvalue problems of the structure, we also determined the specific eigenvalue computation time. SCNMA was twice as fast as the traditional, full-scale NMA. Despite its shorter computation time, the results of our symmetric simulation were consistent with those of the full-scale method.

Figure 2(A) shows the significant torsional angle difference between the open and closed structures. The definition of torsion angle, in this context, is depicted in Figure 2(B). The angle change is calculated from the two different crystallography structures of Mm-cpn but there exists substantial amount of noise because the two different sets of PDB data (3J03, 3IYF) were taken at different resolutions. Despite the noise, the drastic angle change is still distinguishable. This large angle change indicates that the intermediate domain having the peak resides acts like a hinge. Figure 2(C) shows a cartoon model of the upper segment of a wild type closed state single subunit. The hinge point is highlighted by representation using the space-filling model (see arrow). The high flexibility of the intermediate domain has also been reported by many other researchers, including Martin¹⁵ and Saibil.¹⁶ Additionally, Zhang et al. suggested that the current hinge point (helix L) tilts in response to ATP hydrolysis.⁸ A hinge prediction algorithm, called HingeProt,¹⁷ was applied to Mm-cpn and confirmed the result.

Figure 2.

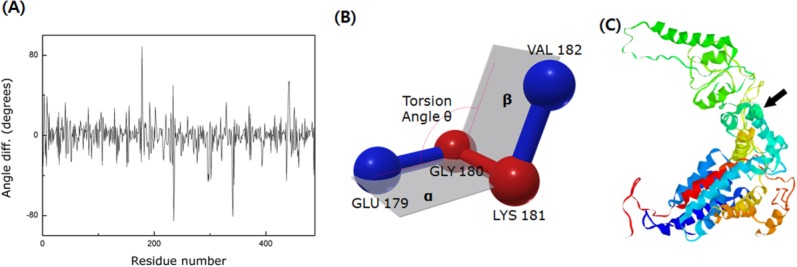
The identification of the hinge region. (A) The torsional angle difference between two models, 3IYF(open form) and 3J03(closed form). Because of the resolution difference between these two models (3IYF has a resolution of 4.8 Å, whereas 3J03 has a resolution of 8.0 Å), there exists substantial amount of noise. However, the significant angle difference in the figure indicates the existence of a hinge point in the intermediate domain. (B) Schematic of the torsion angle. It is defined as the angle between plane α (GLU 179-GLY 180-LYS 181) and plane β (GLY 180 –LYS 181- VAL 182). (C) A cartoon model of the wild type closed structure of Mm-cpn. The black arrow indicates the location of the hinge point (which is also highlighted via the space-filling model).

SCNMA was carried out for two different models of Mm-cpn, the wild type (in vivo) and the lidless type (in vitro). For both models, we analyzed the first four dominant modes (those occurring at the lowest frequencies), which play a major role in the dynamics of Mm-cpn. First, we investigated the in vitro form (closed). As shown in Figure 3, most of the dominant modes showed a typical opening/closing motion that agrees with the various experimental results for chaperonin proteins.

Figure 3.

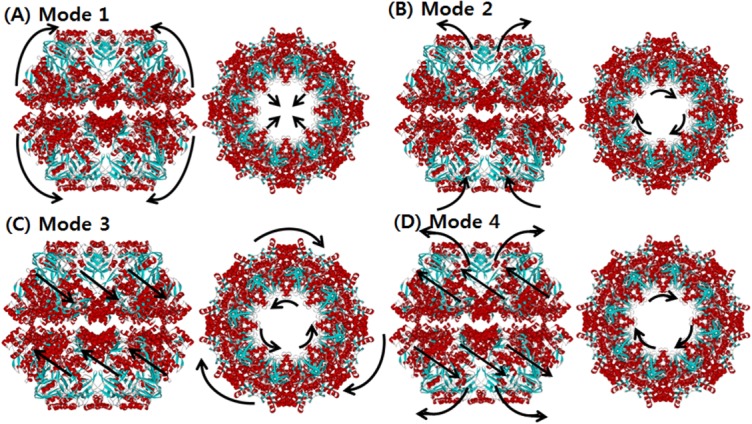
The normal mode shapes of in vitro Mm-cpn. Mode 1 to Mode 4 all show a general opening motion. However, in Modes 2 and 4 the opening motion occurs via a combination of axial motion and shear motion.

Mode 1 showed an alternating breathing motion in the apical domain. The overall dynamics of Mode 1 consisted of two distinctive movements, axial elongation, and spherical expansion. During the axial elongation, the subunit underwent elongation in the direction opposite to each end of the apical domain. During the spherical expansion, the intermediate domain acted as though it were moving away from the central cavity, a motion consistent with a previous experiment, indicating that the intermediate domain serves as a hinge.⁸ However, the equatorial domain moved a lot with respect to the other domains, whereas it serves as a binding ring. This result is strongly supported by Figure 4(A), which shows the relative displacement distribution throughout the entire residue sequence. In the case of the lidless type of Mm-cpn, high mobility was shifted in all three domains throughout the modes. Furthermore, a closer examination of a single subunit identified a particular movement of the equatorial domain—although most of the domain remained relatively stationary, the N and C termini of adjacent subunits were moving away from each other. This unique motion was also confirmed by cryo-EM images of an open wild type Mm-cpn.⁸

Figure 4.

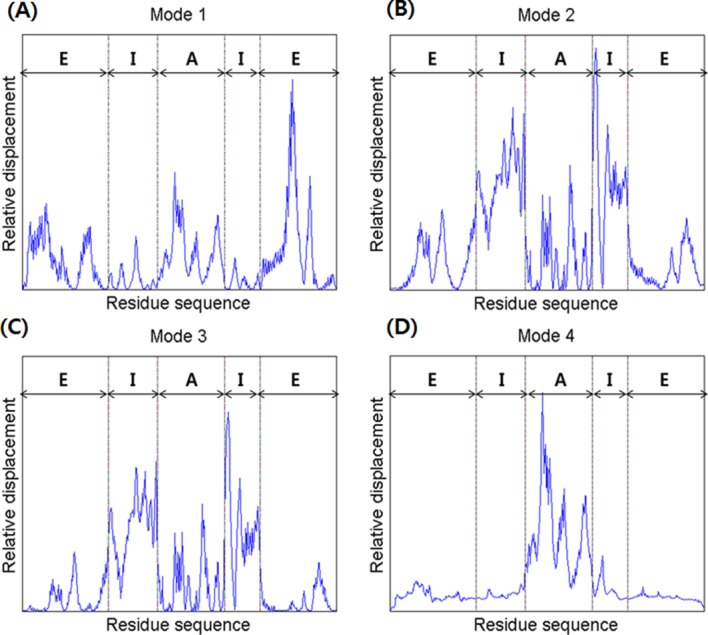
A comparison of the relative displacements of the in vitro (lidless) Mm-cpn, as predicted by SCNMA. The abbreviations “E,” “I,” and “A” represent the equatorial domain (residue numbers 1–135 and 373–491), the intermediate domain (residue numbers 136–212 and 318–372), and the apical domain (residue numbers 213–317), respectively.

In Mode 2, a slight rotation of the apical domain about the axis of symmetry and alternating breathing motions of both the apical and equatorial domains were observed. The breathing motion of Mode 2 is very different from that of Mode 1 in many ways, including its bending directions and high mobility domains. In Mode 2, the apical domain bends upward against the central cavity. This opening motion was also shown in various other modes and coincides with the functional motions of the chaperonin protein. The intermediate domain moved outside to the central cavity, again acting as a hinge. The apical domain also showed torsion about the axis of symmetry. The equatorial domain showed a bending motion similar to that of the apical domain, but it maintained its connection with other equatorial domains to form the body of a ring structure. Another distinctive characteristic of this mode is the high mobility of the intermediate domain, as shown in Figure 4(B). In this figure, which is broken up into five sections, the first section indicates the little fluctuations of the N termini. The second and fourth sections, corresponding to the intermediate domain, show the highest mobility. The third section indicates a relatively low mobility of the entire apical domain. The last section shows the low mobility of the C termini.

In Mode 3, the entire structure underwent a shear opening motion in the counter-clockwise direction (as observed in the top view). As shown in Figure 4(C), the apical domain and the intermediate domain have high mobility, but the equatorial domain remained as an anchor, allowing the volume of the central cavity to remain relatively unchanged.

Mode 4 also included a shear symmetrical opening motion, whereas that of Mode 3 was a symmetrical shear motion of rings moving back to back. In Mode 4, the apical domains of each subunit (both upper and lower ring) moved away from the central cavity (opening motion). The relative displacement plot for Mode 4, shown in Figure 4(D), confirms this shear opening motion and the large relative displacement in the apical domain.

These first four lowest modes cooperate to change the shape of the vacant chamber inside the chaperonin. This result agrees with experimental observations indicating that Group 2 chaperonins open their chambers to take in misfolded proteins.¹⁸ Because the in vitro chaperonin model used in this study does not have a lid, the number of computations needed to create the spring network is far smaller than in the in vivo model. The apical domain showed high mobility throughout all four modes when compared with the other domains, indicating that the apical domain may serve as the substrate-binding site.⁸ A combination of these four lowest modes could represent the actual dynamics of the chaperonin protein.

We also carried out SCNMA to reveal the dynamic characteristics of the in vivo model (wild type). The major structural difference is the inclusion of a lid in vivo. Figure 5 depicts the shapes of the four lowest modes. In Mode 1, a nonsymmetrical opening motion of the apical domain and a clockwise shear of the equatorial domain were observed. The overall conformation was very similar to that observed in Mode 2 of the in vitro model. However, the mobility of the apical domain was lower in vitro. As shown in Figure 6(A), the high mobility of the in vivo Mode 1 was spread across the apical and intermediate domains, whereas movement in the equatorial domain was relatively suppressed. Although the mobility of the apical domain was high, it continued to hold the rings together and showed an alternative breathing motion.

Figure 5.

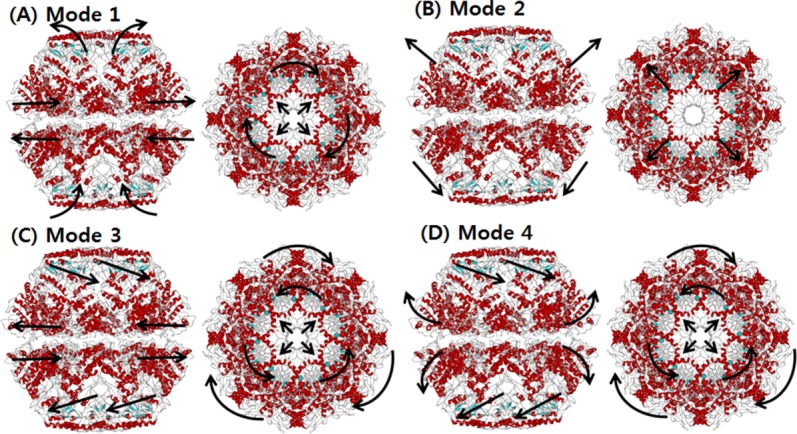
The dominant mode shapes of in vivo Mm-cpn. A general opening motion is observed in Modes 1 through 4. Modes 2 and 3 show a simple opening motion, whereas Modes 1 and 4 indicate a breathing motion.

Figure 6.

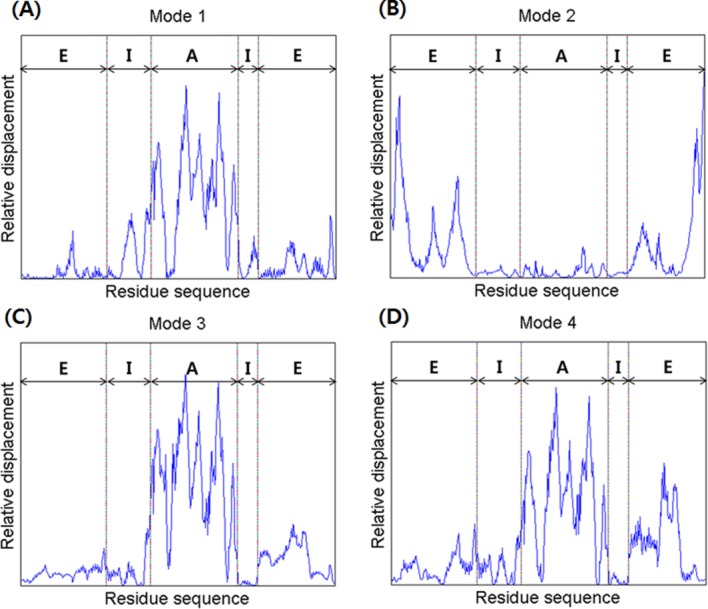
A comparison of the relative displacements of the in vivo (lidded) Mm-cpn, as predicted by symmetry constrained NMA. The abbreviations “E,” “I,” and “A” represent the equatorial domain (residue numbers 1–145 and 401–532), the intermediate domain (residue numbers 146–220 and 367–400), and the apical domain (residue numbers 221–366), respectively.

In Mode 2, an asymmetric global opening motion was observed. The upper structure expanded while the lower structure shrinked. A large motion in the equatorial was observed because of the expanding (shrinking) central cavity. Figure 6(B) also showed that the highest mobility was in the equatorial domain, whereas the other domains remained still.

In Mode 3, a symmetrical shear of the apical domain was observed, similar to that observed in Mode 3 of the in vitro model. Both the upper and lower apical domains simultaneously moved inside to the central cavity. Meanwhile, the intermediate domains acted as hinges. This mode shape is supported by the mobility results for each domain, shown in Figure 6(C). The highest mobility was in the apical domain, whereas the other domains remained still.

A symmetrical (upper and lower subunit) shear of the apical domain, similar to that of Mode 3, was observed in Mode 4, along with a lateral expansion (upper) of the equatorial domain. However, the vibration direction was different than that of the previous mode; the upper apical domain moved in to the central cavity, while the lower apical domain moved away from it. The breathing motion in the equatorial domain was also more vibrant than Mode 3, as is shown in Figure 6(D). This motion is caused by the symmetrical shear motion and compression of the N and C termini that are both located inside the central cavity.

For the closed in vivo model, we confirmed both the breathing and opening motions of its dominant modes. We found that the two closed forms of chaperonin have the same tendency to open the central cavity, whether a lid is present or not. However, there is a significant difference in mobility. Because of the lid, the in vitro model is less flexible than the lidless one. These mobility results suggest that the lid prevents the apical domain itself from opening unless the chaperonin reaches a nucleotide-free state.

Conformational transition of chaperonin

The proposed SCENI was carried out to elucidate chaperonin's conformational transition pathway between its open and closed states. The SCENI was only applied to in vitro Mm-cpn because the structural information for an open form in vivo molecule does not exist. The entire subunit complex appeared to undergo a simple bending motion. The apical domain was initially connected to its neighboring subunits, but it split out individually as the interpolation process continued. This implies that the intraunit connection is much stronger than the interunit connection between subunits.

To validate the transition pathway generated by SCENI, a point of interest (Residues 179-180-181-182) was selected in the intermediate domain, which is presumed to act as the hinge. The torsion angle of the residue of interest was measured to determine the apical domain's bend during the conformational change. As shown in Figure 7, the torsion angle smoothly varied from −10.9° to 82.6°, indicating a large collective movement, although the equatorial domains remained intact throughout the interpolation process.

Figure 7.

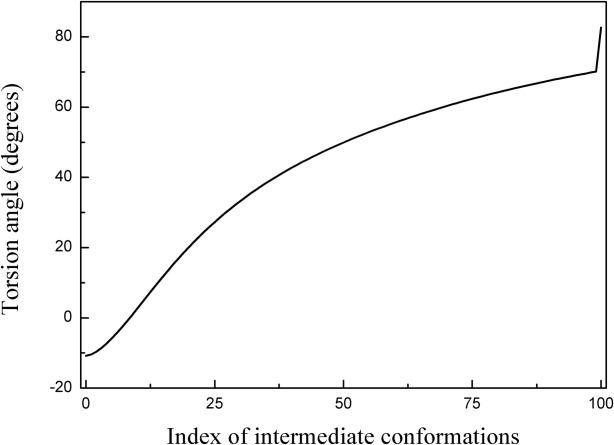
Torsion angle variation at the hinge point (Residues 179–180-181–182) throughout the conformational change from the closed to the open structure of lidless Mm-cpn. The smooth torsion angle change indicates a successful interpolation throughout the entire conformation index (0 to 100).

Figure 8 shows the evolution map of chaperonin from closed to open that was generated by SCENI. Notably, the height of the entire complex gradually increases so that the central cavity can expand enough to envelop an entire misfolded protein.

Figure 8.

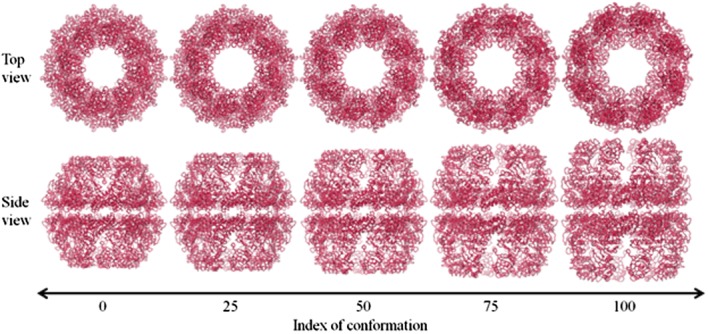
A diagram of the conformational change of chaperonin, as predicted by SCENI. The top and side views over the course of the transient pathway easily demonstrate its opening and breathing motions.

Discussion

The folding mechanism of chaperonin and the role of its lid have been investigated through comparisons between the lidless and wild protein types. To overcome the computational burden caused by the complex's large size (over 8000 residues), SCENM was proposed to take advantage of the symmetry of this eightfold protein.

The SCNMAs for both the lidless and wild type proteins generally showed an opening and closing motion in the central cavity. The existence of the lid slightly altered the mobility of the domains as well as the mode shapes. However, the primary folding mechanism is the same in both types. Hinge motions of the intermediate domain were observed in many different modes. Although one can speculate that a combination of several of the dominant mode shapes revealed by SCNMA would describe the folding mechanism of chaperonin, it is very difficult to determine how much each specific mode contributes to the overall folding pathway.

Additionally, SCENI was applied to the known open and closed structures of lidless Mm-cpn not only to elucidate the folding mechanism of the GroEL complex but also to confirm the previous understanding described in the literature.⁸ A smooth folding pathway was successfully generated, and the exact location of the hinge point in the intermediate domain was identified by evaluating the torsion angle change along the proposed pathway. The SCENI results also agree with the existing literature suggestions.

Both the SCNMA and the SCENI results indicate that the most dominant collective motion is the opening and closing movement. This result coincides with the primary function of Group 2 chaperonins, allowing them to assist the refolding process for damaged or misfolded proteins by accepting them into a central cavity. The proposed symmetry constrained methods will also greatly impact the dynamic analysis and visualization of other symmetric macromolecules, such as virus capsids, reducing computational costs without losing generality.

Methods

Symmetry constrained elastic network model (SCENM)

As found in the research performed by Zhang et al.,⁸ three different crystal structures for chaperonin are available in the Protein Data Bank, and they are classified as one of the two types. The wild type (in vitro) exists in both open and closed forms; the third structure is that of a closed form lidless type (in vivo). The difference between these two types is the presence of an apical domain. To gain a computational advantage, we performed an SCENM that required only the repeated subunit structure and the connectivity of each atom to simulate the full model.

The SCENM has no limitation to consider interconnections among subunits unless the uniformity of interconnection pattern of each unit breaks out. Therefore, SCENM can be applied to both ring structure (which has only interactions with two neighboring subunits like chaperonin) and spherical structure (which has globular interactions with many proximal subunits like virus capsid).¹⁰ Brooks also addressed that only symmetric motion is possible for symmetric structures in his study.¹⁹

Using the coordinates for every atom that were obtained from the crystal structure, we can assume the atoms to be point masses. The Cartesian coordinates of ith atom at time t can be expressed as

(1)

Because this is a coarse-grained model, only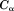 atoms are considered.

We can define a small displacement,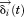, and rewrite the position vector as

(2)

The total kinetic energy of the system can be written as

(3)

We can rewrite the kinetic energy in matrix form using the global mass matrix M so that

(4)

where

(5)

Next, we assume that neighboring atoms within a certain distance are connected to each other via a linear virtual spring, creating a mass-spring system.¹⁰ The total potential energy of that system is

(6)

Using a Taylor series approximation,

(7)

where

(8)

and thus, we can rewrite Eq. (6) as

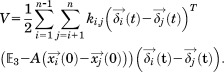(9)

Here, we define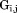 as

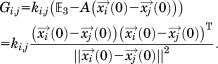(10)

Substituting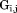 into Eq. (9) yields

(11)

Eq. (11) can be rewritten in quadratic form using global stiffness matrix K to become

(12)

Now, we can derive an equation of motion (EOM) using Lagrange's equations,

(13)

where L = T − V. The final form of the EOM is

(14)

We must then apply the symmetric boundary conditions to the system. The symmetric boundary conditions include the intraconnectivity information from a single subunit and the interconnectivity information from the neighboring subunits. Because chaperonin has a ring-shaped feature made up of eight subunits, we can simply divide Eq. (5) into eight parts. Thus,

(15)

where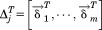 is the x, y, z coordinate set for a single subunit (j = 1, 2, … 8).

Figure 9 illustrates a schematic view of the chaperonin structure. The highlighted feature in red is a single subunit. Each subunit consists of m point mass particles. Because of chaperonin's axis-symmetrical shape, we can rewrite the coordinates using rotation matrices. Thus, the coordinates of each subunit can be rewritten in terms of the first subunit to yield

Figure 9.

A schematic model of the chaperonin's structure. The area highlighted in red indicates a single subunit that was used for symmetry constrained ENM.

(16a)

(16b)

(16c)

(16d)

where

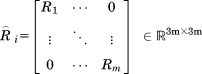(17)

As shown in Figure 10, the connectivity of the atoms is very sparse and repeatable. This type of matrix consumes a large amount of extra memory to simply maintain the matrix size, which leads to long computation times. To resolve this drawback, we noted only the nearest neighboring subunits that were connected to each other via a short cut-off distance.

Figure 10.

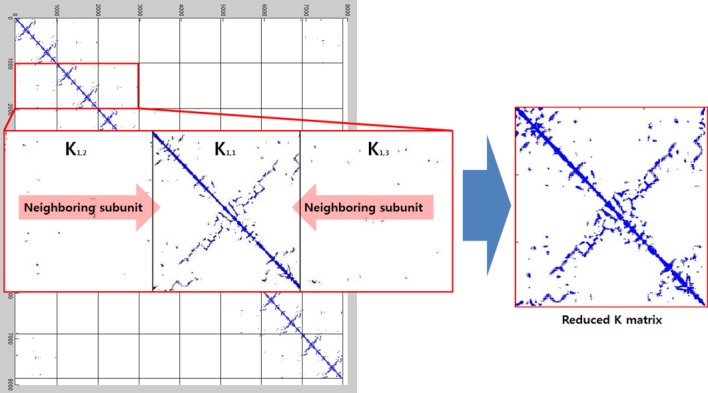
The formation of the reduced K matrix. Symmetry constraints were applied to both the individual subunit's interconnections and the intraconnections with neighboring subunits.

There are more intraconnections within a single subunit than there are interconnections between subunits. This situation allows us to reduce the redundant portion of the connectivity matrix, making it more compact. To do this, we chose three representative neighboring subunits out of eight and created the reduced connectivity matrix. The size of the global stiffness matrix K can also be reduced by eliminating the redundant information, so that

(18)

where and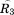 are rotation matrices 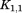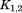and,, and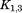 stand for the interconnections between subunits. Figure 10 demonstrates the schematic process of constructing 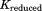from global stiffness matrix K.

Symmetry constrained NMA (SCNMA)

An NMA can reveal the fundamental vibration features of a given protein structure. By comparing the two different intrinsic motions of the in vivo and in vitro proteins, one can understand the role of the lid in the GroEL-GroES complex. Various intrinsic vibration motions were computed from Eq. (22), in which the global stiffness matrix K is replaced by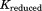 such that

(19)

Multiplying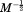 through Eq. (22) yields

(20)

By setting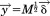, Eq. (23) becomes

(21)

where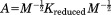. We can also define a similarity transform A such that

(22)

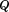contains the normalized eigenvectors of A in column vectors and diagonal matrix contains the eigenvalues of A in its diagonal elements. Equation (19) is then decoupled to become

(23a)

(23b)

where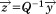 and is the ith eigenvalue of A.

The solution of Eq. (23) is

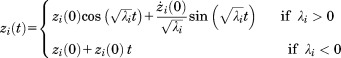(24)

By converting the solution into terms of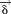, we can define the final solution of EOM to be

(25)

Once we solve this simple eigenvalue problem, we can attain the vibration direction (eigenvectors) of each atom in the order of the low frequencies (eigenvalues). Because the SCNMA result only represents a single subunit, we must duplicate it seven times to recompose the entire ring structure.

Symmetry constrained elastic network interpolation (SCENI)

Elastic network interpolation (ENI) can be used to investigate the conformational change that takes place between the open and closed forms of Mm-cpn. This method generates a smooth pathway between two different crystalline structures obtained from one protein so that the folding process can easily be visualized. Hence, we used only the in vitro protein model because its open and closed crystal structures were both defined. Once we extract the position data from the PDB, we have to minimize the cost function, below, which was proposed by Kim et al.¹⁰

(26)

By taking the derivative, the equation yields

(27)

where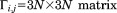,,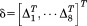, 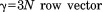and.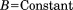

Next, an eightfold symmetry condition is applied to each part of Eq. (31) such that

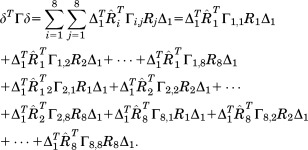(28)

The equation can be simplified to

(29)

Using the same idea, we can rewrite the second part of the equation as

(30)

Thus, the entire equation can be rewritten as

(31)

As an individual SCENI result also represents only a single subunit, we must duplicate it in the same manner that was used for SCNMA.

Definition of torsion angle in a coarse-grained ENM

The torsion angle is defined as “the angle between two planes.” This is also known as the “dihedral angle” and it can be calculated using normal vectors to each of the planes. From Figure 2(B), let GLU 179 as A, GLY 180 as B, LYS 181 as C, and VAL 182 as D. Then define vectors like

(32)

then the magnitude of torsion angle can be define as

(33)

Positive direction of torsion angle is defined clock-wise rotation of plane β with respect to plane α, and vice versa.²⁰