Development and comparative assessment of Raman spectroscopic classification algorithms for lesion discrimination in stereotactic breast biopsies with microcalcifications

Abstract

Microcalcifications are an early mammographic sign of breast cancer and a target for stereotactic breast needle biopsy. Here, we develop and compare different approaches for developing Raman classification algorithms to diagnose invasive and in situ breast cancer, fibrocystic change and fibroadenoma that can be associated with microcalcifications. In this study, Raman spectra were acquired from tissue cores obtained from fresh breast biopsies and analyzed using a constituent-based breast model. Diagnostic algorithms based on the breast model fit coefficients were devised using logistic regression, C4.5 decision tree classification, k-nearest neighbor (k-NN) and support vector machine (SVM) analysis, and subjected to leave-one-out cross validation. The best performing algorithm was based on SVM analysis (with radial basis function), which yielded a positive predictive value of 100% and negative predictive value of 96% for cancer diagnosis. Importantly, these results demonstrate that Raman spectroscopy provides adequate diagnostic information for lesion discrimination even in the presence of microcalcifications, which to the best of our knowledge has not been previously reported.

Raman spectroscopy and multivariate classification provide accurate discrimination among lesions in stereotactic breast biopsies, irrespective of microcalcification status.

1. Introduction

Breast cancer poses a singular public health problem in both developed and developing countries and constitutes approximately 23% of all cancers (excluding non-melanoma skin cancers) in women worldwide [1]. Indeed, it is estimated that one in every eight women is likely to develop breast cancer in her lifetime, which translates to more than 225,000 new cases annually in the US alone [2]. Furthermore, significant economic costs are associated with breast cancer care in the US alone ($7 billion in 2007), a substantive fraction of which (approximately $2 billion) is spent on late-stage breast cancer treatment [3]. Evidently, early detection can alleviate much of the challenges from a healthcare perspective (i.e. by reducing breast cancer morbidity and mortality) as well as the financial burden related to this disease.

In terms of early breast cancer detection methodologies, X-ray mammography is the only accepted routine screening tool [4]. Numerous studies have reported that early detection by screening mammography reduces mortality and increases treatment options [1]. One of the crucial aspects of mammographic investigation is the detection of microcalcifications, which are localized mineral deposits of calcium species that are considered to be early indicators of breast cancer [5]. Microcalcifications discerned radiologically are typically employed as bio-markers for pathology determination, due to the close correlation of type I and II microcalcifications with benign and malignant (including invasive and in situ cancer) lesions, respectively. Despite this acknowledged association with disease type [6], clinical mammograms are unable to reliably discriminate between these two types of microcalcifications. As a consequence, tissue biopsy must be performed to clearly identify whether or not the observed microcalcifications are associated with foci of cancer. To this end, most patients with mammographically detected microcalcifications undergo vacuum-assisted stereotactic core needle biopsies. However, investigators have reported that despite state-of-the-art stereotactic guidance, microcalcifications are not successfully retrieved in nearly 15% of all biopsies performed [7]. Clearly, this represents an undesirable situation as the outcome of the aforementioned cases of unsuccessful retrieval of microcalcifications would be non-diagnostic or false negative biopsies, which would necessitate the patient to undergo a repeat biopsy, frequently as a surgical procedure.

Given the current clinical scenario, there is a substantive unmet need for a real-time clinical tool that can accurately detect microcalcifications as well as diagnose breast lesions in their presence. Such a tool would provide important feedback to radiologists during stereotactic core needle biopsy procedures enabling more efficient retrieval of microcalcifications. In this context, several investigators, as well as our own laboratory, have employed Raman spectroscopy with promising results, due to its exquisite chemical specificity and real-time capability (i.e. stemming from its lack of sample preparation requirements) for disease diagnostics [8–11] including detection of breast cancer [12, 13]. Raman spectroscopy is a fundamental form of molecular spectroscopy that is widely used to investigate the structures and properties of molecules from their vibrational transitions. In Raman scattering, there is a shift between the initial and final vibrational energy states, which appears in the form of characteristic spectral patterns or Raman fingerprints.

Our recent publication has highlighted, for the first time, the ability of Raman spectroscopy to identify microcalcifications from core needle breast biopsy specimens [14]. Previously, our group had also distinguished type I and II breast microcalcifications and discriminated type II microcalcifications associated with benign and malignant breast lesions [12] in Raman microscopy studies of formalin-fixed, paraffin-embedded breast biopsies, using a combination of principal component analysis and logistic regression. Stone and co-workers had subsequently validated and extended our proof-of-concept results in similar paraffin-embedded breast tissue samples using FTIR (Fourier transform infrared) imaging [15] and also used deep Raman spectroscopy to determine the level of carbonate substitution in type II microcalcifications [16].

Nevertheless, for successful clinical translation of Raman spectroscopy, it is imperative that the spectral measurements are able to accurately diagnose the specific type of breast lesion associated with microcalcifications. Our prior attempts in this direction were restricted to diagnosis of breast cancer and benign lesions, such as fibrocystic change (FCC) and fibroadenoma (FA), in the absence of microcalcifications [17, 18]. Like the new algorithms reported here, the algorithm in these studies was based on multivariate analysis (logistic regression) and employed fit coefficients (FC) derived from modeling of the Raman spectra as the relevant inputs. However, this algorithm is unsuitable for breast lesion diagnosis in the presence of microcalcifications due to the substantial Raman spectral contributions from calcium hydroxyapatite (typically associated with type II microcalcifications) and/or calcium oxalate (typically associated with type I microcalcifications).

In this article, we report the first Raman spectroscopy-based algorithms for the diagnosis of breast cancer, irrespective of the presence (or absence) of microcalcifications. These new algorithms are developed on freshly excised tissue from patients undergoing breast core needle biopsies and are therefore not subject to potential variations/changes induced by formalin fixation and paraffin embedding. Importantly, the current algorithms can be used in real-time spectroscopic guidance of stereotactic core needle biopsy procedures, as a large number of the targeted lesions are associated with microcalcifications, and the proposed algorithms enable lesion discrimination even when such calcified deposits are present.

Furthermore, an additional goal of this study is to perform comparative evaluation of discrimination efficiency for multivariate algorithms including logistic regression (LR), decision tree (C4.5), k-nearest-neighbor (kNN) and support vector machine (SVM). Recent cancer research has applied a wide variety of such algorithms for lesion prediction by correlating spectral patterns with the results of histopathological or radiological examination, since the prediction accuracy (and reliability) depends both on the input dataset and the robustness of the discrimination methodology. Here, we seek to combine the physical interpretability of a breast constituent model fit-coefficient based analysis with the accuracy and enhanced robustness provided by these multivariate algorithms. It is worth noting that the aforementioned algorithms provide a representative, but not exhaustive, set of discrimination techniques commonly used in spectral analysis. The objective here is to obtain a concise understanding of the advantages and drawbacks of each through the findings of this study.

2. Materials and methods

2.1 Experimental section

This study was performed on the Raman spectroscopy data set previously acquired for the development of microcalcification detection algorithms in stereotactic core needle breast biopsy specimens [14]. Briefly, a portable Raman spectroscopic instrument was designed and assembled at the Laser Biomedical Research Center (LBRC), Massachusetts Institute of Technology (MIT, Cambridge, MA). This clinical unit consists of an 830 nm diode laser (Process Instruments, Salt Lake City, UT) as an excitation source and f/1.8i spectrograph (HoloSpec, Kaiser) with TE-cooled deep-depletion CCD (PIXIS 256, 1024 × 256 pixel array, Princeton Instruments) for spectral acquisition. A customized optical fiber probe, comprising of a single central excitation fiber surrounded by nine collection fibers (each of 200 μm diameter), is used to deliver light to and from the tissue surface. A detailed description of the probe can be found in our laboratory’s previous publications [19]. Approximately 100 mW of power was incident on a spot size of ca. 1 mm for our investigations. Based on light transport theory as well as Monte Carlo simulations, the sampling depth for our Raman probe is estimated to be 1.27 mm [20]. The tissue Raman spectra were recorded by summing 10 successive frames, each with acquisition time of 0.25 s for a total collection time of 2.5 seconds/spectrum.

Raman spectra were acquired ex vivo from freshly excised (i.e. within 30 minutes of excision) breast tissue cores obtained from 33 female patients (ages 38–79 years) during stereotactic core needle breast biopsies in the Breast Health Center at University Hospitals-Case Medical Center. The tissue core biopsies were approximately 2.0 cm in length and ranged from 1.0 to 2.8 mm in maximum diameter. The aforementioned investigations were approved by the Case Cancer Institutional Review Board and the Massachusetts Institute of Technology Committee On the Use of Humans as Experimental Subjects, in accordance with assurances filed with and approved by the U.S. Department of Health and Human Services. Informed consent was obtained from all subjects prior to their core needle biopsy procedures.

For acquisition of Raman spectra, the optical fiber probe was gently positioned on the tissue surface. To block collection of stray signals the tissue cores themselves were located inside a specially designed black chamber. Raman spectra were recorded from multiple tissue sites of interest from each biopsy core and generally consisted of both grossly normal and grossly abnormal (including lesions with and without microcalcifications) tissue types. The presence of microcalcifications was further validated based on radiographic assessment. It is worth noting that spectra were also acquired from several tissue cores in each biopsy, such that the number of spectra varied from patient to patient.

Following acquisition of tissue Raman spectra, the respective specimen sites were marked with multicolored colloidal inks and were then fixed in 10% neutral buffered formalin and paraffin embedded. Next, tissue sections were obtained and stained with hematoxylin and eosin (H&E) for microscopic examination by an experienced breast pathologist. The radiographic assessments based on the specimen radiograph and the histopathology diagnoses were combined to provide the final gold standard for comparison with spectroscopic results.

Prior to comparison with the radiography and histopathology results, the recorded Raman spectra were analyzed in real time to generate the linear FCs for the constituents of the breast tissue model (including epithelial cell nuclei and cytoplasm, fat, cholesterol-like deposits, β-carotene, collagen, oxyhemoglobin, calcium hydroxyapatite, calcium oxalate and water) and the two fiberoptic probe materials (namely, epoxy and sapphire), a detailed description of which can be found in a previous report [21]. Briefly, ordinary least squares (OLS) fitting was performed on the acquired Raman spectra (with the help of the basis spectra of the above constituents) to generate the model FCs, which offer valuable insight into the morphological and chemical tissue composition. The model FCs were subsequently used to develop the lesion discrimination algorithms using the multivariate classification methods detailed in the subsequent paragraphs.

2.2 Brief description of multivariate classification methods

While the FCs provide substantive insight into the composition of the tissue, the main purpose of such analysis is to establish a quantitative spectral-based classification algorithm to distinguish breast tissues according to specific pathological diagnoses, irrespective of the presence of microcalcifications. To this end, we have employed the FCs in three nonlinear classification models, namely C4.5 decision tree, kNN and SVM, to evaluate their relative performance and compare the results with the more widely used methodology for this type of predictive analysis, logistic regression (LR) [17]. In the following, we provide a brief outline of the underlying concepts and advantages of these methods.

LR is a statistical model extensively used for probabilistic binary classification, though it is not limited to this use. Specifically, LR is a type of regression analysis used for predicting the outcome of a categorical (a variable that can take on a limited number of categories or classes) criterion variable based on one or more predictor variables. In the present study, the categorical variable is the diagnostic classes (namely, normal tissue, FCC, FA and cancer) and the predictor variables are the constituent FCs. Notably, LR, which is a member of the generalized linear models family, is useful because it can transform a predictor variable input in the range of −∞ to +∞ to a probability value between 0 and 1, due to the inherent sigmoidal characteristics of the logistic function. Also, the logit (i.e. log-odds) itself is equal to the corresponding linear regression equation of the predictor variables and thus provides a convenient link to the standard (linear) regression methods without imposition of the latter’s constraints (such as the assumption that the error is normally distributed and is homoscedastic).

Despite its widespread usage in the biomedical analysis, however, LR has its own restrictive assumptions that make it disadvantageous in particular instances. For example, the implicit assumption of linearity in terms of the logit function (versus the predictor variables) may be unreasonable for a range of diagnostic conditions (such as changes in turbidity [22, 23] and temperature [24]). Furthermore, LR is only applicable, strictly speaking, to between-subject study designs and cannot be applied to within-subject ones. Here, our sample set consists of multiple patients (between-subject samples) but also multiple tissue sites per individual patient (within-subject samples), which may potentially violate the LR assumption of independence of errors. Also, the relatively small number of the breast cancer and FA sample sets may produce inaccurate estimates because LR models typically require large sample sizes in comparison to the number of predictor variables used. These limitations are largely absent or considerably more relaxed with the other three classification algorithms tested, described below.

To compare with the above LR model, a decision tree algorithm was first constructed. Such an algorithm repetitively splits the dataset based on a criterion that maximizes the separation of the tissue type (i.e. binary discrimination rule), resulting in a tree-like structure [25, 26]. Importantly, this organization structure from the root node to the leaf node facilitates the ready visualization and interpretation of the model thereby providing an intuitive understanding of the relative importance of different model FCs (so-called “white box” model in contrast to the “black box” models such as SVM and artificial neural networks) in the classification of lesions. In this article, C4.5, a commonly employed statistical classifier, is used to build the decision trees, using the concept of information entropy. In particular, at each node of the tree, the C4.5 algorithm selects one data attribute based on normalized information gain that most effectively splits its set of samples into subsets enriched in one class or the other.

Nevertheless, while decision trees are easy to interpret and reveal information about the underlying relationship between the predictor variable (model FC) and the response variable (tissue diagnostic class), they are often not very accurate in classifying large and complex datasets (such as tissue spectral matrices) [27–29]. To potentially enable more effective classification of the breast tissue lesions, kNN and SVM models were constructed. k-nearest neighbor (kNN) classification uses the data directly for discrimination, without construction of a prior model [30, 31], and therefore is widely used when there is little or no prior knowledge about the distribution of the data. The only adjustable parameter in such a model is k, which represents the number of nearest neighbors considered for estimation of class membership. By appropriately tuning k, the model flexibility can be enhanced or reduced. Typically, larger values of k reduce the effect of noise on the classification, but make boundaries between classes less distinct. The optimal value of k is usually selected by various heuristic techniques, e.g. cross-validation (as detailed in the Algorithm Development sub-section). The advantage of such an algorithm is that the class membership can be articulated in terms of that of its own neighbors and is therefore simple in its interpretation and implementation. Finally, we have also developed support vector machines (SVM) with appropriate kernel functions for non-linear classification. The SVM approach, which is based on statistical learning theory and structural risk minimization, builds optimal separating boundaries between classes by solving a constrained quadratic optimization problem [32, 33]. Using the so-called kernel trick that enables the separation of classes in a higher dimensional space, varying degrees of non-linearity and flexibility can be incorporated in the SVM model.

2.3 Algorithm development

A total of 228 breast biopsy tissue sites were probed using Raman spectroscopy. However, as detailed in our previous publication [14], 69 tissue sites were excluded from further analysis for the following reasons: 1) pertaining to inadequate histopathology/radiology examination (n = 59) (e.g. histopathology diagnosis could not be rendered due to improper paraffin embedding of the biopsy), 2) the spectral data was identified as outliers using Student’s t-test employing a Mahalanobis distance function (n = 10). The previous microcalcification-based classification of the core needle biopsy specimens was performed on a total of 159 tissue sites. In addition, 6 more sites were removed from the current analysis as they were diagnosed with pathologic changes other than the target lesions (fat necrosis, healing reaction and a naked microcalcification without accompanying breast tissue) on closer histopathological examination. Thus, FCs from 153 tissue sites were used to build the multivariate classification models. The 153 tissue sites included at least one site from all 33 patients.

For the LR model, a likelihood ratio test was performed to select the FCs important for lesion diagnosis. The diagnostic FCs, namely calcium hydroxyapatite, cholesterol, fat, collagen, epithelial cell cytoplasm and oxyhemoglobin, reflected the major tissue components that are likely to undergo a substantive change based on the presence of lesion. (It should be noted that the parameters which contribute most to the fit of spectroscopic data to a model may not be the parameters with the most diagnostic utility [34].) The likelihood ratio test also provided the probability thresholds, based on these FCs, which correctly discriminated the most tissue sites. LR code from the Statistics Toolbox in MATLAB (version 7.12, The Mathworks, Inc., MA) was used for developing the LR tissue discrimination models.

To implement C4.5 decision tree classification, J48 (an implementation of C4.5 algorithm) was employed and the analysis was carried out in the Weka data-mining tool [35]. For the kNN and SVM classification models, the open source Orange data mining suite (http://www.ailab.si/orange/) was used [36]. In the kNN algorithm, the Euclidean distance metric was selected for case neighborhood determination. The optimal value of k was selected based on the minimization of classification error in leave-one-out cross-validation (LOOCV) analysis (the protocol for which is explained below). For our dataset, this resulted in an optimal k value of 7. C-SVM was used for SVM analysis [37]. A radial basis function (RBF) kernel with a Gaussian envelope was used to address potential non-linearity in the spectra-class relationship and the cost and kernel parameters were optimized through an automated grid search algorithm.

In order to perform comparative evaluation of the different algorithms and their ability to discriminate lesion types (irrespective of the presence of microcalcifications), we employed LOOCV analysis. A standard recommendation in classification analysis is to not employ the same data samples for training and for prediction – otherwise, the class prediction accuracy may be artificially boosted. To overcome this problem with a limited dataset, LOOCV analysis is frequently pursued. In this procedure, the data from a single tissue site is eliminated, and the specific algorithm (such as LR, kNN etc.) is developed on the remaining tissue sites (optimizing agreement with the gold standard diagnoses). The resulting classification model is then used to predict the class membership of the excluded site. This process is successively applied to each of the sites. The predictions are then compared with the gold standard diagnoses for evaluation of algorithm sensitivity (SE), specificity (SP), positive predictive value (PPV), negative predictive value (NPV), overall accuracy (OA) and the area under the receiver operating characteristic (ROC) curve (AUC) [34].

3. Results

The information embedded in the tissue Raman spectra was first transformed to the chemical and morphological constituent compositional data in terms of the breast model FCs. It is worth noting before commencement of the FC-based analysis that the signal-to-noise ratio (SNR) of the Raman spectra varied slightly based on the tissue type (with the normal breast tissue, lesions without microcalcifications and lesions with microcalcifications showing an average SNR of 38.87 dB, 38.69 dB and 38.30 dB) (the interested reader is referred to the representative spectra shown in Figure 2 of Saha et al. [14]). Despite the small disparities, the large value of the SNR ensures the reproducibility (and precision) of the spectral measurements.

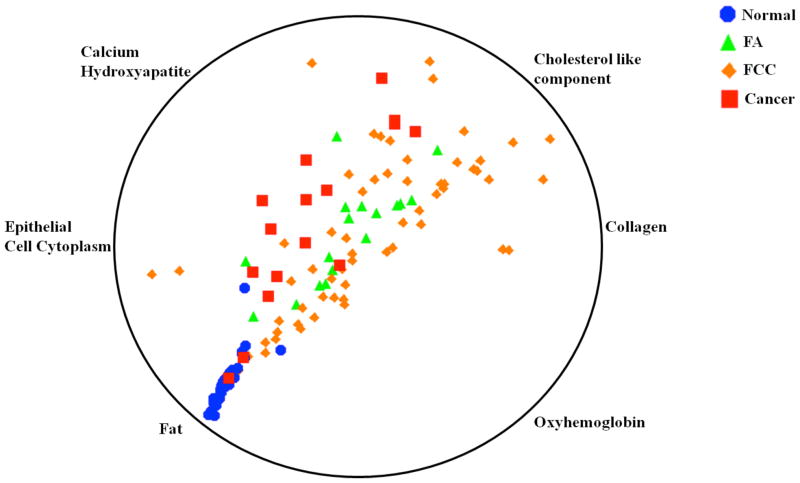
Figure 1 shows a multi-dimensional radial visualization plot of FCs obtained from the tissue site Raman spectra. The FCs plotted here were selected using the likelihood ratio test in LR, as mentioned in the Materials and Methods section. This nonlinear radial visualization method maps the FC data dimensions onto a two dimensional space for the purpose of clustering [38]. The FCs describing tissue site characteristics are equally spaced around the perimeter of a circle and provide dimension anchors, where the values of each dimension (FC) are standardized between 0 and 1. Here, each tissue site is shown as a point inside the unit circle with its location determined by the influence of its dimension anchors [39], thereby providing an intuitive understanding of the importance of specific FCs in determining class labels (i.e. tissue type, irrespective of microcalcification status). From the figure, one can readily observe a certain degree of clustering behavior for each of the tissue classes, especially for normal breast tissue and cancerous lesions. For example, the normal tissue specimens are found to have a substantially larger contribution of fat and smaller contribution of collagen than any of the other categories (which is consistent with our previous findings in breast cancer investigations [14, 17, 18]). In contrast, the benign lesions (namely, FA and FCC) exhibit overlap, probably arising from the competing contributions of collagen and calcium hydroxyapatite (in cases where lesions are associated with microcalcifications). Clearly, a linearly separable algorithm cannot provide adequate discrimination capability for such lesions, although it is easy to see that Raman spectroscopy does provide diagnostic information even when microcalcifications (as indicated by the content of calcium hydroxyapatite) are present.

Figure 1.

Multi-dimensional radial visualization plot of selected breast model fit coefficients obtained from the tissue Raman spectra. The plot illustrates the clustering behavior of the specimens belonging to each tissue histopathology class. Further details of the plot and selection of the fit coefficients are provided in the text.

To quantify this diagnostic information content, we first built LR models using the six FCs (namely, calcium hydroxyapatite, cholesterol, fat, collagen, epithelial cell cytoplasm and oxyhemoglobin) and applied them in a LOOCV protocol. Table 1(A) provides the confusion matrix for the LR models, where each column of the matrix represents the instances in a Raman predicted class, while each row represents the instances in a histopathological reference class. It should be noted that 7 tissue sites (including 1 normal, 1 FCC without microcalcifications, 4 FCC with microcalcifications and 1 ductal carcinoma in situ with microcalcifications) were unallocated based on their relatively low probability of belonging to any class. To ensure consistency in the ensuing analysis, we have removed these 7 tissue sites from further consideration thereby restricting our overall sample set to 146 specimens. These 146 specimens included 53 normal breast tissue (3 of which were associated with microcalcifications), 60 FCC (43 of which are associated with microcalcifications), 17 FA (all of which are associated with microcalcifications) and 16 breast cancer sites (14 of which are associated with microcalcifications). From Table 1(A), we observe that the normal breast tissue and FCC as well as cancer sites are classified with reasonable accuracy. However, a majority of the FA sites (15 out of 17) were misdiagnosed by the LR Raman algorithm as FCC. We suspect that for these tissue sites, microcalcifications are the dominant spectral contributors and the spectral contributions from the other tissue components (such as cholesterol-like, fat and collagen) are similar for FA and FCC lesions. Indeed, there was no FA site without microcalcifications in the analyzed dataset. As a consequence, the classification probability was reasonably similar for either tissue type (namely, FA and FCC) and the misclassifications are due to uncertainty in spectroscopic measurement as well as the fact that FCC has a substantially larger population of specimens in the analyzed dataset thereby skewing the overall algorithm to over-predict its probability of occurrence. Nevertheless, it bears emphasizing that these misclassifications of FA as FCC are of relatively little clinical significance, since the Raman diagnosis would indicate that these biopsies harbor benign breast lesions with microcalcifications. Importantly, however, the current LR algorithm reports 7 false negative and 2 false positive misclassifications of cancer, which is not ideal.

Table 1(A).

Confusion matrix for leave-one-out cross-validation of logistic regression-derived Raman lesion discrimination algorithm.

Reference Diagnosis	LR Raman Diagnosis
		Normal	FA	FCC	Cancer
	Normal	52	1	0	0	53
	FA	1	1	15	0	17
	FCC	7	3	48	2	60
	Cancer	2	0	5	9	16
		62	5	68	11	146

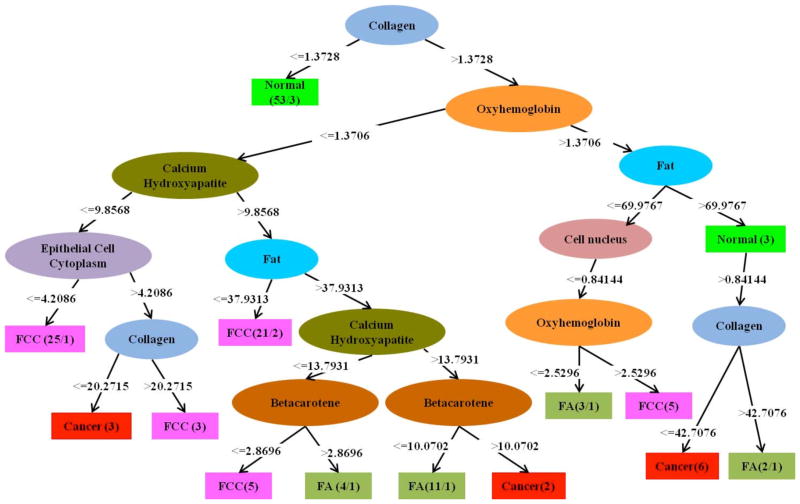
In comparison, as shown in Figure 2, the C4.5 decision tree algorithm employs selective utilization of the FCs to successively construct binary discrimination rules resulting in classification of each tissue site. This provides an alternative perspective on the significance of specific FCs with respect to the radial visualization plot of Figure 1. In accordance with our previous observations from Figure 1, collagen, oxyhemoglobin, fat, and calcium hydroxyapatite were identified as the most important diagnostic FCs. In particular, fat and collagen played key roles in discriminating normal tissue from other lesions. The main advantage of using the decision tree approach over the previous radial visualization plot is that it quantifies the discrimination rules with respect to the predictor variables (FCs). However, in terms of actual discrimination efficiency, the performance of the C4.5 decision tree (Table 1(B)) was considerably inferior compared to the LR models described above. In fact, the total number of misdiagnosed sites for C4.5 is 45 (out of 146 sites), whereas that for LR is 36. Notably, the number of false positives and false negative misdiagnoses of cancer is 7 and 12, respectively, a substantial increase over the LR algorithm.

Figure 2.

Decision tree generated using the C4.5 algorithm on the fit coefficients obtained from the tissue Raman spectra. Here, ellipses indicate intermediate nodes and rectangles represent the final nodes. The binary discrimination rules are represented in the branches following the nodes and the number of specimens distinguished as a specific class is given in the rectangle.

Table 1(B).

Confusion matrix for leave-one-out cross-validation of C4.5 decision tree-derived Raman lesion discrimination algorithm.

Reference Diagnosis	C4.5 Raman Diagnosis
		Normal	FA	FCC	Cancer
	Normal	49	0	2	2	53
	FA	0	6	11	0	17
	FCC	2	11	42	5	60
	Cancer	2	3	7	4	16
		53	20	62	11	146

In order to enhance the discrimination efficiency over the levels obtained using LR, we subsequently developed kNN and SVM models using the aforementioned LOOCV protocol. Unlike the decision tree, which is based on a multistage or hierarchical decision scheme, these classification approaches employ the set of features (FCs) collectively to perform classification in a single decision step. Table 1(C) and 1(D) give the corresponding confusion matrices for kNN and SVM models. It is evident that both of these methods offer much improved discrimination performances in comparison to the decision tree and LR models. In particular, kNN provides better discrimination for FA (where only 7 out of 17 sites, again all with microcalcifications, are misdiagnosed as FCC) in relation to SVM (which misclassifies 9 out of the 17 FA sites as FCC). However, the SVM model does not report any false positives; in contrast, the kNN model shows a single false positive for cancer. Further, both of the models provide the same number of false negatives (6) with 2 of the cancer sites being misclassified as normal and 4 more being misclassified as FCC. For the former two cancer sites (histopathologically assessed to be ductal carcinoma in situ with microcalcifications and lobular carcinoma in situ (without microcalcifications) from two separate patients), the misdiagnoses as normal can be attributed to the excessively high fat FC observed in each case. Additionally, three of the other four cancer sites misclassified as FCC (all ductal carcinoma in situ with microcalcifications) belonged to an individual patient, the spectral data from whom exhibited tissue features that were not accounted for by our fit algorithm. Prominently, the consistency of the kNN and SVM confusion matrices demonstrates that the misclassified sites were not significantly dependent on the type of modeling, but arise from inaccuracies inherent in the spectral-histopathology relationship (such as registration errors between the two types of measurement).

Table 1(C).

Confusion matrix for leave-one-out cross-validation of kNN-derived Raman lesion discrimination algorithm.

Reference Diagnosis	kNN Raman Diagnosis
		Normal	FA	FCC	Cancer
	Normal	50	1	2	0	53
	FA	1	9	7	0	17
	FCC	3	7	49	1	60
	Cancer	2	0	4	10	16
		56	17	62	11	146

Table 1(D).

Confusion matrix for leave-one-out cross-validation of SVM-derived Raman lesion discrimination algorithm

Reference Diagnosis	SVM Raman Diagnosis
		Normal	FA	FCC	Cancer
	Normal	50	1	2	0	53
	FA	2	6	9	0	17
	FCC	4	3	53	0	60
	Cancer	2	0	4	10	16
		58	10	68	10	146

4. Discussion

The results of this study demonstrate that Raman spectroscopy has the potential to discriminate lesions in tissue cores obtained from stereotactic breast needle biopsies. Importantly, we show the ability for lesion classification with a high degree of accuracy even when the lesions are associated with microcalcifications. This investigation, to the best of our knowledge, is the first report of such a finding, which is critical to the successful translation of this technology to the clinic where one of the significant geographical targets for needle biopsies is the presence of microcalcifications. The FC-based analysis reinforces our existing understanding of the tissue composition and its potential changes due to histopathology changes in benign and malignant lesions, and additionally provides a pathway to multivariate classification.

In terms of classification schemes, it is observed that SVM (and to a large extent, kNN) provide remarkably accurate results, especially as related to the discrimination of breast cancer lesions. Table 2 provides a comparative evaluation of the diagnostic performance of each of the classification algorithms (LR, C4.5 decision tree, kNN and SVM) for cancer detection. Given the overlapping populations seen from Figure 1, it is necessary to clearly define the most significant measure of algorithm performance, as there is typically a trade-off between sensitivity and specificity. In this clinical situation, PPV represents the performance metric of greatest interest, as false positives may have serious adverse consequences for the patient [34]. This is usually the case when the disease to be diagnosed is serious, should not be missed and is treatable. Here, one would like to ensure that every patient with a positive Raman diagnosis has cancer; otherwise (in the case of a false positive) the radiologist may retrieve only a single tissue core thereby missing the targeted malignant lesion. Consequently, the patient may have to undergo a second stereotactic or, more ominously, a surgical biopsy in the near future, suffering additional inconvenience and perhaps allowing the cancer to further proliferate. Conversely, even if the Raman algorithm signifies that the tissue to be biopsied is not cancerous when it truly is, the radiologist is likely to remove (unnecessary) additional tissue cores. This represents an undesirable situation but does not pose a major health risk to the patient.

Table 2.

Comparison of diagnostic performance for LR, C4.5, kNN and SVM-derived Raman algorithms for breast cancer lesion prediction. PPV: Positive Predictive Value; NPV: Negative Predictive Value; OA: Overall Accuracy for lesion discrimination. In this clinical situation PPV represents the most significant measure of algorithm performance (further details are mentioned in the text) and is correspondingly highlighted in this table.

Algorithm	Sensitivity	Specificity	NPV	PPV	OA
LR	56.3	98.5	94.8	81.8	75.3
C4.5	25.0	94.6	91.1	36.4	69.2
kNN	62.5	99.2	95.6	90.9	80.8
SVM	62.5	100.0	95.6	100.0	81.5

Viewed from this perspective, it is evident that SVM provides the best diagnostic performance (PPV = 100% and NPV = 96%), closely followed by kNN (PPV = 91% and NPV = 96%). Finally, LR provides PPV and NPV of 82% and 95%, respectively, whereas C4.5 decision tree gives PPV and NPV of 36% and 91%, respectively. Based on these findings, it is reasonable to infer that the latter two algorithms (LR and C4.5) are not optimal in terms of diagnostic performance and SVM (or kNN) should be utilized for development of the final clinical algorithm. Our sample set is not large enough to perform a comprehensive point-by-point evaluation of SVM and kNN, although it appears that the relative performance of these two classification techniques would depend heavily on the specific data set analyzed. Significantly, if the number of predictor variables (fit coefficients or spectral features) increase, prediction accuracy of kNN algorithms tend to decrease. Also, the accuracy of the k-NN algorithm can be severely degraded by the presence of noisy or irrelevant features, which does not serve as a major impediment here because the FCs are derived from the (fairly noise-free) basis spectra. Under such circumstances which may appear if full spectral analysis was pursued, irrelevant attributes easily may overwhelm information from important ones bringing to the forefront the so-called “curse of dimensionality” [40]. Thus, appropriate pre-processing steps focusing on removal of irrelevant attributes would become imperative.

On the other hand, SVM classifiers do not necessitate feature space reduction [41] and as a result can be more readily applied for full spectral analysis. Notably, SVM also provides an advantage over neural networks because it typically offers superior generalization ability and robustness [42]. In addition, it has been reported that SVM model development may require only a small training sample set [43–45], although it bears emphasizing that the burden of proof in a specific study would rest on the investigators to ensure the avoidance of “curse of dataset sparsity” (i.e. too few samples) [40]. It is pertinent to mention that a large weight (for the minimization of regression/classification errors) in the SVM objective function implies that the model bears the risk of over-fitting. In this study, over-fitting is avoided by using leave-one-out cross-validation. Ideally, given a larger dataset, one would like to invoke an independent test set for reporting the final results of the model (that has been optimized using cross-validation) [46]. Such a procedure would further minimize the possibility of over-fitting.

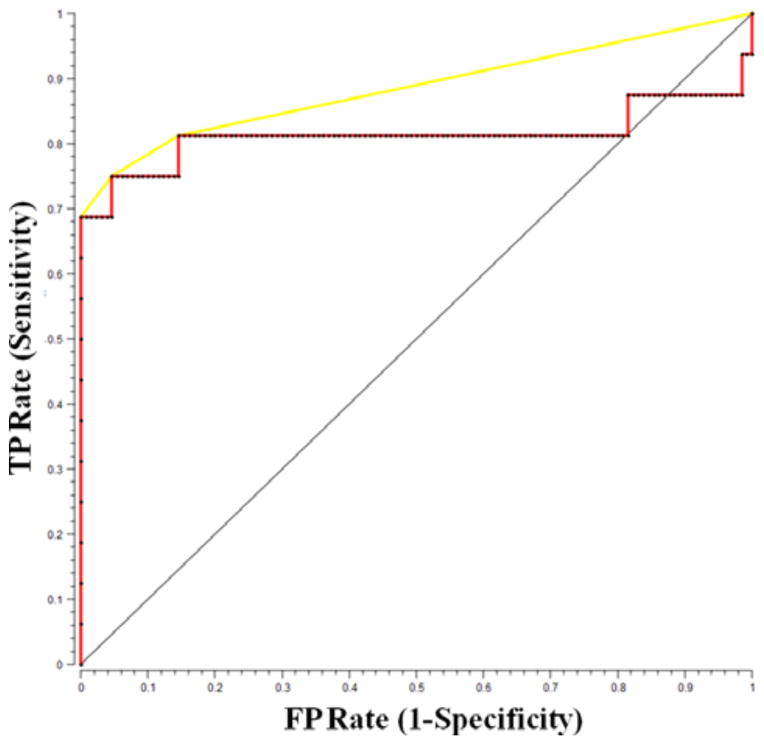
Finally, the receiver operating characteristic (ROC) curve for SVM prediction for breast cancer is shown in Figure 3. For comparison, the ROC curve of two indistinguishable classes (represented by the solid black line) is shown in the figure. The area under the curve (AUC) is determined to be 0.92 whereas the AUC for a perfect algorithm would be 1.00.

Figure 3.

ROC curve for SVM-derived Raman decision algorithm for the diagnosis of breast cancer.

5. Conclusion

We present here a Raman spectroscopic tool for discrimination of lesions in breast tissue obtained during stereotactic breast needle core biopsies, even in the presence of microcalcifications. Raman spectroscopy provides ample diagnostic information due to its exquisite chemical specificity and ability to clearly quantify the chemical composition of the tissue in terms of primary constituents such as collagen, fat and calcium hydroxyapatite. Further, we have performed a comparative assessment of classification methodologies with the resultant optimal SVM-derived Raman diagnostic algorithm exhibiting a PPV of 100% and NPV of 96% in detection of breast cancer lesions. In totality, one can conclude that Raman spectroscopy in combination with a suitable classification tool has the potential to not only detect microcalcifications (based on the calcium oxalate and calcium hydroxyapatite content) [14], but also identify the specific breast lesions associated with the microcalcifications in stereotactic breast biopsies as in this study. This study represents a significant extension of our previous efforts in providing real-time feedback to clinicians during stereotactic breast needle biopsy procedures, potentially decreasing non-diagnostic and false negative biopsies.

In addition to the current investigations, we are actively designing and engineering a side-viewing Raman probe that can be used in conjunction with a vacuum-assisted biopsy needle for true real-time guidance of biopsy procedures. In this regard, other potential excitation-collection schemes such as spatially offset Raman spectroscopy (SORS) [47] can also be investigated. Such clinical studies will allow us to assess the viability of the proposed approach in vivo. It is possible that the PPV and NPV numbers may decrease (to a small extent) when the current Raman algorithm(s) are tested in large-scale studies in more diverse patient populations, thus necessitating suitable fine-tuning of the lesion discrimination algorithms. Also, extensive clinical testing may present the opportunity to diagnose rare lesions that have not been addressed in the preliminary studies. We envision that the final outcome in terms of algorithm development may be a hybrid ensemble of different models (including but not limited to the aforementioned classification techniques), specifically customized for prediction of lesion types with and without microcalcifications. Towards this end, the domain of full-spectral analysis (and its related feature-selected variant [48]) can also be explored, in place of the FC-based analysis outlined in this article.