Indentation and needle insertion properties of the human eye

Abstract

Purpose

Characterization of the biomechanical properties of the human eye has a number of potential utilities. One novel purpose is to provide the basis for development of suitable tissue-mimicking material. The purpose of this study was to determine the indentation and needle insertion characteristics on human eye globes and tissue strips.

Methods

An indenter assessed the elastic response of human eye globes and tissue strips under increasing compressive loads. Needle insertion determined the force (N) needed to penetrate various areas of the eye wall.

Results

The results demonstrated that globes underwent slightly greater indentation at the midline than at the central cornea, and corneal strips indented twofold more than scleral strips, although neither difference was significant (P=0.400 and P=0.100, respectively). Significant differences were observed among various areas of needle insertion (P<0.001). Needle insertion through the anterior sclera (adjacent to the limbus) and posterior sclera (adjacent to the optic nerve) required the greatest amount of force (0.954 and 1.005 N, respectively). The force required to penetrate the central cornea (0.518 N) was significantly lower than all other areas except the midline sclera (0.700 N)

Conclusion

These data form the basis for further research into the development of a tissue-mimicking human eye construct with potential utility as a model for use in ophthalmology research and surgical teaching.

Introduction

Eye models are an integral component of both ophthalmology research and surgical wet-lab teaching, wherein residents-in-training or established ophthalmic surgeons can use these models to master new surgical techniques and clinical procedures. Human cadaveric eyes are difficult and expensive to obtain and fall short of being an ideal model because of tissue degradation. Animal cadaveric eyes are more readily available but are even more removed from the human globe in terms of anatomy and tissue characteristics. Both are biodegradable and pose hygienic/biohazard risks.^{1, 2} Plastic models have poor tissue-mimicking capability.³ Computer-simulated virtual-reality models are expensive, include large hardware, and provide an artificial operating experience.⁴ The existence of a tissue-mimicking construct of the human eye that is not biodegradable and maintains its shape and consistency over time would obviate many of the shortcomings of existing models. Such a model would closely simulate the size, texture, and biomechanical properties of human tissue.

The sclera and cornea have an important role in determining the shape and behaviour of the eye.^{5, 6} The sclera is the fibrous outer protective layer of the human eye. Its mechanical properties are mediated by the content and architecture of its structural proteins. The sclera is composed of irregular, densely packed collagen bundles made up of parallel collagen fibrils. These bundles are arranged in the direction of highest tension around the sclera, forming a crisscross pattern in the plane parallel to the eye surface. The sclera consists of type 1 collagen, which comprises approximately 80% of its dry weight, with glycosaminoglycans (GAGs) and elastin as the other major protein components. Collagen and GAGs are most influential in determining the sclera's response to deformation. Covalent bonds, or cross-links, between these structural proteins serve to increase the stiffness of the tissue.

The cornea is the transparent part of the eye that serves both as a protective layer and as the main refractive component of incoming light.^{7, 8} It is composed of 78% water, 15% collagen, and 5% other proteins. It has a surface area of about 1.3 cm², or 15% of the total eyeball surface. Five distinct layers make up the cornea: the corneal epithelium, Bowman's membrane, stroma, Descemet's membrane, and endothelium. The stroma is a tense tissue consisting of sheets of collagenous material, which comprises about 90% of the cornea's total thickness.

Characterizing the biomechanical properties of the human eye is essential for guiding the development of suitable tissue-mimicking material. The tensile elastic moduli of human sclera and cornea have been extensively described in the literature. However, these values are inconsistent among different authors and vary by up to 100-fold for sclera and 1000-fold for cornea.^{5, 9, 10, 11, 12, 13, 14} Few studies have described the compressive elastic moduli of the sclera and cornea.¹⁵ The insertion of needles into soft tissues has been published by several investigators.^{16, 17, 18} Abolhassani et al provide an excellent review of the tissue mechanics of and modelling needle insertion forces and tissue deformation during needle insertion.¹⁶ The primary factors that affect needle insertion are: tissue layers, elastic/viscoelastic properties of tissue, velocity of insertion, cutting force (needle tip), frictional forces (needle tip and sidewall), tip type (bevelled, triangular, tubular), needle size, bending (due to bevelled needle), needle sharpness. Some have used instrumented needles to determine the forces. Although some work has been conducted on the operational performance of needles in ocular procedures (eg, de Stefano et al¹⁷), studies of the forces required for needle insertion through the ocular tissues are almost absent from the literature.^{17, 18}

In a typical needle puncture, the axial force ramps up to a peak as the needle tip stretches and penetrates the tissue. As the needle advances, there may be additional ramp-peaks and troughs as the needle tip penetrates the layers of tissue. After initial penetration, the adjacent tissue relaxes but produces frictional forces along the needle shaft, which prevents the force from dropping to zero. Upon retraction the forces drop to zero (or negative if the load cell can measure). Podder et al performed the first in vivo force measurements for the manual insertion into human soft tissue (skin, perineal, prostate) associated with the prostate cancer brachytherapy.¹⁹ Their average maximum axial insertion force was about 15 N into perineum and 7 N for the prostate. Finite element modelling has been used to examine the insertion process of a micro-needle into a skin model comprised of three layers.²⁰ Their simulation results show that the stiffness, failure stress, and the thickness of the stratum corneum, the needle tip area and the needle wall angle are the primary control parameters for the tapered microneedle insertion into the multilayered human skin. For hollow microneedles with a large tip diameter, the larger the wall thickness, the larger the insertion force. Recent use of finite element analysis with adaptive cohesive crack modelling has provided some further insights into the needle–tissue interaction.²¹ This has improved the stress field and soft tissue fracture behaviour around the needle tip, showing much higher stress concentrations and greater tissue/tip contact areas than has been demonstrated before.

The suitability of performing penetration experiments using animals as human surrogates is contentious. The relationship of load/strain for fresh corneas from rabbits and humans showed quite different behaviour.²² Although it would seem obvious that the testing of selected animal tissues would replicate human tissues, some reported comparisons contradict this assumption.^{9, 22} Therefore, we chose to only report results for human eyes.

In this exploratory study, we describe the biomechanical properties of the human eye using two testing methods developed at the London site of the National Research Council of Canada (NRC). We assess the deformation response of human eyes under increasing compressive (indentation) loads and determine the force required for needle insertion at various anatomical areas. To our knowledge, indentation and needle insertion tests of this sort on human eyes have not been reported in the literature. These findings will add to the current literature and may be used to better guide the development of tissue-mimicking material for the human eye. Further, as intravitreal injection continues to be a major current method of drug delivery, insights into how the needle interacts with the human tissue may lead to optimization and innovation in this important area.

Materials and methods

Human eyes

Six human eyes, from three donors, were obtained from the Eye Bank of Canada. Three eyes were phakic; three were aphakic. The donors consisted of two males and one female, aged 63–78 years with no known ocular disease. The eyes were stored between 2 and 4 °C in physiologic saline (0.9% (w/v) NaCl) and the testing was conducted within 72 h of enucleation. The surrounding fat, muscle, and episcleral tissues were also carefully removed before testing. In this paper, the eyes are referred to as ‘Human Eye 1', up to ‘Human Eye 6'.

Indentation

An indenter, constructed at the NRC, was used to assess the elastic response of human eye globes and tissue strips under compressive loads. Only the three phakic eyes were used in this experiment to avoid potential confounding factors associated with the compression of an aphakic eye globe as the structural integrity of the latter may have been previously compromised during removal of the lens.

An eye globe was placed into a cavity for stability (Figure 1a). The cavity containing the eye globe was placed on the indentation platform with the indenter shaft raised to its maximum height, between 9 and 12 mm. The indentation platform was raised until the eye globe just touched the bottom of the indenter tip. The indenter shaft was then released onto the desired area of the eye globe and increasing weights were added to the circular platform atop the indenter shaft at 3 s intervals. A video camera recorded the digital screen that displayed the indenter tip height as the loads were applied. During video playback this allowed for determination of the tip height at the moment each weight was placed. The shaft itself weighed 15 g, constituting the ‘minor load'. The ‘major load' was then added in stepwise increments of 15 g. The total load (minor plus major) came to a maximum of 135 g. Two areas were indented on the globes: the midline sclera (equator of the globe) and the central cornea. After globe and needle insertion testing, strips of posterior sclera and central cornea were then excised using surgical scissors, placed directly on the indentation platform, and subjected to the same protocol.

Figure 1.

(a) Indentation of a human eye globe at the midline sclera. (b) Needle insertion through the central cornea.

The data were plotted graphically using Microsoft Excel 2003 with the indenter tip height on the y axis and total load in grams on the x axis. A linear line of best fit was applied to the curve to obtain a slope representing the deformation characteristics of the tested eye component. To evaluate significance, Mann–Whitney U-tests were performed in IBM SPSS Statistics Version 20.0 (IBM, Armonk, NY, USA).

Needle insertion

A Needle Insertion Force and Tracking (NIFT) measurement system, developed at the NRC, was used to characterize the force needed to penetrate various areas of the eye wall (Figure 1b). The NIFT is comprised of an axial force transducer with means for attaching the proximal end of the needle to the force transducer and a magnetic tracking system (Aurora electromagnetic tracking system, Northern Digital Inc., Waterloo, ON, Canada; complete with Tool Development Software). An 18G PrecisionGlide needle (Becton Dickinson & Co., Franklin Lakes, NJ, USA) was attached to NIFT's force transducer via a Luer-Lok connection. One hand was used to hold the eye in a fixed position, whereas the other hand performed the needle insertion. Once recording was initiated, the needle was held for 3–4 s to establish a baseline voltage reading. Then it was pushed through the eye wall and held for another 3–4 s until recording was stopped. Insertions were performed for human cadaveric eyes at the posterior sclera, midline sclera, anterior sclera, corneoscleral limbus, and central cornea as shown in Figure 3. Each area underwent two insertions; for instance, the posterior sclera was penetrated 4 mm from the optic nerve on either side, before moving on to the midline sclera.

The voltage readings obtained from NIFT were converted to Newtons (N). A specific baseline was determined for each needle insertion by averaging the force values during the time when recording was initiated but no needle insertion was taking place. If the baseline differed before and after insertion, the baseline was calculated for both segments. The two values were then averaged and used as the overall baseline force. This baseline force was subtracted from the maximal force of insertion, which was taken as the highest peak on the curve. This enabled a determination of the amount of force required to penetrate the eye wall during each trial and corrected for any baseline force perceived by the transducer.

The data were plotted graphically using Microsoft Excel 2003 with the penetration force on the y axis and the sample number on the x axis. As NIFT takes multiple voltage readings per second, the ‘sample number' is best thought of as a surrogate for ‘time' that is, readings are automatically taken as long as the NIFT recording feature is activated. The data were subjected to a Univariate ANOVA and Tukey post-hoc analyses using SPSS 20.0.

Results

Indentation

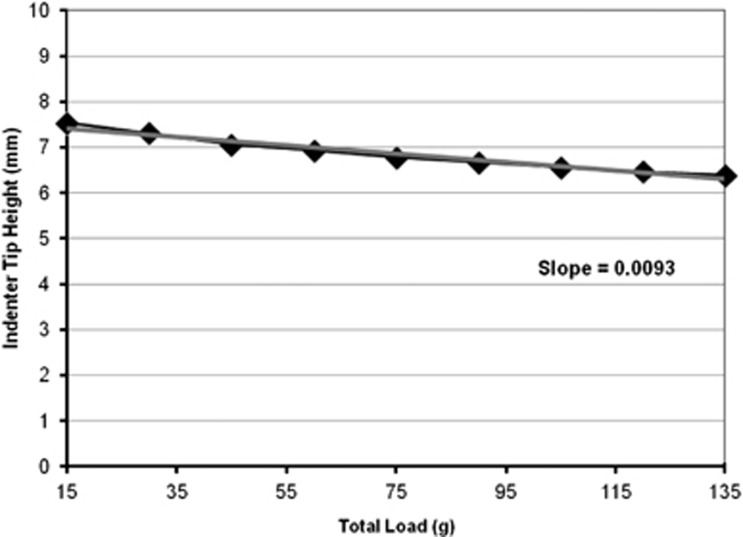
An example of a typical indentation response (Figure 2) shows that the greater the applied load (x axis), the lower the height of the indenter tip (y axis). Using the absolute value of the slope, a greater slope thus indicates a larger deformation under the increasing applied load. The indentation slopes for all three eyes tested are summarized in Table 1. The globes deformed more when indented at the midline sclera than at the central cornea (1.1-fold difference), although this difference was not significant (P=0.400). Corneal strips deformed twofold more than scleral strips during indentation; however, this difference was also not significant (P=0.100).

Figure 2.

Typical indentation response of human eye globe at the midline sclera. The grey line indicates the line of best fit from which the slope was derived.

Table 1. Indentation slopes (μm/g) for the globes and tissue strips of Human Eyes 4 to 6.

Sample	Globe midline sclera	Globe central cornea	Scleral strip	Corneal strip
Human Eye 4	0.0093	0.0072	0.0012	0.0025
Human Eye 5	0.0097	0.0082	0.0011	0.0025
Human Eye 6	0.0079	0.0087	0.0013	0.0022

Needle insertion

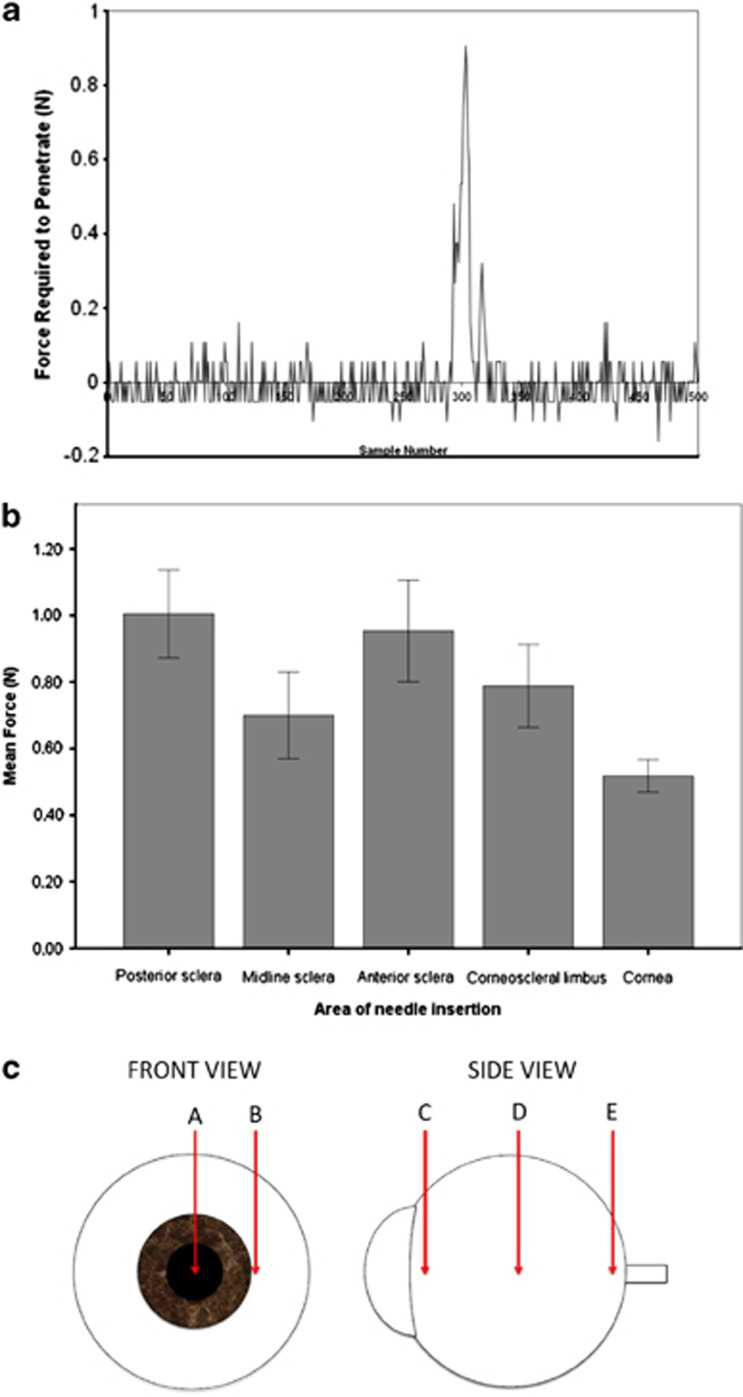
A typical needle insertion curve is shown in Figure 3a. Mean force (±2 SE) required to penetrate each anatomical area is displayed in Figure 3b and c. Significant differences at the 0.05 level were observed among the areas of needle insertion (P<0.001). Needle insertion through the anterior and posterior sclera required the greatest amount of force (0.954 and 1.005 N, respectively) and was not significantly different from each other (P=0.976). The corneoscleral limbus required a slightly greater force (0.788 N) than the midline sclera (0.700 N); however, this difference was not significant (P=0.846). The force required to penetrate the central cornea (0.518 N) was significantly lower than all other areas, but not significantly different from the force required to penetrate the midline sclera (P=0.238). Tukey post-hoc analyses revealed where the significant differences among the areas of needle insertion occurred (Table 2).

Figure 3.

(a) Typical needle insertion curve through the posterior sclera of a human eye. (b) Mean force (N) required to penetrate various areas of the human eye. (c) Schematic illustration of needle insertion sites on a human cadaveric eye. A=central cornea (0.518 N), B=corneoscleral limbus (0.788 N), C=anterior sclera (0.954 N), D=midline sclera (0.7 N), E=posterior sclera (1.005 N).

Table 2. Tukey post hoc for differences in force by area of needle insertion.

Area of needle insertion	Group mean	Mean differences in force (N)
		Posterior sclera	Midline sclera	Anterior sclera	Corneoscleral limbus	Cornea
Posterior sclera	1.005		0.305a	0.051	0.216	0.487a
Midline sclera	0.700			−0.254a	−0.089	0.182
Anterior sclera	0.954				0.165	0.436a
Corneoscleral limbus	0.788					0.270a
Cornea	0.518

^aMean difference is significant at the 0.05 level.

Discussion

Indentation

Unlike the full, taut globes that human eyes resemble in their physiologic environment, the cadaveric eyes lose their initial shape and feel slightly deflated after enucleation and storage. Thus, once the indenter shaft (weighing 15 g) was released and contacted the eye globes, an initial shape deformation occurred. This is why the first height measurement was taken after the indenter shaft contacted the eye (ie, when the eye is exposed to a 15-g mass), rather than the height that was displayed when the indenter shaft is raised to its maximum. This initial response was followed by immediate resistance to further deformation.

The ability of the eye globes to resist deformation under increasing load may be explained by the collagen fibril arrangement in sclera and corneal tissue. At normal intraocular pressure, collagen bundles in the sclera form waves in a semi-relaxed state; however, as the pressure increases, they straighten out to resist further tensile strain.⁶ The cornea also has highly ordered parallel fibrils that make the tissue highly resistant to deformation at a raised intraocular pressure.⁶ Upon the application of a tensile stress, a restoring force is generated by the stretched fibres that balances the applied force and resists deformation, providing the cornea with substantial tensile strength.⁷ During indentation of the eye globes, the focal area of compression to one area of the eye causes tensile stress to spread out over the rest of the eye wall, which resists the deformation accordingly.

Although the small number of samples subjected to indentation limited our ability to detect significant differences, we propose two possible explanations for why the eye globes deformed to a greater extent when indented at the midline sclera than at the central cornea. First, the collagen fibrils of the corneal stroma turn at the corneoscleal limbus and run circumferentially, helping to maintain corneal curvature.⁷ This annular arrangement may have provided extra resistance to deformation as the indenter tip compressed the central cornea. The second explanation relates to the internal anatomy of the eye. The ocular components situated posterior to the cornea, including the lens-iris diaphragm, and associated ciliary body may have added a barrier to compression that was not apparent to the observer.

During indentation of the eye wall strips, a compressive force was applied by the indenter tip and hence the property being measured was truly resistance to compression, rather than a secondary tensile response observed because of the properties of the eye globe. As previously discussed, the primarily circumferential orientation of collagen fibrils allows the sclera and cornea to resist tensile stresses better than compressive forces. In fact, Battaglioli and Kamm found that the compressive elastic modulus of the sclera is 100-fold less than the tensile elastic modulus.¹⁵ A naturally curved tissue strip such as the sclera that has been excised and compressed in a non-physiologic manner resists deformation in a characteristic manner. The circumferentially oriented collagen fibrils are stretched and the radially oriented fibres are compressed along with the general deformation of the tissue matrix.¹⁵ Although the compressive elastic modulus for the cornea has not, to our knowledge, been formally studied, a similar response to compression is likely to occur. It is unclear, then, why the sclera showed greater resistance to compression than the cornea. One reason may be that slight differences in either the structural arrangement of the collagen fibrils or in the composition of the extracellular matrix may provide the sclera with this added compressive stiffness. Indeed, it has been suggested that the corneal ground substance, composed of proteoglycans and GAGs, allows the cornea to resist compressive and shearing forces.^{6, 16}

It is widely perceived that the biomechanical properties of the human eye change with age. The literature is sparse on this topic. In the study by Mortzavi et al, the compressive stress (termed ‘drained equilibrium') decreased with age by about 50% within the age span of 78–89 years.²³ Our indentation of the strips is a compressive force, which would be expected to increase with age, consistent with a less stiff material.

Conversely, Friberg and Lace report that the tensile modulus of elasticity for the globe became stiffer with age from about 1.5 N/m² × 10⁶ at age 16 years to about 3.5 N/m² × 10⁶ at age 81 years.¹¹ Coudrillier et al also reports that older age was predictive of a stiffer response for the posterior sclera.²⁴ Using their regression line, the stiffness increased from 500 kPa (0.5 N/m² × 10⁶) at age 45 years to 4000 kPa (4 N/m² × 10⁶) at age 90 years. Our indentation technique of the globe is similar to the tensile modulus. It would be expected that our indentation results would decrease with age, consistent with a stiffer material. Elsheikh et al found similar results for corneal trephanate expansion tests, with the corneal stiffness increasing by up to 10% between 50 and 100 years of age.²⁵ These changes were attributed to intermolecular and intramolecular collagen cross-linking because of non-enzymatic glycosylation, providing increased stiffness and brittleness. Similar changes in stiffness behaviour were found for the sclera by Schultz et al.⁵

Needle insertion

The magnitude of the axial force for tests in this study was a maximum of about 1 N for an 18-G needle in the anterior sclera. Podder et al measured a maximum axial force of about 9.1 N in different tissue (perineum, prostate), which is considerably higher.¹⁹ Both needles had a regular bevelled tip, same size, smooth wall finish, and stainless steel. However, Pulido et al found peak needle penetration forces for anterior scleral trephinates of 0.29 and 0.61 N with 31 G and 27 G needles, respectively.¹⁸ Given that the nominal scleral thickness of these test specimens and those in the current study would be similar (approximately 0.55 mm), there is some proportionality between the force and the needle diameters, suggesting predominantly frictional forces occurring at peak axial forces. The differences in axial insertion forces described above can be attributed to experimental error, tissue properties, and geometry, and test boundary conditions.

The results of needle insertion appear to correlate with previously published scleral thickness differences at various regions of the eye. The thickness at the posterior pole has been measured between 0.9 and 1.0 mm. It took about 1 N to penetrate the eye wall at this location. The thickness at the equator is between 0.39 and 0.49 mm and the force required to penetrate the midline sclera (ie, the equator) was about 0.7 N. The sclera tends to thicken anteriorly towards the limbus, resulting in a thickness of about 0.55 mm.^{26, 27} By comparison, it took about 0.95 and 0.75 N to penetrate the anterior sclera and limbus, respectively, in the human cadaveric eyes. It should be noted that 3.5–4 mm back from the limbus is a key anatomical area for therapeutic needle insertion.²⁸ Among our testing sites, this corresponds to the anterior sclera. It would thus be particularly important to mimic the needle insertion characteristics of this area accurately in a tissue-mimicking eye construct.

If we are to assume that there is a correlation between scleral thickness and the force of needle insertion, then it should require about half as much force to penetrate the midline sclera than the posterior pole, and slightly more force to penetrate the anterior sclera and corneo-scleral limbus than to penetrate the midline sclera. Although this trend was apparent in our results, the midline sclera, anterior sclera, and corneoscleral limbus all required more force during the needle insertion than would be expected from a strictly corresponding relationship between thickness and penetration force.

There are certain limitations in our study, which may contribute to these inconsistencies. For instance, we have only included scleral, not retinal or choroidal, thickness in our comparisons. As the retina and choroid are very delicate layers, it is unlikely that they contribute any significant additional barrier to needle insertion; however, the omission of their thicknesses could be a source of inaccuracy in our comparisons.

A small subjective component was involved in determining an averaged baseline voltage (later converted to force) of the pre- and post-insertion horizontal segments of the curve, as in some trials these two segments had slightly different baseline values. In addition, although great care was taken while conducting the trials, performing needle insertion by hand results in a small amount of variation in the penetration force with each trial, due to hand tremor and a variable insertion velocity. In future testing, utilization of a robotic needle insertion technique may reduce these inaccuracies by performing needle insertion at a constant, defined velocity with a negligible amount of tremor.

Finally, one of the most important potential confounding factors relates to the order of needle insertion. For each eye, insertions were performed, in order, at the posterior sclera, midline sclera, anterior sclera, limbus, and cornea. A relatively large 18 G gauge needle was used to perform what amounted to at least 10 separate insertions on each eye, given that two insertions were performed for each anatomical area. This caused vitreous leakage from the insertion sites, resulting in a slightly deflated eye globe. It appeared to take more force to penetrate the wall of this type of globe during successive insertions than it did to initially penetrate the posterior sclera of the taut, fully intact eye globe. This may help explain why it took more force than expected to penetrate the midline sclera, anterior sclera, and corneoscleral limbus, as by the time limbal penetration was performed, the eye globe had lost its spherical shape because of vitreous leakage out of the prior insertion sites. Future testing should utilize a pressure transducer system to inject gas or fluid into the eye, effectively controlling pressurization of the globes at physiologic intraocular pressure before needle insertion.

A variety of needles were tested on porcine eyes before conducting human eye measurements, using 18, 25, 27 and 30 G needles (larger gauge corresponds to smaller needle diameter). The 30-G needle is the most common type used in clinical practice.²⁸ Although the smaller diameter needles were less damaging to the eyes, and thus did not cause as much vitreous leakage, they penetrated the eye wall with much less force and did not produce an acceptable signal-to-noise ratio on the resulting curves. Insertions with the18-G (larger diameter) needle yielded the most reproducible force curves, albeit at the expense of the eye globe integrity. Future trials should perform needle insertions at each anatomical position on a fully intact eye globe to increase the accuracy and reproducibility of the measurements.

If it is indeed the case that an increasing amount of force is required to penetrate a deflated eye globe, then needle insertion through the cornea, which has roughly the same thickness as the limbus (0.55 mm),^{29, 30} should require a penetration force that is similar to the limbus and the adjacent anterior sclera. The fact that corneal insertion required the least amount of force overall may be an indication that the corneal collagen arrangement is less resistant to needle insertion than that of the sclera.

The effect of tissue changes with age on our results for needle penetration is difficult to predict as the forces depend on a combination of factors: rate of insertion, wall thickness, interstitial tissue adhesion (friction), and elastic properties at insertion site. However, the work of Elsheikh et al suggests that this may not be as significant as some authors have indicated.²⁵

Conclusions

In this pilot study, we have reported initial data on novel biomechanical aspects of the human eye. These data on indentation and needle insertion properties are a basis for further research, which should focus on refining the measurement techniques and conducting more trials to demonstrate significance. Characterizing these aspects of the human eye also serve as a basis for developing tissue-mimicking material, which can be used to create an accurate human eye model for both surgical education and research applications. Finally, understanding the relationship between the needle and the human eye wall may further provide insights into optimization of drug delivery by this technique.

An improvement to the study would have been to measure or assess the Intra-ocular Pressure (IOP). During the first interaction of the needle with the eye (bending of the ocular tunic before cutting of the sclera with the needle), the IOP is important. The issue then becomes when the peak force occurs. This occurred as the needle passed through the sclera. At this point, as the sclera is compressed and the majority of the force relates to friction along the needle, the IOP becomes irrelevant. The only other issue would be that the shape of the eye just as the needle starts to cut the sclera could be more depressed than with a higher IOP. Again this is not seen as a significant issue. Thus, the early part of the force-displacement curve may be incorrect but the peak force is correct. The effects of IOP changes in this model will be a consideration during future research.

The authors declare no conflict of interest.