Abstract
The determination of the folding dynamics of polypeptides and proteins is critical in characterizing their functions in biological systems. Numerous computational models and methods have been developed for studying structure formation at the atomic level. Due to its small size and simple structure, deca-alanine is used as a model system in molecular dynamics (MD) simulations. The free energy of unfolding in vacuum has been studied extensively using the end-to-end distance of the peptide as the reaction coordinate. However, few studies have been conducted in the presence of explicit solvent. Previous results show a significant decrease in the free energy of extended conformations in water, but the α-helical state is still notably favored over the extended state. Although sufficient in vacuum, we show that end-to-end distance is incapable of capturing the full complexity of deca-alanine folding in water. Using α-helical content as a second reaction coordinate, we deduce a more descriptive free-energy landscape, one which reveals a second energy minimum in the extended conformations that is of comparable free energy to the α-helical state. Equilibrium simulations demonstrate the relative stability of the extended and α-helical states in water as well as the transition between the two states. This work reveals both the necessity and challenge of determining a proper reaction coordinate to fully characterize a given process.
Introduction
Folding of proteins into organized three-dimensional structures capable of fulfilling a biological function is determined by the sequence of amino acids1 and is believed to proceed hierarchically.2,3 The emergence of secondary-structure elements constitutes an early event in the chronology of folding,4 which prefaces the ultimate collapse into well-defined, compact, functional entities. Formation of stretches of secondary structure, the elementary bricks of the protein scaffold, therefore, represents an important milestone on the folding pathway, and a convenient framework to investigate the basic physical principles that underlie protein folding—notably how do elements of secondary structure nucleate and further propagate into an ordered structure, and to what extent is the organization of the peptide chain collective.5 Understanding this key biological process at the theoretical level has greatly benefited from the recent development of novel, dedicated computer architectures6 and the unbridled race to model larger proteins over longer time scales.7,8 Brute-force simulations have now reached a cruising speed that can fold proteins as large as 100 amino-acid residues over tens to hundreds of microseconds,9 still at the price of substantial computational effort. A number of unbiased, all-atom simulations in explicit solvent have proven successful to illuminate the hierarchical nature of folding, shedding light on the possible pathways that connect a random coil to a functional three-dimensional structure.10−13
Substantially shorter importance-sampling14,15 simulations relying on simpler models consisting of short, organized peptide segments can, however, provide valuable insight into the physical and evolutionary principles that govern the intricate conformational transition of a disordered protein chain into a properly folded one.5,16−20 Among suitable candidates of secondary-structure elements for biased simulations are α-helices, the most prevalent motif observed in proteins,21 stabilized by intramolecular interactions, notably through the formation of a hydrogen bond between the carbonyl moiety of the ith residue and the amino moiety of the i+4th residue. Owing to its noteworthy propensity to form α-helices,22 alanine has been the amino acid of predilection in theoretical investigations of conformational equilibria in short peptide segments. Alanine-rich peptides flanked by titratable residues have also been utilized abundantly at the experimental level23 to decipher the transition pathway from a disorganized chain to a nascent chain to an ultimately folded α-helix. In particular, they were at the center of a controversy on the existence of 310-helices,24 a secondary-structure motif arising from the formation of hydrogen bonds between the ith and the i+3-th residues of the peptide chain, conjectured to act as an observable intermediate in the conformational transition toward the α-helical state.
Turning to importance-sampling simulations naturally raises the question of an appropriate choice of a transition coordinate, capable of describing folding of the peptide chain into a well-ordered secondary structure. Even for appreciably short segments, this choice remains an intricate problem, deeply rooted in the large number of degrees of freedom that vary concurrently as the peptide chain evolves toward its native, organized conformation.25 Much of this intricacy lies in the multidimensionality of the true reaction coordinate,26−29 thwarting naive attempts to resort to a limited number of geometric variables, often of low collectivity.30 Fruitful application of collective-variable-based methods rests in large measure upon the fragile hypothesis of time scale separation of slow degrees of freedom, in connection with the reaction coordinate, as well as all other hard, fast degrees of freedom. Mapping the free-energy landscape that underlies the folding of a short peptide, therefore, ultimately reduces to either selecting a few relevant collective variables or throwing into the model a plethora of order parameters to describe the multidimensional transition space.31 The daunting nature of this task explains why biased simulations of complex, intertwined conformational changes remain scarce.32
In the present contribution, we revisit the paradigmatic capped decamer of alanine, henceforth referred to as deca-alanine. Deca-alanine has served on various occasions as a methodological proof of concept, in particular in nonequilibrium work simulations in conjunction with the Jarzynski identity,33 and equilibrium free-energy calculations relying upon the application of a time-dependent bias.34,35 Notwithstanding their rudimentary character, model peptides like deca-alanine offer valuable thermodynamic and kinetic information on folding, under the assumption that a reasonable, nonambiguous transition coordinate can be designed—which is necessarily subservient to the length of the peptide chain. They also help shed light on common shortcomings of importance-sampling simulations of low-dimensionality, notably hidden barriers in orthogonal space, and have proven useful for devising remedies.35−38 Beyond their undeniable utility in methodological developments, they are also sufficiently simple to serve as models of the nascent chain in more realistic biological applications, like the coupled folding–translocation occurring in the SecY complex.39
Here, we extend the exploration of reversible extension of deca-alanine in vacuo34,35 by examining how the aqueous environment reshapes the free-energy landscape that underlies folding. We find that the range of conformational states explored in water is much greater than in a vacuum, making end-to-end distance a highly degenerate transition coordinate. However, by adding a second coordinate describing the helicity of deca-alanine, we demonstrate that its folding pathway in water is more intricate than in a vacuum.
Methods
Simulations of deca-alanine (Ala10) were performed using the 104-atom compact helical model used by Park et al.,33 capped with an acetylated N-terminus and amidated C-terminus, as a starting state, with all hydrogens defined explicitly. For simulations in explicit water, the visualization and analysis program VMD40 was used to place deca-alanine in a cube of 10 850 TIP3P41 water molecules with dimensions 70 Å × 70 Å × 70 Å for a total of 32 659 atoms. Molecular dynamics simulations were carried out using NAMD 2.942 with the CHARMM all-atom force fields (CHARMM22/CMAP43 and CHARMM3644,45). The temperature was fixed at 300 K using Langevin dynamics; the pressure was kept constant at 1 atm using the Langevin piston method.46 The equations of motion were integrated using the RESPA multiple time-step algorithm with a time step of 2 fs used for all bonded interactions, 2 fs for short-range nonbonded interactions, and 4 fs for long-range electrostatic interactions. Long-range electrostatic interactions were calculated using the particle-mesh Ewald method.47 Bonds involving hydrogen atoms were constrained to their equilibrium length, employing the Rattle algorithm.48
PMFs were calculated using both adaptive biasing forces (ABF)34,42,49 and umbrella sampling (US) with the weighted histogram analysis method (WHAM),50 utilizing the collective variables (colvars) module of NAMD 2.9.35 Two reaction coordinates were defined: (ξ) the distance from the carbonyl carbon of the backbone of the first residue to the carbonyl carbon of the last residue and (α) the α-helical content of all 10 alanine residues as defined in the colvars module of NAMD. The α colvar is calculated using a scoring function for the backbone i, i + 4 hydrogen bonding, and the dihedral angles compared to that of a pure α-helix, normalized between 0 and 1. The default parameters for the α colvar as defined in the colvars module were used in all simulations. For two-dimensional PMFs in water, replica-exchange molecular dynamics51 was utilized with US (REMD-US) to increase the sampling efficiency of the entire conformational space. Integration of the 2D PMF to obtain a 1D PMF was calculated according to the following equation:52
| 1 |
where β = (kBT)−1, kB is the Boltzmann constant, T is the temperature, W(x, y) is the 2D PMF, w(x) the corresponding 1D PMF, and (xc, yc) is an arbitrary point in the collective-variable space.
Along the end-to-end distance coordinate, 20 US windows centered at ξ = 12.5 Å, 13.5 Å, ..., 31.5 Å were used with a force constant of 5.0 kcal/Å2·mol for each window. Along the α-helical content coordinate, nine US windows centered at α = 0.1, 0.2, ..., 0.9 were used in vacuum and 17 US windows centered at α = 0.1, 0.15, ..., 0.9 were used in water with a force constant of 500.0 kcal/α2·mol for each window. In vacuum, US windows were simulated for 5–10 ns per window for one-dimensional PMFs and 15 ns per window for two-dimensional PMFs. In water, US windows were simulated for 5 ns per window for one-dimensional PMFs and 20 ns per window for two-dimensional PMFs. The first 1–2 ns were not included in the PMF calculations to ensure the system was in equilibrium. ABF simulations were run for 50–100 ns in total. All ABF simulations used a threshold of 500 samples (“fullsamples”) prior to the application of the bias, unless noted otherwise. Starting states along each reaction coordinate were generated either using steered molecular dynamics (SMD) or from one-dimensional unrestrained ABF trajectories.
Results
One-Dimensional PMFs
To examine the efficacy of our methods, we first determined the PMF of deca-alanine in vacuum using the end-to-end distance reaction coordinate, denoted ξ. Using both the US and ABF approaches (see Methods), we calculated the PMF with the CHARMM22/CMAP and CHARMM36 force fields. The two approaches yield nearly identical free-energy profiles for both force fields (Figure 1). Examination of the simulation trajectories shows that both methods produced only the accordion-like folding/refolding mechanism as shown in Figure 2, where unfolding begins at one end of the peptide and propagates to the other end, suggesting a cooperative folding mechanism.53
Figure 1.
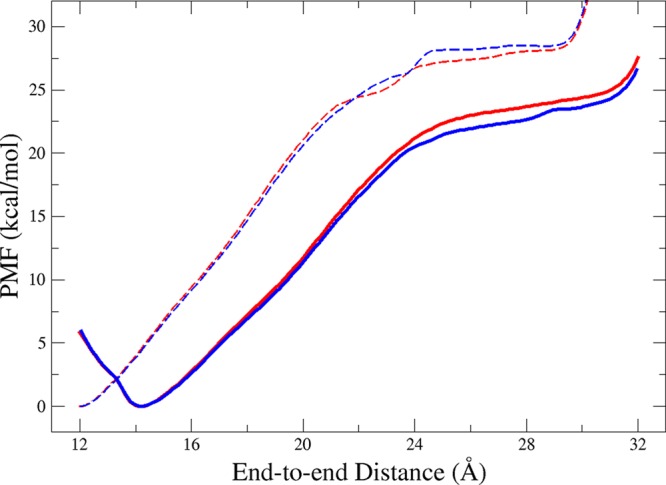
One-dimensional PMF of Ala10 in vacuum using the distance from the N-terminus carbonyl carbon to the C-terminus carbonyl carbon as the reaction coordinate. Red lines represent calculations using ABF, and blue lines represent calculations using US, with solid lines utilizing the CHARMM36 force field and dashed lines utilizing the CHARMM22/CMAP force field.
Figure 2.
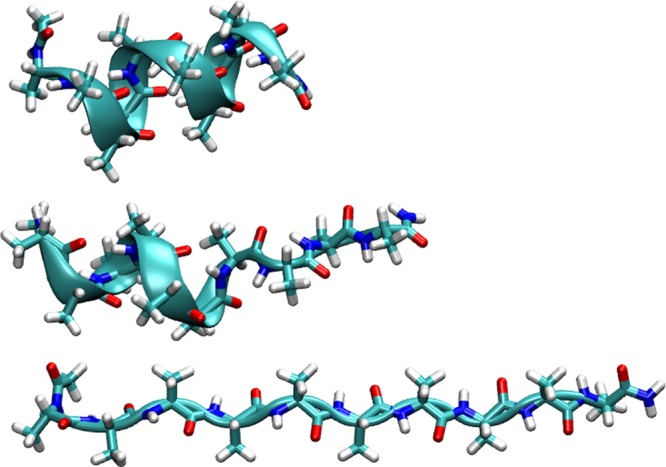
Unfolding of Ala10. This “accordion-like” unfolding mechanism of Ala10 was generated using SMD by pulling on the C-terminus Cα while keeping the N-terminus Cα fixed. Three snapshots of the peptide are shown in various stages of the SMD simulations, drawn using the “licorice” representation for all atoms and a cartoon representation for the backbone structure, where the thick ribbon represents those residues which are in an α-helical state. The top image represents the initial, minimized crystal structure of Ala10 used as the starting state. The middle image represents an intermediate state in which the peptide is partially extended while the remaining portion of the peptide is still in an α-helical state. The bottom image represents the fully extended state.
The results of the CHARMM36 force field agree quite well with previously reported PMFs.54−57 There is only one stable conformation around ξ = 14.2 Å, which corresponds to the pure α-helical state, and there is an energy barrier of ∼25 kcal/mol from the helical to extended state (Figure 1). While the CHARMM22/CMAP force field does yield a minimum near the α-helical state, the entire PMF is shifted by ∼2 Å toward lower end-to-end distances, and the energy barrier between helical and extended states is slightly higher (∼30 kcal/mol). The corrections to the CHARMM22/CMAP force field added to the CHARMM36 force field are evident in the difference in the folding PMFs for Ala10. Since CHARMM36 reproduces the expected free-energy minimum for the α-helical state in a vacuum58 and significantly improves agreement with helix-formation experiments,44 from here on we used solely the CHARMM36 force field.
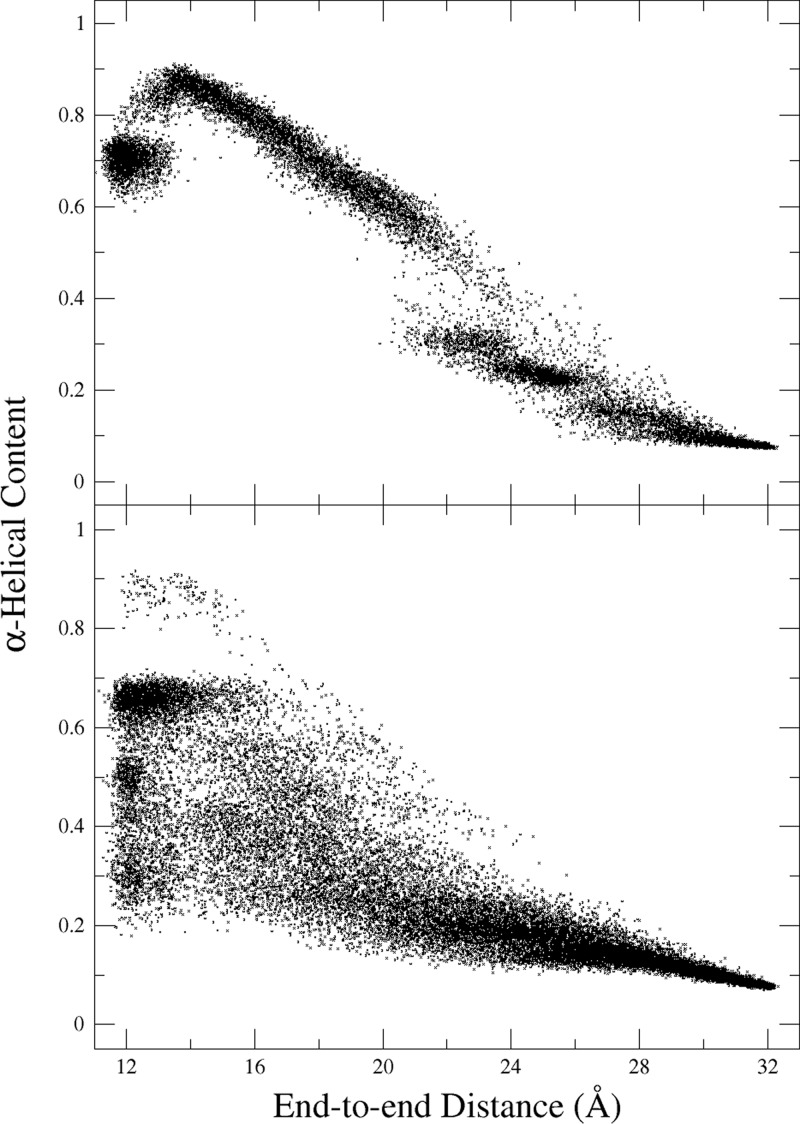
The ABF and US simulations of Ala10 were then repeated in explicit water. Both methods yield a relatively flat PMF, compared to the vacuum PMF, along most of the reaction coordinate (Figure 3, thick, solid lines). The trajectories reveal that there is no longer only the folding/refolding mechanism seen in vacuum; instead, the peptide transitions between extended states and compact, but nonhelical, states. These nonhelical states are characterized by various hairpin structures (Figure 4). Figure 5 shows the prevalence of low-helical, compact states in water as opposed to vacuum, which are “contaminating” the PMF at low end-to-end distances.
Figure 3.
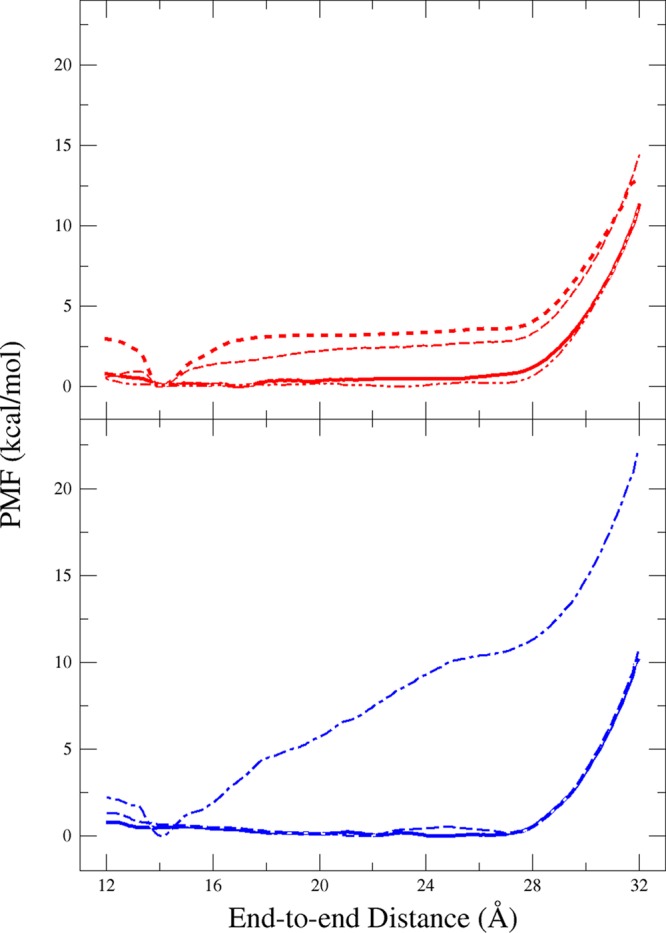
One-dimensional PMF of Ala10 along the end-to-end distance of the peptide calculated using ABF (top) and US (bottom). Top graph: no additional restraints (thick, solid line), no restraints with 50 000 fullsamples (thick, dashed line), 8 Å-radial confinement (thin, dashed line), 10 Å-radial confinement plus antihairpin restraint (thin, dotted-dashed line). Bottom graph: no additional restraints (thick, solid line), 10 Å-radial confinement (thin, dashed line), 10 Å-radial confinement plus antihairpin restraint (thin, dotted-dashed line).
Figure 4.
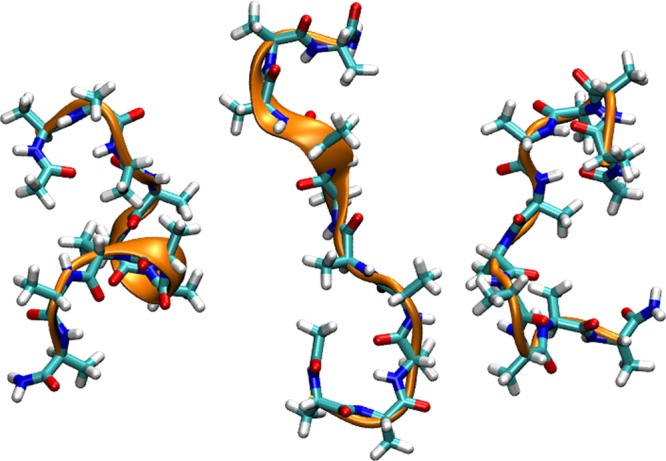
Representative set of compact, low-α-helical content states of Ala10 in water. The Ala10 peptide is shown in the “licorice” representation with the backbone α-helical content represented in orange by a cartoon representation. Water molecules are not shown.
Figure 5.
Scatter plot of states from ABF simulations in vacuum (top) and water (bottom). Top graph: scatter plot of states from 50 ns ABF simulation in vacuum using the CHARMM36 force field. Bottom graph: scatter plot of states from 100-ns ABF simulation in water with 10 Å-radial confinement plus antihairpin restraint.
In order to enforce the α-helical folding/refolding mechanism observed in vacuum, multiple additional restraints were imposed. First, the peptide backbone was confined to a cylindrical tube of radius 10 Å centered along the end-to-end distance vector. This confinement, as well as a smaller tube of radius 8 Å, failed to prevent the formation of compact nonhelical states, and the PMFs produced were either unchanged or inconsistent (Figure 3, dashed lines), likely because convergence was not achieved. An additional antihairpin restraint, which prevents the backbone Cα’s from passing one another in relation to the end-to-end distance vector, was also insufficient to produce the simple folding/refolding mechanism (Figure 3, dotted-dashed lines). The persistent formation by Ala10 of these nonhelical, compact states from extended states reveals a more dynamic folding process than that seen in a vacuum. Indeed, previous simulations of Ala10 have shown that the disordered and extended states are much more soluble in water than the α-helix.59 Instead of running the 1D US simulations longer, because the prevalence of compact, nonhelical states makes it difficult to determine when convergence will be achieved, we switched to a 2D description to ensure adequate sampling of these additional states.
Two-Dimensional PMFs
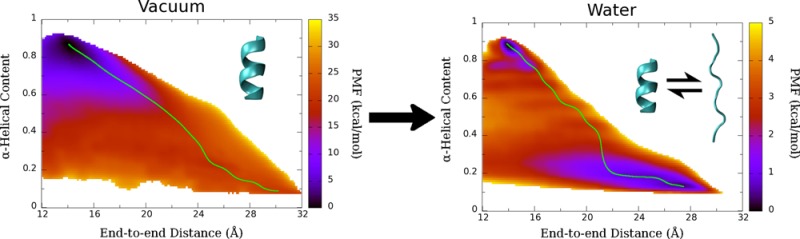
To examine the effects of compact, nonhelical states on the free energy of Ala10 folding, we calculated a two-dimensional PMF using US, with α-helical content as a second reaction coordinate. We first verified this 2D description by calculating the PMF in vacuum with umbrella sampling (Figure 6, top). There is still only one minimum in the pure α-helical state, as was seen in the 1D PMF. In addition, we calculated the least free-energy path,60 which finds the path of least free-energy difference between two local minima on a 2D free-energy surface, from the α-helical state to an extended state. There is close agreement between this path (Figure 6, top inset) and the 1D PMF (Figure 1), suggesting that the folding/refolding mechanism observed in the 1D biased simulations is in fact the primary mechanism of folding for Ala10 in vacuum.
Figure 6.
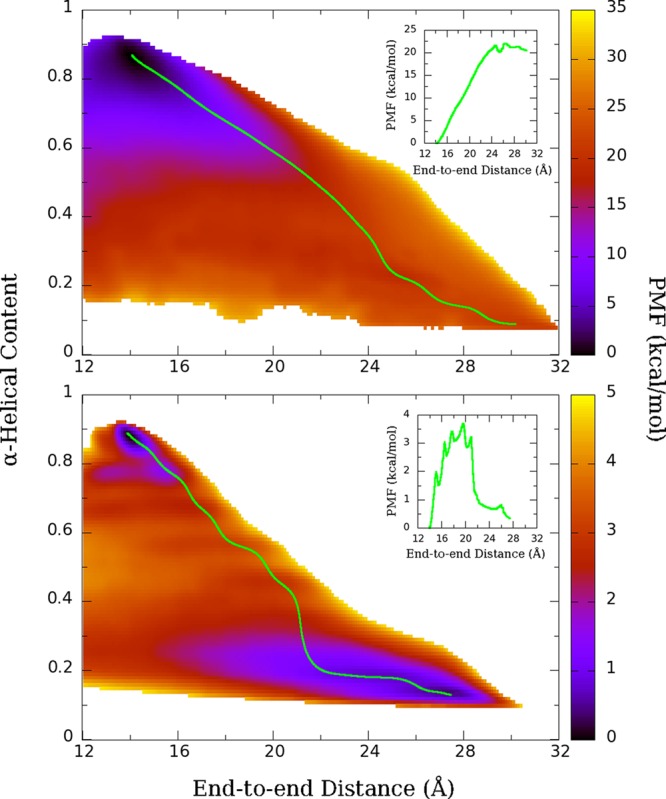
Two-dimensional PMF of Ala10 in vacuum (top) and water (bottom) using end-to-end distance and α-helical content as the two reaction coordinates. Green line represents the least free-energy path from the α-helical state to the extended state. The inset shows the PMF along the least free-energy path, as projected onto the end-to-end distance coordinate.
On the basis of the successful application to the vacuum case, a 2D REMD-US (see Methods) simulation was performed for Ala10 in water. One can immediately see that a free-energy “trough” has appeared along a family of extended, nonhelical states (Figure 6, bottom). These states are also of free energy comparable to the pure α-helix, differing by less than 1 kcal/mol, and the energy barrier between the helical and extended states is now less than 4 kcal/mol. The least free-energy path explores a wider range of extended states before refolding compared with the vacuum case.
One notable feature of the 2D PMF is the appearance of “bands” in the free energy along lines of constant helical content, which were presumed to be indications of poor overlap between neighboring windows when implementing the WHAM algorithm. The poor overlap was confirmed by plotting the histograms (data not shown), and thus, the number of windows along the α coordinate was increased from 9 to 17 (see Methods). However, the bands still remained as seen in Figure 6, bottom graph. These can be seen more explicitly in the PMF along the least free-energy path, which shows five distinct local minima between the α-helical state and the fully extended state (Figure 6, bottom inset). There is less than 1 kcal/mol difference between PMFs calculated for 15 ns per window and 20 ns per window for the entire range of our reaction coordinates, which suggests that the PMFs are converged.
To validate the path as well as our choice of reaction coordinates, we also made a rough estimate of the committor distribution for the free-energy maximum.61,62 Fifty separate conformations were each used to initiate 50 10-ps simulations (2500 simulations and 25 ns in total) with random velocities. The committor was judged to be progressing to the extended state or retreating to the helical state based on the values of ξ and α (see Figure 6, bottom) although full commitment to either minimum would require time scales at least 100× as long (see below). The resulting distribution is peaked at 0.5, with some bias toward values greater than 0.5 (see Figure S1). Overall, the behavior of the committor near the barrier suggests that it is representative of a true transition state.
Equilibrium Simulations
Equilibrium simulations of deca-alanine in water were performed starting from different states for 50 ns each to validate the 2D PMF and to better understand the folding pathway. Starting from a state that is near the α-helical minimum observed in the 2D PMF, in equilibrium the peptide initially samples the region around the minimum. As the simulation progresses, the peptide begins to unfold roughly along the least free-energy path, and similar bands as seen in the PMF also appear in the histogram, despite no biasing being applied (Figure 7). The protein folds and refolds until finally becoming fully extended near the end of the 50-ns simulation.
Figure 7.
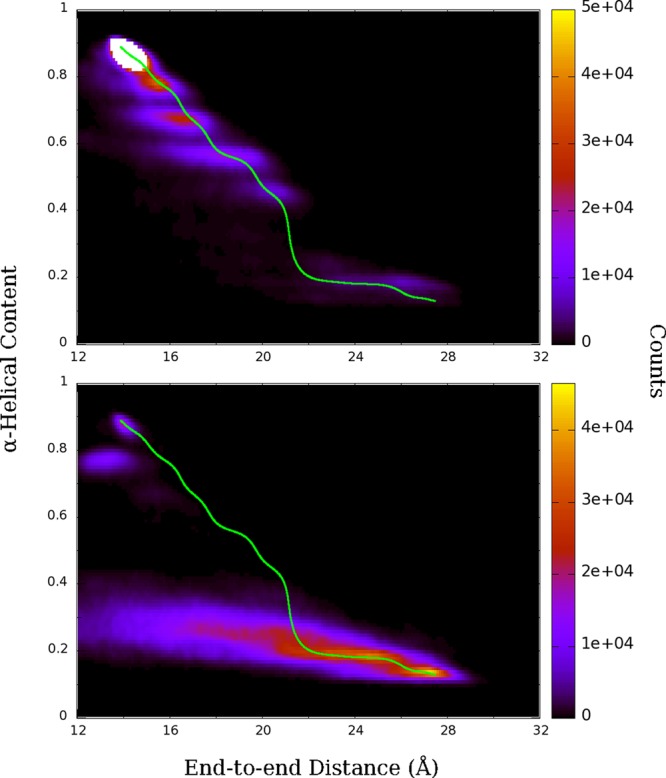
Histograms of 50 ns equilibrium simulations for an α-helical (top) and extended (bottom) starting states. Green lines represent the previously determined least free-energy path.
Starting from an extended state, Ala10 explores the range of extended and compact nonhelical states predicted by the free-energy trough seen in the 2D PMF. The peptide eventually folds into an α-helix near the end of the simulation in much the same manner as in the unfolding case. Examination of the hydrogen bonding of Ala10 with itself and with water during the equilibrium simulations reveals that the transition between helical and extended states occurs in ∼5 ns with the formation or breaking of ∼4 peptide–peptide hydrogen bonds, with a corresponding decrease or increase in water–peptide hydrogen bonds, respectively (Figure S2), in agreement with the results of Ozer et al.63 We see similar results when examining the water–peptide hydrogen bonds from the REMD-US trajectories, with an increase of ∼8–10 hydrogen bonds from folded to extended states (Figure S3).
Based on the success of the two previous equilibrium simulations, we ran 20 additional simulations to get better sampling of the folding mechanism: 10 starting from the α-helical minimum and 10 starting from the extended minimum. With only two exceptions, all initially extended states also sampled the helical state during the 50 ns simulations, while all initially α-helical states sampled the extended states as well. The histograms for these simulations (Figure S4) are practically identical to one another, demonstrating the reproducibility of the conformational equilibria predicted by the PMFs.
Examination of the hydrogen bonding between the ith residue and the i+4th residue for the simulations in which folding was observed reveals some cooperativity at the N-terminus, where the formation of the Ala1–Ala5 hydrogen bond initiates a propagation of hydrogen bond formation toward the C-terminus as the peptide folds from an extended state to an α-helical state (Figure S5, left graphs). In contrast, the C-terminus exhibits less cooperativity, with unfolding typically beginning at the C-terminus and propagating in the opposite direction of folding in the majority of our simulations (Figure S5, right graphs). On average, the N-terminal hydrogen bonds persist longer than those on the C-terminal side while the protein is in a folded conformation. These results are consistent with a previous study which observed that the N-terminus of Ala10 slightly favors the α-helical conformation over the β-sheet conformation, whereas the opposite was observed for the C-terminus.5 We do observe, however, cases in which the N-terminal hydrogen bonds were broken while the C-terminal hydrogen bonds remained intact (Figure S5, bottom right graph), although these occurred much less frequently. The REMD-US trajectories of Ala10 in water yields a similar preference for N-terminal hydrogen bond formation (Figure S6) near the α-helical state. The N-terminal hydrogen bonds also persist for a longer portion of the unfolding pathway (Figure 6, bottom graph) than the C-terminal hydrogen bonds. In addition, we observed very little 310-helical (i, i + 3) hydrogen bonding for both the REMD-US and equilibrium trajectories (data not shown), confirming that the 310-helix is not a folding intermediate. Thus, the folding pathway consists of the breaking or formation of α-helical hydrogen bonds and not the rearrangement of those hydrogen bonds into a 310-helical structure.
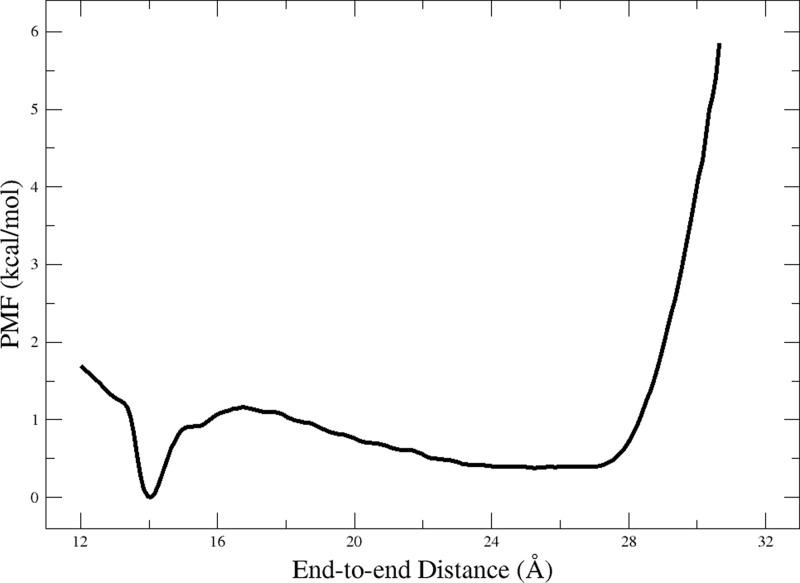
1D PMF from Integration of 2D PMF
After validation of the free energy minima observed in the 2D PMF of Ala10 folding in water by equilibrium simulations, we integrated out the α coordinate according to eq 1 (see Methods) to generate a 1D PMF along the distance coordinate (Figure 8). This integrated PMF still yields the free-energy minimum observed for Ala10 in vacuum around ξ = 14.3 Å. The main difference between the integrated PMF in Figure 8 and the PMF in vacuum (Figure 1) is in the unfolding region (ξ > 15 Å), with the PMF reduced by more than 20 kcal/mol in the extended state. This reduction is comparable to that seen in the previous unrestrained 1D PMFs calculated for Ala10 (see Figure 3). However, by ensuring that Ala10 more fully explores its entire conformational space through biasing of the additional α reaction coordinate, two free energy minima are revealed in the compact states and extended states, respectively, that were not found by biasing of the ξ reaction coordinate alone. The appearance of these new minima supports the suggestion that the previous 1D PMFs had not yet converged. Calculation of the free-energy difference between these two minima establishes that the compact state is slightly favored over the extended states (ΔG = −0.4 kcal/mol), with compact states defined as ξ ≤ 16.75 Å, i.e., below the peak of the energy barrier between the minima.
Figure 8.
One-dimensional PMF of Ala10 in water calculated by integration of the 2D PMF using eq 1.
Discussion
The free energy of folding for Ala10 in vacuum has been used as a benchmark for many free-energy calculation methods, using the end-to-end distance (ξ) of the peptide as the reaction coordinate. This choice of reaction coordinate implicitly presumes a reversible, accordion-like folding/refolding of the peptide. We observed using both US and ABF that in vacuum, this presumption is indeed correct and only the simple folding/unfolding mechanism predicted is found. In the presence of water, however, the folding/unfolding mechanism is much more complex, and biasing the refolding of Ala10 back into an α-helix from an extended state is nontrivial.
Using multiple biasing methods—US and ABF—we discovered that the water-solvated Ala10 will explore an extended range of compact, nonhelical states before refolding back into an α-helix. These compact, nonhelical states appeared to be “contaminating” the low-ξ region of the 1D PMFs calculated from the two biasing methods creating a relatively flat PMF compared to the PMF calculated for Ala10 in vacuum (Figure 3). Calculation of 2D PMFs for the entire (ξ, α) collective-variable space revealed a new free-energy minimum in a family of extended states not observed in vacuum, along with the α-helical minimum that was originally observed in vacuum.
In water, the free energy of the extended states decreased significantly compared to in vacuum, with the α-helical state less than 1 kcal/mol lower in energy than the extended states—a decrease from more than 20 kcal/mol observed in vacuum. A barrier of ∼4 kcal/mol between the two energy minima is also observed in the PMF. Previous studies of Ala10 in water have also shown a decrease in the free-energy difference between extended and helical states. For example, ABF was applied to a zwitterionic form of Ala10 with charged termini to calculate a 1D PMF in water, using the average length of the i, i + 4 hydrogen bonds of the backbone as a reaction coordinate.39 That PMF shows a comparable free-energy barrier of ∼5 kcal/mol between the extended and helical states, with the relative energies differing by ∼1 kcal/mol. The decrease in the free-energy difference was not as pronounced in other studies utilizing adaptive SMD63 and US64 applied to the end-to-end distance of Ala10 with neutral termini. Additionally, neither study discovered the free-energy minimum in the extended states. Levy et al. found that in hydrophilic environments, the α-helix is actually destabilized relative to β-sheet conformations, due to their high conformational entropy compared to that of the α-helix.58 Although we observed a minimum in extended states rather than β-sheet conformations, the extended states are similarly entropically favored over the α-helical state and extend into the range of compact, nonhelical states (Figure 6). As a check on our 2D PMF, we performed 50 ns equilibrium simulations of Ala10 in water starting from α-helical and extended states (Figure 7). These simulations confirmed both minima observed in the 2D PMF. Furthermore, transitions between the two minima demonstrated cooperativity at the N-terminus and noncooperativity at the C-terminus, as expected.5
Although alanine is used as a model for protein folding since it has the highest helix propensity of all amino acids, the folding mechanism for Ala-based peptides is still not very well understood. Experiments studying short Ala-based peptides have led to inconclusive or contradictory observations for the stability of the α-helical state in water. Rohl et al. observed that Ala-based peptides are the only stable helix formers in water for the 20 common amino acids.65 They postulated that reducing the extent of solvation of the coiled backbone could increase stabilization of the helix. Experiments performed by Blondelle et al. showed that peptides of the form Ac–KYAnK–NH2 (10 ≤ n ≤ 14) coexisted as a β-sheet and α-helix to varying extents.66 However, it was later observed that the stability of the helix in these peptides was due to the solubility of the flanking Lys residues, and not the intrinsic helix propensity of Ala.67 This was followed up by Spek et al. stating that although the increase in α-content of KAnK is an artifact of the flanking Lys residues, Ala is intrinsically α-helix stabilizing.68 So, although there is some discrepancy for the stability of secondary structures for Ala-based peptides, the evidence suggests that these peptides do not solely exist as an α-helix in solution as one might suspect based on its strong preference for the helical state in vacuum. Instead they exist in some combination of secondary structures, including α-helices and β-sheets. Indeed, more recently, NMR data for short polyalanine peptides (Ala3–7) show that these peptides exist primarily as polyproline II (PPII) helix-like structures with very little population of the α-helical structure.69
Our results detail the stability, or lack thereof, of the α-helix for short polyalanine peptides in solution. However, one should always be aware of the limitations of the force fields utilized in MD simulations. Best et al. examined a range of force fields and observed that they overemphasized the α-helix structure compared with NMR coupling parameters for the backbone (ϕ, ψ) dihedrals.70 By reweighting the force fields based on these (ϕ, ψ) coupling parameters,69 they were able to yield good agreement with the population of the α-helix, β-sheet, and PPII structures seen in the NMR data. Although there was better agreement with NMR for unblocked (ionic or zwitterionic) termini than with blocked (neutral) termini, by using the reweighting for unblocked peptides, blocked peptides were found to yield α-content of 12–23%. Similar results were found using AGADIR,71 an empirical NMR-based algorithm that determines the α-helical propensity of a peptide based on sequence, which yields a helical propensity of ∼15% for Ac–Ala10–NH2 in water at 300 K.
In this study, we have used the most recent iteration of the CHARMM force field, CHARMM36, introduced in 2012.44,45 One of the major improvements of CHARMM36 is the correction of the α-helical bias introduced into CHARMM22 by the backbone (ϕ, ψ) dihedral CMAP potential. This improvement was achieved by capturing the many-body effects not present in the original CMAP potential. The CMAP potential was optimized to match NMR data for Ala569 and Ac-(AAQAA)3-NH272 in solution, and the side-chain χ1 and χ2 dihedrals were optimized to QM energy surfaces. The result is a better balance between secondary structures, particularly the α-helix and β-sheet, addressing the problem posed originally by Best et al. in 2008.70 In particular, the helical fraction of Ac-(AAQAA)3-NH2 produced by CHARMM36 more closely matches experiments72 than other force fields (a reduction from 95% for CHARMM22/CMAP to 21% for CHARMM36), as well as improved cooperativity for α-helix and β-sheet formation. Thus, the helical fraction of Ala10, as well as its folding mechanism, determined using CHARMM36 should also have better agreement with experimental results, particularly when compared with CHARMM22 and CHARMM22/CMAP, which were utilized in previous unfolding simulations of Ala10 in water.63,64 How the balance between conformational changes in the presence of other peptides and proteins occurs remains uncertain. While it is known that macromolecular crowding can have a significant effect on protein folding in vivo,73,74 a recent study on dipeptide aggregation demonstrated that simulations still have some difficulty reproducing such effects quantitatively.75
Finally, our work emphasizes the challenge and necessity of choosing relevant reaction coordinates to fully characterize a particular system.76 For Ala10, the end-to-end distance is no longer sufficient to capture the diversity of conformations explored in water, thus making it a highly degenerate reaction coordinate (Figure 4). Contributions from compact, nonhelical states can produce a PMF that does not reveal what one intuitively expects it to, namely the accordion-like folding/refolding mechanism shown in Figure 2. By tracking the α-helical content of Ala10 during biased folding simulations, we found many states accessible to the peptide in water that were inaccessible in vacuum. These states arise due to Ala10’s increased flexibility in water, where a loss of intrapeptide hydrogen bonds is compensated by an increase in peptide-water hydrogen bonds (Figures S2, S3). Reaction coordinates suitable for Ala10 in vacuum, therefore, may not be suitable in water.26,58 Since recent studies of Ala10 folding in water have only used the end-to-end distance to characterize the folding pathway, they observe that the preference for the α-helical state is still significant in water compared to the extended states. However, we have shown that the helical and extended states are of comparable stability (|ΔG| < 1 kcal/mol), with both states transitioning from one to the other within the course of 50 ns equilibrium simulations.
Acknowledgments
The authors thank Mahmoud Moradi for stimulating discussions and helpful insights. The research is funded by grant K22-AI100927 from the National Institutes of Health. Simulations were carried out using the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by NSF grant number OCI-1053575.
Supporting Information Available
Six figures of the committor distribution and analysis of hydrogen bonding. This material is available free of charge via the Internet at http://pubs.acs.org/.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Anfinsen C. B. Principles that govern the folding of protein chains. Science 1973, 181, 223–227. [DOI] [PubMed] [Google Scholar]
- Baldwin R. L.; Rose G. D. Is protein folding hierarchic? II. Folding intermediates and transition states. Trends Biochem. Sci. 1999, 24, 77–83. [DOI] [PubMed] [Google Scholar]
- Baldwin R. L.; Rose G. D. Is protein folding hierarchic? I. Local structure and peptide folding. Trends Biochem. Sci. 1999, 24, 26–33. [DOI] [PubMed] [Google Scholar]
- Williams S.; Causgrove T. P.; Gilmanshin R.; Fang K. S.; Callender R. H.; Woodruff W. H.; Dyer R. B. Fast events in protein folding: Helix melting and formation in a small peptide. Biochemistry 1996, 35, 691–697. [DOI] [PubMed] [Google Scholar]
- Young W. S.; Brooks C. L. III. A microscopic view of helix propagation: N and C-terminal helix growth in alanine helices. J. Mol. Biol. 1996, 259, 560–572. [DOI] [PubMed] [Google Scholar]
- Shaw D. E.; et al. Anton, a special-purpose machine for molecular dynamics simulation. SIGARCH Comput. Archit. News 2007, 35, 1–12. [Google Scholar]
- Klepeis J. L.; Lindorff-Larsen K.; Dror R. O.; Shaw D. E. Long-timescale molecular dynamics simulations of protein structure and function. Curr. Opin. Struct. Biol. 2009, 19, 120–127. [DOI] [PubMed] [Google Scholar]
- Bowman G. R.; Voelz V. A.; Pande V. S. Taming the complexity of protein folding. Curr. Opin. Struct. Biol. 2011, 21, 4–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindorff-Larsen K.; Piana S.; Dror R. O.; Shaw D. E. How fast-folding proteins fold. Science 2011, 334, 517–520. [DOI] [PubMed] [Google Scholar]
- Freddolino P. L.; Schulten K. Common structural transitions in explicit-solvent simulations of villin headpiece folding. Biophys. J. 2009, 97, 2338–2347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowman G. R.; Pande V. S. Protein folded states are kinetic hubs. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 10890–10895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beauchamp K. A.; McGibbon R.; Lin Y. S.; Pande V. S. Simple few-state models reveal hidden complexity in protein folding. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 17807–17813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piana S.; Lindorff-Larsen K.; Shaw D. E. Atomic-level description of ubiquitin folding. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 5915–5920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chipot C., Pohorille A.. Free energy calculations. Theory and applications in chemistry and biology; Springer Verlag: Berlin, 2007. [Google Scholar]
- Lelièvre T.; Stoltz G.; Rousset M.. Free energy computations: A mathematical perspective; Imperial College Press: London, 2010. [Google Scholar]
- Tirado-Rives J.; Maxwell D. S.; Jorgensen W. L. Molecular dynamics and Monte Carlo simulations favor the α-helical form for alanine-based peptides in water. J. Am. Chem. Soc. 1993, 115, 11590–11593. [Google Scholar]
- Chipot C.; Pohorille A. Folding and translocation of the undecamer of poly-L-leucine across the water–hexane interface. A multi-nanosecond molecular dynamics study. J. Am. Chem. Soc. 1998, 120, 11912–11924. [DOI] [PubMed] [Google Scholar]
- Collet O.; Chipot C. Non-Arrhenius behavior in the unfolding of a short, hydrophobic α-helix. Complementarity of molecular dynamics and lattice model simulations. J. Am. Chem. Soc. 2003, 125, 6573–6580. [DOI] [PubMed] [Google Scholar]
- Hénin J.; Schulten K.; Chipot C. Conformational equilibrium in alanine-rich peptides probed by reversible stretching simulations. J. Phys. Chem. B 2006, 110, 16718–16723. [DOI] [PubMed] [Google Scholar]
- Gaborek T. J.; Chipot C.; Madura J. D. Conformational free-energy landscapes for a peptide in saline environments. Biophys. J. 2012, 103, 2513–2520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barlow D. J.; Thornton J. M. Helix geometry in proteins. J. Mol. Biol. 1988, 201, 601–619. [DOI] [PubMed] [Google Scholar]
- O’Neil K.; DeGrado W. A thermodynamic scale for the helix-forming tendencies of the commonly occurring amino acids. Science 1990, 250, 646–651. [DOI] [PubMed] [Google Scholar]
- Marqusee S.; Robbins V. H.; Baldwin R. L. Unusually stable helix formation in short alanine-based peptides. Proc. Natl. Acad. Sci. U.S.A. 1989, 86, 5286–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miick S. M.; Martinez G. V.; Fiori W. R.; Todd A. P.; Millhauser G. L. Short alanine-based peptides may form 310-helices in aqueous solution. Nature 1992, 359, 653–655. [DOI] [PubMed] [Google Scholar]
- Chipot C. In New algorithms for macromolecular simulation; Leimkuhler B., Chipot C., Elber R., Laaksonen A., Mark A. E., Schlick T., Schütte C., Skeel R., Eds.; Springer Verlag: Berlin, 2005; Vol. 49, pp 183–209. [Google Scholar]
- Bolhuis P. G.; Dellago C.; Chandler D. Reaction coordinates of biomolecular isomerization. Proc. Natl. Acad. Sci. U.S.A. 2000, 97, 5877–5882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moradi M.; Babin V.; Roland C.; Darden T.; Sagui C. Conformations and free energy landscapes of polyproline peptides. Proc. Natl. Acad. Sci. U.S.A. 2009, 106, 20746–20751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moradi M.; Babin V.; Roland C.; Sagui C. Reaction path ensemble of B-Z-DNA transition: A comprehensive atomistic study. Nucleic Acids Res. 2013, 41, 33–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moradi M.; Tajkhorshid E. Mechanistic picture for conformational transition of a membrane transporter at atomic resolution. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 18916–18921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chipot C. Frontiers in free-energy calculations of biological systems. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2014, 71–89. [Google Scholar]
- Vreede J.; Juraszek J.; Bolhuis P. G. Predicting the reaction coordinates of millisecond light-induced conformational changes in photoactive yellow protein. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 2397–2402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marinelli F.; Pietrucci F.; Laio A.; Piana S. A kinetic model of trp-cage folding from multiple biased molecular dynamics simulations. PLoS Comput. Biol. 2009, 5, e1000452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S.; Khalili-Araghi F.; Tajkhorshid E.; Schulten K. Free energy calculation from steered molecular dynamics simulations using Jarzynski’s equality. J. Chem. Phys. 2003, 119, 3559–3566. [Google Scholar]
- Hénin J.; Chipot C. Overcoming free energy barriers using unconstrained molecular dynamics simulations. J. Chem. Phys. 2004, 121, 2904–2914. [DOI] [PubMed] [Google Scholar]
- Hénin J.; Forin G.; Chipot C.; Klein M. L. Exploring multidimensional free energy landscapes using time-dependent biases on collective variables. J. Chem. Theory Comput. 2010, 6, 35–47. [DOI] [PubMed] [Google Scholar]
- Zheng L.; Chen M.; Yang W. Random walk in orthogonal space to achieve efficient free energy simulation of complex systems. Proc. Natl. Acad. Sci. U.S.A. 2008, 51, 20227–20232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minoukadeh K.; Chipot C.; Lelièvre T. Potential of mean force calculations: A multiple-walker adaptive biasing force approach. J. Chem. Theory Comput. 2010, 6, 1008–1017. [Google Scholar]
- Comer J.; Roux B.; Chipot C.. Achieving ergodic sampling using replica-exchange free-energy calculations. Mol. Simul. 2014, 40. [Google Scholar]
- Gumbart J.; Chipot C.; Schulten K. Free energy of nascent-chain folding in the translocon. J. Am. Chem. Soc. 2011, 133, 7602–7607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD – Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar]
- Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kalé L.; Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKerell A. D. Jr.; Feig M.; Brooks C. L. III. Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004, 25, 1400–1415. [DOI] [PubMed] [Google Scholar]
- Best R. B.; Mittal J.; Feig M.; MacKerell A. D. Jr. Inclusion of many-body effects in the additive CHARMM protein CMAP potential results in enhanced cooperativity of α-helix and β-hairpin formation. Biophys. J. 2012, 103, 1045–1051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best R. B.; Zhu X.; Shim J.; Lopes P. E. M.; Mittal J.; Feig M.; MacKerell A. D. Jr. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone ϕ, ψ and side-chain χ1 and χ2 dihedral angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feller S. E.; Zhang Y.; Pastor R. W.; Brooks B. R. Constant pressure molecular dynamics simulations: The Langevin piston method. J. Chem. Phys. 1995, 103, 4613–4621. [Google Scholar]
- Darden T.; York D.; Pedersen L. G. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar]
- Andersen H. C. Rattle: A “Velocity” version of the shake algorithm for molecular dynamics calculations. J. Chem. Phys. 1983, 52, 24–34. [Google Scholar]
- Darve E.; Pohorille A. Calculating free energies using average force. J. Chem. Phys. 2001, 115, 9169–9183. [Google Scholar]
- Kumar S.; Rosenberg J. M.; Bouzida D.; Swendsen R. H.; Kollman P. A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar]
- Sugita Y.; Kitao A.; Okamoto Y. Multidimensional replica-exchange method for free-energy calculations. J. Chem. Phys. 2000, 113, 6042–6051. [Google Scholar]
- Roux B. Statistical mechanical equilibrium theory of selective ion channels. Biophys. J. 1999, 77, 139–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimm B. H.; Bragg J. K. Theory of phase transition between helix and random coil in polypeptide chains. J. Chem. Phys. 1959, 31, 526–535. [Google Scholar]
- Chipot C.; Hénin J. Exploring the free-energy landscape of a short peptide using an average force. J. Chem. Phys. 2005, 123, 244906. [DOI] [PubMed] [Google Scholar]
- Procacci P.; Marsili S.; Barducci A.; Signorini G. F.; Chelli R. Crooks equation for steered molecular dynamics using a Nosé-Hoover thermostat. J. Chem. Phys. 2006, 125, 164101. [DOI] [PubMed] [Google Scholar]
- Ozer G.; Quirk S.; Hernandez R. Adaptive steered molecular dynamics: Validation of the selection criterion and benchmarking energetics in vacuum. J. Chem. Phys. 2012, 136, 215104. [DOI] [PubMed] [Google Scholar]
- Chelli R.; Gellini C.; Pietraperzia G.; Giovannelli E.; Cardini G. Path-breaking schemes for nonequilibrium free energy calculations. J. Chem. Phys. 2013, 138, 214109. [DOI] [PubMed] [Google Scholar]
- Levy Y.; Jortner J.; Becker O. M. Solvent effects on the energy landscapes and folding kinetics of polyalanine. Proc. Natl. Acad. Sci. U.S.A. 2001, 98, 2188–2193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kokubo H.; Hu C. Y.; Pettitt B. M. Peptide conformational preferences in osmolyte solutions: Transfer free energies of decaalanine. J. Am. Chem. Soc. 2011, 133, 1849–1858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ensing B.; Laio A.; Parrinello M.; Klein M. L. A recipe for the computation of the free energy barrier and the lowest free energy path of concerted reactions. J. Phys. Chem. B 2005, 109, 6676–6687. [DOI] [PubMed] [Google Scholar]
- Pan A. C.; Sezer D.; Roux B. Finding transition pathways using the string method with swarms of trajectories. J. Phys. Chem. B 2008, 112, 3432–3440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ovchinnikov V.; Karplus M.; Vanden-Eijnden E. Free energy of conformational transition paths in biomolecules: The string method and its application to myosin VI. J. Chem. Phys. 2011, 134, 085103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozer G.; Quirk S.; Hernandez R. Thermodynamics of decaalanine stretching in water obtained by adaptive steered molecular dynamics simulations. J. Chem. Theory Comput. 2012, 8, 4837–4844. [DOI] [PubMed] [Google Scholar]
- Stirnemann G.; Kang S.; Zhou R.; Berne B. J. How force unfolding differs from chemical denaturation. Proc. Natl. Acad. Sci. U.S.A. 2014, 111, 3413–3418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohl C. A.; Chakrabartty A.; Baldwin R. L. Helix propagation and N-cap propensities of the amino acids measured in alanine-based peptides in 40 volume percent trifluoroethanol. Protein Sci. 1996, 5, 2623–2637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blondelle S. E.; Forood B.; Houghten R. A.; Pérez-Payá E. Polyalanine-based peptides as models for self-associated b-pleated-sheet complexes. Biochemistry 1997, 36, 8393–8400. [DOI] [PubMed] [Google Scholar]
- Williams L.; Kather K.; Kemp D. S. High helicities of Lys-containing, Ala-rich peptides are primarily attributable to a large, context-dependent Lys stabilization. J. Am. Chem. Soc. 1998, 120, 11033–11043. [Google Scholar]
- Spek E. J.; Olson C. A.; Shi Z.; Kallenbach N. R. Alanine is an intrinsic a-helix stabilizing amino acid. J. Am. Chem. Soc. 1999, 121, 5571–5572. [Google Scholar]
- Graf J.; Nguyen P. H.; Stock G.; Schwalbe H. Stucture and dynamics of the homologous series of alanine peptides: A joint molecular dynamics/NMR study. J. Am. Chem. Soc. 2007, 129, 1179–1189. [DOI] [PubMed] [Google Scholar]
- Best R. B.; Buchete N.-V.; Hummer G. Are current molecular dynamics force fields too helical?. Biophys. J. 2008, 95, L07–L09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacroix E.; Viquera A. R.; Serrano L. Elucidating the folding problem of a-helices: Local motifs, long-range electrostatics, ionic-strength dependence and prediction of NMR parameters. J. Mol. Biol. 1998, 284, 173–191. [DOI] [PubMed] [Google Scholar]
- Shalongo W.; Dugad L.; Stellwagen E. Distribution of helicity within the model peptide Acetyl(AAQAA)3amide. J. Am. Chem. Soc. 1994, 116, 8288–8293. [Google Scholar]
- van den Berg B.; Ellis R. J.; Dobson C. M. Effects of macromolecular crowding on protein folding and aggregation. EMBO J. 1999, 18, 6927–6933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobson C. M. Protein folding and misfolding. Nature 2003, 426, 884–890. [DOI] [PubMed] [Google Scholar]
- Götz A. W.; Bucher D.; Lindert S.; McCammon J. A. Dipeptide aggregation in aqueous solution from fixed point-charge force fields. J. Chem. Theory Comput. 2014, 10, 1631–1637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romo T. D.; Grossfield A. Unknown unknowns: the Challenge of systematic and statistical error in molecular dynamics simulations. Biophys. J. 2014, 106, 1553–1554. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.