Neurodegenerative Disease Diagnosis using Incomplete Multi-Modality Data via Matrix Shrinkage and Completion

Abstract

In this work, we are interested in predicting the diagnostic statuses of potentially neurodegenerated patients using feature values derived from multi-modality neuroimaging data and biological data, which might be incomplete. Collecting the feature values into a matrix, with each row containing a feature vector of a sample, we propose a framework to predict the corresponding associated multiple target outputs (e.g., diagnosis label and clinical scores) from this feature matrix by performing matrix shrinkage following by matrix completion. Specifically, we first combine the feature and target output matrices into a large matrix and then partition this large incomplete matrix into smaller submatrices, each consisting of samples with complete feature values (corresponding to a certain combination of modalities) and target outputs. Treating each target output as the outcome of a prediction task, we apply a 2-step multi-task learning algorithm to select the most discriminative features and samples in each submatrix. Features and samples that are not selected in any of the submatrices are discarded, resulting in a shrunk version of the original large matrix. The missing feature values and unknown target outputs of the shrunk matrix is then completed simultaneously. Experimental results using the ADNI dataset indicate that our proposed framework achieves higher classification accuracy at a greater speed when compared with conventional imputation-based classification methods and also yields competitive performance when compared with the state-of-the-art methods.

1. Introduction

Alzheimers Disease (AD) is the most prevalent form of dementia. It is ultimately fatal and is ranked as the sixth leading cause of death in United States in year 2012 (Alzheimer’s Association, 2013). Neurodegeneration associated with AD is progressive and the symptoms usually begin with gradual memory decline followed by a gradual loss of cognitive and motor abilities that will cause difficulties in the daily lives of the patients. Eventually, the patients will lose the ability to take care of themselves and will need to rely on the intensive care provided by others. This has posed significant medical and socioeconomic challenges to the community (Alzheimer’s Association, 2013).

Owing to the criticality of this issue, it is vital to diagnose AD accurately, especially at its prodormal stage, i.e., amnestic mild-cognitive impairment (MCI), so that an early treatment can be provided to possibly stop or slow down the progression of the disease. MCI, which is defined as a condition where the patient has noticeable cognitive decline, but with-out difficulty in carrying out daily activities, has high probability to develop into AD. With the help of emerging neuroimaging technology, the progress and severity of the neurodegeneration associated with AD or MCI can now be diagnosed and monitored in different ways (modalities). Magnetic resonance imaging (MRI) scans, for instance, provide 3D structural information about the brain, where features such as region-of-interest (ROI)-based volumetric measure and the cortical thickness can be extracted from the MRI to quantify brain atrophy that is usually associated with the diseases (Du et al., 2007; Fan et al., 2007; Klöppel et al., 2008; Desikan et al., 2009; Oliveira Jr et al., 2010; Gerardin et al., 2009; Cuingnet et al., 2011). Flourodeoxyglucose positron emission tomography (FDG-PET), on the other hand, can be used to detect abnormality in term of glucose metabolic rate at brain regions preferentially affected by AD (Higdon et al., 2004; Foster et al., 2007; Chetelat et al., 2003; Chételat et al., 2005; Herholz et al., 2002). Beside neuroimaging techniques, another line of research uses biological and genetic data to develop potential biomarkers for AD diagnosis. The important measurements in biological and genetic data that are closely related to cognitive decline in AD patients include the increase of cerebrospinal fluid (CSF) total-tau (t-tau) and CSF tau hyperphosphorylated at threonine 181 (p-tau), the decrease of CSF amyloid β (Aβ), and the presence of gene apolipoprotein E (APOE) ∊4 allele (Fagan et al., 2007; Morris et al., 2009; Fjell et al., 2010).

Although it is common to use information from only one modality such as structural MRI for diagnosis of AD/MCI, complementary information from multiple modalities (Fjell et al., 2010; Walhovd et al., 2010; Landau et al., 2010; Zhang et al., 2011; Liu et al., 2014) can be combined for more accurate diagnosis. This is supported by the results reported in recent studies (De Leon et al., 2006; Fan et al., 2008; Ye et al., 2008; Hinrichs et al., 2009, 2011; Davatzikos et al., 2011; Zhang and Shen, 2012; Zhang et al., 2011; Liu et al., 2013). To support AD research using multi-modality data, Alzheimer’s Disease Neuroimaging Initiative (ADNI) has been actively collecting data from multiple modalities (e.g., MRI, FDG-PET and CSF data) from AD, MCI and normal control (NC) subjects yearly or half-yearly. Unfortunately, not all the samples in ADNI dataset are completed with the data from all different modalities. For example, while all the samples in the ADNI baseline dataset contain MRI data, only about half of the samples contain FDG-PET data (which is referred as PET throughout the manuscript) and another different half of the samples contain CSF data. The “missing” data in the ADNI dataset is due to several reasons, such as, high measurement cost (i.e., PET scans), poor data quality and unwillingness of the patients to receive invasive tests (i.e., collection of CSF samples through lumber puncture).

There are basically two approaches to deal with missing data in a dataset, i.e., we can either 1) discard the samples with missing data, or 2) impute the missing data. Most existing approaches discard samples with at least one missing modality and perform disease identification based on the remainder of the dataset. However, this approach discards a lot of information that is potentially useful. In fact, if following this approach for multi-modality analysis using MRI, PET and CSF data, about 2/3 of the total samples at ADNI baseline dataset will have to be removed.

The data imputation approach, on the other hand, is more preferable as it provides the possibility to use as many samples as possible in analysis. In fact, incomplete dataset is ubiquitous in many applications and thus various imputation methods have been developed to estimate the missing values based on the available data (Schneider, 2001; Troyanskaya et al., 2001; Zhu et al., 2011). However, these methods work well only when a small portion of the data is missing, but become less effective when a large portion of the data is missing (e.g., PET data in ADNI). Recently, low rank matrix completion (Candès and Recht, 2009) has been proposed to impute missing values in a large matrix through trace norm minimization. This algorithm can effectively recover a large portion of the missing data if the ground truth matrix is low rank and if the missing data are distributed randomly and uniformly (Candès and Recht, 2009). Unfortunately, the latter assumption does not hold in our case since, for each subject, the data from one or more of the modalities might be entirely missing, i.e., the data is missing in blocks.

In this paper, we attempt to identify AD and MCI from the NCs using incomplete multi-modality dataset from the ADNI database. Denoting the incomplete dataset as a matrix with each row representing a feature vector derived from multi-modality data of a sample, conventional approach for solving this problem is to impute the missing data and build a classifier based on the completed matrix. However, it is too time consuming (as matrix size is large) (Xu and Jordan, 1996; Jollois and Nadif, 2007) and inaccurate (as there are too many missing values) to apply the current imputation methods directly. In addition, the errors introduced during the imputation process may affect the performance of the classifier. In this paper, we largely avert the problems of the conventional approach by proposing a framework that 1) shrinks the large incomplete matrix through feature and sample selections, and 2) predicts the output labels directly through matrix completion on the shrunk matrix (i.e., without building another classifier on the completed matrix).

Specifically, we first partition the incomplete dataset into two portions -training set and testing set. Each set is represented by an incomplete feature matrix (each row contains feature vector of a sample), and a corresponding target output matrix (i.e., diagnostic status and clinical scores). Our first goal is to remove redundant/noisy features and samples from the feature matrix so that the imputation problem can be simplified. However, due to the missing values in the feature matrix, feature and sample selections can not be performed directly. We thus partition the feature matrix, together with the target output matrix, into submatrices with only complete data (Ghannad-Rezaie et al., 2010), so that a 2-step multi-task learning algorithm (Obozinski et al., 2006; Zhang and Shen, 2012) can be applied to these sub-matrices to obtain a set of discriminative features and samples. The selected features and samples then form a shrunk, but still incomplete, matrix which is more “friendly” to imputation algorithms, as redundant/noisy features and samples have been removed and there are now a smaller number of missing values that need to be imputed. We propose to impute the missing feature data and target outputs simultaneously using a matrix completion approach. Two matrix completion algorithms are explored: low rank matrix completion and expectation maximization (EM). Experimental results demonstrate that our framework yields faster imputation and more accurate prediction of diagnostic labels than the conventional imputation-based classification approach.

In brief, we propose a framework for a solution for this problem - classification using incomplete multi-modality data with large block of missing data. The contributions of our framework are summarized below:

• Feature selection using incomplete matrix (i.e., matrix with missing values) through data grouping and multi-task learning.

• Sample selection using incomplete matrix through data grouping and multi-task learning.

• Improve imputation effectiveness by focusing only on the imputation of important data.

• Improve classification performance by label imputation.

2. Data

2.1. ADNI background

Data used in the preparation of this article were obtained from the ADNI database (adni.loni.ucla.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public-private partnership. The primary goal of ADNI has been to test whether serial MRI, PET, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials.

The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California - San Francisco. ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date, these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.

2.2. Subjects

We only used the baseline data in this study, amounting to a total of 807 subjects (186 AD, 395 MCI and 226 NC). All 807 subjects have MRI scanned, while only 397 subjects have FDG-PET scanned and 406 subjects have CSF sampled. The general inclusion/exclusion criteria used by ADNI are summarized as follow: 1) Normal subjects: Mini-Mental State Examination (MMSE) scores between 24–30 (inclusive), a Clinical Dementia Rating (CDR) of 0, non-depressed, non MCI, and nondemented; 2) MCI subjects: MMSE scores between 24–30 (inclusive), a memory complaint, have objective memory loss measured by education adjusted scores on Wechsler Memory Scale Logical Memory II, a CDR of 0.5, absence of significant levels of impairment in other cognitive domains, essentially preserved activities of daily living, and an absence of dementia; 3) mild AD: MMSE scores between 20–26 (inclusive), CDR of 0.5 or 1.0, and meets NINCDS/ADRDA criteria for probable AD.

Since MMSE and CDR were used as parts of the criteria in categorizing subjects to different disease groups in ADNI dataset, they might provide complementary information in the data imputation process. Thus, in this study, three clinical scores were also included (CDR global, CDR-SB¹ and MMSE) as target outputs in addition to target label. The information of the subjects (i.e., gender, age and education) and clinical scores (i.e., MMSE and CDR global) used in this study are summarized in Table 1.

Table 1.

Information about ADNI dataset used in this study. (Edu.: Education, std: standard deviation)

	Gender		Age (years)	Edu. (years)	MMSE	CDR
Subjects	male	female	mean ± std.	mean ± std.	mean ± std.	mean ± std.
AD	99	87	75.4 ± 7.6	14.7 ± 3.1	23.3 ± 2.0	0.75 ± 0.25
MCI	254	141	74.9 ± 7.3	15.7 ± 3.0	27.0 ± 1.8	0.50 ± 0.03
NC	118	108	76.0 ± 5.0	16.0 ± 2.9	29.1 ± 1.0	0.00 ± 0.00

2.3. Data processing

The MRI and PET images were pre-processed to extract ROI-based features. For the processing of MRI images, anterior commissure (AC) - posterior commissure (PC) correction was first applied to all the images using MIPAV software². We then resampled the images to 256 × 256 × 256 resolution and used N3 algorithm (Sled et al., 1998) to correct the intensity inhomogeneity. Next, the skull was stripped using the method described in (Wang et al., 2011), followed by manual editing and cerebellum removal. We then used FAST (Zhang et al., 2001) in the FSL package³ to segment the human brain into three different types of tissues: grey matter (GM), white matter (WM) and cerebrospinal fluid (CSF). After registration using HAMMER (Shen and Davatzikos, 2002), we obtained the subject-labeled image based on a template with 93 manually labeled region-of-interests (ROIs) (Kabani, 1998). For each subject, we used the volumes of GM tissue of the 93 ROIs, which were normalized by the total intracranial volume (which is estimated by the summation of GM, WM and CSF volumes from all ROIs), as features. For PET image, we first aligned it to its corresponding MRI image of the same subject through affine transformation, and then computed the average intensity of each ROI in the PET image as feature. In addition, five CSF biomarkers were also used in this study, namely amyloid β (Aβ₄₂), CSF total tau (t-tau) and tau hyperphosphorylated at threonine 181 (p-tau) and two tau ratios with respective to Aβ₄₂ (i.e., t-tau/Aβ₄₂ and p-tau/Aβ₄₂). As a result, there are a total of 93 features derived from the MRI images, 93 features derived from the PET images and 5 features derived from the CSF biomarkers used in this study. Table 2 summarizes the number of samples and the number of features used in this study for each modality. The numbers under the column “All” represent the number of samples with all the three modalities available.

Table 2.

Number of subjects (ADNI database at baseline) and number of features used in this study.

	Modalities
	MRI	PET	CSF	All
Number of features	93	93	5	191
AD subjects	186	93	102	51
MCI subjects	395	203	192	99
NC subjects	226	101	112	52
Total subjects	807	397	406	202

3. Classification through matrix shrinkage and completion

Figure 1 illustrates our framework, which consisted of three components: 1) feature selection, 2) sample selection, and 3) matrix completion. Let X ∈ ℝ^n×d (n samples, d features) and Y ∈ ℝ^n×t (n samples, t targets) denote the feature matrix (that contains features derived from MRI, PET and CSF data) and target matrix (that contains label [−1 1] and clinical scores), respectively. As shown in the leftmost diagram in Figure 1, X is incomplete, and about half of the subjects do not have PET and CSF data. The dataset is divided into two parts, one for training and one for testing. The target outputs for all the training samples are known, but the target outputs for the testing samples are set to unknown for testing purposes. The input features X and clinical scores of Y are first z-normalized across all the samples, by using mean and scale obtained only from the training data. All the missing data are ignored during the normalization process. Then, two stages of multi-task sparse regression are used to remove noisy or redundant features and samples in the training set. The remaining matrix is a matrix with the most discriminative features and samples from the training set. The same set of features selected in the training set are also selected for the testing set. The shrunk training feature matrix together with the testing feature matrix forms a shrunk feature matrix X_s. We then stack X_s with the corresponding target outputs Y_s (where the values is unknown for the testing set) to form an incomplete matrix Z. Finally, a matrix completion algorithm (Goldberg et al., 2010; Ma et al., 2011; Schneider, 2001) is applied to Z, so that missing features and the unknown testing target outputs can be predicted simultaneously. The signs of the imputed target labels are then used as the classification output for the testing samples. The following subsections describe the three main components of the framework in more details.

Figure 1.

Classification via matrix shrinkage and matrix completion. There are three main parts in this framework: feature selection, sample selection and matrix completion. Note that feature selection only involves training set. (X_s, Y_s: Shrunk version of X and Y; Z_c: Completed version of Z.)

3.1. Feature selection

Not all the features are useful in classification. In fact, noisy features may decrease imputation and classification accuracy. In this step, the noisy or redundant features in the incomplete dataset are identified and removed through multi-task sparse regression (with details provided later). However, due to the missing values in the dataset, we can not apply sparse regression directly to the dataset. We first group the incomplete training set into several overlapping submatrices that are comprised of samples with complete feature data for different modality combinations, to which sparse regression algorithm can be applied. Some parts of the submatrices are overlapping as we use a grouping strategy that uses the maximum possible numbers of samples and features for each submatrix, so that as much information as possible is used for sparse regression. For example, Table 3 shows the seven possible types of modality combination, denoted as “combination pattern” (CP), for a dataset of 3 modalities, possibly with incomplete data. As shown in Table 3, a samples with lower CP is a “subset” of some higher CPs, where these higher CPs contain modality data that can be grouped with the lower CP to form a submatrix. For instance, the first row of Table 3 indicates that CP1 is “subset” of CP3, CP5 and CP7, as CP1 contains only “Modality 1” data, which is also part of CP3, CP5 and CP7’s data. Thus, we can combine “Modality 1” data from CP3, CP5 and CP7 with CP1 to form a submatrix that contains the maximum availability of samples with “Modality 1” data.

Table 3.

Grouping of data according to maximum availability of samples for each combination pattern (CP) of modalities. The availability of modalities is represented by binary number at the center column of the Table (‘0’ denotes ‘missing’, ‘1’ denotes ‘available’), while its decimal equivalent is represented by the CP number on the leftmost column of the Table. Samples with lower CP number can be grouped with the samples with higher CP numbers at the last column of the Table to form a submatrix. In this study, the “Modality 1”, “Modality 2” and “Modality 3” represent “MRI”, “PET” and “CSF”, respectively.

Combination pattern (CP)	Availability of data			Subset of CP
	Modality 1	Modality 2	Modality 3
1	1	0	0	3, 5, 7
2	0	1	0	3, 6, 7
3	1	1	0	7
4	0	0	1	5, 6, 7
5	1	0	1	7
6	0	1	1	7
7	1	1	1	−

For the ADNI dataset used in this study, Modality 1, 2 and 3 are used to denote MRI, PET and CSF, respectively. At ADNI baseline, MRI data is complete while PET and CSF data is incomplete, resulting four possible types of data combination, i.e., CP1, CP3, CP5 and CP7. Each CP can borrow data from the higher CPs as indicated in the last column of Table 3 to form a submatrix. The graphical illustration of the submatrices is shown in Figure 2. The red blocks in Figure 2 mark the four submatrices and their corresponding target outputs. Each submatrix has four interrelated target outputs (i.e. 1 label and 3 clinical scores), which can be learned together using a multi-task learning algorithm, by treating the prediction of each output target as a task. Let X_i ∈ ℝ^n_i×d_i and Y_i ∈ ℝ^n_i×t_i denote the input submatrix and its corresponding output matrix for the i-th multi-task learning in the training set, respectively. Then the multi-task sparse regression of each submatrix is given as

$$\underset{{\mathit{\alpha }}_i}{\text{min}}\frac{1}{2}{\Vert {\mathbf{X}}_i{\mathit{\alpha }}_i-{\mathbf{Y}}_i\Vert }_2^2+{\lambda }_f{\Vert {\mathit{\alpha }}_i\Vert }_{2,1},$$ (1)

where n_i, d_i, t_i and α_i ∈ ℝ^d_i×t_i denote the number of samples, the number of features, the number of target outputs and the weight matrix for the i-th multi-task learning, respectively. ‖.‖_2,1 in Eq. (1) is the l_2,1-norm (group-lasso (Yuan and Lin, 2006; Liu et al., 2009)) operator which is defined as ${\sum }_{k=1}^{d_i}{\Vert {\mathit{\alpha }}_i^{(k)}\Vert }_2$, where ${\mathit{\alpha }}_i^{(k)}$ denotes the k-th row of α_i. The use of l₂-norm for ${\mathit{\alpha }}_i^{(k)}$ forces the weights corresponding to the k-th feature (of X_i) across multiple tasks to be grouped together, while the subsequent use of l₁-norm for ${\mathit{\alpha }}_i^{(k)}$ forces certain rows of α_i to be all zero. In other words, Eq. (1) tends to select only common features (corresponding to non-zero-valued rows of α_i) for all the prediction tasks. Thus, α_i is a sparse matrix with a significant number of zero-valued rows that correspond to redundant and irrelevant features in each submatrix. In Figure 2, we arrange α_i according to the feature indices in X, so that the shaded rows in α_i are corresponding to the columns in X_i (illustrated by red block in the Figure), while the empty rows in α_i are corresponding to the features not included in X_i. In this way, each row of α_i is corresponding to the same feature index in X. The features that are selected for at least one of the submatrices (i.e., rows with at least one non-zero value in [α₁ α₂ α₃ α₄]) are finally used for the training and the testing sets. In this study, we determined α_i for each multi-task learning by using 5-fold cross-validation test based on the accuracy of the label (i.e., first column of Y_i) prediction of the training samples. The training and the testing sets with the selected features are then used in sample selection as described in the following subsection.

Figure 2.

Feature selection for incomplete multi-modal data matrix with multiple related target outputs by first grouping the data into submatrices and then using multi-task learning on each submatrix to extract common discriminative features. The red boxes come in pairs, which mark the submatrices that are comprised of largest possible number of samples for each pattern of modality combination and their corresponding target outputs.

3.2. Sample selection

In this step, another multi-task learning is used to select representative samples from the training set that are closely related to the samples in the testing set. This is similar to sparse representation reported by other liter-atures (Huang and Aviyente, 2006; Wright et al., 2010), a subset of samples is selected to represent a test sample. The only difference here is that we perform sparse representation for a group of testing samples, instead of one testing sample, to 1) select common samples from the training set that well represent the samples in the testing set, and 2) remove unrelated or redundant samples from the training set. The procedure of sample selection is similar to feature selection described previously, with some modifications on the input and output matrices of the multi-task learning.

Let X_tr and X_te respectively denote the shrunk training and testing feature matrices from the previous step that contain only the selected features. X_tr and X_te are first transposed (or rotated by 90 degree) so that each column of X_tr^T and X_te^T contains features of a sample. Then X_tr^T and X_te^T are used as the input and output to the multi-task learning, where the task is now defined as the prediction of each testing sample from the training samples. If there are no missing values in X_tr^T and X_te^T, this multi-task learning will select a set of common samples (analogous to common features in feature selection) in the training set for all the prediction tasks. However, due to the missing values in X_tr^T and X_te^T , we can not perform sample selection directly. Instead, similar to feature selection, we group the input matrix (X_tr^T ) into submatrices that contains complete data for the maximum possible number of samples and features. For each submatrix in X_tr^T , all the samples in X_te^T that contain the same set of input features are identified. Each pair of input submatrix and output submatrix with the same features set forms a multi-task learning problem, with its optimization equation given as

$$\underset{{\mathit{\beta }}_i}{\text{min}}\frac{1}{2}{\Vert {{\mathbf{X}}_{\mathbf{t}\mathbf{r}}}_i^T{\mathit{\beta }}_i-{{\mathbf{X}}_{\mathbf{t}\mathbf{e}}}_i^T\Vert }_2^2+{\lambda }_s{\Vert {\mathit{\beta }}_i\Vert }_{2,1},$$ (2)

where ${{\mathbf{X}}_{\mathbf{t}\mathbf{r}}}_i^T\in {ℝ}^{d_i^{\prime }\times n_{tri}}$, ${{\mathbf{X}}_{\mathbf{t}\mathbf{e}}}_i^T\in {ℝ}^{d_i^{\prime }\times n_{tei}}$, β_i ∈ ℝⁿ_tri^×n_tei, $d_i^{\prime }$, n_tri and n_tei denote the input submatrix, output submatrix, weight matrix, length of the selected features, number of training samples, and number of testing samples of the i-th multi-task learning, respectively.

Figure 3 summarizes the illustration of the sample selection. Note that the target matrix is incomplete like the input matrix. This causes different number of targets for each multi-task learning, which is reflected by different width of the weight matrix β_i. Due to the use of ‖.‖_2,1 term in Eq. (2), β_i learned is a sparse matrix with some all-zero rows. Training subjects corresponding to all-zero rows of [β₁ β₂ β₃ β₄] are removed as noisy/irrelevant samples. We assume that removal of noisy or unrelated samples from the training set can consequently improve the accuracy of the missing values imputation, and thus the classification performance. To justify this assumption, we have included a simulation test on our proposed sample selection algorithm using synthetic data in Appendix A.

Figure 3.

Sample selection. In this study, sample selection is realized by modifying the input and output matrices in feature selection illustrated in Figure 2. Specifically, we transpose the training and testing feature matrices, and use the transposed training and testing feature matrices as the input and target output of the multi-task learning, respectively.

3.3. Matrix completion as classification

The original incomplete matrix is shrunk significantly after the feature and sample selection steps. Let X_s and Y_s denote the shrunk version of matrix X and Y, respectively, while n_s and d_s denote the number of remaining samples and data features, respectively. The stacked matrix Z = [X_s Y_s] ∈ ℝ^n_s×(d_s+t) still contains some missing values, including the target outputs of the test set which are to be estimated. The objective of this step is to impute the missing input features, missing target labels, and missing clinical scores simultaneously. Two imputation methods are tested for this step, namely the modified Fixed-point Continuation (FPC) algorithm (Goldberg et al., 2010; Ma et al., 2011) and the regularized expectation maximization (EM) algorithm (Schneider, 2001).

3.3.1. Modified FPC (mFPC)

The multi-task regressions used in the features and samples selection steps have selected the most discriminative input features for the (training) target outputs and the most representative training samples for the testing samples, respectively. As a consequence, the columns of target outputs (Y_s) of the stacked matrix Z could be linearly represented by the columns of data features (X_s); while the rows of the testing samples in Z could be linearly represented by the rows of the training samples. The matrix Z is thus probably low rank (as some rows could be represented by other rows, etc.). However, in practice, measurements in X_s and Y_s could contain certain level of noises. Therefore, the incomplete Z can be completed using trace norm minimization (low trace norm is often used to approximate low rank assumption), together with two regularization terms (i.e., the second and third term in Eq. (3)) to penalize the noises in X_s and Y_s. As the objective of our study is prediction of target labels, we separate the data in Z into two parts: 1) the target labels (P), and 2) the rest of the data (Q). The regularization terms are changed accordingly to have one logistic loss function (L_p(u, v) = log(1 + exp(−uv))) for the output labels (as the output labels can only take value 1 or −1), and one square loss function (L_q(u, v) = 1/2(u − v)²) for the rest of the data (as other data can take any value). The imputation optimization problem is thus given as:

$$\underset{\mathbf{z}}{\text{arg min}}\mu {\Vert \mathbf{Z}\Vert }_{*}+\frac{{\lambda }_m}{|{\mathrm{\Omega }}_{\mathbf{P}}|}\sum _{(i,j)\in {\mathrm{\Omega }}_{\mathbf{P}}}{L}_p(z_{ij},p_{ij})+\frac{1}{|{\mathrm{\Omega }}_{\mathbf{Q}}|}\sum _{(i,j)\in {\mathrm{\Omega }}_{\mathbf{Q}}}{L}_q(z_{ij},q_{ij}),$$ (3)

where Ω_P and Ω_Q denote the set of observed (i.e., non-missing) labels in Y_s and the set of observed values for the rest of the data, respectively; |.| denotes an operator for the number of elements; ‖.‖_* denotes an operator for the trace norm; and z_ij, p_ij and q_ij are the predicted observed values, observed target labels and other observed data, respectively. λ_m and µ are the positive parameters used to control the focus of the minimization problem in Eq. (3). If λ_m is high, Eq. (3) will focus on minimizing the L_p term (second term); if µ is high, Eq. (3) will focus on minimizing the trace norm term (i.e., stronger low rank assumption), and vice versa.

This optimization problem is solved by using the modified FPC algorithm (Goldberg et al., 2010), which consists of two alternating steps for each iteration k:

1. Gradient step:

   $${\mathbf{A}}^k={\mathbf{Z}}^k-\tau g({\mathbf{Z}}^k)$$ (4)

   where τ is the step size and g(Z^k) is the matrix gradient which is defined as:

   $$g(z_{ij})=\{\begin{array}{cc}\frac{{\lambda }_m}{|{\mathrm{\Omega }}_{\mathbf{P}}|}\frac{-p_{ij}}{1+\mathit{\text{exp}}(p_{ij}{z}_{ij})},\hfill & (i,j)\in {\mathrm{\Omega }}_{\mathbf{P}}\hfill \\ \frac{1}{|{\mathrm{\Omega }}_{\mathbf{P}}|}(z_{ij}-q_{ij}),\hfill & (i,j)\in {\mathrm{\Omega }}_{\mathbf{Q}}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (5)
2. Shrinkage step:

   $${\mathbf{Z}}^{k+1}=S_{{\tau }_{\mu }}({\mathbf{A}}^k)$$ (6)

   where S(·) is the matrix shrinkage operator. If SVD of A^k is given as UΛV^T, then the shrinkage operator is given as:

   $$S_{{\tau }_{\mu }}({\mathbf{A}}^k)=\mathbf{U}\text{max}(\mathbf{\Lambda }-\tau \mu ,0){\mathbf{V}}^T$$ (7)

   where max(·) is the elementwise maximum operator.

These two steps are iterated until convergence where the objective function in Eq. (3) at k-th iteration is stable.

3.3.2. Regularized EM (rEM)

We also use the regularized EM (rEM) algorithm developed in (Schneider, 2001) to impute missing values. Symbols defined in this subsection should not be confused with the symbols used in other sections. Let X ∈ ℝ^n×d be an incomplete matrix with n number of samples and d number of variables, its mean vector μ ∈ ℝ^1×d and covariance matrix Σ ∈ ℝ^d×d are to be estimated. For a given sample x ∈ ℝ^1×d with missing values, let x_m ∈ ℝ^1×d_m and x_a ∈ ℝ^1×d_a denote the parts of vector x containing variables with missing values and available values, respectively. Then x_m can be estimated through linear regression model below

$${\mathbf{x}}_{\mathbf{m}}={\mathit{\mu }}_{\mathit{m}}+({\mathbf{x}}_{\mathbf{a}}-{\mathit{\mu }}_{\mathit{a}})\mathbf{B}+\mathbf{e}$$ (8)

where µ_m ∈ ℝ^1×d_m and µ_a ∈ ℝ^1×d_a represent the portions of μ that corresponding to x_m and x_a, respectively, while B ∈ ℝ^d_a^×d_m and e ∈ ℝ^1×d_m are the regression coefficient matrix and random residual vector (with zero mean and unknown covariance matrix C ∈ ℝ^d_m×d_m), respectively. We are now ready to describe the imputation using EM algorithm, which is an iterative process that consists of three steps, 1) expectation step: the mean μ and covariance matrix Σ is estimated, 2) maximization step: the conditional maximum like-lihood estimate (MLE) of the parameters of the regression model (i.e, B and C) is computed, based on the expected value of μ and Σ, and, 3) imputation step: the missing values is estimated using (8) based on the computed parameters. After missing values are imputed, it will iterate back to step 1, where a new set of μ and Σ is estimated based on the completed x, and the whole process is repeated until a convergence condition is met (i.e., the estimated μ and Σ become stable). Regularized EM algorithm consists of the same steps as EM algorithm, with a modification on the maximization step, where the regression coefficients in B are computed through ridge regression method (Hoerl and Kennard, 1970). For more detailed information about rEM algorithm, interested reader may refer to (Schneider, 2001). In our framework, rEM is used to estimate unknown target outputs and missing input features in the matrix completion step.

4. Results and discussions

The proposed framework was tested using the ADNI multi-modality dataset, which includes MRI, PET and CSF data. In this section, the proposed framework is first compared with the baseline frameworks which will be defined in the following subsection. Then, the proposed framework is compared with two state-of-the-art methods (i.e., incomplete Multi-Source Feature (iMSF) learning method and Ingalhalikar’s algorithm for classification based on incomplete dataset) and also an unimodal classifier using only MRI features. In addition, we evaluate the effect of parameters selection (i.e., λ_s, λ_m and µ) of the proposed framework on the classification performance. Finally, we also identify the features that are always being selected in this study.

The classification performance of all the compared methods is evaluated using a 10-fold cross-validation scheme. For each fold, another 5-fold cross-validation scheme is applied on the training dataset to select the best parameters for multi-task learning in feature selection and also for sparse regression based classifier in the baseline methods. The multi-task learning in feature selection and sample selection is realized by using matlab function mcLeastR from SLEP⁴. SLEP is a powerful sparse learning package where it achieves fast convergence in computation by using Nesterov’s method (Liu et al., 2009; Nesterov, 1983) to solve smooth reformulation of the problem and accelerated gradient method (Nesterov, 2007; Liu and Ye, 2010) to solve regularized non-smooth optimization problem. There are infinite choices for λ_f (i.e., multi-task learning parameter in feature selection). Fortunately for the solver mcLeastR that we used, it automatically computes the maximum λ_max value for our problem. Thus, each λ_f value that we input to this solver is treated as a fraction to λ_max, e.g., the true regularization parameter used for λ_f = 0.1 is actually 0.1 × λ_max. Therefore, we choose parameter λ_f from these candidate values: {0.001, 0.005, 0.01, 0.05, 0.1, 0.15, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 }, which roughly cover the whole range of possible λ_f values. The λ_f value used for each fold of experiment is determined based on the highest accuracy of regressed Y label of the training data through 5-fold cross-validation test on the training data. As a result, λ_f is different for each fold of experiment, i.e., different data sparsity for each fold of experiment is assumed. For sample selection, we fix a small value for λ_s, aiming to only remove unrelated samples from the training set. For mFPC matrix completion algorithm, we use grid search to select values of its parameters (i.e., μ and λ_m), i.e., fixed value of μ and λ_m are used for all the folds based on the best classification result in grid search.

Four classification performance measures are used in this study, namely 1) accuracy: the number of correctly classified samples divided by the total number of samples; 2) sensitivity: the number of correctly classified positive samples divided by the total number of positive samples; 3) specificity: the number of correctly classified negative samples divided by the total number of negative samples; and 4) area under receiver operating characteristic (ROC) curve (AUC). The positive samples are referred to AD in AD/NC classification and MCI in MCI/NC classification, respectively.

4.1. Comparison with baseline frameworks

Four imputation methods are included in the baseline framework for comparison in this study:

1. Zero imputation. In this method, the missing portion of the input data matrix is filled with zero. Since all the features were z-normalized (i.e., with zero mean and unit standard deviation) before the imputation process, “zero imputation” is equivalent to fill the missing feature values with the average observed feature values (i.e., all the missing values in a column of data matrix are filled with the mean of the observed values in the same column).

2. k-nearest neighbor (KNN) imputation (Speed, 2003; Troyanskaya et al., 2001). The missing values are filled with a weighted mean of the k nearest-neighbor rows. The weights are inversely proportional to the Euclidean distances from the neighboring rows. We set k = 20 after some empirical tests.

3. Regularized expectation maximization (rEM) (Schneider, 2001). Details are as described in the previous section. We used the default parameter values for the rEM code downloaded from http://www.clidyn.ethz.ch/imputation/index.html.

4. Fixed-point continuation (FPC) (Ma et al., 2011). FPC is one of the low rank matrix completion method that uses the fixed point and Bregman iterative algorithms. It is the original version of Eq. (3) with the regularization terms L_p and L_q replaced by a square loss function for all the observed data. The matlab code for FPC is included in the singular value thresholding (SVT) package⁵. The parameter value of FPC, i.e., µ, is determined empirically.

These imputation methods are used in two baseline frameworks for comparisons:

1. Baseline 1: Conventional method. Impute the incomplete data matrix and then train a classifier using the completed training set data.

2. Baseline 2: Use the proposed feature and sample selection method to shrink the incomplete dataset, impute the missing features in the shrunk incomplete feature matrix, and then train a classifier based on the completed shrunk training set data.

The only difference between the two baseline frameworks above, is that the first baseline framework imputes missing values on the original feature matrix, while the second baseline framework imputes missing values on the shrunk feature matrix. We use sparse regression classifier for the two base-line frameworks, its formulation is given as:

$$\underset{\mathit{\alpha }}{\text{min}}\frac{1}{2}{\Vert \mathbf{X}\mathit{\alpha }-\mathbf{Y}\Vert }_2^2+\lambda {\Vert \mathit{\alpha }\Vert }_{2,1},$$ (9)

where X, Y, and α are defined as the input feature matrix, the output target matrix (including class labels and clinical scores), and the weight matrix, respectively. We obtain α based on the completed training set and multiply it with the completed feature matrix from the testing set to produce regressed outputs. The sign of the regressed output of a testing sample that corresponds to the class label is used as the predicted class label. There is one regularization parameter in Eq. (9), i.e., λ, which is always positive and is primarily used to control features sparsity in X. We determine the value of λ by performing a 5-fold cross-validation test based on the completed training dataset.

Table 4 summarizes the AD/NC classification performance of all the frameworks in comparison. Results reported are the average measurements of 10 repetitions of 10-fold cross-validation test. As shown in the Table 4, all performance of baseline 1 frameworks are improved in baseline 2 framework (i.e., from 0.80–0.83 to 0.85–0.87). In fact, all the four performance measures (i.e., accuracy, sensitivity, specificity and AUC) increase after applying the proposed feature and sample selection steps before the imputation in base-line 2 framework. In addition, the average imputation time is significantly reduced, as shown in the last column of Table 4. For example, FPC and rEM respectively complete the imputation with 8 times and 4 times faster in the baseline 2 framework, if compared with the baseline 1 framework. We thus have shown the efficacy of the proposed feature and sample selection methods in removing the unrelated samples and noisy features, which is beneficial to the imputation process, both in terms of accuracy and speed. In addition, the classification performance is further improved to 0.88–0.89 if the target labels are imputed simultaneously with the incomplete data features using the modified FPC (mFPC) and rEM methods. Although the classification performances of both mFPC and rEM are similar, mFPC performs significantly better than rEM in terms of computation speed. Similar findings are observed for MCI/NC classification as shown in Table 5.

Table 4.

AD/NC classification performance for all the frameworks in comparison. Total of 412 samples used. The best value for each performance measure is highlighted in bold. (Acc: Accuracy, Sen: Sensitivity, Spe: Specificity, AUC: area under ROC curve, time: the average imputation time for each fold, rEM: Regularized EM, mFPC: modified FPC)

Framework	Imputation	Acc.	Sen.	Spe.	AUC	Time(s)
Baseline 1	Zero	0.802	0.802	0.804	0.887	0.00
	KNN	0.830	0.801	0.859	0.904	1.76
	rEM	0.816	0.792	0.840	0.892	84.36
	FPC	0.821	0.812	0.831	0.900	115.35
Baseline 2	Zero	0.853	0.843	0.864	0.922	0.00
	KNN	0.868	0.836	0.894	0.927	0.29
	rEM	0.857	0.833	0.879	0.922	23.76
	FPC	0.858	0.843	0.872	0.923	15.31
Proposed	KNN	0.850	0.745	0.936	0.914	0.32
	rEM	0.885	0.837	0.927	0.944	24.20
	mFPC	0.880	0.852	0.904	0.947	0.39

Table 5.

MCI/NC classification performance for all the compared frame-works. Total of 621 samples used. The best value for each performance measure is highlighted in bold. (Please refer to Table 4 for the meaning of the abbreviations used in this table.)

Framework	Imputation	Acc.	Sen.	Spe.	AUC	Time(s)
Baseline 1	Zero	0.639	0.598	0.710	0.695	0.00
	KNN	0.635	0.623	0.657	0.687	2.72
	rEM	0.650	0.636	0.675	0.696	139.14
	FPC	0.643	0.602	0.714	0.686	130.20
Baseline 2	Zero	0.669	0.631	0.736	0.732	0.00
	KNN	0.666	0.628	0.733	0.724	0.61
	rEM	0.673	0.639	0.733	0.734	34.41
	FPC	0.670	0.632	0.737	0.736	19.06
Proposed	KNN	0.672	0.778	0.486	0.726	0.65
	rEM	0.701	0.866	0.414	0.774	36.56
	mFPC	0.715	0.753	0.649	0.773	1.21

4.2. Comparison with non-imputation state-of-the-art methods

Recently, several algorithms have been proposed to deal with incomplete dataset where the data is missing in blocks. We compare our proposed frame-work with these methods, which are briefly described in the following:

1. Incomplete Multi-source Feature learning (iMSF)⁶ (Yuan et al., 2012; Xiang et al., 2013). The iMSF predicts the target output labels of the incomplete multiple heterogeneous data without involving data imputation. This is a multi-task learning algorithm that is able to deal with missing feature values. The iMSF is available in two versions for multi-task learning part, i.e., the logistic version and the regression version, along with one regularization parameter. We test both versions of iMSF with a range of regularization parameters (i.e., {0.005, 0.01, 0.05, 0.1, 0.2, 0.3 and 0.4}) and finally choose the one with the highest classification accuracy for comparison.

2. Ingalhalikar’s algorithm (Ingalhalikar et al., 2012). This algorithm uses an ensemble classification technique to fuse decision results from multiple classifiers constructed from subsets of data. The data subsets are obtained by applying a grouping strategy similar to ours. We implemented Ingalhalikar’s algorithm and tested it on our dataset. Specifically, we group the data into subsets, select features using signal-to-noise ratio coefficient filter (Guyon and Elisseeff, 2003), use linear discriminant analysis (LDA) as classifier, and finally fuse all the classification results of the subsets into a single result for each sample. We used two fusion methods for this algorithm, i.e., 1) weighted average: each classifier is assigned a weight based on its training classification error, 2) average: all the classifiers are assigned with equal weight.

Tables 6 and 7 show the comparison of classification performance between the proposed framework (using rEM and mFPC imputation methods) and the iMSF and Ingalhalikar’s algorithm. Both tables shows that the proposed framework outperforms the Ingalhalikar’s algorithm but performs competitively to iMSF.

Table 6.

AD/NC classification comparison with iMSF and Ingalhalikar’s algorithm. All the performance measures reported in this table are the means of the respective 10 repetitions of the 10-fold cross-validation test. The best value for each performance measure is highlighted in bold. The significance of the results are indicated by p-value of the t-test (using 100 pairs of AUC values of two methods in comparison) at the last two columns of the Table. p-values that are marked with * indicate that the proposed method is statistically better than the method in comparison at 95% confidence level. (fusion1: weighted average of all the classification outputs from the data sub-sets, fusion2: average of all the classification outputs from the data subsets.)

Framework	Methods	Performance measures				t-test on AUC (p-value)
		Acc	Sen	Spe	AUC	with rEM	with mFPC
Proposed	rEM	0.885 ± 0.050	0.837	0.927	0.944
	mFPC	0.880 ± 0.054	0.852	0.904	0.947
iMSF	regression	0.873 ± 0.056	0.861	0.883	0.932	< 0.0005*	< 0.0005*
	logistic	0.866 ± 0.055	0.809	0.912	0.924	< 0.0005*	< 0.0005*
Ingalhalikar’s	fusion1	0.843 ± 0.061	0.804	0.877	0.905	< 0.0005*	< 0.0005*
	fusion2	0.847 ± 0.058	0.809	0.880	0.913	< 0.0005*	< 0.0005*

Table 7.

MCI/NC classification comparison with iMSF and Ingalhalikar’s algorithm. (Please refer to Table 6 for detailed descriptions of this Table.)

Framework	Methods	Performance measures				t-test on AUC (p-value)
		Acc	Sen	Spe	AUC	with rEM	with mFPC
Proposed	rEM	0.701 ± 0.047	0.866	0.414	0.774
	mFPC	0.715 ± 0.056	0.753	0.649	0.773
iMSF	regression	0.692 ± 0.063	0.649	0.768	0.760	0.001	0.001
	logistic	0.706 ± 0.051	0.818	0.509	0.733	< 0.0005*	< 0.0005*
Ingalhalikar’s	fusion1	0.642 ± 0.062	0.644	0.639	0.664	< 0.0005*	< 0.0005*
	fusion2	0.649 ± 0.063	0.651	0.643	0.689	< 0.0005*	< 0.0005*

iMSF-regression has the highest sensitivity for AD/NC classification and has the highest specificity for MCI/NC classification. iMSF-logistic performs well in MCI/NC classification, may be because that there is non-linear relationship between the features and MCI, which can be better captured by logistic loss function. However, iMSF-logistic does not perform as well in AD/NC classification, if compared with iMSF-regression and our proposed methods. In addition, both versions of iMSF have lower AUC for both categories of classification, if compared with our proposed methods.

Ingalhalikar’s algorithm has the lowest performance in this study if compared with iMSF and our proposed method. The proposed framework, though not involving ensemble procedure, is competitive with state-of-the-art algorithm.

The proposed framework performs the best in term of classification accuracy and AUC values. In term of classification accuracy, the proposed framework using rEM performs the best in AD/NC classification while the proposed framework using mFPC performs the best in MCI/NC classification. Though the performance difference of the proposed framework and iMSF is small in term of classification accuracy (about 1%), there is a sub-stantially significant difference in term of AUC, which is not sensitive to threshold. Both mFPC and rEM imputation algorithms achieve the highest AUC values for both AD/NC and MCI/NC classifications, which are the most important measure in classification.

We performed additional t-tests to examine the significance of our results. We picked AUC values for the t-test, as AUC values are not sensitive to threshold. All the AUC values obtained from the 10 repetitions of the 10-fold cross-validation are used for comparisons, i.e., 100 AUC values from the proposed methods, versus 100 AUC values from the methods of comparison. The null hypothesis is that both methods have no significant difference in term of AUC values, while the alternative hypothesis is there is significant difference in term of AUC values obtained by the two methods at 95% confidence level. We show the p-values of the t-test at the last two columns of the Table 6 and Table 7. The p-values that are marked with * indicates that the differences are significant at 95% confidence level.

Table 6 shows that our proposed framework using rEM and mFPC perform statistically significantly better than all the methods in comparison in both the AD/NC and MCI/NC classifications, in term of AUC values.

4.3. Comparison with unimodal classifier using MRI data

We also compare the performance of the proposed framework with a unimodal classifier using only MRI data, as shown in Table 8. Since all the samples have MRI data, the number of samples used is same as previous experiment. The same sparse regression classifier in Eq. (9) is used in this test. Superior performance of the proposed framework demonstrates the importance of including information from other modalities to improve disease diagnosis accuracy.

Table 8.

Classification comparison with unimodal classifier using only MRI features for AD/NC and MCI/NC classification. The best value for each performance measure is highlighted in bold.

Methods	AD/NC				MCI/NC
	Acc	Sen	Spe	AUC	Acc	Sen	Spe	AUC
Proposed rEM	0.885	0.837	0.927	0.944	0.701	0.866	0.414	0.774
Proposed mFPC	0.880	0.852	0.904	0.947	0.715	0.753	0.649	0.773
MRI only	0.834	0.821	0.847	0.902	0.625	0.582	0.700	0.693

4.4. Effect of parameters selection of mFPC

It is important to select a set of robust parameters for matrix completion, so that the proposed framework works well for most of the situations. Figure 4 shows the classification accuracies and AUC of the proposed mFPC-based framework for a range of λ_m and μ values. As shown in the figure, the classification accuracy is consistently high when small μ and large λ_m are used. With small μ and large λ_m, the objective function in Eq. (3) will focus on the minimization of logistic function (i.e., target label prediction) instead of the minimization of the trace norm (i.e., low rank matrix completion). This implies that the incomplete matrix Z is completed using higher rank than expected. This is probably due to the measurement noise in the dataset, which causes an increase in the rank of Z. Based on the plot in Figure 4, Eq. (3) that satisfy μ ≤ 10⁻³ and λ_m ≥ 0.05 yield reasonably good label prediction.

Figure 4.

Effect of the parameter changes in mFPC algorithm to AD/NC and MCI/NC classification accuracies.

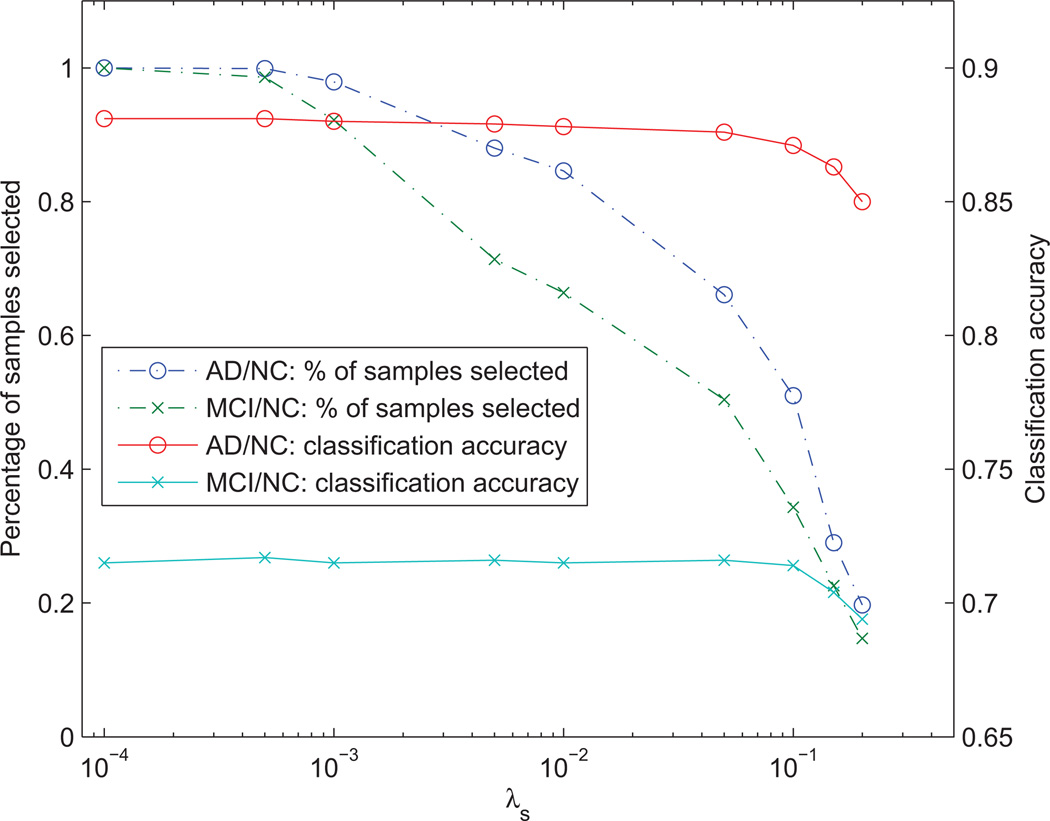
4.5. Effect of λ_s on sample selection

Figure 5 shows the effect of λ_s on sample selection in Eq. (2) to the average number of samples selected (from the training dataset) and the average classification accuracy (i.e., accuracy of the label imputation) of the matrix completion. As shown in Figure 5, the average number of samples selected reduces gradually when λ_s is decreasing, while relatively consistent in terms of classification accuracy for mFPC. This implies that there are a lot of redundant samples in the training set, which can be removed without significantly affecting the accuracy of the label imputation. To examine the performance of sample selection using synthetic data, please refer to Appendix A.

Figure 5.

Effect of the parameter λ_s on the number of samples selected and the corresponding classification accuracies for AD/NC and MCI/NC classification using mFPC of the proposed framework.

One of the possible limitations of the proposed sample selection is that the output space is not considered in the algorithm (as this information is not available for the testing samples), which might cause possible bias in the result if there is measurement noise in the output space. For example, the feature space for highly coherent samples is very similar, but due to measurement noise in the output space, they may have different outputs. In worst case scenario (e.g., using too large λ_s value), the l₁-regularized algorithms (i.e., the l₁-norm part of the l_2,1-norm) may select only one sample and discard the others, which cause bias in the result. This problem can be ameliorated by including the additional l₂-regularization, such as that done in Elastic Net (Zou and Hastie, 2005). This will help retain some coherent samples and allow some averaging effect. Another possible solution is to perform sample selection and output variable estimation iteratively, which we leave it as our future work.

4.6. Most discriminative features

Table 9 shows the statistics of the features selected by the proposed feature selection method for the incomplete ADNI data, during the AD/NC and MCI/NC classifications, respectively. On average, more than 60% of the features is removed for both cases. The number of features selected for each fold varied significantly, e.g., it can go as low as 45 or as high as 120 for AD/NC classification. This is probably because the regularization parameter λ_f in Eq. (1) is chosen from a wide range of values (i.e., {0.001, …, 0.9}).

Table 9.

Numbers of features selected for AD/NC and MCI/NC classifications. (std.: standard deviation; MDFs: Most discriminative features, features that were selected more than 90% of the time for 10 repetitions of 10-fold cross-validation run.)

Classification	Original no. of features	No. of selected features			MDFs
		mean ± std.	min	max	MRI	PET	CSF	Total
AD/NC	191	69.9±14.4	45	120	30	5	1	36
MCI/NC	191	63.0±26.7	19	140	10	5	2	17

In addition, we also include the distribution of the most discriminative features according to modalities in Table 9. We define the most discriminative features (MDFs) as the features that were selected for more than 90% of the times, i.e., more than 90 times in the 10 repetitions of the 10-fold cross-validation run. Most of the MDFs are located in MRI modality, for both the AD/NC and MCI/NC classifications. We also observed that more features were selected for AD/NC than MCI/NC classification. This is probably because MCI, which is the early stage of AD, affects less brain regions (or ROIs) if compared with AD, where its abnormalities are widely spread across brain regions.

Table 10 shows the names of the MDFs for each modality. The common MDFs selected for AD/NC and MCI/NC classifications are also included in Table 10, if exist. The common MDFs for MRI modality include hippocampal formation, middle temporal gyrus, uncus, and amygdala. The atrophy at these ROIs has been reported to be associated with memory and cognitive impairments or closely related to the AD/MCI pathology (De Leon et al., 1997; Convit et al., 2000; Yang et al., 2012; Poulin et al., 2011). For AD/NC classification, since there are many MDFs from MRI, we only list the MDFs that were selected in all cross-validations and repetitions in Table 10.

Table 10.

Most discriminative features (MDFs) selected for each modality. (Please refer to Table 9 for definition of MDF. For MRI’s MDFs in AD/NC classification, only those that are selected 100% of the time are listed here.)

Modality	AD/NC	MCI/NC
MRI	Common MDFs: Hippocampal formation right, hippocampal formation left, middle temporal gyrus left, uncus left, amygdala right.
	Medial frontal gyrus, Angular gyrus right, precuneus right, superior parietal lobule left, precentral gyrus left, perirhinal cortex left, lateral occipitotemporal gyrus right, amygdala left, middle temporal gyrus right, corpus callosum, inferior temporal gyrus right, lateral occipitotemporal gyrus left.	Entorhinal cortex left, cuneus left, lingual gyrus left, temporal pole left, middle occipital gyrus left.
PET	Common MDFs: Middle frontal gyrus right, precuneus right, precuneus left, Medial front-orbital gyrus right.
	Insula right	Angular gyrus left
CSF	t-tau/Aβ42	Aβ42 and t-tau.

On the other hand, the common MDFs for FDG-PET modality include middle frontal gyrus and precuneus, which are similar to the findings in (Mielke et al., 1998; Scarmeas et al., 2004). For CSF biomarkers, the selected MDFs were t-tau/Aβ₄₂ for AD/NC classification and Aβ₄₂ and t-tau for MCI/NC classification.

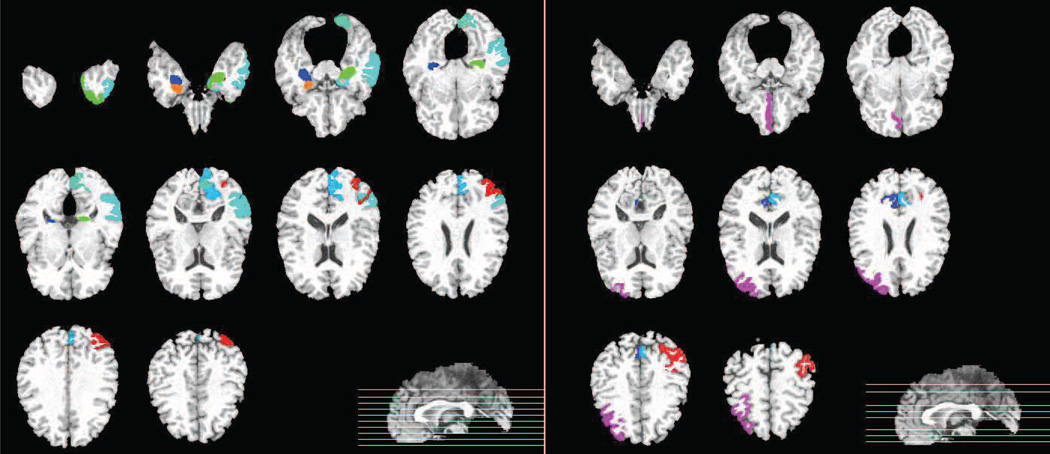
Figures 6 and 7 graphically show the locations of the selected ROI-based features (for MRI and PET modalities) for both the AD/NC and MCI/NC classifications, respectively.

Figure 6.

MDFs in AD/NC classification. (Left: MRI, right: PET)

Figure 7.

MDFs in MCI/NC classification. (Left: MRI, right: PET)

5. Conclusion

In this work, we propose a novel classification framework that is able to deal with datasets with significant amount of missing data (e.g., data missing in blocks). Conventional imputation-based classification approach is slow and inaccurate for this type of dataset. We accomplish accurate label prediction by applying matrix completion on a shrunk version of the data matrix. The matrix shrinkage operation simplifies the imputation task since redundant features and samples have been removed and less missing data needs to be imputed. The experimental results demonstrate the efficacy of feature selection and sample selection in improving the classification performance of the conventional imputation-based classification method, both in terms of speed and accuracy. The proposed framework also yields competitive performance, compared with the state-of-the-art methods such as iMSF and Ingalhalikar’s algorithm. Based on the t-test of their AUC values, the proposed framework using rEM and mFPC are statistically significantly better than iMSF and Ingalhalikar’s algorithm in AD/NC and MCI/NC classifications.

Research Highlights.

• Identify AD/MCI using incomplete dataset via matrix shrinkage and completion.

• A 2-step multi-task learning algorithm is used for feature and sample selection.

• Missing features and the unknown target labels are imputed simultaneously.

• Proposed feature and sample selection improves conventional imputation-based methods.

• Proposed framework outperforms conventional methods in term of speed and accuracy.

Appendix A. Test on sample selection algorithm using synthetic data

Sample selection was used in this work to select samples from the training set that are closely related to the testing samples before imputation of missing values and class labels. We assume that sample selection can remove outlier or unrelated samples from inhomogeneous dataset, and consequently improves the classification performance. To justify our assumption, we have tested the proposed sample selection algorithm by using several sets of synthetic data. The synthetic data with n_s number of samples, n_f number of variables and σ noise level, is generated as follows:

1. Generate a rank-r matrix X_r ∈ ℝ^n_s×n_f by multiplying a randomly generated n_s × r matrix with another randomly generated r × n_f matrix, where elements of both matrices are drawn i.i.d. from a standard normal distribution.

2. Add Gaussian noise N(0, σ²) to each element of matrix X_r.

3. Generate a weight vector w ∈ ℝ^n_f×1 where its elements are drawn i.i.d. from a standard normal distribution.

4. Generate output label Y ∈ ℝ^n_f×1 from Y = sign(X_r × w + N), where N is a noise vector with its elements are drawn i.i.d. from N(0, σ²).

We simulated a multi-modal dataset by generating two different X_r with the same label Y, and arranging them side by side, e.g., X = [X_r1X_r2]. We simulated heterogeneous dataset by generating several X with different rank or w, and stacking them together, e.g., X_het = [X₁; X₂], where X₁ ∈ ℝ^{n_s1 ×2n_f} and X₂ ∈ ℝ^{n_s2 ×2n_f}. We simulated missing data by randomly removing half of the feature data (row by row) from the second modality of X_het (i.e.,X_r2 part for both X₁ and X₂).

Table A.11 shows the details of the generated data. One homogeneous data and two inhomogeneous (heterogeneous) data were generated. The homogenous data was created by using a single matrix X₁, the inhomogeneous data 1 was created by stacking X₁ and X₂, while inhomogeneous data 2 was created by stacking X₁, X₂ and X₃. Each X_m, m = {1, 2, 3} is a “two-modality” simulated data, with each modality containing 80 features (i.e., n_f = 80), respectively. The rank for each modality data is shown in Table A.11. Each synthesized data with four different levels of noise (i.e., σ = {2, 1, 0.5, 0.1}) were used in experiment.

We then tested our framework (specifically the sample selection algorithm) on the synthetic data by using 10-fold cross-validation scheme, similar to the scheme used in this manuscript. The simulation results using homogeneous and 2 types of inhomogeneous data are shown in Figure A.8, A.9 and A.10, respectively. The x-axis of these figures is the λ in sample selection, the higher the λ value, the more the removed training samples. The average number of samples selected from the training set for each fold is shown at the bottom right corner of all the three figures. The other three plots in these figures are the classification accuracies versus λ, using mFPC, KNN and EM imputations, respectively. From the Figure A.8, the classification accuracies for mFPC and KNN are rather stable for all the λ values, as expected for homogeneous data. However, we surprisingly notice that the sample selection improves the classification accuracies for EM imputation using incomplete homogeneous data matrix. This is probably because sample selection removes some noisy samples from the training samples that improves the EM imputation. From the Figure A.9, where the number of “outlier” samples is about 10% of the total samples, the sample selection algorithm slightly improves the classification accuracies for all the three imputation methods, especially when the noise level in the data is higher, i.e., σ = {2, 1}. However, we also notice that there are some declines in classification accuracies for low noise curves (σ = {0.1, 0.5}) using KNN and EM imputations, when higher λ values are used. When the number of “outlier” samples is increased to about 20% of the total samples, the classification accuracies of mFPC and KNN improve significantly, particularly for data with higher noise level, as shown in Figure A.10. The effect of sample selection on EM imputation is not obvious for both the inhomogeneous data matrices 1 and 2.

In summary, these simulation results support our assumption that removing noisy samples (due to Gaussian noise) or unrelated samples (due to inhomogeneous data) from the training dataset can improve classification performance. Sample selection improves mFPC and KNN imputation when the data is more noisy and inhomogeneous, while improves EM imputation when the data is homogeneous.

Table A.11.

Synthetic data: One homogeneous data matrix and two inhomogeneous data matrices. X_m,m = {1, 2, 3} is a simulated two-modality data matrix, e.g., [X_r1X_r2], with n_sm number of samples and rank (r₁r₂), where r₁ and r₂ are the ranks for X_r1 and X_r2, respectively. The inhomogeneous data matrix 1 is simulated by stacking X₁ and X₂, while the inhomogeneous data matrix 2 is simulated by stacking X₁X₂ and X₃ data.

Data matrices	X1		X2		X3
	ns1	rank	ns2	rank	ns3	rank
Homogeneous	100	(60,40)	0	−	0	−
Inhomogeneous 1	100	(60,40)	10	(20,10)	0	−
Inhomogeneous 2	100	(60,40)	10	(20,10)	10	(10,10)

Figure A.8.

Classification result for homogenous data matrix.

Figure A.9.

Classification result for inhomogeneous data matrix 1.

Figure A.10.

Classification result for inhomogeneous data matrix 2.