Abstract
Objective
The generalized matrix learning vector quantization (GMLVQ) is used to estimate the relevance of texture features in their ability to classify interstitial lung disease patterns in high-resolution computed tomography images.
Methodology
After a stochastic gradient descent, the GMLVQ algorithm provides a discriminative distance measure of relevance factors, which can account for pairwise correlations between different texture features and their importance for the classification of healthy and diseased patterns. 65 texture features were extracted from gray-level co-occurrence matrices (GLCMs). These features were ranked and selected according to their relevance obtained by GMLVQ and, for comparison, to a mutual information (MI) criteria. The classification performance for different feature subsets was calculated for a k-nearest-neighbor (kNN) and a random forests classifier (RanForest), and support vector machines with a linear and a radial basis function kernel (SVMlin, SVMrbf).
Results
For all classifiers, feature sets selected by the relevance ranking assessed by GMLVQ had a significantly better classification performance (p < 0.05) for many texture feature sets compared to the MI approach. For kNN, RanForest, and SVMrbf, some of these feature subsets had a significantly better classification performance when compared to the set consisting of all features (p < 0.05).
Conclusion
While this approach estimates the relevance of single features, future considerations of GMLVQ should include the pairwise correlation for the feature ranking, e.g. to reduce the redundancy of two equally relevant features.
Keywords: Feature selection, Relevance learning, Supervised learning, Texture analysis, High-resolution computed tomography of the chest, Interstitial lung disease patterns
1. Introduction
The ability to detect and classify pathological patterns in medical images is a key challenge in computer-aided diagnosis systems that consist of a feature extraction and machine learning task. In high-resolution computed tomography (HRCT) images of the chest, the classification of pathological patterns of interstitial lung diseases (ILDs) is a complicated classification task which requires substantial expertise. Different texture features and classifiers have been proposed to achieve the goal of distinguishing healthy lung patterns from disease patterns [1–3]. A reliable, consistent and reproducible computer-aided diagnosis could improve the radiologists efficiency and avoid surgical lung biopsies for some patients.
One approach to design an image-based, automated detection tool is to extract texture features from regions of interest (ROI) and then use supervised machine learning techniques to classify the ROI as healthy or pathological. Too many features deteriorate the classification performance of the machine learning algorithms summarized as ”curse of dimensionality’ [4]. In addition, irrelevant features degrade the classification performance. Because of these negative effects, it is common to precede the learning with a feature selection stage that strives to eliminate all but the most relevant features.
This study addresses the question how the texture feature can be identified that provide the best information from the underlying lung HRCT images for a specific (classification) problem. This objective can be addressed by estimating the global relevance of each individual texture feature relative to all other texture features in the set. The resulting relevance allows the ranking of texture features for a specific classification problem. The ranks in relevance can then be used (1) to compare the performance of texture features and (2) to select only a subset with the texture features most important for the classification task thereby reducing the dimensionality of the data set and avoiding any over-fitting [4]. With an independent feature selection step, many proposed texture feature approaches can be tested and the best set can then be used for the actual classification task.
The generalized matrix learning vector quantization (GMLVQ) [5] offers such a relevance estimation for features in a supervised pattern classification problem. The GMLVQ algorithm provides a discriminative distance measure of relevance factors, which can account for pairwise correlations between different texture features and their importance in classification using real-world data [6]. From lung HRCT images, texture features were extracted, ranked and selected according to the relevances obtained by GMLVQ. For comparison, features were also selected by a mutual information criteria. The selected features subsets were then evaluated in their ability to classify the lung patterns.
2. Related work
The learning vector quantization (LVQ) approach [7] and its variants (e.g. LVQ3) [8, 9] constitute a popular family of supervised classifiers based on prototypes in the feature space. Specifically, LVQ3 shifts the decision borders toward the Bayesian limits and applies an correction term that ensures that the prototypes approximate the corresponding class distribution. Relevance learning schemes quantify the importance of extracted features for a certain classification task in heterogenous data sets [9]. The GMLVQ is an extension of this concept that provides a matrix of relevances that accounts for correlations between different features. A similar approach is the distinction sensitive LVQ (DSLVQ) [10], which adapts LVQ3 for the weighting factors according to plausible heuristics. In contrast, the GMLVQ update constitutes a stochastic gradient descent on a cost function [8].
Several schemes for adaptive distance learning exist, e.g. the large margin nearest neighbor (LMNN)[11]. A comparison between the LMNN technique and the GMLVQ approach on the basis of a content based image retrieval application revealed that both methods can reach a similar performance; however the computational cost for GMLVQ training is typically lower [12, 13].
Several authors investigated the performance of certain groups of texture features and their combination with classifiers [1–3, 14–18] in lung HRCT images as well as other types of images [19, 20]. In addition, various feature selection schemes based on mutual information were proposed [21, 22].
In this work, the feature selection based on the GMVLQ relevances is compared with a mutual information criteria using a real-world data set.
3. Generalized matrix LVQ
LVQ [7] constitutes a particularly intuitive classification algorithm, which represents data by means of prototypes. LVQ itself constitutes a heuristic algorithm, hence extensions have been proposed for which convergence and ability to represent the data structure can be guaranteed [9, 23]. One particularly crucial aspect of LVQ schemes is the dependency on the underlying metric, usually the Euclidean metric, which may not suit the underlying data structure. Therefore, general metric adaptation has been introduced into LVQ schemes [9, 24]. Recent extensions parameterize the distance measure in terms of a relevance matrix, the rank of which may be controlled explicitly. The algorithm suggested in [5] can be employed for linear dimension reduction and visualization of labeled data.
We consider training data x⃗i ∈ ℝN, i = 1…S with labels yi corresponding to one of C classes respectively. The aim of LVQ is to find m prototypes w⃗j ∈ ℝN with class labels c(w⃗j) ∈ {1,…,C} such that they represent the classification as accurately as possible. A data point x⃗i is assigned to the class of its closest prototype w⃗j, where d(x⃗i, w⃗j) ≤ d(x⃗i, w⃗l) for all l ≠ j and d usually denotes the squared Euclidean distance
| (1) |
Consider a function μ(x⃗i),
| (2) |
where w⃗J denotes the closest prototype with the same class label as x⃗i (c(w⃗J) = yi), and w⃗K is the closest prototype with a different class label (c(w⃗K) ≠ yi). Let Φ(·) denote a monotonically increasing function; then, the general scheme of generalized LVQ (GLVQ) [8] adapts prototype locations by minimizing the cost function
| (3) |
In this contribution, Φ was chosen to be the identity function, Φ(x) = x; other choices include e.g. the logistic function [9]. This cost function aims at an adaptation of the prototypes, such that a large hypothesis margin is obtained and a reliable and robust classification (see [25]) is achieved. A learning algorithm can be derived from the cost function EGLVQ by means of a stochastic gradient descent as shown in [9, 23].
Matrix learning in GLVQ (GMLVQ) [24, 25] substitutes the usual squared Euclidean distance d by a more advanced dissimilarity measure which contains an adaptive dissimilarity measure, thus resulting in a more complex and better adaptable classifier. In [5], it was proposed to choose the dissimilarity as
| (4) |
with an adaptive, symmetric and positive semi-definite matrix Λ ∈ ℝN×N. The dissimilarity measure Eq. (4) possesses the shape of a Mahalanobis distance. Note, however, that the precise matrix is determined in a discriminative way according to the given labeling, such that severe differences from the standard Mahalanobis distance based on correlations can be observed. By setting
| (5) |
with Ω ∈ ℝM×N with M ≤ Nsemi-definiteness and symmetry is guaranteed. Optimization takes place by a stochastic gradient descent of the cost function EGLVQ in Eq. (3), with the distance measure d substituted by dΛ (see Eq. (4)).
The training takes place as an iterative learning scheme picking a sample x⃗i in every step t from the randomized labeled training set and performing an update of both the prototypes w⃗K,J and the matrix. The update of the nearest prototype w⃗J with the same class label like x⃗i and the nearest prototype w⃗K with a different class label is given by
| (6) |
| (7) |
| (8) |
The corresponding update of the matrix reads
| (9) |
| (10) |
with L ∈ {J, K}. After each training step t the matrix is normalized to ∑i[Λ]ii = 1 in order to prevent degeneration to 0. An additional regularization term in the cost function proportional to −ln(det(ΩΩ⊤)) can be used to enforce full rank M of the relevance matrix and prevent over-simplification effects, see [26]. The learning stops after a maximal number of epochs (sweep through the shuffled training set) is reached. At the end of the learning process the algorithm provides a set of prototypes w⃗j, their labels c(w⃗j), and a task specific discriminative distance dΛ.
The diagonal elements Λii of the dissimilarity matrix can be interpreted as overall relevances of every feature i for the classification. The off-diagonal elements Λij with j ≠ i weight the pairwise correlations between features i and j. High absolute values in the matrix denote highly relevant features, while values near zero can be seen as less important for the classification accuracy. So the GMLVQ approach offers typical representatives of the classes in form of prototypes, a discriminative distance measure and feature relevance information suitable for the specific classification task.
The cost function of GMLVQ is non convex and, in consequence, different local optima can occur, which lead to different results and subsequent data visualizations. The non-convexity of the cost function is mainly due to the discrete assignments of data points to one prototype, which may not be unique for real-world data sets with overlapping classes. In the experiments, different assignments and, in consequence, different data representations could be observed, where these representations focus on different relevant facets of the given data sets.
The choice Ω ∈ ℝM×N with M ≤ N transforms the data locally to an M-dimensional feature space. It can be shown that the adaptive distance dΛ(w⃗j, x⃗i) in Eq. (4) equals the squared Euclidean distance in the transformed space under the transformation x⃗ ↦ Ωx⃗, because dΛ(w⃗j, x⃗i) = (Ωx⃗i − w⃗j)2. The target dimension M must be chosen in advance by intrinsic dimension estimation or according to available prior knowledge. For visualization purposes, usually a value of two or three is appropriate.
4. Experiment
4.1. Data
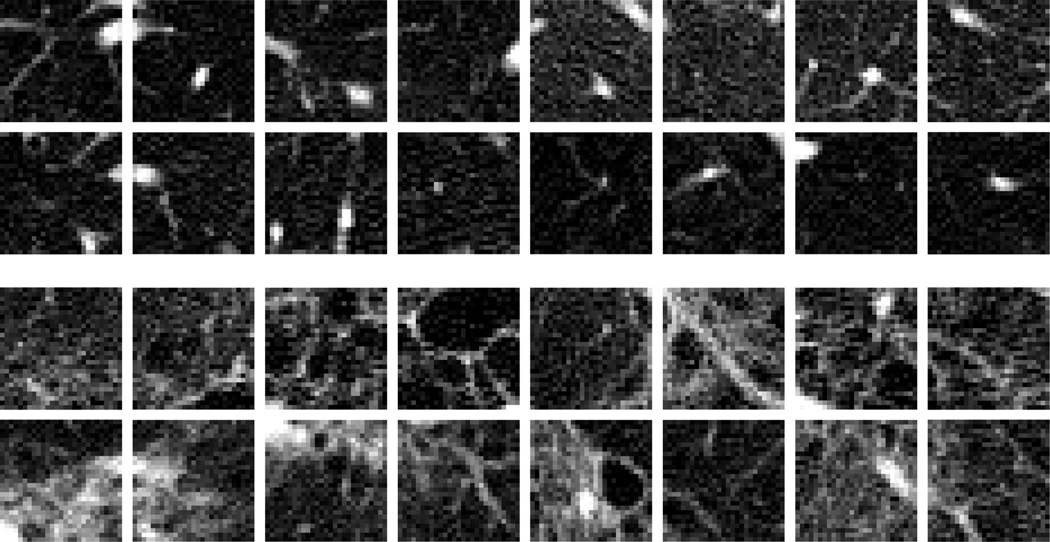
For each of the 14 patients with known occurrence of ILD patterns, a stack of 70 axial images reconstructed with a lung kernel from HRCT of the chest was assessed by an experienced radiologist. The resulting images are comparable to classical HRCT with the exception that not only reconstructions of a small number of slice positions are available. A morphological pattern related to a heterogenous group of ILDs is the so-called honeycombing. All images have a slice thickness of 1mm, an in-plane pixel size of 0.69×0.69 mm, and a slice distance of 5 mm. In this data set, 964 two-dimensional, squared ROIs with an edge length of 23 pixels were defined in 608 healthy and 356 pathological, honeycombing lung patterns (Fig. 1). In each of these ROIs, the set of the following vectors of texture features was calculated.
Figure 1.
ROIs with HRCT image patterns showing examples for healthy lung tissue (upper 2 rows) and pathological lung tissue (lower 2 rows).
4.2. Texture features
Gray level co-occurrence matrices (GLCM) [19] are second order histograms that estimate the joint probability P(gi, gj) for the occurrence of two pixels with the gray levels gi and gj for a given pixel spacing and direction. In each ROI, the gray levels were rescaled (min-max-scaling) to 128 gray level values and texture features were calculated for ndir = 4 offset directions (0°, 45°, 90°, 135°) and five pixel spacings sp = {1, 2, 3, 4, 5}. Pixels pairs were excluded from the GLCM if the neighbor pixel was outside the ROI. To achieve rotation invariant features, the GLCM of the four directions were summed to one matrix. From those isotropic GLCMs, 13 statistical features fi(sp) (i = 1,…,13) were calculated resulting in a set of 65 GLCM texture features. After the calculation, all features were standardized to zero mean and unit variance.
4.3. Mutual information
For a comparison with the estimated feature relevance by GMLVQ, an information theoretic approach to feature selection is used. Mutual information (MI) [4] is a measure of general independence between random variables. For two random variables X and Y, the MI is defined as
| (11) |
where entropy H(·) measures the uncertainty associated with a random variable. The MI I(X, Y) estimates how the uncertainty of e.g. X is reduced if Y has been observed. If X and Y are independent, their MI is zero.
For ROI data set in this study, the MI between the single texture features fi(sp) and the corresponding class labels yi was calculated by approximating the probability density function of each variable using histograms P(·):
| (12) |
Here, the number of classes nc = 2 was used; the number of histogram bins for the texture features nf was determined adaptively according to
| (13) |
where κ is the estimated kurtosis and N the number of ROIs in the data set[21]. Hence, more histogram bins were assigned to non-Gaussian distributed features.
4.4. Classification performance
After the ranking of the texture features, different classifiers were used to test the classification performance on ranked features acquired by the GMLVQ algorithm and the MI approach. Three commonly used classifiers were investigated in this study: a k-nearest neighbor (kNN), support vector machines with a linear and a radial basis function kernel (SVMlin, SVMrbf, respectively), and random forests (RanForest) [27, 28].
Free Parameters of all classifiers were subject to optimization via cross validation in the training phase. In one iteration, the data set is randomly divided into a training set (70%) and a test set (30%); all ROIs of one patient are either included in the training set or the test set. The training set is used to estimate the relevance with GMLVQ and MI ranking and to determine the best classifier parameter in a 10-fold cross-validation. The optimized classifier model was then applied on the independent test set to calculate the accuracy of one iteration. This scheme was repeated 50 times resulting in an accuracy distribution for each texture feature sets and classifier. In addition to a feature set including all features, sets consisting of the best {1,…,20} features according the the GMLVQ and MI ranking were evaluated for their classification performance. A Wilcoxon signed-rank test was used to compare two accuracy distributions.
5. Results
5.1. Feature ranking
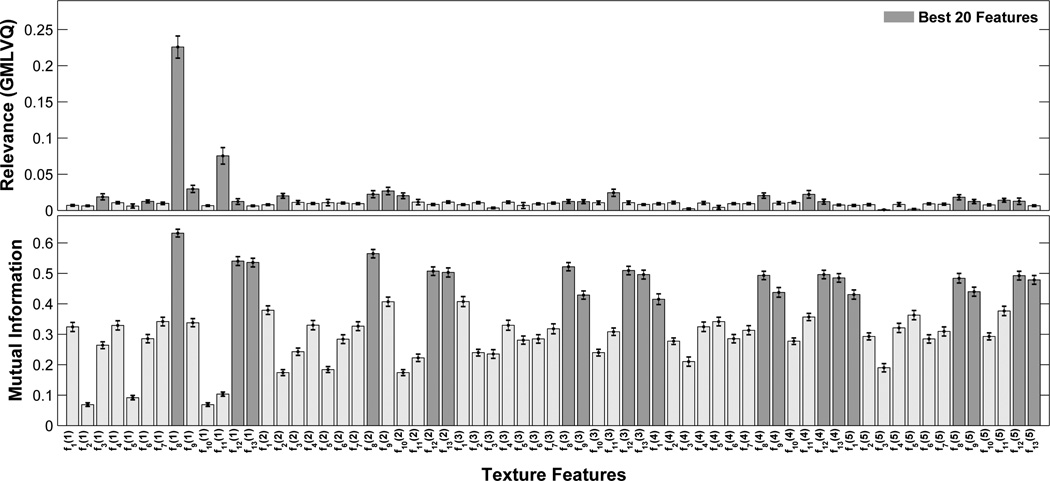
In Fig. (2), the ranking of the used texture feature is shown for the relevance measure obtained by GMLVQ and the MI estimation, and the 20 best features in each ranking scheme are highlighted. Both feature selection approaches identify f8(1) as the most important feature to distinguish the two classes of ROI patterns. However, the second best feature is already different (f11(1) for GMLVQ, f8(2) for MI) and the overall set of the best 20 texture features is not identical as well. The best ranked texture features f8 and f11 define the ’sum of entropy’ and the ’difference entropy’, respectively [19]. For the GMLVQ algorithm, the off-diagonal elements of Λ are shown in Fig. (3), which weight the pairwise correlations between two features.
Figure 2.
Ranking of the used texture features for the relevance measure obtained by GMLVQ (upper panel) and the mutual information MI (lower panel). For the 50 iteration, the mean ranking is shown for each feature; the error bars indicate the corresponding standard deviation. The GMLVQ relevance is calculated from the diagonal elements Λii of the dissimilarity matrix (Eq. 5). The 20 best feature in each ranking approach are marked with black bars. The set of texture features consists of the statistical measures derived from the GLCMs, fi(sp), for i = {1,…,13} and sp = {1,…,5}.
Figure 3.
The matrix Λ with pairwise-correlations between the GLCM features. Dark and bright entries correspond to high negative and positive correlations, respectively. The diagonal elements (see Fig. 2) are set to zero to emphasize the off-diagonal elements.
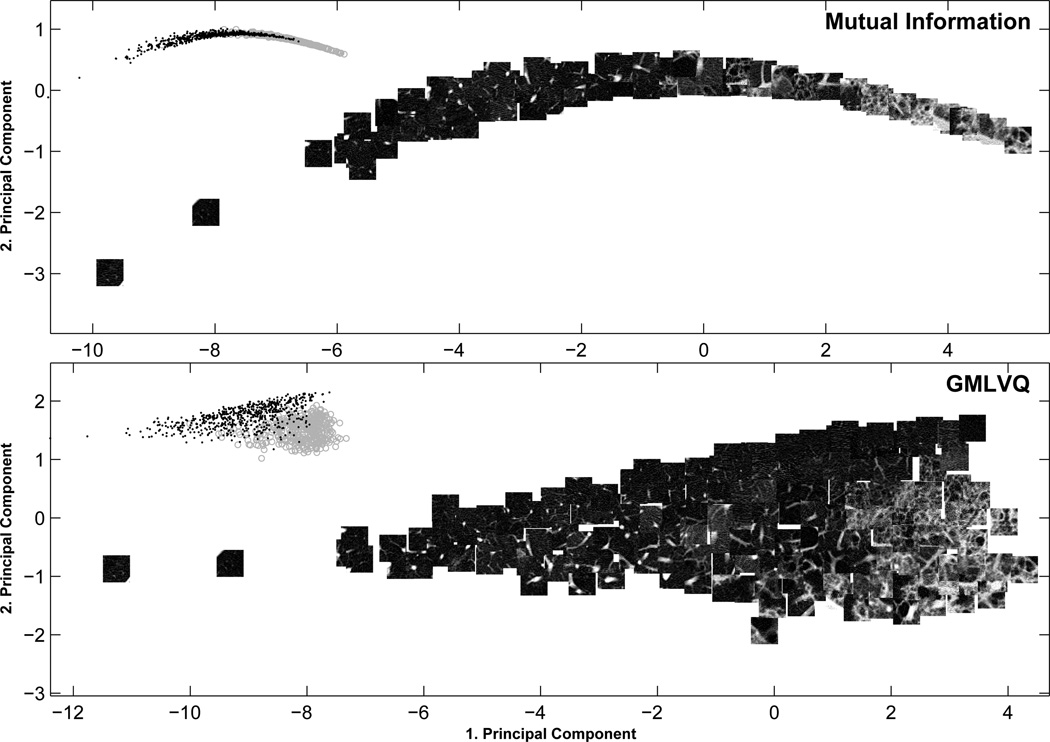
For the classification task, it is interesting to investigate distribution of the feature vectors in the high-dimensional feature space. In Fig. (4), the feature space of the sets including the best 5 features as defined by the two ranking methods are represented by a two-dimensional embedding, where each data point is replaced with the corresponding ROI. The embedding was obtained with a principal component analysis (PCA) leading to the first and second principal components, that include the highest variation found in the data set through a coordinate transformation with the covariance matrix. Using this linear PCA projection, features in the MI ranking seem to be more correlated compared to the GMLVQ ranking (Fig. 4). In addition, the two images classes, healthy and diseased, can be better distinguished in the latter ranking approach.
Figure 4.
Two dimensional projections of feature spaces with a subset of corresponding lung patterns: the first and second principal component are shown for the feature space of the best 5 features for the mutual information (upper panel) and the GMLVQ (lower panel) ranking. The subimages show the complete distributions of the healthy (gray circles) and diseased lung patterns (black dots). These representations reveal the shape of the feature space, especially that the features in the set selected by GMLVQ are less correlated. Note that not all lung pattern images are shown to avoid overlapping.
5.2. Classification performance
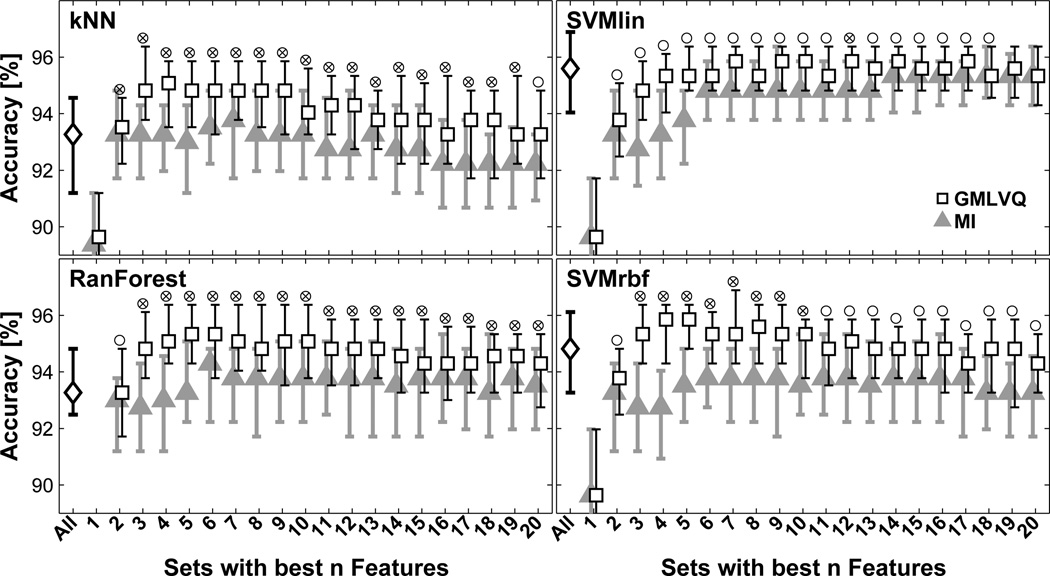
In Fig. (5), the test accuracies obtained by the four classifiers are shown for different feature sets including all features and the best n features selected by GMLVQ and MI rankings. For all classifiers, feature sets selected by the relevance ranking assessed by GMLVQ had a significantly better classification performance for the best {2,…,18} texture features compared to the MI approach (p < 0.05). The other subsets defined by the GMLVQ and MI ranking had a similar performance. For kNN, RanForest, and SVMrbf, some of these feature subsets had a significantly better classification performance when compared to the set consisting of all features, e.g. the best {3,…,10} texture features (p < 0.05). Fore these three classifiers, the best performance was found with sets between 4 to 6 features defined by the GMLVQ ranking; the performance decreased with increasing numbers of features. For SVMlin classifier, the best level of performance was reached with 6 features and remained similar with increasing number of features.
Figure 5.
Classification performance for different features sets and two classifiers. Median test accuracies (error bars indicate the 20th and 80th percentiles) are shown for a set consisting of all features (diamond), and sets with the best n features (n = {1,…,20}) according to the n highest relevances obtained from GMLVQ (squares) and n highest estimations of mutual information MI (triangles). Circles mark significant differences between the two ranking methods; crosses mark a significant better performance of GMLVQ ranking compared to the set including all features (p<0.05).
6. Discussion
In this novel application of the GMLVQ algorithm, the relevance of texture features was estimated in their ability to classify healthy and diseased lung patterns in chest HRCT images. This supervised learning scheme incorporates a stochastic gradient descent on an appropriate error surface and provides a feature selection approach to determine the relevance of several input dimensions for a specific classification task. To this end, GMLVQ weights the texture features corresponding to their ability in discriminating between the two lung tissue classes. In our experiment with real-world data, the feature sets selected by the GMLVQ approach had a similar or a significantly better classification performance compared with feature sets selected by a mutual information ranking. Some of the feature subsets selected by the GMLVQ ranking even improved the overall classification performance of three classifiers.
The common challenge in the field of feature selection is to find sets of features with a low pairwise correlation to avoid redundancy but with a high relevance of the complete set for the classification task. This means that even weak features can be included, if they provided complimentary information to strong features. In general, ranking single features based on their individual performance and then create feature sets according to this ranking may not accommodate these requirements and thus, may not identify the members nor the size of the optimal feature subset. The above ranking-based feature selection method considers only the individual performance of the features and does not consider pairwise correlations between features. However, for this application of interest, the GMLVQ relevance yields a satisfactory performance. While this approach estimates the relevance of single features, future considerations of GMLVQ should include the pairwise correlation (Fig. 3) for the feature ranking, e.g. to reduce the redundancy of two equally relevant features [21, 22].
In order to improve computed-aided diagnosis systems, the presented approach can be used to compare the performance of texture features and to optimize their free parameters in order to find the near optimal settings for subsequent supervised learning tasks. From the broad variety of approaches for texture classification [1], the best set of individual texture features can be identified that is best suited to distinguish between data classes. Most of these texture feature methods have free parameters and it is unclear, which set of parameters leads to the best discrimination between texture classes. For one of these methods, the parameter setting with the best classification performance can be found. For instance, in the presented experiment, the GLCM features with a pixel spacing sp = 5 did not contribute to a significantly better classification performance (Fig. 2). More complex texture feature approaches may benefit from this reduction to the possible parameter space.
In terms of the detection of ILD patterns, a limiting factor of this study was that only one typical pathological lung pattern, i.e. honeycombing, was classified. This represents one of many interstitial lung disease patterns that are common in clinical chest HRCT [1] and should be investigated in future studies. For this endeavor, the GMLVQ approach can be extended for such a multi-class problem to provide feature rankings of individual features for each class. This leads to class specific feature selection and may reveal further insights into the texture quantification and the structure of the feature space.
7. Conclusions
Using the GMLVQ algorithm, the relevance of texture features was estimated in their ability to classify healthy and diseased lung patterns in chest CT images. In our experiment with real-world data, the feature sets selected by the GMLVQ approach had a significantly better classification performance compared with feature sets selected by a mutual information ranking. While this approach estimates the relevance of single features, future considerations of GMLVQ should include the pairwise correlation (Fig. 3) for the feature ranking, e.g. to reduce the redundancy of two equally relevant features [21, 22].
Acknowledgments
This research was funded in part by the Clinical and Translational Science Award 5-28527 within the Upstate New York Translational Research Network (UNYTRN) of the Clinical and Translational Science Institute (CTSI), University of Rochester, and by the Center for Emerging and Innovative Sciences (CEIS), a NYSTAR-designated Center for Advanced Technology. We thank Prof. M.F. Reiser, FACR, FRCR, from the Department of Radiology, University of Munich, Germany, for his support.
References
- 1.Sluimer I, Schilham A, Prokop M, van Ginneken B. Computer analysis of computed tomography scans of the lung: a survey. Medical Imaging, IEEE Transactions on. 2006;25(4):385–405. doi: 10.1109/TMI.2005.862753. [DOI] [PubMed] [Google Scholar]
- 2.Xu Y, van Beek EJ, Hwanjo Y, Guo J, McLennan G, Hoffman EA. Computer-aided Classification of Interstitial Lung Diseases Via MDCT: 3D Adaptive Multiple Feature Method (3D AMFM) Academic Radiology. 2006;13(8):969–978. doi: 10.1016/j.acra.2006.04.017. ISSN 1076-6332. [DOI] [PubMed] [Google Scholar]
- 3.Boehm HF, Fink C, Attenberger U, Becker C, Behr J, Reiser M. Automated classification of normal and pathologic pulmonary tissue by topological texture features extracted from multi-detector CT in 3D. Eur Radiol. 2008;18(12):2745–2755. doi: 10.1007/s00330-008-1082-y. [DOI] [PubMed] [Google Scholar]
- 4.Duda RO, Hart PE, Stork DG. Pattern Classification. New York: Wiley- Interscience Publication; 2000. [Google Scholar]
- 5.Bunte K, Schneider P, Hammer B, Schleif F-M, Villmann T, Biehl M. Tech. Rep. MLR-03-2008. Leipzig University; 2008. [Assessed: February 1st, 2012]. Discriminative Visualization by Limited Rank Matrix Learning. URL http://www.uni-leipzig.de/_compint/mlr/mlr 03 2008.pdf. [Google Scholar]
- 6.Huber MB, Nagarajan MB, Leinsinger G, Eibel R, Ray LA, Wismuller A. Performance of topological texture features to classify fibrotic interstitial lung disease patterns. Medical Physics. 2011;38(4):2035–2044. doi: 10.1118/1.3566070. [DOI] [PubMed] [Google Scholar]
- 7.Kohonen T. Self-Organizing Maps. 3rd edn. New York: Springer, Berlin, Heidelberg; 2001.. [Google Scholar]
- 8.Sato AS, Yamada K. Generalized learning vector quantization. In: Touretzky DS, Mozer MC, Hasselmo ME, editors. Advances in Neural Information Processing Systems. Vol. 8. MIT Press; Cambridge, MA, USA: 1996. pp. 423–429. [Google Scholar]
- 9.Hammer B, Villmann T. Generalized relevance learning vector quantization. Neural Networks. 2002;15(8–9):1059–1068. doi: 10.1016/s0893-6080(02)00079-5. [DOI] [PubMed] [Google Scholar]
- 10.Pregenzer M, Pfurtscheller G, Flotzinger D. Automated feature selection with a distinction sensitive learning vector quantizer. Neurocomputing. 1996;11(1):19–29. ISSN 0925-2312. [Google Scholar]
- 11.Weinberger KQ, Saul LK. Distance Metric Learning for Large Margin Nearest Neighbor Classification. J. Mach. Learn. Res. 2009;10:207–244. ISSN 1532-4435. [Google Scholar]
- 12.Bunte K, Biehl M, Petkov N, Jonkman MF. Adaptive Metrics for Content Based Image Retrieval in Dermatology. In: Verleysen M, editor. Proc. of European Symposium on Artificial Neural Networks (ESANN) Bruges, Belgium: 2009. [Google Scholar]
- 13.Bunte K, Hammer B, Wismuüller A, Biehl M. Adaptive local dissimilarity measures for discriminative dimension reduction of labeled data. Neurocomputing. 2010;73(7–9):1074–1092. ISSN 0925-2312. [Google Scholar]
- 14.Uppaluri R, Hoffman EA, Sonka M, Hartley PG, Hunninghake GW, McLennen G. Computer Recognition of Regional Lung Disease Patterns. Am. J. Respir. Crit. Care Med. 1999;160(2):648–654. doi: 10.1164/ajrccm.160.2.9804094. [DOI] [PubMed] [Google Scholar]
- 15.Sluimer IC, Prokop M, Hartmann I, van Ginneken B. Automated classification of hyperlucency, fibrosis, ground glass, solid, and focal lesions in high-resolution CT of the lung. Medical Physics. 2006;33(7):2610–2620. doi: 10.1118/1.2207131. [DOI] [PubMed] [Google Scholar]
- 16.Korfiatis P, Kalogeropoulou C, Karahaliou A, Kazantzi A, Skiadopoulos S, Costaridou L. Texture classification-based segmentation of lung affected by interstitial pneumonia in high-resolution CT. Medical Physics. 2008;35(12):5290–5302. doi: 10.1118/1.3003066. [DOI] [PubMed] [Google Scholar]
- 17.Uchiyama Y, Katsuragawa S, Abe H, Shiraishi J, Li F, Li Q, et al. Quantitative computerized analysis of diffuse lung disease in high-resolution computed tomography. Medical Physics. 2003;30(9):2440–2454. doi: 10.1118/1.1597431. [DOI] [PubMed] [Google Scholar]
- 18.Depeursinge A, Iavindrasana J, Hidki A, Cohen G, Geissbuhler A, Platon A, et al. Comparative Performance Analysis of State-of-the-Art Classification Algorithms Applied to Lung Tissue Categorization. Journal of Digital Imaging. 2010;23:18–30. doi: 10.1007/s10278-008-9158-4. ISSN 0897-1889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Haralick RM, Shanmugam K, Dinstein I. Textural features for image classification. IEEE Trans. Syst., Man. Cybern. 1973;3(6):610–621. [Google Scholar]
- 20.Anys H, He D-C. Evaluation of textural and multipolarization radar features for crop classification. IEEE Transactions on Geoscience and Remote Sensing. 1995;33(5):1170–1181. [Google Scholar]
- 21.Tourassi GD, Frederick ED, Markey MK, Carey J, Floyd E. Application of the mutual information criterion for feature selection in computer-aided diagnosis. Medical Physics. 2001;28(12):2394–2402. doi: 10.1118/1.1418724. [DOI] [PubMed] [Google Scholar]
- 22.Peng H, Long F, Ding C. Feature Selection Based on Mutual Information: Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005;27(8):1226–1238. doi: 10.1109/TPAMI.2005.159. ISSN 0162-8828. [DOI] [PubMed] [Google Scholar]
- 23.Hammer B, Strickert M, Villmann T. On the Generalization Ability of GRLVQ Networks. Neural Processing Letters. 2005;21(2):109–120. [Google Scholar]
- 24.Schneider P, Biehl M, Hammer B. Relevance Matrices in LVQ. In: Verleysen M, editor. Proc. of European Symposium on Artificial Neural Networks (ESANN) Bruges, Belgium: 2007. pp. 37–42. [Google Scholar]
- 25.Schneider P, Biehl M, Hammer B. Adaptive Relevance Matrices in Learning Vector Quantization. Neural Computation. 2009;21(12):3532–3561. doi: 10.1162/neco.2009.11-08-908. [DOI] [PubMed] [Google Scholar]
- 26.Schneider P, Bunte K, Hammer B, Biehl M. Regularization in Matrix Relevance Learning. IEEE Transactions on Neural Networks. 2010;21(5):831–840. doi: 10.1109/TNN.2010.2042729. [DOI] [PubMed] [Google Scholar]
- 27.Breiman L. Random Forests. Machine Learning. 2001;45:5–32. ISSN 0885-6125. [Google Scholar]
- 28.Jaiantilal A. [Assessed: February 1st, 2012];Random Forest (Regression, Classification and Clustering) implementation for MATLAB (and Standalone) 2010 software available at http://code.google.com/p/randomforest-matlab/