Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Jul 14.
Published in final edited form as: Int J Exp Comput Biomech. 2013 Sep;2(2):105–117. doi: 10.1504/IJECB.2013.056516

Influence of surrounding tissues on biomechanics of aortic wall

Jungsil Kim 1, Brooke Peruski 2, Chris Hunley 3, Sebastian Kwon 4, Seungik Baek 5,*
PMCID: PMC4096287  NIHMSID: NIHMS493087  PMID: 25031610

Abstract

The present study investigates effects of surrounding tissues and non-uniform wall thickness on the biomechanics of the thoracic aorta. We construct two idealised computational models exemplifying the importance of surrounding tissues and non-uniform wall thickness, namely the uniform-thickness model and the histology image-based model. While the former neglects a connective tissue layer surrounding the aorta, the latter takes it into account with non-uniform wall thickness. Using plane strain finite element analysis, stress distributions in the aortic media between the two models are compared. The histology image-based model substantially enhances the uniformity of stress throughout the aortic media. Furthermore, the altered mechanical properties of surrounding tissues change the stress distribution. These results suggest that surrounding tissues and non-uniform wall thickness should be included in biomechanical analysis to better understand regional adaptation of the aortic wall during normal physiological conditions or pathological conditions such as aortic aneurysms and dissections.

Keywords: perivascular tissue, adipose tissue, vascular mechanical homeostasis, aortic dissection.

1 Introduction

The arterial wall adapts sensitively to changes of its mechanical environment. If the mechanical environment is perturbed from the normal mechanical state, cells actively react upon that by changing their activities in production, removal, and organisation of extracellular matrix in order to maintain the preferred state (Humphrey, 2008). It appears that this mechanical homeostasis governs cellular behaviours ranging from normal vascular development (Wagenseil, 2011; Wells and Walter, 2010) to adaptations to sustained changes in flow (Hoi et al., 2008), pressure (Hu et al., 2007; Gleason and Humphrey, 2004) and axial extension (Cardamone et al., 2009; Humphrey et al., 2009); disease processes (Humphrey et al., 2007; Zeinali-Davarani et al., 2011); and vascular responses to clinical treatments (Kwon et al., 2011).

Based on vascular mechanics, various theoretical frameworks and computational simulations have been developed to enhance our understanding of vascular physiopathology and to improve clinical interventions (Humphrey and Rajagopal, 2002; Baek et al., 2007; Watton and Hill, 2009; Sheidaei et al., 2011). However, most previous studies in vascular mechanics have been performed under assumption of uniform thickness of a blood vessel wall without consideration of its surrounding tissues. In the late 1950s, the influence of longitudinal vascular tethering in the dynamic behaviour of vessel segments was studied (Womersley, 1957). Patel and Fry (1966) showed a strong influence of tethering in pressure gradient along the artery and its associated flow through animal experiments. Analytically, a high degree of vascular tethering yields low displacements but high stresses within the vessel wall (Hodis and Zamir, 2009). While these studies focused only on longitudinal constraint imposed by surrounding tissues, Liu et al. (2007) quantified the radial constraint of the surrounding tissue for carotid and femoral arteries. Consequently, removing the surrounding tissue results in the significant increase of the circumferential wall strain and stress, compared to the intact state. Liu et al. (2008) also demonstrated that transmural stress of the coronary artery can be significantly influenced by myocardial support around the vessel, but they used a uniform wall thickness of the vessel in their model.

The thoracic aorta is prone to develop vascular diseases such as aortic aneurysms and dissections. Histologically, the anterior side of the thoracic aorta is surrounded by a thin collagenous tissue layer, while the posterior side is surrounded by collagenous connective tissue as well but mainly by loose adipose tissues. In the present study, we investigate the influence of the surrounding tissues of the aortic wall and non-uniform thickness on mechanical stress. This study uses geometrical measurements of four fresh pig aortas and a histology sample to construct analysis models, and performs parametric study using the material properties obtained from the inflation test data. The results of this study confirm that the aorta model with surrounding tissue results in a comparatively uniform stress level within the aortic media under the in vivo pressure range. In addition, this study shows that stress in the vascular wall can be altered directly by changes in stiffness of the surrounding tissues.

2 Methods

2.1 Histology examination

Four fresh thoracic aortas from six-month-old pigs are used. Aortic rings are isolated from the distal thoracic aorta, keeping the external surrounding tissue intact. They are fixed in 10% formalin solution for three days at room temperature. For dehydration, the tissue is submerged in 70% alcohol for 24 hours, then is solidified in paraffin for the next 24 hours. The solidified tissue is sectioned at 5 μm thickness using a microtome. The sectioned tissue is placed on a glass slide and stained with picrosirius red to detect collagen distribution in the surrounding tissues of the aorta.

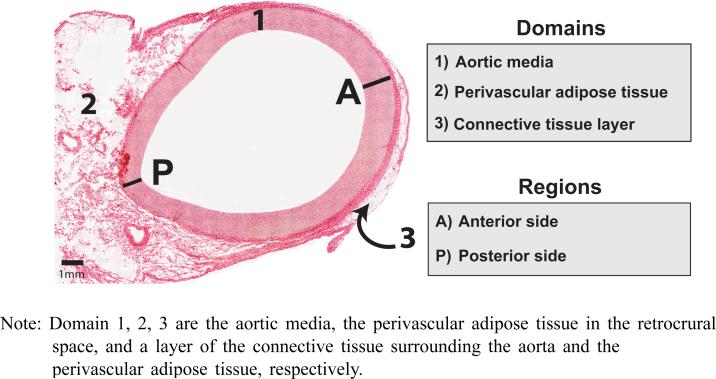
To obtain an entire microscopic view of histology of the aortic cross-section, small areal images of the histology sample under a microscope are captured and multiple consecutive images are combined by overlapping fields of views, which is known as image stitching, using NIS-Elements BR 3.0 (Nikon Instruments Inc., Melville, NY). In a complete view of the histology for the entire cross-section of the aorta (Figure 1), the aortic wall is shown surrounded by connective tissues. The thicknesses of the aortic media and a connective tissue layer are measured along the circumference.

Figure 1.

Figure 1

Open in a new tab

Histology sample of the porcine thoracic aorta (see online version for colours)

Note: Domain 1, 2, 3 are the aortic media, the perivascular adipose tissue in the retrocrural space, and a layer of the connective tissue surrounding the aorta and the perivascular adipose tissue, respectively.

2.2 Measurement and approximation of the fresh aortic media thickness

After removing the loose tethering tissue from the adventitial layer of the fresh aorta, the thicknesses of the aortic wall are measured at eight uniformly spaced points along the circumference. The largest part of the cross-sectional aortic wall is constituted by the media layer, and the wall thickness is assumed to be the same as the media thickness. The measurements are repeated three times and averaged at each point on the circumference.

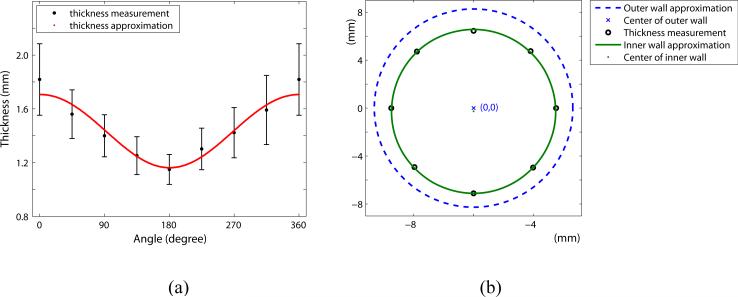
The outer radius measured from four thoracic aortas using a 3D stereo-vision system in our lab (Kim and Baek, 2011) is averaged and used for constructing the geometry of the models. The inner radius is determined by subtracting the aortic wall thickness from the outer radius. We assume that cross-sectional geometries of the inner and outer walls are perfect circles with eccentricity due to the variation of the wall thickness around the circumference. The mean measurement of wall thickness at each point and the geometry of the aortic wall are shown in Figure 2.

Figure 2.

Figure 2

Open in a new tab

(a) Comparison of the aortic wall thickness approximation and measurements along the circumference. 0° , 360° : the anterior side, and 180° : the posterior side (b) Approximation of the cross-sectional geometry of the aorta (see online version for colours)

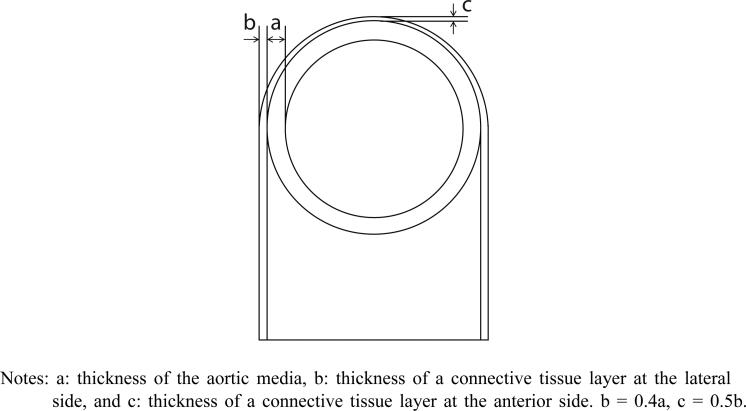
The approximate thickness ratios of the connective tissue layer to the aortic media at anterior and lateral sides are determined by geometrical analogousness of fresh aortic rings and a histology sample. The ratios are used to design the histology image-based model as shown in Figure 3. Finally, idealised two-dimensional finite element models with and without a connective tissue layer are constructed.

Figure 3.

Figure 3

Open in a new tab

Schematic of cross-sectional model of the thoracic aorta

Notes: a: thickness of the aortic media, b: thickness of a connective tissue layer at the lateral side, and c: thickness of a connective tissue layer at the anterior side. b = 0.4a, c = 0.5b.

2.3 Finite element model and analysis

To investigate the effect of surrounding tissue and non-uniform thickness of the aorta on stress distribution within the aortic wall, two finite element models are constructed: a uniform thickness model without a connective tissue layer and a histology image-based model. We assume that both models are bilaterally symmetric. In the uniform thickness model, the thickness of the aortic media is determined by the averaged thickness measurements all around the circumference. On the other hand, the histology image-based model has non-uniform wall thickness with a connective tissue layer. Consequently, three computational domains are considered in the histology image-based model for finite element analysis as defined in Figure 1:

  1. the aortic media

  2. the perivascular connective tissue comprised mainly of adipose tissue in retrocrural space (for convenience, we use ‘perivascular adipose tissue’ in this paper)

  3. a layer of connective tissue surrounding the aorta and the perivascular adipose tissue.

The uniform thickness model consists only of domains 1 and 2.

For two-dimensional analysis, the linear triangular elements (plane strain) are used to generate finite element mesh. The interfaces between each of the two domains are assumed to be coherent, i.e., moving together. The bottom surfaces of the perivascular adipose tissue and connective tissue are assumed to be rigidly attached to the spine and in turn there is no displacement.

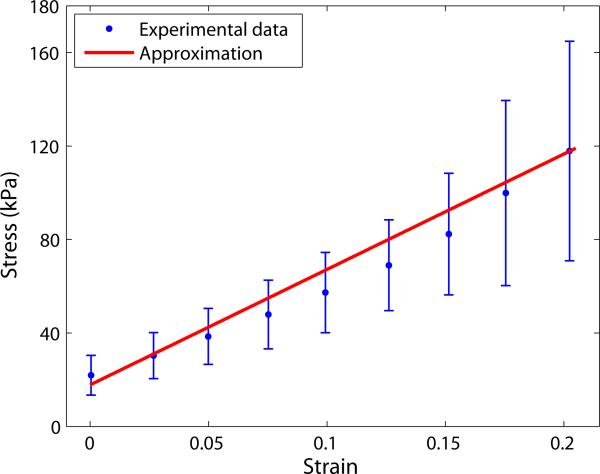
The mechanical properties of the aortic media are prescribed with Young's modulus of 494 kPa and Poisson's ratio of 0.36, which are determined by linear stress-strain relationship in the low-to-medium stress region from the inflation test data. Although it is well known that the mechanical behaviour of blood vessels is non-linear, this study uses a nearly linear mechanical behaviour of the aorta under the pressure of up to 75 mm Hg for the feasibility study on the role of surrounding tissues of the aorta. The Young's moduli of all domains used for the parametric study are listed in Table 1. All domains are assumed to have the same Poisson's ratio and are considered to be linearly elastic and isotropic. Modelling, mesh generation, and analysis are completed by using COMSOL Multiphysics 4.3 (COMSOL, Inc., Burlington, MA).

Table 1.

Young’s moduli used in domains of the uniform thickness model and the histology image-based model for the parametric study

Case Domain 1 Domain 2 Domain 3
1 E 0.25E -
2 E 0.5E -
3 E 0.25E E
4 E 0.5E E
5 E 0.25E 2E
6 E 0 5E 2E
Open in a new tab

Note: E = 494 kPa

3 Results

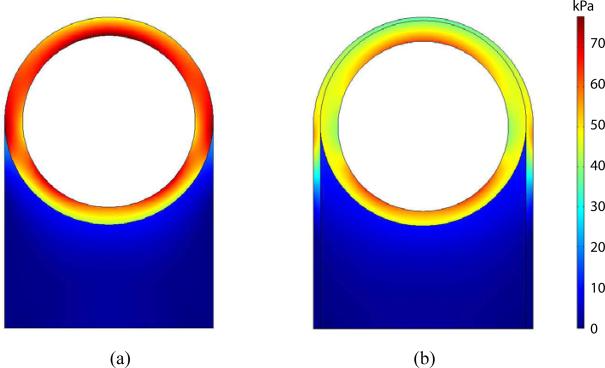
Comparison of the first principal stress distributions between the uniform thickness and histology image-based models is shown in Figure 5, when they are subjected to an internal pressure of 100 mm Hg. The overall stress level within the aortic media is higher in the uniform thickness model than the histology image-based model. In particular, the stress in the anterior region is markedly higher in the uniform thickness model, while the stress difference between the two models in the posterior region is relatively small. Within the aortic media, the stress of the uniform thickness model changes noticeably from the anterior region toward the posterior region. In contrast, the histology image-based model is experienced relatively uniform radial distribution of stress within the aortic wall except the lateral regions at the edge of the perivascular adipose tissue connection. This trend is consistent in the normal physiological pressure ranging from 80–120 mm Hg.

Figure 5.

Figure 5

Open in a new tab

The first principal stress distributions within the uniform thickness model of case 1 (a) and the histology image-based model of case 3 (b) when subjected to an internal pressure of 100 mm Hg (see online version for colours)

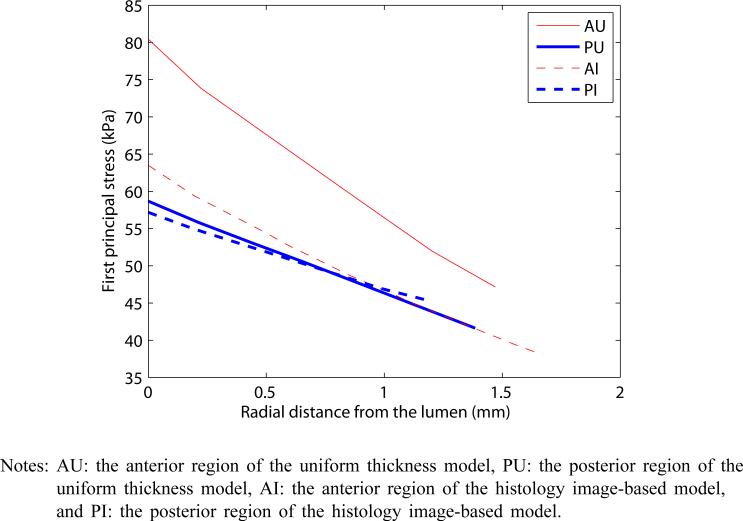
To further highlight the difference between the two models in each of anterior and posterior regions of the aortic media, Figure 6 plots the first principal stress with respect to the radial location within the aortic wall from the lumen. While the stress in the anterior region of the uniform thickness model is remarkably higher than that in the posterior region, note that the principal stresses of histology image-based model are similar between the anterior and posterior regions, creating a sense of uniform stress throughout the aortic wall. For the anterior region, there is a 21.1% drop in stress between the two models at the closest location to the luminal surface and a 19.3% drop at the farthest location at the pressure of 100 mm Hg. These computational results show that the homogeneity of stress within the aortic media greatly improved by using the non-uniform thickness and a connective tissue layer of the aorta.

Figure 6.

Figure 6

Open in a new tab

Comparative plot of the first principal stresses within regions A and P for both models when subjected to an internal pressure of 100 mm Hg (see online version for colours)

Notes: AU: the anterior region of the uniform thickness model, PU: the posterior region of the uniform thickness model, AI: the anterior region of the histology image-based model, and PI: the posterior region of the histology image-based model.

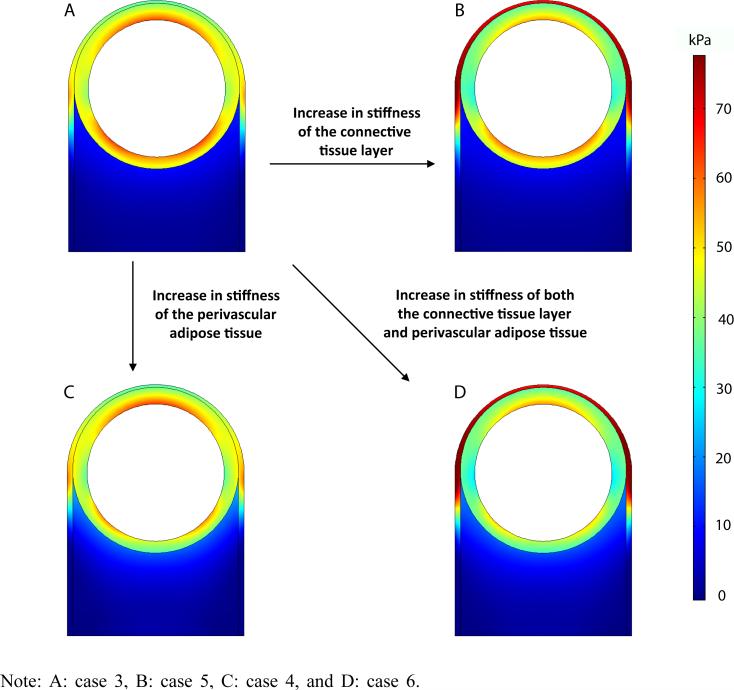
The principal stress in the aortic media changes in unique ways when the properties of the connective tissue layer and perivascular adipose tissue are altered. Referring to Figure 7, when the stiffness of the connective tissue layer is increased, the stress of the aortic media decreases especially in the anterior region (case 5). When the stiffness of the perivascular adipose tissue is increased, the stress of the aortic media decreases in the posterior region (case 4). Therefore, when the stiffness in both connective tissue layer and perivascular adipose tissue are increased, the overall stress in the aortic tissue decreases to form a uniform distribution with overall lower stress (case 6).

Figure 7.

Figure 7

Open in a new tab

The first principal stress distributions with different mechanical of the surrounding tissues when subjected to an internal pressure of 100 mm Hg (see online version for colours)

4 Discussions

Mechanical homeostasis is a key assumption for recent theoretical and computational studies related to the growth and remodelling of blood vessels under various physiopathological conditions. While most previous studies of blood vessels have assumed uniform thickness and have not included surrounding tissue in their models, our study employed an idealised model with surrounding tissue and non-uniform aortic wall thickness based on histology examination of the thoracic aorta. Using finite element analysis, we compared the stress distributions of the histology image-based model with surrounding tissue and the uniform thickness model without a connective tissue layer. When we considered the connective tissue layer of the aorta, there was approximately 19–21% of stress drop in the anterior region and resulted in more uniform stress distribution throughout the vessel wall. Furthermore, we presented the effect of altered mechanical properties of surrounding tissues on the mechanical states of the aortic media. Our finding suggests that non-uniform thickness of the aortic media and surrounding tissues may contribute to the aortic wall maintaining relatively uniform stress distribution.

This result is consistent with a major finding of vascular mechanics during the past four decades, namely that the increases in the complexity of modelling and analysis (e.g., non-linear mechanical behaviour of vessel wall, residual stress, and vasoactive tone) have found more uniform stress within the vessel wall (Humphrey, 2002). The surrounding tissue yields the radial constraint on the aorta and may help to redistribute the external loading circumstantially in accordance with non-uniform thickness of the aortic media. Therefore, our finding with the histology image-based model emphasises the role of the perivascular surrounding tissue in mechanical homeostasis of the aorta.

In recent years, there is a growing interest on the role of perivascular adipose tissue in vascular physiopathology. The perivascular adipose tissue modulates the activities of vascular smooth cells such as contraction, proliferation and migration (Szasz and Webb, 2012); and the contractile response of the aortic ring (Löhn et al., 2002). The amount of adipose tissue is associated with abnormal health conditions, such as hypertension (Gálvez-Prieto et al., 2008) and obesity. Constitutive relationships for the aortic tissue have been heavily studied, but surprisingly little research has been devoted to the mechanical properties of perivascular adipose tissues. Our parametric study, however, implies that changes in mechanical properties of perivascular adipose tissues or the connective tissue layer will affect the mechanical state of aortic wall and induce vascular adaptation in the aorta.

Figures 6 and 7 show that such geometric modifications alone in the model do not yield completely homogenised stress fields, as particularly shown by the stress gradient from luminal surface, although the stress in the aortic media becomes redistributed with surrounding tissue. Further considerations, such as the use of a non-linear constitutive model and inclusion of residual stress, will improve the stress analysis and could result in a fully homogenised stress level within the aortic media. Table 2 summarises the possible model improvements to the current histology image-based model.

Table 2.

Summary of possible model improvements

Anisotropic heterogenous material properties
Periodic internal pressure boundary condition
Inclusion of residual strain in the aortic media
Accurate constitutive relationships for all material domains
Loading contributions from other organs (depending on location)
Open in a new tab

For finite element analysis, we used experimental data for the distal portion of the porcine thoracic aorta. This longitudinal portion of the aorta is placed in the retrocrural space and thus the influence of surrounding organs may be relatively small. The opening angle of this longitudinal portion, which represents the residual stress, is relatively small along the aorta (Han and Fung, 1991). Furthermore, the thoracic aorta exhibits the linear mechanical behaviour up to the physiological level of pressure (Kim and Baek, 2011), although the behaviour of most small arteries is highly non-linear (Danpinid et al., 2010; Shadwick, 1999). Therefore, this portion of the aorta would be appropriate for studying the influence of the surrounding tissue with linear finite element analysis. Nevertheless, further studies are needed for the quantitative study of the effect on surrounding tissues of the aorta with non-linear anisotropic mechanical properties.

This two-dimensional model may also be extended to other locations along the aorta. In such cases, however, one should apply the external boundary conditions to account for the force contribution from organs surrounding the aorta such as lungs in the thoracic region. For example, the area occupied by the retrocrural space would be subjected to changes as the location of interest moves distally from the heart; since the outer boundary of the retrocrural space is delimited by the diaphragmatic crura in humans, the ‘attachment’ of the abdominal aorta to the spine may become negligible (Restrepo et al., 2008).

In closing, although many improvements to the current model are needed to fully capture the biomechanics of the aorta under the physiological accuracy, the model presented in this feasibility study nonetheless demonstrates an important role of the surrounding tissues according to realistic vascular thickness and external tissue in order to better estimate the arterial wall stress in vascular mechanics.

Figure 4.

Figure 4

Open in a new tab

Approximation of the elastic modulus (see online version for colours)

Acknowledgements

This work was supported, in part, by a grant from the NIH (HL115185).

Biography

Biographical notes: Jungsil Kim is a postdoctoral fellow in the Cardiovascular Tissue Mechanics Laboratory at Michigan State University. She is especially interested in the heterogeneous mechanical behaviour of the aorta.

Brooke Peruski is an undergraduate student in the Department of Mechanical Engineering at Michigan State University. Her areas of interest include biomedical design and product development.

Chris Hunley is a former student of the Cardiovacular and Tissue Mechanics Laboratory at Michigan State University. He is currently employed at Heartflow, Inc. in Redwood City, California.

Sebastian Kwon is obtaining his BS in Biomedical Engineering from Johns Hopkins University. He is planning on attending medical school.

Seungik Baek is currently an Associate Professor in the Department of Mechanical Engineering at Michigan State University. His research interests include cardiovascular mechanics and tissue engineering.

Footnotes

Reference to this paper should be made as follows: Kim, J., Peruski, B., Hunley, C., Kwon, S. and Baek, S. (xxxx) ‘Influence of surrounding tissues on biomechanics of aortic wall’, Int. J. Experimental and Computational Biomechanics, Vol. x, No. x, pp.xxx–xxx.

Contributor Information

Jungsil Kim, Department of Mechanical Engineering, Michigan State University, East Lansing, MI 48824-1224, USA kimjun40@egr.msu.edu.

Brooke Peruski, Department of Mechanical Engineering, Michigan State University, East Lansing, MI 48824-1224, USA peruski8@msu.edu.

Chris Hunley, Department of Mechanical Engineering, Michigan State University, East Lansing, MI 48824-1224, USA chris.hunley@gmail.com.

Sebastian Kwon, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD 21218-2608, USA stkwon91@gmail.com.

Seungik Baek, Department of Mechanical Engineering, Michigan State University, 2457 Engineering Building, East Lansing, MI 48824-1226, USA.

References

  1. Baek S, Valentin A, Humphrey JD. Biochemomechanics of cerebral vasospasm and its resolution: II. Constitutive relations and model simulations. Annals of Biomedical Engineering. 2007;35(9):1498–1509. doi: 10.1007/s10439-007-9322-x. [DOI] [PubMed] [Google Scholar]
  2. Cardamone L, Valentin A, Eberth J, Humphrey J. Origin of axial prestretch and residual stress in arteries. Biomechanics and Modeling in Mechanobiology. 2009;8(6):431–446. doi: 10.1007/s10237-008-0146-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Danpinid A, Luo J, Vappou J, Terdtoon P, Konofagou EE. In vivo characterization of the aortic wall stress-strain relationship. Ultrasonics. 2010;50(7):654–665. doi: 10.1016/j.ultras.2010.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Gálvez-Prieto B, Dubrovska G, Cano M, Delgado M, Aranguez I, González M, Ruiz-Gayo M, Gollasch M, Fernández-Alfonso M. A reduction in the amount and anti-contractile effect of periadventitial mesenteric adipose tissue precedes hypertension development in spontaneously hypertensive rats. Hypertension Research. 2008;31(7):1415–1423. doi: 10.1291/hypres.31.1415. [DOI] [PubMed] [Google Scholar]
  5. Gleason RL, Humphrey JD. A mixture model of arterial growth and remodeling in hypertension: altered muscle tone and tissue turnover. Journal of Vascular Research. 2004;41(4):352–363. doi: 10.1159/000080699. [DOI] [PubMed] [Google Scholar]
  6. Han HC, Fung YC. Species dependence of the zero-stress state of aorta: pig versus rat. ASME Journal of Biomechanical Engineering. 1991;113(4):446–1349. doi: 10.1115/1.2895425. [DOI] [PubMed] [Google Scholar]
  7. Hodis S, Zamir M. Arterial wall tethering as a distant boundary condition. Physical Review-Section E-Statistical Nonlinear and Soft Matter Physics. 2009;80(5):51913. doi: 10.1103/PhysRevE.80.051913. [DOI] [PubMed] [Google Scholar]
  8. Hoi Y, Gao L, Tremmel M, Paluch RA, Siddigui AH, Meng H, Mocco J. In vivo assessment of rapid cerebrovascular morphological adaptation following acute blood flow increase. J. Neurosurg. 2008;109(6):1141–1147. doi: 10.3171/JNS.2008.109.12.1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hu JJ, Baek S, Humphrey JD. Stress-strain behavior of the passive basilar artery in normotension and hypertension. Journal of Biomechanics. 2007;40(11):2559–2563. doi: 10.1016/j.jbiomech.2006.11.007. [DOI] [PubMed] [Google Scholar]
  10. Humphrey JD. Cardiovascular Solid Mechanics: Cells, Tissues, and Organs. Springer-Verlag; New York: 2002. [Google Scholar]
  11. Humphrey JD. Vascular adaptation and mechanical homeostasis at tissue, cellular, and sub-cellular levels. Cell Biochemistry and Biophysics. 2008;50(2):53–78. doi: 10.1007/s12013-007-9002-3. [DOI] [PubMed] [Google Scholar]
  12. Humphrey JD, Rajagopal KR. A constrained mixture model for growth and remodeling of soft tissues. Mathematical Models and Methods in Applied Science. 2002;12(3):407–430. [Google Scholar]
  13. Humphrey JD, Baek S, Niklason LE. Biochemomechanics of cerebral vasospasm and its resolution: I. A new hypothesis and theoretical framework. Annals of Biomedical Engineering. 2007;35(9):1485–1497. doi: 10.1007/s10439-007-9321-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Humphrey JD, Eberth JF, Dye WW, Gleason RL. Fundamental role of axial stress in compensatory adaptations by arteries. Journal of Biomechanics. 2009;42(1):1–8. doi: 10.1016/j.jbiomech.2008.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kim J, Baek S. Circumferential variations of mechanical behavior of the porcine thoracic aorta during the inflation test. Journal of Biomechanics. 2011;44(10):1941–1947. doi: 10.1016/j.jbiomech.2011.04.022. [DOI] [PubMed] [Google Scholar]
  16. Kwon ST, Rectenwald JE, Baek S. Intrasac pressure changes and vascular remodeling after endovascular repair of abdominal aortic aneurysms: review and biomechanical model simulation. Journal of Biomechanical Engineering. 2011;133(1):011011. doi: 10.1115/1.4003134. [DOI] [PubMed] [Google Scholar]
  17. Löhn M, Dubrovska G, Lauterbach B, Luft F, Gollasch M, Sharma A. Periadventitial fat releases a vascular relaxing factor. The Journal of the Federation of Ameican Societies for Experimental Biology. 2002;16(9):1057–1063. doi: 10.1096/fj.02-0024com. [DOI] [PubMed] [Google Scholar]
  18. Liu Y, Dang C, Garcia M, Gregersen H, Kassab GS. Surrounding tissues affect the passive mechanics of the vessel wall: theory and experiment. American Journal of Physiology – Heart and Circulatory Physiology. 2007;293(6):H3290–H3300. doi: 10.1152/ajpheart.00666.2007. [DOI] [PubMed] [Google Scholar]
  19. Liu Y, Zhang W, Kassab GS. Effects of myocardial constraint on the passive mechanical behaviors of the coronary vessel wall. American Journal of Physiology – Heart and Circulatory Physiology. 2008;294(1):H514–H523. doi: 10.1152/ajpheart.00670.2007. [DOI] [PubMed] [Google Scholar]
  20. Patel DJ, Fry DL. Longitudinal thethering of arteries in dogs. Circulation Research. 1966;19:1011–1021. doi: 10.1161/01.res.19.6.1011. [DOI] [PubMed] [Google Scholar]
  21. Restrepo CS, Eraso A, Ocazionez D, Lemos J, Martinez S, Lemos DF. The diaphragmatic crura and retrocrural space: normal imaging appearance, variants, and pathologic conditions. RadioGraphics. 2008;28:1289–1305. doi: 10.1148/rg.285075187. [DOI] [PubMed] [Google Scholar]
  22. Shadwick RE. Mechanical design in arteries. Journal of Experimental Biology. 1999;202:3305–3313. doi: 10.1242/jeb.202.23.3305. [DOI] [PubMed] [Google Scholar]
  23. Sheidaei A, Hunley SC, Zeinali-Davarani S, Raguin LG, Baek S. Simulation of abdominal aortic aneurysm growth with updating hemodynamic loads using a realistic geometry. Medical Engineering and Physics. 2011;33(1):80–88. doi: 10.1016/j.medengphy.2010.09.012. [DOI] [PubMed] [Google Scholar]
  24. Szasz T, Webb R. Perivascular adipose tissue: more than just structural support. Clinical Science. 2012;122(1):1–12. doi: 10.1042/CS20110151. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Wagenseil J. A constrained mixture model for developing mouse aorta. Biomechanics and Modeling in Mechanobiology. 2011;10(5):671–687. doi: 10.1007/s10237-010-0265-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Watton PN, Hill NA. Evolving mechanical properties of a model of abdominal aortic aneurysm. Biomechanics and Modeling in Mechanobiology. 2009;8(1):25–42. doi: 10.1007/s10237-007-0115-9. [DOI] [PubMed] [Google Scholar]
  27. Wells SM, Walter EJ. Changes in the mechanical properties and residual strain of elastic tissue in the developing fetal aorta. Annals of Biomedical Engineering. 2010;38(2):345–356. doi: 10.1007/s10439-009-9825-8. [DOI] [PubMed] [Google Scholar]
  28. Womersley JR. Oscillatory flow in arteries: the constrained elastic tube as a model of arterial flow and pulse transmission. Phys. Med. Biol. 1957;2(2):178–187. doi: 10.1088/0031-9155/2/2/305. [DOI] [PubMed] [Google Scholar]
  29. Zeinali-Davarani S, Sheidaei A, Baek S. A finite element model of stress-mediated vascular adaptation: application to abdominal aortic aneurysms. Computer Methods in Biomechanics and Biomedical Engineering. 2011;14(9):803–817. doi: 10.1080/10255842.2010.495344. [DOI] [PubMed] [Google Scholar]

RESOURCES