Imaging human connectomes at the macroscale

Abstract

At macroscopic scales, the human connectome is composed of anatomically distinct brain areas, the structural pathways connecting them, and their functional interactions. Successful annotation of phenotypic associations with variation in the connectome and cataloguing of neurophenotypes promise to transform our understanding of the human brain. This review provides a survey of magnetic resonance imaging-based measurements of functional and structural connectivity. We highlight emerging areas of development and inquiry, and emphasize the importance of integrating structural and functional perspectives on brain architecture.

Introduction

First introduced in 2005¹, the term “connectome” embodies the advances of over a century of neuroscientific innovation and reflects an agenda for a new era. Initially defined as a complete map of neural connections within the brain, the connectome is a multiscale construct that can be examined at varying resolutions. At the extremes are the microscale, which focuses on the study of individual neurons and their synaptic connections, and the macroscale, which examines areas of cortical tissues (commonly ~1cm³or larger). Intermediate is the mesoscale, which, in humans, attends to vertical columns of 80–120 neurons (commonly referred to as micro- or mini-columns)^{1, 2}. Although intimately associated, each resolution provides unique perspectives on the connectome. At the macroscale, and particularly in studies of the human brain, conceptualizations of the connectome have grown to also include information about function³. In this review we will use the term connectome to refer to brain areas, their anatomical connections, and their functional interactions.

Currently, macroscale methodologies are best positioned for mapping and annotating human connectomes with cognitive and behavioral associations. The higher-order, albeit lower-resolution representations, captured at the macroscale most directly relate to regulatory, cognitive, and affective processes. Interpretation of macroscale findings is most amenable to guidance from lesion and brain imaging studies. Further, comprehensive mapping and annotation of the connectome is most achievable at the lower-resolution macroscale, due to reduced computational and analytical demands. Moreover, non-invasive tools for in vivo imaging the human connectome are only available at the macroscale; in vivo microscale studies are currently limited to model organisms and neurosurgical patients.

Among the modalities used for macroconnectomics, MRI is dominant, partly because of widespread availability, safety, and spatial resolution. Diffusion-weighted MRI (dMRI) and functional MRI (fMRI) are especially popular for inferring structural and functional connectivity, respectively⁴. Diffusion-weighted MRI provides cubic-millimeter-resolution portrayals of white matter tracts, and insights into organizing principles guiding their orientation and trajectories; fMRI reveals a universal functional architecture, with variations among individuals meaningfully related to phenotypic variables⁵(e.g., behavioral, psychiatric).

The present review focuses on the mapping, characterization and analysis of macroscale connectomes. We structure our presentation in terms of a mathematical perspective that treats the connectome as a graph of interactions among brain areas. Nodes in the graph are abstract representations of brain areas and edges represent pairwise relationships between nodes. We first review approaches and challenges to parcellating the brain into discrete subunits represented by nodes, and then review the imaging and analytic methodologies used to map and quantify patterns of structural and functional connectivity that are represented by edges in the connectome.

Defining Nodes

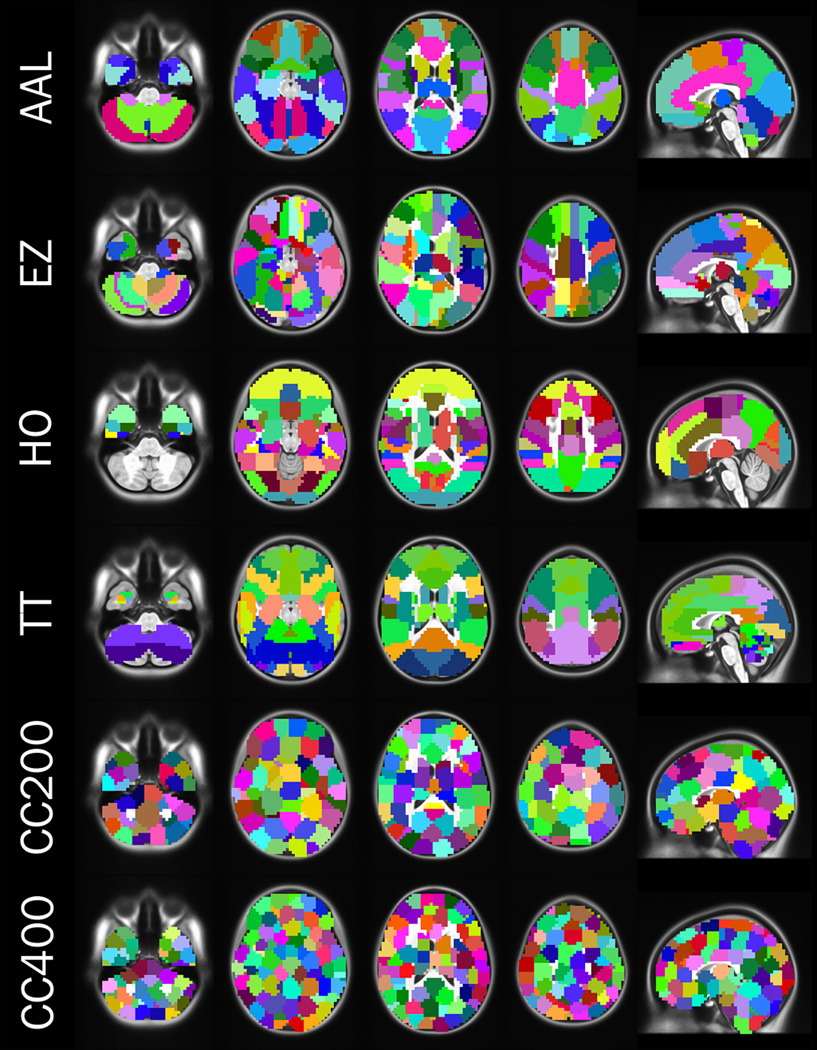
Defining the nodes of a macroscale connectome is a complex task as we lack agreement on how best to define the constituent brain units. Depending on the scope of the investigation, the specific brain subunits represented by nodes can range from the small patches of cortex contained in individual MRI voxels to larger brain areas (e.g., dorsolateral prefrontal cortex). Early parcellation efforts utilized post-mortem architectonic measurements (e.g. cell morphology) of single individuals. Although these resulting atlases are central to neuroscience, no functional or structural connectivity-based information was used in their construction, thus limiting their ability to accurately represent connectomes. For example, despite being represented as a single area in anatomical atlases⁶, the anterior cingulate region contains a number of subregions, each of which are characterized by dramatically different functional⁷and structural⁸connectivity patterns. As demonstrated in figure 1, while the large-scale pattern captured by different parcellation strategies may bear a gross similarity to one another, the specific details conveyed vary substantially (Fig. 1).

Figure 1. Different Parcellations.

We depict several different atlases of brain areas generated using anatomical (rows 1 – 4) and functional (rows 5 – 6) parcellation schemes. AAL (automated anatomical labeling)¹⁰⁹and Harvard Oxford (HO)¹¹⁰are derived from anatomical landmarks (sulci and gyral). The EZ (Eickhoff - Zilles)¹¹¹and TT (Talariach Daemon)¹¹²atlases are derived from post-mortem cyto- and myelo-architectonic segmentations. The CC200 and CC400 atlases are derived from 200 and 400 unit functional parcellations¹¹.

Ideally, information from brain function and structural connectivity should be exploited to delineate brain areas. Meta-analytic approaches can define nodes based on task-based fMRI (T-fMRI) studies⁹. Alternatively, data-driven clustering techniques can subdivide the brain into areas based on homogeneity of functional time series^{10, 11}, or functional or structural connectivity profiles^{8, 11, 12}. Blind source separation techniques can also define network nodes using spatial independence¹³. These methods commonly pool information across individuals, and most can enforce specific properties on resulting brain areas¹¹. One drawback is the need for pre-specification of the number of areas to be generated, which can be estimated based upon homogeneity, accuracy, reproducibility, or stability of the brain areas^{10, 11}. Optimal comparison of connectomes is likely to require parcellation strategies that incorporate information across individuals and modalities, potentially at the cost of quality of fit for single subjects and modalities.

Estimating Structural Connectivity

Structural connectivity encompasses the collection of axonal and dendritic connections among neurons¹. Despite definitional simplicity, structural connectivity is difficult to measure with non-invasive, in vivo imaging approaches. Prior to dMRI, our knowledge was primarily derived from lesions and blunt dissection in humans, or invasive tracing in non-humans. These methodologies remain the gold standard for establishing connectivity, but the non-invasive nature of dMRI makes it the de facto standard for human structural connectivity.

Acquisition

The basic principle underlying the inference of structural connectivity from dMRI is that water diffusion in white matter is hindered, occurring primarily along the path of axons. In contrast, water diffusion in grey matter and cerebral spinal fluid occurs (almost) equally in all directions. By following the motion of water, it is possible to map the orientation(s) of fibers passing through each white matter voxel. In dMRI, a series of images are acquired, each sensitive to diffusion along a specific direction. The number of unique directions acquired varies from six into the hundreds. When combined, these images contain the information necessary to estimate the orientation(s) of fibers passing through each voxel; this information is used to reconstruct large-scale white matter tracts (tractography). See Box 1 for further information about dMRI acquisition.

Box 1. Optimizing fMRI and dMRI image acquisition.

Echo planar imaging (EPI) is the most common method for acquiring functional (fMRI) and diffusion magnetic resonance imaging (dMRI) data. An EPI volume is a set of slices, each acquired after a single excitation. EPI volumes are collected in sequence, representing time-points in fMRI and diffusion directions in dMRI. Gradient echo EPI in fMRI only involves excitation and readout. However, in dMRI an additional 180° rephasing (spin echo) radio frequency pulse, and bipolar diffusion encoding gradients are applied.

$$\text{SNR}\propto I_0\times {\mathrm{\Delta }}_x\times {\mathrm{\Delta }}_y\times {\mathrm{\Delta }}_z\times \sqrt{N_{\text{acq}}\times N_x\times N_y\times N_z\times {\mathrm{\Delta }}_t\times \frac{1}{P_f}}$$ (1)

Signal-to-noise ratio (SNR), spatial distortions and artifacts, and image contrast determine image quality. Image SNR can be represented in terms of parameters such as available signal (I₀), voxel dimensions (Δ_x, Δ_y, Δ_z), number of image acquisitions (Nacq), number of samples in each dimension (N_x, N_y, N_z), time between samples (Δ_t) and parallel imaging factor (Pf) (Eq 1)¹¹⁷. These parameters are described in Table 3. Equation 1 demonstrates how different parameter settings affect SNR; for example, acquiring and averaging 2 volumes (N_↓acq = 2) improves SNR by $\sqrt{2}$ SNR for modern imaging technology is greater than required for most imaging applications, and can be a traded-off to optimize other imaging aspects (i.e., to reduce spatial distortions). Importantly, beyond spatial image considerations, parameter optimizations must be evaluated in terms of impact on the temporal (fMRI) or diffusion (dMRI) signal.

General Considerations for EPI

Spatial distortion

The EPI readout scheme leads to extended readout times and asymmetric bandwidth between areas, in turn increasing T2 decay and in-plane smoothing. Bandwidth corresponds to the number of frequencies allocated to a voxel; any shift in frequency due to magnet field imperfections spatially shifts the signal in proportion to the inverse of the bandwidth¹¹⁸. The bandwidth in the phase encoding direction is a fraction of the bandwidth in the readout direction, making it particularly susceptible to spatial distortions. Increasing bandwidth can minimize spatial distortions, though costing SNR. Parallel imaging techniques increase effective bandwidth and image acquisition rate¹¹⁹. These techniques require calibration scans for proper reconstruction, and any misalignment (e.g., head motion) between these scans and image data produce reconstruction errors¹¹⁹. Alternatively, spatial distortions can be mathematically corrected using maps of the spatial variation in the magnetic field¹⁵.

Image resolution

Image resolution can be increased by reducing the field of view (FOV) or increasing the number of samples along a dimension. Decreasing the FOV produces a proportional decrease in SNR; the FOV must remain larger than the head to avoid excessive ghosting. Increasing the number of samples has less impact on SNR (reduced by square root of the increase¹¹⁷). However, increasing the number of samples in the phase encoding direction substantially increases read out time, which increases the amount of T2 decay experienced during slice acquisition, and leads to increased in-plane smoothness¹¹⁸; parallel imaging mitigates these effects¹¹⁹.

Considerations for fMRI

BOLD contrast

T2* contrast is the most sensitive to the BOLD effect and is optimized using an echo time equal to the T2* of grey matter (TE~30ms at 3T). BOLD can also be measured with spin echo sequences, by using a TE near the T2 of grey matter, though BOLD contrast is low¹²⁰.

Minimizing dropout

Tilting, and positioning imaging slices to prevent slices from intersecting air-tissue interfaces can minimize signal dropout due to susceptibility¹²¹. Slice positioning should focus on areas most vital to the experiment. Reducing TE, which decreases BOLD contrast, and increasing resolution, which decreases SNR, should be avoided. Specialty sequences (e.g., spiral-in/out¹²²and z-shim techniques¹²³) acquire multiple echoes with different dephasing characteristics to reduce susceptibility effects. Alternatively, spin-echo EPI avoids susceptibility artifacts but is much less sensitive to BOLD¹²⁰.

Motion sensitivity

Beyond image misalignment, head motion induces fMRI signal fluctuations due to partial voluming and spin-history effects³⁹. Lower flip angles¹²⁴, longer TR¹²⁵, and interleaved slices minimize spin-history effects by allowing the signal in a slice to fully relax before acquiring its neighboring slice. Spiral sequences are less sensitive to motion during slice acquisition¹²⁶. 3D imaging techniques minimize the impact of within-volume motion, but between-volume motions remain problematic unless a long TR is utilized; long readouts increase the interaction between magnetic field inhomogeneity and motion¹²⁷. Parallel imaging can improve acquisition time, resolution, and bandwidth but requires calibration scans¹¹⁹. Misalignments between the acquired data and calibration scans induce reconstruction errors and motion correlated imaging artifacts¹¹⁹.

Temporal resolution

Number of slices acquired determines temporal resolution. TE fundamentally limits slice acquisition time. Increasing bandwidth, partial Fourier imaging, and parallel imaging can offer marginal speed gains¹¹⁸.

Considerations for dMRI

Diffusion Contrast

Minimizing echo time, and therefore T2 decay, is essential to dMRI. T2 reduces overall MR signal and image SNR, and increases in-plane image blurring. Increasing bandwidth, partial Fourier imaging, parallel imaging, and using stronger diffusion gradients (b-values; high b-values require longer diffusion gradient pulses) can minimize TE¹¹⁸. Higher strength gradient systems enable high b-values (desirable for fiber tracking) in shorter time, though requiring hardware upgrade for most systems. Echo shifting also reduces TE, by relaxing the spin echo condition and shifting the echo train earlier in time¹¹⁸.

Scan Time

TE and number of slices determine dMRI volume TR. The number of diffusion directions, b-values, and averages acquired determine total scan time.

Emerging Acquisition sequences

Multiband and multi-echo imaging are emerging acquisition strategies. In multiband, multiple slices are acquired simultaneously, substantially improving temporal resolution, or increases in spatial resolution per unit time¹²⁸, though at the cost of SNR and spatial smoothness. This improvement enables higher fMRI sampling rates, and more diffusion directions per b-value acquisitions in dMRI¹²⁹– substantially improving estimation of macroscale connectomes¹³⁰. In multi-echo fMRI, two echoes of a slice are acquired at each acquisition (one with low TE, one with a TE optimized for BOLD¹³¹). Systematic noise (heartbeat, respiration, head motion, scanner instability) are measured in the first echo, and removed from the second, enabling signal denoising with practically no SNR cost.

Preprocessing

Following acquisition, dMRI data must be preconditioned before directional information can be extracted, and tractography performed. Little debate exists regarding dMRI data preprocessing (see¹⁴for an exception), though this may reflect the difficulties of preprocessing and its complex impact rather than field consensus.

Correcting image distortions

In vivo dMRI data are plagued with spatial distortions, which are a central focus of preprocessing. In particular, magnetic field inhomogeneities are a major contributor. Areas where materials that differ with respect to magnetic susceptibility (i.e., degree of magnetization achieved in the MRI) interface with one another (e.g. air-tissue interfaces) are particularly prone to such inhomogeneities. These local variations in the magnetic field generate spatial distortions, which can be reduced through parallel imaging techniques or mathematically corrected using estimates of the field variations¹⁵. Another cause of spatial distortion is the interaction between the static magnetic field and currents induced by the rapid switching of gradients with the magnetic field, known as eddy-currents. These artifacts can be reduced using bipolar gradients¹⁶. Image coregistration, i.e. spatial alignment of brain scans, is commonly employed in preprocessing to correct for eddy current distortions and subject head motion¹⁷. However, this method fails for images acquired using very strong diffusion gradients. Model-based approaches that explicitly account for the effects of eddy-currents during image acquisition are emerging as the preferred option¹⁸.

Overlooked Issues

The above preprocessing steps, combined with visual inspection, constitute standard preprocessing. A few important details are often overlooked (see¹⁴for more examples). First, modern scanners are often equipped with antennas that acquire data in parallel through multiple-channels that are subsequently combined. Such parallel imaging techniques can elevate noise levels if the data are submitted to standard reconstruction¹⁹. This can artifactually lower diffusivity estimates along the axons, which increases the tendency of tractography approaches to overfit and generate false positive connections. An alternative reconstruction method has recently been proposed to address this important issue¹⁹. Second, any distortion correction must account for voxel-wise compression or expansion during image coregistration. This is particularly important for dMRI, where distortions vary in direction and magnitude between different gradient orientations, but is largely ignored by current software packages. Finally, image coregistrations contain a rotation component that is applied to each volume, and must therefore be applied to the concurrent gradient orientation²⁰.

Estimating fiber orientation

Prior to delineating tracts and bundles via tractography, fiber orientation(s) must be inferred for white matter voxels individually. The dMRI signal’s sensitivity to water diffusion properties (i.e., rate, direction) enables the estimation of fiber orientation at each voxel. Importantly, each voxel contains thousands of axonal fibers, not just one. Thus, the goal of dMRI analysis is to infer a probability function for each voxel, which captures the different fiber orientations present, and their relative proportions²¹. Referred to as the fiber orientation density function (fODF), estimation of this function at each voxel is the first step in estimating structural connectivity.

The diffusion tensor is a simplistic but viable model for the diffusion profile that provides a simple approximation to the fODF²². Diffusion tensor imaging (DTI) uses a 3×3 matrix to provide an abstract ellipsoid representation of the water diffusion profile for a given voxel. Mathematical decomposition of this matrix yields information regarding the directions (x, y, z) of maximum and minimum water motion (eigenvectors), as well as the amount of diffusion that occurs along each direction (eigenvalues). The direction of maximal diffusion, referred to as the principal diffusion direction, is taken as the best estimate of fiber orientation within a voxel. Formally speaking, in the case of DTI, the fODF is approximated using a delta function or peak aligned with the principal diffusion direction.

The diffusion tensor provides a good estimate of fiber orientations when axons are homogeneously aligned within a voxel. However, this is not always the case. Fibers are known to disperse (i.e., fan), cross, merge, and kiss (i.e., temporarily run adjacent to one another) – all of which can happen within a single voxel and lead to heterogeneity not accounted for by a simple delta function. More complex fODF approximations can account for such heterogeneity within a voxel, though require higher angular coverage^{23, 24}(i.e., more directions) and models that either explicitly or implicitly account for interactions between fiber orientation and the diffusion signal (See²¹for example methods). Complex fODF models better estimate fiber trajectories, particularly when several white matter tracts intersect, and allow recovery of non-dominant pathways invisible to DTI²⁵.

Estimating Edges

Following estimation of voxel-wise fiber orientations, tractography approaches are used to establish structural connectivity between connectome nodes. Three-dimension trajectories, referred to as “streamlines”, are used to trace putative white matter paths. Local fiber orientation information guides the construction of streamlines along the fODF, allowing us to trace major white matter bundles²⁶. Results are typically visualized as 3D renderings of thin curves grouped into bundles (Fig. 2), reminiscent of post-mortem dissection photographs. Importantly, the individual streamlines do not represent actual axons; they depict estimates of the average trajectories of axon bundles, given our assumption that diffusion is least hindered along axons.

Figure 2. Diffusion Imaging of structural connectivity maps.

(A) dMRI-based map of principal tensor orientations of the human brain viewed from below; blue: Superior-inferior, green: anterior-posterior and red: medial-lateral. (B) DTI fiber orientation estimates (red lines) from a region of corpus callosum superimposed on a fractional anisotropy image. Sample streamline depicted in yellow. (C) Pyramidal tract streamlines based on deterministic (left) and probabilistic (right) approaches are depicted (results superimposed on fractional anisotropy image). Image courtesy: Stam Sotiropoulos, http://etheses.nottingham.ac.uk/1164/.

The specific process by which streamlines are developed varies depending on the complexity of the fODF approximations available. With diffusion tensor modeling, the principal diffusion direction at each voxel guides the formation of the streamline; specifically, it provides a candidate for the tangent to the streamline at each voxel. For more complex fODF models, streamlining follows the same principle, though with multiple peak orientations available at each voxel, rather than a single principal diffusion direction. This allows streamlines with differing orientations to pass through the same voxel – which is crucial when heterogeneous fibers are present. While traditional tractography approaches are deterministic, probabilistic approaches account for uncertainty in estimates of local fiber orientations, allowing for estimation of probabilities for any given streamline.

Using streamlining methodologies, it is theoretically possible to measure all connections between grey matter areas. We can estimate both the trajectories and the end points of anatomical pathways. In practice, however, inference of point-to-point connectivity using streamlining is imprecise and error-prone²⁷; improvements in both data quality and modeling are needed to yield more accurate structural connectomes.

Ideally, we should not only be able to infer the existence or absence of connections between nodes, but estimate connection (edge) strengths as well. Anatomical connections are made up of axons; features of these axons, such as density, size, length, and myelination, have important consequences on the propagation of action potentials, and hence information transfer. Measures of microstructural features based on more complex diffusion MRI experiments are emerging²⁸, and may become an important constituent of connectomics. Related measures, such as fractional anisotropy and diffusivity, serve as common proxies for these microstructural complexities, but are extremely sensitive to confounding factors such as partial volume (e.g. voxels containing a mixture of white matter and grey matter) and axonal dispersion^{27, 29}. Accordingly, these measures should be used cautiously to quantify connection strength. Other anatomical factors such as dendrite and spine densities, number of synapses at axon terminals, and synaptic efficacy are much harder to determine noninvasively, though potentially more relevant.

Unfortunately, tractography does not quantify any of the above properties. Often, probabilistic tractography, which estimates the uncertainty of the streamline trajectories, is used to quantify connection strength. Strong connections are expected to have a more significant trace in the diffusion data, and therefore lower uncertainty in their trajectories. This approximation, however, can easily break. For instance, locally non-dominant pathways (e.g., those that cross larger bundles), have higher uncertainty. Uncertainty is also affected by non-relevant factors such as signal-to-noise and partial volume effects. Another issue specific to streamlining is that uncertainty in the streamline’s path increases with the length of tract. Because streamlining operates by propagating uncertainty spatially, connection probabilities inevitably decrease with distance. As a result, tractography-based structural connections are difficult to quantify, threshold, compare between groups, and use for other types of statistical analyses^{27, 29}.

Interpretation and considerations

Tractography pitfalls can be divided into two categories: accuracy (correctness) and precision (reproducibility)¹⁴. Accuracy refers to our ability to infer axonal organization from measurement of water diffusion. In the ideal case, there is no instrumental or physiological noise, yet we can still make erroneous inferences regarding microstructure due to inaccurate modeling. A white matter voxel contains hundreds of thousands of axons, which do not necessarily align³⁰. Fiber ODF models, which account for multiple directions within a voxel (crossing fibers) are replacing tensor models for tractography. However, the sub-voxel organization of axons can be more complex than a simple crossing, and may not always be easily recovered from the diffusion profile. For instance, a collection of axons that bend within a voxel will create a diffusion pattern that may not be easily distinguishable from that of fiber dispersion. One can easily imagine even more complex situations where all these configurations (e.g., bending, dispersion, crossing) happen within the same voxel. Diffusion data from a single voxel cannot unambiguously resolve these complexities. Future approaches may benefit from semi-global models that aggregate diffusion data across multiple adjacent voxels to infer sub-voxel features.

Regarding precision, measurement noise (e.g., instrumental or physiological) and inadequate water diffusion modeling can compromise tensor and fODF estimation, inducing spurious variations in the generated streamlines. Additionally, use of a fixed step size in the generation of streamlines (despite local variations in anatomy), and the discrete nature of voxels (when tracts are continuous) increase measurement error. Probabilistic tractography algorithms try to quantify these errors by estimating the uncertainty in the entire process. Uncertainty in voxel wise fiber orientation can be quantified³¹and propagated into uncertainties regarding the location of streamlines. This process turns 3D point estimates of streamline trajectories into spatial histograms of their locations (Fig. 2c).

Beyond concerns regarding accuracy and precision, identification of fibers in their entirety requires knowledge of where tracts terminate throughout cortex. This remains a challenge for tractography algorithms, which are very good at estimating the location of bundles in deep white matter, but not so good (yet) at identifying where they project into grey matter²⁷. These difficulties result from a lack of detail in white matter architecture modeled through diffusion and biases in cortical projections.

Estimating Functional Connectivity

While the concept of structural connectivity is relatively intuitive given the presence of physical connections between brain areas, its functional counterpart can be more challenging to define. The macroconnectomics field has adopted a neurophysiological perspective of functional connectivity, defining it as the synchronization of neurophysiological events between spatially remote brain areas³². First quantified in early electroencephalography (EEG) and multiunit recordings studies, functional connectivity analyses were adopted by positron emission tomography (PET) and fMRI in 1993³². Although functional connectivity can be measured using a variety of neuroimaging modalities (e.g., PET, fMRI, magnetoencephalography) and different indices related to physiological function (e.g., blood oxygenation level dependent [BOLD], cerebral blood flow, glucose metabolism), BOLD-based fMRI is the most popular technique for inferring functional connectivity.

Functional connectivity studies may be dichotomized based upon the presence or absence of a task (i.e., task-based fMRI [T-fMRI] vs. task-free or “resting state” [R-fMRI]). Task-based approaches focus on the detection of synchronous responses to extrinsic stimulation or tasks, referred to herein as evoked functional connectivity (eFC) or coactivation³³. Evoked functional connectivity can be quantified across the entire period of task performance, or in response to specific event types. Approaches using R-fMRI focus on the detection of synchronized spontaneous activity occurring in the absence of experimenter controlled tasks or stimuli, referred to as intrinsic functional connectivity (iFC)³⁴. Although iFC and eFC patterns can be strikingly similar, especially when eFC is assessed using meta-analytic techniques³⁵or broad comparisons (e.g., task vs. rest), these analyses probe different aspects of the functional architecture³³. Importantly, eFC patterns obtained using one task will not necessarily generalize to another, and aspects of iFC obtained during one state (e.g., wakefulness) may not necessarily generalize to another (e.g., sleep) (see Box 2 for a discussion of states other than wakeful rest).

Box 2 – iFC and Conscious States.

An emerging literature has demonstrated the impact of cognitive⁹⁷, physiological¹³²and pathological states¹³³on functional connectivity. Consciousness has received particular attention, with numerous studies examining physiological states (e.g., sleep), induced states (e.g., anesthesia, hypnosis) and pathological states (e.g., coma, vegetative syndrome, and minimally conscious state¹³³). iFC patterns detected in these states are grossly similar to those observed during wakefulness, though direct comparison reveals state-related iFC changes. For example, the default and lateral networks each exhibit decreased functional connectivity among network components (i.e., within network connectivity) during sleep, suggesting decreased integration of information. Complementary findings of decreased negative iFC between these networks and others may suggest decreased segregation as well,¹³⁴. These results suggest that while sleep-based studies may be useful in populations not amenable to examination in wakeful states (e.g., toddlers), comparison of findings across states may be problematic. Of note, changes in thalamocortical connectivity are reported during anesthesia, non-rapid eye movement (non-REM) sleep and vegetative states¹³⁵, but the specific role of thalamocortical circuitry in consciousness remains underexplored. These studies also suggest potential clinical applications of iFC, such as improving recognition of consciousness following recovery from coma.

Acquisition

BOLD is the predominant fMRI technique in functional connectivity (see³⁶for alternative cerebral blood flow-based technique). BOLD is measured using ultra-fast imaging sequences that are sensitive to relative concentrations of deoxyhemoglobin, which is paramagnetic (i.e., dephases the MR signal) in contrast to oxyhemoglobin, which is diamagnetic³⁷; the resulting measurement is an indirect measure of neural activation. Datasets for functional connectivity analysis using fMRI are typically obtained in 5–30 minutes, as a participant either performs an experimental task (T-fMRI), or rests quietly in the scanner (typically while awake; R-fMRI). See Box 1 for a discussion of determinants of BOLD imaging acquisition quality.

Preprocessing

Preprocessing aims to remove confounding variation from data and facilitate comparison across subjects. Structured nuisance signals and anatomical variation can obscure functional connectivity measurements if left unaccounted for. Despite considerable effort, we lack consensus regarding the optimal set of preprocessing steps, their ordering and their implementation. Most preprocessing steps originated with task activation approaches. However, their usage and implications are greater for functional connectivity approaches due to the increased risk of spurious findings given that the independent and dependent variables can be contaminated by the same noise signals (e.g., motion, respiration). Comprehensive comparison of preprocessing strategies and their implications for eFC and iFC analyses remain elusive, in part due to lack of objective benchmarks. The preprocessing steps described below are post-hoc corrections. However, optimization of acquisition strategies to minimize the impact of noise sources is preferred (see Box 1).

Slice Timing Correction

The slices of an fMRI volume are acquired at different times, creating effective shifts in time-series obtained at different slices. Although some question its necessity³⁸, correction by temporal-interpolation is recommended to avoid the potential for deleterious impact of these lags on signal denoising and time-series extraction from brain areas.

Motion Correction

Head motion results in a misalignment of brain areas between volumes typically accounted for using 3D image registration techniques. Additionally, head motion induces artifactual fMRI signal fluctuations due to changes in slice tissue composition (partial voluming), and residual magnetization from prior slice excitations (spin history effects)³⁹. These motion artifacts are typically modeled and removed in a regression framework, containing predictors calculated from motion parameters estimated during coregistration⁴⁰. Although effective, modeling based approaches do not completely remove motion-related fluctuations in the fMRI signal^41–43. To address this issue, the “scrubbing” of offending volumes via removal⁴¹or spike regression⁴⁴has been proposed. Importantly, excluding time-points alters the temporal structure of the data, thereby compromising analyses that rely on this structure (e.g., temporal dynamics, spectral analysis, estimating temporal autocorrelation). Regardless of the motion correction scheme employed, it is necessary to account for motion in group level analyses^{42, 45}.

Physiological Noise Correction

Cardiac pulsation and respiration can induce fMRI signal fluctuations, which led to early criticisms attributing iFC to these physiological signals rather than neural signals⁴⁶. The cardiac cycle generates pulsatile motion throughout the brain⁴⁷. Respiratory movement of the chest and abdomen induce changes in the magnetic field, producing intensity fluctuations in fMRI images⁴⁷. Additionally, changes in cardiac rhythm as well as rate and depth of breathing create longer-term effects. Respiration and pulse can be recorded to model and subsequently remove their impact⁴⁷. Although accepted as ideal, this is not commonly performed. Instead, signals present in white matter and cerebrospinal fluid are taken as surrogates for respiration and cardiac effects, and regressed from the fMRI time-series. Incorporating spatial variation in the noise captured by the white matter signal provides superior denoising (e.g., ANATICOR⁴⁸). Blind source separation techniques provide another means of physiological correction (e.g., Corsica⁴⁹).

Global Signal Regression (GSR)

The mean time-series across the whole brain is commonly regressed from the data. In this model, the global signal is considered a non-specific measure of noise whose removal improves the specificity of iFC⁵⁰, decreases motion-effects⁴⁴, and removes inter-session and inter-site effects. However, awareness that GSR centers the correlation distribution at zero, and thus introduces negative connections⁵¹and can alter inter-individual differences⁵², has made its use controversial. In this regard, it is important to note that functional correlation coefficients obtained after GSR are relative values, not absolute. Additionally, electrophysiological demonstrations of globally synchronous neural signals in grey matter⁵³call into question the interpretation of the global signal as simply noise.

Temporal Filtering

Bandpass filtering (0.001<f<0.08) is usually included. This frequency range targets removal of low frequency scanner drift and frequencies above those traditionally associated with functional connectivity^{34, 54}. However, complete removal of physiological noise is unlikely, due to artifacts induced by the low temporal resolution of fMRI (e.g. aliasing)⁴⁶. Concerns about temporal filtering include reductions in the degrees of freedom for the time-series and recent demonstrations of functional connectivity at frequencies higher than 0.1 Hz for several brain areas, suggesting that low-pass filtering is removing valuable signal⁵⁵. Thus, despite historical precedent, inclusion of low-pass filtering merits further consideration.

Spatial Normalization and Smoothing

Another aspect of preprocessing is conditioning the data for comparison across subjects. Spatial normalization addresses morphological variation across individuals by transforming them to a common stereotactic space; population- and study-specific templates are increasingly used to optimize correspondence. Spatial smoothing further improves the correspondence of brain areas across individuals, and increases the signal-to-noise ratio⁵⁶.

Estimating Edges

Several mathematical modeling techniques can be used to define functional relationships, differing primarily in the stringency with which they define functional connectivity. Functional connectivity simply implies a statistical dependency between activities observed in brain areas, and is an umbrella term for a wide range of dependency measures, each providing a different perspective³². For example, mutual information measures statistical dependency from the joint probability distribution function and is sensitive to linear and non-linear relationships, whereas Pearson’s correlation is primarily sensitive to linear relationships⁵⁷. Effective connectivity, on the other hand, requires a mathematically precise (directional) description of the interactions between brain areas⁵⁸. Importantly, this leads to a plurality of graphs that can be derived from functional connectivity, each characterizing functional interactions from a different perspective.

Estimating iFC from R-fMRI typically begins with extraction of the mean time-series across voxels in each brain node (i.e., parcellation-defined brain area). Intrinsic functional connectivity is commonly estimated from bivariate tests for statistical dependency (e.g., Pearson’s correlation, mutual information, spectral coherence) between every possible pairing of time-series⁵⁹. Although these approaches perform well in simple simulations⁵⁹, the limited number of observations results in noisy estimates of statistical relationships, which can be reduced using regularization (shrinkage) methods⁶⁰. A limitation of bivariate approaches is that they do not take into account multiple brain areas simultaneously. Hence they cannot distinguish direct from indirect interactions (mediated by shared relationships with other areas). Partial correlation (related to the inverse covariance matrix) estimates the conditional linear dependency between two brain areas, after accounting for interactions with every other area⁶¹. Although considered preferential to bivariate approaches, the number of brain areas commonly exceeds the degrees of freedom, preventing unique specification of partial correlations. In these cases, regularization techniques (e.g., graphical lasso, elastic net) can assist in finding a solution⁵⁹. Additionally, information can be pooled across individuals to optimize estimation parameters⁶². Note that some, but not all, of these approaches enforce symmetry; in other words, one can obtain dependency in one direction but not the other (see Box 3).

Box 3 - Directionality in functional connectomics.

Commonly referred to as effective connectivity, the mapping of directional relationships is essential for characterizing information flow in functional connectivity studies¹³⁶. Identification of neural drivers can facilitate our understanding of control systems, as well as ectopic foci leading to pathological conditions (e.g., epilepsy¹³⁷). While invasive tracing and stimulation techniques are powerful tools for mapping directional relationships in non-human populations¹³⁸, they are not generally applicable in humans. Here, we provide an overview of non-invasive approaches to establishing directionality.

Statistical Techniques

Before reviewing statistical effective connectivity approaches, we note that despite nomenclature, their findings should not be interpreted as indicating causality, but rather the directionality of information flow. Structural Equation Modeling (SEM) and Dynamic Causal Modeling (DCM) approaches evaluate the fit of hypothesized models of directional interactions among nodes with measured fMRI data. SEM is a covariance-based approach that represents each node as an exogenous variable (i.e., predicting the activity of another node), endogenous variable (i.e., activity is predicted by another node), or both¹³⁹; effective connectivity is modeled at the hemodynamic (BOLD response) level. In contrast, DCM is a generative approach, modeling effective connectivity at the neuronal level based upon a given biophysical model and employs a forward model to produce the downstream fMRI activity. Models can be evaluated individually; however, common-practice is to compare models representing competing hypotheses regarding causality to identify the “best fit” model. Concerns exist regarding the feasibility of successfully identifying a “best fit” model from a large population of putative models¹⁴⁰. SEM and DCM approaches are limited in the number of nodes and interactions they can model efficiently. Primarily intended for confirmatory analysis, exploratory implementations of SEM¹⁴¹and DCM¹³⁶are emerging for use with R-fMRI.

Granger causality analysis (GCA) is a model-free, data-driven effective connectivity approach¹⁴²that investigates whether past values of the time-series for one node could improve the prediction of the current value in another¹⁴³. In contrast to SEM and DCM, GCA can assess numerous nodes simultaneously. Application of GCA to R-fMRI¹⁴⁴is particularly controversial due to: 1) limitations imposed by the sluggish and variable hemodynamic response function (HRF), 2) slow sampling rate (e.g., TR ≥ 2s)⁵⁹, and 3) assumptions that HRF characteristics are constant across nodes⁵⁹. Attempts to rehabilitate GCA for R-fMRI include: HRF deconvolution prior to GCA¹³⁷, accounting for regional variation in the HRF using breath-hold scans, and faster sampling rates¹⁴⁵. Nonetheless, using GCA with R-fMRI remains problematic.

Lesion Studies

Lesion studies directly perturb the system and therefore can be compelling in establishing causality when carried out in a controlled manner. From this perspective, changes in the activity of a node following disruption of inputs from another are taken to infer causal influences. In the ideal paradigm, scans are obtained pre- and post-occurrence of a given lesion. For example, Johnston et al.¹⁴⁶scanned a 6-year-old child pre- and post-callosotomy, revealing disruptions specific to interhemispheric connectivity. Lesion studies are, however, commonly limited to post-lesion scans, taken after naturally-occurring lesions (e.g., stroke, congenital abnormality, neoplasm, seizure focus). Although useful for testing predictions or generating novel hypotheses, findings of such studies cannot be considered definitive.

Brain Stimulation

The gold standard for establishing directional influences is the demonstration that direct stimulation of node A impacts node B, but not the converse. In this regard, intraoperative studies of corticocortical evoked potentials (CCEP) –which involve the tracking of electrical signals from stimulation sites to other locations– are powerful tools¹⁴⁷, though with limited applicability (i.e., neurosurgical patients). Non-invasive stimulation techniques with a broader range of applications are slowly evolving. Transcranial magnetic stimulation (TMS) is capable of producing temporary, and reversible neural excitation or suppression in targeted cortical areas. Concurrent TMS–fMRI studies have revealed causal relationships within motor circuits¹⁴⁸and the visual system¹⁴⁹. Transcranial direct current stimulation (tDCS) and transcranial alternating current stimulation (tACS) approaches deliver weak currents to targeted brain areas, and are emerging as less expensive and technically demanding alternatives to TMS, though delivering focal stimulation is challenging¹⁵⁰.

A number of approaches exist for estimating eFC. Several authors have borrowed approaches from iFC, assuming the time-series spans the entire task⁶³or from concatenated blocks of specific task conditions⁶⁴. Psychophysiological interaction (PPI)³⁹analyses directly model interactions between patterns of functional connectivity and the experimental stimulus design, potentially offering greater specificity of findings. Others have measured eFC from “coactivation” using a series of fitted regression coefficients⁶⁵or binarized (by applying a threshold to regression coefficients) time-series⁶⁶generated from a first level task analysis. Regression coefficient-series are then compared using correlation or partial correlation^{33, 65}. Binarized time-series can be compared from the joint distribution of the two values using measures akin to mutual information⁶⁶. Finally, meta-analytical approaches provide a means of measuring eFC across studies and often tasks, detecting patterns of coactivation across statistical maps generated from the literature^{35, 67}.

A variety of data-driven techniques are also used for identifying iFC and eFC patterns. Examples include self-organizing maps⁶⁸, principal component analysis, normalized cut clustering⁶⁹, and independent component analysis⁷⁰. These methods are more appropriate for identifying nodes of connectome graphs (see node section) than edges, although exceptions exist⁵⁹.

Once functional connectivity is estimated, some applications require it to be thresholded or binarized (i.e., a connection is present or not). Threshold selection is not straightforward, but can be accomplished by applying a test of statistical significance to each edge. When using parametric statistics, care must be taken to adjust the degrees of freedom for temporal autocorrelation. Alternatively, this can be addressed using non-parametric tests of significance such as wavestrapping⁷¹or circular block bootstrap⁷². Sparse covariance estimation methods can also be employed.

Interpretations and Considerations

A common pursuit of T-fMRI and R-fMRI studies is to fractionate the connectome into a set of spatially and functionally distinct networks that can each be annotated in terms of the specific functional (e.g. cognitive, affective, or visceral) domain they subserve. Impressively, they have converged on similar definitions of 8–20 spatially and functionally distinct networks - though numerous studies have suggested the actual number of networks is substantially greater¹³. The concordance of T-fMRI and R-fMRI findings suggests the brain's intrinsic functional architecture provides a framework for moment-to-moment responses to the external world. As summarized by Smith et al.⁶⁷, it appears that “the full repertoire of functional networks utilized by the brain in action is continuously and dynamically ‘active’ even when at ‘rest’.”

When considering the visualization of functional connectivity (Fig. 3), an important question is: “what are we missing?” While functional connectivity is often represented with static graphs, neurophysiological models have long asserted the transient nature of many functional interactions. Specifically, distributed neural assemblies appear to change their patterns of interaction with one another from one cognitive act or state to another. Consistent with this notion, eFC studies have noted significant task-dependency in their findings, even when looking at the same regions^{33, 39}. Perhaps most exciting, recent iFC studies have observed dynamic changes in iFC patterns over a 5–minute scan⁷³. These findings suggest that commonly employed metrics of iFC are incomplete, only capturing the “mean” connectivity over time. If true, the implications would be multifold: 1) findings of hypo- or hyper-connectivity in population studies would need to be reassessed, as they may reflect a different distribution of time spent in the various iFC configurations between populations, 2) the detection of changing eFC patterns over the course of task performance may prove to be a means of explaining observed behavioral variability. Of note, an increasing number of studies are highlighting the potential value of examining transition zones between functional areas in the brain⁵. Examination of temporal dynamics may inform such efforts, by mapping changes in the boundary over time and providing greater clarity for findings.

Figure 3. Visualizing the Connectome.

(A) Classical anatomical-tracing style depiction of iFC for posteromedial cortex subdivisions (reproduced with permission from Margulies et al., 2009¹¹³). (B) Matrix representation of functional brain connections predictive of diagnostic status in depression (reproduced with permission from Craddock et al., 2009⁹⁰). (C) Flatmap-based representation of the CoCoMac atlas of the Macaque connectome (reproduced with permission from Knock et al., 2009¹¹⁴). (D) Connectogram depicts brain areas (nodes) as columns in the circular band, differing connectivity metrics in separate layers and connections with lines, lobes are differentiated by color and left/right halves corresponds to hemispheres (reproduced with permission from van Horn et al., 2012¹¹⁵).

In addition to naturally occurring variations in iFC over time, studies have suggested that iFC can be systematically impacted by cognitive demands prior to R-fMRI data acquisition. By comparing iFC during R-fMRI scans collected before and after task performance⁷⁴, studies have shown that iFC strength within and between networks is altered in a task-dependent manner. For example, R-fMRI based functional connectivity between the inferior frontal gyrus and visual areas was found to vary depending on the category of stimuli viewed prior to the R-fMRI scan⁷⁵. Further, across participants, the degree to which iFC was modulated correlated with subsequent memory for the stimuli. In addition to exhibiting plasticity related to tasks performed close in time to the measurements, iFC is modulated by direct stimulation protocols including median nerve stimulation⁷⁶, heat pain⁷⁷, transcranial magnetic stimulation (TMS)⁷⁸and transcranial direct current stimulation (tDCS)⁷⁹. This suggests that R-fMRI may have utility in identifying targets for stimulation protocols as well as assessing their efficacy (e.g., in the context of the treatment of depression⁸⁰).

This iFC-based evidence of experience-induced plasticity provide strong support for the hypothesis that iFC reflects a history of coactivation among areas. However, they also suggest a corollary - correlated intrinsic activity plays a role in learning and memory consolidation⁸¹. The demonstration of brain-behavior correlations between task-related modulations of iFC and subsequent behavior (e.g., recall) supports this hypothesis. If short-term iFC alterations reflect experience-induced plasticity, then enduring changes would be expected following extended practice or training. Several studies suggest this is the case⁸². Studies of long-term training-induced plasticity have the potential to inform our understanding of mechanisms involved in remediation-based recovery of function, or even to index the efficacy of treatment interventions. For example, in a preliminary retrospective study, differences in iFC were observed between children with dyslexia who were successfully remediated by reading interventions versus children who had received no treatment⁸³.

Statistical analysis of the connectome

Once connectomes graphs are estimated, the next goal is to annotate them in terms of their relevance to higher order cognitive processes, neuropsychiatric diagnoses, or other phenotypic variables⁵. These associations are most often inferred by performing a categorical or dimensional statistical analysis that compares connectivity across a population of individuals, or within an individual across time or treatments⁸⁴. Many of the same statistical approaches are appropriate for the analysis of connectome graphs regardless of whether they were constructed with functional or structural datasets. However, the interpretation of the results must always consider the idiosyncratic differences between structural and functional connectivity. For example, functional connections are typically weighted, and can be positive or negative. Structural connectivity graphs tend to be unweighted and are strictly non-negative²⁷. Additionally, structural connections can be thought of as pathways along which information can flow, but functional connections cannot be interpreted in the same manner⁸⁵.

A Bag of Edges

The simplest approach to comparing graphs is to treat them as a bag, or collection of edges, and perform statistical analyses at each edge one at a time, without taking into account interactions or relationships between them (i.e., edgewise statistics)⁸⁴. Such univariate approaches (e.g., T-tests, F-tests, or regression) allow researchers to identify easily interpretable relationships between categorical or dimensional variables and edge weights. However, this approach results in a large number of statistical tests, which require correction for multiple comparisons to adequately control for the number of false positives. Standard correction techniques such as false discovery rate⁸⁶that do not model the dependencies between edges may result in overly liberal or conservative corrections⁸⁷. Alternate correction techniques such as the network-based statistic⁸⁸or group Benjamini-Hochberg⁸⁹leverage information about the group structure of connectome graphs to increase statistical power, while maintaining control of false positives.

Alternatively, multivariate regression and classification techniques evaluate the relationship between the entire connectome graphs and their associated phenotypic variables with a single statistical test^{90, 91}. Although powerful for connectome-phenotype relationships, they obscure information about the involvement of individual edges. Extracting this information, if desired, requires a return to edge-specific tests, and the need for multiple comparison correction⁹⁰. Of note, while these multivariate techniques tend to be applied to bag-of-edges representations, which ignore graph structure, they can also be performed using graph distance measures that preserve topological information when comparing graphs⁹².

Node and graph-level statistics: Invariants

Graphical representations of connectomes contain a wealth of information about brain architecture beyond the presence and strength of bivariate connections, which can be described using a variety of node-level and graph-level statistics. These measures are called invariants in graph theory parlance, or topological measures in network theory, because they are not unique to particular representations of the graph. The most commonly employed node invariants are centrality measures that indicate a node’s relative influence in a graph. Several different centrality metrics are available that measure a node’s importance based on the number and strength of direct connections (degree centrality⁹³), the importance of neighboring nodes (eigenvector⁹⁴or Page Rank⁹⁵centrality), and their role in connecting other pairs of nodes (betweenness⁸⁵). The various measures provide different perspectives on a node’s role in the graph, and when combined can provide a more holistic understanding of connectome-phenotype relationships⁹⁵.

Similarly, a range of graph-level invariants is employed for studying structural and functional connectivity. In particular, graphs are commonly assessed in terms of their local and global efficiency. Local efficiency assesses the degree to which neighbors are densely interconnected, while global efficiency captures the number of connections that must be traversed to connect any two nodes⁹³. The relationships of these two measures to what would be obtained from random graphs with similar properties can be combined to assess the small-worldness of a graph⁹³. Small-world graphs balance integration and segregation to obtain fast and cost-efficient propagation of information through the graph, as well as robustness to single-node failures⁹⁶. The cost-efficiency of a graph can be inferred from the difference between global efficiency and the number of edges in the graph⁹³. An additional invariant is modularity, which quantifies the degree to which a graph can be segregated into densely intraconnected but sparsely interconnected modules and allows direct comparison of module membership between graphs⁸⁵.

Each of the previously described node and graph invariants can be statistically evaluated to identify relationships with categorical and dimensional phenotypes. Although invariants can increase statistical power by decreasing the number of multiple comparisons, the resulting relationships can be more difficult to interpret. When comparing invariants between graphs it is important to consider the impact of potential differences in graph properties (e.g. number of edges) that can systematically differ between individuals or groups and confound interpretation of findings⁹³. Additionally, since the distributional properties of most invariants are poorly characterized, non-parametric statistical tests are preferred⁹³.

Finally, researchers frequently aim to identify connectivity patterns predictive of a phenotypic variable (e.g., diagnosis⁹⁰, age⁹¹or brain state⁹⁷). Predictive modeling directly assesses the ability of a connectivity pattern to predict the phenotype of an individual, in contrast to inferential statistics, which evaluate improbability of a set of relationships arising by chance⁹⁸. Predictive modeling is typically supervised, with the training set consisting of connectivity graphs and their associated phenotypes⁹⁹. One can assess the predictive accuracy via cross-validation⁹⁹or other model selection techniques. Predictive modeling has primarily focused on invariants and bags-of-edges^{90, 100}style approaches.

Translational Connectomics

MRI-based approaches to connectomics research are rapidly transforming neuroscience in animal models as well, by removing barriers to longitudinal examinations associated with invasive techniques (e.g., animal sacrifice, injection of toxic chemicals). The recent Mouse BIRN initiative (http://www.loni.ucla.edu/BIRN/Projects/Mouse/) provides an initial demonstration of the potential to complement cross-sectional atlases of the developing brain generated using histological approaches with longitudinal atlases obtained using dMRI. Simultaneously, R-fMRI is emerging as a powerful tool for comparative functional neuroanatomy studies. Initial work has demonstrated impressive correspondence between the iFC observed in humans and macaques for homologous functional networks supporting an array of functions, including those that are putatively “human” (e.g., language, self-referential, cognition)¹⁰¹. Evidence of homologies with patterns of iFC in lower mammals, such as rats, further underscores this translational potential¹⁰². Armed with increasingly powerful imaging-based tools, macroscale connectomic studies in animal models are poised to provide a mechanistic understanding of brain function through the combination of non-invasive imaging with direct structural, pharmacological, molecular, and genetic manipulations that are impossible in humans.

Despite the rich promise of translational connectomics, methodological issues must also be addressed. For example, iFC can be examined in awake rats that have been habituated to restraint in the loud MRI environment¹⁰³. However, most studies are conducted under anesthesia – in particular, using the general anesthetic isoflurane¹⁰⁴which can confound findings due to its effects on neural excitability. The sedating alpha-2 adrenergic agonist medetomidine may be preferable, as it avoids such confounds¹⁰⁵. Dose-response studies are few¹⁰⁴and are essential. Initial translational studies in monkeys, rats and mice have relied on preprocessing and analytical approaches identical to those developed in humans¹⁰³. While their success is encouraging, differences in physiological (e.g., cardiac, respiration) and imaging parameters must be explored to arrive at optimal strategies. Finally, we note that the many questions raised regarding the interpretation of dMRI and R-fMRI techniques in humans also apply to animal studies.

Towards Neurophenotypes and Clinical Applications

An overarching goal of the connectomics era is the derivation of “neurophenotypes”¹⁰⁶, a concept that remains poorly specified despite increasing investigator enthusiasm. An individual’s macroscale connectome and its subgraphs contribute to the specification of their neurophenotype. A central goal of connectomics is to catalog neurophenotypes and relate them to phenotypic profiles⁴. This can be accomplished through data-driven approaches focused on the detection of commonalities and distinctions in connectomes, or that can be reverse-engineered from phenotypic profiles. The breadth of phenotyping can vary depending on the application, though it typically consists of some combination of cognitive, affective, behavioral, neurological or psychiatric variables. When cataloging neurophenotypes based upon macroscale connectomes, the specificity of findings will depend on their nature, granularity of node definitions and quality of neuroimaging data employed. Similarly, when sorting neurophenotypes based on phenotypic profiles, specificity will be determined by the precision and comprehensiveness (i.e., number and breadth of independent features) of the phenotyping available to statistical analysis. Importantly, future work will need to find a balance between categorical and dimensional perspectives of neurophenotypes.

Beyond the derivation of a fundamental understanding of brain architecture and its implications for behavior and cognition, a major reason for the excitement surrounding connectomics is the promise of clinical utility because of the ability to obtain individually-relevant reliable brain indices (see Table 1 for initiatives that are accelerating the pace of macroconnectomics research). Recent years have witnessed an explosion in the number of neurological and psychiatric disorders studied with dMRI and R-fMRI (see Table 2). Hopes of attaining clinically useful diagnostic tools are increasingly espoused in the literature. However, leaders in the field have recently suggested that the attainment of tools capable of stratifying individuals based upon disease risk, prognosis and treatment response may prove to be a more fruitful goal than focusing on diagnosis¹⁰⁷. Regardless, a key requirement remains: attaining large-scale datasets representative of the human population. In this regard, the macroconnectomics community has supported several large-scale data-sharing initiatives dedicated to rapidly aggregating the necessary data¹⁰⁸.

Table 1.

Large-scale initiatives macroscale connectomics inititatives (See¹¹⁶ for additional information regarding these initiatives and others).

INITIATIVES PROMISING TO ACCELERATE THE PACE OF MACROSCALE CONNECTOMICS RESEARCH
Brain Genomics Superstruct (US). Aims to collect a large-scale imaging dataset to explore brain-behavior relationships and their genetic influences. The initiative has collected R-fMRI, dMRI, and saliva samples from over 3,000 adults, along with comprehensive phenotyping (cognitive, personality, lifestyle), and the resultant repository containing 1500 completed, quality pass datasets is expected to be publicly available within the next year.
Brainnetome (http://www.brainnetome.org; China). Attempts to characterize brain networks with multimodal neuroimaging techniques, from the microscale (microtechnique, ultramicrotomy, staining and visualization techniques) to the most macroscale (EEG, fMRI, dMRI). R-fMRI and diffusion imaging datasets, along with behavioral and blood data from more than 1000 schizophrenia patients, 300 Alzheimer’s Disease / mild cognitive impairment (MCI) patients, 120 stroke patients, 50 glioma patients and 2000 healthy controls collected from eleven hospitals and imaging centers.
Consortium of Neuroimagers for the Non-invasive Exploration of Brain Connectivity and Tracts (http://www.brain-connect.eu; EU). Consortium focused on studying the brain's microstructure, tracts and connectivity using dMRI. Target deliverables include optimized acquisition protocols, analytic tools and a connectivity atlas.
Developing Human Connectome Project (EU). Recently awarded initiative that will comprehensively map and model the human connectome for 1000 babies, including in utero and in vivo imaging (from 20 to 44 weeks post-conceptional age).
NIH Human Connectome Project: WU-Minn consortium (http://humanconnectome.org; US). State-of-the-art multimodal imaging initiative (MEG, EEG, R-fMRI, T-fMRI, dMRI), that makes use of a twin-design (1200 healthy aduts, including twin pairs and their siblings from 300 families) to provide insights into the genetic bases of the human connectome. The initiative is making use of “low TR” multiband imaging sequences for R-fMRI and dMRI, which it has refined and is currently distributing to interested centers. All data and tools developed through the initiative will be openly shared.
NIH Human Connectome Project: MGH/Harvard-UCLA consortium (http://humanconnectome.org; US). Initiative focusing on the unraveling the full connectivity map using the first “Connectome Scanner”, which is designed to carry out diffusion using ultrahigh gradient strength (4–8 times the strength of conventional systems). Efforts to optimize dMRI technology will focus on increasing the spatial resolution, quality, and speed of acquisition.
1000 Functional Connectomes Project (FCP; http://fcon_1000.projects.nitrc.org; global). Grass-roots data-sharing initiative that brought together over 1200 previously collected R-fMRI datasets from 33 independent sites

Table 2.

Neuropsychiatric disorders most commonly studied using macroscale functional and structural connectivity. Determined by the number (count) of R-fMRI and dMRI papers dedicated to the neuropsychiatric diagnosis. Calculated from the Child Mind Institute Librarian (Resting State and DTI libraries; http://www.mendeley.com/profiles/cmi-librarian/).

Neuropsychiatric Diagnoses	R-fMRI Count	dMRI Count
Schizophrenia	100	283
Alzheimer's Disease	89	201
Depression	81	101
Epilepsy and Seizures	62	179
Mild Cognitive Impairment	58	115
Other Neurological Disorders	45	50
Substance Dependence	40	94
Attention Deficit Hyperactivity Disorder	32	37
Autism Spectrum Disorders	26	86
Multiple Sclerosis	22	211
Parkinson's Disease	19	73
Traumatic Brain Injury	18	259
Sleep Disorders	17	7
Stroke	15	182
Anxiety Disorders	15	16
Coma and Vegetative State	15	9
Obsessive Compulsive Disorder	12	27
Amyotrophic Lateral Sclerosis	10	84
Bipolar Disorder	10	61

Conclusion

The connectomics era is the culmination of more than a century of conceptual and methodological innovation. MRI-based approaches to mapping and annotating the connectome at the macroscale are transforming basic, translational and clinical neuroscience research by overcoming barriers to progress faced by more traditional invasive methodologies. This review has broadly surveyed the many challenges that remain at hand in the acquisition, preprocessing and analysis of brain-imaging data. Failure to consider the many complexities could jeopardize this burgeoning field through the introduction of spurious, irreproducible findings associated with suboptimal methodologies. Conversely, increased attention to the acquisition of high quality data, combined with optimized preprocessing and analytic methodologies can serve to accelerate the pace at which connectomes can be meaningfully annotated, and their variations catalogued.

Table 3.

Magnetic Resonance Imaging Parameters

Parameter	Definition	Impact
Echo Time (TE)	The time between slice excitation and acquiring the center of k-space.	Determines impact of T2 and T2* on the images.
Repetition Time (TR)	The time between acquisitions of adjacent fMRI volumes (sampling period).	Impacts the signal available for imaging (I0), impacted by the number of slices. Longer TRs reduce motion sensitivity.
Bandwidth (BW; 1/Δt)	The range of frequencies mapped to a voxel.	Lower bandwidth settings can increase artifacts due to inadequate shimming or susceptibility, and distortions in the phase-encoding direction (e.g. ‘scalloping’)
Flip Angle (α)	The amount of rotation applied to proton spins by the excitation pulse.	Impacts the signal available for imaging (I0). Flip angles larger or smaller that the Ernst angle for a given TR will reduce I0. Low flip angles may reduce motion sensitivity, and in-flow effects and improve T1 contrast of images.
Spatial Resolution (Δx, Δy, Δz, Nx, Ny)	The volume of tissue sampled in a given voxel. Determined by field of view (FOV) and the number of points sampled in a slice.	SNR is significantly impacted by voxel volume; higher spatial resolution have lower SNR, e.g. a 2mm iso voxel has only ~30% of the SNR of a 3mm iso voxel, holding all other factors constant.
Parallel Imaging (Pf)	Methods such as GRAPPA and SENSE can decrease TR, and reduce spatial distortions by sampling k-space lines in parallel. Decreases in TR are rate-limited by TE required for BOLD contrast.	Can allow faster image acquisition, but at a reduction of SNR by 1/parallelization factor, holding all other factors constant. Will increase temporal noise resulting from head motion, respiration, or pulsatile effects.
Nacq	The number of acquisitions that are acquired and subsequently averaged.	Improves SNR, does not make sense for fMRI, but commonly used for dMRI.