Ab Initio Path-Integral Calculations of Kinetic and Equilibrium Isotope Effects on Base-Catalyzed RNA Transphosphorylation Models

Abstract

Detailed understandings of the reaction mechanisms of RNA catalysis in various environments can have profound importance for many applications, ranging from the design of new biotechnologies to the unraveling of the evolutionary origin of life. An integral step in the nucleolytic RNA catalysis is self-cleavage of RNA strands by 2′-O-transphosphorylation. Key to elucidating a reaction mechanism is determining the molecular structure and bonding characteristics of transition state. A direct and powerful probe of transition state is measuring isotope effects on biochemical reactions, particularly if we can reproduce isotope effect values from quantum calculations. This paper significantly extends the scope of our previous joint experimental and theoretical work in examining isotope effects on enzymatic and non-enzymatic 2′-O-transphosphorylation reaction models that mimic reactions catalyzed by RNA enzymes (ribozymes), and protein enzymes such as ribonuclease A (RNase A). Native reactions are studied, as well as reactions with thio substitutions representing chemical modifications often used in experiments to probe mechanism. Here, we report and compare results from eight levels of electronic-structure calculations for constructing the potential energy surfaces in kinetic and equilibrium isotope effects (KIE and EIE) computations, including a “gold-standard” coupled-cluster level of theory [CCSD(T)]. In addition to the widely-used Bigeleisen equation for estimating KIE and EIE values, internuclear anharmonicity and quantum tunneling effects were also computed using our recently-developed ab initio path-integral method, i.e., automated integration-free path-integral (AIF-PI) method. The results of this work establish an important set of benchmarks that serve to guide calculations of KIE and EIE for RNA catalysis.

Introduction

Elucidation of RNA catalytic mechanisms has a wide range of implications and applications, from the evolutionary origin of life and cell signaling to the design of new biotechnologies and therapeutics.^[1–7] Of particular importance are the nucleolytic RNA enzymes (ribozymes) that catalyzes a 2′-O-transphosphorylation for the self-cleavage processes of RNA strands. ^[1–17] Every potential reaction path associated with the 2′-O-transphosphorylation is characterized by its own rate-limiting transition state, which, by its nature (in contrast to reactant and product states), is unstable and thus is very hard to be captured in experiment (it is also generally true for other biochemical reactions as well). As a result, determining the molecular structure and bonding of the rate-limiting transition state is a key component in unraveling the catalytic mechanisms of these ribozymes.^{[8–11, 18–29]}

To shed some light on the nature of the transition-state structure and bonding, studying equilibrium and kinetic isotope effects (EIE and KIE) on a biochemical reaction is a popular and powerful approach.^{[8, 9, 18–22, 26–29]} The EIE is defined as the ratio of equilibrium constant of light isotope to that of heavy isotope:

$$\text{EIE}\equiv \frac{\text{Equilibrium}\text{constant}(\text{light}\text{isotope})}{\text{Equilibrium}\text{constant}(\text{heavy}\text{isotope})}$$ (1)

And the KIE is defined as the ratio of reaction rate of light isotope to that of heavy isotope:

$$\text{KIE}\equiv \frac{\text{Rate}(\text{light}\text{isotope})}{\text{Rate}(\text{heavy}\text{isotope})}$$ (2)

If KIE value is larger than unity, then we call it as “normal KIE” because the reaction rate of light isotope is faster than that of heavy isotope. On the contrary, an “inverse KIE” means that the KIE value is smaller than unity, i.e., the reaction rate of light isotope is slower than that of heavy isotope. This reaction rate ratio, i.e., KIE, is very sensitive to the rate-limiting transition state. Therefore, measuring KIE values has been considered as a (most) direct and powerful experimental probe of transition state.^{[8, 9, 18–22, 26–29]} Furthermore, for some cases of 2′-O-transphosphorylation, the O2′ position may or may not be deprotonated in a pre-equilibrium step. Hence, it is also important to study the EIE on the 2′-OH deprotonation as well.^{[8, 9, 30]}

Nevertheless, such important experimental numerical values cannot directly tell us what the structure of the rate-limiting transition state precisely is. As a result, isotope effects computation and computational visualization provide us with a complementary approach for identifying the structure of the rate-limiting transition state.

This is because, in contrast to experiment, prior to calculating the numerical values of isotope effects, we first hypothesize a reaction path to determine an explicit molecular structure of the rate-limiting transition state.^{[8–11, 18–29]} Subsequently, we would like to validate whether or not our computed isotope-effect values associated with the hypothetical transition-state structure match with experimental results. If so, then we can safely conclude that the enzymatic mechanism, along with the molecular structure, bonding, and other properties of the rate-limiting transition state, are successfully determined in silico that otherwise can only be qualitatively inferred.^{[8, 9, 18–22, 26–29]}

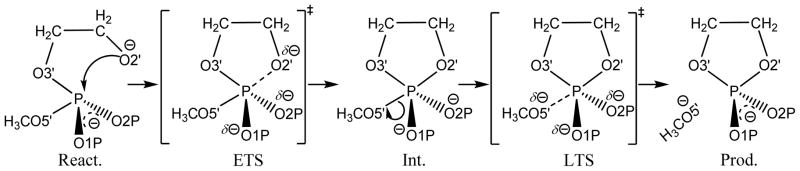
Indeed, previously, a collaborative computational and experimental investigation has been coordinated to study the isotope effects on the base-catalyzed RNA transphosphorylation. As demonstrated in our previous communication,^[9] a simplest model for studying the essence of the transphosphorylation is the reverse, dianionic, in-line methanolysis of ethylene phosphate. The general mechanism of the methanolysis is shown in Scheme 1, in which the phosphoryl oxygen positions are labeled in accordance with their RNA counterparts.

Scheme 1.

General reaction scheme for the (associative) reverse of dianionic in-line methanolysis of ethylene phosphate: a model for RNA phosphate transesterification under alkaline conditions. “React.”, “ETS”, “Int.”, “LTS”, and “Prod.” stand for reactant, early transition state, intermediate, late transition state, and product, respectively. In the present work, the native reaction in the scheme is studied in both gas and solution phases as well as reactions that have single sulfur substitutions in the bridging 3′- (S3′) and leaving group 5′-positions (S5′). Note: as revealed by our calculations, not all of the states in the scheme exist for every reaction (see text for details).

In that communication,^[9] the free-energy profile^{[31, 32]} for the reaction mechanism illustrated in Scheme 1 was generated via molecular dynamics (MD) simulations^[33] using potential energy constructed on the fly by density-functional quantum mechanical/molecular mechanical (QM/MM) approach in explicit solvent.^[31] These high-level and expensive free-energy simulations were performed with a modified version of the CHARMM program (based on c36a2 version),^[34] interfacing with the Q-Chem program.^[35] As a result, the dynamic fluctuations of the solute and the degrees of freedom of the water molecules are all incorporated. In addition, the adiabatic energy profile was also determined by implicit solvent of the polarizable continuum model (PCM).^[36–41] The levels of density-functional theory (DFT)^{[42, 43]} for both profiles in explicit and implicit solvation models are the same, which are the hybrid B3LYP^[44] exchange-correlation functional with the 6-31+G(d) basis set.^{[45, 46]} We have concluded that the DFT QM/MM free-energy profile and the PCM adiabatic energy profile are quite similar.^[9] Both are in an associative mechanism and possess early and late transition states (ETS and LTS). Both LTS are the rate-limiting transition states, with 24.1 and 21.0 kcal/mol barriers, respectively.^[9] The calculated PCM barrier (21.0 kcal/mol) is close to the experimental derived rate for UpG phosphate transesterification (19.9 kcal/mol), extrapolated at the infinite pH limit.^[9] Moreover, the calculated and experimental KIE values are also in good agreement, in particular our calculations clearly indicate that the rate-limiting transition state is shifted from LTS to ETS with thio substitution at either 3′ or 5′ position. All these results suggest that our PCM calculations are able to describe the core of the solvent effects on the energy profile for computing the KIE and EIE values.

Subsequently, another coordinated work of experiment and theory about isotope effects was just published for determining the altered transition-state structures of the 2′-O-transphosphorylation catalyzed by ribonuclease A (RNase A).^[8]

By virtue of all these successful stories about the computations on isotope effects on the 2′-O-transphosphorylation, there has been a definite need for a detailed comparative study on the accuracy, robustness, and computing time at various levels of electronic-structure and internuclear quantum theories. As a result, in this article, KIE and EIE calculations on the base-catalyzed RNA transphosphorylation in both gas and solution phases at a total of eight different levels of electronic-structure theory are reported. These eight levels of theory for constructing the potential energy surfaces range from the single-Slater-determinant Hartree-Fock method (HF)^{[45, 46]} and two popular density-functional theories (DFT),^{[42–44, 47, 48]} to the multi-Slater-determinant Møller-Plesset (MP) perturbation method,^{[45, 49]} single-and-double-substitution coupled-cluster CCSD theory, and a “gold-standard” partial-triple-substitution coupled-cluster CCSD(T) theory.^{[45, 50, 51]} And the three basis sets that were tested are 3-21+G*, 6-31+G(d), and 6-311+G(d,p).^{[45, 46]} Furthermore, internuclear quantum-statistical effects were taken care by the conventional Bigeleisen equation^{[8, 9, 22, 52, 53]} as well as by our recently developed automated integration-free path-integral (AIF-PI) method for calculating anharmonicity and quantum tunneling effects.^{[9, 22, 31, 54–56]} We hope our benchmark reported herein can establish a mini database serving a guide for future more accurate and more efficient isotope-effect computations and free-energy simulations on more complex biomolecular systems of RNA catalysis.

Computational Details

The molecular structures of the native and thio-substituted anionic and dianionic reactants, and the transition-state structures were minimized in the gas phase and in aqueous solution using Hartree-Fock theory,^45,46 second order Møller-Plesset perturbation method (MP2),^45,49 and density-functional theory (DFT),^{[42–44, 47, 48]} with the inclusion of the polarizable continuum model (PCM)^[36–41] for treating the solvent effects. Two popular hybrid-exchange-correlation density-functionals, B3LYP^[44] and M06-2X,^{[47, 48]} were employed. The three different basis sets we used in this work are those most frequently used in biomolecular applications: 3-21+G*, 6-31+G(d), and 6-311+G(d,p).^45,46 Coupled-cluster single-point energy calculations at the levels of CCSD/6-311+G(d,p) and “gold-standard” CCSD(T)/6-311+G(d,p)^45,50,51 were performed on each of the minimized structures in both gas and solution phases. Vibrational frequency analyses were carried out to confirm the nature of the minimum and saddle points, and to compute quantum thermal corrections in the decoupled rigid-rotor harmonic-oscillator approximation.^[57] The software package Gaussian 09 was used for all the electronic-structure calculations.^[41] An essential feature of Gaussian 09 that enables these calculations to be performed was the implementation of a continuous surface charge formalism based on a smooth boundary element solvation method that afforded continuity, smoothness, and robustness of the solvent reaction field and its derivatives with respect to nuclear positions.^[36–41] We have used the UAKS radii optimized at the PB0/6-31G(d) level of theory^57,58 to define the molecular cavity for the PCM model,^{[58, 59]} with special tuning of the 2′-OH, and X5′ positions so as to be fixed along the reaction coordinate and close to the QM/MM and experimental barrier values. All fixed atomic radii used in the present work, and the gas-phase and solution-phase minimized structures are given in the Supporting Information.

The most widely-used formalism to compute equilibrium and kinetic isotope effects (EIE and KIE) is the Bigeleisen equations^{[8, 9, 22, 52, 53]} (fulfilling the Redlich-Teller product rule^{[52, 53]}), in which the EIE and KIE are evaluated in terms of harmonic vibrational frequencies, and neglecting quantum tunneling:

$${\text{EIE}}_{\text{BE}}=\frac{{\displaystyle \prod _{i=1}^{3N-6}}\frac{{\mathrm{\Omega }}_{i,l_0}^P/sinh\left(\beta \hslash {\mathrm{\Omega }}_{i,l_0}^P/2\right)}{{\mathrm{\Omega }}_{i,h_0}^P/sinh\left(\beta \hslash {\mathrm{\Omega }}_{i,h_0}^P/2\right)}}{{\displaystyle \prod _{i=1}^{3N-6}}\frac{{\mathrm{\Omega }}_{i,l_0}^R/sinh\left(\beta \hslash {\mathrm{\Omega }}_{i,l_0}^R/2\right)}{{\mathrm{\Omega }}_{i,h_0}^R/sinh\left(\beta \hslash {\mathrm{\Omega }}_{i,h_0}^R/2\right)}}$$ (3)

$${\text{KIE}}_{\text{BE}}=\left(\frac{{\omega }_{l_0}^{‡}}{{\omega }_{h_0}^{‡}}\right)\frac{{\displaystyle \prod _{i=1}^{3N-7}}\frac{{\mathrm{\Omega }}_{i,l_0}^{‡}/sinh\left(\beta \hslash {\mathrm{\Omega }}_{i,l_0}^{‡}/2\right)}{{\mathrm{\Omega }}_{i,h_0}^{‡}/sinh\left(\beta \hslash {\mathrm{\Omega }}_{i,h_0}^{‡}/2\right)}}{{\displaystyle \prod _{i=1}^{3N-6}}\frac{{\mathrm{\Omega }}_{i,l_0}^R/sinh\left(\beta \hslash {\mathrm{\Omega }}_{i,l_0}^R/2\right)}{{\mathrm{\Omega }}_{i,h_0}^R/sinh\left(\beta \hslash {\mathrm{\Omega }}_{i,h_0}^R/2\right)}}$$ (4)

where ħ is Planck’s constant divided by 2π, β = 1/k_BT, k_B is Boltzmann’s constant, T is absolute temperature, the superscripts ‡, P, and R denote the transition state, product state, and reactant state, respectively, ω^‡ is the imaginary frequency at the transition state, l₀ indicates the light isotope and h₀ is the heavy isotope, N is the number of nuclei, i is the index running over all normal modes, and Ω_i is the real frequency for the ith normal mode.

To go beyond the harmonic approximation and to include quantum tunneling effects in the framework of the Feynman centroid path integral, we refine the Bigeleisen equations as follows:^{[9, 22, 60]}

$${\text{EIE}}_{\text{PI}}=\frac{exp\left[-\beta \left(W_{l_0}^P-W_{h_0}^P\right)\right]}{exp\left[-\beta \left(W_{l_0}^R-W_{h_0}^R\right)\right]}$$ (5)

$${\text{KIE}}_{\text{PI}}=\left(\frac{{\omega }_{l_0}^{‡}}{{\omega }_{h_0}^{‡}}\right)\frac{exp\left[-\beta \left(W_{l_0}^{‡}-W_{l_0}^{‡}\right)\right]}{exp\left[-\beta \left(W_{l_0}^R-W_{h_0}^R\right)\right]}$$ (6)

where W is the centroid effective potential energy calculated at the centroid position of path integrals.^{[31, 54, 61–69]} The mass (isotope) and temperature dependent nature of the centroid potential energy W distinguishes itself from the (ab initio) Born-Oppenheimer potential energy. The latter is independent of (nuclear) mass and temperature. Note that our refined Bigeleisen equations, i.e., Eq. (5) and Eq. (6), reduce back to the well-known Bigeleisen equations [i.e., Eq. (3) and Eq. (4)] when the centroid potential is computed in the decoupled rigid-rotor harmonic-oscillator approximation (and neglecting tunneling effects; Appendix B in Ref. [^[60]] provides a proof). In addition, Eq. (5) and Eq. (6) are consistent with the path-integral transition-state theory (PI-QTST),^{[65, 67, 70–72]} and the reaction coordinate is defined as the centroid positions of nuclear coordinates, which in turn are the imaginary time-average positions of nuclei. The mass-dependent property of the centroid potential in the formulation of the PI-QTST has also been applied to chemical reactions in condensed phases.^{[63–67, 70, 73–81]}

In this work, with the treatment of solvent effects by a dielectric continuum, we used our automated integration-free path-integral (AIF-PI) method^{[31, 54–56]} to determine the values of W, and then in turn used Eq. (5) and Eq. (6) to compute primary EIE and KIE values along the reaction path of intrinsic reaction coordinate (IRC) on the ab initio potential energy surface.^{[9, 22]} Our AIF-PI method is based on the powerful and remarkably accurate Kleinert’s variational perturbation (KP) theory [which has been shown accurate even at the limit of zero temperature (absolute zero)],^{[61, 82–87]} and makes use of the decoupled instantaneous normal coordinate approximation (DINCA) to render the KP theory be applicable to actual molecular systems.^{[31, 54–56, 88]} Our previous studies on a series of proton-transfer reactions demonstrate that performing ab initio path-integral calculations with our AIF-PI method can accurately and economically include anharmonicity and tunneling contributions to the KIE values calculated from Eq. (6). These two contributions are important in order to have quantitative agreement with experimental results.^[22] Furthermore, we also have successfully used our AIF-PI method to compute KIE on heavy atoms.^[9] Since the molecular structures at the stationary points of the original gas-phase and solution-phase Born-Oppenheimer potential energy surfaces (PES) should be similar to those on the gas-phase and solution-phase centroid PES (their difference is usually in the order of magnitude of about 0.01 Å),^[56] the molecular structures of the reactant and transition states were not re-optimized on the basis of the centroid potential.^{[9, 22]}

In the AIF-PI method, we interpolated the original gas-phase and solution-phase PES along each normal mode by a twentieth order polynomial at a step size of 0.1 Å.^{[31, 54–56]} The centroid potential is computed up to the second order of Kleinert’s variational perturbation expansion. Thus, the notation for this level of theory is KP2/P20, where Pm denotes an mth order polynomial representation of the original PES along each normal mode coordinate. Through a series of rigorous tests, we found that KP2/P20 is generally a good choice for the AIF-PI method. The calculated values of the centroid potential are usually within a few percent from the exact.^{[31, 54–56]}

In this work, the entire system is quantized (16 or more atoms) to compute harmonic or Bigeleisen EIE and KIE values. Additionally, for estimating the anharmonic and tunneling effect corrections to the Bigeleisen EIE and KIE values, we further quantize the following six to seven nuclei using the AIF-PI method: the phosphorus atom and all the five (oxygen or sulfur) atoms that can potentially form covalent bonds to the phosphorus atom, including the O2′ of nucleophile and X5′ of leaving groups, in addition to the hydrogen connected with the O2′ (i.e., the H of 2′-OH) for the case of anionic ethylene phosphate bonded with methanol group. All our path-integral calculations were performed using our AIF-PI program implemented for use with Mathematica.^[89]

Results and Discussion

Computational Costs

Table 1 shows the computational costs of all eight levels of electronic structure theory, in terms of the computing times of single-point energy, force, and frequency calculations on the LTS structure of the native reaction in solution, using four processors and sharing 4GB Memory. HF/3-21+G* indeed is the computationally cheapest level of theory. DFT methods with the larger basis sets, 6-31+G(d) and 6-311+G(d,p), are obviously more computationally expensive, though are still affordable [e.g., the computing time for a frequency analysis at the level of M06-2X/6-311+G(d,p) is about 17 minutes].

Table 1.

Computing times of single-point energy, force, and frequency calculations at the eight levels of electronic structure theory. The number of basis functions in this table for 3-21+G*, 6-31+G(d), and 6-311+G(d,p) are 141, 189, and 248, respectively. All calculations were performed with four processors of Intel Xeon E7-4870 2.40GHz, sharing 4GB memory of 1066MHz quad ranked LV RDIMMs, on a single-compute-node machine (jiraiya) that has forty processors of Intel Xeon E7-4870 2.40GHz (4×10C), sharing 1TB memory of 1066MHz quad ranked LV RDIMMs (64×16GB). The LTS structures are the optimized structures in solution respectively for each level of theory, except for CCSD and CCSD(T) single-point energy calculations. In these CCSD and CCSD(T) calculations, we used the optimized structure in solution at the MP2/6-311+G(d,p) level.

Native LTS in Solution	4 processors, 4GB Memory Computing Time (hh:mm:ss)[a]
Electronic Struct. Theory	Energy	Force	Frequency
HF/3-21+G*	00:00:09	00:00:13	00:01:07
B3LYP/6-31+G(d)	00:00:34	00:00:42	00:04:35
M06-2X-6-31+G(d)	00:00:48	00:00:57	00:06:32
B3LYP/6-311+G(d,p)	00:01:17	00:01:34	00:11:25
M06-2X/6-311+G(d,p)	00:01:26	00:01:45	00:17:35
MP2/6-311+G(d,p)	00:01:19	00:04:04	02:10:38
CCSD/6-311+G(d,p)	01:51:14	--[b]	--[b]
CCSD(T)/6-311+G(d,p)	04:54:00	--[b]	--[b]

^[a] hh = hours in two digits, mm = minutes in two digits, ss = seconds in two digits.

^[b] The calculation was not performed.

Noteworthily, the computational cost for a single-point energy calculation at the MP2/6-311+G(d,p) level is virtually the same as those calculations at a DFT level using the same basis set. Nevertheless, the force and frequency analysis at the MP2 level are (significantly) more computationally expensive than the DFT methods, particularly true for the frequency analysis.

According to Table 1, CCSD is so computationally expensive that its single-point energy calculation took more or less the same amount of time as a frequency analysis at the MP2 level. The computational cost grows even much more terrifically for the “gold standard” CCSD(T) level of theory, as its single-point energy calculation took more than double of the computing time for a single-point energy calculation at the CCSD level.

As shown in Table S1 (Supporting Information), similar conclusions as the above can be drawn when we increase the number of processors and the amount of the sharing memory from four to sixteen, and from 4GB to 100GB, respectively. One final remark is that the computing time for a single-point energy calculation at the CCSD(T) level using sixteen processors is more or less the same as a frequency analysis at the MP2 level using four processors.

Energetics

Table 2 lists the energy values for stationary points of the native and thio-substituted S3′ and S5′ reactions in both gas and solution phases, calculated at the six different levels of electronic structure theory. The corresponding energy profiles in both gas and solution phases at MP2/6-311+G(d,p) level are shown in Figure 1. By comparing the results between gas and solution phases, it is clear that the solvation effects greatly reduce the rate-limiting barriers for all reactions. The extent of the reduction is most profound for the native reaction (by ~20 to 30 kcal/mol), followed by the S3′ reaction (by ~15 to 20 kcal/mol), and then the S5′ reaction (by ~10 to 15 kcal/mol).

Table 2.

Single-level relative free energy calculated for stationary points along the intrinsic reaction coordinate of the (A) native, (B) S3′, and (C) S5′ simplest models of RNA transphosphorylation in both gas and solution phases.^[a]

Native (37°C)	Gas (kcal/mol)			Solution (kcal/mol)
Electronic Struct. Theory	ΔG‡ETS	ΔGInt	ΔG‡LTS	ΔG‡ETS	ΔGInt	ΔG‡LTS
HF/3-21+G*	--	--	57.8	23.6	23.2	29.1
B3LYP/6-31+G(d)	--	--	41.3	18.6	18.3	21.0
M06-2X/6-31+G(d)	--	--	41.6	15.5	13.5	19.2
B3LYP/6-311+G(d,p)	--	--	41.1	18.5[b]	--[c]	20.9
M06-2X/6-311+G(d,p)	--	--	42.2	15.2	13.9	19.4
MP2/6-311+G(d,p)	--	--	41.4	17.7	17.4	20.7
(A)

S3′ (37°C)	Gas (kcal/mol)			Solution (kcal/mol)
Electronic Struct. Theory	ΔG‡ETS	ΔGInt	ΔG‡LTS	ΔG‡ETS	ΔGInt	ΔG‡LTS
HF/3-21+G*	40.8	--[c]	39.9	20.2	17.0	20.3
B3LYP/6-31+G(d)	34.6	34.0	35.5	16.9	16.0	17.8
M06-2X/6-31+G(d)	33.0	29.4	34.4	13.7	9.5	14.4
B3LYP/6-311+G(d,p)	33.8	33.5	34.7	16.3	15.9	17.2
M06-2X/6-311+G(d,p)	31.9	28.7	33.6	12.7[d]	9.1[d]	13.4[d]
MP2/6-311+G(d,p)	32.4	31.4	33.2	15.8	14.0	16.4
(B)

S5′ (37°C)	Gas (kcal/mol)			Solution (kcal/mol)
Electronic Struct. Theory	ΔG‡ETS	ΔGInt	ΔG‡LTS	ΔG‡ETS	ΔGInt	ΔG‡LTS
HF/3-21+G*	35.8	--	--	19.5	--	--
B3LYP/6-31+G(d)	26.6	--	--	16.6	--	--
M06-2X/6-31+G(d)	26.4	--	--	13.1	--	--
B3LYP/6-311+G(d,p)	25.9	--	--	16.4	--	--
M06-2X/6-311+G(d,p)	25.6	--	--	13.2	--	--
MP2/6-311+G(d,p)	27.0	--	--	15.7	--	--
(C)

^[a] Thermal corrections of free energy are computed in the decoupled rigid-rotor harmonic-oscillator approximation. The PCM energy profiles shown in Figure 1 are shifted by thermal corrections at their respective rate-limiting transition states. “--” denotes the molecular structure of that particular state could not be determined.

^[b] The ETS is determined but along with very small value of non-reactive imaginary frequency.

^[c] No intermediate could be determined by us that satisfies all default criteria in Gaussian 09.^[41]

^[d] The reactant is determined but along with very small value of non-reactive imaginary frequency.

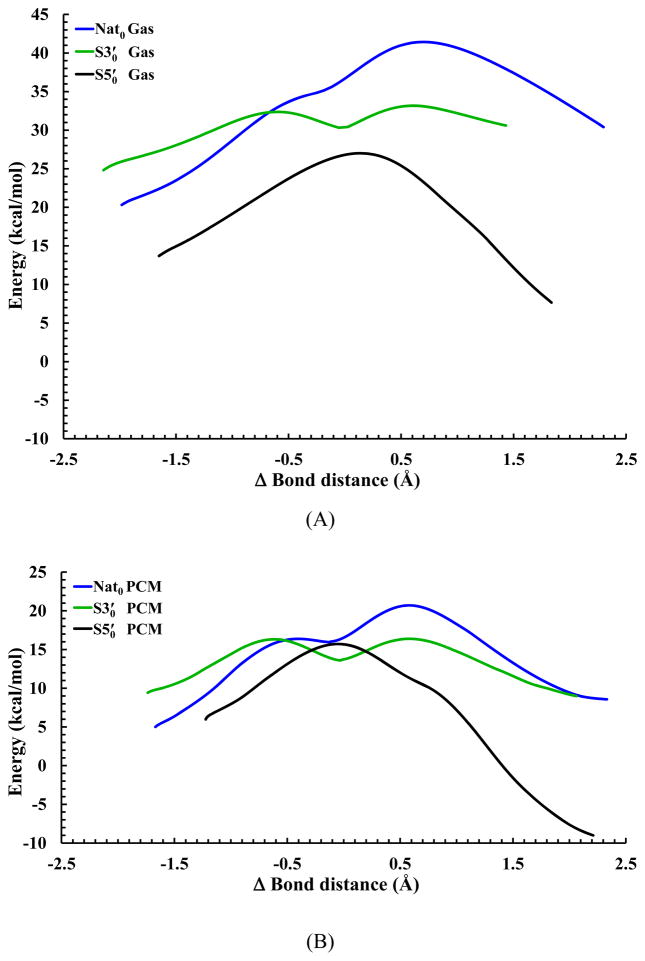
Figure 1.

Adiabatic energy profiles for the native, S3′, and S5′ simplest models of RNA transphosphorylation in both (A) gas and (B) solution phases, as a function of the difference in bond length (Δbond) between the breaking P—X5′ bond (X = O for native and S3′; X = S for S5′) and the forming P—O2′ bond (Δbond = P—X5′ - P—O2′). The level of all the electronic structure calculations is at MP2/6-311+G(d,p). The profiles are mapped from the intrinsic reaction coordinate paths and have been shifted to match the respective rate-limiting free-energy barriers calculated in the decoupled rigid-rotor harmonic-oscillator approximation at 37°C. Other than this shift, however, there is no zero-point energy or thermal corrections included in the profiles.

In the gas-phase native reaction, neither ETS nor intermediate (Scheme 1) could be determined at all six levels of theory. However, the polarization by the aqueous environment stabilizes the pentavalent phosphorane more than the LTS, which in turn induces a non-rate-limiting ETS and a transient intermediate in the solution-phase native reaction at all six levels of theory, except interestingly, no intermediate could be located at the B3LYP/6-311+G(d,p) level that satisfies all default criteria in Gaussian 09.^[41]

In contrast to the gas-phase native reaction, both ETS and metastable intermediate do exist in the gas-phase S3′ reaction at all six levels of theory, except interestingly, no intermediate could be located at the HF/3-21+G* level that satisfies all default criteria in Gaussian 09.^[41] For the S5′ reaction in both gas and solution phases, as opposed to both native and S3′ reactions, only ETS can be determined. There is no LTS, and thus no transient intermediate can be located at all six levels of theory.

In addition to these six levels of theory, we have also carried out expensive single-point-energy coupled-cluster electronic-structure calculations, up to the “gold standard” CCSD(T)/6-311+G(d,p) level,^45,50,51 on the stationary points of these six levels of theory, i.e., dual-level calculations. Results are presented in Table 3 for CCSD(T) and Table S2 (Supporting Information) for CCSD, in which all single-point CCSD(T) and CCSD energy calculations are only for electronic structure, and are not included in the nuclear thermal corrections. By comparing the results between Table 2 and Table 3, it is evident that among those six single levels of theory, MP2/6-311+G(d,p) is the most accurate for our simplest models of RNA phosphate transesterification. This is because as shown in Table S3 (Supporting Information), the theory that exhibits the smallest root-mean-square deviation (RMSD) between its single-level calculations, and its counterpart of dual-level CCSD(T)/6-311+G(d,p) single-point energy calculations is MP2/6-311+G(d,p). This RMSD of MP2/6-311+G(d,p) is merely 0.2 kcal/mol (the largest deviation is just 0.3 kcal/mol). In other words, it should also be safely to interpret that among all single and dual levels of theory presented in this paper (a total of twelve levels of theory), the most accurate calculations for our simplest models of RNA transphosphorylation are at the CCSD(T)/6-311+G(d,p)//MP2/6-311+G(d,p) dual level.

Table 3.

Dual-level CCSD(T) relative free energy calculated for stationary points along the intrinsic reaction coordinate of the (A) native, (B) S3′, and (C) S5′ simplest models of RNA transphosphorylation in both gas and solution phases.^[a]

Native (37°C)	Gas (kcal/mol)			Solution (kcal/mol)
Electronic Struct. Theory CCSD(T)/6-311+G(d,p) //	ΔG‡ETS	ΔGInt	ΔG‡LTS	ΔG‡ETS	ΔGInt	ΔG‡LTS
HF/3-21+G*	--	--	40.8	17.5	17.5	20.2
B3LYP/6-31+G(d)	--	--	41.3	17.4	17.0	20.3
M06-2X/6-31+G(d)	--	--	41.0	17.1	17.3	20.1
B3LYP/6-311+G(d,p)	--	--	41.5	17.2[b]	--[c]	20.2
M06-2X/6-311+G(d,p)	--	--	41.4	17.2	17.1	20.2
MP2/6-311+G(d,p)	--	--	41.1	17.6	17.5	20.5
(A)

S3′ (37°C)	Gas (kcal/mol)			Solution (kcal/mol)
Electronic Struct. Theory CCSD(T)/6-311+G(d,p) //	ΔG‡ETS	ΔGInt	ΔG‡LTS	ΔG‡ETS	ΔGInt	ΔG‡LTS
HF/3-21+G*	32.2	--[c]	33.5	16.0	14.7	16.2
B3LYP/6-31+G(d)	32.3	31.4	33.5	15.0	13.5	15.7
M06-2X/6-31+G(d)	32.8	32.6	33.5	14.9	13.6	15.1
B3LYP/6-311+G(d,p)	32.3	31.5	33.8	15.0	13.6	15.9
M06-2X/6-311+G(d,p)	32.2	32.0	33.2	14.4[d]	13.1[d]	14.7[d]
MP2/6-311+G(d,p)	32.2	31.6	33.0	15.5	14.2	16.2
(B)

S5′ (37°C)	Gas (kcal/mol)			Solution (kcal/mol)
Electronic Struct. Theory CCSD(T)/6-311+G(d,p) //	ΔG‡ETS	ΔGInt	ΔG‡LTS	ΔG‡ETS	ΔGInt	ΔG‡LTS
HF/3-21+G*	25.9	--	--	15.6	--	--
B3LYP/6-31+G(d)	26.5	--	--	16.3	--	--
M06-2X/6-31+G(d)	27.1	--	--	15.5	--	--
B3LYP/6-311+G(d,p)	26.7	--	--	16.5	--	--
M06-2X/6-311+G(d,p)	26.7	--	--	15.8	--	--
MP2/6-311+G(d,p)	26.8	--	--	15.7	--	--
(C)

^[a] CCSD(T) is not included in the thermal corrections. “--” denotes the molecular structure of that particular state could not be determined.

^[b] As in Table 2, the ETS is determined but along with very small value of non-reactive imaginary frequency.

^[c] As in Table 2, no intermediate could be determined by us that satisfies all default criteria in Gaussian 09.^[41]

^[d] As in Table 2, the reactant is determined but along with very small value of non-reactive imaginary frequency.

Yet, a very notable finding in this paper is actually located by comparing the results among Table S3, Table S4, and Table S5 (Supporting Information). As shown in Table S3 (Supporting Information), the RMSD of HF/3-21+G* from its dual-level CCSD(T) counterpart is obviously the largest, at the huge value of 8 kcal/mol, and the same largest huge value of 8 kcal/mol is also found in Table S4 (Supporting Information) that lists RMSD of all six single levels of calculations with respect to CCSD(T)/6-311+G(d,p)//MP2/6-311+G(d,p) (which should be the most accurate level of theory considered in this paper). However, the RMSD between the dual-level CCSD(T) of HF/3-21+G* and the dual-level CCSD(T) of MP2/6-311+G(d,p) is only 0.4 kcal/mol, which is (tied at) the smallest value comparing to all other four levels of theory listed in Table S5 (Supporting Information). All these striking results about dual-level calculations could serve as an important precursor towards some future work of high-level and affordable on-the-fly ab initio QM/MM free-energy simulations for actual RNA catalysis. This is because oftentimes even in molecular simulations, it could be possible to treat the entire active site on the fly at the HF/3-21+G* level for the purpose of sampling the phase space. Subsequently, we could systematically refine the ab initio QM/MM free-energy profile by means of a free-energy perturbation method with a small number of high-level calculations.

According to Table S3, Table S4, and Table S5 (Supporting Information), the overall performances of two popular density functionals, B3LYP and M06-2X, are quite similar [and definitely better than single-level HF/3-21+G*], though B3LYP might have the edge, in particular M06-2X tends to overstabilize the transient intermediates for both native and S3′ reactions quite a bit (Table 2). Interestingly, increasing the size of basis set from 6-31+G(d) to 6-311+G(d,p) does not necessarily increase the accuracy for both B3LYP and M06-2X functionals at either single [Table S4 (Supporting Information)] or dual levels [Table S5 (Supporting Information)]; however, their respective dual-level counterparts with single-point energy of CCSD(T)/6-311+G(d,p) still oftentimes improve the accuracy of the single level [Table S3 (Supporting Information)]. Note that the M06-2X overstabilization of the transient intermediates in both gas and solution phases has been generally rescued by dual level calculations, but the dual-level energy for the native intermediate minimized at the M06-2X/6-31+G(d) somehow is higher than the corresponding dual-level energy for the ETS by about 0.2 kcal/mol (Table 3). In comparison, for the case of the dual-level CCSD(T) of MP2/6-311+G(d,p) (i.e., the most accurate level considered in this paper), the energy of the metastable native intermediate is actually about 0.1 kcal/mol lower than the ETS.

CCSD(T) is generally considered as “gold standard”.^45,50,51 By comparing Table 3 with Table S2 (Supporting Information), we can see that the performance of the single-point-energy calculations at the CCSD level [without (T)] is actually not that close to those at the CCSD(T) level. In Table S6 (Supporting Information), we lists the RMSD between single-level calculations, and their respective counterparts of dual-level calculations that have single-point energy of CCSD/6-311+G(d,p). In contrast to the case for CCSD(T) shown in Table S3 (Supporting Information), this time for CCSD, no level of theory can have RMSD smaller than 1 kcal/mol [Table S6 (Supporting Information)]. Moreover, from Table S7 (Supporting Information), all six dual-level calculations with single-point energy of CCSD/6-311+G(d,p) exhibit RMSD of ~1 to 2 kcal/mol from our most accurate level of theory: CCSD(T)/6-311+G(d,p)//MP2/6-311+G(d,p).

With regard to the agreement between the calculated barriers with experiment, in Table 4 we present the most relevant available experimental results that we have found in the literature for the native, S3′, and S5′ reactions in solution. Note that none of experimental results shown in Table 4 is the actual methanolysis of ethylene phosphate that we calculated in this paper (Scheme 1). Most of the experiments are RNA transphosphorylation of dinucleotides with different combinations of the nucleobases, and often under different experimental conditions.

Table 4.

Most relevant available experimental results of (A) native, (B) S3′, and (C) S5′ reactions in solution to compare with the calculated barriers of our simplest models of RNA phosphate transesterification. “--” denotes the experimental data could not be found.

Native pH	Liu et al.[a]		Harris et al.[b]		Iyer et al.[c]		Thomson et al.[d]		Weinstein et al.[e]		Dantzman et al.[f]
	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)
8	--	--	54266	27.6	--	--	--	--	--	--	12[m]	21.5
9	--	--	5427	26.2	--	--	--	--	--	--	--	--
10	--	--	543	24.8	--	--	--	--	7289[j]	24.1	--	--
10.06	4800[i]	27.3[i]	473	24.7	--	--	--	--	--	--	--	--
11	--	--	54	23.4	--	--	--	--	729[k]	22.8	--	--
11.5	--	--	17	22.7	--	--	825	25.1	--	--	--	--
12	--	--	6	22	--	--	--	--	--	--	--	--
13	--	--	0.7	20.7	--	--	--	--	37[l]	21.1	--	--
Infinity	--	--	0.2	19.9	--	--	--	--	--	--	--	--
(A)

S3′ pH	Liu et al.[a]		Harris et al.[b]		Iyer et al.[c]		Thomson et al.[d]		Weinstein et al.[e]		Dantzman et al.[f]
	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)
8	--	--	--	--	--	--	--	--	--	--	--	--
9	--	--	--	--	11552[i]	30.5	--	--	--	--	--	--
10	--	--	--	--	5403[j]	30	--	--	7[o]	20.2	--	--
10.06	25	23.9	--	--	--	--	--	--	--	--	--	--
11	--	--	--	--	650[k]	28.5	--	--	0.4[p]	18.5	--	--
11.5	--	--	--	--	249[l]	27.8	--	--	--	--	--	--
12	--	--	--	--	87[m]	27.1	--	--	--	--	--	--
13	--	--	--	--	20.5[n]	26	--	--	0.02[q]	16.8	--	--
Infinity	--	--	--	--	--	--	--	--	--	--	--	--
(B)

S5′ pH	Liu et al.[a]		Harris et al.[b]		Iyer et al.[c]		Thomson et al.[d]		Weinstein et al.[e]		Dantzman et al.[f]
	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)	t1/2[g] (min)	Barrier[h] (kcal/mol)
8	132	23.4	--	--	9176[i]	30.3	46[o]	23.3	--	--	--	--
9	29	22.5	--	--	6496[j]	30.1	4	21.7	--	--	--	--
10	--	--	--	--	1155[k]	28.9	--	--	--	--	--	--
10.06	--	--	--	--	--	--	--	--	--	--	--	--
11	--	--	--	--	116[l]	27.3	--	--	--	--	--	--
11.5	--	--	--	--	32.6[m]	26.4	--	--	--	--	--	--
12	--	--	--	--	15.4[n]	25.8	--	--	--	--	--	--
13	--	--	--	--	--	--	--	--	--	--	--	--
Infinity	--	--	--	--	--	--	--	--	--	--	--	--
(C)

^[a] 50°C, UpU, Ref.[^[92–94]].

^[b] 37°C, UpG, Eq. (1) in Ref.[^[14]].

^[c] 80°C, mNB, Ref.[^[91]].

^[d] 37°C, UpU, Ref.[^[95]].

^[e] 10°C, IpU, Ref.[^[90]].

^[f] 25°C, UppNp, Ref.[^[96]].

^[g] If the time of half life (t_1/2) is not given in the reference papers, then t_1/2 is derived from the first order rate constant k as follows: t_1/2 = (ln 2)/k.

^[h] The energy barrier is converted from the rate constant by conventional transition-state theory.

^[i] 4800 to 5400 min, 27.3 to 27.4 kcal/mol.

^[j] The extracted value of k is ~10^−5.8 s⁻¹, from the Fig. 4 in Ref. [^[90]].

^[k] The extracted value of k is ~10^−4.8 s⁻¹, from the Fig.4 in Ref. [^[90]].

^[l] The extracted value of k is ~10^−3.5 s⁻¹, from the Fig. 4 in Ref. [^[90]].

^[m] The extracted value of k is ~10⁻³ s⁻¹, from the Fig. 3 in Ref. [^[96]].

^[a] 50°C, UspU, Ref.[^[92–94]].

^[b] 37°C, UspG, Eq. (1) in Ref.[^[14]].

^[c] 80°C, S3′mNB, Ref.[^[91]].

^[d] 37°C, UspU, Ref.[^[95]].

^[e] 10°C, IspU, Ref.[^[90]].

^[f] 25°C, UsppNp, Ref.[^[96]].

^[g] If the time of half life (t_1/2) is not given in the reference papers, then t_1/2 is derived from the first order rate constant k as follows: t_1/2 = (ln 2)/k.

^[h] The energy barrier is converted from the rate constant by conventional transition state theory.

^[i] The extracted value of k is ~10⁻⁶ s⁻¹, from the Fig. S2 in Ref. [^[91]].

^[j] The extracted value of k is ~10^−5.67 s⁻¹, from the Fig. S2 in Ref. [^[91]].

^[k] The extracted value of k is ~10^−4.75 s⁻¹, from the Fig. S2 in Ref. [^[91]].

^[l] The extracted value of k is ~10^−4.33 s⁻¹, from the Fig. S2 in Ref. [^[91]].

^[m] The extracted value of k is ~10^−3.875 s⁻¹, from the Fig. S2 in Ref. [^[91]].

^[n] The extracted value of k is ~10^−3.25 s⁻¹, from the Fig. S2 in Ref. [^[91]].

^[o] The extracted value of k is ~10^−2.8 s⁻¹, from the Fig. 4 in Ref. [^[90]].

^[p] The extracted value of k is ~10^−1.5 s⁻¹, from the Fig. 4 in Ref. [^[90]].

^[q] The extracted value of k is ~10^−0.2 s⁻¹, from the Fig. 4 in Ref. [^[90]].

^[a] 30°C, UpsU, Ref.[^[92–94]].

^[b] 37°C, UpsG, Eq. (1) in Ref.[^[14]].

^[c] 80°C, S5′mNB, Ref.[^[91]].

^[d] 37°C, UpsU, Ref.[^[95]].

^[e] 10°C, IpsU, Ref.[^[90]].

^[f] 25°C, UpspNp, Ref.[^[96]].

^[g] If the time of half life (t_1/2) is not given in the reference papers, then t_1/2 is derived from the first order rate constant k as follows: t_1/2 = (ln 2)/k.

^[h] The energy barrier is converted from the rate constant by conventional transition state theory.

^[i] The extracted value of k is ~10^−5.9 s⁻¹, from the Fig. S3 in Ref. [^[91]].

^[j] The extracted value of k is ~10^−5.75 s⁻¹, from the Fig. S3 in Ref. [^[91]].

^[k] The extracted value of k is ~10⁻⁵ s⁻¹, from the Fig. S3 in Ref. [^[91]].

^[l] The extracted value of k is ~10⁻⁴ s⁻¹, from the Fig. S3 in Ref. [^[91]].

^[m] The extracted value of k is ~10^−3.45 s⁻¹, from the Fig. S3 in Ref. [^[91]].

^[n] The extracted value of k is ~10^−3.125 s⁻¹, from the Fig. S3 in Ref. [^[91]].

^[o] The extracted value of k is ~10^−3.6 s⁻¹, from the Fig. 2 in Ref. [^[95]].

Nevertheless, by comparing the experimental results of the IpU and IspU reactions measured by Weinstein and Cech et al,^[90] we could conclude that in general S3′ reactions should be faster than the native ones. Similarly, by comparing the experimental results of the S3′mNB and S5′mNB reactions measured by Iyer and Hengge,^[91] we could also conclude that in general S5′ reactions should be faster than S3′ reactions by just a little bit. These two conclusions are consistent with our calculated results (Table 2 and Table 3).

Breaking/Forming Bond Orders and Bond Distances

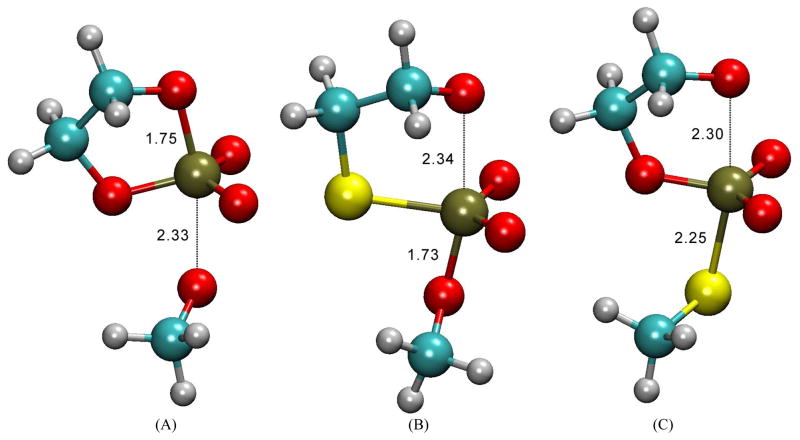
As indirectly suggested by the minimal values of dual-level RMSD in Table S5 (Supporting Information), all values of breaking/forming bond orders and bond distances associated with the transition states shown in Table 5, Table S8 (Supporting Information), and Table 6 (which are all either calculated at single or dual levels) are in fact quite close to one another. They are all virtually within only 0.1 or 0.1 Å from one another for bond orders and distances, respectively. This finding further supports the aforementioned idea that it could be quite possible and accurate to have dual-level and systematic types of on-the-fly ab initio QM/MM free-energy simulations for actual RNA catalysis. Furthermore, according to the data shown in these three tables [Table 5, Table S8 (Supporting Information), and Table 6], we have the same conclusions as in our previous study that the rate-limiting transition states for the native reactions in both gas and solution phases (which are LTS) exhibit cleavage of the exocyclic P—O5′ is advanced. Take the MP2 structure of LTS in solution as an example, P—O5′ distance is 2.33 Å and its bond order is 0.14, whereas P—O2′ bond is at 1.75 Å and its bond order is 0.53 (Figure 2).

Table 5.

Single-level Wiberg bond order (bond index) for stationary points along the intrinsic reaction coordinate of the (A) native, (B) S3′, and (C) S5′ simplest models of RNA transphosphorylation in both gas and solution phases.^[a]

Native	Gas (Å)						Solution (Å)
Electronic Struct. Theory	ETS		Int		LTS		ETS		Int		LTS
	BOO5′	BOO2′	BOO5′	BOO2′	BOO5′	BOO2′	BOO5′	BOO2′	BOO5′	BOO2′	BOO5′	BOO2′
HF/3-21+G*	--	--	--	--	0.11	0.47	0.52	0.28	0.48	0.41	0.18	0.53
B3LYP/6-31+G(d)	--	--	--	--	0.15	0.44	0.50	0.29	0.47	0.40	0.21	0.52
M06-2X/6-31+G(d)	--	--	--	--	0.12	0.46	0.53	0.20	0.46	0.42	0.16	0.53
B3LYP/6-311+G(d,p)	--	--	--	--	0.14	0.45	0.51[b]	0.33[b]	--[c]	--[c]	0.20	0.54
M06-2X/6-311+G(d,p)	--	--	--	--	0.10	0.48	0.55	0.21	0.49	0.42	0.14	0.56
MP2/6-311+G(d,p)	--	--	--	--	0.09	0.46	0.52	0.24	0.47	0.39	0.14	0.53
(A)

S3′	Gas (Å)						Solution (Å)
Electronic Struct. Theory	ETS		Int		LTS		ETS		Int		LTS
	BOO5′	BOO2′	BOO5′	BOO2′	BOO5′	BOO2′	BOO5′	BOO2′	BOO5′	BOO2′	BOO5′	BOO2′
HF/3-21+G*	0.49	0.15	--[c]	--[c]	0.14	0.49	0.54	0.19	0.45	0.45	0.18	0.54
B3LYP/6-31+G(d)	0.47	0.23	0.43	0.43	0.19	0.47	0.52	0.22	0.44	0.43	0.20	0.53
M06-2X/6-31+G(d)	0.49	0.15	0.44	0.44	0.11	0.49	0.53	0.16	0.44	0.44	0.14	0.54
B3LYP/6-311+G(d,p)	0.47	0.23	0.43	0.42	0.19	0.48	0.53	0.22	0.45	0.43	0.20	0.54
M06-2X/6-311+G(d,p)	0.51	0.13	0.44	0.45	0.10	0.51	0.56	0.15	0.46	0.45	0.13	0.57
MP2/6-311+G(d,p)	0.48	0.14	0.42	0.42	0.12	0.47	0.53	0.14	0.44	0.43	0.14	0.53
(B)

S5′	Gas (Å)						Solution (Å)
Electronic Struct. Theory	ETS		Int		LTS		ETS		Int		LTS
	BOS5′	BOO2′	BOS5′	BOO2′	BOS5′	BOO2′	BOS5′	BOO2′	BOS5′	BOO2′	BOS5′	BOO2′
HF/3-21+G*	0.48	0.16	--	--	--	--	0.72	0.20	--	--	--	--
B3LYP/6-31+G(d)	0.41	0.18	--	--	--	--	0.66	0.22	--	--	--	--
M06-2X/6-31+G(d)	0.50	0.16	--	--	--	--	0.68	0.18	--	--	--	--
B3LYP/6-311+G(d,p)	0.39	0.17	--	--	--	--	0.65	0.22	--	--	--	--
M06-2X/6-311+G(d,p)	0.49	0.15	--	--	--	--	0.67	0.18	--	--	--	--
MP2/6-311+G(d,p)	0.45	0.16	--	--	--	--	0.71	0.16	--	--	--	--
(C)

^[a] BO_O5′ is the bond order between O5′ and P, BO_O2′ is the bond order between O2′ and P, BO_S5′ is the bond order between S5′ and P. “--” denotes the molecular structure of that particular state could not be determined.

^[b] As in Table 2, the ETS is determined but along with very small value of non-reactive imaginary frequency.

^[c] As in Table 2, no minimum point could be determined by us that satisfies all default criteria in Gaussian 09.^[41]

Table 6.

Breaking and forming bond distances for stationary points along the intrinsic reaction coordinate of the (A) native, (B) S3′, and (C) S5′ simplest models of RNA transphosphorylation in both gas and solution phases.

Native	Gas (Å)						Solution (Å)
Electronic Struct. Theory	ETS		Int		LTS		ETS		Int		LTS
	rO5′	rO2′	rO5′	rO2′	rO5′	rO2′	rO5′	rO2′	rO5′	rO2′	rO5′	rO2′
HF/3-21+G*	--	--	--	--	2.55	1.75	1.70	2.09	1.75	1.86	2.29	1.71
B3LYP/6-31+G(d)	--	--	--	--	2.49	1.84	1.77	2.13	1.82	1.93	2.31	1.77
M06-2X/6-31+G(d)	--	--	--	--	2.52	1.79	1.72	2.28	1.80	1.87	2.38	1.72
B3LYP/6-311+G(d,p)	--	--	--	--	2.49	1.85	1.78[b]	2.05[b]	--[c]	--[c]	2.30	1.77
M06-2X/6-311+G(d,p)	--	--	--	--	2.53	1.79	1.72	2.25	1.79	1.89	2.38	1.72
MP2/6-311+G(d,p)	--	--	--	--	2.52	1.82	1.75	2.15	1.80	1.92	2.33	1.75
(A)

S3′	Gas (Å)						Solution (Å)
Electronic Struct. Theory	ETS		Int		LTS		ETS		Int		LTS
	rO5′	rO2′	rO5′	rO2′	rO5′	rO2′	rO5′	rO2′	rO5′	rO2′	rO5′	rO2′
HF/3-21+G*	1.72	2.41	--[c]	--[c]	2.38	1.72	1.68	2.30	1.78	1.80	2.28	1.69
B3LYP/6-31+G(d)	1.80	2.29	1.88	1.89	2.35	1.81	1.75	2.30	1.85	1.89	2.30	1.76
M06-2X/6-31+G(d)	1.75	2.46	1.83	1.83	2.51	1.75	1.70	2.40	1.81	1.83	2.41	1.71
B3LYP/6-311+G(d,p)	1.81	2.27	1.89	1.91	2.34	1.82	1.75	2.29	1.85	1.90	2.28	1.76
M06-2X/6-311+G(d,p)	1.75	2.47	1.84	1.84	2.52	1.75	1.70	2.40	1.81	1.84	2.42	1.71
MP2/6-311+G(d,p)	1.78	2.38	1.87	1.88	2.40	1.79	1.73	2.34	1.83	1.86	2.32	1.74
(B)

S5′	Gas (Å)						Solution (Å)
Electronic Struct. Theory	ETS		Int		LTS		ETS		Int		LTS
	rS5′	rO2′	rS5′	rO2′	rS5′	rO2′	rS5′	rO2′	rS5′	rO2′	rS5′	rO2′
HF/3-21+G*	2.42	2.38	--	--	--	--	2.21	2.24	--	--	--	--
B3LYP/6-31+G(d)	2.57	2.41	--	--	--	--	2.29	2.31	--	--	--	--
M06-2X/6-31+G(d)	2.41	2.42	--	--	--	--	2.25	2.34	--	--	--	--
B3LYP/6-311+G(d,p)	2.60	2.41	--	--	--	--	2.31	2.29	--	--	--	--
M06-2X/6-311+G(d,p)	2.42	2.41	--	--	--	--	2.26	2.33	--	--	--	--
MP2/6-311+G(d,p)	2.49	2.35	--	--	--	--	2.25	2.30	--	--	--	--
(C)

^[a] r_O5′ is the distance between O5′ and P, r_O2′ is the distance between O2′ and P, r_S5′ is the distance between S5′ and P. “--” denotes the molecular structure of that particular state could not be determined.

^[b] As in Table 2, the ETS is determined but along with very small value of non-reactive imaginary frequency.

^[c] As in Table 2, no minimum point could be determined by us that satisfies all default criteria in Gaussian 09.^[41]

Figure 2.

Rate-limiting transition-state structures that match with experimental KIE values for the (A) native, (B) S3′, (C) S5′ reactions, respectively. These structures were optimized at the MP2/6-311+G(d,p) level. The bond distances are given in Å.

On the other hand, the ETS for both S3′ and S5′ reactions in solution, which are the rate-limiting transition states in accordance with the experimental and calculated KIE data,^[9] show the covalent bond between P—O2′ (the nucleophilic bond) is far from being formed (Figure 2), in particular the fast leaving group of S5′ makes the LTS in the S5′ reaction extinct. For example, the MP2 structure of S3′-ETS in solution has the bond distance of P—O5′ at 1.73 Å and its bond order is 0.53, while the P—O2′ distance is 2.34 Å and its bond order is 0.14 (Figure 2).

Equilibrium Isotope Effects on 2′-OH deprotonation

In the base-catalyzed reaction mechanism, previously we showed that the O2′ has already been deprotonated in the reactant state.^[9] However, during the actual RNA catalysis, we should have the 2′-OH for the ground state instead.^[8] Therefore, it is of particular interest in determining the equilibrium isotope effects (EIE) on the 2′-OH deprotonation.^{[8, 9, 14, 30]}

Single levels and dual levels of EIE for our simplest native and thio-substituted models in the gas phase are listed in Table S9 and Table S10 (Supporting Information), respectively. All these EIE values were computed from the Bigeleisen equation [Eq. (3)]. Since frequency analyses at coupled-cluster level are extremely expensive, and as what we have discussed above, CCSD(T)/6-311+G(d,p)//MP2/6-311+G(d,p) are the most accurate level of theory in this work, all the dual-level calculations of EIE and KIE in this work were performed with frequency analyses at the MP2/6-311+G(d,p) level.

Similar to the cases in breaking/forming bond orders and bond distances, the differences in EIE between the single-level values and their dual-level counterparts in the gas phase are basically insignificant [Table S9 vs. Table S10 (Supporting Information)]. For the gas-phase native reaction, the largest EIE is on the O2′ among all twelve single and dual levels of theory, ranging from 1.029 to 1.039, in which the MP2 EIE value is 1.031. The second largest EIE is on the O5′ ranging from 1.005 to 1.006 among all twelve single and dual levels of theory, in which the MP2 EIE value is 1.0059. The EIE values on the remaining phosphoryl oxygens are close to unity, ranging from 1.000 to 1.003, at all twelve single and dual levels of theory. Similar values of EIE can also be found for both S3′ and S5′ reactions in the gas phase, with a note that ^18,34E_Lea values are reduced to be in the range of 1.002.

For all the reactions in solution, as shown in Table 7 and Table S11 (Supporting Information), the differences in EIE between the single-level values and their dual-level counterparts are even more minimal. For the solution-phase native reaction, the largest EIE is still on the O2′ among all twelve single and dual levels of theory. But, comparing to their gas-phase counterparts, their EIE values on the O2′ in solution have been slightly reduced to be around 1.025, in which the MP2 value is 1.0218. These EIE values are similar to the EIE value, 1.0245, reported by Humphry et al. for deprotonation of the hydroxyl of 2-hydroxypropyl-p-nitrophenyl phosphate (HpPNP).^{[9, 30]}

Table 7.

Equilibrium isotope effects on nucleophile (2′-OH) deprotonation of the (A) native, (B) S3′, and (C) S5′ simplest models of RNA transphosphorylation in solution. All values are computed from the Bigeleisen equation.

Native (37°C)	Equilibrium Isotope Effects in Solution (ratio of isotopic equilibrium constants) Nucleophile (2′-OH) deprotonation
Electronic Struct. Theory	18ENuc	18ELea	18EO3′	18EO1P	18EO2P
HF/3-21+G*	1.0245	1.0020	0.9985	0.9991	0.9999
B3LYP/6-31+G(d)	1.0210	1.0007	1.0012	0.9999	1.0008
M06-2X/6-31+G(d)	1.0214	1.0015	0.9975	1.0000	0.9998
B3LYP/6-311+G(d,p)	1.0220	1.0007	1.0013	0.9997	1.0011
M06-2X/6-311+G(d,p)	1.0222	1.0016	0.9977	0.9999	1.0001
MP2/6-311+G(d,p)	1.0218	1.0020	0.9984	1.0004	1.0003
(A)

S3′ (37°C)	Equilibrium Isotope Effects in Solution (ratio of isotopic equilibrium constants) Nucleophile (2′-OH) deprotonation
Electronic Struct. Theory	18ENuc	18ELea	34ES3′	18EO1P	18EO2P
HF/3-21+G*	1.0266	1.0002	1.0000	1.0003	0.9995
B3LYP/6-31+G(d)	1.0196	1.0005	1.0003	1.0007	1.0006
M06-2X/6-31+G(d)	1.0244	1.0002	1.0009	1.0005	0.9998
B3LYP/6-311+G(d,p)	1.0208	1.0005	1.0003	1.0008	1.0006
M06-2X/6-311+G(d,p)	1.0255[a]	1.0003[a]	1.0009[a]	1.0005[a]	1.0000[a]
MP2/6-311+G(d,p)	1.0271	1.0001	1.0007	1.0004	1.0004
(B)

S5′ (37°C)	Equilibrium Isotope Effects in Solution (ratio of isotopic equilibrium constants) Nucleophile (2′-OH) deprotonation
Electronic Struct. Theory	18ENuc	34ELea	18EO3′	18EO1P	18EO2P
HF/3-21+G*	1.0259	0.9997	1.0001	1.0002	1.0014
B3LYP/6-31+G(d)	1.0204	1.0002	1.0026	1.0011	1.0004
M06-2X/6-31+G(d)	1.0215	0.9994	1.0024	1.0005	1.0011
B3LYP/6-311+G(d,p)	1.0215	1.0002	1.0027	1.0012	1.0004
M06-2X/6-311+G(d,p)	1.0222	0.9993	1.0022	1.0004	1.0012
MP2/6-311+G(d,p)	1.0225	0.9999	1.0002	1.0004	1.0001
(C)

^[a] As in Table 2, the ground state after deprotonation is determined but along with very small value of non-reactive imaginary frequency.

Similar to the gas-phase results, the second largest EIE for the native reaction in solution is on the O5′, at the values of ~1.002, except the ones using B3LYP functional at the values of ~1.0007 [Table 7 and Table S11 (Supporting Information)]. The EIE values on the remaining phosphoryl oxygens are also close to unity, ranging from 0.998 to 1.000, at all twelve single and dual levels of theory. Similar values of EIE can also be found for both S3′ and S5′ reactions in the solution phase, with a note that ^18,34E_Lea values are reduced to be ~1.000.

Remarkably, for the S5′ reaction in solution [Table 7 and Table S11 (Supporting Information)], both single-level and dual-level calculations of EIE on the O3′ at the HF/3-21+G* level outperform the B3LYP and M06-2X functionals, in which the latter even have larger basis sets. The accurate MP2 value of EIE is 1.0002, whereas the HF values are ~1.0004. And the two functional values are not accurate, which are at the values of ~1.0020, off by one order of magnitude in terms of error percentage.

Kinetic Isotope Effects on RNA Transphosphorylation

Similar to what we have discussed in the previous section for EIE, since frequency analyses at coupled-cluster level are prohibitively expensive and CCSD(T)/6-311+G(d,p)//MP2/6-311+G(d,p) are the most accurate level of theory in this study, all the dual-level calculations of EIE and KIE in this work were carried out with frequency analyses at the MP2/6-311+G(d,p) level.

Table S12 and Table S13 (Supporting Information) list single and dual levels of KIE in the gas phase. All these KIE values were calculated from the Bigeleisen equation [Eq. (4)]. Similar to the calculations for EIE, for all reactions in the gas phase, we cannot find significant difference in the KIE values computed at the single levels from their dual-level counterparts. Moreover, all the KIE values computed at all twelve single and dual levels are actually quite close to one another. For the gas-phase native reaction, all the twelve KIE values of LTS on the O2′, O5′, O3′, O1P, and O2P are in the vicinities of 0.960, 1.070, 1.005, 1.001, and 1.001, respectively, in which the MP2 KIE values are 0.9727, 1.0669, 1.0084, 1.0011, and 0.9999, respectively. For the gas-phase S3′ reaction, all the KIE values of ETS on the O2′, O5′, S3′, O1P, and O2P are in the vicinities of 1.025, 1.010, 1.002, 1.001, and 1.001, respectively, in which the MP2 KIE values are 1.0250, 1.0115, 1.0024, 1.0009, and 1.0008, respectively. In addition, the KIE of LTS on the O2′, O5′, S3′, O1P, and O2P are in the ranges of 0.960, 1.060, 1.003, 1.001, and 1.001, respectively, in which the MP2 KIE values are 0.9738, 1.0591, 1.0041, 1.0013, and 1.0009, respectively. For the gas-phase S5′ reaction, all the KIE values of ETS on the O2′, S5′, O3′, O1P, and O2P are in the ranges of 1.015, 1.005, 1.002, 1.000, and 1.000, respectively, in which the MP2 KIE values are 1.0117, 1.0051, 1.0030, 1.0002, and 1.0010, respectively.

On the other hand, Table 8 and Table S14 (Supporting Information) show single and dual levels of KIE in solution. Once again, we cannot find significant difference in the KIE values computed at the single levels from their dual-level counterparts. Further, again, all the KIE values computed at all twelve single and dual levels are in excellent agreement with one another. As what we conclude in the previous study,^[9] by comparing our KIE values to the most relevant experimental KIE data, we have determined that the rate-limiting transition state for the native reaction is LTS, whereas for the S3′, and S5′ reactions are ETS.

Table 8.

Kinetic isotope effects on the (A) native, (B) S3′, and (C) S5′ simplest models of RNA transphosphorylation in solution. All values are computed from the Bigeleisen equation. “--” denotes the molecular structure of that particular state could not be determined.

Native (37°C)	Kinetic Isotope Effects in Solution (ratio of isotopic reaction rates)
Electronic Struct. Theory	ETS					LTS
	18kNuc	18kLea	18kO3′	18kO1P	18kO2P	18kNuc	18kLea	18kO3′	18kO1P	18kO2P
HF/3-21+G*	1.0105	1.0063	1.0022	1.0037	1.0046	0.9515	1.0805	1.0022	1.0038	1.0035
B3LYP/6-31+G(d)	1.0169	1.0064	1.0051	1.0041	1.0039	0.9673	1.0607	1.0051	1.0049	1.0026
M06-2X/6-31+G(d)	1.0239	1.0060	1.0040	1.0031	1.0023	0.9630	1.0716	1.0050	1.0039	1.0027
B3LYP/6-311+G(d,p)	1.0117[a]	1.0078[a]	1.0064[a]	1.0049[a]	1.0046[a]	0.9677	1.0602	1.0057	1.0050	1.0024
M06-2X/6-311+G(d,p)	1.0229	1.0064	1.0043	1.0035	1.0026	0.9635	1.0719	1.0054	1.0042	1.0024
MP2/6-311+G(d,p)	1.0190	1.0075	1.0046	1.0047	1.0045	0.9665	1.0683	1.0043	1.0039	1.0029
(A)

S3′ (37°C)	Kinetic Isotope Effects in Solution (ratio of isotopic reaction rates)
Electronic Struct. Theory	ETS					LTS
	18kNuc	18kLea	34kS3′	18kO1P	18kO2P	18kNuc	18kLea	34kS3′	18kO1P	18kO2P
HF/3-21+G*	1.0209	1.0076	1.0007	1.0024	1.0023	0.9510	1.0697	1.0008	1.0019	1.0013
B3LYP/6-31+G(d)	1.0250	1.0086	1.0010	1.0033	1.0038	0.9709	1.0575	1.0014	1.0017	1.0026
M06-2X/6-31+G(d)	1.0276	1.0075	1.0010	1.0016	1.0024	0.9646	1.0714	1.0009	1.0007	1.0013
B3LYP/6-311+G(d,p)	1.0242	1.0092	1.0010	1.0034	1.0038	0.9713	1.0557	1.0015	1.0014	1.0021
M06-2X/6-311+G(d,p)	1.0277[b]	1.0076[b]	1.0011[b]	1.0021[b]	1.0021[b]	0.9641[b]	1.0723[b]	1.0010[b]	1.0007[b]	1.0011[b]
MP2/6-311+G(d,p)	1.0264	1.0088	1.0011	1.0035	1.0030	0.9659	1.0666	1.0013	1.0020	1.0024
(B)

S5′ (37°C)	Kinetic Isotope Effects in Solution (ratio of isotopic reaction rates)
Electronic Struct. Theory	ETS					LTS
	18kNuc	34kLea	18kO3′	18kO1P	18kO2P	18kNuc	34kLea	18kO3′	18kO1P	18kO2P
HF/3-21+G*	1.0150	1.0022	1.0036	1.0025	1.0033	--	--	--	--	--
B3LYP/6-31+G(d)	1.0198	1.0021	1.0051	1.0037	1.0037	--	--	--	--	--
M06-2X/6-31+G(d)	1.0203	1.0022	1.0027	1.0030	1.0016	--	--	--	--	--
B3LYP/6-311+G(d,p)	1.0187	1.0020	1.0056	1.0039	1.0039	--	--	--	--	--
M06-2X/6-311+G(d,p)	1.0196	1.0019	1.0035	1.0027	1.0018	--	--	--	--	--
MP2/6-311+G(d,p)	1.0211	1.0019	1.0064	1.0037	1.0040	--	--	--	--	--
(C)

^[a] As in Table 2, the ETS is determined but along with very small value of non-reactive imaginary frequency.

^[b] As in Table 2, the reactant is determined but along with very small value of non-reactive imaginary frequency.

For the solution-phase native reaction, the twelve KIE values of LTS on the O2′, O5′, O3′, O1P, and O2P are in the ranges of 0.960, 1.070, 1.004, 1.004, and 1.003, respectively, in which the MP2 KIE values are 0.9665, 1.0683, 1.0043, 1.0039, and 1.0029, respectively [Table 8 and Table S14 (Supporting Information)]. For the solution-phase S3′ reaction, the twelve KIE values of ETS on the O2′, O5′, S3′, O1P, and O2P are in the vicinities of 1.025, 1.008, 1.001, 1.002, and 1.002, respectively, in which the MP2 KIE values are 1.0264, 1.0088, 1.0011, 1.0035, and 1.0030, respectively [Table 8 and Table S14 (Supporting Information)]. For the solution-phase S5′ reaction, the twelve KIE values of ETS on the O2′, S5′, O3′, O1P, and O2P are in the vicinities of 1.020, 1.002, 1.004, 1.003, and 1.003, respectively, in which the MP2 KIE values are 1.0211, 1.0019, 1.0064, 1.0037, and 1.0040, respectively (Table 8 and Table S14).

Overall, impressively, EIE and KIE calculations at the HF/3-21+G* level are at least semi-quantitatively accurate, even with no need to perform extra MP2 frequency analysis. Once again, this finding strongly indicates that systematic and dual-level on-the-fly ab initio QM/MM free-energy simulations for actual RNA catalysis could be very promising, even for EIE and KIE calculations.

Another fascinating finding for our EIE and KIE calculations can be located by comparing the values in the gas phase with those in solution [Table 8 vs. Table S12 (Supporting Information)]. Even though, the solvent effects considerably reduce the energy barriers by at least ~10 kcal/mol to at most ~34 kcal/mol (Table 2), the intrinsic or the gas-phase EIE and KIE values are only marginally affected by the aqueous environment.

Beyond the Bigeleisen Equations: Ab Initio Path-Integral Calculations of Equilibrium and Kinetic Isotope Effects

Table 9, Table 10, Table S15, and Table S16 (Supporting Information) show primary EIE and KIE values computed with our path-integral method, AIF-PI, for going beyond the Bigeleisen Equations. The potential energy surface is constructed at the ab initio electronic-structure level of MP2/6-311+G(d,p) theory, which is the most accurate single-level of theory we considered in this work. Our AIF-PI method, which is based on the impressively powerful and accurate Kleinert’s variational perturbation (KP) theory, can systematically include the anharmonicity and tunneling effects in EIE and KIE calculations [i.e., Eq. (5) and (6)]. Otherwise, the anharmonicity and tunneling effects are ignored in the widely-used Bigeleisen equations [i.e., Eq. (3) and (4)]. Our previous studies on a series of proton-transfer reactions demonstrate that performing ab initio path-integral calculations with our AIF-PI method can accurately and economically include anharmonicity and tunneling contributions to the KIE values calculated from Eq. (6). These two contributions are important in order to have quantitative agreement with experiment.^{[18, 19, 22]} In this work, although the entire system is quantized for computing the harmonic EIE and KIE values, we only further quantize six or seven atoms to estimate the anharmonic and tunneling effects. More information on our AIF-PI method is available in the section of Computational Details.

Table 9.

Ab initio path-integral calculations of equilibrium isotope effects on nucleophile (2′-OH) deprotonation of the (A) native, (B) S3′, and (C) S5′ simplest models of RNA transphosphorylation in solution. “Full Harmonic” is the value computed from the Bigeleisen equation, in which the entire system is quantized. “Partial” means only six or seven atoms are further quantized to compute the anharmonicity, which is excluded in the Bigeleisen equation. See Computational Details for the meanings of the notations of KP1/KP2 and P20.

Native (37°C) Electronic Struct. Theory	Ab Initio Path-Integral Calculations Equilibrium Isotope Effects in Solution Nucleophile (2′-OH) deprotonation
MP2/6-311+G(d,p)	18ENuc	18ELea
Full Harmonic	1.0218	1.0020
Partial Harmonic	1.0212	1.0020
Partial KP1/P20	1.0273	1.0044
Partial KP2/P20	1.0261	1.0044
Full Harmonic × Partial(KP1/Harmonic)	1.0279	1.0045
Full Harmonic × Partial(KP2/Harmonic)	1.0268	1.0044
(A)

S3′ (37°C) Electronic Struct. Theory	Ab Initio Path-Integral Calculations Equilibrium Isotope Effects in Solution Nucleophile (2′-OH) deprotonation
MP2/6-311+G(d,p)	18ENuc	18ELea
Full Harmonic	1.0271	1.0001
Partial Harmonic	1.0266	1.0001
Partial KP1/P20	1.0230	1.0005
Partial KP2/P20	1.0224	1.0005
Full Harmonic × Partial(KP1/Harmonic)	1.0235	1.0005
Full Harmonic × Partial(KP2/Harmonic)	1.0228	1.0005
(B)

S5′ (37°C) Electronic Struct. Theory	Ab Initio Path-Integral Calculations Equilibrium Isotope Effects in Solution Nucleophile (2′-OH) deprotonation
MP2/6-311+G(d,p)	18ENuc	18ELea
Full Harmonic	1.0225	0.9999
Partial Harmonic	1.0220	0.9999
Partial KP1/P20	1.0194	0.9997
Partial KP2/P20	1.0186	0.9997
Full Harmonic × Partial(KP1/Harmonic)	1.0199	0.9997
Full Harmonic × Partial(KP2/Harmonic)	1.0191	0.9997
(C)

Table 10.

Ab initio path-integral calculations of kinetic isotope effects on the (A) native, (B) S3′, and (C) S5′ simplest models of RNA transphosphorylation in solution. “Full Harmonic” is the value computed from the Bigeleisen equation, in which the entire system is quantized. “Partial” means only six atoms are further quantized to compute the anharmonicity and tunneling effects, which are excluded in the Bigeleisen equation. See Computational Details for the meanings of the notations of KP1/KP2 and P20. “--” denotes the molecular structure of that particular state could not be determined.

Native (37°C) Electronic Struct. Theory	Ab Initio Path-Integral Calculations Kinetic Isotope Effects in Solution
	ETS		LTS
MP2/6-311+G(d,p)	18kNuc	18kLea	18kNuc	18kLea
Full Harmonic	1.0190	1.0075	0.9665	1.0683
Partial Harmonic	1.0207	1.0067	0.9680	1.0685
Partial KP1/P20	1.0205	1.0048	0.9682	1.0659
Partial KP2/P20	1.0205	1.0048	0.9681	1.0660
Full Harmonic × Partial(KP1/Harmonic)	1.0189	1.0056	0.9667	1.0657
Full Harmonic × Partial(KP2/Harmonic)	1.0188	1.0056	0.9666	1.0658
(A)

S3′ (37°C) Electronic Struct. Theory	Ab Initio Path-Integral Calculations Kinetic Isotope Effects in Solution
	ETS		LTS
MP2/6-311+G(d,p)	18kNuc	18kLea	18kNuc	18kLea
Full Harmonic	1.0264	1.0088	0.9659	1.0666
Partial Harmonic	1.0287	1.0085	0.9673	1.0659
Partial KP1/P20	1.0285	1.0072	0.9667	1.0658
Partial KP2/P20	1.0285	1.0073	0.9667	1.0658
Full Harmonic × Partial(KP1/Harmonic)	1.0262	1.0076	0.9653	1.0665
Full Harmonic × Partial(KP2/Harmonic)	1.0262	1.0077	0.9653	1.0666
(B)

S5′ (37°C) Electronic Struct. Theory	Ab Initio Path-Integral Calculations Kinetic Isotope Effects in Solution
	ETS		LTS
MP2/6-311+G(d,p)	18kNuc	34kLea	18kNuc	34kLea
Full Harmonic	1.0211	1.0019	--	--
Partial Harmonic	1.0243	1.0018	--	--
Partial KP1/P20	1.0245	1.0019	--	--
Partial KP2/P20	1.0245	1.0019	--	--
Full Harmonic × Partial(KP1/Harmonic)	1.0213	1.0019	--	--
Full Harmonic × Partial(KP2/Harmonic)	1.0213	1.0019	--	--
(C)

Based on the EIE and KIE values presented in Table 9, Table 10, Table S15, and Table S16 (Supporting Information), we conclude that further quantizing only six or seven atoms should be enough for estimating the anharmonicity and tunneling effects. This is because the largest difference between the full harmonic (entire system is quantized) and partial harmonic (only six or seven atoms are quantized) values is about 0.3% (in computing ¹⁸k_Nuc value for the S5′ reaction in solution; Table 10). Moreover, even the largest tunneling contribution to the KIE values is only about 0.04% (in computing ¹⁸k_Nuc value for the S5′ reaction in solution; Table 10). And most of our other calculated values of tunneling contributions are actually smaller than the largest 0.04% by at least one order of magnitude. Therefore, for simplicity, we do not explicitly list the KIE tunneling contributions in the tables.

Regarding the contributions from anharmonicity, we conclude that it is more quantitatively significant to EIE than KIE calculations. This finding is consistent with the fact that there is a hydrogen atom further quantized in the anharmonic EIE calculation. But for the KIE calculations, all six atoms that are further quantized are heavy. We found that the largest anharmonic contribution is about 1% in computing ¹⁸E_Nuc for both S3′ and S5′ reactions in the gas phase [Table S15 (Supporting Information)]. For all the reactions in the solution phase, the largest anharmonic contribution is about 0.5% in computing ¹⁸E_Nuc for the native reaction in solution (Table 9). By contrast, the anharmonicity contributions to the KIE values are smaller. For all the reactions in both gas and solution phases, the largest anharmonic contribution is about 0.25% in computing ¹⁸k_Lea value for the LTS of the native reaction in solution (Table 10).

The convergence of the KP1 and KP2 calculations are phenomenal. The largest difference between KP1 and KP2 values are in EIE calculations for the reactions in solution, which is only about 0.1%. For all other EIE and KIE calculations, their difference is smaller than or in the order of magnitude of 0.01%. Since Kleinert’s variational perturbation (KP) theory has been well-known for its exponentially and uniformly convergent property (which is even true at the limit of absolute zero temperature), we believe that our path-integral calculations up to KP2 should be quite accurate.

Overall, in contrast to our previous studies on a series of proton-transfer reactions,^[22] we found that since all our isotope effects are on heavy atoms, in general anharmonicity and tunneling contributions are not significant to both EIE and KIE on our simplest models of RNA transphosphorylation. However, in order to have better quantitative agreement with experiment, we might need to include anharmonic contribution to the EIE calculations for the nucleophile (2′-OH) deprotonation, as there is a hydrogen atom directly bonded with the nucleophile O2′. For example, after adding the anharmonic contribution, now the ¹⁸E_Nuc for the native reaction in solution is increased from 1.0218 to 1.0268 (Table 9).

Conclusions

In this comprehensive paper, we thoroughly compare various levels of electronic-structure and internuclear quantum-statistical theories for KIE and EIE computations on a simplest model for the base-catalyzed 2′-O-transphosphorylation. We find that in terms of energetics, MP2/6-311+G(d,p) is the most accurate single-level theory that we considered in this work [Table S3 (Supporting Information)]. Its RMSD from its dual-level counterpart that has single-point energy of CCSD(T)/6-311+G(d,p) is only 0.2 kcal/mol (0.3 kcal/mol is the largest deviation). Although the accuracy of the computationally least expensive HF/3-21+G* is generally not good enough [Table S4 (Supporting Information)], its dual-level CCSD(T) counterpart provides us with one of the most accurate results [Table S5 (Supporting Information)]. For density functional theory (DFT), in general the performances of two popular functionals B3LYP and M06-2X are similar, but B3LYP might be a bit more accurate and M06-2X tends to overstabilize the transient intermediate for both native and S3′ reactions (in the gas and solution phases). Notably, CCSD and CCSD(T) results differ non-trivially, emphasizing the importance of the perturbative triple correction [Table S7 (Supporting Information)]. All the computed energy barriers for the native, S3′, and S5′ reactions are consistent with the most relevant experimental results that we have found in the literature, i.e., S3′ reactions are faster than the natives ones, whereas the fastest reactions belong to the S5′ (Table 2 and Table 3 and Table 4). Regarding the breaking/forming bond orders and bond distances associated with the transition states, all the values calculated at the single or dual levels are more or less the same as one another [Table 5 and Table S8 (Supporting Information) and Table 6].

For the calculations of the equilibrium isotope effects (EIE) on the 2′-OH deprotonation, we could not find important differences between the single-level and dual-level values in the gas phase, as well as in the solution phase [Table S9, Table S10 (Supporting Information), Table 7, and Table S11 (Supporting Information)]. Terrifically, for the S5′ reaction in solution, both single-level and dual-level calculations at the economical HF/3-21+G* level returns us more accurate results than those at the B3LYP and M06-2X levels of theory [Table 7 and Table S11 (Supporting Information)].

Similarly, for the calculations of the kinetic isotope effects (KIE) on the base-catalyzed 2′-O-transphosphorylation, no significant differences could be found between the single-level and dual-level results in the gas phase, as well as in the solution phase [Table S12, Table S13, Table 8, and Table S14 (Supporting Information)]. As shown in our previous work, by the comparison of our KIE values to the most relevant experimental KIE results, we have concluded that for the native reaction, the rate-limiting transition state is LTS, while ETS is the rate-limiting one for both S3′ and S5′ reactions.

Overall, by comparing the values of isotope effects in the gas phase with those in the solution phase, we are a little bit astonished by the fact that although the solvent effect substantially lowers the energy barriers by ~10 to 34 kcal/mol (Table 2), the inherent or the gas-phase isotope-effects values are fairly insensitive to the solvation environment.

In addition, remarkably, EIE and KIE values computed at the HF/3-21+G* level are at least semi-quantitatively accurate, even true for single-level results. Together with all the other findings in this study about the accuracy of the HF/3-21+G* results, a solid theoretical basis is already formed towards more systematic and more accurate dual-level on-the-fly ab initio QM/MM free-energy and isotope effects calculations on more intricate biomolecular systems associated with the 2′-O-transphosphorylation.

In regard to our ab initio path-integral calculations of EIE and KIE using our AIF-PI method, we showed that further-quantization of only six to seven atoms should be enough for estimating anharmonicity and tunneling effects (on top of harmonic quantization for all atoms), in which the largest tunneling contribution is only ~0.04% (most of our other calculated values of tunneling effects are even smaller than 0.04% by at least one order of magnitude), whereas the largest anharmonic contribution is about 1% for computing ¹⁸E_Nuc. Therefore, we may conclude that in general anharmonicity and tunneling contributions are not particularly important to both EIE and KIE on our simplest models for the base-catalyzed 2′-O-transphosphorylation. Nonetheless, we should include anharmonic contribution to the EIE on the 2′-OH deprotonation. Finally, the systematic manner and the impressively fast convergence property of the powerful Kleinert variational perturbation (KP) theory are also demonstrated. The largest difference in the isotope-effects calculations between first order and second order of KP expansions (i.e., between KP1 and KP2) is only about 0.1%, while all other differences are smaller than or in the order of magnitude of 0.01%.