Abstract
The ill-posed nature of the MEG (or related EEG) source localization problem requires the incorporation of prior assumptions when choosing an appropriate solution out of an infinite set of candidates. Bayesian approaches are useful in this capacity because they allow these assumptions to be explicitly quantified using postulated prior distributions. However, the means by which these priors are chosen, as well as the estimation and inference procedures that are subsequently adopted to affect localization, have led to a daunting array of algorithms with seemingly very different properties and assumptions. From the vantage point of a simple Gaussian scale mixture model with flexible covariance components, this paper analyzes and extends several broad categories of Bayesian inference directly applicable to source localization including empirical Bayesian approaches, standard MAP estimation, and multiple variational Bayesian (VB) approximations. Theoretical properties related to convergence, global and local minima, and localization bias are analyzed and fast algorithms are derived that improve upon existing methods. This perspective leads to explicit connections between many established algorithms and suggests natural extensions for handling unknown dipole orientations, extended source configurations, correlated sources, temporal smoothness, and computational expediency. Specific imaging methods elucidated under this paradigm include weighted minimum ℓ2-norm, FOCUSS, MCE, VESTAL, sLORETA, ReML and covariance component estimation, beamforming, variational Bayes, the Laplace approximation, and automatic relevance determination (ARD). Perhaps surprisingly, all of these methods can be formulated as particular cases of covariance component estimation using different concave regularization terms and optimization rules, making general theoretical analyses and algorithmic extensions/improvements particularly relevant.
I. Introduction
Magnetoencephalography (MEG) and electroencephalography (EEG) use an array of sensors to take electromagnetic field (or voltage potential) measurements from on or near the scalp surface with excellent temporal resolution. In both cases, the observed field is generated by the same synchronous, compact current sources located within the brain. Because the mapping from source activity configuration to sensor measurement is many to one, accurately determining the spatial locations of these unknown sources is extremely difficult. The relevant localization problem can be posed as follows: The measured electromagnetic signal is B ∈ ℝdb×n, where db equals the number of sensors and n is the number of time points at which measurements are made. The unknown sources S ∈ ℝds×n are the (discretized) current values at ds candidate locations distributed throughout the cortex. These candidate locations are obtained by segmenting a structural MR scan of a human subject and tesselating the gray matter surface with a set of vertices. B and S are related by the likelihood model
| (1) |
where L is the so-called lead-field matrix, the i-th column of which represents the signal vector that would be observed at the scalp given a unit current source at the i-th vertex with a fixed orientation (flexible orientations can be incorporated by including multiple columns per location, one for each directional component). Multiple methods based on the physical properties of the brain and Maxwell’s equations are available for this computation [37]. Finally,
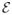 is a noise-plus-interference term where we assume, for simplicity, that columns are drawn independently from
is a noise-plus-interference term where we assume, for simplicity, that columns are drawn independently from
 (0, Σε). However, temporal correlations can easily be incorporated if desired using the method outlined in [13]. Additionally, here we will mostly assume that Σε is known; however, robust procedures for its estimation can be found in [25] and can naturally be incorporated into the proposed model.1
(0, Σε). However, temporal correlations can easily be incorporated if desired using the method outlined in [13]. Additionally, here we will mostly assume that Σε is known; however, robust procedures for its estimation can be found in [25] and can naturally be incorporated into the proposed model.1
To obtain reasonable spatial resolution, the number of candidate source locations will necessarily be much larger than the number of sensors (ds ≫ db). The salient inverse problem then becomes the ill-posed estimation of these activity or source regions, which are reflected by the nonzero rows of the source estimate matrix Ŝ. Because the inverse model is severely underdetermined, all efforts at source reconstruction are heavily dependent on prior assumptions, which in a Bayesian framework are embedded in the distribution p(S).
If under a given experimental or clinical paradigm this p(S) were somehow known exactly, then the posterior distribution p(S|B) can be computed via Bayes rule:
| (2) |
This distribution contains all possible information about the unknown S conditioned on the observed data B [4]. Two fundamental problems prevent using p(S|B) for source localization. First, for most priors p(S), the distribution p(B) given by
| (3) |
cannot be computed. Because this quantity, which is sometimes referred to as the model evidence, is required to compute posterior moments and is also sometimes used to facilitate model selection [13], [22], this deficiency can be very problematic. Of course if only a point estimate for S is desired, then this normalizing distribution may not be needed. For example, a popular estimator involves finding the value of S that maximizes the posterior distribution, often called the maximum a posteriori or MAP estimate, and is invariant to p(B). However MAP estimates may be unrepresentative of posterior mass and are unfortunately intractable to compute for most p(S) given reasonable computational resources. Secondly, we do not actually know the prior p(S) and so some appropriate distribution must be assumed, perhaps based on neurophysiological constraints or computational considerations. In fact, it is this choice, whether implicitly or explicitly, that differentiates a wide variety of localization methods at a very high level.
Such a prior is often considered to be fixed and known, as in the case of minimum ℓ2-norm approaches [2], minimum current estimation (MCE) [18], [44], FOCUSS [7], [16], sLORETA [30], and minimum variance beamformers [45]. Alternatively, a number of empirical Bayesian approaches have been proposed that attempt a form of model selection by using the data to guide the search for an appropriate p(S). In this scenario, candidate priors are distinguished by a set of flexible hyperparameters γ that must be estimated via a variety of data-driven iterative procedures. Examples include hierarchical covariance component models [12], [24], [31], automatic relevance determination (ARD) [22], [26], [33], [34], [41], and several related variational Bayesian methods [13], [14], [27], [29], [36], [38].
While seemingly quite different in many respects, we present a generalized framework that encompasses all of these methods and points to intimate connections between algorithms. The underlying motivation here is to leverage analytical tools and ideas from machine learning, Bayesian inference, and convex analysis that have not as of yet been fully exploited in the context of MEG/EEG source localization. Specifically, we address how a simple Gaussian scale mixture prior [29] with flexible covariance components underlie and generalize all of the above. This process demonstrates a number of surprising similarities or out-right equivalences between what might otherwise appear to be very different methodologies. We also analyze several properties of this framework related to: (i) computational speed and convergence guarantees, (ii) properties of locally- and globally-optimal source reconstructions with respect to emergent cost functions, and (iii) theoretical localization bias recovering basic source configurations. Wherever possible, results are derived in a general setting and therefore can largely propagate down to specific cases such as the methods listed above. Overall, we envision that by providing a unifying theoretical perspective and comprehensive analyses, neuroelectromagnetic imaging practitioners will be better able to assess the relative strengths of many Bayesian strategies with respect to particular applications; it will also help ensure that different methods are used to their full potential and not underutilized. Moreover, this process points to several promising directions for future research.
The remainder of the paper is organized as follows. Section II introduces the basic Gaussian scale mixture model and three primary inference possibilities - empirical Bayes or hyperparameter MAP (γ-MAP), basic MAP estimation of sources (S-MAP), and variational Bayesian methods (VB). Section III describes γ-MAP in detail using the notion of automatic relevance determination for determining an optimal weighting of covariance components. Fast algorithms are derived as well as theoretical analysis of convergence, local minima, and localization bias. Section IV re-derives and extends basic S-MAP source estimation procedures in light of the Gaussian scale mixture model and discusses similar properties and connections with γ-MAP. In particular, S-MAP is shown to be equivalent to empirical Bayes using a somewhat different regularization term for estimating hyperparameters. We then present two types of variational Bayesian algorithms in Section V, the mean-field and Laplace approximations, and discuss close connections with γ-MAP. Finally, sLORETA and beamforming are analyzed in Section VI while Section VII gives a comprehensive summary of the ideas and contributions of the paper. Portions of this work have appeared previously in conference proceedings [50].
II. Bayesian Modeling Using General Gaussian Scale Mixtures and Arbitrary Covariance Components
In this section, we present a general-purpose Bayesian framework for source localization and discuss a central distinction between fixed-prior MAP estimation schemes and empirical Bayesian approaches that adopt a flexible, parameterized prior. While often derived using different assumptions and methodology, they can be related via a simple hierarchical structure based on general Gaussian scale mixture distributions with arbitrary covariance components. Numerous special cases of this model have been considered previously in the context of MEG source localization and related problems as will discussed in subsequent sections.
A. The Model
To begin we invoke the noise model from (1), which fully defines the assumed likelihood
| (4) |
where denotes the weighted matrix norm . While the unknown noise covariance can also be parameterized and seamlessly estimated from the data via the proposed paradigm, for simplicity we assume that Σε is known and fixed. Next we adopt the following source prior for S:
| (5) |
This is equivalent to applying a zero-mean Gaussian distribution with covariance Σs to each column of S. Here γ ≜ [γ1,…, γdγ]T is a vector of dγ nonnegative hyperparameters that control the relative contribution of each covariance basis matrix Ci. While the hyperparameters are unknown, the set of components
| (6) |
is assumed to be fixed and known. Such a formulation is extremely flexible however, because a rich variety of candidate covariance bases can be proposed as will be discussed in more detail in Section II-C. Moreover, this structure has been advocated by a number of others in the context of neuroelectromagnetic source imaging [12], [24], [31]. Finally, we assume a hyperprior on γ of the form
| (7) |
where each fi(·) is an unspecified function that is assumed to be known. The implicit prior on S, obtained by integrating out (marginalizing) the unknown γ, is known as a Gaussian scale mixture:
| (8) |
B. Estimation and Inference
Estimation and inference using the proposed model can be carried out in multiple ways depending how the unknown quantities S and γ are handled. This leads to a natural partitioning of a variety of inverse methods. We briefly summarize three possibilities before discussing the details and close interrelationships in Sections III through V.
1) Hyperparameter MAP/Empirical Bayes (γ-MAP)
The first option comes from the recognition that if γ were known (and so Σs is known as well), then the conditional distribution p(S|B, γ) ∝ p(B|S)p(S|γ) is a fully specified Gaussian distribution with mean and covariance given by
| (9) |
| (10) |
where sj denotes the j-th column of S and individual columns are uncorrelated. It is then common to use the simple estimator Ŝ= Ep(S|B, γ) [S] for the unknown sources. However, since γ is actually not known, a suitable approximation γ̂ ≈ γ must first be found. One principled way to accomplish this is to integrate out the sources S and then solve
| (11) |
This treatment is sometimes referred to as empirical Bayes [4], because the γ-dependent prior on S, p(S|γ), is empirically learned from the data, often using expectation-maximization (EM) algorithms which treat S as hidden data [8]. Additionally, the process of marginalization provides a natural regularizing mechanism that can shrink many elements of γ to exactly zero, in effect pruning the associated covariance component from the model, with only the relevant components remaining. Consequently, estimation under this model is sometimes called automatic relevance determination (ARD) [23], [26], [41] and will be explored further in Section III. This procedure can also be leveraged to obtain a rigorous lower bound on log p(B). While knowing p(S|B) is useful for source estimation given a particular model, access to p(B) (or equivalently log p(B)) can assist model selection [13], [22].
2) Source-Space MAP (S-MAP)
The second option follows directly from (8). Specifically, if we integrate out the unknown γ, we can treat p(S) as the effective prior and attempt to compute a MAP estimate of S via
| (12) |
This option will be addressed in detail in Section IV and follows from ideas in [7], [29]. While it may not be immediately transparent, solving S-MAP also leads to a shrinking and pruning of superfluous covariance components. In short, this occurs because the hierarchical model upon which (12) is based leads to a convenient, iterative EM algorithm-based implementation, which treats the hyperparameters γ as hidden data and computes their expectation for the E-step. Over the course of learning, this expectation collapes to zero for many of the irrelevant hyperparameters, removing them from the model in much the same way as γ-MAP. In fact, this affiliation will be made much more explicit in Section IV-B, where we convert S-MAP problems involving the proposed hierarchical model to a dual formulation in γ-space.
3) Variational Bayesian (VB) Approximations
A third possibility involves finding formal approximations to p(S|B) as well as the marginal p(B) using an intermediary approximation for p(γ|B). Because of the intractable integrations involved in obtaining either distribution, practical implementation requires additional assumptions leading to different types of approximation strategies as outlined in Section V. First, the so-called mean-field approximation [1], [3] makes the simplifying assumption that the joint distribution over unknowns S and γ factorizes, meaning p(S, γ|B) ≈ p̂(S|B)p̂(γ|B), where p̂(S|B) and p̂(γ|B) are chosen to minimize the Kullback-Leibler divergence between the factorized and full posterior. This is accomplished via an iterative process akin to EM, effectively using two E-steps (one for S and one for γ). It also produces a rigorous lower bound on log p(B) similar to γ-MAP. A second possibility proposed in [14], [13] applies a second-order Laplace approximation to the posterior on the hyperparameters (after marginalizing over the sources S), which is then iteratively matched to the true posterior; the result can then be used to approximate p(S|B) and log p(B). We emphasize two crucial points:
Perhaps surprisingly, both of the VB methods described above lead to posterior approximations p̂(S|B) = p(S|B, γ = γ̂), where γ̂ is equivalently computed via γ-MAP.2 Consequently, VB enjoys the same component pruning (or ARD) and much of the γ-MAP analysis of Section III can be applied directly to VB.
The only meaningful difference between VB and γ-MAP, at least in the context of the proposed generative model, involves approximations to the model evidence log p(B), with different VB and γ-MAP methods giving different estimates. These ideas will be discussed further in Section III-C and Section V.
While details and assumptions may differ γ-MAP, S-MAP, and VB can all be leveraged to obtain a point estimate of S expressed in the Tikhonov regularized form [35]
| (13) |
with
| (14) |
Importantly, because each method intrinsically sets γ̂i = 0 for superfluous covariance components, to an extent that will be made explicit in Sections III through V, we can in principle allow the cardinality of
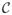 to be very large and rely on the data-driven learning processes, either γ-MAP, S-MAP, or VB, to select the most appropriate subset. Specific choices for
to be very large and rely on the data-driven learning processes, either γ-MAP, S-MAP, or VB, to select the most appropriate subset. Specific choices for
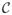 lead to a wide variety of established algorithms as will be discussed next.
lead to a wide variety of established algorithms as will be discussed next.
C. Selections for
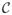
In the simplest case, the single-component assumption Σs = γ1C1 = γ1I, where I is an identity matrix, leads to a weighted minimum-ℓ2-norm solution [2]. More interesting covariance component terms have been used to effect spatial smoothness, depth bias compensation, and candidate locations of likely activity [24], [31]. With regard to the latter, it has been suggested that prior information about a source location can be codified by including a second term C2, i.e.,
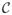 = {C1, C2}, with all zeros except a patch of 1’s along the diagonal signifying a location of probable source activity, perhaps based on fMRI data [31]. For γ-MAP, S-MAP, and VB, we will obtain a source estimate representing a trade-off (modulated by the relative values of the associated γ̂1 and γ̂2) between honoring the prior information imposed by C2 and the smoothness implied by C1. The limitation of this proposal is that we generally do not know, a priori, the regions where activity is occurring with both high spatial and temporal resolution. Therefore, we cannot reliably known how to choose an appropriate location-prior term C2 in many situations.
= {C1, C2}, with all zeros except a patch of 1’s along the diagonal signifying a location of probable source activity, perhaps based on fMRI data [31]. For γ-MAP, S-MAP, and VB, we will obtain a source estimate representing a trade-off (modulated by the relative values of the associated γ̂1 and γ̂2) between honoring the prior information imposed by C2 and the smoothness implied by C1. The limitation of this proposal is that we generally do not know, a priori, the regions where activity is occurring with both high spatial and temporal resolution. Therefore, we cannot reliably known how to choose an appropriate location-prior term C2 in many situations.
A potential solution to this dilemma is to try out many different (or even all possible) combinations of location priors, For example, if we assume the underlying source currents are formed from a collection of dipolar point sources located at each vertex of the lead-field grid, then we may choose
, where each ei is a standard indexing vector of zeros with a ‘1’ for the i-th element (and so
encodes a prior preference for a single dipolar source at location i).3 This specification for the prior involves the counterintuitive addition of an unknown hyperparameter for every candidate source location which, on casual analysis may seem prone to severe overfitting (in contrast to [31], which uses only one or two fixed location priors). As suggested previously however, γ-MAP, S-MAP, and VB all possess an intrinsic, sparsity-based regularization mechanism. This ameliorates the overfitting problem substantially and effectively reduces the space of possible active source locations by choosing a small relevant subset of active dipolar locations. Such a procedure has been empirically successful in the context of neural networks [26], compressed sensing [19], kernel machines [11], [41], and multiple dipole fitting for MEG [33], a significant benefit to the latter being that the optimal number of dipoles need not be known a priori. For S-MAP algorithms, we will show that this selection of
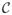 leads to a generalized version of FOCUSS and MCE [7], for γ-MAP and VB, a general form of sparse Bayesian learning (SBL) [46], a variant of automatic relevance determination (ARD) [26].
leads to a generalized version of FOCUSS and MCE [7], for γ-MAP and VB, a general form of sparse Bayesian learning (SBL) [46], a variant of automatic relevance determination (ARD) [26].
In contrast, to model sources with some spatial extent, we can choose , where each ψi represents, for example, a ds × 1 geodesic neural basis vector that specifies an a priori weight location and activity extent [32], [34]. In this scenario, the number of covariance components satisfies dγ = vds, where v is the number of scales we wish to examine in a multi-resolution decomposition, and can be quite large (dγ ≈ 106). The net result of this formulation is a source prior composed of a mixture of Gaussian kernels of varying scales and locations. The number of mixture components is learned from the data and is naturally forced to be small (sparse) to a degree which will be quantified later. In general, the methodology is quite flexible and other prior specifications can be included as well, such as temporal and spectral constraints [21] or the components from [13].
In conclusion, there are two senses with which to understand the notion of covariance component selection. First, there is the selection of which components to include in the model before any estimation takes place, i.e., the choice of
 . Second, there is the selection that occurs within
. Second, there is the selection that occurs within
 as a natural byproduct of many hyperparameters being driven to zero during the learning process. Such components are necessarily pruned by the model; those that remain have therefore been ‘selected’ in some sense. Here we have argued that in many cases the later, data-driven selection can be used to ease the burden of often ad hoc user-specified selections. This notion will be examined in detail in later sections where theoretical and empirical evidence will be presented.
as a natural byproduct of many hyperparameters being driven to zero during the learning process. Such components are necessarily pruned by the model; those that remain have therefore been ‘selected’ in some sense. Here we have argued that in many cases the later, data-driven selection can be used to ease the burden of often ad hoc user-specified selections. This notion will be examined in detail in later sections where theoretical and empirical evidence will be presented.
III. Hyperparameter MAP Estimation (γ-MAP)
γ-MAP obtains a point estimate for the unknown γ by first integrating out the unknown sources S producing the hyperparameter likelihood equation
| (15) |
where
| (16) |
To estimate γ we then solve
| (17) |
which is equivalent to minimizing the cost function
| (18) |
where Cb ≜ n−1BBT is the empirical covariance. This cost function is composed of three parts. The first is a data fit term based on the dissimilarity between the empirical covariance Cb and the model covariance Σb; in general, this factor encourages γ to be large. The second term provides the primary regularizing or sparsifying effect, penalizing a measure of the volume formed by the model covariance Σb.4 Since the volume of any high dimensional space is more effectively reduced by collapsing individual dimensions as close to zero as possible (as opposed to reducing all dimensions isometrically), this penalty term promotes a model covariance that is maximally degenerate (or non-spherical), which pushes elements of γ to exactly zero. Much more detail on this phenomena can be found in [46].
Finally, the third term follows directly from the hyperprior, which we have thus far assumed to be arbitrary. This term can be useful for incorporating specific prior information, perhaps from fMRI data or some other imaging modality. It can also be used to expedite hyperparameter pruning or conversely, to soften the pruning process or prevent pruning altogether. One popular choice is the inverse-Gamma hyperprior given by
| (19) |
for the i-th hyperparameter, where is a standard Gamma function and ai, bi ≥ 0 are shape parameters. In [38], the latter are determined by fMRI data. In the limit as ai, bi → 0, then (19) converges to a noninformative Jeffreys prior; when optimization is performed in log γi space as is customary in some applications [41], the effective prior is flat and can therefore be ignored. In contrast, for ai = bi → ∞, all hyperparameters are constrained to have equal value and essentially no learning (or pruning) occurs. Consequently, the standard weighted minimum ℓ2-norm solution can be seen as a special case. A detailed treatment of what types of hyperpriors lead to covariance component pruning can be found in [49].
For simplicity of exposition, and because of proven effectiveness in practice, we will often concern ourselves with flat hyperpriors when considering the γ-MAP option. Further theoretical justification for this selection can be found in Section III-B and [46]. Hence the third term in (18) vanishes and the only regularization will come from the log |·| term. In this context, the optimization problem with respect to the unknown hyperparameters is sometimes referred to as type-II maximum likelihood [4]. It is also equivalent to the restricted maximum likelihood (ReML) cost function [12]. However, the proposed optimization methods (Section III-A) can be easily modified to handle a wide variety of alternative choices for fi(·).
Regardless of how γ is optimized, once some γ̂ is obtained, we compute Σ̂s using (14), which fully specifies our assumed empirical prior on S. To the extent that the ‘learned’ prior p(S|γ̂) is realistic, this posterior quantifies regions of significant current density and point estimates for the unknown sources can be obtained by evaluating the posterior mean computed using (13).
A. Optimization
The primary objective of this section is to minimize (18) with respect to γ. For simplicity, we will first present updates with fi(γi) = 0 (i.e., a flat hyperprior).5 We then address natural adaptations to the more general cases (e.g., not just conjugate priors). Of course one option is to treat the problem as a general nonlinear optimization task and perform gradient descent or some other generic procedure. In contrast, here we will focus on methods specifically tailored for minimizing (18) using principled methodology. We begin with methods based directly on the EM algorithm and then diverge to alternatives that draw on convex analysis to achieve faster convergence. The algorithms presented here can also be applied to VB as discussed in Section V.
A common approach to this problem in the context of EEG/MEG comes from [12], [13] and is implemented via the SPM software platform.6 Here a restricted maximum likelihood (ReML) method is proposed for optimization which utilizes what amounts to EM-based updates treating S as hidden data [8]. For the E-step, the mean and covariance of S are computed given some estimate of the hyperparameters γ̂. For the M-step, we then must update γ̂ using these moments as the true values. Unfortunately, the optimal value of γ̂ cannot be obtained in closed form for arbitrary
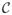 (although for certain special cases it can), so a second-order Fisher scoring procedure is adopted to approximate the desired solution. While effective for estimating small numbers of hyperparameters [24], [31], this approach requires inverting a dγ × dγ Fisher information matrix, which is not computationally feasible for large dγ. Moreover, unlike exact EM implementations, there is no guarantee that (18) will be decreased at each iteration.
(although for certain special cases it can), so a second-order Fisher scoring procedure is adopted to approximate the desired solution. While effective for estimating small numbers of hyperparameters [24], [31], this approach requires inverting a dγ × dγ Fisher information matrix, which is not computationally feasible for large dγ. Moreover, unlike exact EM implementations, there is no guarantee that (18) will be decreased at each iteration.
Consequently, here we present alternative optimization procedures that expand upon ideas from [22], [38], [41], [50], apply to the arbitrary covariance model discussed above, and naturally guarantee that γi ≥ 0 for all i. All of these methods rely on reparameterizing the generative model such that the implicit M-step can be solved in closed form.
First we note that
 (γ) only depends on the data B through the db × db sample correlation matrix Cb. Therefore, to reduce the computational burden, we replace B with a matrix B ∈ ℝdb×rank(B) such that BBT = BBT. This removes any per-iteration dependency on n, which can potentially be large, without altering that actual cost function. It also implies that, for purposes of computing γ, the number of columns of S is reduced to match rank(B).
(γ) only depends on the data B through the db × db sample correlation matrix Cb. Therefore, to reduce the computational burden, we replace B with a matrix B ∈ ℝdb×rank(B) such that BBT = BBT. This removes any per-iteration dependency on n, which can potentially be large, without altering that actual cost function. It also implies that, for purposes of computing γ, the number of columns of S is reduced to match rank(B).
Next we introduce the decomposition
| (20) |
where each Ai is selected such that and A ≜ [A1 ··· Adγ], . In Section II-C, both ei and ψi were special cases of Ai. Letting L ≜ [L1, …, Ldγ] = L[A1 ··· Adγ], this allows us to re-express the original hierarchical Bayesian model as
| (21) |
where
 is the standard Frobenius norm
. The hyperprior remains unaltered. It is easily verified by the rules for transformation of random variables that (21) and the original model are consistent. It also follows that
is the standard Frobenius norm
. The hyperprior remains unaltered. It is easily verified by the rules for transformation of random variables that (21) and the original model are consistent. It also follows that
| (22) |
where Σs is the diagonal, γ-dependent prior covariance of the pseudo-sources.7
1) EM Algorithm
We will now treat S as the hidden data as opposed to the actual sources S and exploit the diagonal structure of the pseudo-source covariance Σs in implementing the EM algorithm. For the E-step, given the value of γ at the k-th iteration, the pseudo-sources are Gaussian with mean and covariance given by
| (23) |
where sj is the j-the column of S (and columns are independent of one another). The M-step then solves
| (24) |
where
| (25) |
The expression (24) can be computed analytically because the diagonal pseudo-source covariance effectively decouples the maximization problem, allowing a closed-form solution for each γi individually. This leads to the M-step updates
| (26) |
The combined update for the (k + 1)-th iteration (obtained by plugging (23) into (26) is then
| (27) |
Given the appropriate simplifying assumptions on the form of Σs and some additional algebraic manipulations, (27) reduces to the algorithm from [38], even though the later was derived under a very different variational Bayes (VB) framework. Section V will examine why this should be the case.
The EM procedure can also be modified to provide an alternative update that handles the case where fi(γi) ≠ 0 in a variety of cases (including when p(γ) is not a conjugate prior). For example, if any of the following conditions hold, then a simple EM algorithm (or generalized EM algorithm [8]) can be derived:
has an analytical solution for all i and c1, c2 ≥ 0.
fi(γi) is concave with respect to γi.
fi(γi) is concave with respect to .
While space precludes a detailed treatment of each of these here, the end result is a straightforward modification to the M-step. For example, assuming the third condition above holds, then we can derive the generalized EM update
| (28) |
where and is the derivative with respect to γi. This is gauranteed to reduce (or leave unchanged) the cost function (18) at every iteration.
Noting that off-diagonal elements of the trace term on the righthand side of (27) and (28) need not be computed, the per-iteration cost of EM updates is at most . This expense can be significantly reduced still further in cases where different pseudo lead-field components, e.g., some Li and Lj, contain one or more columns in common. This situation occurs if we desire to use the geodesic basis functions with flexible orientation constraints, as opposed to the fixed orientations assumed in Section II-C. In general, the linear dependence on dγ is one of the attractive aspects of this method, effectively allowing for extremely large numbers of hyperparameters and covariance components.
The problem then with (27) is not the per-iteration complexity but the convergence rate, which we have observed to be prohibitively slow in practical situations with high-resolution lead-field matrices and large numbers of hyperparameters (see Appendix A for a toy example). The only reported localization results using this type of EM algorithm are from [38], where a relatively low resolution lead-field matrix is used in conjunction with a simplifying heuristic that constrains some of the hyperparameter values.
2) MacKay Updates
To avoid constraints based on computational limitations, which can potentially degrade the quality of source estimates, a faster update rule is needed. To this end, we modified the procedure of [22], which involves taking the gradient of
 (γ) with respect to γ, rearranging terms, and forming the fixed-point update
(γ) with respect to γ, rearranging terms, and forming the fixed-point update
| (29) |
The complexity of each iteration is the same as before, only now the convergence rate can be orders of magnitude faster and shown in Appendix A. And the updates can be extended to a variety of hyperpriors fi(γi), although we omit details here. As an additional point of interest, for the appropriate selection of
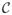 , the hyperparameters obtained after a single iteration of (29) lead to the sLORETA estimate of source activity. This connection will be discussed further in Section VI-B.
, the hyperparameters obtained after a single iteration of (29) lead to the sLORETA estimate of source activity. This connection will be discussed further in Section VI-B.
Unlike the EM method, one criticism of (29) is that there currently exists no proof that it represents a proper descent function (meaning
 (γ(k+1)) ≤
(γ(k+1)) ≤
 (γ(k)) at every iteration), although we have never observed an exception in practice. While we can show that (29) is equivalent to iteratively solving a particular min-max problem in search of a saddle point (see Appendix B), provable descent is still suspect.
(γ(k)) at every iteration), although we have never observed an exception in practice. While we can show that (29) is equivalent to iteratively solving a particular min-max problem in search of a saddle point (see Appendix B), provable descent is still suspect.
3) Convexity-Based Approach
We now derive a related update rule that is both significantly faster than EM and is proven to produce γ vectors such that
 (γ(k+1)) ≤
(γ(k+1)) ≤
 (γ(k)) for every iteration k. Using a dual-form representation of
(γ(k)) for every iteration k. Using a dual-form representation of
 (γ) that leads to a tractable auxiliary cost function, this update is given by
(γ) that leads to a tractable auxiliary cost function, this update is given by
| (30) |
Details of the derivation are given in Appendix B and empirical validation on a simple toy problem is shown in Appendix A. The auxiliary function upon which (30) is based can also be iteratively minimized by solving a series of convex, weighted second-order cone (SOC) problems [48], although specifics are beyond the scope of this paper. Consequently, γ-MAP can be implemented using standard convexity-based optimization tools designed for large problems. This perspective also leads to a variety of desirable analytical properties [48].
Finally, the extension to non-zero fi(γi) is very straightforward in two situations:
has an analytical solution for all i and c1, c2 ≥ 0.
fi(γi) is concave for all i.
The second condition from above leads to the modified update
| (31) |
which is guaranteed to reduce (18) at each iteration (this result follows from the derivation in Appendix B).
B. Analysis of γ-MAP
Previously, we have claimed that the γ-MAP process naturally forces excessive/irrelevant hyperparameters to converge to zero, thereby reducing model complexity. Note that, somewhat counterintuitively, this occurs even when a flat hyperprior is assumed. While this observation has been verified empirically by ourselves and others in various application settings, there has been relatively little corroborating theoretical evidence, largely because of the difficulty in analyzing the potentially multimodal, non-convex γ-MAP cost function. As such, we provide the following result:
Theorem 1
Every local minimum of the generalized γ-MAP cost function (18) is achieved at a solution with at most rank (B) nonzero hyperparameters if fi(γi) is concave and non-decreasing for all i (this includes fi(γi) = 0, or equivalently pi(γi) = 1).
The proof follows from a straightforward extension of [51, Theorem 2] and the fact that the γ-MAP cost only depends on the rank(B) matrix Cb = n−1BBT. Theorem 1 comprises a worst-case bound that is only tight in very nuanced situations; in practice, for any reasonable value of Σε, the number of nonzero hyperparameters is typically much smaller than db. The bound holds for all Σε, including Σε = 0, indicating that some measure of hyperparameter pruning, and therefore covariance component pruning, is built into the γ-MAP framework irrespective of the noise-based regularization. Moreover, the number of nonzero hyperparameters decreases monotonically to zero as Σε is increased. And so there is always some sufficiently large such that all hyperparameters converge to exactly zero. Therefore, we can be confident that the pruning mechanism of γ-MAP is not merely an empirical phenomena. Nor is it dependent on a particular sparse hyperprior, the result holds when a flat (uniform) hyperprior is assumed.
The number of observation vectors n also plays an important role in shaping γ-MAP solutions. Increasing n has two primary benefits: (i) it facilitates convergence to the global minimum (as opposed to getting stuck in a suboptimal extrema) and (ii), it improves the quality of this minimum by mitigating the effects of noise [46]. With perfectly correlated (dipolar) sources, primarily only the later benefit is in effect. For example, with low noise and perfectly correlated sources, the estimation problem reduces to an equivalent problem with n = 1, so the local minima profile of the cost function does not improve with increasing n. Of course standard γ-MAP can still be very effective in this scenario [34], [46]. In contrast, geometric arguments can be made to show that uncorrelated sources with large n offer the best opportunity for local minima avoidance. More details about how γ-MAP functions when temporally correlated sources are present can be found in [47] as well as Section VI-A where beamforming is discussed. Finally, a third benefit to using n > 1 is that it leads to temporal smoothing of estimated time courses (i.e., rows of Ŝ). This occurs because the selected covariance components do not change across time, as would be the case if a separate set of hyperparameters were estimated at each time point. This distinction will be illustrated in subsequent papers.
Further theoretical support for γ-MAP is possible in the context of localization bias assuming simple source configurations. For example, substantial import has been devoted to quantifying localization bias when estimating a single dipolar source. Recently it has been shown, both empirically [30] and theoretically [40], that the sLORETA algorithm has zero location bias under this condition at high SNR. Because γ-MAP can be viewed as an iterative enhancement of the sLORETA as mentioned previously (and discussed further in Section VI-B), the question naturally arises whether γ-MAP retains this desirable property. In fact, it can be shown that this is indeed the case in two general situations. We assume that the lead-field matrix L represents a sufficiently high sampling of the source space such that any active dipole aligns with some lead-field column. Unbiasedness can also be shown in the continuous case for both sLORETA and general γ-MAP, but the discrete scenario is more straightforward and of course more relevant to any practical task.
Theorem 2
Assume that
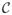 includes (among others) ds covariance components of the form
. Then in the absence of noise (high SNR), and assuming fi(γi) = 0, γ-MAP has zero localization bias when estimating a single dipolar source, regardless of the value of n.
includes (among others) ds covariance components of the form
. Then in the absence of noise (high SNR), and assuming fi(γi) = 0, γ-MAP has zero localization bias when estimating a single dipolar source, regardless of the value of n.
If we are willing to tolerate some additional assumptions, then this theorem can be significantly expanded. For example, multiple dipolar sources can be localized with zero bias if they are perfectly uncorrelated (orthogonal) across time and assuming some mild technical conditions [46]. This result formalizes the notion, mentioned above, that γ-MAP performs best with uncorrelated sources. Turning to the more realistic scenario where noise is present gives the following:
Theorem 3
Let
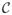 be constructed as above and assume the noise covariance matrix Σε is known up to a scale factor and fi(γi) = 0. Then given a single dipolar source, in the limit as n becomes large the γ-MAP cost function is unimodal, and a source estimate with zero localization bias achieves the global minimum.
be constructed as above and assume the noise covariance matrix Σε is known up to a scale factor and fi(γi) = 0. Then given a single dipolar source, in the limit as n becomes large the γ-MAP cost function is unimodal, and a source estimate with zero localization bias achieves the global minimum.
For most reasonable lead-fields and covariance components, this global minimum will be unique, and so the unbiased solution will be found as in the noiseless case. As for proofs, all the theoretical results pertaining to localization bias in this section follow from local minima properties of ML covariance component estimates. While details have been deferred to [47], the basic idea is that if the outerproduct BBT can be expressed as some non-negative linear combination of the available covariance components, then the γ-MAP cost function is unimodal and Σ̂b = n−1BBT at any minimizing solution. This Σ̂b in turn produces unbiased source estimates in a variety of situations.
While theoretical results of this kind are admittedly limited in applicability, many iterative Bayesian schemes in fact fail to exhibit similar performance. For example, all of the S-MAP algorithms we are aware of, including FOCUSS and MCE methods, provably have a localization bias in the general setting, although in particular cases there may be no bias. When we move to more complex source configurations with possible correlations and noise, theoretical results are not available; however, empirical tests provide a useful means of comparison (results will be presented in forthcoming papers).
C. An Alternative Perspective on γ-MAP and a Bound on log p(B)
For purposes of model selection, a rigorous bound on log p(B) can be derived using principles from convex analysis that have been successfully applied in general-purpose probabistic graphical models [20]. The basic idea follows from an intrinsic property of Gaussian scale mixtures outlined in [29] that readily adapts to the present context. As in Section III-A, we choose to work with the pseudo-source parameterization for convenience. To begin, we define the function gi(·) via
| (32) |
which is always possible since p(Si|γi) only depends on Si through the Frobenius norm operator.8 It can be shown that, for any pi(γi), the gi(·) which results from the above marginalization will be a concave, non-decreasing function of its argument [29]. From convex analysis [6], this property implies that gi(·) can always be expressed as a minimum over upper-bounding lines or
| (33) |
where is the concave conjugate of gi(·) defined via the duality relationship
| (34) |
For what follows, it is not crucial that these expression be fully digested; however, [20] contains a very accessible treatment of conjugate duality and related concepts that are applicable here. The implication of (33) is that now p(Si) can be written in the variational form
| (35) |
where we have used the substitution to highlight the connection with γ-MAP. Now suppose that we would like to compute a tractable approximation to p(B, S) that can be normalized to produce some p̂(S|B) (and therefore a posterior estimate p̂(S|B) of the real sources as well) and provides a bound on log p(B) that can be used for model selection. Both objectives are easily accomplished using (35). By dropping the maximization, we obtain the rigorous lower bound on p(B, S) given by
| (36) |
To find the optimal approximation, we minimize
| (37) |
to obtain some γ̂. This is of course the same as the γ-MAP cost function with . If these fi(γi) so obtained are concave and non-decreasing, then the sparsity bound from Theorem 1 will hold. Additionally, none of the γ-MAP optimization methods detailed in Section III-A require the hyperprior to be normalized, so these approaches can be applied equally well here when convenient for optimizing (37) to give some γ̂. Once this value is determined, the approximate distribution
| (38) |
is Gaussian with moments given by (23) computed using γ = γ̂. Finally, for purposes of model comparison, the convex variational formulation gives the following rigorous lower bound:
| (39) |
Later in Section V we will describe related bounds produced by alternative variational Bayesian methods.
IV. Source-Space MAP Estimation (S-MAP)
S-MAP methods operate in source space by intergrating out γ and then computing a MAP estimate Ŝ. There are (at least) two ways to go about this depending on how the integration is performed with respect to the hierarchical model from Section II. The most direct method involves solving
| (40) |
However, in a general setting this can be a difficult optimization problem and furthermore, the nature of the underlying cost function is not immediately transparent. Consequently, we advocate an indirect alternative utilizing the pseudo-source decomposition given by S described previously, which leads to an efficient EM implementation and a readily interpretable cost function. It also demonstrates that both FOCUSS and MCE can be viewed as EM algorithms that are readily generalized to handle more complex spatio-temporal constraints. Explicitly, we will minimize
| (41) |
where gi(·) is defined as in (32).
For many choices of the hyperprior, the associated gi(·) may not be available in closed form. Moreover, it is often more convenient and transparent to directly assume the form of gi(·) rather than infer its value from some postulated hyperprior. In fact, based on results in [29], virtually any non-decreasing, concave function gi(·) of interest can be generated by the proposed hierarchical model. In other words, there will always exist some pi(γi), possibly improper, such that the stated Gaussian mixture representation will produce any desired concave gi(·).9 A generalized version of MCE and FOCUSS can be produced from the selection
| (42) |
which is concave and amenable to a Gaussian scale-mixture representation for any p ∈ (0, 2] and constant ci > 0. This is key because, even if the corresponding pi(γi) that produced a particular gi(·) is unavailable or unwieldy, effective EM update rules can still be developed based on the associated unknown scale-mixture [29] as will be discussed in Section IV-A. The value of ci can be chosen to account for dimensionality differences of the pseudo-sources Si, provide symmetry with γ-MAP, and to allow update rules and cost functions that reduce to regular FOCUSS and MCE with the appropriate simplifications. While space precludes a detailed treatment, the selection accomplishes these objectives. To retrieve the exact FOCUSS and MCE cost functions, we must further assume n = 1, Σε = λI (where λ is a non-negative scalar), and Ai = ei for i = 1, …, ds. Under these assumptions (41) reduces to
| (43) |
where b is the observation vector (consistent with n = 1) and s is the associated source vector. With p = 1, (43) is the regularized MCE cost function. In the limit p → 0, the second term converges (up to a constant which does not affect the final solution) to and we retrieve the basic FOCUSS cost function.
Before we proceed, a couple of points are worth noting regarding the general case. First, if A is invertible, then solving (40) and (41) lead to an identical estimate for S. Secondly, while an infinite set of decompositions can be found for each covariance component, the cost function (41) is invariant to the particular one that is chosen, meaning that the estimate Ŝ will be the same. Consequently, Ai can be computed in the most convenient fashion.
A. Optimization
Presumably, there are a variety of ways to optimize (41). One particularly straightforward and convenient method exploits the hierarchical structure inherent in the assumed Bayesian model. This leads to simple and efficient EM-based update rules as follows [7], [11], [29].10 It also demonstrates that the canonical FOCUSS iterations are equivalent to principled EM updates. Likewise, regularized MCE solutions can also be obtained in the same manner.
Ultimately, we would like to estimate each Si, which in turn gives us the true sources S. If we knew the values of the hyperparameters γ this would be straightforward; however, these are of course unknown. Consequently, in the EM framework γ is treated as hidden data whose distribution (or relevant expectation) is computed during the E-step. The M-step then computes the MAP estimate of S assuming γ equals the appropriate expectation.
For the (k+1)-th E-step, the expected value of each is required under the distribution p (γ|B, S(k)) (see the M-step below) and can be computed analytically assuming gi(·) is differentiable, regardless of the underlying form of p(γ). Using results pertaining to Gaussian scale mixtures [29] and the assumption gi(z) ∝ zp/2, it can be shown that the relevant sufficient statistic is
| (44) |
The associated M-step is then readily computed using
| (45) |
giving the i-th pseudo-source update rule
| (46) |
S(k+1) = AS(k+1) is then the (k + 1)-th estimate of the true sources. Each iteration of this procedure decreases the cost function (41) and convergence to some fixed point is guaranteed. Also, by substituting (46) into (44) and treating as an estimate of γi, the combined iteration expressed in terms of γ alone becomes
| (47) |
We note that B-dependency is limited to BBT, so we can replace B with B as before. Each iteration then produces a refined estimate of the unknown hyperparameters γ just as with the γ-MAP algorithms from Section III-A, implying that in some sense we are performing covariance component estimation akin to γ-MAP. The updates, while not equivalent, are very related. For example, when p → 0, (47) equals the first term of the γ-MAP update (27) or the numerator in (29). The exact connection between S-MAP and γ-MAP will be made explicit in Section IV-B. Regardless, from a computational standpoint, the S-MAP updates described here are of the same per-iteration complexity as the γ-MAP updates from Section III-A.
As a final point of comparison, given the simplifying assumptions n = 1 and Ai = ei as before, (47) reduces to
| (48) |
where ℓi is the i-th column of L. Not surprisingly, we recover the exact FOCUSS updates when p → 0 and a FOCUSS-like update for MCE when p = 1.11 Note however, that while previous applications of MCE and FOCUSS to neuroelectromagnetic source imaging using n = 1 require a separate iterative solution to be computed at each time point in isolation, here the entire S can be computed at once with n > 1 for about the same computational cost as a single FOCUSS run. The benefits of the generalized versions of FOCUSS and MCE, beyond mere computational expediency, will be discussed further below.
B. Analysis of S-MAP
The nature of the EM updates for S-MAP, where an estimate of γ is obtained via the E-step, suggest that this approach is indirectly performing some form of covariance component estimation. But if this is actually the case, it remains unclear exactly what cost function these covariance component estimates are minimizing. This is unlike γ-MAP, where γ is explicitly selected to minimize (18). The following theorem details the relationship between the S-MAP solution and a particular covariance component-based cost function.
Theorem 4
Let γ̂ be a minimum of the cost function
| (49) |
where p ∈ (0, 2) and γ ≥ 0. Then
| (50) |
satisfies, , where S* is a minimum of (41).
The proof is beyond the scope of this paper; however, it follows by extension of convexity results in [49] to the proposed hierarchical model.12 Moreover, while Theorem 4 only pertains to the selection gi(z) ∝ zp/2 for simplicity, the result is readily generalized to any concave, non-decreasing gi(·), and therefore any S-MAP problem with a source prior that can be expressed as a Gaussian scale mixture.
Several things are worth noting regarding
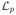 (γ). First, the data fit term is equivalent to that employed by the γ-MAP cost function. Consequently, the fundamental difference between S-MAP and γ-MAP ultimately lies in the regularization mechanism of the covariance components. Unlike γ-MAP, the penalty term in (49) is a separable summation that depends on the value of p to affect hyperparameter pruning; there is no volume-based penalty as in (18). For p ≤ 1, this penalty is concave in γ and leads to the following result:
(γ). First, the data fit term is equivalent to that employed by the γ-MAP cost function. Consequently, the fundamental difference between S-MAP and γ-MAP ultimately lies in the regularization mechanism of the covariance components. Unlike γ-MAP, the penalty term in (49) is a separable summation that depends on the value of p to affect hyperparameter pruning; there is no volume-based penalty as in (18). For p ≤ 1, this penalty is concave in γ and leads to the following result:
Theorem 5
Assuming p ≤ 1, every local minimum of
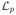 (γ) is achieved at a solution with at most rank(B)
nonzero hyperparameters.
(γ) is achieved at a solution with at most rank(B)
nonzero hyperparameters.
The proof is directly analogous to that of Theorem 1; both demonstrate how concave regularization terms lead to hyperparameter pruning. As a direct consequence of this result, we note that hyperparameter pruning directly leads to pruning of pseudo-sources as previously claimed:
Corollary 1
Assuming p ≤ 1, every local minimum of the generalized MAP cost function (41) is achieved at a solution Ŝ = Σi AiŜi such that at most rank(B)
pseudo-sources Ŝi satisfy
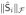 > 0.
> 0.
This result implies that, rather than promoting sparsity at the level of individual source elements at a given voxel and time (as occurs with standard MCE and FOCUSS when n = 1, Ci = ei), here sparsity is encouraged at the level of the pseudo-sources Si.13 The functions gi(·) operate on the Frobenius norm of each Si and favor solutions with
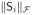 = 0 for many indeces i. As before, the bound from Theorem 5 is extremely weak; in practice many more components will be pruned. However, an equally key feature of this model is that within a nonzero Si, smooth (non-sparse) solutions are favored by virtue of the Frobenius norm operator. This is why, for example, S-MAP (like γ-MAP) does not produce overly discontinuous source estimates across time as will occur if regular FOCUSS (or MCE) is applied individually to each time point. Because each Si spans all time points, and smoothness is encouraged within each Si, the resulting source estimate is a superposition of smooth temporal bases. This is also explains why, when given the appropriate Ai [36], dipole orientations need not be biased to the coordinate axis [18].
= 0 for many indeces i. As before, the bound from Theorem 5 is extremely weak; in practice many more components will be pruned. However, an equally key feature of this model is that within a nonzero Si, smooth (non-sparse) solutions are favored by virtue of the Frobenius norm operator. This is why, for example, S-MAP (like γ-MAP) does not produce overly discontinuous source estimates across time as will occur if regular FOCUSS (or MCE) is applied individually to each time point. Because each Si spans all time points, and smoothness is encouraged within each Si, the resulting source estimate is a superposition of smooth temporal bases. This is also explains why, when given the appropriate Ai [36], dipole orientations need not be biased to the coordinate axis [18].
While the sparsity bounds for S-MAP do not provide any distinction from γ-MAP, this does not imply that actual performance in practical situations will be the same or even similar. This is because Theorems 1 and 5, which are worst-case bounds applying to component pruning at any local minimum, say nothing about the probability of achieving the global minimum or the quality of this global minimum even if it is achieved. In these respects the selection of gi(·), or in particular the value of p, can have a very significant impact.
The simple choice p = 1 leads to a convex cost function devoid of non-global minima; the update rules from Section IV-A will converge to a global solution. However, the resulting generalized MCE estimate associated with this global minimum can potentially have problems recovering certain standard source configurations. In fact, MCE solutions, commonly referred to as minimum ℓ1-norm solutions, have been studied exhaustively in the statistics and signal processing communities regarding the ability to recover sparse (i.e., dipolar-like) sources. Specifically, conditions are stipulated whereby minimum ℓ1-norm solutions are guaranteed to locate some number of nonzero coefficients (or sources) in an underdetermined linear model [9], [15], [17], [42]. While derived primarily for the simplified case where n = 1, Ai = ei, they nontheless elucidate concerns in the more general setting. For example, one of the earliest and most straightforward of these results, which applies when Σε = 0, can be posed as follows:
Assume we have observed a single measurement vector b produced by the generative model b = Ls0, where s0 is a dipolar source vector meaning that most elements are equal to exactly zero or equivalently, ||s0||0 is small.14 Moreover, assume that no other solution to b = Ls satisfies ||s||0 ≤ ||s0||0, meaning no solution with fewer number of equivalent dipoles could have produced b. Then the following result from [9] dictates a rigorous, computable condition whereby the MCE solution is guaranteed to successfully locate all dipoles.
Theorem 6: (adapted from Donoho and Elad, 2003)
Given an arbitrary lead-field L with columns ℓi normalized such that , ∀i = 1, …, ds, and given G ≜ LT L and κ ≜ maxi≠j |Gij|, if s0 satisfies
| (51) |
then the MCE solution is guaranteed to equal s0.
While elegant in theory, in practice Theorem 6 is very difficult to apply. For example, the lead-fields L required for MEG/EEG source localization (when suitably normalized as required by the theorem) typically have κ ≈ 1, meaning some columns tend to be highly correlated. This implies that only sparse solutions with at most one nonzero element are guaranteed to be found, and even this will only occur for suitably normalized lead-fields. Therefore with unnormalized lead-fields, localization bias can still occur when estimating single dipolar sources with no noise (unlike γ-MAP which can be invariant to to column normalization schemes in this respect). Additionally, the above bound is tight, meaning a lead-field matrix can always be constructed such that the MCE solution will sometimes fail to find s0 if ||s0||0 ≥ 1/2(1 + 1/κ). Further analysis of general equivalence conditions and performance bounds for MCE-like algorithms are derived in [10], [43]. However again, these are all more applicable to applications such as compressed sensing, where the columns of the analogous L are not highly correlated, than to neuroelectromagnetic localization problems. Moreover, the potential difficulty dealing with correlated (or coherent) lead-field columns persists in the more general scenario involving n > 1 and Ai ≠ ei.
To summarize then, the problem with MCE is not the existence of local minima. Rather, it is that the global minimum may be unrepresentative of the true source distribution even for simple dipolar source configurations. In this situation, and especially when lead-field columns are highly correlated, the MCE solution may fail to find sufficiently sparse source representations consistent with the assumption of a few equivalent current dipoles. We anticipate that this issue could persist with more complex covariance components and source configurations. Regardless, the unimodal, convex nature of the generalized MCE cost function remains a very attractive advantage over γ-MAP.
In contrast, if p < 1 (which implies that gi(z2) is strictly concave in z), then more pseudo sources will be pruned at any global solution, which often implies that those which remain may be more suitable than the MCE estimate. Certainly this is true when estimating dipolar sources, but it likely holds in more general situations as well. However, local minima can be an unfortunate menace with p < 1. For example, the canonical FOCUSS algorithm, which implies p → 0, has a combinatorial number of local minima satisfying
| (52) |
Obviously this number will be huge for practical lead-field matrices, which largely explains the sensitivity of FOCUSS to initialization and noise. While the FOCUSS cost function can be shown to have zero localization bias at the global solution, because of the tendency to become stuck at local optima, in practice a bias can be observed when recovering even a single dipolar source. Other selections of p between zero and one can lead to a similar fate.
In the general case, a natural trade-off exists with S-MAP procedures: greater sparsity of solutions at the global minimum the less possibility that this minimum is biased, but the higher the chance of suboptimal convergence to a biased local minimum. In this regard the optimal balance could well be application dependent; however, these factors crucially disallow any theoretical bias results analogous to those given for γ-MAP in Section III-B. So in this respect γ-MAP maintains a distinct advantage, which is further elaborated in [46] in a somewhat different context. However, S-MAP is nonetheless capable of successfully handling large numbers of diverse covariance components, and therefore simultaneous constraints on the source space. This addresses many of the concerns raised in [24] pertaining to existing MAP methods.
Finally, to link (49) to more traditional weighted minimum ℓ2-norm methods, we note that
| (53) |
When this expression is plugged into (49), subsequent minimization forces all γi → 1, and the resulting estimate Ŝ is the standard weighted minimum norm estimate.
V. Variational Bayes
Sections III and IV describe two complementary yet distinctive means of utilizing a simple Gaussian scale mixture model to affect source localization. From the perspective of a Bayesian purist however, the pursuit of MAP estimates for unknown quantities of interest, whether parameters S or hyperparameters γ, can be misleading since these estimates discount uncertainty and may not reflect regions of significant probability mass, unlike (for example) the posterior mean. Variational Bayesian methods, which have successfully been applied to a wide variety of hierarchical Bayesian models in the machine learning literature [1], [3], offer an alternative to γ-MAP and S-MAP that putatively tackle these concerns. The principle idea here is that all unknown quantities should either be marginalized (intergrated out) when possible or approximated with tractable distributions that reflect underlying uncertainty and have computable posterior moments.15 Practically, we would like to account for ambiguity regarding γ when estimating p(S|B), and potentially, we would also like a good approximation for p(B), or a bound on the model evidence log p(B), for application to model selection [13], [22].
In this section we will briefly consider two possible variational approximations germane to the source localization problem: the mean-field approximation (VB-MF), and a fixed-form, Laplace approximation (VB-LA). It turns out that both are related to γ-MAP but with important distinctions.
A. Mean-Field Approximation (VB-MF)
The basic strategy here is to replace intractable posterior distributions with approximate ones that, while greatly simplified and amenable to simple inference procedures, still retain important characteristics of the full model. In the context of our presumed model structure, both the posterior source distribution p(S|B), which is maximized with S-MAP, as well as the hyperparameter posterior p(γ|B), which is maximized via γ-MAP, are quite complex and can only be expressed up to some unknown scaling factor (the integration required for normalization is intractable). Likewise, the joint posterior p(S, γ|B) over all unknowns is likewise intractable and complex. VB attempts to simplify this situation by finding an approximate joint posterior that factorizes as
| (54) |
where p̂(S|B) and p̂(γ|B) are amenable to closed-form computation of posterior quantities such as means and variances (unlike the full posteriors upon which our model is built). This is possible because the enforced factorization, often called the mean-field approximation reflecting its origins in statistical physics, simplifies things significantly [1], [3]. The cost function optimized to find this approximate distribution is
| (55) |
where q(S) and q(γ) are arbitrary probability distributions and KL[·||·] indicates the Kullback-Leibler divergence measure.
Recall that γ-MAP iterations effectively compute an approximate distribution for S (E-step) and then a point estimate for γ (M-step); S-MAP does the exact opposite. In contrast, here an approximating distribution is required for both parameters S and hyperparameters γ. While it is often contended that conjugate hyperpriors must be employed such that (55) is solvable [5], in fact this problem can be solved by coordinate descent over q(S) and q(γ) for virtually any hyperprior [29] in the following sense.
Assume first that q(γ) is held fixed to some q(k)(γ) and we are optimizing (55) with respect to q(S). This can be solved via
| (56) |
If we define
| (57) |
then (56) simplifies to
| (58) |
The final distribution is Gaussian with moments given by (23) using γ = γ̄(k). Note that we can also use B for computational convenience. So this update is equivalent to the E-step of γ-MAP.
Updates for q(k+1)(γ) proceed in a similar fashion with fixed q(S) = q(k+1)(S) giving
| (59) |
where the factorization over γi is a natural consequence of the mean-field approximation; it does not follow from an additional assumption. Regardless, the posterior distributions over each γi are not available in closed form, except when a conjugate prior is used for p(γ). However, the update for q(k+1)(S) above only requires γ̄(k+1) at each iteration, not the entire distribution. The latter can be computed using
| (60) |
where p̂(
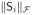 ) ≜ p(Si) and p̄′(·) is the associated first derivative. The derivation follows from [28], [29].
) ≜ p(Si) and p̄′(·) is the associated first derivative. The derivation follows from [28], [29].
Two things are worth pointing out with respect to this result. First, it implies that we can maximize (55) with respect to p̂(S|B) without ever explicitly computing p̂(γ|B) in full. This is accomplished by iteratively updating each S̄i and γ̄i. Secondly, we have the following:
Theorem 7
Let p̂(S|B) denote the distribution that solves (55) assuming some arbitrary hyperprior . Then there exists a hyperprior and corresponding γ-MAP estimate γ̃ = arg maxγ p(B|γ) Πip̃i(γi) such that
| (61) |
The selection achieves this result, where is the concave conjugate of gi(·) defined via (32).
The proof, which can be derived from results in [29], has been omitted for brevity. Theorem 7 implies that the p̂(S|B) obtained from the mean-field approximation offers nothing new that could not already be obtained via γ-MAP (although the hyperprior needed for equivalence will generally not be the same as used by VB-MF, i.e., fi(γi) ≠ f̃i(γi)). Consequently, although we are in principle accounting for uncertainty in γ when arriving at the posterior on S, we do not actually obtain a new class of approximations by this added sophistication.
The analysis here sheds some light on existing localization algorithms. For example, in [38] a VB-MF algorithm is developed for localizing sources with some spatial extent and potentially some prior knowledge from fMRI. The underlying cost function can be shown to be a special case of (55) assuming that Σs is parameterized via
| (62) |
and so dγ = 2ds.16 When fMRI data is available, it is incorporated into a conjugate inverse Gamma hyperprior on γ, as is also commonly done with γ-MAP methods [5]. Optimization is then performed using update rules that reduce to special cases of (58) and (60). Unfortunately, because these EM updates are prohibitively slow in practice, some heuristics are proposed to facilitate the estimation process [38]. Of course in light of the fact that minimizing the VB-MF cost can be accomplished via γ-MAP for this model (assuming the appropriate f(γ)), the faster updates described in Section III-A could easily be substituted. With these results in mind then, the general methods of [12], [24], [31] and [33], [34], [41] as well as the variational method of [38] are all identical with respect to their underlying source estimates p̂(S|B); they differ only in which covariance component set
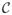 and possibly hyperpriors are assumed, and in how optimization is performed.
and possibly hyperpriors are assumed, and in how optimization is performed.
Before proceeding, however, we should point out that there is a drawback to using (60) in place of a full update on q(γ). For purposes of model comparison, it is sometimes desirable to have an estimate of log p(B) [13], [22]. One popular estimator which strictly lower bounds log p(B) and falls out of the VB framework is given by
| (63) |
where the inequality follows by the non-negativity of the Kullback-Leibler divergence. The quantity F is sometimes referred to the variational free energy. Evaluation of F requires the full distribution p̂(γ|B) and therefore necessitates using conjugate priors or further approximations. One possibility, which involves the use of a fixed-form Gaussian assumption, is discussed in the next section and in Appendix D.
B. Laplace (Fixed-Form) Approximation (VB-LA)
The Laplace approximation has been advocated in [14] for addressing a variety of general problems in neuroimaging. Application to MEG/EEG source localization as outlined in [13] is tailored to finding a tractable posterior distribution on the hyperparameters and then using this p̂(γ|B) to find approximations to p(S|B) and log p(B) (the pseudo-sources S are not used in the formulation in [13]). To facilitate this process, the hyperparameters are re-parameterized via the transformation γi ≜ log γi, ∀i, which now alows them to have positive or negative values. The Laplace approximation then involves the assumption that the posterior distribution of these new hyperparameters λ ≜ [λ1, …, λdγ]T satisfies
| (64) |
There are a variety of ways μλ and Σλ can be chosen to form the best approximation. Although not explicitly presented this way, the method from [13] is equivalent to the following procedure. First, a MAP estimate of λ is computed by maximizing log p(B, λ) using a seconder-order Fisher scoring procedure, although as before this method is not guaranteed to increase the cost function and requires a very expensive matrix inverse. However, because log p(B, λ = log γ) = log p(B|γ)p(λ = log γ) is equivalent to the γ-MAP cost function (up to a scaling factor and constant terms), the optimization methods from Section III-A could be applied as well. As stated previously, these methods do not require that the hyperprior be properly normalized, so the fact that p(λ = log γ) is not a proper density with respect to γ is not an issue.
Once the mode λ̂ is obtained, we set μλ = λ̂. The second-order statistics of the true and approximate distributions are then matched at this mode using Σλ = −[ℓ″(μλ)]−1, where ℓ(μλ) ≜ log p(B, λ = μλ) and ℓ″(μλ) is the corresponding Hessian matrix evaluated at μλ.
We still need approximate distributions for p(S|B) and p(B). For p(S|B), it is suggested in [13] to use p(S|B, λ = μλ), which is equivalent to a γ-MAP estimator with γ = exp(μ̂λ); however, uncertainty regarding λ as reflected by Σλ does not effect p(S|B, λ = μλ). So in this respect, like the previous variational method, there is no advantage over γ-MAP. Regarding p(B), an approximation to log p(B) is derived that requires an additional assumption.
Because of the non-negativity of the KL divergence, it always holds that
| (65) |
Unfortunately however, this bound cannot be computed in closed form, so the computable approximation
| (66) |
is used as a surrogate. The derivation can be found in Appendix C. While the original F does constitute a rigorous bound on log p(B), F̂ does not. This is easily seen by noting that
| (67) |
The extra terms can be positive or negative and, because log p(λ = μλ|B) is unknown and intractable, there is no way of knowing how F̂ relates to log p(B). Therefore, since F̂ can be greater than log p(B), it could potentially distort efforts to use this approximation for model selecton (e.g., it could artificially inflate the model evidence), although empirical results from [13] suggest that it can be informative in practice nonetheless. A second potential issue with F̂ is the computational complexity required to compute −log |ℓ″(μ̂λ)|; this is a calculation like the Fisher scoring procedure. Although this only need be computed once after μλ is obtained (if we use the methods from Section III-A), this can still be an extremely expensive and possibly numerically instable task if dγ is large.
The Laplace approximation could certainly be implemented with a variety of hyperpriors. In [13], a Gaussian distribution (with user-specified mean and covariance) is assumed on λ. This is equivalent to assuming a log-normal prior on γ. With this assumption, (66) is equivalent to Eq. (5) in [13].
As a final consideration, the limitations of this method can potentially be ameliorated by combining the Laplace and mean-field approximations. This possibility is explored in depth in Appendix D, where an alternative learning procedure, with several attractive properties, is developed.
C. Summary
The approximate distribution p̂(S|B) obtained from both variational methods is equivalent to a γ-MAP estimate given the appropriate equalizing hyperprior. Consequently, the optimization procedures for this purpose described in Section III-A can be directly applied if desired. Likewise, the sparsifying properties of the underlying γ-MAP cost functions carry over as well (see Section III-B). Additionally, when the mean-field approximation is used, the particular parameterization of the unknown hyperparameters (e.g., γ vs. λ has no affect on p̂(S|B). This is because the only quantity required for this approximation is the expected value of each ; this quantity is invariant to the parameterization. This is quite unlike the Laplace approximation, which crucially depends on the non-linear re-parameterization of γ.
More substantial differences exist regarding the estimated bound on log p(B). With VB-MF, we get a principled bound that can only be computed in closed form when conjugate priors on γ are present, although Appendix D presents one way to circumvent this difficulty. Because the VB-MF posterior on the hyperparameters naturally factorizes (regardless of the parameterization) via (59), this bound is independent of any correlations between the hyperparameters and is easy to compute. In contrast, the VB-LA gives an approximation to log p(B) that can potentially be utilized with a variety of hyperpriors; however, a rigorous bound is not produced and so formal model comparison can be biased. The approximation also depends on correlations between hyperparameters and can be expensive to compute if dγ is extremely large.
As discussed in Section III-C, direct γ-MAP can also be used to obtain a flexible bound on log p(B) that can be used in a variety of situations and does not depend on conjugacy. In general, it has not yet been established which approximation technique leads to the tightest lower bound on log p(B) or the most effective metric in practice.
VI. Connections with Other Statistical Tomographic Methods
Thus far, we have attempted to relate and extend three large classes of Bayesian inverse methods, all of which turn out to be performing covariance component estimation/pruning using different sparsity promoting regularization procedures. This section provides further connections to beamforming and sLORETA.
A. Minimum Variance Adaptive Beamforming
Beamformers are spatial filters that pass source signals in particular focused locations while suppressing interference from elsewhere. The widely-used minimum variance adaptive beamformer (MVAB) creates such filters using a sample covariance estimate; however, the quality of this estimate deteriorates when the sources are correlated or the number of samples n is small [39], [52].
But the simpler γ-MAP strategy can also be used to enhance beamforming in a way that is particularly robust to source correlations and limited data [47]. Specifically, the estimated γ-MAP data covariance matrix
| (68) |
can be used to replace the problematic sample covariance Cb = n−1BBT. In [47], we prove that this substitution has the natural ability to remove the undesirable effects of correlations or limited data. When n becomes large and assuming uncorrelated sources, this method reduces to the exact MVAB. Simulations using MEG and direction-of-arrival data [47] support these conclusions. Additionally, the method can potentially enhance a variety of traditional signal processing methods that rely on robust sample covariance estimates.
In comparing this idea with the VB approach for estimating source correlations in [36], it is important to make a distinction between estimating the correlation between sources and estimating the locations of correlated sources. In [47] we attempt only the latter using the natural decorrelating mechanism of γ-MAP, although actual source correlations can still be estimated empirically using the Ŝ so obtained (which is localized but not actually decorrelated). The simplicity of this approach means that efficient update rules and analyses of global and local minima are possible as discussed in Section III-B and [47]. In contrast, the added complexity involved in explicitly learning source correlations using the method in [36] leads to expensive learning rules (quadratic in ds) and some ambiguity regarding convergence properties and the nature of minimizing solutions.
B. sLORETA
Standardized low resolution brain electromagnetic tomography (sLORETA) begins with a weighted minimum ℓ2-norm (WMN) estimate using Σs = I and Σε = λI and then standardizes the solution using the covariance of the resulting WMN estimator [30]. This process is designed to compensate for deep current sources, which otherwise may be mapped to superficial cortical locations. The sLORETA procedure is easy to compute analytically and has been show to exhibit zero localization bias if only a single dipolar source is present [40].
We now describe how sLORETA provides an interesting link between the γ-MAP updates and the iterative FOCUSS source localization algorithm. The connection is most transparent when we assume fixed dipole orientations in each voxel and substitute the prior covariance into (29), giving the modified update
| (69) |
where Γ ≜ diag[γ], ℓi is the i-th column of L, b is a single measurement vector, and R(k) is the effective resolution matrix given the hyperparameters at the current iteration. The j-th column of R (called a point-spread function) equals the source estimate obtained using when the true source is a unit dipole at location j [40].
Continuing, if we assume that initialization of γ-MAP occurs with γ(0) = 1 (as is customary), then the hyperparameters produced after a single iteration of γ-MAP are equivalent to computing the sLORETA estimate for standardized current density power [30] (this assumes fixed orientation constraints). In this context, the inclusion of R as a normalization factor helps to compensate for depth bias, which is the propensity for deep current sources within the brain to be underrepresented at the scalp surface [30], [33]. So γ-MAP can be interpreted as a recursive refinement of what amounts to the non-adaptive, linear sLORETA estimate. In fact, the basic MacKay γ-MAP update equations have been derived independently from this perspective [33]. Additionally, during this iterative process it typically retains zero location bias in the sense described in Section III-B.
As a further avenue for comparison, if we assume that R = I for all iterations, then the update (69) is equivalent to the original FOCUSS iterations regularized using λ. Therefore, γ-MAP can be viewed in some sense as taking the recursive FOCUSS update rules and including the sLORETA normalization that, among other things, allows for some level of depth bias compensation.
VII. Discussion
The efficacy of modern Bayesian techniques for quantifying uncertainty and explicitly accounting for prior assumptions make them attractive candidates for source localization. However, it is not always transparent how these methods relate, nor how they can be extended to handle more challenging problems, nor which ones should be expected to perform best in various situations relevant to MEG/EEG source imaging. Starting from a hierarchical Bayesian model constructed using Gaussian scale mixtures with flexible covariance components, we analyze and, where possible, extend three broad classes of Bayesian inference methods: γ-MAP, which involves integrating out the unknown sources and optimizing the hyperparameters, and S-MAP, which integrates out the hyperparameters and directly optimizes over the sources, and variational approximation methods, which attempt to account for uncertainty in all unknowns. Together, these three encompass a surprisingly wide range of existing source reconstruction approaches, which makes general theoretical analyses and algorithmic extensions/improvements pertaining to them particularly relevant. Specific highlights of this endeavor are as follows:
γ-MAP, S-MAP, and VB can be viewed as procedures for learning a source covariance model using a set of predetermined symmetric, positive semi-definite covariance components. The number of components in this set, each of which acts as a constraint on the source space, can be extremely large, potentially much larger than the number of sensors. However, a natural pruning mechanism effectively discards components that are unsupported by the data. This occurs because of an intrinsic sparsity preference in the Gaussian scale mixture model, which is manifested in an explicit sparsity-inducing regularization term. Consequently, it is not crucial that the user/analyst manually determine an optimal set of components a priori; many components can be included initially allowing the learning process to remove superfluous ones.
-
The wide variety of Bayesian source localization methods that fall under this framework can be differentiated by the following factors:
Selection of covariance component regularization term per the discussion in Sections III-B and IV-B. Note that this will implicitly determine whether we are performing S-MAP, γ-MAP, or VB.
Choice of initial covariance component set
 ,
,Optimization method/Update rules, and
Approximation to log p(B); this determines whether we are ultimately performing γ-MAP or VB.
Covariance component possibilities include geodesic neural basis functions for estimating distributed sources [34], spatial smoothing factors [24], indicator matrices to couple dipole components or learn flexible orientations [36], fMRI-based factors [31], and temporal and spectral constraints [21].
With large numbers of covariance components, S-MAP, γ-MAP, and VB provably remove or prune a certain number of components which are not necessary for representing the observed data.
In principle, the noise-plus-interference covariance Σε can be jointly estimated as well, competing with all the other components to model the data (see [11] for a special case of the latter in the context of kernel regression). However, identifiability issues can be a concern here [46] and so we consider it wiser to estimate Σε via other means (e.g., using VBFA applied to prestimulus data [53]).
The latent structure inherent to the Gaussian scale-mixture model leads to an efficient, principled family of update rules for γ-MAP, S-MAP, and VB. This facilitates the estimation of complex covariance structures modulated by very large numbers of hyperparameters (e.g., 100, 000+) with relatively little difficulty.
Previous focal source imaging techniques such as FOCUSS and MCE display undesirable discontinuities across time as well significant biases in estimating dipole orientations. Consequently, various heuristics have been proposed to address these deficiencies [18], [44]. However, the general spatio-temporal framework of γ-MAP and S-MAP handles both of these concerns in a robust, principled fashion by the nature of their underlying cost function.
The standard weighted minimum ℓ2 norm method can be viewed as a limiting case of both S-MAP and γ-MAP.
γ-MAP provides a useful covariance estimate that can be used to improve the performance of the minimum variance adaptive beamformer when sources are correlated or n is small.
sLORETA is equivalent to performing a single iteration of a particular γ-MAP optimization procedure. Consequently, the latter can be viewed as an iterative refinement of sLORETA. This is exactly analogous to the view of FOCUSS as an iterative refinement of a weighted minimum ℓ2-norm estimate.
γ-MAP and VB have theoretically zero localization bias estimating perfectly uncorrelated dipoles given the appropriate hyperprior and initial set of covariance components.
The role of the hyperprior p(γ) is heavily dependent on whether we are performing γ-MAP, S-MAP, or VB. In the S-MAP framework, the hyperprior functions through its role in creating the concave regularization function g(·). In practice, it is much more transparent to formulate a model directly based on a desired g(·) as opposed to working with some supposedly plausible hyperprior p(γ) and then inferring the what the associated g(·) would be. In contrast, with γ-MAP and VB the opposite is true. Choosing a model based on the desirability of some g(·) can lead to a model with an underlying p(γ) that performs poorly. These issues are discussed in detail (albeit in a somewhat different context) in [49].
Both VB and γ-MAP give rigorous bounds on the model evidence log p(B).
In summary, we hope that these ideas help to bring an insightful perspective to Bayesian source imaging methods, reduce confusion about how different techniques relate, expand the range of feasible applications, and ensure that γ-MAP, S-MAP, and VB are not underutilized. We also observe a number of surprising similarities or out-right equivalences between what might otherwise appear to be very different methodologies. Additionally, there are numerous promising directions for future research, including time-frequency extensions, alternative covariance component parameterizations, and robust interference suppression.
Acknowledgments
This research was supported by NIH grants R01DC04855 and R01DC006435. Also, special thanks to Rey Ramírez, Jason Palmer, Hagai Attias, and Kensuke Sekihara for helpful discussions.
Appendix A: Empirical Comparison of Convergence Rates for γ-MAP Algorithms
Several different iterative schemes are discussed in Section III-A for implementing γ-MAP. While the per-iteration cost is the same for all methods, the convergence rates can be very different. This appendix presents an example of the relative convergence rates on a simple toy problem. A simulated 2D dipolar source was generated and projected to the sensors using the experimental paradigm described in [53]. The signal was corrupted by 10dB additive Gaussian sensor noise. For each algorithm, a flat hyperprior was assumed and ; a single covariance component was used for each voxel and orientation giving dγ = 3450 total components. Figure 1 displays the reduction in the γ-MAP cost function (18) as a function of the iteration number. Consistent with previous observations, the EM updates are considerably slower in reducing the cost. In contrast, the principled updates formed using the convexity-based auxiliary function are relatively similar to the MacKay fixed-point iterations.
Fig. 1.
Convergence comparisons for three methods of performing γ-MAP.
Appendix B: Derivation of Alternative γ-MAP Update Rules
In this section, we re-express the γ-MAP cost function
 (γ) in a more convenient form leading to the update rule (30) and a proof that
(γ) in a more convenient form leading to the update rule (30) and a proof that
 (γ(k+1)) ≤
(γ(k+1)) ≤
 (γ(k)) at each iteration. In fact, a wide variety of alternative, convergent update rules can be developed by decoupling
(γ(k)) at each iteration. In fact, a wide variety of alternative, convergent update rules can be developed by decoupling
 (γ) using auxiliary functions and an additional set of parameters that can be easily optimized, along with γ, using coordinate descent.
(γ) using auxiliary functions and an additional set of parameters that can be easily optimized, along with γ, using coordinate descent.
To begin, the data fit term can be expressed as
| (70) |
where
. Likewise, because the log-determinant term of
 (γ) is concave in γ (see [46]), it can be expressed as an minimum over upper-bounding hyperplanes via
(γ) is concave in γ (see [46]), it can be expressed as an minimum over upper-bounding hyperplanes via
| (71) |
where h*(z) is the concave conjugate of log |Σb|. For our purposes below, we will never actually have to compute h*(z).
Dropping the minimizations and combining terms from (70) and (71) leads to the modified cost function
| (72) |
where by construction
| (73) |
It is straightforward to show that if {γ̂, X̂, ẑ} is a local minimum to
 (γ, X, z), then γ̂ is a local minimum to
(γ, X, z), then γ̂ is a local minimum to
 (γ). Likewise, if {γ̂, X̂, ẑ} is a global minimum of
(γ). Likewise, if {γ̂, X̂, ẑ} is a global minimum of
 (γ, X, z), then γ̂ globally minimizes
(γ, X, z), then γ̂ globally minimizes
 (γ).
(γ).
Since direct optimization of
 (γ) may be difficult, we can instead iteratively optimize
(γ) may be difficult, we can instead iteratively optimize
 (γ, X, z) via coordinate descent over γ, X, and z. In each case, when two are held fixed, the third can be globally minimized in closed form. (In the case of γ this occurs because each γi can be optimized independently given fixed values for X and z.) This ensures that each cycle will reduce
(γ, X, z) via coordinate descent over γ, X, and z. In each case, when two are held fixed, the third can be globally minimized in closed form. (In the case of γ this occurs because each γi can be optimized independently given fixed values for X and z.) This ensures that each cycle will reduce
 (γ, X, z), but more importantly, will reduce
(γ, X, z), but more importantly, will reduce
 (γ) (or leave it unchanged if a fixed-point or limit cycle is reached). The associated update rules from this process are as follows.
(γ) (or leave it unchanged if a fixed-point or limit cycle is reached). The associated update rules from this process are as follows.
With z and X fixed, the minimizing γ is obtained by solving
| (74) |
This leads to the update
| (75) |
The optimal X (with γ and z fixed) is just the standard weighted minimum-norm solution given by
| (76) |
for each i. Finally, the minimizing z equals the slope at the current γ of log |Σb|. As such, we have
| (77) |
By merging these three rules into a single γ update, we arrive at the exact γ-MAP iteration given by (30).
By using a slightly different set of auxiliary functions, other updates (e.g., the standard EM rule), can be easily derived. Also, this process can be used to show that the fixed-point update (29) is iteratively solving a particular min-max problem in search of a saddle point. To accomplish this we define
| (78) |
where the logarithm is understood to apply elementwise. We then note that
| (79) |
By computing the Hessian with respect to y and rearranging terms, this expression can be shown to be convex in y. It therefore admits the representation
| (80) |
where now h*(z) is the convex conjugate. Substituting this expression into (72) leads to an iterative min-max procedure, whereby a lower bound is repeatedly minimized, followed by subsequent tightening (maximization) of the bound. Unfortunately though, proving convergence in this context is more difficult.
Appendix C: Derivation of Approximate Variational Free Energy from [13]
The variational free energy from Section V-B can be manipulated via
| (81) |
where H[·] is the differential entropy. The remaining integral is intractable however, so a second-order Taylor series approximation of ℓ(λ) ≜ log p(λ, B) about μλ is adopted. Note that this second Laplacian assumption is separate and different from the original assumption that p(λ|B) is Gaussian. (Unlike the original, there is no re-normalization after the second-order approximation, which ultimately leads to the extra terms in (67).) This gives
| (82) |
where and . Plugging this result into (81) gives
| (83) |
Combining (83) with (81), we arrive at
| (84) |
If we assume Σλ = − [ℓ″(μλ)]−1, then (84) reduces to
| (85) |
which is the expression given in [13] (assuming the appropriate hyperprior on p(λ).
It is worth pointing out that, for fixed μλ, the selection Σλ = − [ℓ″(μλ)]−1 minimizes (84) with respect to Σλ. However, selecting μλ to be the maximum of ℓ(λ) and then choosing Σλ as above is not guaranteed to jointly maximize F̂ over μλ and Σλ. This is because of the μλ-dependency of ℓ″(μλ). So the Laplace procedure discussed in Section V-B is not explicitly maximizing F̂. Of course maximizing F̂ is not necessarily the ideal objective anyway, since F̂ is not a strict lower bound on log p(B).
Appendix D: Combining the Laplace (Fixed-Form) and Mean-Field Approximations
The mean-field approximation assumes that p(S, γ|B) ≈ p̂(S|B)p̂(γ|B). While the optimal p̂(S|B) can be computed in closed-form using the method outlined in Section V-A, p̂(γ|B), and therefore the variational bound on log p(B) cannot in general (unless a conjugate hyperprior is used). In contast, the fixed-form assumption from Section V-B works with a variety of hyperpriors but does not lead to a rigorous bound on log p(B) and can be expensive to compute.
One potential remedy is to combine the two approaches. This involves reparameterizing via λi ≜ log γi as before then assuming the approximate posterior distribution of these new hyperparameters λ ≜ [λ1, …, λdγ]T is
| (86) |
Note that the optimal distribution for q(S) is Gaussian with no fixed-form assumptions (we will again work with the pseudo-source parameterization for convenience). We will also assume that the (non-conjugate) prior on λ is iid Gaussian, with
| (87) |
This assumption provides consistency with [13] but is by no means required by what follows. Given these provisions, the goal is to minimize KL[q(S)q(λ)||p(S, λ|B)] which is equivalent to maximizing
| (88) |
Optimization over q(S) given a fixed is simple. All we need to know about q(k)(λ) is
| (89) |
The optimal q(k+1)(S) is then Gaussian, with moments given by (23) with from above.
Optimization over q(λ) given fixed q(S) = q(k+1)(S) is a bit more complicated. We have
| (90) |
where is defined as in Section V-A. Because the natural factorization in (90), the optimal q(λ) will factor as well and we can solve for each q(λi) separately. Thus, (90) reduces to
| (91) |
Thus far we have placed no restrictions on q(λ); we now apply the fixed-form, Gaussian approximation to (91). Using
| (92) |
the relevant optimization problem becomes
| (93) |
This optimization problem is jointly convex in μλ,i and Σλ,ii and so can be minimized (or partially minimized for generalized EM) via a variety of simple procedures. This must of course be repeated for each i.
This formulation is attractive for several reasons. First, at each iteration, the approximation q(S) is dependent on the posterior variance Σλ; the more uncertain we are about λi, the more likely it is that we force the estimated covariance component to zero through (89). Secondly, we get strict, lower bound on log p(B) that can be derived in closed-form and does not require the expensive computation of a full posterior covariance on λ. Finally, a conjugate prior is not required to proceed.
If we are averse to the computation of (93) at every iteration, we could instead follow the Laplace approximation from Section V-B to get
 (λ|μλ, Σλ) and then compute a single update of (89) to find q(S) and subsequently F. This would still give a proper bound on log p(B) and a Σλ-dependent estimate of p(S|B), but would only require the diagonal elements of Σλ.
(λ|μλ, Σλ) and then compute a single update of (89) to find q(S) and subsequently F. This would still give a proper bound on log p(B) and a Σλ-dependent estimate of p(S|B), but would only require the diagonal elements of Σλ.
Footnotes
Joint estimation of S and Σε can also potentially lead to identifiability issues.
The associated hyperprior required for equality here need not be the same however; see Section V.
Here we assume dipoles with orientations constrained to be orthogonal to the cortical surface; however, the method is easily extended to handle unconstrained dipoles [36].
The determinant of a matrix is equal to the product of its eigenvalues, which is a well-known volumetric measure.
Note also that as n becomes large, the effect of the hyperprior becomes inconsequential anyway.
Because each Si is effectively described by a diagonal prior covariance parameterized by γi, and since each Si is assumed independent, the total covariance of S will be diagonal. The diagonal section associated with Si of length ri is given by γi1ri, where 1ri is an ri × 1 vector of ones.
Thus far we have assumed that γi parameterizes a linear weighting on covariance components. However, the function gi(·) is invariant to this parameterization because of the marginalization. Consequently, for what follows, the particular parameterization (e.g., precision vs. variance or some other non-linear variant) is irrelevant.
The variational representation from Section III-C allows any concave gi(·) to be generated and also yields identical EM-like updates (to those discussed in the next section).
Traditionally, the EM algorithm has been employed to obtain iterative maximum likelihood (ML) parameter estimates; however, the procedure is easily adapted to compute MAP estimates as well.
Technically, the updates can be combined in hyperparameter space, as we have done above for consistency with γ-MAP, or directly in source space, as is often displayed in the literature [16]. For the latter, we substitute the γ update (44) into (46) resulting in an iteration over the sources that is identical to regularized FOCUSS [16].
Roughly speaking, the EM iterations (44) and (46) can be viewed as coordinate descent over a particular auxiliary cost function dependent on both S and γ. This auxiliary function can be solved analytically for S giving the above expression, which only depends on γ. So the EM algorithm for S-MAP can be viewed equivalently as minimizing (49) over γ or (41) over S. Additionally, this duality can be extended the other way as well; γ-MAP can be expressed explicitly in S-space as a proper S-MAP method [48].
While bounds such as Corollary 1 have been derived for the special case n = 1, Ci = ei using concavity results directly in S-space [35], the methodology is insufficient for the general case because the S-MAP cost function is not concave in S-space.
||·||0 denotes the ℓ0 quasi-norm, which is simply a count of the number of nonzero elements in a vector.
γ-MAP accomplishes this in some sense given the convex bounding perspective of Section III-C.
Recall from Section II-C that ψj is a Gaussian geodesic basis function.
Contributor Information
David Wipf, Email: dwipf@mrsc.ucsf.edu.
Srikantan Nagarajan, Email: sri@mrsc.ucsf.edu.
References
- 1.Attias H. Advances in Neural Information Processing Systems. Vol. 12. MIT Press; 2000. A variational Bayesian framework for graphical models. [Google Scholar]
- 2.Baillet S, Mosher J, Leahy R. Electromagnetic brain mapping. IEEE Signal Processing Magazine. 2001 Nov;:14–30. [Google Scholar]
- 3.Beal M, Ghahrarmani Z. Bayesian Statistics. Vol. 7. Oxford University Press; 2002. The variational Bayesian EM algorithm for incomplete data: With application to scoring graphical model structures. [Google Scholar]
- 4.Berger J. Statistical Decision Theory and Bayesian Analysis. 2. New York: Springer-Verlag; 1985. [Google Scholar]
- 5.Bishop C, Tipping M. Variational relevance vector machines. Proc. 16th Conf. on Uncertainty in Artificial Intelligence; 2000. pp. 46–53. [Google Scholar]
- 6.Boyd S, Vandenberghe L. Convex Optimization. Cambridge University Press; 2004. [Google Scholar]
- 7.Cotter S, Rao B, Engan K, Kreutz-Delgado K. Sparse solutions to linear inverse problems with multiple measurement vectors. IEEE Trans Signal Processing. 2005 Apr;53(7):2477–2488. [Google Scholar]
- 8.Dempster A, Rubin D, Tsutakawa R. Estimation in covariance components models. J American Statistical Association. 1981 Jun;76:341–353. [Google Scholar]
- 9.Donoho D, Elad M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ1 minimization. Proc National Academy of Sciences. 2003 Mar;100(5):2197–2202. doi: 10.1073/pnas.0437847100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Donoho D, Elad M, Temlyakov V. Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Trans Information Theory. 2006 Jan;52(1):6–18. [Google Scholar]
- 11.Figueiredo M. Advances in Neural Information Processing Systems. Vol. 14. MIT Press; 2002. Adaptive sparseness using Jeffreys prior; pp. 697–704. [Google Scholar]
- 12.Friston K, Penny W, Phillips C, Kiebel S, Hinton G, Ashburner J. Classical and Bayesian inference in neuroimaging: Theory. NeuroImage. 2002;16:465–483. doi: 10.1006/nimg.2002.1090. [DOI] [PubMed] [Google Scholar]
- 13.Friston K, Harrison L, Daunizeau J, Kiebel S, Phillips C, Trujillo-Barreto N, Henson R, Flandin G, Mattout J. Multiple Sparse Priors for the MEG/EEG Inverse Problem. NeuroImage. 2007;39:1104–1120. doi: 10.1016/j.neuroimage.2007.09.048. [DOI] [PubMed] [Google Scholar]
- 14.Friston K, Mattout J, Trujillo-Barreto N, Ashburner J, Penny W. Variationl free energy and the Laplace approximation. NeuroImage. 2006;34:220–234. doi: 10.1016/j.neuroimage.2006.08.035. [DOI] [PubMed] [Google Scholar]
- 15.Fuchs J. On sparse representations in arbitrary redundant bases. IEEE Transactions on Information Theory. 2004 Jun;50(6):1341–1344. [Google Scholar]
- 16.Gorodnitsky I, George J, Rao B. Neuromagnetic source imaging with FOCUSS: A recursive weighted minimum norm algorithm. Journal Electroencephalography and Clinical Neurophysiology. 1995 Oct;95(4):231–251. doi: 10.1016/0013-4694(95)00107-a. [DOI] [PubMed] [Google Scholar]
- 17.Gribonval R, Nielsen M. Sparse representations in unions of bases. IEEE Trans Information Theory. 2003 Dec;49:3320–3325. [Google Scholar]
- 18.Huang M, Dale A, Song T, Halgren E, Harrington D, Podgorny I, Canive J, Lewis S, Lee R. Vector-based spatial-temporal minimum ℓ1-norm solution for MEG. NeuroImage. 2006;31(3):1025–37. doi: 10.1016/j.neuroimage.2006.01.029. [DOI] [PubMed] [Google Scholar]
- 19.Ji S, Xue Y, Carin L. Bayesian compressive sensing. IEEE Trans Signal Processing. (to appear) [Google Scholar]
- 20.Jordan M, Ghahramani Z, Jaakkola T, Saul L. An introduction to variational methods for graphical models. Machine Learning. 1999;37(2):183–233. [Google Scholar]
- 21.Limpiti T, Veen BV, Wakai R. Cortical patch basis model for spatially extended neural activity. IEEE Trans Biomedical Engineering. 2006 Sep;53(9):1740–1754. doi: 10.1109/TBME.2006.873743. [DOI] [PubMed] [Google Scholar]
- 22.MacKay D. Bayesian interpolation. Neural Computation. 1992;4(3):415–447. [Google Scholar]
- 23.MacKay D. Bayesian non-linear modeling for the energy prediction competition. ASHRAE Transactions. 1994;100(2):1053–1062. [Google Scholar]
- 24.Mattout J, Phillips C, Penny W, Rugg M, Friston K. MEG source localization under multiple constraints: An extended Bayesian framework. NeuroImage. 2006;30:753–767. doi: 10.1016/j.neuroimage.2005.10.037. [DOI] [PubMed] [Google Scholar]
- 25.Nagarajan S, Attias H, Hild K, Sekihara K. A graphical model for estimating stimulus-evoked brain responses in noisy MEG data with large background brain activity. NeuroImage. 2006;30(2):400–416. doi: 10.1016/j.neuroimage.2005.09.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Neal R. Bayesian Learning for Neural Networks. New York: Springer-Verlag; 1996. [Google Scholar]
- 27.Nummenmaa A, Auranen T, Hämäläinen M, Jääskeläinen I, Lampinen J, Sams M, Vehtari A. Hierarchical Bayesian estimates of distributed MEG sources: Theoretical aspects and comparison of variational and MCMC methods. Neuroimage. 2007;35(2):669–685. doi: 10.1016/j.neuroimage.2006.05.001. [DOI] [PubMed] [Google Scholar]
- 28.Palmer J, Kreutz-Delgado K. Modeling and estimation of dependent subspaces with non-radially symmetric and skewed densities. in preparation. [Google Scholar]
- 29.Palmer J, Wipf D, Kreutz-Delgado K, Rao B. Advances in Neural Information Processing Systems. Vol. 18. MIT Press; 2006. Variational EM algorithms for non-Gaussian latent variable models; pp. 1059–1066. [Google Scholar]
- 30.Pascual-Marqui R. Standardized low resolution brain electromagnetic tomography (sLORETA): Technical details. Methods and Findings in Experimental and Clinical Pharmacology. 2002;24(Suppl D):5–12. [PubMed] [Google Scholar]
- 31.Phillips C, Mattout J, Rugg M, Maquet P, Friston K. An empirical Bayesian solution to the source reconstruction problem in EEG. NeuroImage. 2005 Jan;24:997–1011. doi: 10.1016/j.neuroimage.2004.10.030. [DOI] [PubMed] [Google Scholar]
- 32.Phillips C, Rugg M, Friston K. Anatomically informed basis functions for EEG source localization: combining functional and anatomical constraints. NeuroImage. 2002 Jul;13(3 pt 1):678–95. doi: 10.1006/nimg.2002.1143. [DOI] [PubMed] [Google Scholar]
- 33.Ramírez R. PhD Thesis. New York University; May, 2005. Neuromagnetic source imaging of spontaneous and evoked human brain dynamics. [Google Scholar]
- 34.Ramírez R, Makeig S. Neuroelectromagnetic source imaging using multiscale geodesic neural bases and sparse Bayesian learning. Human Brain Mapping, 12th Annual Meeting; Florence, Italy. June 2006. [Google Scholar]
- 35.Rao B, Engan K, Cotter SF, Palmer J, Kreutz-Delgado K. Subset selection in noise based on diversity measure minimization. IEEE Trans Signal Processing. 2003 Mar;51(3):760–770. [Google Scholar]
- 36.Sahani M, Nagarajan S. Advances in Neural Information Processing Systems. Vol. 16. MIT Press; 2004. Reconstructing MEG sources with unknown correlations. [Google Scholar]
- 37.Sarvas J. Basic methematical and electromagnetic concepts of the biomagnetic inverse problem. Phys Med Biol. 1987;32:11–22. doi: 10.1088/0031-9155/32/1/004. [DOI] [PubMed] [Google Scholar]
- 38.Sato M, Yoshioka T, Kajihara S, Toyama K, Goda N, Doya K, Kawato M. Hierarchical Bayesian estimation for MEG inverse problem. NeuroImage. 2004;23:806–826. doi: 10.1016/j.neuroimage.2004.06.037. [DOI] [PubMed] [Google Scholar]
- 39.Sekihara K, Nagarajan S, Poeppel D, Marantz A. Performance of an MEG adaptive-beamformer technique in the presence of correlated neural activities: Effects on signal intensity and time-course estimates. IEEE Trans Biomedical Engineering. 2002;40(10):1534–1546. doi: 10.1109/tbme.2002.805485. [DOI] [PubMed] [Google Scholar]
- 40.Sekihara K, Sahani M, Nagarajan S. Localization bias and spatial resolution of adaptive and non-adaptive spatial filters for MEG source reconstruction. NeuroImage. 2005;25:1056–1067. doi: 10.1016/j.neuroimage.2004.11.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Tipping M. Sparse Bayesian learning and the relevance vector machine. J Machine Learning Research. 2001;1:211–244. [Google Scholar]
- 42.Tropp J. Greed is good: Algorithmic results for sparse approximation. IEEE Trans Information Theory. 2004 Oct;50(10):2231–2242. [Google Scholar]
- 43.Tropp J. Just relax: Convex programming methods for identifying sparse signals. IEEE Trans Information Theory. 2006 Mar;52(3):1030–1051. [Google Scholar]
- 44.Uutela K, Hämäläinen M, Somersalo E. Visualization of magnetoencephalographic data using minimum current estimates. NeuroImage. 1999;10:173–180. doi: 10.1006/nimg.1999.0454. [DOI] [PubMed] [Google Scholar]
- 45.Veen BV, van Drongelen W, Yuchtman M, Suzuki A. Localization of brain electrical activity via linearly constrained minimum variance spatial filtering. IEEE Trans Biomedical Engineering. 1997;44(9):867–880. doi: 10.1109/10.623056. [DOI] [PubMed] [Google Scholar]
- 46.Wipf D. PhD Thesis. University of California; San Diego: 2006. Bayesian methods for finding sparse representations. [Google Scholar]
- 47.Wipf D, Nagarajan S. Beamforming using the relevance vector machine. International Conference on Machine Learning; June 2007. [Google Scholar]
- 48.Wipf D, Nagarajan S. A new view of automatic relevance determination. Advancies in Neural Information Processing Systems. 2008;20 (to appear) [Google Scholar]
- 49.Wipf D, Palmer J, Rao B, Kreutz-Delgado K. Performance analysis of latent variable models with sparse priors. IEEE International Conf. Acoustics, Speech, and Signal Processing; April 2007. [Google Scholar]
- 50.Wipf D, Ramírez R, Palmer J, Makeig S, Rao B. Advances in Neural Information Processing Systems. Vol. 19. MIT Press; 2007. Analysis of empirical Bayesian methods for neuroelectromagnetic source localization. [Google Scholar]
- 51.Wipf D, Rao B. Sparse Bayesian learning for basis selection. IEEE Trans Signal Processing. 2004 Aug;52(8):2153–2164. [Google Scholar]
- 52.Zoltowski M. On the performance analysis of the MVDR beamformer in the presence of correlated interference. IEEE Trans Signal Processing. 1988;36:945–947. [Google Scholar]
- 53.Zumer J, Attias H, Sekihara K, Nagarajan S. A probabilistic algorithm for interference suppression and source reconstruction from MEG/EEG data. Advancies in Neural Information Processing Systems. 2007;19 [Google Scholar]



