Abstract
Using a reduced subset of SNPs in a linear mixed model can improve power for genome-wide association studies, yet this can result in insufficient correction for population stratification. We propose a hybrid approach using principal components that does not inflate statistics in the presence of population stratification and improves power over standard linear mixed models.
Keywords: mixed models, population stratification, GWAS
IN recent years, there has been extensive research on linear mixed models (LMM) to calculate genome-wide association study (GWAS) statistics (Kang et al. 2008, 2010; Segura et al. 2012; Svishcheva et al. 2012; Zhou and Stephens 2012; Yang et al. 2014). While linear mixed models implicitly assume that all SNPs have an effect on the phenotype (an infinitesimal genetic architecture), it is widely believed that disease phenotypes do not follow an infinitesimal model and that modeling a genetic architecture where most SNPs have negligible effect and some have modest effect (a noninfinitesimal genetic architecture) would increase power. As a step in that direction, Listgarten et al. (2012; Lippert et al. 2013) recently developed the state-of-the-art FaST-LMM Select method, which constructs a genetic relationship matrix (GRM) from a subset of top associated SNPs that are more likely to be causal. However, as a recent Perspective article (Yang et al. 2014) shows, limiting the GRM to a subset of SNPs can result in insufficient correction for population stratification, leading to significantly inflated statistics and false positive associations (Table 1, Table 2, Supporting Information, Figure S2, Figure S3, Figure S4, and File S1).
Table 1. Extent of null statistic inflation as measured by λGC [median Wald statistic on test null SNPs divided by the theoretical median under the null distribution (Devlin and Roeder 1999)].
| Mean λGC (SE) | Pop. strat., P = 0.05 | Pop. strat., P = 0.005 | P = 0.05 | P = 0.005 |
|---|---|---|---|---|
| Linear regression | 3.8 (0.4) | 4.5 (0.5) | 1.01 (0.01) | 1.01 (0.01) |
| Linear regression with PCs | 1.02 (0.01) | 1.03 (0.01) | 1.01 (0.01) | 1.02 (0.01) |
| LMM | 1.01 (0.01) | 1.02 (0.01) | 1.01 (0.01) | 1.01 (0.01) |
| FaST-LMM Select | 1.04 (0.01) | 1.26 (0.03) | 1.01 (0.01) | 0.99 (0.01) |
| PC-Select | 1.01 (0.01) | 1.01 (0.01) | 1.01 (0.01) | 0.99 (0.01) |
We tabulate λGC for linear regression, linear regression with PCs, standard LMM, FaST-LMM Select, and PC-Select on simulated genotypes and phenotypes with and without population stratification as the fraction of causal SNPs (P = 0.05, 0.005) varies. Values shown are mean λGC over 100 simulations with standard errors (SE) in parentheses. FaST-LMM Select inflates statistics in the presence of population stratification when few SNPs are causal (P = 0.005), which may result in false positives. Pop. strat., population stratification.
Table 2. Extent of null statistic inflation measured by λGC.
| Mean λGC (SE) | Pop. strat., P = 0.05 | Pop. strat., P = 0.005 | P = 0.05 | P = 0.005 |
|---|---|---|---|---|
| Linear regression | 1.58 (0.02) | 1.55 (0.02) | 1.03 (0.01) | 1.04 (0.01) |
| Linear regression with PCs | 1.01 (0.01) | 1.00 (0.01) | 1.01 (0.01) | 1.02 (0.01) |
| LMM | 1.02 (0.01) | 1.01 (0.01) | 1.00 (0.01) | 1.02 (0.01) |
| FaST-LMM Select | 1.02 (0.01) | 1.06 (0.01) | 1.00 (0.01) | 1.02 (0.01) |
| PC-Select | 1.01 (0.01) | 1.01 (0.01) | 1.00 (0.01) | 1.01 (0.01) |
We tabulate λGC for linear regression, linear regression with PCs, standard LMM, FaST-LMM Select, and PC-Select on real genotypes and simulated phenotypes with and without population stratification as the fraction of causal SNPs (P = 0.05, 0.005) varies. Values shown are mean λGC over 200 simulations with standard errors (SE) in parentheses. FaST-LMM Select inflates statistics in the presence of population stratification when few SNPs are causal (P = 0.005), which may result in false positives.
As a solution to this problem, we propose PC-Select, a novel hybrid approach that includes the principal components (PCs) of the genotype matrix as fixed effects in FaST-LMM Select. PC-Select leverages the advantages of the FaST-LMM Select framework while correcting for population stratification. The two main steps of FaST-LMM Select are ranking SNPs by linear regression P-values to form the GRM with the top-ranked SNPs and then calculating association statistics in a mixed-model framework, using this GRM. We used the top five PCs as fixed effects in both of these steps (see Materials and Methods). [We follow the recommendations in the literature (Price et al. 2006) and use a fixed number of PCs. We have found that five PCs are generally sufficient to correct for stratification in simulated and real data sets. Alternatively, the number of PCs may be selected through cross-validation or Tracy–Widom statistics (Patterson et al. 2006).] As a result, PC-Select yields noninflated test statistics in the presence of population stratification and maintains high power to detect causal SNPs.
Specifically, to examine inflation and power, we followed the simulation procedure in Yang et al. (2014) and generated data sets each containing 10,000 SNPs for 1000 individuals. To avoid a loss in power for LMM that can occur when candidate SNPs are included in the GRM (Listgarten et al. 2012; Yang et al. 2014), we separately simulated a set of candidate SNPs to compute test statistics. We sampled individuals from two populations with Fst = 0.05, ancestral minor allele frequencies uniform in [0.1, 0.5], and mean phenotypic difference 0.25 SD. To simulate causal SNPs in the GRM, we selected a fraction P = 0.05 or 0.005 of the SNPs at random and sampled Gaussian effect sizes (variance equal to 0.5 divided by the number of casual SNPs in the GRM) for these SNPs. We generated 500 candidate test null SNPs that were not causal, and to measure inflation we calculated λGC, the median Wald statistic on these SNPs divided by the theoretical median under the null distribution (Devlin and Roeder 1999). To investigate power, we generated 50 causal candidate SNPs with normally distributed effect sizes (variance equal to 0.5 divided by the number of causal candidate SNPs) and measured mean Wald statistic on these SNPs. We split the variability from causal SNPs evenly between the GRM and the causal candidate SNPs. We repeated all simulations 100 times and report the mean and standard error.
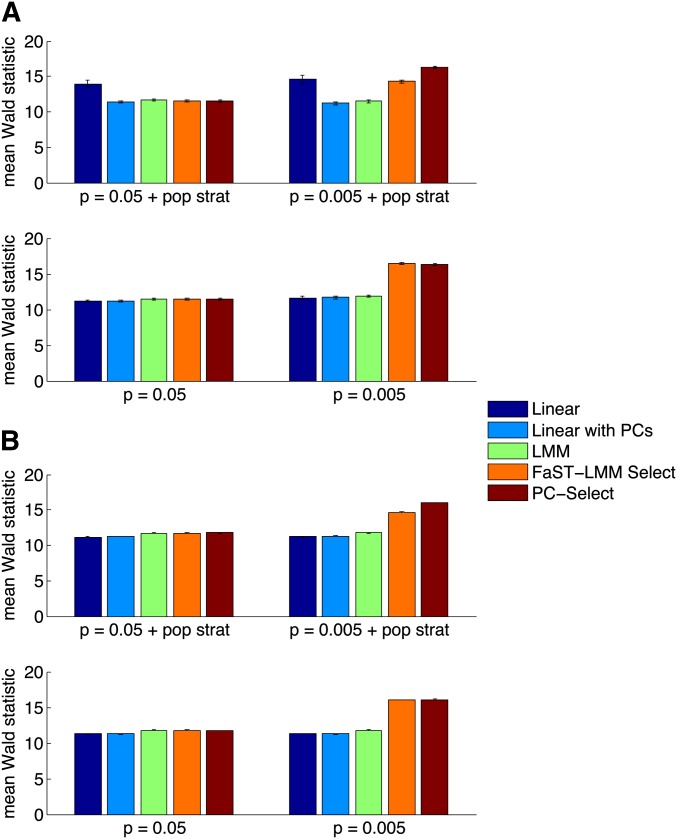
We found that when few SNPs were causal (P = 0.005), FaST-LMM Select inflated null statistics in the presence of population stratification (λGC = 1.26 ± 0.03), whereas PC-Select was properly calibrated (λGC = 1.01 ± 0.01) (Table 1). Moreover, FaST-LMM Select lost power in the presence of population stratification (measured by the mean Wald statistic on causal SNPs: 14.3 ± 0.2 with stratification vs. 16.4 ± 0.1 without), whereas PC-Select’s power in simulations with and without population stratification was not significantly different (16.3 ± 0.1 vs. 16.3 ± 0.1) (Figure 1). Thus, even though PC-Select corrected for stratification, this advantage did not come at the expense of power. This gain is likely because the PCs reduce noise in selecting subsets of SNPs for the GRM in the presence of population stratification. In addition, PC-Select chose fewer SNPs than FaST-LMM Select to include in the GRM (over 100 simulations, mean SNPs chosen: ∼20 vs. ∼240, Figure S1), yielding potential computational savings. When many SNPs were causal (P = 0.05), both methods used nearly all SNPs in the GRM (over 100 simulations, mean SNPs chosen: ∼9400 and ∼8800 of 10,000, respectively), achieving similar performance to standard LMM.
Figure 1.
(A and B) Comparison of power for linear regression, linear regression with PCs, standard LMM, FaST-LMM Select, and PC-Select on simulated genotypes and phenotypes (A) and real genotypes and simulated phenotypes (B) with and without population stratification as the fraction of casual SNPs (P = 0.05, 0.005) varies. To measure power, we plot the mean Wald statistic on test causal SNPs. In all cases, PC-Select has the highest power of the methods that do not inflate statistics.
We also investigated a recent extension of FaST-LMM Select, the genard method (Hoffman 2013) that fits a data-adaptive low-rank GRM; however, we found that it did not have increased power over LMM in our simulations (Figure S5), which is consistent with previous simulations in a similar context (Hoffman 2013).
Next, we evaluated inflation and power on real genotypes with simulated phenotypes in a similar manner. We analyzed 5000 individuals randomly subsampled from a multiple-sclerosis (MS) study genotyped on Illumina arrays (Sawcer et al. 2011) made available via Wellcome Trust Case Control Consortium 2 (WTCCC2) (see Materials and Methods). As before, we separated GRM SNPs and candidate SNPs to avoid proximal contamination and provide a fair comparison of methods. We randomly sampled 50,000 SNPs for the GRM from chromosomes 3 to 22, 250 causal SNPs from chromosome 1, and 500 null SNPs from chromosome 2. To simulate environmental variance aligned with population structure, we added 0.25 times the first PC (after the PC had been normalized to variance 1) to each individual’s phenotype. Otherwise, we generated phenotypes as before and report simulations over 200 randomly generated phenotypes.
We again found that when few SNPs were causal (P = 0.005), FaST-LMM Select inflated null statistics in the presence of population stratification (λGC = 1.06 ± 0.01), whereas PC-Select was properly calibrated (λGC = 1.01 ± 0.01) (Table 2). Moreover, FaST-LMM Select lost power in the presence of population stratification (measured by the mean Wald statistic on causal SNPs: 14.64 ± 0.05 with stratification vs. 16.02 ± 0.05 without); in contrast, PC-Select’s power in simulations with and without population stratification was not significantly different (16.02 ± 0.05 vs. 16.08 ± 0.05) (Figure 1). In all of our simulations, PC-Select produced noninflated statistics and high power.
Finally, we analyzed data from 10,204 MS cases and 5429 controls genotyped on Illumina arrays (Sawcer et al. 2011) made available via WTCCC2 (see Materials and Methods). The cases and controls were not matched for ancestry and thus exhibited substantial population stratification. Evaluated over all SNPs, PC-Select had λGC = 1.24 and FaST-LMM Select had λGC = 1.20. Due to polygenicity, we expect λGC on all markers to be >1. On the same data, Yang et al. (2014) report λGC = 1.23 and 1.20 for linear regression with PCs and LMM, respectively, which they show is consistent with polygenicity. To evaluate power, we considered Wald statistics at 75 known associated SNPs (see Materials and Methods and Table S1 for Wald statistics). PC-Select consistently gave larger Wald statistics than FaST-LMM Select (63 of 75 markers; P = 2 × 10−9, mean Wald statistic 12.07 vs. 11.30). Based on cross-validation, both PC-Select and FaST-LMM Select chose to use all markers. This may indicate that the disease is not caused by a small number of loci with large effects or that our sample size is too small to capture this effect. Although PC-Select and FaST-LMM Select chose to use all SNPs and thus neither method inflated statistics, we emphasize that without a priori knowledge about the genetic architecture, PC-Select automatically tunes the number of SNPs to include in the GRM to optimize power and simultaneously protects against population stratification at no cost to power.
Janss et al. (2012) caution against using PCs as fixed effects in combination with a random effect derived from the GRM when estimating heritability. This may result in an ill-posed model because the PCs enter both as fixed effects and implicitly through the random effect. We avoid this issue when estimating variance components by using the PCs as fixed effects in a restricted maximum-likelihood (REML) approach, which projects the genotype matrix into a subspace orthogonal to the PCs, effectively removing them from the random effect. We also note that population structure and PCs have previously been used successfully as fixed effects (or separate random effects) in mixed-model settings to address confounding from population structure and from unusually differentiated markers (Yu et al. 2006; Zhao et al. 2007; Price et al. 2010, 2013; Sul and Eskin 2013).
Using PCs in a linear model does not correct for family relatedness and cryptic relatedness (Price et al. 2010). As suggested by Yang et al. (2014), due to the large length of segments shared identical-by-descent, using a subset of SNPs may correct for cryptic relatedness. Listgarten et al. (2012) show that using a subset of SNPs in the GRM does not inflate statistics on the WTCCC data, where inflation is likely primarily due to cryptic relatedness. We expect that PC-Select will not be inflated by cryptic relatedness for the same reasons. In most human data sets with unrelated individuals, family relatedness is not an issue; however, for data sets with strong family relatedness, we suspect there may be cases where both PC-Select and FaST-LMM Select inflate statistics.
PC-Select has the same asymptotic runtime as FaST-LMM Select, quadratic in the number of individuals and linear in the number of markers. In practice, the runtime for the additional step of computing the PCs for the genotype matrix is minimal because both methods require several spectral decompositions of matrices of nearly the same size for the cross-validation step. It should be noted that while the asymptotic runtime of PC-Select and FaST-LMM Select is the same as that of previously published exact LMM methods (Lippert et al. 2011; Zhou and Stephens 2012), the actual runtime of both methods is ostensibly longer by a factor of 10 due to the cross-validation step. The cross-validation step is parallelizable, so in practice this is not a significant limitation.
Including PCs as fixed effects allows PC-Select to infer ancestry from all SNPs simultaneously, while at the same time maintaining the benefits of using a statistically chosen subset of the SNPs to estimate the GRM (Listgarten et al. 2012; Lippert et al. 2013). As we have shown, using a combination of PCs and a subset of SNPs in the GRM gives the best of both worlds.
Materials and Methods
MS data set
We analyzed data from 10,204 MS cases and 5429 controls [the National Blood Service (NBS) and the 1958 Birth Cohort (1958BC)] genotyped on Illumina arrays made available to researchers via WTCCC2 (http://wtccc.org.uk/ccc2/). We follow the quality-control standards in Yang et al. (2014). Although Sawcer et al. (2011) analyzed United Kingdom (UK) and non-UK samples separately followed by meta-analysis in most of their analyses, the data made available to researchers include both UK and non-UK cases but only UK controls. We retained all samples to maximize sample size. We considered markers that were present in each of MS, NBS, and 1958BC data sets and removed markers with >0.5% missing data, P < 0.01 for allele-frequency difference between NBS and 1958BC, P < 0.05 for deviation from Hardy–Weinberg equilibrium, P < 0.05 for differential missingness between cases and controls, or minor allele frequency <0.1% in any data set, leaving 360,557 markers. The 75 known associated markers were defined by including, for each MS-associated marker listed in the National Human Genome Research Institute (NHGRI) GWAS catalog (http://genome.gov/gwastudies/), a single best tag at r2 > 0.4 from the set of 360,557 markers if available.
Statistical methods
PC-Select follows a similar framework to that of FaST-LMM Select (Lippert et al. 2011, 2013; Listgarten et al. 2012). For completeness, we list the steps and equations we used.
First, we describe a method for computing association statistics, and then in subsequent sections we describe the steps of PC-Select.
Association statistics:
The phenotype y, covariates X, and genotypes W are mean centered. Additionally, each genotype is divided by where is the estimated minor allele frequency. Then the phenotype is modeled as
where α is a vector of weights for the covariates, and K is the GRM. This model naturally leads to an association statistic based on the Wald statistic.
To calculate the association statistic for SNP w, we add w as a fixed-effect covariate to the previous model and test whether its coefficient is significantly different from 0. Specifically, consider the model
where β is the coefficient for the test SNP. We estimate and by REML. The fixed-effect coefficients (β, α) are estimated by maximum likelihood.
It is straightforward to construct the Wald statistic to test whether β ≠ 0. Let and Q = [w; X]. Then is equal to the first entry of (QTV−1Q)−1QTV−1y and is equal to the first entry of (QTV−1Q)−1. The test statistic is
which is asymptotically χ2 distributed with 1 d.f.
PC-Select:
Now we describe the PC-Select method:
Step 1: Extracting PCs: We extract the top five PCs from a GRM formed using all of the genotype data, WWT, to use as fixed-effect covariates. We use X to denote the matrix of user-specified covariates and the top five PCs.
Step 2: Ranking SNPs by linear regression: Second, we rank the SNPs by a linear regression test statistic. Linear regression test statistics are calculated by fixing to 0 and using the procedure described above to calculate Wald statistics.
-
Step 3: Determining the GRM: As in FaST-LMM Select, PC-Select uses a subset of the SNPs that are likely to be causal. In this step, we determine k, the number of top SNPs (as ranked in Step 2) to include in the GRM. We use 10-fold cross-validation on predictive log-likelihood to choose the number of top SNPs. We choose k from a list of user-defined possibilities (e.g., k ∈ {100, 1000, 3000, 10,000, 30,000, …}). First, we randomly divide individuals into 10 equal groups or folds. For each fold i, we form a test set from the individuals in fold i and use the rest of the individuals as a training set. For each choice of k, we consider a subset of the genotype matrix consisting only of the top k SNPs (the ranking of the SNPs is recomputed per fold, using the training data). For notational simplicity, we also refer to the reduced genotype matrix by W, and it will be clear from context if this refers to the full genotype matrix or a subset. Let Wi denote the genotypes from fold i and W−i represent the genotypes from the rest of the folds (similarly for y and X). We wish to evaluate the predictive log-likelihood of yi given the training information (y−i, X−i, Xi) to assess the predictive power of using only the top k SNPs in the GRM.
Specifically, to evaluate the predictive log-likelihood, we start by forming a GRM from the training set Then we estimate and from the training set by REML. We estimate α by ML with these variance parameters fixed. Then under the model
where and the predictive distribution of the phenotypes given the training parameters, is normally distributed with mean
and covariance
This can be evaluated efficiently, using the spectral decompositions computed in the REML step (Lippert et al. 2011; Listgarten et al. 2012). We average the predictive log-likelihood over each of the 10 folds and choose the k that gives the highest average log-likelihood.
-
Step 4:
Calculating association statistics: Finally, with the number of top SNPs to use in the GRM fixed, we calculate association statistics for each SNP. Let W be the genotype matrix using the top k SNPs chosen in the previous step. To avoid proximal contamination (Listgarten et al. 2012), we use a leave-one-chromosome-out procedure (Yang et al. 2014). For each test SNP w (which is not necessarily in W), we exclude the chromosome including that SNP from the GRM and calculate the Wald statistic for w with this GRM. We do this efficiently by precomputing and storing the GRM, excluding each chromosome in turn.
Supplementary Material
Acknowledgments
We thank Po-Ru Loh, Sean Simmons, and Jian Peng for helpful discussions. This study makes use of data generated by the Wellcome Trust Case Control Consortium. This research was funded by National Institutes of Health grants R01 GM108348 and R01 HG006399.
Footnotes
Communicating editor: I. Hoeschele
Literature Cited
- Devlin B., Roeder K., 1999. Genomic control for association studies. Biometrics 55(4): 997–1004. [DOI] [PubMed] [Google Scholar]
- Hoffman G. E., 2013. Correcting for population structure and kinship using the linear mixed model: theory and extensions. PLoS ONE 8(10): e75707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janss L., de los Campos G., Sheehan N., Sorensen D., 2012. Inferences from genomic models in stratified populations. Genetics 192: 693–704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang H. M., Zaitlen N. A., Wade C. M., Kirby A., Heckerman D., et al. , 2008. Efficient control of population structure in model organism association mapping. Genetics 178: 1709–1723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang H. M., Sul J. H., Zaitlen N. A., Kong S.-y., Freimer N. B., et al. , 2010. Variance component model to account for sample structure in genome-wide association studies. Nat. Genet. 42(4): 348–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lippert C., Listgarten J., Liu Y., Kadie C. M., Davidson R. I., et al. , 2011. FaST linear mixed models for genome-wide association studies. Nat. Methods 8(10): 833–835. [DOI] [PubMed] [Google Scholar]
- Lippert C., Quon G., Kang E. Y., Kadie C. M., Listgarte J., et al. , 2013. The benefits of selecting phenotype-specific variants for applications of mixed models in genomics. Sci. Rep. 3: 1815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Listgarten J., Lippert C., Kadie C. M., Davidson R. I., Eskin E., et al. , 2012. Improved linear mixed models for genome-wide association studies. Nat. Methods 9(6): 525–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson N., Price A. L., Reich D., 2006. Population structure and eigenanalysis. PLoS Genet. 2(12): e190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price A. L., Patterson N. J., Plenge R. M., Weinblatt M. E., Shadick N. A., et al. , 2006. Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 38(8): 904–909. [DOI] [PubMed] [Google Scholar]
- Price A. L., Zaitlen N. A., Reich D., Patterson N., 2010. New approaches to population stratification in genome-wide association studies. Nat. Rev. Genet. 11(7): 459–463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price A. L., Zaitlen N. A., Reich D., Patterson N., 2013. Response to Sul and Eskin. Nat. Rev. Genet. 14(4): 300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawcer S., Hellenthal G., Pirinen M., Spencer C., Patsopoulos N., et al. , 2011. Genetic risk and a primary role for cell-mediated immune mechanisms in multiple sclerosis. Nature 476(7359): 214–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segura V., Vilhjálmsson B. J., Platt A., Korte A., Seren Ü., et al. , 2012. An efficient multi-locus mixed-model approach for genome-wide association studies in structured populations. Nat. Genet. 44(7): 825–830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sul J. H., Eskin E., 2013. Mixed models can correct for population structure for genomic regions under selection. Nat. Rev. Genet. 14(4): 300. [DOI] [PubMed] [Google Scholar]
- Svishcheva G. R., Axenovich T. I., Belonogova N. M., van Duijn C. M., Aulchenko Y. S., 2012. Rapid variance components-based method for whole-genome association analysis. Nat. Genet. 44: 1166–1170. [DOI] [PubMed] [Google Scholar]
- Yang J., Zaitlen N. A., Goddard M. E., Visscher P. M., Price A. L., 2014. Advantages and pitfalls in the application of mixed-model association methods. Nat. Genet. 46(2): 100–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu J., Pressoir G., Briggs W. H., Bi I. V., Yamasaki M., et al. , 2006. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 38(2): 203–208. [DOI] [PubMed] [Google Scholar]
- Zhao K., Aranzana M. J., Kim S., Lister C., Shindo C., et al. , 2007. An Arabidopsis example of association mapping in structured samples. PLoS Genet. 3(1): e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou X., Stephens M., 2012. Genome-wide efficient mixed-model analysis for association studies. Nat. Genet. 44(7): 821–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.