Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Aug 1.
Published in final edited form as: Gene. 2014 May 22;546(1):25–34. doi: 10.1016/j.gene.2014.05.043

K-mer natural vector and its application to the phylogenetic analysis of genetic sequences

Jia Wen a,b, Raymond H Chan b, Shek-Chung Yau c, Rong L He d, Stephen S T Yau e,*
PMCID: PMC4096558  NIHMSID: NIHMS602411  PMID: 24858075

Abstract

Based on the well-known k-mer model, we propose a k-mer natural vector model for representing a genetic sequence based on the numbers and distributions of k-mers in the sequence. We show that there exists a one-to-one correspondence between a genetic sequence and its associated k-mer natural vector. The k-mer natural vector method can be easily and quickly used to perform phylogenetic analysis of genetic sequences without requiring evolutionary models or human intervention. Whole or partial genomes can be handled more effective with our proposed method. It is applied to the phylogenetic analysis of genetic sequences, and the obtaining results fully demonstrate that the k-mer natural vector method is a very powerful tool for analysing and annotating genetic sequences and determining evolutionary relationships both in terms of accuracy and efficiency.

Keywords: K-mer model, Natural vector, Phylogenetic analysis

1. Introduction

Phylogenetic analysis of genetic sequences has become essential for researching the evolutionary relationships between all types of organisms (from bacteria to humans) (Nei, 1996). Phylogenetic analysis is also important for clarifying the evolutionary pattern of multigene families (Atchley et al., 1994; Goodwin et al., 1996; Ota and Nei, 1994), as well as for understanding adaptive evolution at the molecular level (Chandrasekharan et al., 1996; Jermann et al., 1995; Wistow, 1993). It also provides deep insight into the mechanism for the maintenance of polymorphic alleles in populations (Figueroa et al., 1988; Takahata, 1993). The results of phylogenetic analysis are represented by phylogenetic tree, in which sequences are grouped based on sequence similarities.

Methods for phylogenetic analysis commonly depend on multiple sequence alignment, which assumes some sort of evolutionary model, and yields results that are often controversial. Although most alignment-based methods can precisely represent evolutionary relationships between genetic sequences, they frequently lead to very complicated computation. Alignment-free methods, which are based on numerical characterizations of genetic sequences, are proposed to compensate for the ineffectiveness of traditional alignment-based methods.

Among all alignment-free methods, the k-mer model method may be the best developed one. The classic string representation based on the k-mer model was first used for the comparison of genome sequences by Blaisdell (1986), and the counts of k-mers appearing in the sequence were used for the comparison of regulatory sequences by Kantorovitz et al. (2007). Later, various frequency-based methods were introduced for sequence comparison presented by Wu et al. (1997, 2001, 2005), Korf and Rose (2009), Sims et al. (2009a, 2009b) and Jun et al. (2010). The advantage of k-mer model approach is that the phylogenetic tree can be constructed much faster than using sequence alignment, and it can be used for comparison of whole genomes. However, the deficiency of the k-mer model is that the relationships between the k-mers within a sequence are more or less neglected (Yang and Wang, 2013; Yu, 2013).

The original natural vector approach is an alternative alignment-free method which produces a one-to-one association between genetic sequences and vectors in a finite dimensional space (Deng et al., 2011). One of the strengths of this approach is that the natural vector incorporates the normalized central moments to account for the interrelationships between different portions of genetic sequences. But the obtaining results show that the original natural vector approach cannot accurately depict evolutionary relationships of species considered in phylogenetic analysis of genetic sequences.

In this paper, we integrate original natural vector with k-mer model to produce k-mer natural vector that contains both types of information: the information stored in the k-mer counts as well as information about the relationships between k-mers appearing in the sequence. We can prove that the correspondence between a genetic sequence and its associated k-mer natural vector is one-to-one by mathematical proof. Moreover, the k-mer natural vector method is applied to the phylogenetic analysis of genetic sequences, and the obtaining results show that our new method can not only effectively overcome the deficient of former k-mer model methods, but also further improve accuracy in depicting evolutionary relationships of genetic sequences compared with sequence alignment methods and some published methods.

2. Materials and Methods

2.1. K-mer model of genetic sequence

The k-mer model of a genetic sequence can be described as follows: Consider a genetic sequence s of length L, `N1N2…NL', where Nl ∈{A,C,G,T}, l =1,2,…,L. A string of consecutive k nucleotides within a genetic sequence is called a k-mer. The k-mers appearing in a sequence can be enumerated by using a sliding window of length k, shifting one base each time from position 1 to L −k +1, until the entire sequence has been scanned.

Given any k, there are 4k different possible permutations of k-mers that may appear: [1], [2], …, [4k]. For any genetic sequence s, the k-mer counting vector n(s,k) is defined by n(s,k) = ns[1],ns[2], …,ns[4k]), where ns[i] is the number of times the k-mer [i] occurs in sequence s.

2.2. K-mer natural vector

The k-mer natural vector is defined to be the concatenation of the following three vectors, each of which is of length 4k: The k-mer counting vector n(s,k) as defined above. The k-mer mean distance vector (μ[1],μ[2], …,μ[4k]), where μ[i] is defined to be the arithmetic mean of the distances from various occurrences of the k-mer [i] to the first base in the sequence. If a specific k-mer [i] does not exist in a genetic sequence, μ[i] is defined to be zero.

The normalized central moment vector (D2[1],D2[2],⋯,D2[4k]). In general, for any m, the normalized central moments are defined as follows:

Dm[i]=∑j=1n[i](s[i][j]−μ[i])mn[i]m−1(L−k+1)m−1,m=1,2,⋯,n[i],

where n[i] denotes the number of times [i] appearing in the genetic sequence, L is the length of genetic sequence, s[i][j] is the distance from the first base to the j -th [i]in sequence s, and μ[i] is the mean of distances from the various occurrences of [i] to the first base. Thus, we get a sequence of normalized central moments which are natural parameters associated with k-mers distributions within the genetic sequence.

When k=1, the k-mer natural vector is the same to the original natural vector. Thus the k-mer natural vector method is a generalization of the original natural vector model.

If the distribution of each k-mer is different, two genetic sequences cannot be similar even though they contain the same set of k-mers and the same total distance measurement. Although each subset of numerical parameters maybe not sufficient to annotate genetic sequences, the combined numerical parameters are sufficient to characterize each genetic sequence. We can mathematically prove that the correspondence between a genetic sequence and its associated k-mer natural vector is one-to-one for each given k in the Text S1 of Appendix A. Because all the first central moments are zero, we do not need to include them as part of k-mer natural vector.

The k-mer natural vector is obtained by concatenating the first group of parameters (the frequency of occurrence of each k-mer in the sequence) and the second group of parameters (the mean distance of each k-mer to the first base) to the normalized central moments, and the k-mer natural vector implies the information on the relationships of k-mers for each fixed k. Because of this, our k-mer natural vector model overcomes the deficiency of previous k-mer model methods.

It is shown that the 3×4k -dimensional vector (n[i],μ[i],D2[i]) is enough to represent a genetic sequence, and not necessary to include normalized central moments higher than second order for the comparison of genetic sequences, in that, the high central moments hardly make any contribution, and the 3×4k -dimensional natural vector mapping restricted on all the datasets is still one-to-one mapping.

For each fixed k, there are 4k different possible k-mers in the sequence. The computational complexity of our k-mer natural vector is o(n·m2·4k), where n is the maximum length of the sequences, and m is the number of sequences in the dataset. Our proposed method is fast, because it only needs to read the sequence once to compute k-mer natural vector. Moreover, the running time comparisons for our k-mer natural vector methods, clustalW, and Muscle are presented in the Text S2 of Appendix A.

2.3. The choice ofk

Because the parameter k has a great influence on the results of evolutionary relationships and on the complexity of computation for k-mer model, it is very important and difficult to choose a suitable k for different length of genetic sequences considered in phylogenetic analysis. Some researchers have explored the selection of the optimum value k* for k-mer model. For example, Wu et al. proposed an optimal word size for dissimilarity measurement that depends on the length of sequences being considered, i.e., k* should be increased when the sequence length increases (Wu et al., 2005). Another investigation was done by Sims et al. (2009), who reported that the optimal length of word lies within an approximate range with lower bound log4n, where n is the length of sequence, and the upper bound given by the criterion that phylogenetic tree topology for length k must be parallel to that of k +1.

Searching for the optimum value k* for k-mer model, we apply our proposed method to some real datasets (Deng et al., 2011; Yu, 2013; Huang et al., 2011; Ingman et al., 2000; Chan et al., 2012), and the optimal k* over the range of k considered for k-mer natural vector model is chosen based on the following strategy: if the result of phylogenetic tree for value k is relatively stable to that of k+1, we choose k*=k; otherwise k* is equal to the maximum over the range of k values considered. We infer that the optimal k* for our k-mer natural vector is within a range

[ceil(log4min(L)),ceil(log4max(L))+1],

where L is the set of lengths of genetic sequences considered in phylogenetic analysis. This explicit range for choosing the optimum value k* is much shorter than that considered by previous k-mer model methods. Additionally, the optimal k* obtained by k-mer natural vector is less than those selected by other k-mer model methods (Qi et al., 2004; Yu et al., 2005; Chan et al., 2012) for the same candidate dataset (18S rRNAs dataset), which indicates that our k-mer natural vector method needs lower computational time, and can more easily extract the features that are hidden in genetic sequence.

2.4. Distance metric

Since each genetic sequence can be uniquely represented by a k-mer natural vector, a distance metric can be used to quantify the evolutionary relationships of genetic sequences. The similarity between a pair of genetic sequences can be computed by the correlation angle between their natural vectors, because the correlation angle can eliminate the effects of high dimensionality (Berry et al., 1999; Wen and Zhang, 2009). In this paper, we select the distance metric defined below to measure the similarities of genetic sequences, which has been widely used in the k-mer model (Qi et al., 2004; Stuart et al., 2002, 2004).

Let v1 and v2 be the k-mer natural vectors of genetic sequences s1 and s2, respectively, the distance between sequences s1 and s2 can be computed as follows:

d(s1,s2)=1−cos(ν1,ν2)=1−ν1⋅ν2∣ν1‖ν2∣,

where cos(v1, v2) is the cosine angle of vectors v1 and v2, and |v1|,|v2| are the norms of vector v1 and v2, respectively.

Once the distance matrix constructed by the distances among all genetic sequences considered for phylogenetic analysis is obtained, the evolutionary tree can be drawn by the methods of Unweighted Pair Group Method with Arithmetic Mean (UPGMA) or Neighbour Joining (NJ) using MEGA 5.10. (Tamura et al., 2011).

3. Results and Discussion

To demonstrate the validity of k-mer natural vector method, we apply our proposed method to the phylogenetic analysis of real datasets: the mitochondrial genome sequences and 18S rRNA sequences in which both long and short genetic sequences are considered. All genetic sequences are treated as linear sequences.

3.1. Phylogenetic analysis of 31 mammal mitochondrial genomes

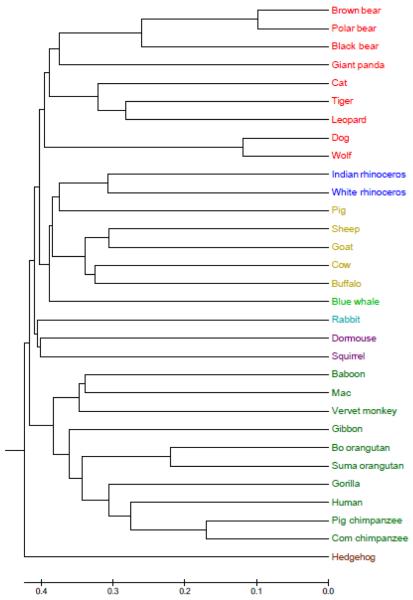
We first analyse the mitochondrial genome sequences of 31 species using our proposed method. This data was previously analysed using the original natural vector approach (Deng et al., 2011). The descriptions of the 31 mitochondrial genome sequences are listed in the Table S1 of Appendix A, the lengths of which are from 16338 to 17447 base pairs (bp). The mitochondrial genetic sequences that are not highly conserved have a rapid mutation rate, so they are suitable for exploring the evolutionary relationships of different species (Yu et al., 2010; Huang et al., 2011). The phylogenetic tree of 31 mitochondrial genomes is shown in Figure 1 by UPGMA method when k=9.

Figure 1.

Figure 1

Open in a new tab

Phylogenetic tree of 31 mitochondrial genome sequences based on 9-mer natural vector. All 31 genomes are correctly clustered into eight known clusters: Carnivora (red), Perissodactyla (blue), Artiodactyla (yellow), Cetacea (light green), Lagomorpha (light blue), Rodentia (purple), Primates (green) and Erinaceomorpha (light green), which agrees with results from standard biological taxonomy and evolutionary relationships of species.

Looking at Figure 1, all 31 genomes are correctly clustered into eight known clusters: Carnivora (red), Perissodactyla (blue), Artiodactyla (yellow), Cetacea (light green), Lagomorpha (light blue), Rodentia (purple), Primates (green) and Erinaceomorpha (brown). Since whales evolved from the primitive artiodactyl, blue whale clusters with artiodactyls to form Cetartiodactyla, which integrate with rhinoceroses to constitute Euungulata. Hence, our results can be considered as the evidence for Euungulata Theory. Additionally, rabbit clusters with dormouse and squirrel, in that, they are all in Glires. The resulting phylogenetic tree agrees with those from standard biological taxonomy, evolutionary relationships of species and some published papers (Yu et al., 2010; Huang et al., 2011; Liu et al., 2001; Raina et al., 2005; Kullberg et al., 2006). Compared with Figure 3 of (Deng et al., 2011) drawn by the original natural vector method, the accuracy of evolutionary relationships has been greatly improved, which can be easily seen from the evolutionary relationships within the subgroups of Primates and Carnivora, respectively.

Figure 3.

Figure 3

Open in a new tab

Phylogenetic tree of 53 human mitochondrial genome sequences based on 8-mer natural vector. The 53 mtDNAs are mainly divided into two parts: non-Africans (red and green) and Africans (blue, yellow, brown and purple), and humans in each group correctly cluster, which is consistent with known evidences of human evolution and human migration.

To further show the utility of our k-mer natural vector method, we perform multiple sequence alignment on the same dataset that we considered, using MEGA 5.10 implementation of the clustalW algorithm. The phylogenetic tree drawn for multiple sequence alignment is shown in Figure 2 by UPGMA method, where the species are coloured the same as Figure 1. Here, we only consider the differences between phylogenetic trees corresponding to the k-mer natural vector and clustalW, respectively. When clustalW is applied to 31 mitochondrial genome sequences, squirrel seems closer rabbit in Figure 2, rather than dormouse in Figure 1, which does not agree with standard biological taxonomy, in that, squirrel and dormouse are rodents.

Figure 2.

Figure 2

Open in a new tab

Phylogenetic tree of 31 mitochondrial genome sequences obtained by multiple sequence alignment (clustalW).

3.2. Phylogenetic analysis of 53 human mitochondrial genomes

We also apply our method to investigate variations in human mitochondrial genomes and to explore the origin of modern humans. Because mtDNA has a high substitution rate (Brown et al., 1979), less recombination (Olivio et al., 1983), and maternal inheritance (Giles et al., 1980), it is usually utilized as a tool in human evolution. Due to the variations of substitution rates and parallel mutation, these studies focusing on the control region of mtDNA might lead to incorrect phylogenetic inferences (Tamura and Nei, 1993; Maddison et al., 1992).

To improve the information obtained from mtDNA for studies of human evolution, Ingman et al. described the global mtDNA diversity in humans based on sequence alignment of complete mtDNA sequences (excluding D-loops) from 53 diverse origins (Ingman et al., 2000). It has been verified that the portion of a mtDNA sequence that is outside any D-loops evolves in a roughly `clock-like' manner, enabling a more accurate measure of mutation rate, and therefore improved time estimates for evolutionary events. The 53 human mtDNAs (excluding D-loops) are unique and vary in length from 15440 to 15450 base pairs (bp). They are described in the Table S2 of Appendix A and the phylogenetic tree for them is shown in Figure 3 by NJ method when k=8.

From Figure 3, the 53 mtDNA sequences are divided into two parts: non-Africans (red and green) and Africans (blue, yellow, brown, and purple). Humans in each group correctly cluster, which is consistent with known evidences of human evolution and human migration. Compared with Figure 2 of Ingman et al. (2000), the evolutionary relationships between all Africans and most non-Africans are the same, and differences only exist in several non-Africans.

Moreover, we also apply the ClustalW to these 53 human mtDNA sequences, and the obtaining phylogenetic tree is shown in Figure 4 by NJ method, which is the similar to the results of our proposed method shown in Figure 3. Moreover, our k-mer natural vector method seems to get better results.

Figure 4.

Figure 4

Open in a new tab

Phylogenetic tree of 53 human mitochondrial genome sequences obtained by multiple sequence alignment (clustalW).

For example, sequence alignment method would imply that two mtDNA samples from Japanese were not closely connected, but our method (see Figure 3) shows the contrary. If we take Guarani and Siberian-Inuit as references, the lengths of four mtDNAs considered are all 15449. The mismatches between Japanese1 and Japanese2, Guarani, Siberian-Inuit are 12, 16, and 15, respectively, and mismatches between Japanese2 and Guarani, Siberian-Inuit equal 14 and 13, respectively. Hence, the two Japanese should close connected in the phylogenetic tree, and phylogenetic tree obtained by our method looks more reasonable.

3.3. Phylogenetic analysis of 40 tetrapod 18S rRNA sequences

Additionally, our method is used to analyse the phylogeny of 40 tetrapod 18S rRNA sequences. The 18S sequence was considered odd, providing significantly different estimates of phylogeny in higher organisms (Huelsenbeck et al., 1996). The phylogenetic relationship amongst tetrapod species has been widely discussed in the area of phylogeny and evolution. A controversial problem among tetrapod is whether birds are more closely related to crocodilians, or to mammals. The evolutionary analysis of tetrapod 18S rRNAs generates a clustering of birds with mammals (Xia et al., 2003), whereas evidences from molecules, palaeontology, and morphology showed that birds should cluster with crocodilians (Hedges et al., 1990), which is more acceptable to biologists. We investigate this question by applying our method to the tetrapod dataset shown in Figure 3 of (Chan et al., 2011) which contains 40 sequences whose lengths are from 1733 to 2235 base pairs (bp).

The phylogenetic tree based on our proposed method is shown in Figure 5 by NJ method when k=6. This phylogenetic tree contains four clades: Birds (green), Crocodilians (blue), Mammals (red) and Amphibians (purple), and the species in each clade are correctly grouped together. The results are similar to those obtained from sequence alignment and what is found in some phylogenetic analyses (Xia et al., 2003; Hedges et al., 1990; Chan et al., 2011; Rzhetsky and Nei, 1992; Hedges, 1994; Seutin et al., 1994; Caspers et al., 1996; Janke and Arnason, 1997; Zardoya and Meyer, 1998; Ausio et al., 1999; Dixon and Hillis, 1993). It can be seen that birds group with crocodilians rather than group with mammals in Figure 5. This result conforms to results from traditional classification and the results in Hedges et al., (1990) and Chan et al., (2012). Compared with Figure 3 of Chan et al. (2012), our result is relatively better. Rattus and Mus group together, and Homo is closer to Oryctolagus, rather than Mus and Rattus, which conform to the evolutionary relationships of species and results obtained by sequence alignment. Although in our Figure 5, Homo K03432 is not clustered to the rest of Homo by NJ algorithm, however after inspecting the distance matrix, we find that the nearest neighbour of Homo K03432 is Homo M10089. Similarly, the nearest neighbour of Oryctolagus X00640 is Oryctolagus X06776.

Figure 5.

Figure 5

Open in a new tab

Phylogenetic tree of 40 18S rRNA sequences based on 6-mer natural vector. The phylogenetic tree of 18S rRNAs contains four clades: Birds (green), Crocodilians (blue), Mammals (red) and Amphibians (purple), and the species in each clade correctly group together that conform to results from traditional classification.

Finally, we applied clustalW to the tetrapod 18S rRNA sequences, and the result is shown in Figure 6. Although Homo and Oryctolagus do not group well, our proposed method has yielded a valuable result: birds group with crocodilians in Figure 5, rather than mammals shown in Figure 6, which conforms to traditional classification and evidences from molecules, morphology, and palaeontology. It is important to certify that bird should group with crocodilians, rather than with mammals, which would be more meaningful in biological evolution.

Figure 6.

Figure 6

Open in a new tab

Phylogenetic tree of 40 18S rRNA sequences obtained by multiple sequence alignment (clustalW).

4. Conclusions

In this paper, the k-mer natural vector method is proposed by combining the original natural vector with the k-mer model for genetic sequences. The number and distribution of k-mers in a genetic sequence are the components of k-mer natural vector, which contains information of relationships between k-mers in a sequence. The correspondence between a genetic sequence and its associated k-mer natural vector can be mathematically proven to be one-to-one. With this representation, each genetic sequence can be characterized by a multidimensional vector. Our proposed method makes it easy to compare genetic sequences, which is more effective for handling whole or partial genomes than sequence alignment methods. The phylogenetic analysis of genetic sequences done by our proposed method does not assume some sort of evolutionary model, and avoids high computational complexity associated with sequence alignment. Its applications to real datasets have shown that the k-mer natural vector method is a powerful tool for the phylogenetic analysis of genetic sequences. It not only improves the accuracy of evolutionary relationships to some extent, but it also reduces computational time for phylogenetic analysis. However, the k-mer natural vector method is still in the process of being improved.

Supplementary Material

01

Highlights.

  • A one-to-one correspondence between genetic sequence and its k-mer natural vector.

  • Phylogenetic analysis does not need any evolutionary model or human intervene.

  • Whole or partial genomes can be handled more effective with our proposed method.

  • Our method is a very powerful tool for analysing and annotating genetic sequences.

Acknowledgements

We thank Dr. Max Benson for his critically reading and editing our manuscript. This work is supported by Scientific Research Fund of Heilongjiang Education Department (12513097), Youth Fund of Suihua University (KQ1202004), U.S. NSF grant DMS-1120824, China NSF grant 31271408, and Tsinghua University.

Abbreviations

A

adenosine

C

cytidine

G

guanosine

T

thymidine

bp

base pairs

UPGMA

Unweighted Pair Group Method with Arithmetic Mean

NJ

Neighbour Joining

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflict of interest We certify that there is no conflict of interest. There is no limitation on access to data or other material critical to the work being reported.

References

  1. Atchley WR, Fitch WM, Bronner FM. Molecular evolution of the MyoD family of transcription factors. Proc. Natl. Acad. Sci. USA. 1994;91:11522–11526. doi: 10.1073/pnas.91.24.11522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ausio J, Soley JT, Burger W, Lewis JD, Barreda D, Cheng KM. The histidine-rich protamine from ostrich and tinamou sperm: A link between reptile and bird protamines. Biochemistry. 1999;38:180–184. doi: 10.1021/bi981621w. [DOI] [PubMed] [Google Scholar]
  3. Berry MW, Drmac Z, Jessup ER. Matrices, vector spaces, and information retrieval. SIAM Rewiew. 1999;41:335–362. [Google Scholar]
  4. Blaisdell BE. A measure of the similarity of sets of sequences not requiring sequence alignment. Proc. Natl. Acad. Sci. USA. 1986;83:5155–5159. doi: 10.1073/pnas.83.14.5155. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Brown WM, George MJ, Wilson AC. Rapid evolution of animal mitochondrial DNA. Proc. Natl. Acad. Sci. USA. 1979;76:1967–1971. doi: 10.1073/pnas.76.4.1967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Caspers GJ, Reinders GJ, Leunissen JA, Wattel J, Dejong WW. Protein sequences indicate that turtles branched off from the amniote tree after mammals. J. Mol. Evol. 1996;42:580–586. doi: 10.1007/BF02352288. [DOI] [PubMed] [Google Scholar]
  7. Chan RH, Chan TH, Yeung HM, Wang RW. Composition vector method based on maximum entropy principle for sequence comparison. IEEE/ACM Trans. Comput. Biol. Bioinform. 2012;9:79–87. doi: 10.1109/TCBB.2011.45. [DOI] [PubMed] [Google Scholar]
  8. Chandrasekharan UM, Sanker S, Glynias MJ, Karnik SS, Husain A. Angiotensin II-forming activity in a reconstructed ancestral chymase. Science. 1996;271:502–505. doi: 10.1126/science.271.5248.502. [DOI] [PubMed] [Google Scholar]
  9. Deng M, Yu C, Liang Q, He RL, Yau SS. A novel method of characterizing genetic sequences: genome space with biological distance and applications. PLoS One. 2011;6:e17293. doi: 10.1371/journal.pone.0017293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Dixon MT, Hillis DM. Ribosomal RNA secondary structure: Compensatory mutations and implications for phylogenetic analysis. Mol. Biol. Evol. 1993;10:256–267. doi: 10.1093/oxfordjournals.molbev.a039998. [DOI] [PubMed] [Google Scholar]
  11. Figueroa F, Gunther E, Klein J. MHC polymorphism pre-dating speciation. Nature. 1988;335:265–267. doi: 10.1038/335265a0. [DOI] [PubMed] [Google Scholar]
  12. Giles RE, Blanc H, Cann HM, Wallace DC. Maternal inheritance of human mitochondrial DNA. Proc. Natl. Acad. Sci. USA. 1980;77:6715–6719. doi: 10.1073/pnas.77.11.6715. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Goodwin RL, Baumann H, Berger FG. Patterns of divergence during evolution of α1-proteinase inhibitors in mammals. Mol. Biol. Evol. 1996;13:346–358. doi: 10.1093/oxfordjournals.molbev.a025594. [DOI] [PubMed] [Google Scholar]
  14. Hedges SB. Molecular evidence for the origin of birds. Proc. Natl. Acad. Sci. USA. 1994;91:2621–2624. doi: 10.1073/pnas.91.7.2621. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hedges SB, Moberg KD, Maxson LR. Tetrapod phylogeny inferred from 18S and 28S ribosomal RNA sequence and a review of the evidence for amniote relationships. Mol. Biol. Evol. 1990;7:607–633. doi: 10.1093/oxfordjournals.molbev.a040628. [DOI] [PubMed] [Google Scholar]
  16. Huang G, Zhou H, Li YF, Xu L. Alignment-free comparison of genome sequences by a new numerical characterization. J. Theor. Biol. 2011;281:107–112. doi: 10.1016/j.jtbi.2011.04.003. [DOI] [PubMed] [Google Scholar]
  17. Huelsenbeck JP, Bull JJ, Cunningham CW. Combining data in phylogenetic analysis. Trends Ecol. Evol. 1996;11:152–158. doi: 10.1016/0169-5347(96)10006-9. [DOI] [PubMed] [Google Scholar]
  18. Ingman M, Kaessmann H, Pääbo S, Gyllensten U. Mitochondrial genome variation and the origin of modern humans. Nature. 2000;408:708–713. doi: 10.1038/35047064. [DOI] [PubMed] [Google Scholar]
  19. Janke A, Arnason U. The complete mitochondrial genome of Alligator mississippiensis and the separation between recent archosauria (birds and crocodiles) Mol. Biol. Evol. 1997;14:1266–1272. doi: 10.1093/oxfordjournals.molbev.a025736. [DOI] [PubMed] [Google Scholar]
  20. Jermann RM, Opitz JG, Stackhouse J, Benner SA. Reconstructing the evolutionary history of the artiodactyl ribonuclease superfamily. Nature. 1995;374:57–59. doi: 10.1038/374057a0. [DOI] [PubMed] [Google Scholar]
  21. Jun SR, Sims GE, Wu GA, Kim SH. Whole-proteome phylogeny of prokaryotes by feature frequency profiles: an alignment-free method with optimal feature resolution. Proc. Natl. Acad. Sci. USA. 2010;107:133–138. doi: 10.1073/pnas.0913033107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kantorovitz MR, Robinson GE, Sinha S. A statistical method for alignment-free comparison of regulatory sequences. Bioinformatics. 2007;23:i249–i255. doi: 10.1093/bioinformatics/btm211. [DOI] [PubMed] [Google Scholar]
  23. Korf IF, Rose AB. Applying word-based algorithms: the IMEter. Methods Mol. Biol. 2009;553:287–301. doi: 10.1007/978-1-60327-563-7_14. [DOI] [PubMed] [Google Scholar]
  24. Kullberg M, Nilsson M, Arnason U, Harley EH, Janke A. Housekeeping genes for phylogenetic analysis of eutherian relationships. Mol. Biol. Evol. 2006;23:1493–1503. doi: 10.1093/molbev/msl027. [DOI] [PubMed] [Google Scholar]
  25. Liu FG, Miyamoto MM, Freire NP, Ong PQ, Tennant MR, Yong TS, Gugel KF. Molecular and morphological supertrees for eutherian (placental) mammals. Science. 2001;291:1786–1789. doi: 10.1126/science.1056346. [DOI] [PubMed] [Google Scholar]
  26. Maddison DR, Ruvolo M, Swofford DL. Geographic origins of human mitochondrial DNA: phylogenetic evidence from control region sequences. Syst. Biol. 1992;41:111–124. [Google Scholar]
  27. Nei M. Phylogenetic analysis in molecular evolutionary genetic. Annu. Rev. Genet. 1996;30:371–403. doi: 10.1146/annurev.genet.30.1.371. [DOI] [PubMed] [Google Scholar]
  28. Olivio PD, VandeWalle MJ, Laipis PJ, Hauswirth WW. Nucleotide sequence evidence for rapid genotypic shifts in the bovine mitochondrial DNA D-loop. Nature. 1983;306:400–402. doi: 10.1038/306400a0. [DOI] [PubMed] [Google Scholar]
  29. Ota T, Nei M. Divergent evolution and evolution by the birth-and-death process in the immunoglobulin VH gene family. Mol. Biol. Evol. 1994;11:469–482. doi: 10.1093/oxfordjournals.molbev.a040127. [DOI] [PubMed] [Google Scholar]
  30. Qi J, Wang B, Hao BL. Whole proteome prokaryote phylogeny without sequence alignment: a k-string comparison approach. J. Mol. Evol. 2004;58:1–11. doi: 10.1007/s00239-003-2493-7. [DOI] [PubMed] [Google Scholar]
  31. Raina SZ, Faith JJ, Disotell TR, Seligmann H, Stewart CB, Pollock DD. Evolution of base-substitution gradients in primate mitochondrial genomes. Genome Res. 2005;15:665–673. doi: 10.1101/gr.3128605. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Rzhetsky A, Nei M. A simple method for estimating and testing minimum-evolution tree. Mol. Biol. Evol. 1992;9:945–967. [Google Scholar]
  33. Seutin G, Lang BF, Mindell DP, Morais R. Evolution of the WANCY region in amniote mitochondrial DNA. Mol. Biol. Evol. 1994;11:329–340. doi: 10.1093/oxfordjournals.molbev.a040116. [DOI] [PubMed] [Google Scholar]
  34. Sims GE, Jun SR, Wu GA, Kim SH. Alignment-free genome comparison with feature frequency profiles (FFP) and optimal resolutions. Proc. Natl. Acad. Sci. USA. 2009;106:2677–2682. doi: 10.1073/pnas.0813249106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Sims GE, Jun SR, Wu GA, Kim SH. Whole-genome phylogeny of mammals: evolutionary information in genic and non-genic regions. Proc. Natl. Acad. Sci. USA. 2009;106:17077–17082. doi: 10.1073/pnas.0909377106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Stuart GW, Berry MW. An SVD-based comparison of nine whole eukaryotic genomes supports a coelomate rather than ecdysozoan linkage. BMC Bioinformatics. 2004;5:204. doi: 10.1186/1471-2105-5-204. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Stuart GW, Moffett K, Leader JJ. A comprehensive vertebrate phylogeny using vector representations of protein sequences from whole genomes. Mol. Biol. Evol. 2002;19:554–562. doi: 10.1093/oxfordjournals.molbev.a004111. [DOI] [PubMed] [Google Scholar]
  38. Takahata N. Allelic genealogy and human evolution. Mol. Biol. Evol. 1993;10:2–22. doi: 10.1093/oxfordjournals.molbev.a039995. [DOI] [PubMed] [Google Scholar]
  39. Tamura K, Nei M. Estimation of the number of nucleotide substitutions in the control region of mitochondrial DNA in humans and chimpanzees. Mol. Biol. Evol. 1993;10:512–526. doi: 10.1093/oxfordjournals.molbev.a040023. [DOI] [PubMed] [Google Scholar]
  40. Tamura K, Peterson D, Peterson N, Stecher G, Nei M, Kumar S. MEGA5: Molecular Evolutionary Genetics Analysis using Maximum Likelihood, Evolutionary Distance, and Maximum Parsimony Methods. Mol. Biol. Evol. 2011;28:2731–2739. doi: 10.1093/molbev/msr121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Wen J, Zhang YY. A 2D graphical representation of protein sequence and its numerical characterization. Chem. Phys. Lett. 2009;476:281–286. [Google Scholar]
  42. Wistow G. Lens crystallins: gene recruitment and evolutionary dynamism. Trends Biochem. Sci. 1993;18:301–306. doi: 10.1016/0968-0004(93)90041-k. [DOI] [PubMed] [Google Scholar]
  43. Wu TJ, Burke JP, Davison DB. A measure of DNA sequence dissimilarity based on Mahalanobis distance between frequencies of words. Biometrics. 1997;53:1431–1439. [PubMed] [Google Scholar]
  44. Wu TJ, Hsieh YC, Li LA. Statistical measures of DNA dissimilarity under Markov chain models of base composition. Biometrics. 2001;57:441–448. doi: 10.1111/j.0006-341x.2001.00441.x. [DOI] [PubMed] [Google Scholar]
  45. Wu TJ, Huang YH, Li LA. Optimal word sizes for dissimilarity measures and estimation of the degree of dissimilarity between DNA sequences. Bioinformatics. 2005;21:4125–4132. doi: 10.1093/bioinformatics/bti658. [DOI] [PubMed] [Google Scholar]
  46. Xia X, Xie Z, Kjer KM. 18S ribosomal RNA and tetrapod phylogeny. Syst. Biol. 2003;52:283–295. doi: 10.1080/10635150390196948. [DOI] [PubMed] [Google Scholar]
  47. Yang XW, Wang TM. A novel statistical measure for sequence comparison on the basis of k-word counts. J. Theor. Biol. 2013;318:91–100. doi: 10.1016/j.jtbi.2012.10.035. [DOI] [PubMed] [Google Scholar]
  48. Yu C, Deng M, Cheng SY, Yau SC, He RL, Yau SS. Protein space: a natural method for realizing the nature of protein universe. J. Theo. Biol. 2013;318:197–204. doi: 10.1016/j.jtbi.2012.11.005. [DOI] [PubMed] [Google Scholar]
  49. Yu C, Liang Q, Yin C, He RL, Yau SS. A Novel Construction of Genome Space with Biological Geometry. DNA Res. 2010;17:155–168. doi: 10.1093/dnares/dsq008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Yu C, Hernandez T, Zheng H, Yau SC, Huang HH, He RL, Yang J, Yau SS. Real time classification of viruses in 12 dimensions. PLoS One. 2013;8:e64328. doi: 10.1371/journal.pone.0064328. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Yu HJ. Segmented K-mer and its application on similarity analysis of mitochondrial genome sequences. Gene. 2013;518:419–424. doi: 10.1016/j.gene.2012.12.079. [DOI] [PubMed] [Google Scholar]
  52. Yu ZG, Zhou LQ, Anh V, Chu KH, Long SC, Deng JQ. Phylogeny of prokaryotes and chloroplasts revealed by a simple composition approach on all protein sequences from whole genome without sequence alignment. Jour. Mol. Evol. 2005;60:538–545. doi: 10.1007/s00239-004-0255-9. [DOI] [PubMed] [Google Scholar]
  53. Zardoya R, Meyer A. Complete mitochondrial genome suggests diapsid affinities of turtles. Proc. Natl. Acad. Sci. USA. 1998;95:14226–14231. doi: 10.1073/pnas.95.24.14226. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
NIHMS602411-supplement-01.docx (105.8KB, docx)

RESOURCES