Continuum Approaches to Understanding Ion and Peptide Interactions with the Membrane

Abstract

Experimental and computational studies have shown that cellular membranes deform to stabilize the inclusion of transmembrane (TM) proteins harboring charge. Recent analysis suggests that membrane bending helps to expose charged and polar residues to the aqueous environment and polar head groups. We previously used elasticity theory to identify membrane distortions that minimize the insertion of charged TM peptides into the membrane. Here, we extend our work by showing that it also provides a novel, computationally efficient method for exploring the energetics of ion and small peptide penetration into membranes. First, we show that the continuum method accurately reproduces energy profiles and membrane shapes generated from molecular simulations of bare ion permeation at a fraction of the computational cost. Next, we demonstrate that the dependence of the ion insertion energy on the membrane thickness arises primarily from the elastic properties of the membrane. Moreover, the continuum model readily provides a free energy decomposition into components not easily determined from molecular dynamics. Finally, we show that the energetics of membrane deformation strongly depend on membrane patch size both for ions and peptides. This dependence is particularly strong for peptides based on simulations of a known amphipathic, membrane binding peptide from the human pathogen Toxoplasma gondii. In total, we address shortcomings and advantages that arise from using a variety of computational methods in distinct biological contexts.

Introduction

The cell membrane serves as a critical barrier differentiating the interior of the cell from the extracellular medium. It is inextricably linked to cellular identity—without a membrane, a cell cannot control its internal chemistry. Loss of membrane integrity often leads to cell death, and organisms have evolved strategies to kill other cells by attacking their membranes, as in the mechanisms of many antibiotics. Strikingly, cells induce their own deaths by compromising the integrity of their membranes during apoptosis through decoupling the cytoskeletal network from the membrane, which leads to blebbing (Mills et al. 1998).

Chemical and physical principles underlie the membrane's dual role as a barrier to the external environment and regulator of nutrient transport into and out of the cell. Packed hydrophobic lipids form a low-dielectric barrier to charged and polar molecules, while membrane-spanning channels and pumps exert control over the passage of ions and macromolecules. Such transmembrane (TM) proteins typically consist of hydrophobic amino acids that are energetically stabilized in the low-dielectric membrane. However, proteins with functionally important, highly charged moieties also reside in the hydrophobic bilayer core, suggesting that some mechanism must exist to mitigate the electrostatic cost of their insertion. In particular, in vitro translocation experiments suggest that TM segments harboring a central, charged residue partition into the bilayer at a small energetic cost of only 2–3 kcal/mol (Hessa et al. 2005). Recent molecular dynamics (MD) simulations have demonstrated that an arginine residue positioned in the bilayer core may “snorkel”, bringing water and ions into the bilayer to interact favorably with the buried amino acid, incurring an energy penalty associated with membrane rearrangement (MacCallum et al. 2007; Dorairaj and Allen 2007). Membrane deformations and distortions, therefore, represent a potential mechanism for charge insertion into the bilayer.

Membrane elasticity likely facilitates a range of biological processes, from the large-scale deformations required for vesicle budding and fusion to the localized permeation of small molecules across bilayers. Carrier-mediated ion transport and bare ion permeation constitute two distinct contexts in which to further investigate how membrane bending modulates membrane transport phenomena. For example, ionophores such as Streptomyces-derived valinomycin selectively chelate potassium ions and shuttle them across host cell bilayers, disrupting their electrochemical gradient. Similarly, the threat of bare permeation of small ions and water molecules to high-fidelity nucleic acid replication might have spurred the development of the phospholipid bilayer as an early and critical evolutionary adaptation on the molecular level (Mansy and Szostak 2008; Budin and Szostak 2011). Nonetheless, bare ion permeation, while rare, does occur, although its mechanism remains disputed in the literature.

At present, ion permeation is thought to occur via two distinct mechanisms: solubility-diffusion and transient pore formation (Paula et al. 1996, 1998; Marrink et al. 2009). In the former, the ion must partition into the hydrophobic core, surmounting a considerable energy barrier, diffuse across the core, and resolvate as it exits the opposite membrane leaflet (Dilger et al. 1979; Finkelstein 1987). However, rates for bare ion permeation predicted from solubility-diffusion theory disagree with experiment by several orders of magnitude (Parsegian 1969). Paula et al. (1996, 1998) investigated how potassium permeation depends on bilayer thickness and found that crossing rates for thin bilayers are best understood by transient pore formation, while crossing rates for thick bilayers are explained by the solubility-diffusion model. Further support for the transient pore model comes from simulation, where studies have demonstrated that electroporation, membrane tension, or the presence of anti-microbial peptides all induce hydrophilic, transient pores, which serve as pathways for ions, lipids and other small molecules (Kandasamy and Larson 2006; Tieleman and Marrink 2006; Marrink et al. 2009; Bennett and Tieleman 2011). In these studies, the primary barrier to permeation is the cost of creating a toroidal pore in the membrane. A third theory, closely related to transient pore formation, suggests that charged molecules at the membrane surface induce the formation of water-head group defects that penetrate deep into the membrane, allowing for the permeation of charges and water molecules through a temporary, electrostatically-favorable environment (Tepper and Voth 2006; Khavrutskii et al. 2009; Li et al. 2012).

While there have been previous studies that have used analytic and continuum approaches to understand bare ion permeation (Parsegian 1969; Finkelstein 1987; Paula et al. 1996, 1998), more recent attempts to compare continuum approaches with detailed MD simulations suggest a failure in the continuum methods (Li et al. 2012). We believe that this failure is largely due to the inability of most continuum implementations to account for the deformable nature of the membrane. Recently, we developed a method that overcomes this shortcoming by using elasticity theory to predict membrane distortions around TM proteins harboring charged, buried residues (Choe et al. 2008; Callenberg et al. 2012). Bending drastically reduces the energy required to insert these proteins into the membrane, and our model is in quantitative agreement with results from atomistic MD simulations, but requires a fraction of the computational cost. To date, we have only assessed the model's ability to predict the static configurations and stability of embedded membrane proteins, but here, we extend our work by considering the penetration of ions and peptides into the membrane from solution. We show that membrane flexibility largely reconciles previous discrepancies between MD simulations and continuum calculations. Snapshots from coarse-grained MD simulations of ion penetration are compared with snapshots from the continuum model, revealing the importance of system size in providing qualitative agreement between different approaches. Additionally, our model produces very similar free energy profiles to all-atom MD simulations of charged groups moving into bilayers of different thickness (Li et al. 2012). A free energy decomposition, which is easily performed with our approach, reveals that the increase in energy required to penetrate thick bilayers is almost entirely due to the increased bilayer bending energy. Finally, we use coarse-grained simulations of peptide association with the membrane to show that computed free energy profiles depend heavily on the system size, as revealed by our ion penetration studies.

Methods

Description of the Continuum Model

Previously, we developed a continuum membrane model and search algorithm to calculate insertion energies and membrane distortions for single pass TM proteins (Choe et al. 2008; Callenberg et al. 2012). Briefly, in our model the total energetic stability of the solute in the membrane, ΔG_total, is approximated by the following equation:

$$\Delta G_{\text{total}}=\Delta G_{\mathrm{mem}}+\Delta G_{\mathrm{elec}}+\Delta G_{\mathrm{np}},$$ (1)

where the first term on the right hand side (ΔG_mem) is the energy associated with distortions in the membrane caused by embedding the solute, the second term (ΔG_elec) is the electrostatic cost required to move the charged solute from solution into the low-dielectric environment of the membrane, and the final term (ΔG_np) is the nonpolar or hydrophobic energy gained by removing portions of the solute surface from water and burying them in the membrane. All energiesare calculated with respect to the molecule free in solution far from an unstressed membrane; therefore, negative values indicate stabilization in the membrane. This model is in excellent agreement with free energies calculated from simulations (Choe et al. 2008), and the model supports experimental observations on the stability of voltage sensors from voltage-gated potassium channels (Callenberg et al. 2012).

All of the energies presented in this manuscript are equilibrium values calculated from static configurations. The exact computational details closely follow the procedure outlined in our previous manuscript (Callenberg et al. 2012) and additional details can be found in Choe et al. (2008). Briefly, the energetic terms and procedure are calculated as follows.

Membrane Deformation Energy (ΔG_mem)

We use linear elasticity theory to determine the shape and energetic cost of deforming the bilayer at the site of ion penetration. Specifically, we use a modified Helfrich Hamiltonian, which includes terms for membrane bending, compression and tension (de Gennes 1969; Helfrich 1973; Harroun et al. 1999):

$$\Delta G_{\mathrm{mem}}=\frac{1}{2}{\int }_{\Omega }\left[\frac{K_{\mathrm{a}}}{L_0^2}{(u^{-}-u^{+})}^2+\frac{K_{\mathrm{c}}}{2}\left({\left({\nabla }^2{u}^{-}\right)}^2+{\left({\nabla }^2{u}^{+}\right)}^2\right)+\frac{\alpha }{2}\left({(\nabla u^{-})}^2+{(\nabla u^{+})}^2\right)\right]\mathrm{d}x\mathrm{d}y,$$ (2)

where u⁺ is the shape of the upper leaflet and u^– is the shape of the lower leaflet, L₀ is the equilibrium thickness of the membrane, K_a is the compression modulus, K_c is the membrane bending modulus, and α is the surface tension. The surfaces are represented in the Monge gauge, and correspondingly, the integral extends over the entire x–y domain, Ω. The functional derivative of Eq. 2 with respect to variations in u⁺ and u^– gives the following partial differential equations (PDEs) that determine the shapes of each leaflet:

$$\begin{array}{cc}\hfill {\nabla }^4{u}^{+}-& \frac{\alpha }{K_{\mathrm{c}}}{\nabla }^2{u}^{+}+\frac{2K_{\mathrm{a}}}{K_{\mathrm{c}}{L}_0^2}(u^{+}-u^{-})=0,\hfill \\ \hfill {\nabla }^4{u}^{-}-& \frac{\alpha }{K_{\mathrm{c}}}{\nabla }^2{u}^{-}+\frac{2K_{\mathrm{a}}}{K_{\mathrm{c}}{L}_0^2}(u^{-}-u^{+})=0.\hfill \end{array}$$ (3)

The last term on the left hand side of each equation couples the upper and lower leaflets. Thus, Eq. 3 is the set of equations that result from minimizing Eq. 2 for a given set of boundary conditions. To minimize the total energy of the system, we employ Powell's method to identify the optimal boundary condition for Eq. 3 that produce the membrane shape that minimizes all of the energy terms shown in Eq. 1. More specifically, the coupled set of fourth-order equations requires two boundary conditions to be specified on the inner boundary, where the bilayer contacts the ion, and at the outer boundary, far from the ion. We assume that the membrane is flat at its equilibrium thickness, L₀, far from the ion. At the ion, we impose a radially symmetric contact height for the upper and lower leaflets, and we impose contact angles that determine the slope, or curvature, of the membrane as it meets the ion (Fig. 1). Thus, four independent parameters determine the boundary conditions at the inner boundary. We determined these values by carrying out a search on all four parameters to find the membrane shapes that minimize the total energy in Eq. 1 as discussed in reference (Callenberg et al. 2012). In some cases described in the “Results” section, we optimized only the contact angle of the leaflet undergoing ion penetration and imposed a contact angle of zero on the opposite leaflet. The PDEs in Eq. 3 were solved using a second-order finite difference method written in radial coordinates (r and θ), and the membrane bending energy was determined by using a second-order scheme to compute the integral in Eq. 2. While the solver is a general 2D solver, the solutions for the ion–membrane systems described in this paper only vary in r, not θ, due to the underlying symmetry of the system and could have been represented with a 1D solver. However, we can also use the 2D solver to address more complex problems that lack radial symmetry, and it is highly accurate and fast compared to the electrostatics calculations performed here. All code was written in Matlab (The MathWorks, Inc., Natick, MA).

Fig. 1.

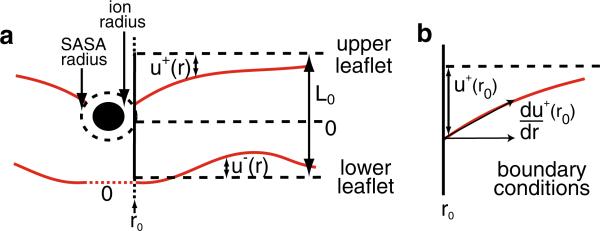
Geometry of the system in the continuum model. a Cross section showing membrane distortions in the upper and lower leaflets. Solid red lines indicate the membrane–water interfaces. Dashed black lines indicate the equilibrium heights of the membrane leaflets and the midplane at z = 0. u⁺ and u^– represent the displacement from equilibrium for the upper and lower leaflets, respectively. The equilibrium bilayer thickness is L₀. The inner boundary conditions are applied at r₀, where the solvent accessible surface area (SASA) of the ion contacts the membrane. b The contact point u⁺(r₀) is determined from the search angle that minimizes the total energy Eq. 1. The ion–membrane contact angle, du⁺/dr, is a free parameter in the model that is optimized during energy minimization. The contact point and angle on the lower leaflet are treated in similar manners (Color figure online)

Electrostatic Energy (ΔG_elec)

We solve the non-linear Poisson–Boltzmann equation to determine the cost of inserting a charged molecule into a neutral, uncharged bilayer:

$$-\nabla \cdot [∊\left(\mathit{r}\right)\nabla \varphi \left(\mathit{r}\right)]+{\kappa }^2\left(\mathit{r}\right)\sinh \left[\varphi \left(\mathit{r}\right)\right]=\frac{e}{k_{\mathrm{B}}T}4\pi \rho \left(\mathit{r}\right),$$ (4)

where φ/(r) = Φ(r)/k_BT is the reduced electrostatic potential at position r; κ is the Debye–Huckel screening coefficient to account for ionic shielding, ε is the spatially-dependent dielectric constant, e is the electron charge and ρ is the charge density within the protein. The electrostatic potential is solved using the software APBS (Baker et al. 2001) along with scripts for including the dielectric influence of the membrane similar to those found in APBSmem (Callenberg et al. 2010). The electrostatic energy of the ion in the membrane compared to solution, ΔG_elec, is calculated by subtracting the total energy of the molecule in the membrane from the value in solution, far from the membrane. This energy is usually referred to as the Born solvation energy, ΔG_Born.

In a separate electrostatics calculation, we include the influence of the membrane dipole potential by adding a sheet of dipole charges at the interface between the head group and the hydrocarbon core, one sheet for the upper leaflet and one for the lower leaflet. This term accounts for the large electrostatic role that the membrane dipole plays in charge permeation events, and we tune the charges and the separation distance of the dipoles to achieve +300 mV at the center of the membrane, which is estimated for phosphatidylcholine (PC) bilayers (Wang et al. 2006). For this calculation, we solve the linearized form of the Poisson–Boltzmann equation to expedite the calculations. First, we calculate the total electrostatic energy of the charged molecule in the bilayer with the dipole potential on. Next, we subtract off the “self” dipole energies by turning off the charge on the permeating molecule and re-performing the calculation with the dipole charges still on. Finally, we subtract the electrostatic energy of the charged molecule with the dipole potential turned off. These three terms added in this way provide the interaction energy between the ion and the membrane dipole potential, ΔG_dipole. Care was taken to avoid double counting of charge–charge interactions. The total electrostatic energy is then given by the sum of the Born solvation energy and the dipole energy: ΔG_elec = ΔG_Born + ΔG_dipole. We found that including the dipole in the electrostatics calculation throughout the search, rather than as a separate calculation, only resulted in less than a 1 kcal/mol difference in the final energy for all membrane configurations, with the exception of the DSPC-like continuum bilayer configurations at z = –1 and 0 Å from bilayer center, which resulted in a 1.5 kcal/mol difference.

Nonpolar Energy (ΔG_np)

The nonpolar energy arises from the tendency of water to exclude molecules, resulting in the clustering of hydrophobic proteins and the stabilization of molecules in the membrane. We model the nonpolar energy, ΔG_np, as proportional to the difference in the ion's solvent accessible surface area (SASA) in the membrane compared to solution:

$$\Delta G_{\mathrm{np}}=a\cdot (A_{\mathrm{mem}}-A_{\mathrm{sol}}),$$ (5)

where A_mem is the ion SASA in the membrane, A_sol is the total ion SASA, and a = 0.028 (kcal/mol)/Ų. The constant a was determined based on the partitioning of small non-polar molecules between aqueous and organic phases (Sitkoff et al. 1994). SASA values are calculated with a modified Shrake–Rupley algorithm (1973) using the solvent-accessible surface representation of the ion with a water probe radius of 1.4 Å. In the presence of the membrane, if the point on the surface of the ion lies between the upper, u⁺ and lower, u^–, leaflets then it is considered occluded and does not contribute to A_mem. Matlab's cubic interpolation function was used to navigate between the position of the point on the ion surface and the grid points describing the upper and lower membrane surfaces.

Minimizing the Total Energy

To simulate the permeation of an ion, we systematically translated the molecule in steps of 1 Å along an axis orthogonal to the membrane normal, which we call the z axis. For each position, we carried out a search using Powell's method (1964) to determine the deformation that minimized the total energy of the system in Eq. 1. Initially, during the search, the contact height of the upper and lower leaflets as well as the slope of membrane contact with the ion were varied (Fig. 1b). To facilitate convergence of the search, we used the final, optimal membrane configuration from one calculation as the starting guess for the subsequent position along the pathway.

Continuum Setup and Parameters

We created input files containing radii and charge for the potassium ion and chloride ion calculations, assigning them their respective charges of +1 and –1, and we used unhydrated ionic radii, 1.39 Å for K⁺ and 1.81 Å for Cl^– (Shannon 1976). We also specified r₀, the radius of the solute inclusion. See Fig. 1 for an illustration of the geometry of the system. For K⁺ and Cl^–, we have no way to determine the extent of ion hydration as it permeates the membrane. Thus, for K⁺, we treat r₀ as equivalent to the SASA radius. We then set the r₀ for Cl^– equal to r₀ for K⁺ but recognize that even slight increases in r₀ lower the cost of ion insertion into the membrane (data not shown).

To capture the effect of increasing bilayer thickness on ion permeation in our continuum model, we also considered how lipid alkyl tail length, a variable in MD simulations and experiments, corresponds to bilayer thickness, and how this in turn affects the elastic properties of the bilayer. Several groups have shown that increasing hydrocarbon chain length leads to a linear increase in bilayer thickness and that the bending modulus, K_c increases systematically as lipid chain length increases (Lewis and Engelman 1983; Rawicz et al. 2000). However, the compression modulus, K_a, does not vary significantly between different lipid chain lengths. We therefore used empirical data to add lipid-specific information to our continuum model while maintaining its computational efficiency. Rawicz and co-workers developed an empirical relation to describe the hydrophobic thickness to K_a and K_c:

$$K_{\mathrm{c}}=\frac{L_{\mathrm{c}}^2}{24}{K}_{\mathrm{a}},$$ (6)

where 24 is an empirical constant and L_c is the equilibrium hydrocarbon thickness, which is equal to the entire bilayer thickness, L₀, minus twice the thickness of the head group region. For all calculations, we used 8 Å as the head group thickness (Helm et al. 1987). We computed K_c from an average K_a of 230 mN/m (Rawicz et al. 2000) and from hydrophobic thicknesses of simulated PC bilayers reported by Li et al. (2012), with the exception of DSPC. For the hydrophobic thickness of DSPC, which was simulated at a higher temperature than the other lipid types, we calculated the average increase in hydrophobic thickness among the other bilayers and added this value to the thickness of DPPC.

We also had to select an outer radius parameter to use as the outer boundary for membrane deformations in the continuum model. In order to bring the sizes of the continuum and coarse-grained lipid patches into agreement, we chose an outer radius for the continuum model such that twice the radius equaled the length of one side of the coarse-grained lipid patch. Since the surface area taken up by individual lipids decreases slightly as tail length increases, we used lipid surface area values reported by Li and co-workers to estimate the outer radius that would provide equivalent surface area to that of a 48 PC lipid patch. Please see Tables 1 and 2 for continuum calculation parameters.

Table 1.

Parameters for all continuum calculations

Parameters	Values
Electrostatics grid dimensions	161 x 161 x 161 Å3
Coarse grid lengths	200 x 200 x 200 Å3
Fine grid lengths	50 x 50 x 50 Å3
Radial points	1,400
Counter-ions	0.1 M symmetric salt
Protein dielectric	2.0
Membrane dielectric	2.0
Head group dielectric	80.0
Solvent dielectric	80.0
Solvent probe radius	1.4 Å
Surface sphere density	10.0 grid points/Å2
Temperature	298.15 K
Membrane thickness	See Table 2
Head group thickness	8.0 Å
Bending modulus (Kc)	See Table 2
Compression modulus (Ka)	2.30 x 10-11 N/Å
Surface tension (α)	3.00 x 10—13 NÅ
Outer boundary radius	800 or 19.5 Å

Table 2.

Elastic membrane material properties

Lipid types	Carbon atoms	L0(Å)	Kc (NÅ)
DDPC	10	32.0	2.5 x 10—10
DLPC	12	36.3	4.0 x 10—10
DMPC	14	39.9	5.5 x 10—10
DPPC	16	43.6	7.0 x 10—10
DSPC	18	47.7	5.9 x 10—10

Coarse-Grained Simulations and Free Energy Calculations

We performed coarse-grained MD simulations using GROMACS version 4.5.3 (Hess et al. 2008) and the MARTINI forcefield version 2.0 with polarizable water (Yesylevskyy et al. 2010). Following the protocols outlined by the Sansom Lab (Bond et al. 2008; Wee et al. 2011), umbrella sampling combined with weighted histogram analysis method (WHAM) were used to construct free energy profiles for peptide helices or permeating ions (Kumar et al. 1992). The z-position of the ion or center of mass (COM) of the helix were harmonically restrained with respect to the COM of the membrane, and this distance was chosen as the reaction coordinate. For cation simulations, Na⁺ was used rather than K⁺, which has not been parameterized in MARTINI. Meanwhile, K⁺ was used in the continuum model due to the prevalence of K⁺ permeation data in the literature. Ion/helix positions were sampled from one side of the membrane to the other in 1 Å steps. In each simulation, the ion/helix was initially placed at the restraint minimum in a pre-equilibrated bilayer. The membrane starts in a flat state that is identical across all simulations, and the protein is translated to many different starting positions across the bilayer prior to minimization and production runs (Fig. 5b). The long axis of the helix was initially parallel to the membrane normal with the N-terminus always pointing in the positive z direction. Minimization and equilibration successfully removed steric clashes between the embedded ion/helix and the lipids. We could possibly have benefited from a speed up in convergence by using the final configuration from the previous ion position to initiate new simulations. However, we were also interested in the ability of the coarse-grained membrane to undergo large scale conformational changes in a limited time, so we initiated all simulations from a flat membrane, a universally accepted approach for molecular simulation. After energy minimization, MD was performed for 60 ns. The first 10 ns of each simulation were discarded as equilibration.

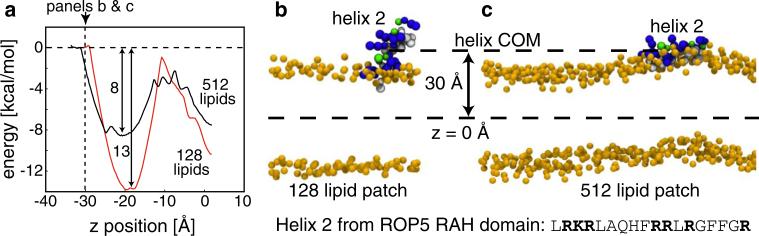
Fig. 5.

Free energy of ROP5 RAH helix 2 binding to a membrane. a The potential of mean force (PMF) for ROP5 RAH helix 2 translated from the lower bath into the center of the bilayer. The PMFs are flat in water, but exhibit a sharp downward slope at –32 Å (512 patch, black curve) and –28 Å (128 patch, red curve) when the membrane starts to bend to interact with the helix. The large patch is able to bend to reach the helix before the small patch leading to robust differences between the two PMFs. The interfacial region near –20 Å is the most stable position for both simulations, but the binding is predicted to be 5 kcal/mol more stable for the small patch than the large patch. The interface between the head group and aqueous environment in the unstrained membrane is indicated by the vertical dashed line. b, c Significant membrane deformations are observed in the large coarse-grained system, but not the small system. When helix 2 from the ROP5 protein is restrained at ±30, +30 Åis shown here, from the center of a DPPC bilayer, a large membrane patch is able to undergo a large scale conformational change to allow the helix to go completely interfacial (c), while the small patch is unable to accommodate such a bending mode (b). Only the distance from the helix COM to the membrane COM are restrained, and the orientation of the helix is free to rotate. Without membrane bending, the distance restraint prevents the entire helix from embedding in the membrane interface (b). These differences in system size give rise to differences in the energetics of helix association with the membrane in panel a (Color figure online)

We used semi-isotropic pressure coupling with a Berendsen barostat (Berendsen et al. 1984) at 1 bar in x and y with a coupling of 1 ps and a compressibility of 3.0 × 10^–5. Particle mesh Ewald electrostatics were used with a 1 Å grid spacing. The software g_wham was used to calculate the potential of mean force (PMF) using WHAM (Hub et al. 2010; Kumar et al. 1992). Two hundred bins were used to construct the histogram, and the energy in bulk solution at ±30 Å was defined to be 0.

All coarse-grained simulations started from an identical pre-equilibrated DPPC bilayer composed of either 128 lipids and 2,000 waters or 512 lipids and 8,000 waters at 320 K. Ions were added as necessary to neutralize the system. The sequence of helix 2 from the arginine-rich amphipathic helix (RAH) domain of Toxoplasma gondii rhoptry protein 5 (ROP5) was obtained from the ToxoDB online resource (LRKRLAQHFRRLRGFFGR). An idealized alpha helix was created with this sequence using VMD Molefacture plugin version 1.2 (Humphrey et al. 1996). The secondary structure was harmonically restrained with a force constant of 1,000 kJ/mol during all simulations.

Results

Continuum Membrane Models Match Molecular Simulation

We first explored the ability of the continuum model to match deformations observed in simulations of ion and charged molecule permeation studies. We moved K⁺ from the upper solution at z = +30 Å to the lower solution at z = –30 Å in 1 Å steps. At each step, we carried out a search algorithm to identify the contact values of the upper and lower leaflets and the membrane contact slope, or curvature, that minimized the total free energy in Eq. 1. The membrane was modeled as a large 800 Å radial patch with thickness and compression moduli derived for DPPC lipids (see Table 2), and in the flat, unstressed case it spans from +21.8 to –21.8 Å, centered at zero.

Four equilibrium snapshots of the ion at different positions along the permeation pathway are shown in Fig. 2a. The membrane adopts a low energy, large wavelength deformation to avoid the high energy electrostatic penalty of direct ion penetration into the hydrocarbon region. The far field boundaries are not shown, so the large scale deformation is not visible in each panel; therefore, the membrane shapes appear flat and unstrained only involving a global translation up or down along the z axis. The insertion energy, ΔG_tot, required to move the ion from bulk solution close to the center of the bilayer at z = –1 Å shown in the second panel of Fig. 2a, is nearly 0 kcal/mol. While physically intuitive, this result does not match the large 20–30 kcal/mol energies predicted for cation penetration into the core based on all-atom MD simulations (Tepper and Voth 2006; Li et al. 2012). Moreover, the membrane shape is completely different from published MD studies, and we hypothesized that this may be the result of MD simulations being performed on small patches of membrane (Tepper and Voth 2006; Leontiadou et al. 2007; MacCallum et al. 2007; Li et al. 2012).

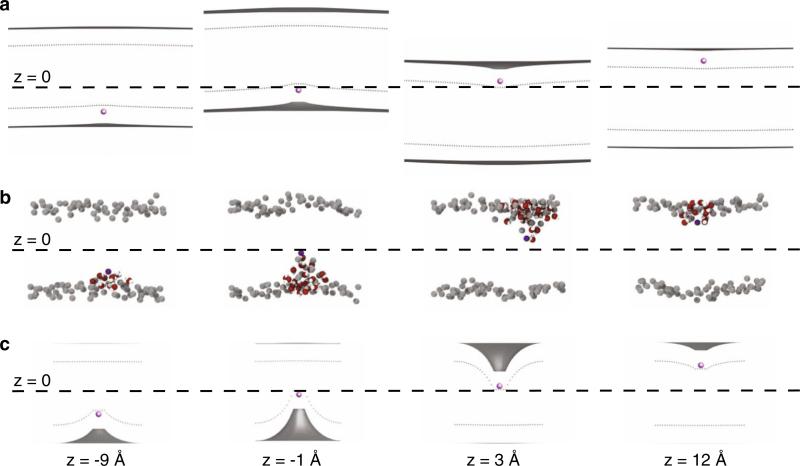
Fig. 2.

Continuum membrane bending is qualitatively similar to deformations observed in coarse-grained simulations. a Configurations from the continuum membrane bending model for a large patch of membrane with boundary conditions applied at 800 Å from the ion. Panels a–c all show four snapshots of a cation (purple) placed at –9, –1, +3, and +12 Å with respect to the center of mass of the membrane. In panels a and c, the gray surfaces are the membrane–water interfaces, which separate the head group region from aqueous solution. The interfaces between the head group region and the membrane core are shown as gray dotted curves. A search was carried out to identify the optimum membrane shape that minimizes the system energy for each ion position. The membrane undergoes large deflections in the z direction to avoid penetration of the ion into the hydrocarbon core. These deflections are most pronounced when the ion is near the center at z = –1 and +3 Å causing shifts up and down, respectively. When the ion is at –9 and +12 Å the bilayer undergoes very little deflection from the flat, unstrained state. b Snapshots from a coarse-grained MD simulation of Na⁺ penetrating a DPPC bilayer using the MARTINI forcefield. The membrane is approximately square with a side length of 65 Å, and it is composed of 128 DPPC lipids. The phosphate beads are gray, and penetrating waters are red and white. Starting with an identical flat, equilibrated bilayer, 71 independent umbrella sampling simulations were performed with the ion restrained at positions along the membrane normal. The small leaflet deformations occur at –9 and +12 Å, but large membrane bending occurs when the ion is near the center of the bilayer in the middle two snapshots. c Configurations from the continuum model for a small patch of membrane with a 19.5 Å radius. For this small patch, more similar in size to the system in panel b, the membrane is not able to adopt a low energy, large scale deformation to avoid penetration by the ion. The leaflet being penetrated bends sharply, while the opposite leaflet adopts a more gentle bend to relieve compression just as in the coarse-grained simulations in panel b (Color figure online)

To elucidate the source of these differences, we carried out our own MD simulations of a cation penetrating a bilayer using the coarse-grained MARTINI force field (Yesylevskyy et al. 2010) (Fig. 2b). MARTINI has been extensively used to simulate membrane distortions, ranging from TM and lipid fusion pores to large scale lipid rearrangement (Yoo et al. 2013; Marrink and Tieleman 2013). We constructed a small membrane composed of 128 DPPC lipids approximately 65 Å × 65 Å in area, comparable to patch sizes employed in all-atom MD simulations. Umbrella sampling was then used to harmonically restrain the cation at positions along the z axis ranging from –30 to +30 Å, with respect to the membrane COM, and representative snapshots were extracted from simulations at –9, –1, 3 and 12 Å (Fig. 2b). Consistent with past MD simulations, the coarse grained simulations reveal deep penetration of the ion into the membrane, which causes a severe deformation of the adjacent lipids. However, there was no large scale deflection of the membrane in the ±z direction, as observed in panel a, since the patch is not large enough to accommodate a long wavelength distortion given its small lateral extent.

Next, we carried out continuum calculations as in panel a, but with a much smaller patch size of radius 19.5 Å, comparable to the system size in the all-atom MD simulations of Li et al. (2012). Interestingly, the resulting minimized membrane configurations are now qualitatively similar to the MD simulations (compare Fig. 2b, c). The membrane is now too small to undergo a large deflection to keep the ion in the head group region, and instead the leaflets undergo bending to position the ion in the head group as it penetrates the bilayer. This result demonstrates that qualitative features of ion penetration into the membrane can be captured with a continuum model, and it highlights the importance of membrane size when exploring ion and small molecule permeation.

Ion Free Energy Profiles from Continuum Model Match Profiles from Molecular Simulations

Next, we wanted to determine if our model produces energy values that are consistent with previous all-atom studies of ion permeation, and we wanted to understand the role of membrane bending in this process. First, we computed the total free energy according to Eq. 1 for K⁺ and Cl^– movement across a non-deformable membrane in 1 Å steps (red and blue dashed lines in Fig. 3, respectively). The energy profile for an ion permeating a non-deformable bilayer exhibits a sharp increase as the ion leaves the high-dielectric head group region and then flattens out in the low-dielectric core between ± 8 Å. The electrostatic cost of moving a charged solute into a low-dielectric region largely accounts for this effect, which is mediated slightly by the favorable change in the nonpolar energy arising from removing a solute from solution. Additionally, the anion is stabilized an additional ~20 kcal/mol compared to the cation because both ions experience the full effect of the +300 mV dipole potential. Importantly, these energy profiles do not match the “witch's hat” profiles produced by all-atom MD simulations, which show that the permeation profiles are sharply peaked near the bilayer center.

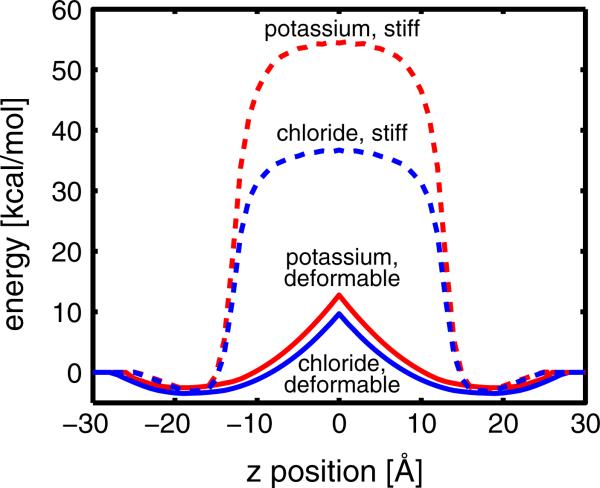
Fig. 3.

Free energy profiles along the transmembrane coordinate for a cation and an anion. We translated K⁺ (red curves) or Cl^– (blue curves) across the membrane in 1 Å steps with the ion initially positioned in bulk solvent approximately 6 Å from the membrane–water interface (z = –30 Å). Dashed lines correspond to calculations carried out on a stiff, unbending bilayer, while solid lines correspond to calculations carried out using the membrane bending model and minimizing the total energy in Eq. 1. Bending dramatically reduces the energy required to move ions into the center of the membrane by 12–30 kcal/mol. The membrane dipole reduces Cl^– penetration by ~20 kcal/mol over K⁺ in the non-deformable model (difference between dashed curves), but only by 2–3 kcal/mol in the membrane bending model (difference between solid curves) because ions never experience the full dipole potential in the later case (Color figure online)

When we recompute the energy profile for ion permeation through a deformable membrane with DPPC-like bilayer properties, we see that the model reproduces sharply peaked energy profiles in qualitative agreement with MD (Tepper and Voth 2006; Khavrutskii et al. 2009; Li et al. 2012) (red and blue solid lines in Fig. 3). From the snapshots in Fig. 2c, we predicted that ion residence in the head group throughout the permeation process minimizes the electrostatic barrier to permeation while incurring an elastic cost for bending the membrane. Previously, we observed this interplay between electrostatics and elastostatics when we examined the insertion of arginine-containing helices into continuum elastic bilayers (Callenberg et al. 2012). Membrane bending lowers the energetic barrier to ion permeation by over 25 kcal/mol for K⁺, revealing that the cost of bending the membrane is small relative to the electrostatic penalty of burying charge in the membrane.

Our model also stabilizes both cations and anions in the head group region at ±18 Å. Stabilization occurs because the head group dielectric is assumed to be the same as water, minimizing the electrostatic penalty, while desolvating the ions maximizes the nonpolar advantage of insertion. Another important feature of these profiles is that the energy difference between K⁺ and Cl^– is markedly reduced in the deformable model (solid) compared to the flat membrane profiles (dashed). As discussed in the last paragraph, selectivity arises from the positive dipole potential, which we model as two thin dipole sheets at the head group–hydrocarbon core interfaces. Since the ions remain largely in the head group region during penetration, they never fully cross this interface and hence never experience the full dipole potential. The fact that the ions never fully penetrate into the core of the continuum membrane is discussed in more detail in the “Discussion” section.

Permeation Barriers Increase with Increased Membrane Thickness

We next sought to examine membrane permeation in a variety of lipidic environments, which has implications for the analysis of small molecule permeability through different types of biological membranes. At present, the only systematic atomistic MD simulations exploring the influence of membrane thickness were carried out on MGuanH⁺, which is a charged analog of the arginine side chain. We use those energy profiles here to qualitatively compare with our profiles for ion penetration. We translated a K⁺ ion in 1 Å steps across membranes comparable to those used by Li et al. (2012) whose physical dimensions and material properties are listed in Table 2. The energy required to move the ion into the middle of the bilayer increases dramatically as the membrane thickness increases (Fig. 4a), which is in excellent agreement with the dependence observed in the energy profiles for MGuanH⁺ permeation, shown in the inset. Both our continuum results and the all-atom MD are in qualitative agreement with the experimental finding that ion permeability values drastically increase with bilayer thickness (Paula et al. 1996). The absolute value of the energies reported at the membrane center are different for K⁺ and MGuanH⁺, which is not surprising given their chemical differences. Also, the MGuanH⁺ profiles plateau near z = 0 Å for thinner membranes, DDPC and DLPC, which is not observed in our continuum profiles and is likely due to membrane reorganization as discussed later.

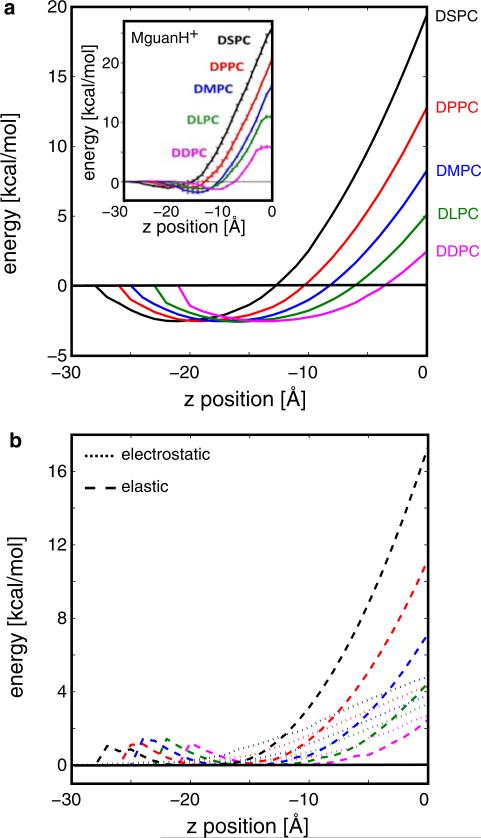
Fig. 4.

Free energy profiles for K⁺ penetration into bilayers of different thicknesses. a For all thicknesses, the ion is stabilized as it enters the head group region, but rises to a sharp-peak at the membrane center. The penetration energy increases with membrane thickness with values at the center ranging from 3 to 18 kcal/mol. The inset shows similar free energy profiles obtained from atomistic MD simulations carried out on the positively charged arginine side chain analogue, MGuanH⁺ (Li et al. 2012). The equilibrium thickness (L₀) and bending modulus (K_c) were increased to match the known properties of lipids being modeled, and values are given in Table 2. The compression modulus (K_a) was held constant since it is thought to be independent of the hydrophobic thickness. In all cases, L₀ for each lipid type is similar between the MD simulations and continuum model except for DSPC, as discussed in the “Methods” section. b Elastic (dashed) and electrostatic (dotted) energy contributions to the insertion energy values in panel a. The color scheme is the same as panel a. As the ion first enters the head group between –28 and –22 Å, depending on the lipid type, there is a small jump in the bending energy due to the bilayer bending up to meet the ion. Near the center of the bilayer, the elastic energy term dominates for thicker bilayers, but the elastic and electrostatic components are similar for thinner bilayers. The nonpolar energy term is not shown since it is relatively simple: it decreases by a set amount as the ion penetrates the head group, and then it remains flat

We also determined the individual energy contributions from the elastic, electrostatic, and nonpolar components of the model (Fig. 4b). Interestingly, while the elastic component of the free energy increases quadratically with increasing bilayer thickness, the electrostatic and nonpolar contributions depend very weakly on bilayer thickness (Fig. 4b). Likewise, only the elastic component of the free energy is affected by changes in lipid patch size (data not shown), a result that is most likely a direct consequence of our elastic treatment of the membrane. Thus, the increase in energy observed in Fig. 4a with increasing bilayer thickness is a direct consequence of the ion penetrating a longer distance to reach the center of thicker membranes.

Membrane Patch Size Influences Binding Energies

Our initial observation in Fig. 2a was that calculations on large membrane systems do not match observed deformations from MD simulations, and simply restricting the membrane size in our continuum model allowed us to accurately match results from MD (Fig. 2c). We wanted to ask the converse question; that is, do MD simulations carried out on large membranes provide qualitatively and quantitatively different answers than simulations performed on small membranes? To answer this question, we again carried out MARTINI simulations, but this time on a protein segment known to bind membranes: helix 2 from the RAH domain of T. gondii ROP5 (Reese and Boothroyd 2009; El Hajj et al. 2007). We hypothesized that the simulation of a small, known membrane binding segment would elicit a more detectable dependence on membrane patch size than the simulation of a single ion, which is true based on our CG simulations of ions (data not shown). ROP5 is a rhoptry protein secreted by the human pathogen T. gondii during infection of a host cell and is a very potent virulence factor in this organism (Reese et al. 2011; Behnke et al. 2011). Its binding to the parasitophorous vacuole membrane (PVM), which surrounds the parasite, is driven by a specific RAH domain consisting of three putative alpha-helices (Reese and Boothroyd 2009). The RAH domain is both necessary and sufficient for membrane binding, and deletion of helix 2 of the RAH domain most effectively reduces ROP5 binding to the PVM (Reese and Boothroyd 2009), leading to the hypothesis that helix 2 has the highest binding affinity to the membrane. It is postulated, but not known, that the RAH helices of ROP5 bind interfacially to the PVM (Reese and Boothroyd 2009).

The binding energy for ROP5 helix 2 is reported in Fig. 5a for both a small membrane patch of 128 lipids (red curve) and a large membrane patch with 512 lipids (black curve). As expected based on its amphipathic character (see bottom of Fig. 5 for sequence), the helix is most stable at the membrane–water interface (–20 Å). It adopts a conformation with the hydrophobic face buried in the membrane core and the arginine residues exposed to water, regardless of lipid patch size (snapshots not shown). This configuration is consistent with what has been proposed for the ROP5 RAH domain helices (Reese and Boothroyd 2009). Interestingly, the free energy curves are not identical for these two systems. While the energy barriers at the center of the bilayer are nearly identical, the shape of the PMFs are quite different, leading to different estimates of the interfacial binding energy, –8 versus –13 kcal/mol, for small and large patches, respectively (Fig. 5a). We observe that when a small number of lipids are simulated with the helix restrained at ±30 Å from the membrane center, large scale membrane bending does not occur, and the helix remains largely solvated in water (Fig. 5b). The distance restraint prevents the helix from getting closer to the membrane and going interfacial, while the small size of the membrane patch makes it prohibitively difficult to bend and fully contact the helix. However, simulations of the same situation with the larger patch size show a large scale deformation of the bilayer that embeds the hydrophobic residues in the membrane (Fig. 5c). We performed three additional simulations with different random seeds for each system and found this difference in membrane behavior was consistent; the large patch always bent, while the smaller patch never exhibited large scale bending during the length of the entire simulation. The behavior is in exact agreement with our continuum model shown in Fig. 2a in which the membrane undergoes large scale deformations to minimize the energy of the system. In small patch size simulations, it is not possible for the membrane to undergo such large scale deformations, and the results are necessarily higher energy compared to the larger systems.

Discussion

Our continuum model produces shapes (Fig. 2b, c) and energetics (Fig. 4a) that are qualitatively consistent with fully atomistic and coarse-grained simulations of ion penetration into membranes. This connection is encouraging since ion, ionophore and peptide permeation across membranes is of extreme interest from both a basic biological stand point and a pharmacological perspective. Computational approaches to understanding these phenomena are needed to gain atomic level insight and provide predictive power. One advantage of a continuum model is that the reduction of the system size, by treating the membrane and water as a continuum, leads to energy calculations that are thousands of times faster than corresponding atomistic simulations (Callenberg et al. 2012). Another benefit of our approach is that it is quite easy to determine the contribution of each energy term in the model to the total energy. The decomposition in Fig. 4b shows that the dependence of insertion energy on membrane thickness is largely described by the increase in elastic energy required to bend thicker membranes. Such a decomposition can be difficult for atomistic simulations because it requires averaging over many configurations and macroscopic energies such as elasticity are not easily computed.

Calculations in Fig. 4a show that both cations and anions are stabilized in the head group region, which is in agreement with recent experiments (Knecht and Klasczyk 2013). This property is not captured by most all-atom MD simulations (Tepper and Voth 2006; Khavrutskii et al. 2009), but it has been reported that Cl^– binds to the head group using the GROMACS force field, albeit more weakly than Na⁺ (Pandit et al. 2003). Furthermore, it has been argued that stabilization of anions in the PC head group may not be possible with classic MD, but may require a polarizable force field (Knecht and Klasczyk 2013; Woolf 2013). Such calculations are even more computationally demanding than classic all-atom MD, again highlighting the usefulness of our continuum approach, which already reproduces the correct anion/cation stabilization, and can be further tuned to match experiment. Additionally, our model suggests that ions that have moved into the bilayer do not sense the full strength of the membrane dipole potential because they remain in the head group region. This was also observed by Vorobyov and colleagues who used all-atom MD to show a similar result for MGuanH⁺ permeation (Vorobyov et al. 2010).

Unfortunately, our model does not lend much insight into the nature of the transition state for passive ion permeation. The presence of the ion induces deformations in the membrane shape, which supports the ion-induced defect model (Li et al. 2012). However, when the ion is at the center of the membrane, symmetry is broken depending on which side the ion originated (Fig. 6). The left hand snapshot shows the ion at the center of the membrane, where it still remains in the lower head group, separated from the upper leaflet by the hydrophobic core. Moving the ion 1 Å farther produces a snap through bifurcation in which the ion becomes localized in the upper leaflet (right). Thus, our model does not capture the configurations in which the ion is either exposed to the hydrophobic core (solubility-diffusion model) or in which a pore defect is created through the bilayer (transient pore formation model). Pore formation involves a topological change in the membrane, which is not possible in our current elastic energy formulation. As we continue to formulate more accurate continuum models of the membrane, we may be able to incorporate topological changes, which would allow us to return to the question of permeation and predicting permeabilities with our model.

Fig. 6.

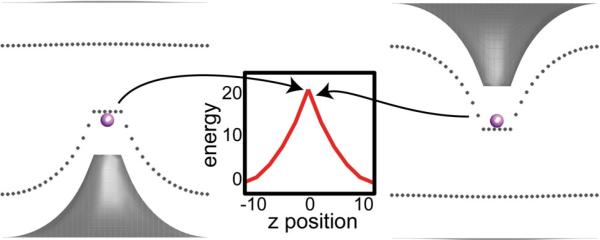
The continuum model fails to reproduce the transition state for ion permeation. Membrane configurations from the continuum model for a K⁺ at the center of the membrane (left) and just to the right of the membrane center (right). The relevant portion of the energy profile from Fig. 3 is shown in the middle

Perhaps our most important observation is that computed energy profiles for ion and peptide association with the membrane depend on the size of the membrane patch. Only by matching lipid patch size could we achieve consistency between continuum and coarse-grained models. Our continuum model shows that if the membrane patch is large enough, low energy, long wavelength deformations in the bilayer allow for protein–membrane interactions over long distances (Callenberg et al. 2012), and this is highlighted in our qualitative, coarse grained simulations of ROP5 (Fig. 5a). The underlying free energy profiles are quite different for the small patch and the large patch, leading to considerable variation in the predicted membrane binding energies (–13 vs. –8 kcal/mol, respectively). Our continuum model explains why the larger patch size is able to interact with the peptide held farther away from the membrane center, but it does not explain why the small patch binds so much tighter. We hypothesize that the peptide suppresses entropic fluctuations in the large membrane, which are not present in the small patch, but we have no calculations to support this notion. Moreover, it is not clear which simulation setup is most appropriate for comparing with experimental binding energy values. One way to remove the dependence on patch size is to define the membrane COM using a small number of lipid molecules within a cutoff radius of the permeating molecule, as was done by Bennett and Tieleman (2011) for all-atom simulations on MGuanH⁺. This definition selects higher energy configurations, but it also uncouples the long wavelength behavior of the membrane to the local changes that accompany permeation. Nonetheless, while the application of a restraining potential to a large bilayer represents one way to overcome size differences among models, it is also prohibitive for the study of large scale membrane deformations. Importantly, our results complement the recent findings of the Patel group, which used all-atom simulations to demonstrate that MGuanH⁺ permeation through a large lipid patch incurs a small energetic cost relative to permeation through a small patch (Hu et al. 2013)—exactly what we found for K⁺ in the “Continuum Membrane Models Match Molecular Simulation” section.

The idea of membrane patch size as a determinant of deformation energy has implications in other biological contexts as well. In one study, continuum and coarse-grained models of membrane fusion pores predicted nearly identical membrane configurations and curvatures when the lateral dimensions of the simulated bilayers were matched in both systems (Yoo et al. 2013). Increasing patch size dramatically changed the shape of bowing during energy minimization of the continuum model, suggesting that the membrane area available during fusion directly affects the energetics of pore formation. With this in mind, the importance of patch size may have been overlooked in previous studies of membrane inclusion induced deformations. In one study, the authors concluded that a range of inclusion radii and monolayer thicknesses led to only small changes in the induced membrane curvature during the insertion of a cylinder into a continuum membrane (Campelo et al. 2008). However, the significance of this observation was assessed for only a single lateral dimension of the membrane. For other patch sizes, our data suggest that as dimensions increase, strain will spread out over the lateral dimensions of the membrane, reducing the elastic energy and changing the curvature of the deformation. Similarly, the size of the membrane patch available for bending could alter, for example, the affinity of BAR domain proteins with the membrane and induce curvature that aids fusion pore formation (Zimmerberg and Kozlov 2005).

While our continuum model accurately describes large scale deformations, difficult to capture via molecular simulations, it does not capture small length scale changes at the single lipid level. Kim et al. (2012) recently described the membrane deformation profile around the membrane spanning antibiotic peptide gramicidin A. They showed that the membrane surface undergoes non-monotonic changes in height in the first few lipid shells surrounding the peptide, and our experience leads us to agree with their conclusion that such solutions are not possible given the class of elastic models we are using. The impact of these undulations on membrane–protein function and system energetics must be further explored, and it may take more sophisticated continuum models to describe membrane structure at this level of detail. Given these considerations, we believe that a multi-pronged computational approach to membrane permeation is needed to describe both large scale deformations with continuum models and small length scale interactions with all-atom MD. For instance, the membrane geometry could first be optimized around a protein with the continuum model and then the shape could subsequently be used as a constraint for packing all-atom lipids into the system. The Weinstein Lab has already implemented a method that combines both all-atom MD and continuum methods to better understand the energetics of their membrane–protein systems (Mondal et al. 2011). Similarly, the Jacobson Laboratory has created a hybrid approach that uses molecular simulation together with simple solubility-diffusion models through flat membranes to rapidly assess neutral cyclic peptide and small molecule membrane permeability (Rezai et al. 2006a, b; Leung et al. 2012). The incorporation of our membrane bending model into this latter framework may make it possible to explore the permeation of charged and highly polar molecules and peptides, offering opportunities for high-throughput design and screening of novel membrane permeable compounds.