Label Free Cell-Tracking and Division Detection Based on 2D Time-Lapse Images For Lineage Analysis of Early Embryo Development

Abstract

In this paper we report a database and a series of techniques related to the problem of tracking cells, and detecting their divisions, in time-lapse movies of mammalian embryos. Our contributions are: (1) a method for counting embryos in a well, and cropping each individual embryo across frames, to create individual movies for cell tracking; (2) a semi-automated method for cell tracking that works up to the 8-cell stage, along with a software implementation available to the public (this software was used to build the reported database); (3) an algorithm for automatic tracking up to the 4-cell stage, based on histograms of mirror symmetry coefficients captured using wavelets; (4) a cell-tracking database containing 100 annotated examples of mammalian embryos up to the 8-cell stage; (5) statistical analysis of various timing distributions obtained from those examples.

1. Introduction

In recent years, a number of studies related to time-lapse imaging of early embryos have been published (Payne et al. (1997), Hardarson et al. (2002), Mio and Maeda (2008), Wong et al. (2010), Nakahara et al. (2010), Meseguer et al. (2011), Cicconet et al. (2013), Chavez et al. (2012), Wong et al. (2013), Conaghan et al. (2013)).

For human in vitro fertilized (IVF) embryos, certain measurements relating to cell division timing have been shown to correlate with embryonic viability in a clinical setting (Wong et al. (2010), Meseguer et al. (2011), Wong et al. (2013), Conaghan et al. (2013)). The relevance of cell cycle timing statistics stems from the fact that embryonic development depends on the proper coordination of many cellular events in space and time. In model organisms, the contribution of different genes to early developmental events can be studied by silencing gene activity using RNA interference (RNAi) and analyzing any resulting changes in cellular behavior (including cell cycle timing) in early embryos (e.g. Sonnichsen et al. (2005)).

These applications motivated us to study the problem of cell tracking and division detection in time-lapse images of early mouse embryos. The input is a series of images of a well containing about ten embryos, from the first cell until after the blastocyst cavitation phase. In this paper, we report algorithms aiming to:

1. detect, in the first frame, the locations of the embryos, track each embryo for the duration of the movie, and create cropped movies displaying one particular embryo in the center of the frames;

2. for each embryo, track individual cells, and detect when they divide (up to the 8-cell stage¹).

It is possible to capture timing information without tracking cells. In Meseguer et al. (2011), for instance, the sum of absolute differences between pixels for consecutive frames is used to detect cell division events. This approach allows the duration of first and second generation cells to be evaluated, under the assumption that all 2nd-generation cells divide before any 3rd-generation cell does. However, evaluating the timing of 3rd generation cells requires knowledge of which 2nd-generation cell was their progenitor². Thus, we are interested in building a lineage tree of cells (Figure 1), which requires cell tracking in addition to detection of cell division times.As a result, we can measure individual cell duration times as well as gather information about the synchronicity of divisions for cells of the same generation.’

Figure 1.

Our main goal is to capture spatio-temporal information related to the lineage tree of each embryo, rather than just the times when a cell division event occurs. This allows gathering statistics of cell duration for different generations of cells, as well as measuring synchronicity of cell divisions for cells that are “siblings.”

In this spirit, our approach resembles more that of Wong et al. (2010), in which cell tracking is considered. Our method differs in two main directions. First, we do not use a brute force approach for the automated tracker³. Rather, we analyze cell division based on circularity information, using histograms of centers that are captured using a bank of Morlet wavelets (Bruna and Mallat (2012)). Second, our semi-automated tracker works for one additional generation, allowing timing analysis up to the 8-cell stage.

Our contributions are:

1. a method for counting embryos in a well, and cropping each individual embryo across frames, to create individual movies for cell tracking – Subsection 3.1;

2. a semi-automated method for cell tracking that works up to the 8-cell stage, along with a software implementation available to the public – Subsection 3.2;

3. an algorithm for automatic tracking up to the 4-cell stage, based on histograms of mirror symmetry coefficients captured using wavelets – Subsection 3.3;

4. a cell-tracking database containing 100 annotated examples of mouse embryos up to the 8-cell stage, to be publicly available for other researchers – Section 4;

5. statistical analysis of various timing distributions obtained from those examples – Section 5.

Regarding item 5 above, more specifically we provide: (1) statistics of cell duration for 1st-, 2nd- and 3rd-generation cells; (2) statistics of synchronicity of division for 2nd- and 3rd- generation cells; (3) statistics of cell radii per generation, and total volume of the embryo, assuming the cells are spheres of the measured radii. In summary, our measurements show that for mouse embryos, under standard laboratory conditions:

1. 1st-generation cells divide about 1h:38min after pronuclear envelope breakdown⁴;

2. The duration of 2nd-generation cells is about 19h:29min;

3. The duration of 3rd-generation cells is about 11h:26min;

4. 2nd-generation sibling cells divide about 42min apart in time, and 3rd-generation siblings about 35min apart;

5. The radii of 1st-, 2nd-, and 3rd-generation cells are about 36.09μm, 27.41μm, and 21.14μm, respectively

6. There is an apparent reduction in the total volume of cells up to the 8-cell stage: in the 2nd generation it is 88% that of the 1st generation, and total volume is 92% in the 3rd generation relative to the 2nd generation.

The last observation was surprising, since intuitively we expected total cell volume to be conserved in each generation. This apparent reduction in volume most likely arises from changes in osmotic balance during cell culture (since cells adjust their volume in response to the tonicity of their environment), but could in part reflect the depletion of stored maternal products, which are metabolized throughout embryogenesis both to produce energy for cellular processes (e.g. cell division) and to synthesize new cellular components (e.g. membrane, chromatin).

Although our methods relate to a specific problem in biology, the technique we introduce for event detection in a sequence of frames (Subsection 3.3) is of general interest in Computer Vision. The algorithm consists of monitoring the output of a shape descriptor (in our case, a descriptor of circularity), looking for points in the time-series where the evidence for the existence of that shape reduces drastically. This idea can be used in other tracking scenarios to infer time points at which a target object disappears from the field of view. In our case the target object is a cell, but it could in principle be any shape (e.g., face, car, hand), as long as its descriptor is relatively invariant between successive frames⁵.

Furthermore, by making our cell-tracking database available, we not only facilitate reproducibility, but we also contribute to other researchers working on techniques such as tracking and shape analysis. We are already using the database ourselves to test novel methods in basic Computer Vision problems such as circle and ellipse detection (Cicconet et al. (2014)).

On Related Research

While the literature on cell tracking for mammalian embryos is relatively small, a large body of publications is available for cell tracking in general, dealing with model organisms such as zebrafish, Drosophila, and C. elegans (e.g., Bao et al. (2006), Hamahashi et al. (2007), Melani et al. (2007), Castro-Gonzlez et al. (2010)), Mikut et al. (2013), Bellaiche et al. (2012), Kang et al. (2012)).

Many of these techniques require “labeling” cells (that is, marking them with dyes or fluorophores) and/or reconstructing 3D geometry using stacks of images in different focal planes (z-stacks). The methods discussed in this paper are “label-free” and are designed for images that are grayscale and bi-dimensional.

In terms of algorithms, the main difference between this paper and our previous work (Cicconet et al. (2013)) is in how we handle cell division. Previously, we looked at pixel variances at the image and cell levels, and we computed likelihoods of cell presence from the accumulator space of a wavelet-based circular Hough transform (Cicconet et al. (2013)). In Subsection 3.2 we report a strategy in which human interaction determines the frames of cell division with 100 percent accuracy. In Subsection 3.3 we introduce an improved automatic method for division detection, based on mirror symmetry between pairs of pixels with tangents.

Technically, the methods of this paper aim at the same problem and similar input data as discussed in Wong et al. (2010) and Meseguer et al. (2011). Wong et al. (2010) also perform cell tracking by looking at cell boundaries, but use particle filters and model cells as ellipses, whereas we use Dynamic Programming and model cells as circles. Also, in Wong et al. (2010) division detection is embodied in the particle filter, instead of being an independent module. Meseguer et al. (2011) do not perform cell tracking, and division detection happens globally (by looking at the entire frame), not at the individual level of the cells.

2. Materials and Methods

Mouse embryos were collected from 4-6 week old superovulated CB6F1 female mice (BALB/c × C57BL/6; Charles River, Wilmington, MA). For RNAi, zygotes at the pronuclear stage (i.e. prior to fusion of the paternal and maternal genetic material in the first cell cycle) were injected with 400-700bp long double-stranded RNA corresponding to target gene sequences. Control (untreated or mock-injected) and RNAi-treated zygotes were cultured in a constant environment of 37°C, 5% CO₂, and 95% humidity for up to 120 hours (5 days), during which time images were captured every 420s (at 7 minute intervals). Under these conditions, control embryos consistently achieved > 95% development to the blastocyst stage.

Time-lapse recordings were collected using an Eclipse TI inverted microscope (Nikon Instruments, Inc., NY) with Hoffman modulation optics, a heated stage-top incubator (Tokai Hit Co., Ltd., Japan) with an independent air circulation and heating Air-Therm ATX system (WPI, Inc., FL) mounted on an XYZ motorized stage (Nikon), and NIS Elements imaging software (Nikon) running on a Dell Precision Workstation T7400.

3. Computational Analysis

3.1. Cropping

The input images, of size 2784 by 2080 pixels, are as shown in Figure 2 (a). As we want to analyze each embryo individually, a cropping step is necessary. The first phase of processing consists of automatically locating the centers of the embryos in the first frame of the time-lapse sequence. This is sometimes referred to as a “segmentation” problem in the literature. There are many possible solution techniques for segmenting a circular shape (every embryo is a singular, nearly circular cell, in the first frame), based on level sets (Li et al. (2010)), sliding-band filters (Quelhas et al. (2010)), Hough transforms (Cicconet et al. (2013)), mirror symmetry coefficients (Cicconet et al. (2014)), and a number of other methods. Since we want not only to locate embryos in the first frame, but also to track them (that is, their cells as a whole) for the (almost) entire video, we opted for a method based on texture rather than shape.

Figure 2.

To locate the embryos in a well, the input image (a) is processed for high local contrast detection (b). This “contrast” image is convolved with a Gaussian. In the output (c), we look for local maxima, which provide the locations (and counting) of the embryos (d).

There are three steps. First we generate a “texture” image, which we shall call K (Figure 2 (b)), of the same size as the input image I. The value K_i,j in each pixel of location (i, j) in K is defined by looking at a neighborhood 2 × 2 of (i, j) (which we call W^i,j). In the second step, we convolve K with a Gaussian, producing $\stackrel{‒}{K}$, which highlights clusters of areas of high contrast in K (Figure 2 (c)). Finally, we search for local maxima in $\stackrel{‒}{K}$, which correspond to the centers of cells. Details are as follows.

Let I be an input image. We first reduce the size of I (by resizing the edges to a quarter of the originals). We then process I for local contrast enhancement with adaptive histogram equalization, producing $\stackrel{‒}{I}$, of size m rows by n columns. Let J, of size m × n, be defined as

$$J_{2(i-1)+1,2(j-1)+1}=\max W^{i,j}-\min W^{i,j}$$

for $i=1,\dots ,\frac{m}{2},j=1,\dots ,\frac{n}{2}$, and J_. = 0 otherwise, where

$$W^{i,j}={\stackrel{‒}{I}}_{2(i-1)+1\cdots 2(i-1)+2,2(j-1)+1\cdots 2(j-1)+2}$$

are 2 × 2 block matrices⁶. Define K_m×n, such that

$$\begin{array}{cc}\hfill K_{i,j}& =1\text{if}{J}_{i,j}>\frac{1}{10}\max J,\hfill \\ \hfill K_{i,j}& =0,\text{otherwise},\hfill \end{array}$$

for i = 1, … , m, j = 1, … , n.

K indicates pixels where the contrast in $\stackrel{‒}{I}$ is high (an example is shown in Figure 2 (b)). Convolving K with a Gaussian filter (of standard deviation σ = 20), we obtain $\stackrel{‒}{K}$ – as seen in Figure 2 (c) – in which the local maxima are located approximately around the centers of the embryo cells. Finding these allows counting and labeling of the embryos (Figure 2 (d)).

Afterwards, each embryo is tracked along the remaining frames. Supposing ${\stackrel{‒}{K}}_t$ is the matrix $\stackrel{‒}{K}$ as defined above for frame t, the location of an embryo at frame t is determined by looking for a local maximum in ${\stackrel{‒}{K}}_t$ nearby its location in frame t − 1. An individualized movie of each embryo is then generated by cropping a region of interest around the tracked path for it, in the images of full resolution (as in I defined above).

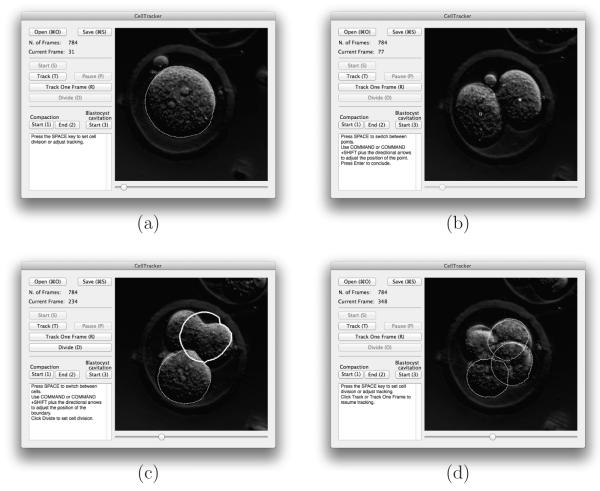
The size of each cropped embryo frame is about 480 by 480 pixels, and the first cells have radii of approximately 110 pixels. Some examples are shown in the screenshots of Figure 3.

Figure 3.

Some screenshots of CellTracker in different phases. (a) Tracking the first cell. (b) Setting the initial points of second generation cells right after the first cell divides. (c) Highlighting which 2nd-generation cell is to divide. (d) Tracking three 3rd-generation cells.

3.2. Semi-Automated Cell Tracking

There are two main challenges in studying the developmental trajectory of early embryos: (1) tracking cells, and (2) detecting the times of division for individual cells. Both problems increase in complexity as time advances and the number of cells increases, but the second problem is significantly more difficult (in part because it requires the solution of the first). Any method that detects divisions independent of tracking would not permit discovering which cell is dividing, and therefore would not allow building the timing-tree of Figure 1 beyond the 4-cell stage.

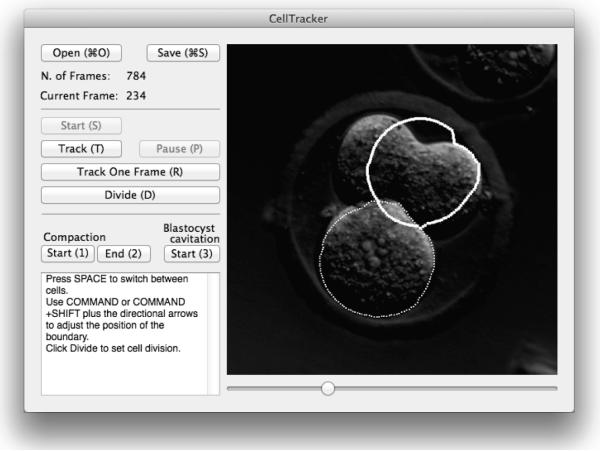
We developed a semi-automated method that circumvents the problem of division detection by handing it to the user, while the system performs only cell tracking. The user can also correct the trajectory of a particular cell when the tracking algorithm misses it. The software, called CellTracker, allows the “scoring” of an embryo in about 2 minutes for a trained user. An average embryo’s video contains about 350 frames. Some screenshots are shown in Figure 3. Figure 4 provides a larger version for GUI readability.

Figure 4.

CellTracker screenshot (larger version of Figure 3 (c)).

Before getting into the user-interaction aspects of the tool, we briefly describe how cell tracking is performed.

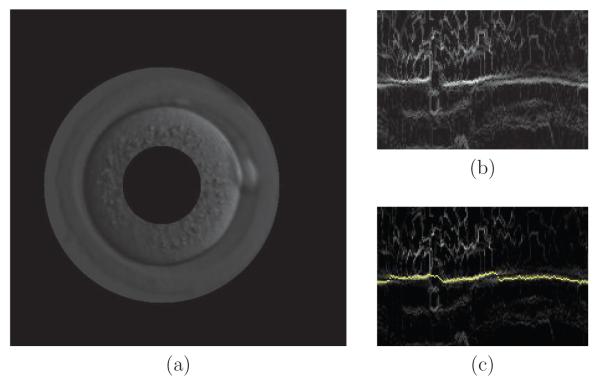
The idea is to track the boundary of the cell, which is nearly circular, using Dynamic Programming. This approach was introduced in Geiger et al. (1995) and used for cell tracking in our previous work Cicconet et al. (2013). Roughly speaking, a “tubular neighborhood” around the boundary of the circle estimated to fit the current cell is mapped into a rectangle, and the path of minimal cost from left to right in such rectangle is searched for. Figure 5 illustrates this.

Figure 5.

For each frame, there is an initial guess for the circle that better approximates the boundary of each cell. Following this circle around, a band of the original image is taken (a) and its gradient mapped to a rectangular image (b). The yellow line in (c) shows the solution by Dynamic Programming that fits the boundary.

CellTracker works on folders containing frames in the tiff or png image formats. It can track cells up to the third generation, and has buttons to register the frames when embryo compaction starts and ends, as well as the frame when blastocyst cavitation starts (compaction and cavitation are important events in early embryo development).

In the first frame, the user sets the approximate location of the center of the first cell. The software uses fixed parameters for the estimated radii of cells in the first three generations; thus, for the initial cell and all subsequent division events, setting the estimated radius of the daughter cells is not necessary. After tracking each frame, the estimated radius of each cell is automatically updated.

Once the location of any cell center is set, tracking can be performed. The software enters a loop and continues until the last frame is reached or until the user instructs it to pause. If cells are properly tracked, the user waits until the tracking passes a frame when cell division occurs, then pauses and navigates back to that frame. At this point, the user toggles among the current cells and selects the one that is to divide. This either triggers initialization of the centers of the two daughter cells (for 1st and 2nd generation cell divisions) or terminates tracking (for third generation divisions). At any point, the user can pause and reset the boundary location of any tracked cell, in case the boundary was not followed properly, i.e. the software “missed” the cell. Some screenshots taken during the tracking of an embryo are shown in Figure 3.

A number of statistical results gathered by CellTracker that relate to cell duration and size are reported in Section 5. While CellTracker’s main purpose is to record temporal information, it also saves the path of each cell, from birth to division, as well as its estimated radius. This allows computing additional statistics, such as the estimated total volume of cells in the embryo. The cell paths are important for the construction of the cell tracking database, which we will discuss in Section 4.

A video demonstrating the usage of CellTracker is available as supplementary material. CellTracker is available for download at http://celltracking.bio.nyu.edu.

3.3. Automated Cell Tracking

CellTracker works very robustly up to the 8-cell stage. Although it has limitations in cases where the overlap between two cells is high (their boundaries visually coincide), even in those situations it can be used to record timing information, provided the overlapping cells are “siblings” (that is, they come from the same dividing cell). Still, as a semi-automated method, it requires extensive human supervision.

In this section we report a fully automated method that works up to the 4-cell stage. Like in CellTracker, the algorithm uses Dynamic Programming for cell boundary tracking. To detect division events, it relies on circularity information, computed using a measurement of mirror symmetry (Geiger et al., 2003; Cicconet et al., 2014) between pairs of pixels with their tangents, captured using Morlet wavelet filters (Bruna and Mallat, 2012).

The algorithm works “offline”, in the sense that when a particular frame is analyzed, information from past and future frames are taken into account. A frame is visited at least g + 1 times, where g is the generation of the “youngest” cell visible in the frame.

Broadly speaking, the algorithm has three main steps:

1. Frames are pre-processed for the computation of centers histograms, and their clusters.

2. Frames are analyzed sequentially for cell division detection.

3. The locations of the centers of the daughter cells in the frame of division are initialized.

We now describe these tasks in detail.

3.3.1. Centers Histogram

We model cells as nearly circular shapes. This provides a simpler implementation in comparison to more accurate models – where cells are ellipsoids, for instance. Still, our method is robust to deviations from circularity.

Our division detection algorithm and the initial locations of the daughter cells – in the frame right after a division is detected – are based on what we call the centers histogram.

Let I_m×n be an image (corresponding to a particular frame of the cropped embryo), and J its gradient:

$$J(i,j)=\Vert \nabla I(i,j)\Vert ,\forall i=1,\dots ,m,j=1,\dots ,n$$

Using a bank of Morlet wavelet filters, we capture a list of pairs (point, slope) from J, that is, a list of points with associated tangents (modulus π, for we are only interested in the slope, not the direction). We name this list as

$$L=\left\{\right(p\left(t\right),a\left(t\right)),t=1,\dots ,T\},$$ (1)

where, for each t, p(t) is a point of high maximum wavelet response, and a(t) is the angle of the wavelet of maximum response at that point.

For simplicity, let us call every pair (p(t), a(t)) a rod⁷, represented as ρ(t). Next, we go over every pair ρ(t₁), ρ(t₂) in L and test them for mirror symmetry. The concept of mirror symmetry is defined with details in Cicconet et al. (2014) – intuitively, two rods ρ(t₁) and ρ(t₂) are mirror symmetric if the “reflection” of ρ(t₁) by a mirror set at the bisector of the line connecting p(t₁) and p(t₂) coincides with ρ(t₂).

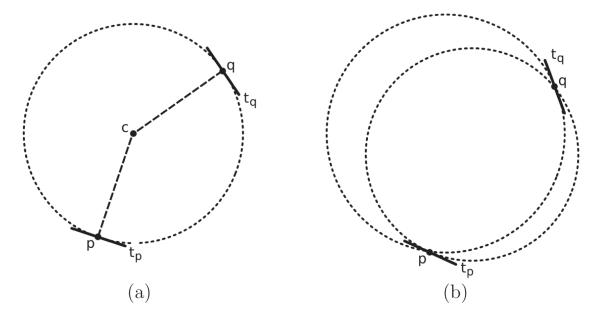
It turns out that, if two rods ρ(t₁) and ρ(t₂) are mirror symmetric, then they uniquely define a circle, with center c_t1,t2 and radius r_t1,t2, whose boundary crosses p(t₁) and p(t₂), with tangents parallel to a(t₁) and a(t₂), respectively. Figure 6 (a) illustrates a circle defined by a pair of mirror-symmetric rods.

Figure 6.

Circle detection using mirror symmetry. (a) When rods (p, t_p) and (q, t_q) are mirror symmetric, they uniquely define a circle with tangents parallel to t_p and t_q. The centers of circles like this provide histograms that are used for cell-division detection. (b) It’s not possible to draw a circle fitting rods that are not mirror symmetric, since one of the tangents doesn’t match.

Let

$$C=\left\{\right(c_k,r_k),k=1,\dots ,K\}$$ (2)

be the set of pairs (center, radius) defined by mirror-symmetric rods in L. Let r_g1, r_g2, and r_g3 be the estimated radii for cells of generations 1, 2, and 3, respectively, and w a “window” parameter (we use w = 5). We define the centers histogram H_m×n×3 as follows.

$$H(i,j,h)=\#\{k\in \{1,\dots ,K\}:c_k=(i,j),r_{g_h}-w\le r_k\le r_{g_h}+w)\},$$ (3)

for c_k and r_k as defined in Equation 2, # the “number of elements” operator, and h = 1, 2, 3.

For the next phase of the algorithm, we will also need a set of “local maxima” in every dimension of H: (at most) 1 local maximum for H(., ., 1), (at most) 2 for H(., ., 2), and (at most) 4 for H(., ., 3). The rationale is this: H(., ., 1) accumulates the evidence that there is a circle of radius r_g1 in the image; thus, in frames corresponding to the first cell, we expect H(., ., 1) to have a clear cluster around the center of the cell; when the first cell divides, H(., ., 2) – which accumulates evidence for circles of radius r_g2 – is expected to have (two) clusters around the centers of the two daughter cells; and so forth.

We quoted the term local maxima in the previous paragraph because H(., ., h) is not smooth, and therefore presents many local maxima around the corresponding cell centers. To cope with this, we convolve H(., ., h) with a Gaussian kernel (of σ = 5), producing $\stackrel{‒}{H}(.,.,h)$, and locate the local maxima in $\stackrel{‒}{H}(.,.,h)$ instead. We define

$$M_h=\left\{\right(x,y):(x,y\left)\text{one of the}{n}_h\text{largest local maxima in}\stackrel{‒}{H}\right(.,.,h\left)\right\},$$ (4)

where n_h = 1, 2, 4 for h = 1, 2, 3, respectively.

3.3.2. Division Detection

Our division detection method is based on the number of votes for a circle of a particular radius in a neighborhood of the estimated center of that circle, such center given by the tracking module.

Let f₁ and f₂ be frame indices for which cells of generation 1 and 2 are expected to have divided already. That is: it is known that the first cell usually divides around frame 50, so we chose f₁ > 50 (in our implementation we set f₁ = 100). Second generation cells are expected to divide around frame 220, so we define f₂ = 300. (f₁ and f₂ should be such that, taking the variances of division times into account, the first generation cells are expected to divide in frames before f₁, and second generation cells before f₂⁸.

The tracking method then scans the frames 3 times, as depicted in Figure 7. The first scan extends from frame 1 to frame f₁, aiming to track the trajectory of the first cell and detect the frame t₁ of the first cell division. The second scan extends from frame t₁ + 1 to frame f₂; it aims to track the trajectories of the two 2nd-generation cells and to detect frames t₂ and t₃, corresponding to the second and third divisions, respectively. While this is sufficient to obtain division times up to the 4-cell stage, we perform a third scan, extending from frame t₂ + 1 to frame f₂, in order to verify if the 3rd generation cells are tracked properly (the second scan only tracks 2nd generation cells).

Figure 7.

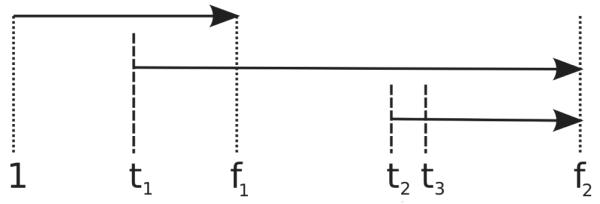
Pipeline of the tracking algorithm. The first run is for detecting the first division time (t₁). The division times of second generation cells (t₂ and t₃) are searched for in the second run. One additional pass is performed for debugging/visualization purposes.

We now explain how the events curve for the detection of the first division is computed. The procedure for the other divisions is similar.

During the first run, we compute a path of centers

$$P=\{c_t,t=1,\dots ,f_1\},$$ (5)

given by the boundary-tracking module. In this run the tracking is performed with settings for a 1st-generation cell, and they are not changed when the cell divides. What happens in terms of boundary tracking is that the method tends to fit either one of the daughter cells or a blob of cells after division. Regardless, what is important is that, in a few frames after division, P follows an estimated trajectory for the center of the cell as if it had not divided.

Now, for a frame of index t, let S_t be the square block of edge r_g1/2, centered at c_t, in the histogram $\stackrel{‒}{H}(.,.,1)$ for that frame. (r_g1, we recall, is the estimated radius of a 1st-generation cell.) We define the events curve E = {e₁, … , e_f1} for first division detection by setting

$$e_t=\sum _{i,j=1}^{r_{g_1}∕2}{S}_{t_{i,j}},\forall t=1,\dots ,f_1.$$ (6)

That is, e_t is the sum of the elements in S_t. We also refer to E as the “likelihood” curve – as in Figure 9 – since it corresponds to the likelihood of a circle of a particular radius being in each frame. Figure 8 shows cropped examples of $\stackrel{‒}{H}(.,.,1)$ and $\stackrel{‒}{H}(.,.,2)$ around the frame centers, for frames around cell divisions. Figure 9 shows some examples of events curves.

Figure 9.

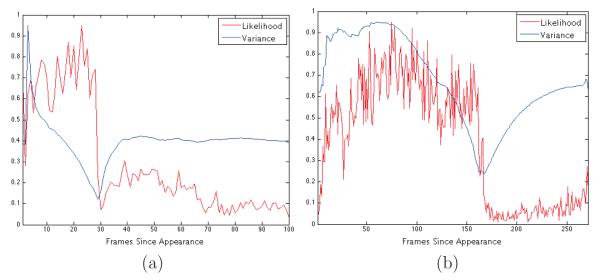
Event detection curves for division detection in first (a) and second (b) generation cells. The point of global minimum in a variance curve provides the point of division.

Figure 8.

Sequences of $\stackrel{‒}{H}(.,.,1)$ and $\stackrel{‒}{H}(.,.,2)$ (cropped around the frame centers), for frames around cell divisions. Notice how the histograms change considerably when divisions occur.

The events curve is, ideally, a two-step piecewise constant function, and detecting the division frame amounts precisely to finding the point where such a function changes values. (While we are only interested in the division point, below we also include the computation of the piecewise function, to clarify the intuition behind the method.)

The frame of division is the global minimum of a cost function {α(t), t = 1, …, f₁}, computed as follows. For each t = 2, …, f₁, split the {set E in two segments, $E_t^{-}=\{e_1,\dots ,e_{t-1}\}$ and $E_t^{+}=\{e_t,\dots ,e_{f_1}\}$, and define α(t) = variance(E⁻) + variance(E⁺). For completeness, define α(1) = α(2). The frame of division will be $\widehat{t}=\arg \min \alpha \left(t\right)$, and the two-step piecewise constant function ϕ that best fits E is

$$\varphi \left(t\right)=\mathit{mean}\left(E_{\widehat{t}}^{-}\right)\text{for}t=1,\dots ,\widehat{j}-1,\text{and}$$ (7)

$$\varphi \left(t\right)=\mathit{mean}\left(E_{\widehat{t}}^{+}\right)\text{for}t=\widehat{j},\dots ,n.$$ (8)

Figure 9 shows some examples of events (likelihood) curves and corresponding cost (variance) functions, scaled to fit in the same field of view.

3.3.3. Initializing Daughter Cell Locations

Here we make use of the local maxima stored in M_h (Equation 4). To initialize the positions of the two cells after the 1st-generation cell divides, we look at the points in the sets M₂ corresponding to n frames following the frame of division (including the frame of division). In general, the two daughter cells do not move too much in their initial frames. Therefore, if n is sufficiently small, the aggregate set of local maxima from the n sets M₂ just mentioned should have two well-localized clusters, close to the approximate center of the mother cell before division. The centroids of such clusters – which we compute using the k-means algorithm – provide the initial positions for the daughter cells. We use n = 6 in our implementation.

4. Cell-Tracking Database

We selected 100 Control examples, scored with CellTracker, for a cell-tracking movie database.

The database contains for each video: (1) the uncompressed frames, up to the 10th frame after the appearance of the 8th cell; (2) a text file with the trajectories of all the cells, from appearance to division (for cells of generations 1 to 3), where a trajectory is a sequence of pairs (center, radius); (3) a movie file showing the trajectories of the cells – examples of frames are shown in Figure 10.

Figure 10.

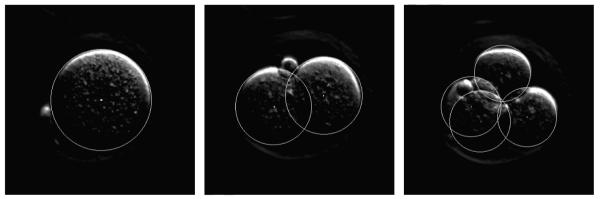
Some frames of a video in the cell-tracking database.

We are making these examples available so that other Computer Vision and Image Analysis researchers have access to ground-truth data for the development of cell-tracking and division detection algorithms. The corresponding webpage will keep track of reported performance results, starting from the ones obtained with the techniques described in this paper.

The cell-tracking database is available at http://celltracking.bio.nyu.edu.

5. Results

In this section we report performance results for the cell counting method described in Subsection 3.1 and the automated tracking algorithm of Subsection 3.3. We also give a few examples of the types of data analysis that can be conducted based on information gathered with CellTracker (Subsection 3.2).

5.1. Counting Embryos

Our method for cropping each embryo’s trajectory in the well (to create individual time-lapse movies) performs embryo counting in the first step. Since at that point each embryo consists of one cell only, the algorithm can be evaluated in terms of its performance for counting cells.

We evaluated the performance of cell counting using 112 images similar to the one shown in Figure 2(a), comprising a total of 1442 embryos. The recall and precision rates were 0.9979 and 0.9993, respectively. For the same dataset, the state-of-the-art method described in Quelhas et al. (2010) (code available online) achieves recall of 0.9986 and precision of 0.9017.

5.2. Semi-Automated Tracking

We used CellTracker to score 103 control embryos up to the 8-cell stage. 100 of these are available in the tracking database, and 92 (in which pronuclear envelope breakdown was clearly visible) were used for the statistical analysis shown below.

Table 1 and Figure 11 display some statistics of the analyzed data, in particular data related to the durations and synchronicity of division for cells in different generations. The duration of first-generation cells (t1) was measured from the frame of pronuclear envelope breakdown. This occurs in all zygotes in preparation for the first mitotic division and provides a common reference timepoint that can be used as a developmental registration mark for comparisons between time-lapse recordings.

Table 1.

Medians of timing measurements, in frames and hours:minutes. t1, t2, t3: durations of 1st, 2nd, and 3rd generation cells, respectively. s2: absolute difference, in frames, between times in which sibling cells of 2nd-generation divide (the “s” is for “synchronicity”). s3: analogous of s2 for 3rd-generation cells. All examples go to 8-cell stage. See Figure 11 for more statistical analysis.

	t1	t2	t3	s2	s3
frames	14.0	167.0	98.0	6.0	5.0
HH:MM	01:38	19:29	11:26	00:42	00:35

Figure 11.

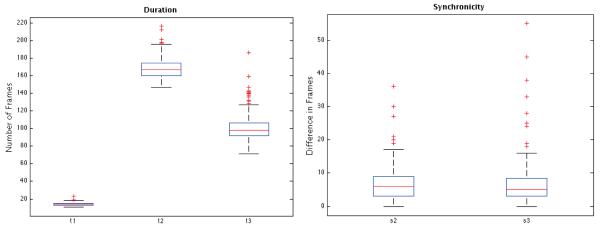
Box plots of measurements described in Table 1, obtained from a subset of 92 embryos in the cell tracking database (those embryos for which pronuclear envelope breakdown was clearly visible). To convert the vertical axis in clock time, recall that consecutive frames are 7 minutes apart.

Figure 12, showing data captured from all 103 control embryos, approaches the question of total volume up to the 8-cell stage. According to the adopted model of cells as spheres with radii estimated with CellTracker, total volume actually decreases.

Figure 12.

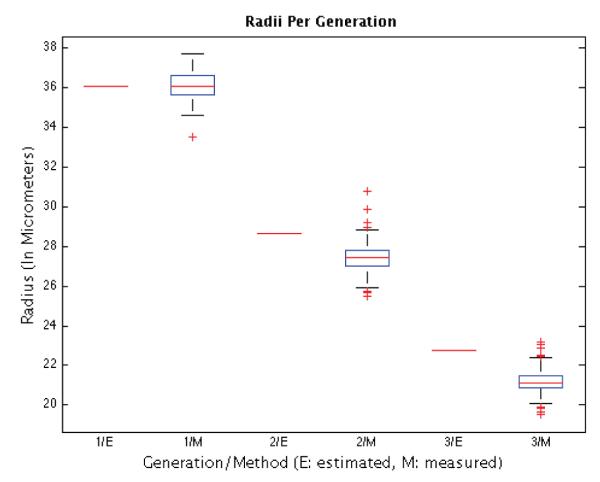
Analysis of total cell volume by CellTracker. Columns 1, 3, and 5 show estimated median radii for 1st, 2nd, and 3rd generation cells, respectively, assuming conservation of total volume and spherical cells. Columns 2, 4, and 6 show box plots of measured radii for 1st, 2nd, and 3rd generation cells, respectively. Using the medians as estimators of radii, the total volume decreases up to the 8-cell stage, to 88% and 92% that of the previous generation in the 2nd and 3rd generation, respectively. The conservation of volume predicts a radius that is off by 4.5% for 2nd-generation cells and by 7.6% for 3rd generation cells. The estimated medians correspond to radii of approximately 27.41μm for a 2nd-generation cell, and of 21.14μm for a third generation cell. We normalized the plot so that the median for 1st-generation cells is 36.09μm (this value is the median of the radii of 59 1st-generation cells of distinct non-injected embryos, measured using the NIS-Elements imaging software).

User interaction is required primarily to set the frames of divisions for every cell, and occasionally to correct the boundary location of a particular cell when the tracking module misses it. For the results reported in Table 1 and Figure 11, additional manual scoring was performed to annotate the frame of pronuclear envelope breakdown.

5.3. Automated Tracking

We evaluated the accuracy of the automated tracking algorithm as applied to 100 control embryos at two different thresholds. When accuracy is defined as a difference of up to 3 frames between manual and automatic detection, the automated tracking algorithm achieved an accuracy of 92%, 70%, and 58%, respectively, for detecting 1st, 2nd, and 3rd generation divisions. When accuracy is defined as a difference of up to 5 frames, accuracy increases to 95%, 78%, and 63%, respectively⁹.

In comparison, the sum of absolute pixel-to-pixel differences for consecutive frames (as in Meseguer et al. (2011)) finds the first division with 78% accuracy when 3 frames of error flexibility are given, and with 80% accuracy for a 5-frames precision window.

Our previous implementation (Cicconet et al. (2013)) performs with 61%, 33%, and 26% of accuracy (in 150 embryos).

Considering the correct finding of all three division times up to the 3rd division our method performs with 46% accuracy (when time discrepancy is of less than 3 frames; 55% when discrepancy is of less than 5 frames).

Wong et al. (2010) only report partial performance results on small datasets. For instance, 14 human embryos from a set of 100 were used to evaluate the measurement of time between first and second mitoses, and results were compared to manual annotations. “Excellent agreement between the two methods” was obtained, but only in 8 cases (those for which embryos “reached the blastocyst stage with good morphology”).

The main limitation of our method is related to noise in the events curves used for division detection (Figure 9), which leads to computation of the wrong local minima. Less often, a division is not detected when a cell divides perpendicularly to the focal plane, since such events provide no evidence of change in the centers histogram.

5.4. On Computation Time

Counting embryos on the first frame takes about 0.35 seconds. The automatic cell-tracking algorithm up to the 4-cell stage runs in about 4 minutes per embryo. These methods were implemented in Matlab R2011b (64-bit).

Tracking happens in a real-time fashion (there’s no perceived waiting-time between frames). The software was implemented in Objective-C, using Xcode (thus, it runs natively on Apple Macintosh computers only).

All experiments were performed on an iMac with 2.8 HGz Intel Core i7 processor and 16 GB RAM, running Mac OS 10.8 or 10.9.

6. Conclusion

In this work we described two methods for cell tracking and division detection in time-lapse videos of mouse embryos. The semi-automated method (available as a software implementation called CellTracker) works up to the 8-cell stage, and relies on user interaction for cell division. The automatic tracking algorithm goes up to the 4-cell stage. Its division detection module is based on histograms of mirror symmetry coefficients, which provide evidence for the existence of cells of particular radii in each frame.

We also release with this paper a cell-tracking database, containing 100 annotated examples of mouse embryos up to the 8-cell stage. The database was built using CellTracker, and thus represents an accurate “gold standard” reference dataset according to careful manual annotation that provides a benchmark for the development and assessment of Computer Vision methods in areas such as tracking and shape analysis.

Both the software and the database are available at http://celltracking.bio.nyu.edu.

We hope CellTracker will be used by IVF (In Vitro Fertilization) researchers to improve the understanding of how the division times and shape features of a human embryo correlate with its developmental competence for uterine re-implantation.