Abstract
Estimation of age-group differences and intra-individual change across distinct developmental periods is often challenged by the use of age-appropriate (but non-parallel) measures. We present a short version of the Behavior Assessment System (Reynolds & Kamphaus, 1998), Parent Rating Scales for Children (PRS-C) and Adolescents (PRS-A), which uses only their common-items to derive estimates of the initial constructs optimized for developmental studies. Measurement invariance of a three-factor model (Externalizing, Internalizing, Adaptive Skills) was tested across age-groups (161 mothers using PRS-C; 200 mothers using PRS-A) and over time (115 mothers using PRS-C at baseline and PRS-A five years later) with the original versus short PRS. Results indicated that the short PRS holds a sufficient level of invariance for a robust estimation of age-group differences and intra-individual change, as compared to the original PRS, which held only weak invariance leading to flawed developmental inferences. Importance of test-content parallelism for developmental studies is discussed.
Keywords: BASC, parent rating scale, measurement invariance, scale parallelism, developmental change
In the context of developmental research, studies are often challenged with the use of developmentally appropriate measures that vary in content according to child age, although tapping presumably into the same underlying psychological construct. Despite an apparent level of conceptual comparability, even slight variations in test content may preclude a rigorous estimation of both age-group differences and intra-individual change across distinct developmental periods. As pointed out by Marsh, Nagengast, and Morin (2013), “unless the underlying factors really do reflect the same construct and the measurements themselves are operating in the same way (across groups, over age and time, or across different levels of continuous variables), mean differences and other comparisons are likely to be invalid” (Marsh et al., 2013, p.1199). Issues related to the equivalence of assessments and the controversies of “changing persons versus changing tests” have whetted the appetites of methodologists for decades (Nesselroade, 1984). However, despite attempts to outline best practice in the matter (e.g., Marsh et al., 2009; Marsh et al., 2013; Pentz & Chou, 1994; Vandenberg & Lance, 2000; Widaman, Ferrer, & Conger, 2010), such methodological considerations are still regularly disregarded in contemporary theoretical and applied developmental research.
In this report, we estimate and illustrate the need to maximize test-content parallelism in developmental studies, specifically regarding estimation of age group differences and developmental change, using the Behavior Assessment System for Children (BASC; Reynolds & Kamphaus, 1998). The BASC is an international reference for the assessment of adaptive and maladaptive behavioral and psychological adjustment of children and adolescents in community and home settings. This multidimensional assessment system includes three forms of Parent Rating Scales (PRS) to represent age-appropriate content: the preschool form (PRS-P) for children under age 6, the child form (PRS-C) for children between 6 and 11 years old, and the adolescent form (PRS-A) for children between 12 and 18 years old. Here we examine specifically the PRS-C and PRS-A forms, which comprise 138 and 126 items, respectively. Both are rated on a four-point frequency scale (ranging from “0 = the behavior never occurs” to “3 = the behavior almost always occurs”) and compose nine clinical scales (Aggression, Anxiety, Attention Problems, Atypicality, Conduct Problems, Depression, Hyperactivity, Somatization and Withdrawal) and three adaptive skills scales (Leadership, Social Skills and Adaptability). Because the Adaptability scale is not available in the PRS-A form, this scale was discarded in all analyses presented in this report (see method section and discussion). By construction, PRS scales are used to derive three clinical composite indexes: (a) externalizing problems (Hyperactivity, Aggression, Attention Problems, Conduct Problems), which are characterized by disruptive or “uncontrolled” behavior, (b) internalizing problems (Anxiety, Depression, Somatization, Withdrawal), which represent psychological maladjustment not marked by acting-out behavior, and (c) adaptive skills (Leadership, Social Skills), mostly summarized by interpersonal or social competency.
Although BASC-PRS subscales and composite index tap conceptually into the same underlying constructs across forms, test scores are obtained using different items depending on the version (i.e., PRS-C or PRS-A) for the particular age cohort studied. Despite these differences, researchers have often considered the PRS-C and PRS-A forms to consist of three “identical” composite scores (e.g., Zeller, Saelens, Roehrig, Kirk, & Daniels, 2004) and they have, therefore, indistinctly or inconsistently merged scores obtained with both forms in the same analyses (e.g., Lopata et al., 2010; Luthar & Sexton, 2007; Seymour et al., 2012; Volker et al., 2010; Zeller et al., 2004). Failing to address this lack of parallelism between forms, normed-referenced scores (T-scores) are often used to increase the comparability of scores obtained with the PRS-C and PRS-A forms. However, this strategy interferes even more with the interpretation of results as (a) it does not solve the initial issue of test-content differences (and thus potential differences in substantive meaning of the constructs measured), and (b) it disturbs individual rank-orders by norming them in reference groups that differ according to the child’s age. As a result, some researchers have been more cautious and have separated their analyses depending on the PRS form used (e.g., Merrell, Streeter, Boelter, Caldarella, & Gentry, 2001). At the same time, they have only paid little attention to the impact of the variations in the PRS forms’ content on the substantive meaning of the test scores for younger (PRS-C) versus older individuals (PRS-A), and accordingly, on their possible consequence (e.g., changes in the meaning of the measure over time) for the estimation and interpretation of age-group difference and intra-individual change.
Confirmatory factor analyses and structural equation modeling of latent variables (LV) are robust approaches to address such developmental effects, for example, by modeling inter-individual change over time with latent difference models (Steyer, Eid, & Schwenkmezger, 1997) or examining age-group differences in latent means. These approaches explicitly take into account measurement error that may bias estimates of the relations among the underlying constructs (e.g., Kline, 2010). Importantly, these approaches allow for the test of measurement invariance (i.e., whether latent constructs have the same substantive meaning, and thus, are comparable), an essential prerequisite that has to be established in order to infer valid comparisons of latent variable means across groups or over time (e.g., De Beuckelaer & Swinnen, 2010; Meredith & Horn, 2001).
In a cross-sectional context, measurement invariance establishes whether a given measure taps a particular latent construct (e.g., externalizing behavior) similarly across various groups (e.g., different age groups) so that meaningful inferences can be made across the groups. For the BASC PRS, this means that the latent structure of both PRS-C and PRS-A forms should be identical in order to represent the same underlying constructs and, thus, allow for meaningful comparisons between children and adolescents. In a longitudinal context, the assumption of measurement invariance over time (i.e., the relations between the observed scores and their underlying latent variables do not change over time) has to be empirically tested before drawing conclusions about intra-individual change in latent means. Besides simulation studies that have addressed the consequences of failure to measurement invariance in developmental research (e.g., De Beuckelaer & Swinnen, 2010), there are only few practical examples available to applied developmental researchers concerned with using age-appropriate measures in their studies.
The BASC PRS is especially informative and illustrative in this regard as it allows for the estimation of possible bias in developmental analyses resulting from the use of non-parallel scales content for targeted age groups (such as the PRS-C and PRS-A). In order to illustrate this bias, here we examine the level of cross-sectional (age-group) and longitudinal invariance reached with non-parallel scale forms (i.e., the original PRS-C and PRS-A scores) as compared to a version of these scales that are maximized for content parallelism.
Present study
Although the number of items varies across the BASC PRS-C and PRS-A forms, there is an overlap of 85 identical items (representing 61.5% and 67.5% of the items in the PRS-C and PRS-A, respectively). The purpose of this study was to develop a content invariant short version of the PRS scales that purposefully capitalizes on these overlapping items to derive estimates of the initial constructs that are comparable in content across age groups and over time. Supporting this purpose, Reynolds and Kamphaus’ (1998) structural analysis of the BASC PRS across children and adolescents forms suggest that these identical items function in the same way regardless of the PRS form. Building on this result, the main goal of this study was to evaluate the extent to which the resulting “Comparable Scales Scores” (CSS) properly address the issues of (a) age-group differences and (b) intra-individual change across distinct developmental periods, as the CSS should presumably achieve an adequate level of measurement invariance. To do so, we conducted a series of structural comparisons between the original PRS scales scores and the new CSS set. For this purpose, we used data gathered from a two-wave longitudinal research study, comprised of a sample of at-risk mothers and their school-age children and adolescents. These subjects were tested at baseline and re-assessed after a period of five years (see Barbot, Hunter, Grigorenko, & Luthar, 2013; Luthar & Sexton, 2007; Yoo, Brown, & Luthar, 2009).
Specifically, to address measurement invariance and mean level differences of the original PRS versus the CSS between children and adolescents, we compared cross-sectionally a sample of children rated by their mothers with the PRS-C form and a sample of adolescents rated with the PRS-A form. To address intra-individual change across distinct developmental periods (childhood through adolescence), we examined a sub-sample of participants followed-up after five years, using the PRS-C form at baseline and the PRS-A form at follow-up, to investigate longitudinal measurement invariance and latent change estimates yielded by the original scores versus the CSS. Together, this study was intended to substantiate the robustness of the BASC PRS short-form scores (CSS) for developmental investigation while estimating the potential adverse impact of relying on unparalleled test-content in such investigations.
Method
Participants
At time of recruitment (Time 1, T1), the sample consisted of 361 mother-child and mother-adolescent dyads living in an urban area of Connecticut recruited from community settings and from outpatient treatment facilities for drug abuse and other mental health problems. Mothers’ age ranged from 23.5 to 55.8 years (M = 38.2 years, SD = 6.2 years). Per study inclusion criteria, each participant was the biological mother of a child between 8 and 17 years old (54% girls, 46% boys, MageGirls = 12.7, SD = 2.9, MageBoys = 12.3, SD = 2.7), was the child’s legal guardian, and lived with the child. This sample was divided into two distinct age groups according to the BASC-PRS form that was used by the mothers to rate their child’s behavioral and psychological adjustment. Accordingly, the mother-child group included 161 mothers of children between the age 8 and 11 (51% girls, 49% boys, MageGirls = 9.5, SD = 1.2, MageBoys = 9.4, SD = 1.2) and the mother-adolescent group comprised 200 mothers of adolescents between the age 12 and 17 (56% girls, 44% boys; MageGirls = 14.3, SD = 1.8; MageBoys = 14.1, SD = 1.8). Among the participants followed-up longitudinally, we examined a cohort of 115 mothers who rated their child using the PRS-C at baseline (50.5% girls, 49.5% boys, MageGirls = 9.4, SD = 1.6, MageBoys = 9.5, SD = 1.6) and the PRS-A at follow-up (Time 2, T2) after an average of five years (MageGirls = 14.2, SD = 1.4, MageBoys = 14.3, SD = 1.4). Self-reported ethnicities of the interviewed mothers were African-American (51.5%), Caucasian (34.2%), Hispanic (6.3%), Native American (.8%), Asian (.3%), Mixed and others (7%), with similar ethnicity distribution across age groups.
Measure and Procedure
Mothers who expressed interest in participation were screened to determine eligibility for the main research program after which research procedures, risks, and benefits were explained to eligible participants and informed consent was obtained (see Luthar & Sexton, 2007). Among a set of measures and interviews conducted by trained interviewers as part of the main study, the Parent Rating Scales (PRS) of the Behavior Assessment System for Children (BASC; Reynolds & Kamphaus, 1998), was administered at each measurement occasion in its child (PRS-C) or adolescent form (PRS-A) according to the age of the rated child. Note that the BASC-II was published in 2004 as a second version of the previous edition used in this study. Even though there are some differences between both versions regarding test content, the present study mainly aims to illustrate how to use the scales in developmental research. Procedures and data analytic strategies are therefore, applicable to research using the BASC-II which also include non-overlapping items between PRS-C and PRS-A.
In the present study, original PRS scale scores were derived by averaging item scores pertaining to each scale independently for data collected with PRS-C and PRS-A forms. CSS scores1 were derived by averaging responses obtained with only the common overlapping items across forms (PRS-C and PRS-A) in their corresponding scale, in order to maximize the similarity of the constructs measured across age groups and over time. The Adaptability scale was therefore entirely dropped from this CSS scoring procedure given its absence in the PRS-A form.
In order to compare on a same basis the “performance” of original vs. CSS scores, we homogenized the distributional features of all scores into normal distributions by using the Rankit transformation method (e.g., Solomon & Sawilowsky, 2009). Rankit is a useful and widely applicable rank-based inverse normal transformation that has shown excellent performance to approximate the intended standard deviation of the transformed distribution, while maximizing statistical power and control Type I error rate for tests of correlations (Bishara & Hittner, 2012). More importantly for our purpose here, this simple transformation can approximately normalize any distribution shape (Bishara & Hittner, 2012), which was useful to reduce the effect of data distributions when comparing model fit and level of invariance reached by both scores sets based on Maximum Likelihood estimation (an estimator that relies on assumption of multivariate normality). However, note that this procedure is specific to the available data because it generates rankits for each data point based on expected values from the order statistic of a particular sample. Thus, although this procedure optimizes distributional features, it hampers direct comparisons of results across studies.
For both sets of scores, this transformation was conducted on a dataset including both T1 and T2 data from children and adolescents (further mapped into a longitudinal dataset after normalization), in order to maintain the relative mean-differences and rank-order relations over time. Correlations between the rankit transformed scores and the corresponding raw score ranged between .85 and 1 with an average of .96 for each scoring method and across measurement occasion, suggesting that the data transformation into normal scores did not substantially interfere with the initial scores’ rank-orders.
Data Analyses
After a series of preliminary analyses examining the distributional features and reliability estimates of the observed variables used in this study, three sets of confirmatory factor analyses (CFA) were conducted separately for the original PRS scores and the CSS to (a) confirm the baseline measurement model following the PRS underlying theoretical structure (Reynolds & Kamphaus, 1998); (b) examine cross-sectional measurement invariance across two age-groups (factorial equivalence and mean level differences); and (c) examine longitudinal measurement invariance (rank-order stability and estimated change in latent means) across distinct developmental periods.
Full information maximum likelihood estimation was used to estimate all model parameters using AMOS 18 (Arbuckle, 2009). To identify the metric of the latent factor models and to provide a scale to the underlying LV, the factor loading of one observed variable was fixed to 1 (i.e., a marker indicator). Model fit was evaluated using the Chi-square likelihood ratio test (χ2) and the χ2/df ratio, the Comparative Fit Index (CFI) and the Root Mean Square Error of Approximation (RMSEA) with its 90% confidence interval. General guidelines in the literature (e.g., Kline, 2010) suggest that a non-significant χ2 -- although rarely observed due to its sensitivity to sample size and model parsimony -- a χ2/df ratio below two, a CFI higher than .95, and a RMSEA lower than .08 indicate an acceptable fit of the model to the observed data. All invariance decisions were based both on the non-significance of the Δχ2 between the unconstrained and the more constrained (invariant) models, as well as a difference in CFI (ΔCFI) lower than .010 (Byrne, 2010; Cheung & Rensvold, 2002).
Baseline measurement models
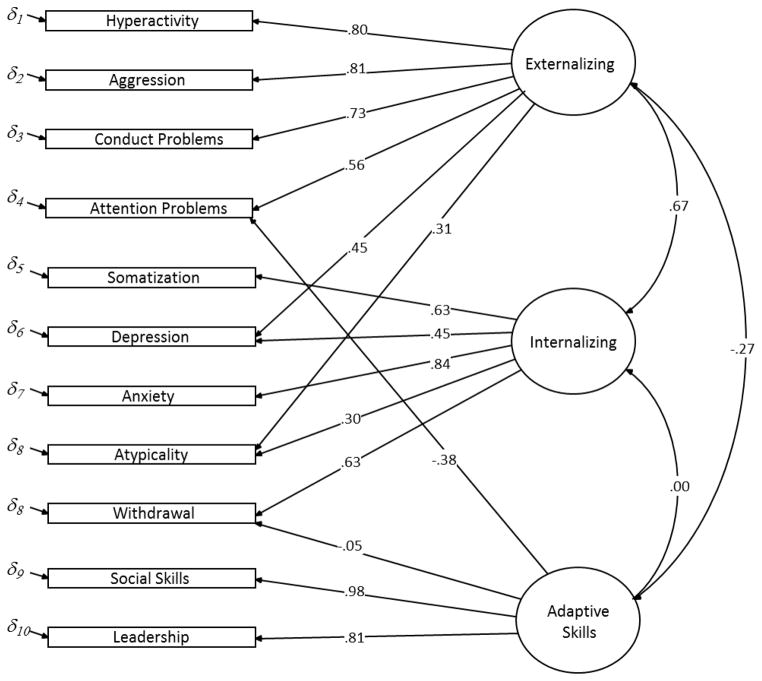
The PRS measurement model following the theoretical structure outlined by Reynolds and Kamphaus’ (1998) “final model” was tested. Accordingly, the three composite indices of the PRS (Internalizing, Externalizing and Adaptive Skills) were modeled as LVs by loading each PRS scale into their corresponding index(es) (see Figure 1). In line with Reynolds and Kamphaus’s final model, four indicators were allowed to load on more than one LV. Specifically, Atypicality was specified as an additional indicator of both the Internalizing and Externalizing LVs, consistent with theoretical expectations suggesting that Atypicality refers to a range of features such as unusual behavior (Externalizing) and mood swings (Internalizing). In addition, the Depression scale was modestly loaded onto the Externalizing LV (along with the main indicators Hyperactivity, Aggression, Conduct Problems, and Attention problems), and all these indicators showed loadings of similar magnitude compared to the original solution presented by Reynolds and Kamphaus (1998). Withdrawal, Somatization, Depression, Anxiety and Atypicality were specified as indicators of the Internalizing LV, yielding again scale-factors loadings of similar extent to the original solution presented by Reynolds and Kamphaus (1998). Finally, Attention problems and Withdrawal were modeled as additional indicators of the Adaptive Skills LV (in addition to the main indicators Social Skills and Leadership), with a lower loading for Attention Problems (−.38) compared to Reynolds and Kamphaus (1998), and a negligible loading for Withdrawal. Because the PRS composite indices represent behavioral dimensions that are distinct but not independent (Reynolds & Kamphaus, 1998), correlations between LVs were estimated freely.
Figure 1.
BASC-PRS baseline measurement model (based on CSS scores). Factor loadings (standardized estimates) and intercorrelations are estimated on the basis of the PRS short form scores at the first measurement occasion (Comparable Scale Scores- CSS), N = 361.
Cross-sectional measurement invariance across age groups
Within both sets of scores (original and CSS), the parallelism of PRS-C and PRS-A forms was explored to estimate the extent to which both forms were structurally comparable. By doing so, we sought to ensure that the constructs measured had the same substantive meaning across forms in order to derive a valid estimation of latent means differences between groups (PRS-C vs. PRS-A). Multi-group CFAs (child group vs. adolescent group at T1) were employed, allowing for the simultaneous fit of the baseline measurement model for the original PRS scores and the CSS to several covariance matrices (one for each PRS form) and the derivation of a weighted combination of model fit across forms (Byrne, Shavelson, & Muthén, 1989). Four levels of factorial invariance stringency were tested, each level adding a new set of constraints to the previous (e.g., Bollen, 1989; Byrne et al., 1989).
Although the four steps to test increasingly stringent set of constraints toward strict factorial invariance often follow Meredith (1993) and the like (e.g., Widaman & Reise, 1997), we, instead, relied on an alternative sequence of steps that is increasingly used as it is thought to be more appropriate to estimate scalar invariance (e. g., Marsh et al., 2013; Wicherts & Dolan, 2010). Indeed, Meredith (1993) and Widaman and Reise (1997)’s approach entails a strong factorial invariance model in which measurement intercepts and factor loadings are restricted to be equal across groups while unique variances are allowed to differ between groups. Next, a strict factorial invariance model adds to the strong factorial invariance model the constraint of unique factor variances invariance across groups. DeShon (2004) has built on this seminal work to reemphasize that the evaluation of metric invariance requires homogeneous unique factor variances across groups since measures cannot be operating in an equivalent fashion across groups if one group has larger uniqueness than another. Such group difference in parts of the uniqueness can “mask” differences in intercepts in a way that mean differences in the uniqueness are “absorbed” by the intercept because uniqueness means are restricted to be zero.
As a result, the four invariance steps tested were as follow (see Wicherts & Dolan, 2010): In the configural invariance model (least restricted), the baseline model was fitted simultaneously to PRS-C and PRS-A data, with the only constraints being an identical number of LVs and factor-loading pattern across PRS forms. The metric/weak invariance model added the constraint of equal factor loadings across PRS forms. Next, the equal uniqueness variance model added the constraint of equal unique variance of subscales across PRS forms. Because this set of analyses focused on metric equivalence across groups and not on latent mean differences, means of the LVs were fixed to 0 and intercepts of the indicators were freely estimated. Finally, the strict factorial invariance model used the previously described equal uniqueness model where the intercepts of each marker indicator were fixed to zero, while the intercepts of the other indicators were set to be equal across groups. In order to estimate the LV means, this model also relaxed the constraint of LVs means fixed to 0 in the equal uniqueness variance model. Because strict factorial invariance may be overly restrictive in some applications (e.g., Allum, Sturgis, & Read, 2010), partial invariance model was developed. Following common practice in the matter (e.g., Millsap, 2011), parameters’ constraints were relaxed using modification indices suggested by the software. Specifically, the least invariant intercepts and uniqueness variances were successively relaxed when yielding a significant overall improvement in model fit as reflected by the difference in Chi-square values (see specific parameters in the Results section). However, at least two intercepts were constrained for each LV, which is the minimal parameterization to estimate validly latent mean differences (e.g., Allum et al., 2010; Byrne et al., 1989; Steenkamp & Baumgartner, 1998). The most restricted model (highest level of invariance stringency) was used to estimate means differences between groups.
Longitudinal measurement invariance
In order to test for mean intra-individual change over time, the baseline model was extended into a longitudinal multivariate factor model (e.g., McArdle & Nesselroade, 1994) with lagged autocorrelation between common LV, and cross-lagged correlation between the other LVs (autocorrelation of uniqueness term between common-indicators was freely estimated). Measurement invariance over time (e.g., Meredith & Horn, 2001) was tested, where a configural invariance model (no restrictions on factor loadings and covariance structure across measurement occasion) was compared to models with the same level of invariance stringency as presented in the cross-sectional comparison analyses (i.e., with successive, additional restrictions on factor loadings, uniqueness, and indicators intercepts). Similarly, partial invariance models were tested longitudinally, and the most restricted model (highest level of invariance stringency) was used to estimate mean change over time.
Results
Preliminary Analyses
Screening of the data for distributional properties indicated a tendency toward non-normal distribution, in particular for the Atypicality scale (at both T1 and T2). After treatment of the data with the rankit transformation, distributional features were much closer to the normal distribution with |skewness| values not exceeding .80 at T1 and 1.27 at T2, and |kurtosis| values not exceeding .57 at T1 and .77 at T2. Table 1 presents the number of items and internal consistency coefficients for the original PRS scores and the CSS, as well as the correlation between original scores and CSS. Both scoring versions yielded overall satisfactory internal consistency with an average Coefficient α of .80, .75, .83 and .78 for PRS-C original scores, PRS-C CSS, PRS-A Original scores and PRS-A CSS, respectively. Although all reliability coefficients appear to be on the acceptable range, Table 1 also reflects substantial differences of some reliability coefficients according to the form PRS-C vs. PRS-A (e.g., Atypicality, Depression), which represents a threat to measurement invariance and further supports the selected sequence of steps toward strict invariance discussed above (see also, DeShon 2004; Lubke & Dolan, 2003; Marsh et al.,2013; Wicherts & Dolan, 2010). Not surprisingly, CSS yielded slightly lower internal consistency coefficients partly due to the reduced number of items contributing to each scale. Importantly, correlations between the original scores and the CSS were high with an average r = .90 for the PRS-C form, and r = .91 for the PRS-A form, suggesting that the CSS values are conceptually similar to the initial constructs (averaging 81% of shared variance).
Table 1.
Descriptive Statistics and Internal Consistencies of the Original PRS Scores and CSS Scores
| PRS-C (N = 161) | PRS-A (N = 200) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
||||||||||
| Scale | Original | CSS | ro-c | Original | CSS | ro-c | ||||
| Items | α | Items | α | Items | α | Items | α | |||
| Hyperactivity | 10 | .82 | 7 | .78 | .91 | 10 | .81 | 7 | .72 | .90 |
| Aggression | 13 | .86 | 8 | .74 | .90 | 11 | .85 | 8 | .78 | .91 |
| Conduct Problems | 11 | .82 | 8 | .75 | .89 | 14 | .87 | 8 | .82 | .91 |
| Anxiety | 11 | .81 | 5 | .72 | .84 | 10 | .80 | 5 | .66 | .90 |
| Depression | 12 | .85 | 8 | .78 | .91 | 11 | .86 | 8 | .94 | .92 |
| Somatization | 13 | .77 | 9 | .74 | .94 | 12 | .83 | 9 | .79 | .93 |
| Atypicality | 12 | .72 | 8 | .62 | .81 | 11 | .83 | 8 | .81 | .73 |
| Withdrawal | 8 | .63 | 5 | .62 | .83 | 8 | .73 | 5 | .62 | .91 |
| Attention Problems | 7 | .82 | 5 | .77 | .91 | 7 | .78 | 5 | .66 | .96 |
| Social Skills | 14 | .90 | 11 | .88 | .99 | 12 | .89 | 11 | .88 | .99 |
| Leadership | 11 | .84 | 11 | .84 | 1 | 12 | .86 | 11 | .85 | .99 |
| Average | 11.1 | .80 | 7.7 | .75 | .90 | 10.7 | .83 | 7.7 | .78 | .91 |
Notes. PRS-C = parent rating scale for children; PRS-A = parent rating scale for adolescents; Original = original PRS scores; CSS = Comparable PRS Scale Scores; α = Cronbach’s Alpha; roc = correlation between original scores and CSS.
Baseline Measurement Models
The baseline model was tested separately for T1 and T2 data based on the original scores versus the CSS. Because preliminary results showed the presence of a negative uniqueness variance of small magnitude for one indicator (Social Skills), the unique variance of that indicator was specified (i.e., fixed to .02) prior to all model estimation, to prevent further estimation problems. The baseline model using original scores yielded a limited fit to the data at T1 (χ2 [df = 38] = 131.2, p < .001, CFI = .956, RMSEA [90%-CI] = .083[.067–098]) and satisfactory fit at T2 (χ2 [df = 38] = 60.1, p < .05, CFI = .980, RMSEA [90%-CI] = .040[.019–059]). In contrast, the baseline model using CSS scores showed a better fit at T1 (χ2 [df = 38] = 97.7, p < .001, CFI = .968, RMSEA [90%-CI] = .066[.050–082]), and even a better fit at T2 (χ2 [df = 38] = 57.1, p < .05, CFI = .979, RMSEA [90%-CI] = .037[.014–056]).
This baseline model, with its scale-factor loadings and factor intercorrelations estimated on the basis of the CSS at T1, is depicted in Figure 1. As illustrated in Figure 1, and consistent with Reynolds and Kamphaus (1998), the Externalizing LV mostly explained variance in the marker indicator Aggression followed by Hyperactivity and Conduct Problem. The Internalizing LV was mainly represented by Anxiety, Somatization, and Withdrawal. The Social skills and Leadership scales were highly loaded on the Adaptive Skills LV. This pattern was consistent across measurement occasions and score sets.
Cross-Sectional Comparisons Across Age-Groups
Measurement Invariance across age-groups
Using data collected at T1, the baseline model was tested for measurement invariance across age-groups, operationalized here by the PRS form administered: “child” group (corresponding to the administration of the PRS-C), and “adolescent” group (corresponding to the administration of the PRS-A). Multi-group CFAs were employed in order to test measurement invariance using the original score set and the CSS set, successively. With both scores sets, between-group differences in LV means were modeled by restricting LV means in one arbitrary group (child) to equal zero. As indicated in Table 2, although all models yielded a similar and overall adequate fit to the data (except for the strict factorial invariance models), the CSS set held a higher level of measurement invariance across the child and adolescent forms (the equal uniqueness model being associated with an acceptable level of invariance; Δχ2 [df = 23] = 41.2, p = .011, ΔCFI = .010), in comparison to the original score associated with a significant degradation in model fit, after the weak invariance condition (Δχ2 [df = 23] = 58.6, p < .001, ΔCFI = .016). Anecdotally, invariance of the baseline model using CSS was also tested as a function of other relevant background factors and suggested strict invariance according to gender (χ2 [df = 28] = 43.1, p = .034, ΔCFI = .008), and ethnicity (χ2 [df = 56] = 73.1, p = .062, ΔCFI = .009).
Table 2.
Invariance Testing of Cross-Sectional (age-group) Models
| PRS Original Scores | PRS CSS Scores | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
||||||||||||
| Model (df) | χ2 | χ2/df | Δχ2 | CFI | ΔCFI | RMSEA (CI) | χ2 | χ2/df | Δχ2 | CFI | ΔCFI | RMSEA (CI) |
| Configural invariance (75) | 145.6*** | 1.94 | _ | .968 | _ | .051 (.039 – .064) | 140.9*** | 1.88 | _ | .966 | _ | .049 (.037 – .062) |
| Metric/weak invariance (87) | 168.8*** | 1.94 | .026 | .963 | .005 | .051 (.040 – .063) | 160.0*** | 1.84 | .086 | .962 | .004 | .048 (.036 – .060) |
| Equal uniqueness (98) | 204.2*** | 2.08 | .001 | .952 | .016 | .055 (.044 – .066) | 182.1*** | 1.86 | .007 | .956 | .010 | .049 (.038 –.060) |
| Strict factorial invariance (106) | 362.4*** | 3.42 | .001 | .884 | .084 | .082 (.073 – .091) | 252.3*** | 2.38 | .001 | .924 | .042 | .062 (.052 –.072) |
| Partial invariance (99/102) | 191.1*** | 1.93 | .005 | .958 | .010 | .051 (.040 – .062) | 186.4*** | 1.83 | .014 | .956 | .010 | .048 (.037 –.059) |
Notes. Invariance testing using the “final model” as baseline and based on T1 data; χ2 = chi-square; df = degrees of freedom; p = p value of the chi-square test; Δχ2 = p value of the chi-square difference test; CFI = Comparative fit index; ΔCFI = difference in the CFI value (assuming baseline model to be correct); RMSEA = root mean square error of approximation; CI = 90% confidence interval of RMSEA value.
p < .001
However, both CSS and Original scores sets failed to reach the strict invariance condition (between PRS-C and PRS-A), so partial invariance models were developed. Confirming the lack of measurement invariance of the original scores set, its associated partial invariance model involved relaxing five invariance constraints on indicators intercepts (Somatization, Depression, Attention Problems, Conduct Problems, Atypicality) and two invariance constraints on indicators uniqueness (Somatization and Hyperactivity) to reach a satisfactory level of partial invariance (i.e., based on the ΔCFI; see Byrne, 2010; Cheung & Rensvold, 2002). Differences in Latent means obtained with the strict invariance and partial invariance model were very small (differences translating in Cohen’s d ranging from 0 to .16, with a mean of .08). In contrast to the Original scores set, the partial invariance model using the CSS relaxed only four invariance constraints on indicators intercepts (Conduct Problems, Hyperactivity, Somatization, Withdrawal) to reach an acceptable level of partial invariance (Δχ2 [df = 31] = 186.4, p = .014, ΔCFI = .010). Despite substantial improvement in model fit with the partial invariance model, LV means estimated by both models (i.e., strict invariance and partial invariance) were highly similar (differences in LVs means translates in Cohen’s d ranging from 0 to .06, with a mean of .02).
Estimation of mean differences between age-groups
In order to inform the impact of lack of test content parallelism with the original PRS score set, age-group differences in latent means were estimated with both the original scores (associated with a limited level of invariance, precluding for a reliable estimation of latent means and group differences) and the CSS (holding a satisfactory level of invariance for a valid estimation of latent mean differences). In both cases, the most invariant model was used (i.e., partial invariance) and the latent means of the child group were fixed to zero, so that the estimated latent means for the adolescent group could directly be interpreted as between-group differences. As an initial step, a model testing the equality of latent means between groups rejected the null hypothesis when compared against the partial scalar invariance model (with latent means freely estimated across groups), with both the original scores set (Δχ2 [df = 3] = 41.2, p < .001) and the CSS set (Δχ2 [df = 3] = 12.1, p = .008), suggesting significant mean differences in LVs between groups, especially when considered with the original scores set.
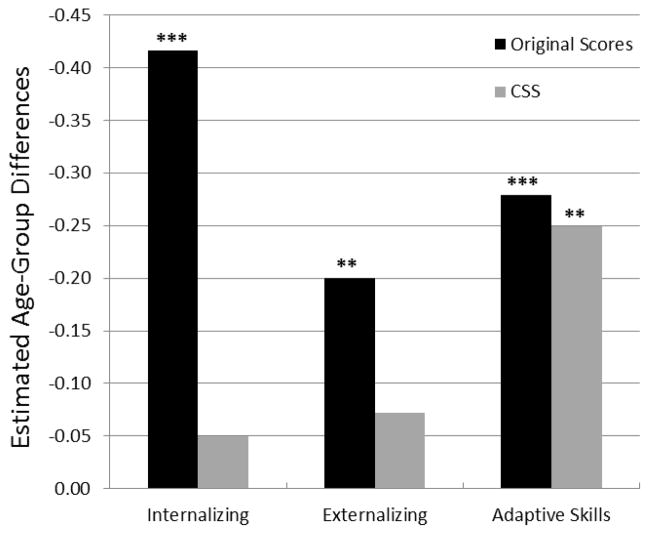
Table 3 displays the estimated variances of each LV for the child group (latent means being fixed to zero), as well as estimated variances and means of each LV for the adolescent group (estimated latent means for the adolescent group being directly interpreted as between-group difference). As presented in Table 3 and illustrated in Figure 2, both original scores set and CSS set yields significant mean age-group difference on the Adaptive Skills LV that are similar in size (the adolescent sample being associated with significantly lower means that the child sample; Cohen’s d = 0.35 using original scores and 0.32 using CSS scores, respectively). However, the original scores set also yields significant mean age-group difference on both the Internalizing (Cohen’s d = 0.70) and Externalizing (Cohen’s d = 0.34) LVs, while the CSS set is associated with small and non-significant group-differences on these LVs (Cohen’s d = 0.09 and 0.13 for Internalizing and Externalizing, respectively). Complementary analyses (in a model where means of the child group were freely estimated as well) suggest that latent means obtained with the original score set seem to be artificially inflated for the child group, and deflated for the adolescent group, thus overestimating group differences in latent means, and increasing the risk of Type 1 error.
Table 3.
Estimates of Age Group Differences using Original Scores versus CSS Scores
| PRS Original Scores | PRS CSS Scores | |||||
|---|---|---|---|---|---|---|
|
|
||||||
| Parameter | Unst. | SE | p | Unst. | SE | p |
| Adolescent Sample Mean | ||||||
| Internalizing | −.416 | .077 | .001 | −.050 | .072 | .482 |
| Externalizing | −.200 | .069 | .004 | −.072 | .068 | .289 |
| Adaptive Skills | −.279 | .077 | .001 | −.249 | .085 | .003 |
| Child Sample Variance | ||||||
| Internalizing | .353 | .064 | .001 | .348 | .067 | .001 |
| Externalizing | .350 | .061 | .001 | .324 | .060 | .001 |
| Adaptive Skills | .616 | .084 | .001 | .613 | .084 | .001 |
| Adolescent Sample Variance | ||||||
| Internalizing | .362 | .062 | .001 | .325 | .059 | .001 |
| Externalizing | .337 | .056 | .001 | .284 | .051 | .001 |
| Adaptive Skills | .658 | .083 | .001 | .632 | .081 | .001 |
Notes. Total N = 361; Child group (PRS-C), N = 161; Adolescent group (PRS-A), N = 200; Estimates of the partial invariance models. Unst. = unstandardized estimates. SE = Standard error.
Figure 2. Estimated latent means on each PRS clinical index for the Adolescent sample using the original scores and CSS.
Values reflect estimates of the most restricted models (partial invariant models). Latent means of the child group (PRS-C) are fixed to 0. Child group (PRS-C), N = 161, Adolescent group (PRS-A), N = 200. ***p < .001, **p < .01,
Longitudinal Comparisons
Longitudinal measurement invariance and rank-order stability
In this analytical set, the baseline model was extended into a longitudinal multivariate factor model, where the four level of invariance stringency were tested successively for both the PRS original score set, and the CSS set. Results (see Table 4) indicate an evident lack of invariance across the child and adolescent PRS forms when using the original score set, even in the comparably more “lenient” weak invariance condition (Δχ2 [df = 12] = 30.08, p = .002, ΔCFI = −.011). In contrast, the CSS set held a higher level of measurement invariance across the child and adolescent forms, the equal uniqueness model being associated with a slight improvement in model fit (Δχ2 [df = 23] = 12.1, p = .97, ΔCFI = .006).
Table 4.
Longitudinal Invariance Testing
| PRS Original Scores | PRS CSS Scores | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
||||||||||||
| Model (df) | χ2 | χ2/df | Δχ2 | CFI | ΔCFI | RMSEA (CI) | χ2 | χ2/df | Δχ2 | CFI | ΔCFI | RMSEA (CI) |
| Configural invariance (176) | 238.5*** | 1.36 | _ | .967 | _ | .056 (.036 – .074) | 201.3 | 1.14 | _ | .985 | _ | .035 (.000 – .057) |
| Metric/weak invariance (188) | 269.3*** | 1.43 | .002 | .956 | .011 | .062 (.045 – .078) | 209.3 | 1.11 | .785 | .987 | .002 | .032 (.000 – .053) |
| Equal uniqueness (199) | 284.9*** | 1.43 | .003 | .954 | .013 | .062 (.045 – .078) | 213.4 | 1.07 | .969 | .991 | .006 | .025 (.000 – .049) |
| Strict factorial invariance (207) | 399.9*** | 1.93 | .001 | .897 | .070 | .091 (.078 – .105) | 328.2*** | 1.58 | .001 | .926 | .059 | .072 (.057 – .086) |
| Partial invariance (201a/205b) | 282.1*** | 1.40 | .012 | .957 | .010 | .060 (.043 – .076) | 228.0 | 1.11 | .587 | .986 | .001 | .031 (.000 –. 052) |
Notes. Sample includes only the participants using PRS-C at T1 and PRS-A at T2 (N = 115); LCS = Latent change score model. χ2 = chi-square; df = degrees of freedom; p = p value of the chi-square test; Δχ2 = p value of the chi-square difference test; CFI = Comparative fit index; ΔCFI = absolute difference in the CFI value (assuming baseline model to be correct); RMSEA = root mean square error of approximation; CI = 90% confidence interval of RMSEA value.
6 additional parameters are freely estimated in the partial invariance model using the Original scores set.
2 additional parameters are freely estimated in the partial invariance model using the CSS set.
p < .05,
p < .01,
p < .001.
However, similar to the age-group differences analytical set, strict factorial invariance was not met with both score sets, so partial invariant models were developed. Again, six invariance constraints were relaxed when using the original score set (five on indicators intercepts including Somatization, Attention Problems, Depression, Conduct Problem, and Leadership, and one on Somatization uniqueness), to reach a just acceptable level of invariance (Δχ2 [df = 25] = 43.6, p = .012, ΔCFI = .010). This model yielded LVs means estimates in a similar range than those obtained with the strict factorial model (Cohen’s d for mean differences ranging from 0 to .16, with a mean of .08). In contrast, the longitudinal partial invariance model using the CSS set relaxed only two invariance constraints on indicators intercepts (Conduct Problems, and Anxiety), and was associated with excellent fit to the data (χ2 [df = 205] = 228.0, p = .13, CFI = .986, RMSEA [90%-CI] = .031[.000 – 052]), as well as similar LV means estimates in comparison to the strict factorial model (Cohen’s d for mean differences ranging from 0 to .17, with a mean of .08).
The most invariant model (partial invariance) was used as the basis of the estimation of rank-order stability (cross-lagged correlation between common-factors) yielding stability coefficients of .68, .55 and .69 for, respectively, the Internalizing, Externalizing, and Social Competence LVs estimated using the original scores set, and .72, .51, and .64 for the same LVs estimated using the CSS set (the differences of the correlation coefficient estimates obtained with both scores sets are not statistically significant). Therefore, it appears that despite the limited longitudinal measurement invariance with the original PRS scores set, no substantial interference in the estimation of rank-order stability was observed, with rank-order estimates on the moderate to high stability range (given the rather long delay) close to those estimated using the CSS.
Mean-level stability and change
Given the high level of measurement invariance observed with the CSS set, estimates of intra-individual change from baseline (T1) to follow-up (T2) could be interpreted validly. With only configural invariance, the original scores set was likely to yield biased estimates of mean change. To inform differences in estimates according to the original vs. CSS scores sets, between-individual differences in intra-individual change was modeled in the partial invariance models by restricting LVs means to equal zero at the first measurement occasion, so that estimated means at the second measurement occasion could directly be interpreted as latent mean change (latent difference between T1 and T2).
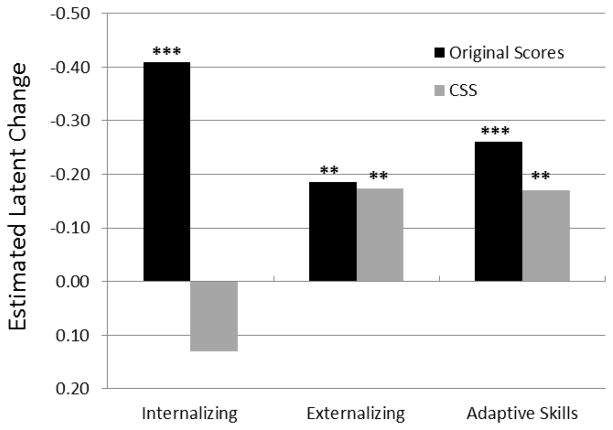
Estimates of mean intra-individual change (as reflected by latent mean at T2) are presented in Table 5, along with Time 1 and Time 2 estimated variances. Variance at T1 represents between-individual differences in initial level, while T2 variance captures between-individual differences in intra-individual change. Similar to the age-group differences observed in the cross-sectional analyses, the original PRS scores yielded significant change over time for all LVs (in particular on the Internalizing LV; Cohen’s d = 0.64, 0.31, and 0.29, for Internalizing, Externalizing, and Adaptive Skills, respectively), while the short form (CSS) yielded significant and smaller change only for the Externalizing (Cohen’s d = 0.32) and Adaptive Skills (Cohen’s d = 0.21) LV, with an overall decrease over time. As illustrated in Figure 3, if both original scores and CSS sets yield significant mean decreases on the Externalizing problems and Adaptive Skills LV over time (and similar in size) the original scores set also yields significant and rather large decreases on the Internalizing LVs, while the CSS set is associated with overall stability on this LV. Again, the original scores set appears to increase the risk of Type 1 error, with overestimation of average developmental change when non-parallel forms are used at each measurement occasion (PRS-C, then PRS-A).
Table 5.
Estimation of Mean Intra-individual Change over Time (Latent change scores) using Original Scores and CSS sets
| PRS Original Scores | PRS CSS Scores | |||||
|---|---|---|---|---|---|---|
|
|
||||||
| Parameter | Unst. | SE | p | Unst. | SE | p |
| Time 2 Latent Means | ||||||
| Internalizing | −.409 | .068 | .001 | .131 | .068 | .054 |
| Externalizing | −.185 | .062 | .003 | −.173 | .058 | .003 |
| Adaptive Skills | −.261 | .082 | .001 | −.170 | ..071 | .016 |
| Time 1 Variance | ||||||
| Internalizing | .361 | .077 | .001 | .431 | .092 | .001 |
| Externalizing | .321 | .069 | .001 | .261 | .064 | .001 |
| Adaptive Skills | .797 | .133 | .001 | .700 | .120 | .001 |
| Time 2 Variance | ||||||
| Internalizing | .470 | .098 | .001 | .500 | .106 | .001 |
| Externalizing | .396 | .084 | .001 | .309 | .075 | .001 |
| Adaptive Skills | .828 | .137 | .001 | .680 | .117 | .001 |
Note. N = 115, Unst. = unstandardized estimates. SE = Standard error. LVs means at T1 are set to equal zero so that the presented estimated means at T2 can be directly interpreted as latent mean latent difference between T1 and T2.
Figure 3. Estimated latent change over time on each PRS clinical index using the original scores and CSS.
Values reflect estimates based on the partial invariant models. T1 uses PRS-C, T2 uses PRS-A. Mean at T1 are fixed to 0 so that T2 means are interpreted as latent difference between T1 and T2. N = 115. ***p < .001, **p < .01, *p < .05.
Discussion
This study demonstrated the robustness of comparable scale scores (CSS) derived from the BASC Parent Rating Scale (PRS) using an overlap of 85 items between child and adolescent forms for use in developmental investigations. Specifically, while the CSS derived from the short PRS version were adequately internally consistent and conceptually tapped the same underlying constructs compared to the original PRS forms (average of 81% of shared variance with the original scores), they yielded a sufficient level of measurement invariance for estimating validly (a) age-group latent mean differences and (b) developmental change in the PRS clinical indices. In contrast, the original PRS version failed to reach the desirable level of measurement invariance needed for the valid estimation of these developmental effects, leading to overestimated child scores (PRS-C) and underestimated adolescents scores (PRS-A), which resulted in misleading inferences in developmental investigations (increased Type I errors). In sum, using the original BASC PRS scales, larger between-group and across-time mean differences on the underlying latent variables (Internalizing, Externalizing and Adaptive Skills) were observed, most likely due to the effects of the non-common items (which were eliminated in the PRS Short form that used the “common” sets of items only). Therefore, research results that have disregarded the issue of item content overlap across age-groups in developmental analyses should be interpreted cautiously. Using the BASC PRS, we have illustrated how this lack of parallelism ultimately resulted in flawed inferences, but it could translate to other major biases using other measures (according to the way age-specific content impacts test scores).
Interestingly, flawed inferences regarding mean differences in our study depend on the clinical index under consideration. Specifically, the Internalizing index was associated with largest discrepancies in mean differences when comparing the original scores and the CSS. It is also the index that included the least common items between PRS-C and PRS-A forms (65% common). In contrast, results regarding Adaptive Skills are associated with fewer discrepancies between score sets, and this index included the highest overlap in content (90% common items). This observation indicates that the risk of Type I error and flawed inferences regarding the estimation of developmental effects may be related to the proportion of common items. However, it should also be noted that the proportion of common items in the Adaptive Skills index was artificially improved in this study, since the Adaptability scale was removed from the original PRS-C (given its absence in the PRS-A). Therefore, developmental studies using the index derived from the full original scales would limit comparability across the PRS-C and PRS-A even more (i.e., non-invariance at a configural level), and equally result in biased estimates of developmental effects. In sum, when researchers use collections of items–some of which are “common” and some of which are “non-common”–mean differences across groups or over time may be confounded by the presence of the “non-common” items. Therefore, researchers should pay attention to item sampling in developmental investigation and make sure to use only common items, so that mean differences are more readily interpreted, provided that an adequate level of factorial invariance has been achieved.
Our study also suggested that the lack of test content parallelism may primarily be a threat for inference regarding means, while inferences regarding rank-order stability seem to be accurate. This assumption deserves further research, since in this study, rank-order stability was estimated only with a sample of participants who were all administered the PRS-C at baseline and the PRS-A at follow-up (i.e., measurement biases may have intervened in a systematic fashion which did not disturb rank-orders). Further, the use of the Rankit transformation may have optimized the comparability of the rank-order stability coefficient obtained with both scores sets, in which case, such transformation may prove useful for studies using non-parallel test content and focusing on rank-order stability and change. Thus, under practical considerations, it is possible that an instrument that does not reach a sufficient level of content parallelism and measurement invariance between age-groups or over time may still be used in developmental investigations. Specifically, our study suggests that (a) high level of measurement invariance is needed for making valid inferences regarding latent mean differences, while (b) a lower level of measurement invariance may be sufficient to examine validly rank-order stability and change (e.g., cross-lagged correlation between common-factors).
We must however note that, even when ensuring the parallelism of test-content between the PRS-C and PRS-A forms, strict factorial invariance was not established. In turn, eliminating non-common items does not grant factorial invariance, although greatly maximizing it. As noted earlier, strict factorial invariance may be overly restrictive in some applications (e.g., Allum, Sturgis, & Read, 2010), so partial invariance models may be developed (e.g., Byrne et al., 1989). In this situation, the investigator may follow iterative procedures of establishing a maximum level of measurement invariance that constraints intercepts (with at least the intercepts of a marker indicator and a reference indicator) of observed variables to be invariant over time and across groups (see Millsap, 2011, for an overview). Increasingly available statistical techniques accommodate the development of partially invariant models reasonably well, allowing for the isolation of the source of group differences (or test forms differences), and ending with a solution that accommodates both groups with a higher level of parallelism. However, this specification has important methodological and conceptual implications.
Methodologically, a partially invariant model is characterized by a mixture of invariant and group-specific parameter estimates (Millsap, 2011). Thus, group differences in intercepts of the observed variables indicate that a part of the predicted observed scores differs at various levels of the latent factor, which resembles differential item functioning (DIF). Conceptually, a partial invariance model means that only a subset of the observed variables could be regarded as unbiased. For instance, depending on their direction, intercept differences may lead to an overestimation or an underestimation of group differences in latent means (Wicherts & Dolan, 2010). Practically, there is much debate on whether partial invariance is a sufficient condition to validly estimate latent means (e.g., Robert, Lee & Chan, 2006). In their review of numerous invariance studies, Schmitt and Kuljanin (2006) indicate than more than half have applied partial invariance and they have observed that partial invariance made little difference in the estimates of structural model parameters. It is likely that whether or not latent means can be validly compared depends on the number and the magnitude of non-invariant intercepts. Some authors have suggested that at least two intercepts should be constrained for each LV (e.g., Allum et al., 2010; Byrne et al., 1989; Steenkamp & Baumgartner, 1998), which is essentially the case in the present study. Others have suggested a “compensation” mechanism between nonequivalent intercepts of the same magnitude but opposite direction, which could result in a true comparability of latent means (e.g., Robert et al. 2006).
Although we did not follow this particular recommendation here, we illustrated how increased level of non-equivalence (such as for the PRS original score set) yielded quite different estimates in comparison to the CSS score set eliminating all non-common items across the PRS-C-and PRS-A forms. Given the limitation associated with a “data-driven” approach to impose partial measurement invariance, we argue for future studies using the BASC scales to cross-validate the results observed here, in particular, evidence of highest level of measurement invariance with the CSS score set, and conclusions regarding mean age-group differences, mean intra-individual change, and rank order-stability.
In sum, this study illustrated how the use of age-appropriate test forms may ironically preclude a robust estimation of developmental effects, as it fails to achieve a minimal level of measurement invariance needed for such an investigation. This illustration was, however, based on deliberately conservative invariance decisions (models with a high level of invariance stringency were favored). Although most models (non-invariant) showed fit indexes sufficient for publication, they provided a biased estimate of latent means and latent mean differences which would have been unnoticed if invariance was not carefully tested. This demonstration was meant to re-emphasize that even slight variation in test content produces scores that vary in substantive meaning to the same extent, complicating their interpretation when included in the same analyses, and most importantly, biasing inferences regarding age-group differences and longitudinal change central to developmental investigations.
Therefore, our study illustrated that maximizing test-content parallelism is a basic condition to improve construct comparability across distinct developmental periods. Such “metric” requirements may be difficult to accommodate considering the practical requirement of presenting test material appropriate for targeted age groups. Nevertheless, as suggested in this study, scores capitalizing on common items across forms (CSS) shared a large amount of the variance with the original scores, suggesting that only a limited portion of the variance in the original scores was attributed to age-specific contents (and measurement error). Therefore, as illustrated here, it seems reasonable to develop alternative scoring methods that maximize the use of overlapping items across various age-appropriate forms (presumably central to the construct) without substantially harming the construct validity of the concept to be measured. Similarly, application of variance decomposition techniques (e.g., Barbot et al., 2012; Flora, Curran, Hussong, & Edwards, 2008; McArdle, Grimm, Hamagami, Bowles, & Meredith, 2009) to isolate overlapping-items variance from age-specific items variance may be a promising avenue of exploration to achieve the compromise of capturing age-group differences and developmental change using various developmentally appropriate test forms.
Our argument for the need to maximize test-content parallelism and establish cross-sectional and longitudinal measurement invariance has important implications for drawing conclusions from longitudinal studies spanning childhood and adolescence. The present study illustrated that biased estimates of mean differences could be obtained if measurement invariance was not established. This could, for example, lead to biased conclusions about the long-term impact of an intervention. Moreover, if outcome scores are not comparable across time, findings of continuity and change could potentially be misinformed due to the insufficient equivalence of the measurement scale. Thus, intervention studies that focus on examining the long-term effectiveness of a treatment across developmental periods should employ measures that allow mean changes over time. This is particularly important in intervention studies that assess the baseline level of a construct in a child at a young age via other informant’s ratings (such as parents or teachers) and then longitudinally track the development of the child into adolescence using the same instrument. These studies should carefully examine and establish cross-sectional measurement invariance across age groups (e.g., children and adolescents) when planning the long-term course of the study. For this purpose, some researchers have recognized the need to optimize their measures for applied developmental research by establishing measurement invariance across age groups within normative samples (e.g., Prince-Embury & Courville, 2008; Ladd, 2006).
Conclusion
In this report, we illustrated the importance of the issue of test content parallelism and its consequences for measurement invariance outlined in the developmental and individual differences literature (e.g., Curran, 2014). Essentially, when applied researcher use instruments with collections of items – some of which are “common” and some of which are “non-common” – then, mean differences across groups or time may be confounded by the presence of the “non-common” items. If one restricts one’s attention only to the common items, then mean differences are more readily interpreted, provided that an adequate level of factorial invariance has been achieved. Our investigation provided not only evidence of the relevance of a BASC-PRS short form for use in developmental studies, but also re-emphasizes the need to carefully investigate measurement invariance in such studies. Although the use of age-specific test scores is undeniably relevant and recommended for practical purpose (in particular age-normed scores such as T scores), reliance on them for developmental studies is unwarranted. Because alternative forms of the same measure for targeted age-groups tap conceptually into the same underlying psychological construct, some degree of parallelism can be reasonably achieved despite age-specific typical behaviors represented in the test content. To this end, researchers and test developers should attempt to maximize item content that is reasonably universal at every stage of development and is sufficiently central to the construct of interest. This is especially achievable with adult-informant rated scales (such as the BASC PRS or Teacher Rating Scale), where comprehension is not an issue precluding the development of items that are identical across age-groups.
Research Highlights.
We show the need to maximize test-content parallelism in applied developmental studies.
We compare the level of measurement invariance reached with parallel vs. non-parallel scales.
We estimate biases resulting from using non-parallel scales for two age groups.
Only scales with parallel content hold a level of invariance proper for developmental studies.
Acknowledgments
Preparation of this manuscript was supported by NIDA DA010726, R01-DA11498 and R01-DA14385 (PI: Luthar). We thank Macrina Cooper-White and Kristen Piering for editorial assistance, as well as two anonymous reviewers for valuable suggestions.
Footnotes
Scoring program for this PRS Short form is available upon request from the first author.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Allum N, Sturgis P, Read S. Evaluating change in social and political trust in europe using multiple group confirmatory factor analysis with structured means. In: Davidov E, Schmidt P, Billiet J, editors. Methods for cross-cultural analysis: Basic strategies and applications. London, GB: Taylor & Francis; 2010. pp. 58–77. European Association of Methodology Series ed. [Google Scholar]
- Arbuckle J. Amos 18 user’s guide. SPSS Incorporated; 2009. [Google Scholar]
- Barbot B, Haeffel GJ, Macomber D, Hart L, Chapman J, Grigorenko EL. Development and validation of the delinquency reduction outcome profile (DROP) in a sample of incarcerated juveniles: A multiconstruct/multisituational scoring approach. Psychological Assessment. 2012;24(4):901–912. doi: 10.1037/a0028193. [DOI] [PubMed] [Google Scholar]
- Barbot B, Hunter S, Grigorenko EL, Luthar SS. Dynamic of change in pathological personality trait dimensions: A latent change analysis among at-risk women. Journal of Psychopathology and Behavioral Assessment. 2013;35(2):173–185. doi: 10.1007/s10862-012-9331-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishara AJ, Hittner JB. Testing the significance of a correlation with nonnormal data: Comparison of pearson, spearman, transformation, and resampling approaches. Psychological Methods. 2012;17(3):399–417. doi: 10.1037/a0028087. [DOI] [PubMed] [Google Scholar]
- Bollen KA. Structural equations with latent variables. New York: Wiley; 1989. [Google Scholar]
- Byrne B. Structural equation modeling using AMOS. 2. New York: Routledge; 2010. [Google Scholar]
- Byrne B, Shavelson R, Muthén B. Testing for the equivalence of factor covariance and mean structures: The issue of partial measurement invariance. Psychological Bulletin. 1989;105(3):456–466. doi: 10.1037/0033-2909.105.3.456. [DOI] [Google Scholar]
- Cheung GW, Rensvold RB. Evaluating goodness-of-fit indexes for testing measurement invariance. Structural Equation Modeling: A Multidisciplinary Journal. 2002;9(2):233–255. [Google Scholar]
- Curran PJ. Commentary: The critical role of measurement (and space elevators) in the study of child development. Journal of Pediatric Psychology. 2014;39(2):258–261. doi: 10.1093/jpepsy/jst145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Beuckelaer A, Swinnen G. Biased latent variable mean comparisons due to measurement non-invariance: A simulation study. In: Davidov E, Schmidt P, Billiet J, editors. Methods for cross-cultural analysis: Basic strategies and applications. London, GB: Taylor & Francis Group; 2010. pp. 119–149. European Association of Methodology Series ed. [Google Scholar]
- DeShon RP. Measures are not invariant across groups without error variance homogeneity. Psychology Science. 2004;46:137–149. [Google Scholar]
- Ferrer E, McArdle JJ. Longitudinal modeling of developmental changes in psychological research. Current Directions in Psychological Science. 2010;19(3):149–154. doi: 10.1177/0963721410370300. [DOI] [Google Scholar]
- Flora DB, Curran PJ, Hussong AM, Edwards MC. Incorporating measurement nonequivalence in a cross-study latent growth curve analysis. Structural Equation Modeling. 2008;15(4):676–704. doi: 10.1080/10705510802339080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kline RB. Principles and practice of structural equation modeling. 3. New York, NY: The Guilford Press; 2010. [Google Scholar]
- Ladd GW. Peer rejection, aggressive or withdrawn behavior, and psychological maladjustment from ages 5 to 12: an examination of four predictive models. Child Development. 2006;77(4):822–846. doi: 10.1111/j.1467-8624.2006.00905.x. [DOI] [PubMed] [Google Scholar]
- Lopata C, Toomey JA, Fox JD, Volker MA, Chow SY, Thomeer ML, Smerbeck AM. Anxiety and depression in children with HFASDs: Symptom levels and source differences. Journal of Abnormal Child Psychology. 2010;38(6):765–776. doi: 10.1007/s10802-010-9406-1. [DOI] [PubMed] [Google Scholar]
- Lubke GH, Dolan CV. Can unequal residual variances across groups mask differences in residual means in the common factor model? Structural Equation Modeling. 2003;10(2):175–192. [Google Scholar]
- Luthar SS, Sexton CC. Maternal drug abuse versus maternal depression: Vulnerability and resilience among school-age and adolescent offspring. Development and Psychopathology. 2007;19(1):205–225. doi: 10.1017/S0954579407070113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marsh HW, Muthén B, Asparouhov T, Lüdtke O, Robitzsch A, Morin AJS, Trautwein U. Exploratory structural equation modeling, integrating CFA and EFA: Application to students’ evaluations of university teaching. Structural Equation Modeling: A Multidisciplinary Journal. 2009;16(3):439–476. doi: 10.1080/10705510903008220. [DOI] [Google Scholar]
- Marsh HW, Nagengast B, Morin AJS. Measurement invariance of big-five factors over the life span: ESEM tests of gender, age, plasticity, maturity, and la dolce vita effects. Developmental Psychology. 2013;49(6):1149–1218. doi: 10.1037/a0026913. [DOI] [PubMed] [Google Scholar]
- McArdle J. Latent variable modeling of differences and changes with longitudinal data. Annual Review of Psychology. 2009;60(1):577–605. doi: 10.1146/annurev.psych.60.110707.163612. [DOI] [PubMed] [Google Scholar]
- McArdle JJ, Grimm KJ, Hamagami F, Bowles RP, Meredith W. Modeling life-span growth curves of cognition using longitudinal data with multiple samples and changing scales of measurement. Psychological Methods. 2009;14(2):126–149. doi: 10.1037/a0015857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McArdle J, Nesselroade JR. Using multivariate data to structure developmental change. In: Cohen S, Reese H, editors. Life-span developmental psychology: Methodological contributions. Hillsdale, NJ: Lawrence Erlbaum Associates, Inc; 1994. pp. 223–267. [Google Scholar]
- Meredith W. Measurement invariance, factor analysis and factorial invariance. Psychometrika. 1993;58(4):525–543. [Google Scholar]
- Meredith W, Horn J. The role of factorial invariance in modeling growth and change. In: Linda M, Sayer AG, editors. New methods for the analysis of change. Washington, DC, US: American Psychological Association; 2001. pp. 203–240. [DOI] [Google Scholar]
- Merrell KW, Streeter AL, Boelter EW, Caldarella P, Gentry A. Validity of the home and community social behavior scales: Comparisons with five behavior-rating scales. Psychology in the Schools. 2001;38(4):313–325. doi: 10.1002/pits.1021. [DOI] [Google Scholar]
- Millsap RE. Statistical approaches to measurement invariance. Routledge; New York: 2011. [Google Scholar]
- Nesselroade JR. Concepts of intraindividual variability and change: Impressions of cattell’s influence on lifespan development psychology. Multivariate Behavioral Research. 1984;19(2–3):269–286. doi: 10.1080/00273171.1984.9676929. [DOI] [PubMed] [Google Scholar]
- Pentz MA, Chou C. Measurement invariance in longitudinal clinical research assuming change from development and intervention. Journal of Consulting and Clinical Psychology. 1994;62(3):450–462. doi: 10.1037/0022-006X.62.3.450. [DOI] [PubMed] [Google Scholar]
- Prince-Embury S, Courville T. Measurement invariance of the resiliency scales for child and adolescents with respect to sex and age cohorts. Canadian Journal of School Psychology. 2008;23(1):26–40. [Google Scholar]
- Reynolds C, Kamphaus RW. Behavior assessment system for children. Circle Pines, MN: American Guidance Service; 1998. [Google Scholar]
- Robert C, Lee WC, CHAN K. An empirical analysis of measurement equivalence with the indcol measure of individualism and collectivism: Implications for valid cross-cultural inference. Personnel Psychology. 2006;59(1):65–99. [Google Scholar]
- Schmitt N, Kuljanin G. Measurement invariance: Review of practice and implications. Human Resource Management Review. 2008;18(4):210–222. [Google Scholar]
- Seymour KE, Chronis-Tuscano A, Halldorsdottir T, Stupica B, Owens K, Sacks T. Emotion regulation mediates the relationship between ADHD and depressive symptoms in youth. Journal of Abnormal Child Psychology. 2012;40(4):1–12. doi: 10.1007/s10802-011-9593-4. [DOI] [PubMed] [Google Scholar]
- Solomon SR, Sawilowsky SS. Impact of rank-based normalizing transformations on the accuracy of test scores. Journal of Modern Applied Statistical Methods. 2009;9(2):448–462. [Google Scholar]
- Steenkamp JEM, Baumgartner H. Assessing measurement invariance in cross-national consumer research. Journal of Consumer Research. 1998;25(1):78–90. doi: 10.1086/209528. [DOI] [Google Scholar]
- Steyer R, Eid M, Schwenkmezger P. Modeling true intraindividual change: True change as a latent variable. Methods of Psychological Research–Online. 1997;2:21–33. [Google Scholar]
- Vandenberg RJ, Lance CE. A review and synthesis of the measurement invariance literature: Suggestions, practices, and recommendations for organizational research. Organizational Research Methods. 2000;3(1):4–70. doi: 10.1177/109442810031002. [DOI] [Google Scholar]
- Volker MA, Lopata C, Smerbeck AM, Knoll VA, Thomeer ML, Toomey JA, Rodgers JD. BASC-2 PRS profiles for students with high-functioning autism spectrum disorders. Journal of Autism and Developmental Disorders. 2010;40(2):188–199. doi: 10.1007/s10803-009-0849-6. [DOI] [PubMed] [Google Scholar]
- Wicherts JM, Dolan CV. Measurement invariance in confirmatory factor analysis: An illustration using IQ test performance of minorities. Educational Measurement: Issues and Practice. 2010;29(3):39–47. [Google Scholar]
- Widaman KF, Ferrer E, Conger RD. Factorial invariance within longitudinal structural equation models: Measuring the same construct across time. Child Development Perspectives. 2010;4(1):10–18. doi: 10.1111/j.1750-8606.2009.00110.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Widaman KF, Reise SP. In: Exploring the measurement invariance of psychological instruments: Applications in the substance use domain. Bryant KJ, Windle M, West SG, editors. Washington, DC, US: American Psychological Association; 1997. pp. 281–324. [DOI] [Google Scholar]
- Yoo JP, Brown PJ, Luthar SS. Children with Co-Occurring anxiety and externalizing disorders: Family risks and implications for competence. American Journal of Orthopsychiatry. 2009;79(4):532–540. doi: 10.1037/a0017848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeller MH, Saelens BE, Roehrig H, Kirk S, Daniels SR. Psychological adjustment of obese youth presenting for weight management treatment. Obesity Research. 2004;12(10):1576–1586. doi: 10.1038/oby.2004.197. [DOI] [PubMed] [Google Scholar]