MEG Source Imaging Method using Fast L1 Minimum-norm and its Applications to Signals with Brain Noise and Human Resting-state Source Amplitude Images

Abstract

The present study developed a fast MEG source imaging technique based on Fast Vector-based Spatio-Temporal Analysis using a L1-minimum-norm (Fast-VESTAL) and then used the method to obtain the source amplitude images of resting-state magnetoencephalography (MEG) signals for different frequency bands. The Fast-VESTAL technique consists of two steps. First, L1-minimum-norm MEG source images were obtained for the dominant spatial modes of sensor-waveform covariance matrix. Next, accurate source time-courses with millisecond temporal resolution were obtained using an inverse operator constructed from the spatial source images of Step 1. Using simulations, Fast-VESTAL’s performance of was assessed for its 1) ability to localize multiple correlated sources; 2) ability to faithfully recover source time-courses; 3) robustness to different SNR conditions including SNR with negative dB levels; 4) capability to handle correlated brain noise; and 5) statistical maps of MEG source images. An objective pre-whitening method was also developed and integrated with Fast-VESTAL to remove correlated brain noise. Fast-VESTAL’s performance was then examined in the analysis of human mediannerve MEG responses. The results demonstrated that this method easily distinguished sources in the entire somatosensory network. Next, Fast-VESTAL was applied to obtain the first whole-head MEG source-amplitude images from resting-state signals in 41 healthy control subjects, for all standard frequency bands. Comparisons between resting-state MEG sources images and known neurophysiology were provided. Additionally, in simulations and cases with MEG human responses, the results obtained from using conventional beamformer technique were compared with those from Fast-VESTAL, which highlighted the beamformer’s problems of signal leaking and distorted source time-courses.

Introduction

MEG is a functional imaging technique that directly measures neuronal activity with millisecond temporal resolution. The key outcomes of MEG source imaging are the source locations and the source time-courses of neuronal activities responsible for the observed MEG field distribution. However, if no constraint is imposed, there are many sets of source configurations that can generate essentially the same MEG field distribution. To deal with this non-uniqueness, constraints must be imposed on sources by stipulating a “source model”. A conventional source model for MEG is a set of equivalent current dipoles (ECDs), a model that assumes focal neuronal current that can be modeled by one or more point-like dipoles. Automated multiple-dipole model algorithms such as multiple signal classification (MUSIC) (Mosher et al., 1992; Mosher and Leahy, 1998; Mosher et al., 1999a) and multi-start spatiotemporal (MSST) multiple-dipole modeling (Huang et al., 1998; Aine et al., 2000; Huang et al., 2000; Shih et al., 2000; Stephen et al., 2002; Hanlon et al., 2003; Stephen et al., 2003; Huang et al., 2004) have been studied and applied to the analysis of human MEG data. Yet, the ability of dipole models to adequately characterize neuronal responses is limited, due to 1) difficulties in modeling extended sources with ECDs and 2) problems in accurately estimating the number of dipoles in advance (Huang et al., 1998). Another type of source-modeling technique involves minimum L2-norm solutions (e.g., dSPM (Dale et al., 2000), MNE (Hamalainen, 2005), sLORETA (Pascual-Marqui, 2002)). In these approaches, source space (brain volume or cortex) is divided into a grid containing a large number of dipoles (typically several thousands). The inverse procedure obtains the dipole moment distribution across different grid nodes by minimizing the total power (L2 norm). This solution is obtained using a direct linear inverse operator (pseudo-inverse with regularization) of the lead-fields. However, the spatial resolution of the minimum L2-norm solution is low and often provides distributed reconstructions even if true generators are focal. Cross-talk between source time-courses of nearby grid points can also be high. The third type of source modeling is spatial filtering, which makes assumptions about the temporal properties of source time-courses. Conventional single-core beamformer approaches fall into this framework, and assume that different source time-courses are uncorrelated (Van Veen et al., 1997; Gross and Ioannides, 1999; Robinson and Vrba, 1999; Gross et al., 2001; Sekihara et al., 2001; Hillebrand and Barnes, 2003; Barnes and Hillebrand, 2003). The extent to which this “uncorrelated assumption” limits the application of the conventional beamformer remains debated (Dalal et al., 2006; Brookes et al., 2007; Diwakar et al., 2011a; Diwakar et al., 2011b), as most beamformer publications have not directly addressed the signal leaking and distortion problems of reconstructed source time-courses when neuronal sources are correlated. In evoked responses, electro-neurophysiology studies show that sources can be highly correlated because brain regions work together to achieve a task goal (Kandel et al., 2000).

Recent developments of dual-core Beamformer techniques from our lab and others sought to address the problem for highly-correlated sources and partially overcame this problem (Brookes et al., 2007; Diwakar et al., 2011a; Diwakar et al., 2011b). In addition, a recently-developed source reconstruction algorithm, Champagne (Owen et al., 2012), which uses an iterative approach to optimize a cost function related to the logarithm of the trace in data model covariance, performed better than several conventional approaches and was robust to noise, although its ability to accurately obtain the source time-courses was not evaluated (Owen et al., 2012).

A high-resolution MEG time-domain inverse imaging method was developed earlier in our lab, namely the VEctor-based Spatial-Temporal Analysis, which was based on a L1-minimum-norm solution (VESTAL or Standard-VESTAL), in which temporal information in the data is used to enhance the stability of the reconstructed L1-minimum norm solution (Huang et al., 2006). Advantages are that Standard-VESTAL: 1) can model many dipolar and non-dipolar sources; 2) requires no pre-determination of the number of sources (model order); 3) can resolve 100% temporally correlated sources; and 4) has substantially higher spatial resolution than many lead-field-based MEG source modeling techniques (Huang et al., 2006; Brang et al., 2010; Huang et al., 2010). Recently, Standard-VESTAL was expanded from the time-domain to the frequency-domain to effectively image oscillatory MEG signals, including complicated MEG slow-waves in patients with traumatic brain injury (Huang et al., 2009; Huang et al., 2012). The computational costs of Standard-VESTAL in the time- and frequency-domains are manageable, but they increase linearly with the number of time samples or frequency bins.

The present study presents an MEG source imaging technique based on L1-minimum-norm solution, called “Fast-VESTAL,” that immensely improves computational speed and other aspects of the source images. Using simulations, the performance of Fast-VESTAL is assessed for its: 1) ability to localize multiple correlated sources; 2) ability to faithfully recover source time-courses; 3) robustness to different SNR conditions (including SNR with negative dB levels); 4) capability to handle correlated brain noise; and 5) statistical maps of MEG source images. To handle signal with correlated brain noise, a new objective pre-whitening method was developed to separate noise and signal subspaces, and successfully remove correlated brain noise from the data. Then the results are presented from the application of Fast-VESTAL to the analysis of human MEG responses evoked by median-nerve stimulation. In addition, for the first time, the whole-brain Fast-VESTAL source-amplitude images are reported in different frequency bands for resting-state MEG data in 41 healthy subjects. Resting-state electromagnetic signals are one of the most widely examined human brain responses, dating back to the EEG alpha recording. Building on the work of Wienbruch and colleagues for low-frequency bands (Wienbruch, 2007), the present study produces a comprehensive set of source-based neuronal amplitude/power images that cover the whole brain for all frequency bands for the resting-state MEG/EEG recording. Comparisons between resting-state MEG sources-amplitude images and known neurophysiology are also provided. Lastly, performances of Fast-VESTAL, Standard-VESTAL, and conventional beamformer technique were compared for simulations and human MEG data.

Material and Methods

Theory of MEG Source Imaging using Fast-VESTAL

Source Imaging of the Dominant Spatial Modes

First, we take an imaging (lead-field) approach and divide the source space (gray-matter brain volume) into a grid of thousands of potential source locations. MEG time-domain signal in sensor-space can then be expressed in a data matrix: B = [b(t₁),b(t₂),…,b(t_T)], where t₁, t₂,…, t_T are time samples and T is the total number of time samples and b(t_i) is a M×1 vector containing the magnetic fields at M sensor sites at time sample t_i. This M×T data matrix can be expressed as:

$$\mathbf{B}=\mathbf{G}\mathbf{Q}+\mathbf{N}$$ Eq. (1)

where G is an M×2P gain (lead-field) matrix calculated from MEG forward modeling for the pre-defined source grid with P dipole locations, with each dipole location having two orthogonal orientations (i.e., θand ϕ). N is an M×T noise matrix. Q is a 2P×T source time-course matrix. In the spherical MEG forward head model, θand ϕ represent the two tangential orientations for each dipole location, whereas in a realistic MEG forward model using the boundary element method (BEM), the θand ϕ-orientations are obtained as the two dominant orientations from the singular-value decomposition (SVD) of the M×3 lead-field matrix for each dipole, as previously documented (Huang et al., 2006). The noise term in Eq. (1) is assumed to be Gaussian white noise. If correlated noise exists, pre-whitening procedures can be applied (Sekihara et al., 1997; Sekihara et al., 1999; Huang et al., 2006). In the present study, a new objective pre-whitening method was developed to effectively remove correlated brain and environmental noise from the data (see below). The inverse solution in Eq. (1) obtains the source time-courses Q for given MEG sensor wave-forms B. In general, for each time-sample, since the number of unknown parameters is far greater than the number of sensor measurements (i.e. 2P>>M), MEG source imaging is dealing with a highly under-determined problem, and there are a large number of solutions that fit the data. To reduce the ambiguity, additional constraints (source models) are needed.

In the present Fast-VESTAL approach, we first remove the time-dependent features from Eq. (1) and only focus on the spatial profiles. This is done by performing a SVD for the M×T MEG sensor waveform data matrix:

$$\mathbf{B}={\mathbf{U}}_B{\mathbf{S}}_B{\mathbf{V}}_B^T$$ Eq. (2)

In the typical case of M<T, the dimensions for U_B, S_B, and V_B are M×M, M×T, and T×T, respectively. All temporal information in the MEG sensor waveform can be represented as a linear combination of the singular vectors in the matrix V_B. In addition, SVD is performed for the gain matrix G:

$$\mathbf{G}={\mathbf{U}}_G{\mathbf{S}}_G{\mathbf{V}}_G^T$$ Eq. (3)

The dimensions for U_G, S_G, and V_G are M×M, M×2P, and 2P×2P, respectively. Substituting Eqs. (2)(3) into Eq. (1) and multiplying the result with V_B from the right side, we have:

$${\mathbf{U}}_B{\mathbf{S}}_B={\mathbf{U}}_G{\mathbf{S}}_G{\mathbf{V}}_G^T\mathbf{H}$$ Eq. (4)

The 2P×M matrix H = QV_B is called the source spatial map matrix for the given time window, and is independent of individual time samples. In the above deviation, we also use the fact that the white noise is uncorrelated with the MEG neuronal signals NV_B = 0.

Each column of U_B S_B is defined as a spatial mode of MEG sensor-waveforms. The significance of Eq. (4) is that each spatial mode in the sensor-waveforms be expressed as a linear combination of the corresponding source imaging maps (i.e., the columns of H). It is clear that the number of signal (i.e., dominant) spatial modes in a given MEG data set (usually ranges from a few to a tens of seconds) is substantially less than the number of time samples in the data (~100s to ~100,000s). Thus, by solving Eq. (4), the computational cost can be substantially reduced. This step of using temporal projection is similar to the temporal dimension reduction component of the Multiple Sparse Priors (MSP) method of Friston and colleagues (Friston et al., 2008).

Spatial-profile and Covariance Matrices of Sensor Waveforms

In practice, if the number of time samples is large, calculating the SVD of the sensor waveform matrix as in Eq. (2) can be time- and memory-consuming. However, what is really needed in the left hand side of Eq. (4) is U_B S_B, and this can be easily obtained as the SVD of the M×M, sensor-waveform-based, spatial-profile matrix R = BB^T:

$$\mathbf{R}=\mathbf{B}{\mathbf{B}}^T={\mathbf{U}}_B{\mathbf{S}}_B{{\mathbf{S}}_B}^T{{\mathbf{U}}_B}^T={\mathbf{U}}_B{\mathbf{\Sigma }}_B{{\mathbf{U}}_B}^T$$ Eq. (5)

where the diagonal elements in S_B are simply the square root (SQRT) of the corresponding eigenvalues of R which are the diagonal elements in Σ_B. If the sensor waveforms B are zero-mean across time for each MEG channel, R is the same as the sensor covariance matrix multiplied by the number of time samples T.

Fast-VESTAL Solution

Eq. (4) is under-determined, just like Eq. (1), with the number of unknown variables in each column of H = [h₁,h₂,…, h_k,…, h_M] (i.e., 2P) much larger than the number of measurements in each column of U_BS_B = [s₁u₁, s₂u₂,…,s_ku_k,…, s_Mu_M,] (i.e., M), so additional constraint(s) are needed to obtain a unique solution for Eq. (4). Here, the number of signal (dominant) spatial modes k is usually much smaller than the number of MEG sensor measurementsM. After multiplying from the left side with ${\mathbf{U}}_G^T$, for individual dominant spatial modes of Eq. (4), Eq. (4) can be written as:

$${\mathbf{U}}_G^T{\mathbf{u}}_i{s}_i={\mathbf{S}}_G{\mathbf{V}}_G^T{\mathbf{h}}_i,i=1,2,\dots ,k$$ Eq. (6)

where i =1,2,…, k are the indices of spatial modes in sensor space. The Fast-VESTAL solution to Eq. (6) is:

$$\text{min}({\mathbf{w}}^T|{\mathbf{h}}_i|),\text{subject to constrains}{\mathbf{S}}_G{{\mathbf{V}}_G}^T{\mathbf{h}}_i\cong {\mathbf{U}}_G^T{\mathbf{u}}_i{s}_i,i=1,2,\dots ,k$$ Eq. (7)

where the 2P×1vector h_i is the source imaging map associated with the dominant spatial mode vector u_i (dimension M×1) of the sensor-domain. In Eq. (7), w is a 2P×1 weighting vector chosen to remove potential bias towards grid nodes at the superficial layer and it is usually taken to be the column norm of the G matrix (Matsuura and Okabe, 1997; Uutela et al., 1999; Huang et al., 2006) or a Gaussian function (Ioannides et al., 1993). In the present study, $\mathbf{w}=\sqrt{\mathit{\text{diag}}({\mathbf{V}}_G{\mathbf{V}}_G^T)}$ was chosen to remove some small bias for the reconstructed source locations in the above choices of w.

In general, the solution to Eq. (7) is a non-linear minimization procedure since the source imaging maps h_i (associated with dominance spatial mode u_i) can be either positive or negative. However, in practice, one can always replace the absolute values in |h_i| with the following two sets of non-negative values related to h_i, and solve the set of equations through linear programming (LP). Specifically, with the introduction of two new non-negative variables ${\mathbf{h}}_i^a$ and ${\mathbf{h}}_i^b$ (Eiselt et al., 1987), Eq. (7) can be re-written as:

$$\text{min}\left({\mathbf{w}}^T\right({\mathbf{h}}_i^a+{\mathbf{h}}_i^b\left)\right)\text{subject to}{\mathbf{S}}_G{{\mathbf{V}}_G}^T{\mathbf{h}}_i\cong {\mathbf{U}}_G^T{\mathbf{u}}_i{s}_i,{\mathbf{h}}_i={\mathbf{h}}_i^a-{\mathbf{h}}_i^a,i=1,2,\dots ,k,$$ Eq. (8)

Eq. (8) can be solved readily by several LP packages. In the present study, SeDuMi (http://sedumi.ie.lehigh.edu/) is used to solve the above equation-set to get source imaging h_i for each dominant spatial mode u_i of sensor-domain signal. This step is repeated for all dominant spatial modes to obtain the final Fast-VESTAL source image matrix H. The computational cost of Fast-VESTAL is proportional to the number of dominant (signal-related) spatial modes k which is usually much fewer than the number of time samples.

The Fast-VESTAL source imaging result can be plotted on the source grid as:

$$\mathbf{A}=\sqrt{\mathit{\text{diag}}\left(\mathbf{H}{\mathbf{H}}^T\right)/T}$$ Eq. (9)

which is the 2P×1 root-mean-square (RMS) source amplitude value, mean across time at each grid node. The main feature of A is that it is highly sparse, with many of its elements being either zero or close to zero, as a direct consequence of L1-norm minimization.

One problem that must be addressed by the minimum L1-norm approach is that the solution has a small tendency (bias) towards the coordinate axes. For example, in spherical MEG head model, for a dipole at the i^th node of the grid, the vector-based L1-minimum norm solution can also be expressed as minimizing $\sum _{i=1}^P{w}_i{\omega }_i(|\text{cos}({\psi }_i)|+|\text{sin}({\psi }_i)|)$ where ψ_i is the angle between total dipole moment and the orientation of the elevation in a tangential plane containing the dipole node, and ${\omega }_i=\sqrt{{\left({\omega }_i^{\theta }\right)}^2+{\left({\omega }_i^{\varphi }\right)}^2}$ is the non-negative dipole strength. This will introduce a bias towards the coordinate axes (Fig. 1 in (Huang et al., 2006)). To handle this small bias, an additional correction factor ${(|\text{cos}({\psi }_i^e)|+|\text{sin}({\psi }_i^e)|)}^{-1}$ was included in the weighting vector w in Eq. (8) for one more iteration, where ${\psi }_i^e$ is the angle associated with the estimated orientation based on L1-minimum norm solution without the correction factor (Huang et al., 2006; Huang et al., 2012).

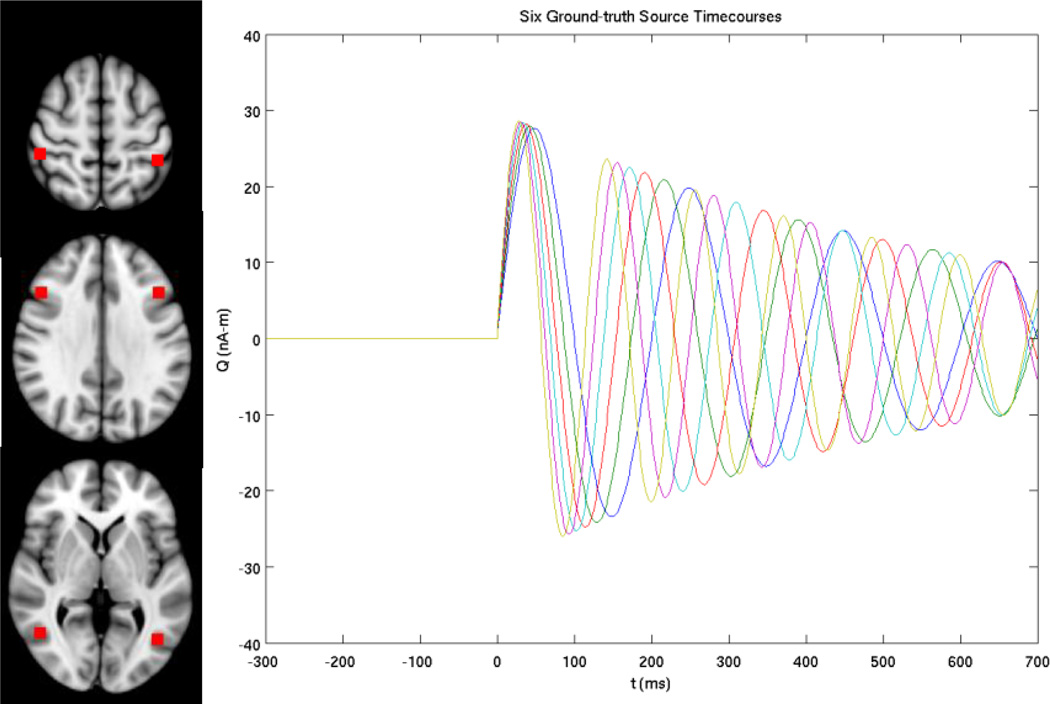
Figure 1.

Left panel: ground-truth locations of six simulated sources. Right panel: six correlated source time-courses used in computer simulations to mimic evoked response, with 300 ms for pre-stimulus and 700 ms for post-stimulus intervals.

Obtain the Source Time-courses in Fast-VESTAL

A main advantage of MEG over other functional imaging techniques (e.g., fMRI and PET) is its excellent temporal resolution. To capitalize on this, it is essential that a source imaging approach not only accurately localizes the neuronal activities, but also faithfully recovers the source time-courses with high temporal resolution.

In the present study, the spatial images obtained by Fast-VESTAL in Eq. (9) were used to obtain the source time-courses. Here, an inverse operator matrix was adopted and directly applied to the sensor waveform matrix B(t). First, the Fast-VESTAL spatial image in Eq. (9) is assigned as a weighting variable to the gain (lead-field) matrix:

$$\mathbf{G̃}=\mathbf{G}•\left(\mathbf{J}{\mathbf{A}}^T\right)$$ Eq. (10)

where J = [1,1,…, 1]^T is a M×1 vector of ones, and • indicates the element-wise matrix product. G̃ is the M×2P weighted gain (lead-field) matrix with each of the 2P columns weighted by the 2P elements from A in Eq. (9). Since the source maps from the Fast-VESTAL are highly sparse with most of its elements being zero or near zero, the M×2P weighted gain matrix G̃ is also sparse. Using the SVD of this weighted gain matrix,

$$\mathbf{G̃}={\mathbf{U}}_{\mathrm{G̃}}{\mathbf{S}}_{\mathrm{G̃}}{\mathbf{V}}_{\mathrm{G̃}}^T$$ Eq. (11)

Then the 2P×M linear inverse matrix G̃⁺ for G̃ can be constructed as:

$${\mathbf{G̃}}^{+}={\mathbf{V}}_{\mathrm{G̃}}{({\mathbf{S}}_{\mathrm{G̃}}+\alpha \mathbf{I})}^{-1}{\mathbf{U}}_{\mathrm{G̃}}^T$$ Eq. (12)

in which I is an identity matrix and α is the regularization parameter. The reconstructed, best-fitting, source time-courses of Fast-VESTAL solution are then obtained using such a linear inverse operator G̃⁺

$$\mathbf{Q̂}\cong [{\mathbf{G̃}}^{+}•(\mathbf{A}{\mathbf{J}}^T\left)\right]\mathbf{B}={\mathbf{G̃}}_{\mathbf{A}}^{+}\mathbf{B}$$ Eq. (13)

Here, the 2P×M inverse operator matrix ${\mathbf{G̃}}_A^{+}$ is called the Fast-VESTAL source time-course operator. The millisecond-by-millisecond source time-course matrix Q̂ (dimension 2P×T) is simply obtained by applying ${\mathbf{G̃}}_A^{+}$ to the sensor waveform matrix B as shown in Eq. (13). In short, the estimated Fast-VESTAL source time-course Q̂ is related to the A in Eq. (13), and A is related to Fast-VESTAL spatial source map matrix H in Eq. (9).

The goodness-of-fit to the MEG Sensor Signals

The goodness-of-fit to the MEG sensor waveform may be obtained by comparing the predicted sensor waveform using the best-fitting source time-courses from Eq. (13) to the measured MEG sensor waveforms. In fact, the goodness-of-fit can be calculated directly from Eq. (13) without needing to calculate the predicted MEG sensor waveforms. In this approach, the best-fitting source spatial-profile matrix or the source covariance matrix can also be obtained as:

$${\mathbf{R̂}}_{\mathit{\text{SOURCE}}}={\mathbf{G̃}}_{\mathbf{A}}^{+}\mathbf{R}{\mathbf{G̃}}_{\mathbf{A}}^{{+}^T}$$ Eq. (14)

Then, the best-fitting sensor spatial-profile matrix or the sensor covariance matrix can be expressed as:

$$\mathbf{R̂}=\mathbf{G}{\mathbf{R̂}}_{\mathit{\text{SOURCE}}}{\mathbf{G}}^T$$ Eq. (15)

The goodness-of-fit measure of the MEG sensor signals is then calculated using the diagonal elements of both the measured and the predicted sensor spatial-profile matrix or the sensor covariance matrix:

$$\mathit{\text{Goodness}}\_\mathit{\text{of}}\_\mathit{\text{fit}}=(1-\frac{\sum _{i=1}^M{(R_{ii}-{\mathrm{R̂}}_{ii})}^2}{\sum _{i=1}^M{R_{ii}}^2})\times 100\%$$ Eq. (16)

Setup for Computer Simulations using White Noise

In the present study, computer simulations were used to assess three key issues related to the performance of Fast-VESTAL: 1) the algorithm’s ability to localize multiple correlated sources, 2) the algorithm’s performance for different SNR conditions with white as well as real brain noise, and 3) the algorithm’s accuracy of reconstruction of source time-courses.

The source grid used by Fast-VESTAL was obtained by sampling the gray-matter areas from the T1-weighted MRI of each subject (Huang et al., 2012). The processing pipeline includes the following steps: 1) The T1-weighted MR images from a subject are registered to a standard atlas (e.g., MNI-152) using registration programs in FSL (www.fmrib.ox.ac.uk/fsl/). 2) The cortical, subcortical, and cerebellum gray-matter masks with pre-defined brain regions from the standard atlas in FSL are transferred to the individual subject’s coordinates, using the inverse of the transformation in the first step. In this step, the Harvard-Oxford Atlas (part of the FSL software) is used to parcellate gray matter into 96 cortical gray-matter regions (48 in each hemisphere), 15 subcortical regions, and the cerebellum. 3) The regional masks in the subject are re-sampled to a cubic source grid with 5mm size for Fast-VESTAL analysis, which leads to a grid with ~7,000 nodes. A realistic BEM head model was used for MEG forward calculation, with the BEM mesh obtained from tessellating the inner skull surface from the MRI into ~6000 triangular elements with ~5mm size.

The performance of Fast-VESTAL was first examined using six simulated dipolar sources (Fig. 1, left panel). Correlated source time-courses (ground-truth) were assigned to these sources to mimic evoked responses with 300 ms pre-stimulus and 700 post-stimulus intervals (Fig. 1, right panel). MEG sensor waveforms were calculated using the BEM model (Mosher et al., 1999b; Huang et al., 2007) for the sensor configuration of Elekta/Neuromag VectorView™ whole-head MEG system (Elekta-Neuromag, Helsinki, Finland) with 306 MEG channels that contains 204 planar gradiometers and 102 magnetometers. These 6 sources were placed as follows: two at L-R middle frontal gyri, two in L-R postcentral gyri and superior parietal lobules, and two in L-R lateral occipital cortex (Fig. 1). The ground-truth orientations of these 6 sources were [−0.14, −0.75, 0.64], [−0.52, 0.40, 0.76], [−0.78, 0.17, −0.60], [0.01, 0.99, 0.11], [−0.16, 0.14, 0.98], and [0.47, 0.80, −0.37], respectively. Three different levels of random white noise were added to the sensor wave forms to examine Fast-VESTAL’s performance in reconstructing the source locations and source time-courses. After adding the three levels of white noise, the SNRs of the noisy MEG sensor waveforms were at 3.74 (White-noise Level-1), 1.24 (White-noise Level-2), and 0.53 (White-noise Level-3) respectively for the entire interval, and were at 4.46, 1.48, and 0.64 respectively for the post-stimulus interval, as measured by Frobenius norms (see Results). Since statistical analyses (see below) depend on some noise in the pre-stimulus interval, a negligible amount of white noise (“Level-0”) to the noiseless was added to MEG sensor waveform with the SNR > 10⁶. Since the SNR was quite high for Level-0, this condition is referred to as “Noiseless” throughout this paper.

The selection of the number of dominant signal modes k in S_B in Eq. (4) is straightforward for data with white noise. The selection of k was based on the “L-shaped” nature of the singular value curve of the MEG sensor signal in Eq. (2) or equivalently the SQRT of eigenvalues of the sensor covariance matrix in Eq. (5), allowing us to effectively separate the signal subspace from the noise subspace (see Results)-- a procedure widely used in processing MEG data (Mosher et al., 1992; Mosher and Leahy, 1998; Huang et al., 2006; Sekihara et al., 2008).

New Objective Pre-whitening Method to Handle Correlated Brain Noise with Pre-whitening, Eigenvalue Plots, and Objective Threshold

When studying human MEG responses, correlated environment noise and especially brain noise are common; this is different from white noise. In situations with correlated noise, the determination of signal (i.e., dominant) spatial modes k becomes challenging. The pre-whitening method has been introduced to handle correlated noise (e.g., (Sekihara et al., 1997; Sekihara et al., 1999)). In these studies using simulated correlated noise, if one has complete knowledge of the correlated noise, the pre-whitening step effectively determines the signal subspace and removes the correlated noise. However, it remains a topic of research as to how correlated brain noise should be handled in realistic situations when only incomplete or non-simultaneously collected information about the correlated noise is available. A typical example is evoked MEG responses, wherein brain (correlated) noise can be estimated during the pre-stimulus interval, but not during the post-stimulus interval when the evoked signal mixes with the brain noise. Another example is when brain noise used for pre-whitening is collected before or after the actual task session. So in practice, one must find: 1) an objective way to measure the efficacy of the prewhitening step, 2) an additional procedure to further remove residual correlated noise when prewhitening step is not completely successful, and 3) an objective way to identify noise subspace in the pre-whitened signal covariance matrix.

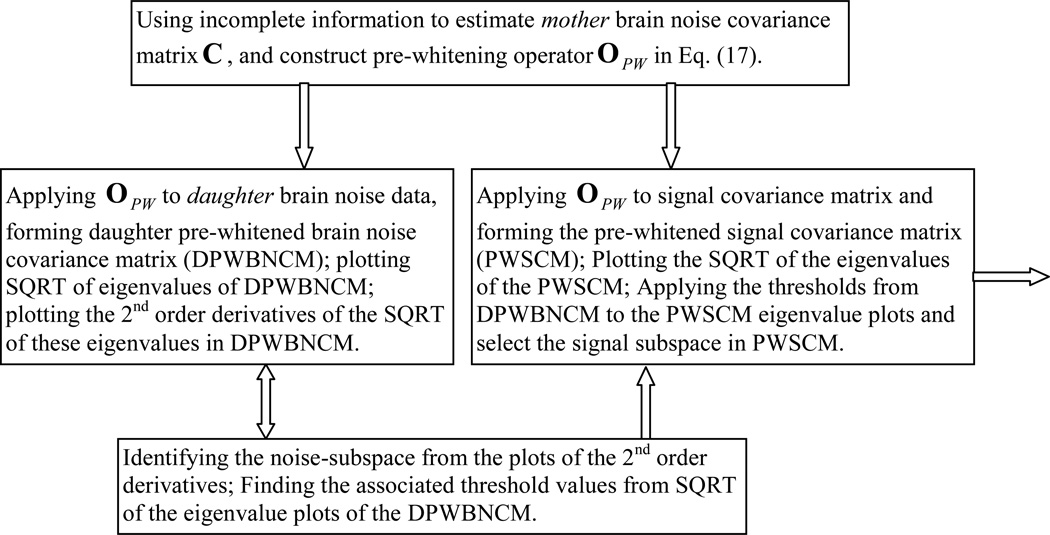
In the present study, a new Objective Pre-whitening Method (OPWM) was developed to address the above challenges for effectively removing correlated brain noise. Our OPWM contained four steps as shown in Fig. 2: 1) Estimating a “mother” correlated brain noise covariance matrix based on incomplete information and constructing a pre-whitening operator (see below), which was then applied to a series of “daughter” brain noise data sets, thereby forming a series of daughter pre-whitened brain noise covariance matrices (DPWBNCM); 2) plotting the SQRT of eigenvalues of these DPWBNCM, and plotting the second-order derivatives of the SQRT of eigenvalues of DPWBNCM. If the pre-whitening step does not completely remove the correlated brain noise (it is often the case), the leading second-order derivatives will be substantially different from zero. 3) Identifying the noise-subspace from the plots of the second-order derivatives of eigenvalues of DPWBNCM and finding the associated threshold values from the SQRT of the eigenvalue plots of the DPWBNCM; and 4) Applying the pre-whitening operator to the signal covariance matrix to obtain the pre-whitened signal covariance matrix (PWSCM), and then applying the thresholds from the DPWBNCM in Step 3 to the PWSCM eigenvalue plots and selecting the signal subspace in the PWSCM.

Figure 2.

A flow-chart of the Objective Pre-whitening Method (OPWM) for removing correlated brain noise from the data. The same process was applied to remove correlated environmental noise when replacing the DPWBNCM in the chart with the daughter pre-whitened empty-room covariance matrix (DPWERCM).

Pre-whitening Step

In the pre-whitening step, eigenvalue decomposition (EVD) is first performed on an estimated M×M mother noise covariance matrix (see later for how to obtain such a matrix) $\mathbf{C}={\mathbf{U}}_C{\mathbf{\Omega }}_C{\mathbf{U}}_C^T$, and then an M×M pre-whitening operator is constructed:

$${\mathbf{O}}_{PW}={\mathbf{U}}_C{\mathbf{\Omega }}_C^{-1/2}{\mathbf{U}}_C^T$$ Eq. (17)

Next, the pre-whitening operators are applied to the gain matrices in Eqs. (1)(2)(11), MEG sensor waveforms in Eqs. (1)(2)(13), or sensor covariance matrices in Eqs. (5)(14):

$${\mathbf{G}}_{PW}={\mathbf{O}}_{PW}\mathbf{G};{\mathbf{G̃}}_{PW}={\mathbf{O}}_{PW}\mathbf{G̃};\mathbf{B}{(t)}_{PW}={\mathbf{O}}_{PW}\mathbf{B}(t);{\mathbf{R}}_{PW}={\mathbf{O}}_{PW}\mathbf{R}{\mathbf{O}}_{PW}^T$$ Eq. (18)

The rest of the formulation of Fast-VESTAL takes the same format when replacing these matrices with their corresponding pre-whitening ones. Note that after the pre-whitening step, the MEG sensor waveforms and sensor covariance matrices will become dimensionless (i.e., ratio scores). In our implementation of Eq. (17), the calculation of ${\mathbf{\Omega }}_C^{-1/2}$ was based on the top 60 largest singular values in Ω_C, due to the fact that the later matrix becomes rank 64 after applying MaxFilter to any data set in the Elekta MEG system (Taulu et al., 2004a; Taulu et al., 2004b; Song et al., 2008).

Brain-noise data

To examine the robustness of Fast-VESTAL in realistic situations of correlated brain noise, MEG brain-noise was collected from a healthy subject when he was watching a fixation point for over 2 hours, in multiple sessions of 5-minute recordings from different days. After co-registering these data sessions and removing epochs containing eye-blinks, eye-movements, and other artifacts using MaxFilter (see below), the fixation brain signals were divided into a pool of over 6,100 epochs that were free of artifacts, each of 1000 ms duration. Using these data, three levels of brain noise were constructed to match the noise levels of the three white-noise conditions based on Frobenius norms. The numbers of randomly selected epochs for signal averaging in each of the three brain-noise conditions were: 125, 14, and 3, respectively. These conditions were referred as brain-noise Levels-1, 2, and 3.

Assessing the efficacy of pre-whitening using only brain-noise data

Before the realistic brain noise was added to the simulated signal to challenge the performance of the Fast-VESTAL algorithm, the robustness of the estimated mother noise-covariance matrix in removing correlated brain noise was first examined. In practice, the estimation of the mother noise covariance is always based on partial information. Thus, the estimated mother covariance matrix of correlated brain noise was constructed using the pre-stimulus interval partial data (not the entire interval), assuming that the pre-whitening step removes the correlated noise for the entire interval, including the post-stimulus section.

A Monte-Carlo approach was used to evaluate the efficacy of the pre-whitening approach. For each brain-noise condition, 40 sets of epochs, each epoch lasting 1000 ms, were randomly selected from our pool of over 6,100 epochs of human brain-noise recordings. Specifically, for the brain-noise Level-1 condition, each of the 40 sets of epochs contained 125 trials that were then averaged (i.e., 5,000 total epochs). In each set, the mother brain-noise covariance matrix was estimated from the first 300 ms interval of the averaged data, and the pre-whitening step was run through the entire 1000 ms interval (i.e., daughter brain-noise condition) using Eqs. (17) and (18). Next, the SQRT of the eigenvalues of the daughter pre-whitened brain-noise covariance matrix (DPWBNCM) was plotted for the entire interval. As shown in the Results section, these plots and their second-order derivatives objectively assessed the quality of the pre-whitening step and provided an objective way to separate signal subspace from the noise subspace. This procedure was repeated for the conditions with brain-noise Level-2 (14 trials averaging) and Level-3 (3 trials averaging). It is important to emphasize that no simulated signal was added during this procedure – only brain-noise data were involved in the analyses.

Analyzing Human Median-nerve MEG response

The performance of Fast-VESTAL was further examined using human MEG responses evoked by unilateral median-nerve stimulation. This task is particularly relevant, owing to our excellent understanding of the underlying neuronal activity, which allows us to predict with a high degree of confidence where sources should be found, and hence to confirm or refute the correctness of the calculated source localizations. MEG recordings were conducted from a healthy subject as he underwent right median-nerve stimulation using a bipolar Grass™ constant current stimulator. The stimuli were square-wave electric pulses (0.2 ms duration) delivered at about 1 Hz (ISI: 800 ms to 1200 ms). The intensity of the stimulation was adjusted until robust thumb twitches were observed. Magnetic fields evoked by median-nerve stimulation were measured using our Elekta/Neuromag™ whole-head Vectorview™ MEG system in a 6-layer magnetically shielded room (IMEDCO-AG, Switzerland) (Cohen et al., 2002). EOG electrodes were used to detect eye blinks and eye movements. An interval of 500 ms post-stimulus was recorded, using 300 ms pre-stimulus data for constructing the noise covariance matrix for pre-whitening. Data were sampled at 1000 Hz and run through a high-pass filter with 0.1 Hz cut-off and through a notch filter (58–62 Hz) to remove 60Hz power-line noise. Two hundred artifact-free responses were averaged with respect to the stimulus trigger to increase the SNR. Maxfilter, also known as signal space separation (Taulu et al., 2004a; Taulu et al., 2004b; Song et al., 2008), was used to remove external interferences. A five-minute session of resting-state brain noise (eyes-open), collected from the same subject on a different day, was used to examine the efficacy of the pre-whitening step and to identify the noise subspace.

MEG Resting-state Recording in Healthy Subjects

To examine the performance of Fast-VESTAL technique for spontaneous data, Fast-VESTAL was applied to obtain whole-brain source imaging for resting-state MEG data in standard frequency bands. Study participants included 41 healthy control subjects with no history of neurological or psychiatric disorders (age 26.7 ± 8.4 years, 34 males). Three blocks of resting-state MEG data with eyes-closed for 5 minutes were collected for each block using the same Elekta/Neuromag VectorView™ whole-head MEG system. During the recording, subjects were instructed to keep their eyes closed and empty their mind. Data were sampled at 1000 Hz and were run through a high-pass filter with 0.1 Hz cut-off and a low-pass filter with 330 Hz cut-off. Eye blinks, eye movements, and heart signals were monitored. Precautions were taken to ensure head stability: foam wedges were inserted between the subject’s head and the inside of the unit, and a Velcro strap was placed under the subject’s chin and anchored in superior and posterior axes. The head positions were measured to ensure that head movement across different sessions was less than 5 mm (usually 2–3 mm).

MEG eyes-closed data were first run through MaxFilter to remove external interferences (e.g., magnetic artifacts due to metal objects, strong cardiac signals, environment noise, etc.) and to co-register the MEG data by removing the small head movements across the three 5-min eyesclosed sessions. Next, residual artifacts near the sensor array due to eye movements and residual cardiac signals were removed using Independent Component Analysis. The software is our customized version of ICALAB (bsp.brain.riken.jp/ICALAB/). The EKG artifacts in the MEG data were also removed when the MEG data were passed through MaxFilter. This feature of MaxFilter has been described previously (Taulu et al., 2004a; Taulu et al., 2004b; Song et al., 2008). Removal of EKG artifacts using MaxFilter is quite straightforward since EKG signals clearly represent magnetic fields in the Vector Spherical Harmonic Expansion (in signal space separation), external to the MEG sensor array.

Structural MRIs of the subject’s head were collected using a General Electric 1.5T Excite MRI scanner (ver. 14 software release). The acquisition contains a standard high-resolution anatomical volume with a resolution of 0.94×0.94×1.2 mm³ using a T1-weighted 3D-IR-FSPGR pulse sequence. To co-register the MEG with MRI coordinate systems, three anatomical landmarks (i.e., left and right pre-auricular points, and nasion) were measured for each subject using the Probe Position Identification system (Polhemus, USA). By identifying the same three points on the subject's MR images using MRILAB software developed by Elekta/Neuromag, a transformation matrix involving both rotation and translation between the MEG and MR coordinate systems was generated. To increase the reliability of the MEG-MR co-registration, approximately 80 points on the scalp were digitized with the Polhemus system, in addition to the three landmarks, and those points were co-registered onto the scalp surface of the MR images. Based on our experience with the MEG median-nerve task, which reliably produces primary somatosensory cortex responses for hand representations that are associated with unique anatomical landmarks (Huang et al., 2000; Huang et al., 2006), the MEG-MR co-registration error is expected to be less than 3 mm. The T1-weighted images were also used to extract the innermost skull surface (SEGLAB software developed by Elekta/Neuromag). The innermost skull surface was used to construct a realistic head model for MEG forward calculation based on the BEM model (Mosher et al., 1999b; Huang et al., 2007).

To analyze the human resting-state data and assess statistical significance (see below), 41 sets of “empty-room” data sets were acquired when no human subjects were inside the MEG scanner. An extra set of empty-room data was used to estimate the mother noise covariance matrix in the OPWM step. These empty-room data sets (each lasting about 2 minutes) were collected over a 3-year period that coincided with the human resting-state recordings. The new OPWM developed for simulated signal with brain noise and the human median-nerve response was applied in the resting-state data analyses. Here, to remove the correlated noise from the environment, an estimated mother noise covariance matrix was first constructed using the extra empty-room data set, and the pre-whitening operator Eq. (17) was then built from the mother noise covariance matrix. Next, the pre-whitening operator was applied to each of the 41daughter empty-room data sets to create the daughter pre-whitened empty-room covariance matrices (DPWERCM). The SQRT of the eigenvalues from the DPWERCM provided the objective threshold for distinguishing noise subspace from the signal subspace. This threshold was used in the Fast-VESTAL analysis of the pre-whitened data covariance matrices for the 41 empty-room data sets and the resting-state data from 41 human subjects (see Results). For comparison, a beamformer analysis was applied to the same 82 pre-whitened data sets.

Assessing the Statistical Significance of the Fast-VESTAL Results

An approach was developed to assess the statistical significance of the Fast-VESTAL results and then was used to construct statistical maps of the neuronal activities. For the simulation data with different noise levels, F-tests assessed the variances between the post-stimulus 700 ms interval over the pre-stimulus 300 ms interval for each grid node. The F-value maps for the Fast-VESTAL solution were constructed for the ~7000 grid nodes. False discovery rate (FDR) corrected for multiple comparisons (corrected p=0.01) was employed. Additional thresholding based on the post-stimulus RMS value of 0.3 nA-m was applied. Grid nodes with activities below the threshold were considered not detectable and excluded from the statistical analysis.

To assess statistical significance in the analyses of resting-state MEG data, Fast-VESTAL was used to analyze 41 data sets from human resting-state recordings and 41 empty-room data after pre-whitening and objective selection of the signal subspace (see above). After a square-root transformation, all source images were registered to the MNI-152 brain-atlas coordinates using FLIRT software in FSL, and spatially smoothed using 5-mm Gaussian kernel to reduce inter-subject anatomical difference. The Fast-VESTAL results from the empty-room data sets served as the control group to evaluate the statistical significance of source amplitudes from the human resting-state data in two-tailed t-tests. T-test values were plotted as statistical maps across the grid nodes, using FDR correction (corrected p=0.01). The same statistical procedures were applied to the source images obtained from the beamformer analysis.

Other Parameter Settings in Fast-VESTAL

As with any MEG source imaging technique, optimal performance of Fast-VESTAL depends on the settings of certain parameters. In Fast-VESTAL, three parameters need to be set: 1) the number of dominant singular values in S_G from the SVG of the MEG gain (lead-field) matrix G in Eq. (4); 2) the regularization parameter α in the inverse operator G̃⁺ in Eq. (12) to obtain the Fast-VESTAL source time-courses; and 3) the number of dominant signal modes k in S_B from the SVD of the MEG sensor waveform in Eq. (2), or equivalently in the sensor covariance matrix in Eq. (5) for white-noise conditions, and the corresponding ones in Eq. (18) for signal with correlated brain-noise after the pre-whitening step. In previous sections, detailed descriptions of the new approach were provided, and the results demonstrated that this approach can differentiate the noise subspace from the signal subspace and objectively estimates dominant signal modes k, for the conditions with real correlated brain-noise.

The setting of the other two parameters was straightforward without any iterations and/or updating procedures. In all simulations and processing of empirical MEG data using Fast-VESTAL, the parameter α was set at 5% of the largest singular values in S_G̃ in Eq. (12), the number of dominant singular values in S_G was set to 80 in Eq. (4), and all other smaller singular values in S_G were set to be zero. These settings were independent of the MEG signals or the noise levels (see Results).

Results

Computer Simulation Result with White Noise, Correlated Sources, and Different SNRs

Different levels of white noise were added to the MEG sensor waveforms calculated from the 6 sources, which are shown in Figs. 3(A)(E)(I)(M) where 204 planar gradiometers were superimposed. SNR was defined as the ratio of the Frobenius norms of the noiseless MEG sensor waveform matrix over the random white sensor noise waveform matrix. For the whole 1000 ms time interval, the SNRs for the simulated noisy data sets were at 1.86×10⁶ (125.4 dB); 3.74 (11.45 dB); 1.24 (1.90 dB); and 0.53 (−5.49 dB), corresponding to noise Levels 0 (“noiseless”), 1, 2, and 3 respectively. For just the post-stimulus interval, the SNRS were at 2.23×10⁶ (126.9 dB) for the “noiseless” Level-0; at 4.46 (12.90 dB) for Level-1; at 1.48 (3.45 dB) for Level-2; and at 0.64 (−3.95 dB) for Level-3. Fast-VESTAL was used to reconstruct the source locations and source time-courses. In all cases, the number of dominant signal modes in S_B (i.e., size of the signal subspace) was selected to be 6, based on the “L-shape” singular value curve (see below). Standard-VESTAL and beamformer methods were also used to reconstruct the location and source time-courses. The noise features in the sensor waveforms from 102 magnetometers was similar (not shown) to that of the gradiometers.

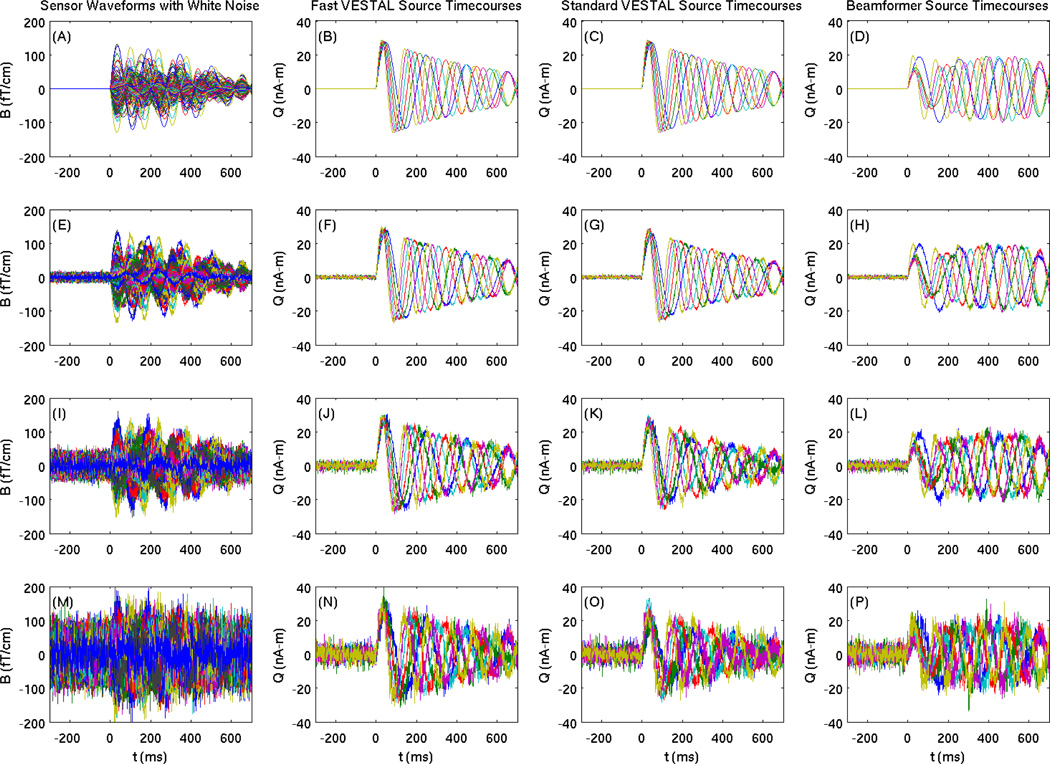
Figure 3.

Simulated MEG sensor waveforms added white noise (first column) and source time-courses reconstructed from Fast-VESTAL (second column), Standard-VESTAL (third column), and beamformer (fourth column). Each row displays the data for different white-noise levels. Row 1: white-noise Level-0 (post-stimulus SNR=2.23×10⁶ or 126.9dB); Row 2: white-noise Level-1 with post-stimulus SNR=4.46 or 12.90 dB; Row 3: white-noise Level-2 with poststimulus SNR=1.48 or 3.45 dB; and Row 4: white-noise Level-3 with post-stimulus SNR=0.64 or −3.95 dB.

Source Time-course Reconstruction

The 6 source time-courses reconstructed by Fast-VESTAL (Eq. (13)) for the noise levels 0–3 are shown in Figs. 3(B)(F)(J)(N). Good reconstructions, in terms of shape, onset, and amplitude, were obtained for all 6 source time-courses, including the high-noise-level condition. In calculating each of the reconstructed source time-courses, the activities were summed up via SVD from all voxels within 10 mm from the center voxel with the strongest activities in each of the 6 clusters.

The reconstructed source time-courses from the Standard-VESTAL (Figs. 3(C)(G)(K)(O)) were highly similar to those from the Fast-VESTAL, although more noise was seen in the standard VESTL results for the high noise levels (Fig. 3(K)(O)). For noise Level-0 (noiseless), the reconstructed source time-courses from both Fast-VESTAL (Fig. 3(B)) and Standard-VESTAL (Fig. 3(C)) were virtually identical to the ground-truth source time-courses with strong correlations (Fig. 1). In addition, a beamformer was used to analyze the same simulated data with the reconstructed source time-courses shown in Figs. 3(D)(H)(L)(P). In the beamformer solution, the nodes with maximum F-values (see below) within 10 cm from the true source locations were selected. All constructed source time-courses using the beamformer exhibited substantial distortions, even for the noiseless condition.

Table 1 lists the percent variance explained (PVE) in the reconstructed source time-courses relative to the ground-truth source time-courses by Fast-VESTAL, Standard-VESTAL, and the beamformer solutions. For each source, the PVE of source time-courses was defined as: $PV{E}_q=(1-\frac{\sum _i{(q_i(t)-{\mathrm{q̂}}_i(t))}^2}{\sum _i{q}_i{(t)}^2})\times 100\%$, where the q(t) and q̂(t) are the ground-truth and reconstructed source time-courses, respectively. The upper-left panel of the table lists the range of PVE for the 6 sources at different white-noise levels. The PVE values from Fast-VESTAL solutions were in the upper 90s% to 100% range for white-noise Levels 0–2, and between 83.9% to 94.5% for the Level-3 condition where the SNR was substantially less than one. The PVE values from the Standard-VESTAL solution were quite high as well, but less than those from the Fast-VESTAL. In contrast, the PVE from the beamformer-reconstructed sources were markedly lower, even at the noiseless (Level-0) condition, indicating substantial distortions in the reconstructed source time-courses.

Table 1.

1) The percent variance explained (PVE) in the reconstructed source time-courses; 2) PVE of inter-source cross correlation (ICC) among reconstructed source time-courses (lower-left triangle in Fig. 4). The comparisons are made for the solutions from Fast-VESTAL, Standard-VESTAL, and Beamformer; and arranged separately for white noise (left half) from the real brain noise (right half). Orientations errors were also listed.

Source Time-course PVE (%), White Noise				Source Time-courses PVE (%), Brain Noise
Noise Levels	Fast VESTAL	Std VESTAL	Beamformer	Fast VESTAL	Std VESTAL	Beamformer
Level-0	100.0 – 100.0	100.0 – 100.0	77.5 – 89.9	---	---	---
Level-1	99.6 – 99.9	99.0 – 99.8	77.2 – 89.5	97.7 – 99.2	95.7 – 99.4	60.0 – 91.6
Level-2	96.9 – 98.9	86.8 – 95.7	74.2 – 87.3	87.4 – 96.2	70.5 – 90.5	58.7 – 78.3
Level-3	83.9 – 94.5	78.1 – 93.3	60.7 – 77.9	43.6 – 87.3	33.5 – 85.7	9.3 – 59.0
ICC PVE (%), White Noise				ICC PVE (%), Brain Noise
Level-0	100.0	100.0	8.7	---	---	---
Level-1	99.7	99.5	8.7	99.5	92.4	18.4
Level-2	99.7	93.5	8.9	96.9	71.1	18.2
Level-3	98.4	92.4	13.2	60.2	45.1	15.5
Orientation error (deg), White Noise				Orientation error (deg), Brain Noise
Level-0	0.0 – 0.0	0.0 – 0.0	0.2 – 8.0	---	---	---
Level-1	0.1 – 0.5	0.2 – 0.7	0.3 – 8.1	0.1 – 1.5	0.4 – 2.1	0.7 – 13.6
Level-2	0.2 – 2.0	0.3 – 3.1	0.6 – 8.2	0.6 – 6.5	0.6 – 8.5	0.9 – 20.4
Level-3	0.7 – 13.1	1.2 – 12.5	0.9 – 16.8	0.7 – 18.5	1.0 – 21.5	1.4 – 24.4

Inter-source Cross Correlation Exam

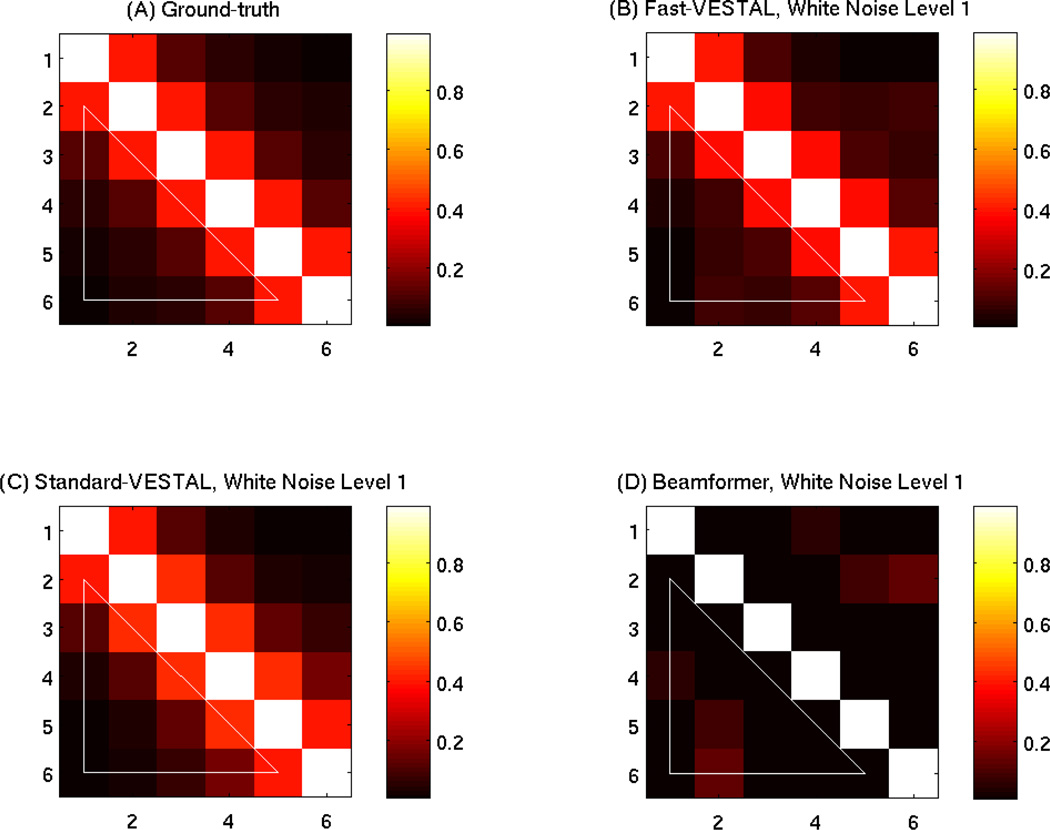
Another important measure of reconstructed source time-courses is the inter-source cross correlation (ICC). The ICC assessed if the reconstructed source time-courses preserved the inter-relationship of the time-courses among different sources. Figure 4(A) plots the cross-correlation matrix of the 6 ground-truth source time-courses. The diagonal elements are all one since each source 100% correlated with itself. The rest of the ICC values (highlighted by the white triangle in the lower-left corner) vary from 0.01 to 0.40. The ICC from both Fast-VESTAL in Fig. 4(B) and Standard-VESTAL in 4(C) for the white-noise Level-1 condition closely matched the ground truth. In contrast, the ICC from the beamformer reconstructed source time-courses showed markedly reduced correlations over the ground truth.

Figure 4.

Cross correlation coefficient matrix for the 6 simulated source. (A): using ground-truth source time-courses; (B): using time-courses reconstructed by Fast-VESTAL at white-noise Level-1; (C): by Standard-VESTAL; (D): by beamformer. The coefficients under the lower-left white triangles were used to calculate the inter-source cross correlation (ICC) and their percent variance explained to the ground-truth values, as listed in Table 1.

The PVE values (relative to the ground-truth) were also calculated for the ICC measures under the white triangles in the cross-correlation matrices in Fig. 4 from the three source modeling techniques, which are shown in the middle-left panel of Table 1. As highlighted in bold, the PVE values for the ICC from Fast-VESTAL are above 98%, markedly higher than those from the beamformer, which are 13.2% or lower. The performance of Standard-VESTAL was also good with PVE for ICC all above 92%, yet slightly inferior to the values obtained by Fast-VESTAL.

Statistical Maps and Source Location Reconstruction for Signals with White Noise

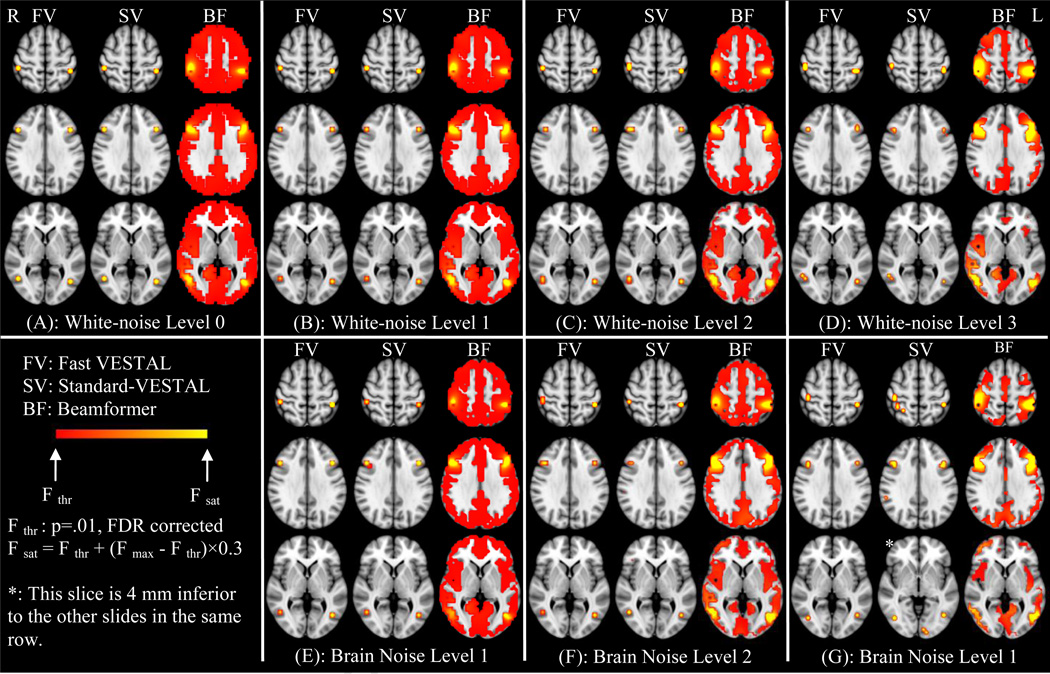
An approach was developed to assess the statistical significance of the Fast-VESTAL results and to construct statistical maps of the neuronal activities. For the simulation data with different white-noise levels, F-test assessed the statistical significance of variances between post-stimulus 700 ms interval over the pre-stimulus 300 ms interval for each grid node. The F-value maps from the Fast-VESTAL, Standard-VESTAL, and the beamformer solutions are shown in the 4-upper panels of Fig. 5 for white-noise Levels 0–3. The range of the F-values across different noise levels were orders of magnitudes different, due to different SNRs. To display the F-values in a comparable fashion, the threshold of the color scale was set to the F-value corresponding to corrected p-value of 0.01 (FDR), whereas the saturation value of the color scale was set to be F_satuation = F_threshold + (F_max − F_threshold)×0.3. Here, F_max was the maximum F-value in the brain volume for a specific noise level condition.

Figure 5.

F-value maps (post-stimulus over pre-stimulus) of source activity for the 6 simulated sources reconstructed from FV: Fast-VESTAL; SV: Standard-VESTAL; BF: beamformer. The upper four panels were for white-noise Level-0 (A); white-noise Level-1 (B); white-noise Level-2 (C); and white-noise Level-3 (D). The three lower panels were for brain-noise Level-1 (E) with 125 trial-averaging; brain-noise Level-2 (F) with 14 trial-averaging; and brain-noise Level-3 (G) with 3 trial-averaging.

For noise Level-0, the maps from Fast-VESTAL and Standard-VESTAL were virtually identical to the ground-truth locations of the 6 simulated sources (Fig. 1). The statistical maps from the beamformer solution revealed the 6 local maxima that matched the ground-truth locations. However, the spatial extent of the beamformer local maxima was markedly larger than those obtained from the two VESTAL techniques, with above threshold F-values in widespread areas throughout the brain, suggesting potential signal leakage from the beamformer solution. Good source location reconstructions were also obtained from both Fast-VESTAL and Standard- VESTAL for white-noise Levels 1–3 as shown in Figs. 5(B)(C)(D), although some activities spread to the neighboring voxels for the highly noisy condition (i.e., Level-3). In contrast, substantial signal leakage was observed in the beamformer solution for all three noise-level conditions.

Monte-Carlo Brain Noise Analysis of Pre-whitening Efficacy and the Objective Threshold of Noise Subspace

The robustness of Fast-VESTAL was examined using correlated MEG brain noise collected from a healthy subject when he was watching a fixation point for over 2 hours in multiple 5-minute sessions. The brain-noise data were divided into a pool of over 6,100 artifact-free epochs (1000 ms duration). Then Monte-Carlo analyses were performed, in which three conditions of brain noise were constructed that approximately matched the noise levels of the white-noise conditions based on Frobenius norms. The number of randomly selected epochs for trialaveraging in the brain-noise Level-1, 2, and 3 conditions was 125, 14, and 3, respectively.

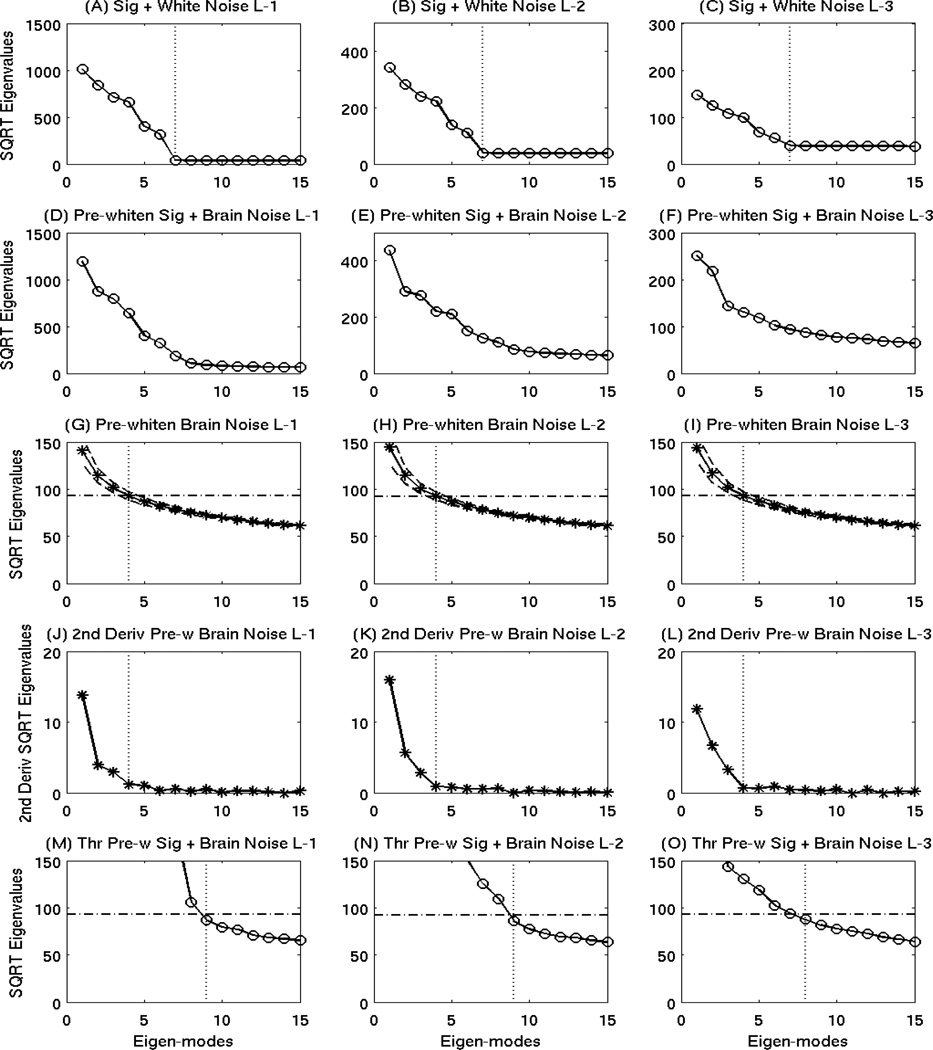
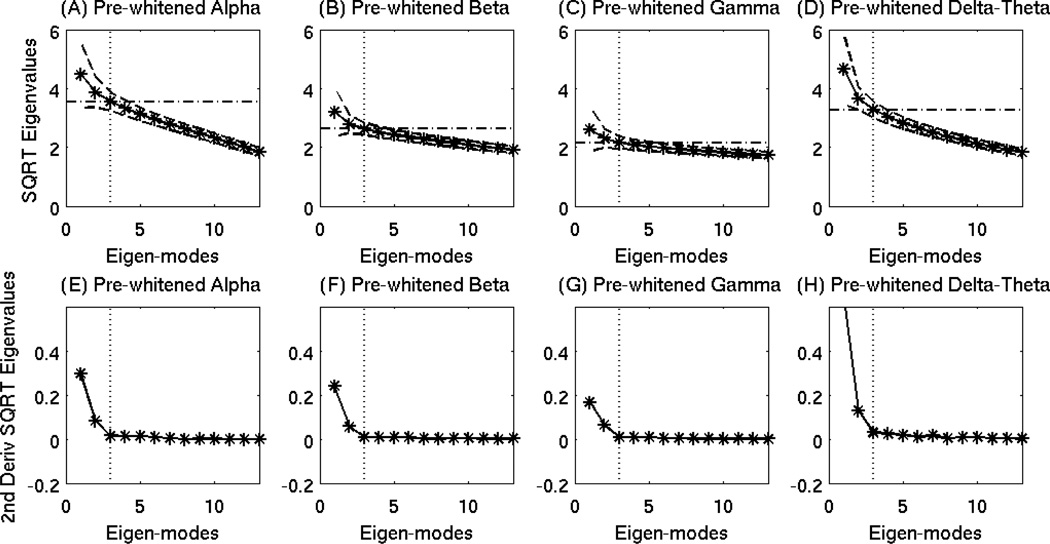
One key issue for the signal with correlated brain noise is that the boundary between signal subspace and noise subspace is blurred, which makes determining the number of signal (dominant) spatial modes k in Eqs. (6)–(8) more challenging than for cases with white noise. In Fig. 6(A)(B)(C), the SQRT plots of the eigenvalues in the sensor covariance matrices from simulated signal (white-noise Levels 1–3) clearly showed different characteristics between the signal subspace (i.e., Spatial Modes 1–6) and the flat noise subspace. The vertical dotted lines mark the beginning of the noise subspace (i.e., number 7). However, there is no clear boundary between signal subspace and noise subspace for the conditions of simulated signal with different levels of real brain noise added as shown in Fig. 6(D)(E)(F). This is a common and difficult problem for analyzing MEG signals with real correlated brain-noise.

Figure 6.

Objective thresholding in OPWM to separate noise subspace from signal subspace. Row 1: the SQRT plots of the eigenvalues in the sensor covariance matrices from simulated signal with white-noise Levels 1–3. Vertical dotted lines indicated the beginning of the noise subspace. Row 2: SQRT plots of the eigenvalues in pre-whitened sensor covariance matrices from simulated signal with brain-noise Levels 1–3. No clear distinctions were seen between noise and signal subspaces. Row 3: SQRT plots of eigenvalues in pre-whitened sensor covariance matrices for daughter brain-noise conditions from the Monte-Carlo analysis. The dash-dotted lines were the thresholds associated with the beginning eigenmode from noise subspace determined in Row 4. Row 4: second-order derivatives of the SQRT plots of eigenvalues in Row 3. Clear cutoffs of the noise and signal subspaces are seen as indicated by vertical dotted lines. Row 5: Application of the objective threshold to curves from Row 2.

To solve this problem, the efficacy of removing brain noise from the data for the entire 1000 ms epoch was first examined when the estimated (mother) brain-noise covariance matrix was constructed using only a portion of the interval. Here, we were only analyzing epochs with brain noise: no simulated signal was added in this test. First, 40 Monte-Carlo analyses was performed to examine epochs for each brain-noise level condition. For example, for the brain-noise Level-1, 40 sets of 1000 ms epochs were examined, and within each set, 125 trials (i.e., 5,000 random epochs were involved) were averaged. In each set, pre-whitening to the whole 1000 ms epoch was performed following Eqs. (17) and (18), by using only the first 300 ms to construct the mother noise covariance matrix. For brain-noise Level-1 condition with 125 trials, asterisks connected by a solid line in Fig. 6(G) show the SQRT of the eigenvalues of the daughter pre-whitened brain-noise covariance matrices (DPWBNCM) from the entire 1000 ms interval. The two dashed lines indicate the range of one standard deviation across the 40 sets of Monte-Carlo analysis. Very similar results were seen for brain-noise condition Level-2 with 14 trials (Fig. 6(H)) and for Level-3 with 3 trials (Fig. 6(I)).

The important characteristic of the SQRT plots of the eigenvalues from the DPWBNCM for the entire 1000 interval was their second-order derivatives, plotted in Fig. 6(J). The leading eigenvalues were different from zero suggesting the pre-whitening step did not completely remove the correlated brain noise as one would expect. However, a clear boundary was visible between the signal subspace (i.e, eigenmodes 1–3) indicating residual brain signal after prewhitening, and noise subspace as marked by the vertical dotted line for the condition of brainnoise Level-1. Obvious distinctions between residual signal subspace and noise subspace were also observed for brain-noise Level-2 (Fig. 6(K)) and Level-3 (Fig. 6(L)), using the second-order derivative approach. Now, knowing the cutoff of the noise subspace (i.e.,4^th eigenmode), one can go back to Fig. 6(G)(H)(I) and identify the objective threshold of noise subspace in the actual SQRT of the eigenvalue plots, which is the value associated with the fourth eigenmode as indicated by the horizontal lines. The objective thresholds (horizontal lines) were virtually identical across all three brain-noise conditions. All of the eigenmodes with their associated eigenvalue SQRTs above the lines belong to the signal subspace.

Finally, objective thresholds were applied to the simulated data that contained signals from the 6 simulated sources with different levels of brain noise added. For signal with brain-noise Level-1, Fig. 6(M) showed the same SQRT of the eigenvalues as in Fig. 6(D), but at a zoom-in scale. The horizontal line exhibited the same objective threshold obtained from the brain-noise Monte-Carlo analysis in Fig. 6(G). Eigenvalues below the threshold belong to the noise subspace, the beginning of which is designated by the dotted vertical line in Fig. 6(M) (i.e., 9^th eigenmode). The same threshold approach was applied to simulated signal with real brain-noise Levels 2 and 3. As indicated by the dotted lines in Fig. 6 (N) and 6(O), the noise subspace starts at the ninth and eighth eigenmodes for brain-noise Level-2 and 3, respectively.

Computer Simulation Results with Real Brain Noise, Correlated Sources, and Different SNRs

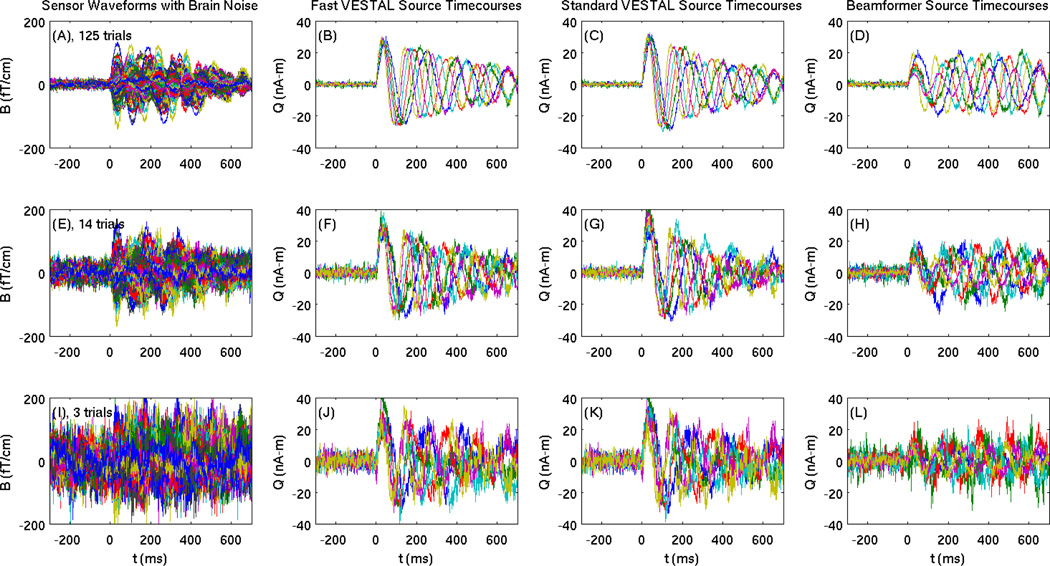
The realistic brain noise was added to the simulated signal to challenge the performance of Fast-VESTAL. Following the pre-whitening step and the objective threshold method described in the previous section, the source time-courses and location maps were reconstructed using Fast-VESTAL, Standard-VESTAL, and the beamformer solution. Figures 7(A) displays the MEG sensor waveforms containing simulated signals from 6 sources plus the real brain noise after 125 trial averages (Level 1 brain noise). The reconstructed source time-courses from Fast-VESTAL (Fig. 7(B)) matched the ground truth source time-courses well. Reconstructed source timecourses from Standard-VESTAL were reasonably good (Fig. 7(C)), but inferior to Fast-VESTAL. Obvious distortions were seen in the reconstructed source time-courses from the beamformer solution (Fig. 7(D)). For Level-2 brain noise with 14 trials of averaging (sensor waveforms shown in Fig. 7(E)), reconstructed source time-courses from Fast-VESTAL (Fig. 7(F)) and Standard-VESTAL (Fig. 7(G)) again outperformed those from the beamformer solution (Fig. 7(H)). For the simulated signal with high (i.e., Level-3) brain noise with only 3 trials of averaging, the signal in the post-stimulus interval is barely visible in the MEG sensor waveforms in Fig. 7(I), yet the reconstructed source time-courses from Fast-VESTAL (Fig. 7(J)) and Standard-VESTAL (Fig. 7(K)) still appeared to capture the main signature of the true source time-courses, although they were noisier than the other noise conditions. Distortion in the source time-courses was particularly marked from the beamformer solution (Fig. 7(L)).

Figure 7.

Simulated MEG sensor waveforms with different levels of real brain noise and the reconstructed source time-courses. Colum 1: MEG sensor waveforms with brain-noise Levels 1–3. The associated number of trials for averaging was 125 (Level-1), 14 (Level-2), and 3 (Level-3), respectively. Column 2: reconstructed source time-courses from Fast-VESTAL. Column 3: from Standard-VESTAL. Column 4: from beamformer.

For all three conditions with real brain noise, the upper-right panel in Table 1 lists the PVE relative to the ground-truth source time-courses using the source time-courses that were reconstructed from Fast-VESTAL, Standard-VESTAL, and the beamformer solution. All values are lower than the corresponding white-noise conditions, especially for the brain-noise Level-3. Fast-VESTAL showed the highest PVE, followed by Standard-VESTAL and the beamformer solution. The middle-right panel in Table 1 lists the inter-source correlation PVE values for the signal with three levels of real brain noise. FAST-VESTAL showed the highest ICC PVE, with values above 95% for Levels 1 and 3, but only 60.2% for Level-3. This contrasted with the moderate ICC PVE values from Standard-VESTAL and the notably low values from the beamformer solution.

Source Orientation Reconstruction

The bottom panel of Table 1 lists the errors in source orientation for each solution. Orientation errors were calculated for the center voxel with the strongest activities within 10 mm from the true source locations. The source-orientation parameters were obtained accurately by Fast-VESTAL for the simulated data. For white and brain-noise Levels 0–2, the orientation errors were less than 10 degrees. The largest error in source orientation was 18.5 degrees for brain-noise Level-3 condition. Orientation errors from Standard-VESTAL and beamformer solutions were also reasonably small, but somewhat larger than those from Fast-VESTAL.

Cutoff of the Singular Values in the Gain Matrix in Fast-VESTAL

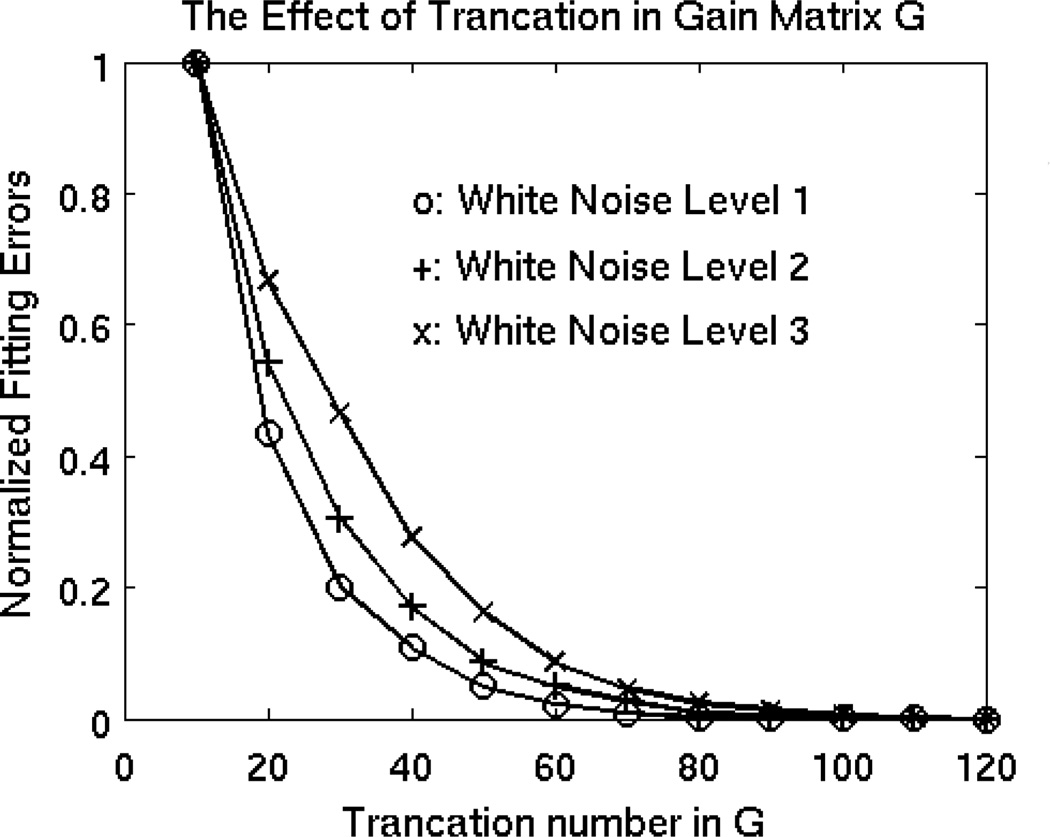
The number of dominant singular values in S_G was set to 80 in Eq. (4) and all other smaller singular values in S_G were set to be zero. Figure 8 plots the normalized error of the Fast-VESTAL-predicted MEG sensor waveforms over the ground truth, as a function of the singular value cut-off in S_G. In all three conditions with different white-noise levels, the errors of prediction reached the saturation level ~80.

Figure 8.

Normalized error of the Fast-VESTAL predicted MEG sensor waveforms over the ground truth, as a function of the singular value cut-off in the gain matrix. In all three conditions with different white-noise levels, the errors of prediction reach the saturation level ~80.

Human Median-nerve Results for Fast-VESTAL and Beamformer

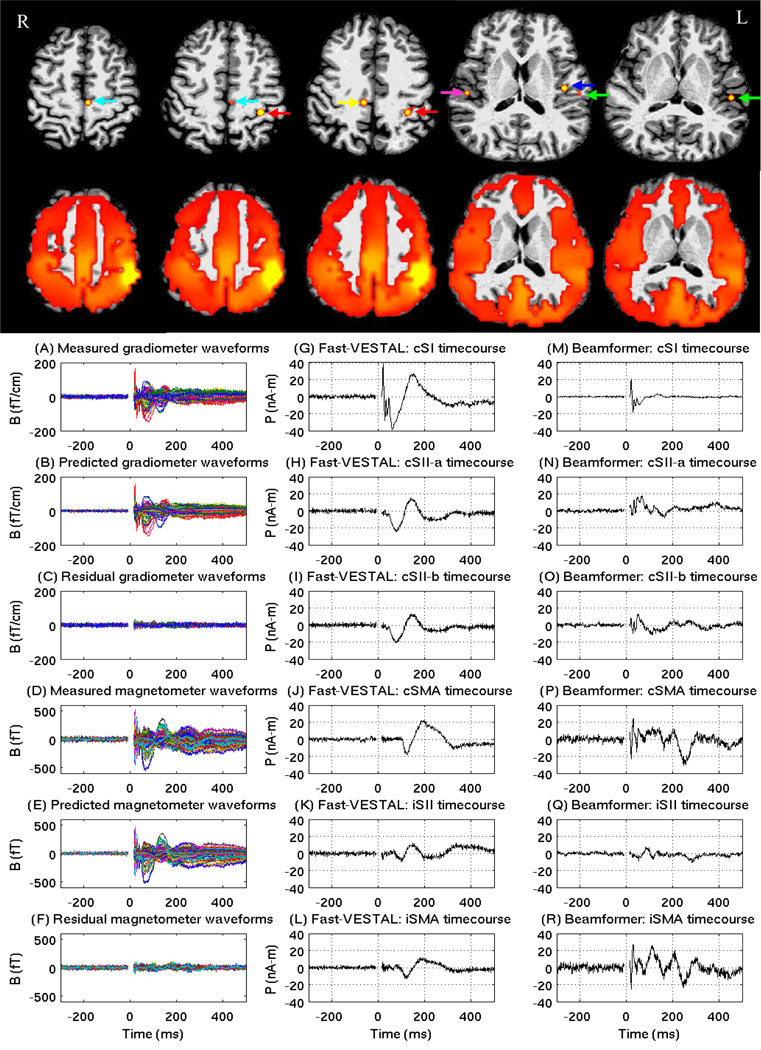
Fast-VESTAL was applied to a data set containing MEG responses evoked by right mediannerve stimulation in a healthy subject. Figure 9(A)(D) shows the measured sensor-waveforms of MEG responses for the −300 ms – 500 ms duration evoked by the right median-nerve stimulation, with 204 gradiometers and 102 magnetometers superimposed, respectively. The −10 ms to 15 ms gap was removed from the analysis due to the large artifact from the electrical stimuli. The remaining −300 ms to −10 ms pre-stimulus interval was used to construct the estimated noise covariance matrix and to pre-whiten the response for the entire interval. To examine the efficacy of the pre-whitening step and identify the noise subspace, a five-minute session of brain-noise recording collected from the same subject, but on a different day, was divided into ~310 artifact-free epochs, each lasting 800 ms, with the first 300 ms used to estimate the mother brain-noise covariance matrix. The number of dominant spatial modes was selected using the same OPWM that was developed for the simulated signal with correlated brain noise.

Figure 9.

Upper Panels, Top row: F-value maps of axial MRI view for the locations of 6 sources obtained by Fast-VESTAL for right median nerve stimulation. The color scale for the F-value was the same as in Fig. 5. Red arrow for cSI; Blue arrow for cSII-a; Green arrow for cSII-b; Cyan arrow for cSMA; Magenta arrowfor iSII; Yellow arrow for iSMA. Row two: F-value maps of the beamformer solution. Low panels, Left column: measured and predicted MEG sensor waveforms from Fast-VESTAL; Middle column: Fast-VETSLA source time-courses for the above sources; Right column: source time-courses from beamformer.

The predicted MEG sensor waveforms in Figures 9(B)(E) from the Fast-VESTAL solution matched the measurement very well. Figures 9(C)(F) show that mainly noise remained in the residual waveforms (i.e., measured minus predicted). The upper panel of Figure 9 shows the spatial maps of significance sources, based on the F-tests of source time-courses in the post-stimulus interval versus the pre-stimulus baseline. Six sources were obtained by Fast-VESTAL for the responses evoked by right median nerve stimulation: one in contralateral (left) primary somatosensory cortex (cSI), two in contralateral secondary somatosensory areas (cSII-a and cSII-b), one in contralateral supplementary motor area (cSMA), one in ipsilateral (right) secondary somatosensory area (iSII), and one in ipsilateral supplementary motor area (iSMA). The color scale in Figure 9 was set in the same manner as for the F-test spatial maps in simulations (Fig. 5).

The plots in Figure 9(G)–(L) show the time-courses of the 6 sources from Fast-VESTAL. The cSI time-course showed sharp early-components that peaked at ~20ms and ~30 ms with opposite polarities (Fig. 9(G)). These sharp transient components were not observed in the time-courses of the other sources. Two slow components at ~60 ms and ~150 ms were also seen in the cSI time-courses. The time-courses of the two cSII sources (i.e., cSII-a and cSII-b) were very similar with peak latencies of the first and second components at ~75 ms and ~140 ms, respectively (Figs. 9(H)(I)). The time-course of cSMA shows two slow components with peak latencies at ~125 ms and ~180 ms, respectively (Fig. 9(J)). The amplitude of the iSII source was weaker than for cSII, with peak latencies at ~90 ms and ~150 ms (Fig. 9(K)). The iSMA time-course showed similar peak latencies as those of cSMA, but with weaker amplitude (Fig. 9(L)). Table 2 lists the cross-correlation coefficients among these 6 sources, which varied between 12% and 98%.

Table 2.

Fast-VESTAL cross correlation coefficients among the time-courses from 6 sources evoked by median-nerve stimuli in post-stimulus interval.

	cSI	cSII-a	cSII-b	cSMA	iSII	iSMA
cSI
cSII-a	0.71
cSII-b	0.77	0.98
cSMA	0.25	0.32	0.18
iSII	0.12	0.65	0.61	0.60
iSMA	0.22	0.31	0.16	0.95	0.51

For comparison, we also performed the beamformer analysis on the same median-nerve data with 200 trials. There is controversy surrounding whether the signal covariance matrix should be reconstructed using the averaged signal or the un-averaged trials. Analysis was performed using both approaches and virtually the same results were obtained. Figure 9 presents the beamformer results using the approach with un-averaged trials. The upper panel of Figure 9 (second row) displays the statistically significant sources, based on F-tests of source time-courses in the post-stimulus interval versus the pre-stimulus baseline. The sole local maximum in this statistical map was in the cSI area. No clearly distinguishable local maxima were observed in other brain regions such as cSII or iSII. As for the simulated cases, the beamformer solution exhibited widespread signal leakage to other regions.

Out of curiosity, the beamformer source time-courses were plotted in Figure 9(M)–(R) of the same six areas for which the Fast-VESTAL solution showed strong activities. Since many of these areas did not show visible local maxima, the same locations obtained from the Fast-VESTAL solution had to be used as seeds for obtaining the beamformer source time-courses. The early and sharp components of the cSI time-course (Fig. 9(M)) were similar to that obtained by Fast-VESTAL (Fig. 9(G)), but the late slow components were missing in the beamformer solution. The remaining source time-courses from beamformer appear substantially different from those obtained from Fast-VESTAL. Many beamformer-derived source time-courses showed the strong early and sharp components that were absent in Fast-VESTAL, except for cSI source.

Whole-brain Source Amplitude Imaging for Resting-state MEG Signals using Fast-VESTAL

Fast-VESTAL was used to obtain the source amplitude (RMS) images of human resting-state (eyes-closed) MEG signals from 41 healthy control subjects and from 41 sets of empty-room data. In each human and empty-room data set, the MEG sensor covariance matrix for the restingstate recording was calculated for four different frequency bands, namely in alpha (8–10 Hz), beta (15–30 Hz), gamma (30–100 Hz), and low frequency (1–7 Hz) bands, after artifact removal and noise reduction pre-processing steps (see the Methods Section). Fast-VESTAL source images were obtained using the sensor covariance matrix and then transformed from the subject’s native coordinates to the MNI-152 atlas coordinates.

Figure 10 shows the process of using OPWM to separate the noise subspace from the signal subspace in the empty room data. After the pre-whitening step using the pre-whitening operator built from the mother noise covariance matrix of an extra empty-room data set (see Methods), the SQRTs of the eigenvalues for the daughter pre-whitened empty room covariance matrix or DPWERCM were calculated from each of the 41 empty-room data sets. Figures 10(A)–10(D) display the mean (solid lines) and standard deviations (dashed lines) for such SQRT of the eigenvalues of DPWERCM, across 41 empty-room sets, for alpha, beta, gamma, and delta plus theta bands, respectively. As for the simulated case in Figure 6, the second-order derivatives of the SQRTs of the eigenvalues from PWERCM show the clear cut of the noise-subspace at the eigenmode 3 for all bands. The thresholds for the SQRT of the eigenvalues for DPWERCM for the starts of the noise subspace were obtained from the horizontal dash-dotted lines in Figure 10(A)–10(D) for all frequency bands. Such thresholds were used to determine the cutoffs of the signal subspaces (spatial modes) in the pre-whitened covariance matrices for 41 the empty-room data and the 41 human resting-state data in the Fast-VESTAL data analyses. For each of the 41 empty-room datasets, a minimum of 2 spatial modes were used in the Fast-VESTAL analysis.

Figure 10.

OPWM separate noise and signal subspaces in empty room data. Top row: SQRT of eigenvalues from the daughter pre-whitened empty room covariance matrix (DPWERCM) for alpha (A), beta (B), gamma (C), and delta + theta (D) frequency bands. Bottom row: second-order derivatives of the SQRT of the eigenvalues. The vertical dotted lines show the beginning of the noise subspace, which are then used in the top row to determine the threshold of noise subspace (dash-dotted lines in top row).

The t-value maps for the Fast-VESTAL solutions from human subjects versus the emptyroom were shown in the 4 upper panels in the upper panel (top 4 rows) of Figure 11 for different frequency bands in MNI-152 brain atlas coordinates, using the registration and smoothing steps described previously. The ranges of the t-values across bands were markedly different due to the different SNR levels from human rhythms (e.g., the SNRs in the alpha band were much larger than those in the gamma band). To effectively plot these t-values in a comparable fashion, the color scales in Figure 11 were chosen in the following way: the threshold of the color scale was set to the t-value corresponding to a corrected p-value of 0.01 (FDR), and the saturation value of the color scale was set as t_satuation = t_threshold + (t_max − t_threshold)×0.5. Here, t_max was the maximum t-value in the brain volume for that specific noise-level condition.

Figure 11.

Upper panels (Rows 1–4): Whole brain t-value maps of the Fast-VESTAL source amplitude images that cover cortex, sub-cortical areas, and cerebellum for resting-state (eyes-closed) in alpha, beta, gamma, and delta + theta frequency bands. Lower panels (Rows 5–8): t-value maps of beamformer source amplitudes images for different frequency bands.

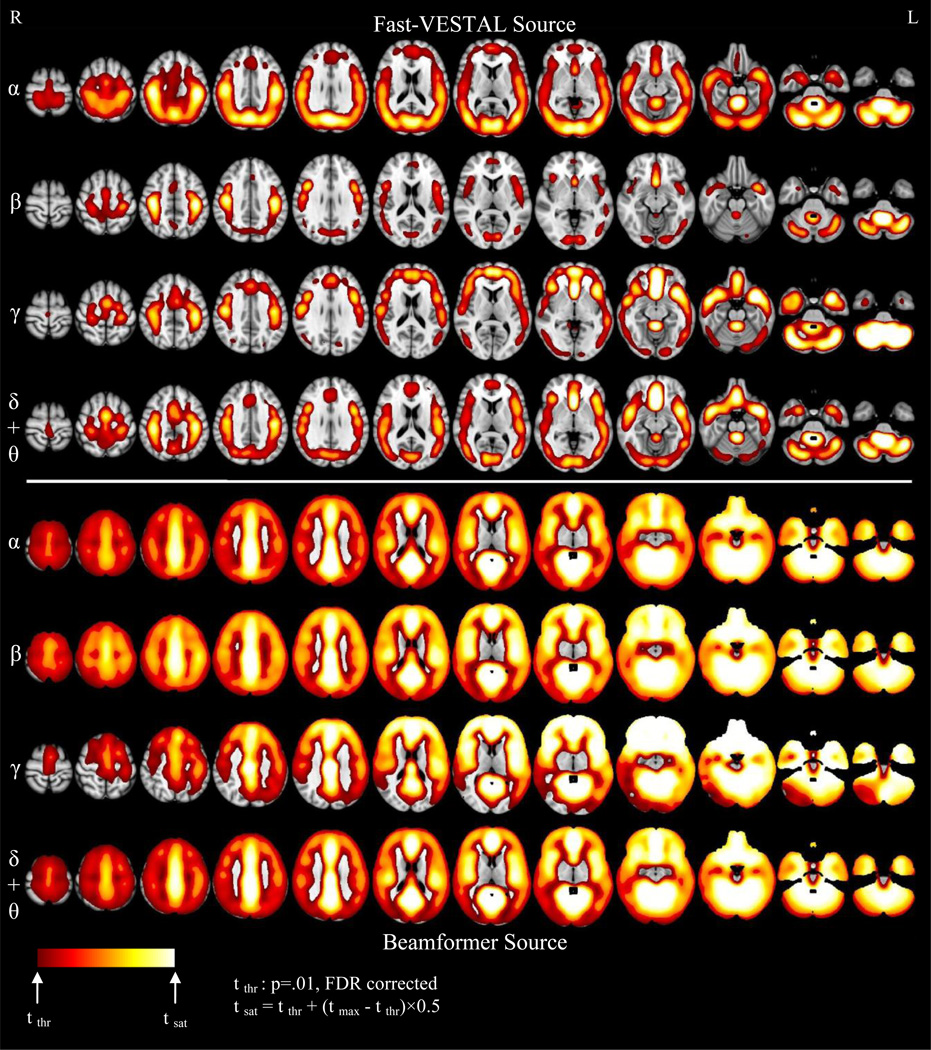
Alpha-band Source Amplitude Images

For the alpha band (first row in Fig. 11), the source amplitude images show strong cortical activity from the bilateral intracalcarine cortices, supracalcarine cortices, cuneus and precuneus, postcentral gyri, superior parietal lobules, and midline subcallosal cortices. Considerable alpha-band activity is also evident in the bilateral lateral-occipital cortices, angular gyri, and parietal operculum, and posterior aspects of superior and middle temporal gyri. Cerebella and brain-stem also show strong alpha activity. An interesting phenomenon is that frontal cortices do not show as strong alpha activity as the posterior portions of the brain.

Beta-band Source Amplitude Images

A different picture was seen for the MEG source images in the beta band (second row in Fig. 11). The bilateral postcentral gyri and midline subcallosal cortices show strong beta-band activity. However, beta-band activity is not as pronounced as alpha-band activity in bilateral intracalcarine and lateral-occipital cortices, supracalcarine cortices cuneus and precuneus, parietal operculum, and temporal lobes. Beta-band activity is significant in frontal areas (bilateral precentral gyri, frontal operculum, and anterior aspect of midline paracingulate and cingulate gyri). Strong beta-band activity is still seen in the brain-stem, but is not as pronounced in the cerebella.

Gamma-band Source Amplitude Images

Many interesting patterns of activity were seen in the gamma band (third row of Fig. 11). Strong activity was notable from midline paracingulate and cingulate gyri, bilateral superior and middle frontal sulci, frontal operculum and midline subcallosal cortices. In addition, bilateral precentral gyri, supramarginal gyri, parietal operculum, angular gyri, superior parietal lobules, middle temporal gyri, and midline precuneus also show substantial activity. Furthermore, bilateral anterior hippocampi, amygdala, and the temporal poles show strong gamma-band activity, which is markedly more prominent than the activity from the same regions in alpha or beta bands. Bilateral cerebella and brain-stem show strongest gamma-band activities among all bands, in the relative scale. Interestingly, the occipital lobe and posterior temporal lobe do not exhibit strong gamma-band activity.

Low Frequency-band Source Amplitude Images

The bottom row of Fig. 11 shows strong low-frequency activity (1–7 Hz) from bilateral intracalcarine cortices, supracalcarine cortices, midline paracingulate, frontal medial cortices, subcallosal cortices, and midline posterior cingulate. Considerable low-frequency activity is also seen in the bilateral Heschl’s gyri, frontal operculum, precentral and poscentral gyri, angular gyri, parietal operculum, and middle temporal gyri. Bilateral anterior hippocampi, amygdala, temporal poles, and brain stem also show strong low-frequency activity.

Beamformer Source Amplitude Images

The source images obtained by the beamformer solution for the human resting-state data were substantially different from those obtained by Fast-VESTAL. The bottom four rows in Fig. 11 show the beamformer source-amplitude images as t-value maps between 41 healthy subjects versus 41 empty-room data sets. The different frequency bands were largely undifferentiated by the beamformer maps. In all bands, almost all brain areas showed activity, except in subcortical regions and in superior portions of the cortex for gamma band activity. The regions that the exhibited the highest activity were the midline structures and the cerebellum.

Fast-VESTAL‘s Low Computational Costs

The computational cost of the conventional VESTAL is already relatively low (Huang et al., 2006) compared with many non-linear optimization approaches such as non-linear multipledipole modeling (see review in (Huang et al., 1998)), and is substantially lower than that of Standard-VESTAL. In the above examples, the total number of time-samples was 1000, 777, and ~900,000 for the simulated data, human median-nerve, and human resting-state signals, respectively. Despite the high variability in the number of time-samples in these datasets, the total analysis time was typically in the range of tens of seconds to obtain source images on a source grid with ~7,000 nodes using Fast-VESTAL for each dataset. The computational cost of Fast-VESTAL is approximately proportional to the number dominance (signal-related) spatial modes k when solving Eq. (8), and is not directly related to the number of time samples as for the Standard-VESTAL. It takes about 10 seconds to solve the L1-minimum solution and obtain a volume of source images for each dominance (signal-related) spatial mode in Eq. (8). The time Δ_L1 for solving one L1-minimum norm problem is almost the same for one spatial mode in Fast-VESTAL, for one time-sample in Standard time-domain VESTAL, and for one frequency-bin in Standard frequency-domain VESTAL. The total computational cost is ~ k × Δ_L1 for Fast-VESTAL and T × Δ_L1 for Standard time-domain VESTAL. For the simulation cases with 6 spatial modes and 1000 time samples, the Fast-VESTAL solution was approximately 1000/6 = 166.7 times faster than Standard-VESTAL. All programs were developed in MATLAB and all analyses done on a Dell Precision 7500 Workstation with Dual Intel Xeon X5550 Processors (each with 8M Cache, 2.67 GHz, and 6.40 GT/s QPI) and with 24 GB system RAM. Although Fast-VESTAL is inherently a good candidate for parallel processing, no parallel processing was performed in the present study.

Discussion

Performances of Fast-VESTAL and Standard-VESTAL versus Beamformer for Simulated Data

In extensive evaluations using simulated and real data, the performance of Fast-VESTAL for whole-brain source localization was equal or superior to that of the Standard-VESTAL and beamformer methods, in several respects. First, Fast-VESTAL and Standard-VESTAL showed superior performances over beamformer in the robustness for accurately obtaining correlated source time-courses, even at poor SNR levels and with real brain noise (Figs. 3 and 7). Quantitative assessments (Fig. 4 and middle panels of Table 1) supported this feature with Fastand Standard-VESTAL demonstrating PVE values for the ICC over 90% in most cases, whereas values from the beamformer solution were extremely low. We believe that the reason for the very good performance of Fast- and Standard-VESTAL in obtaining source time-courses and maintaining high ICC is that no temporal constraints are imposed on the solutions. This is not the case in beamformer techniques, which assume that source time-courses are uncorrelated (Van Veen et al., 1997; Gross and Ioannides, 1999; Robinson and Vrba, 1999; Gross et al., 2001; Sekihara et al., 2001; Hillebrand and Barnes, 2003; Barnes and Hillebrand, 2003), and independent component analysis, which assumes that the source time-courses are statistically independent (Makeig et al., 1997; Vigario and Oja, 2000; Vigario et al., 2000; Barros et al., 2000; Jung et al., 2001).

Second, Fast-VESTAL showed its substantial improvement on computational speed over the Standard-VESTAL technique (Huang et al., 2006). In fact, the computational cost of Fast-VESTAL is basically independent of the time samples in the data, but instead proportional to the number of spatial modes in the sensor-spatial-profile matrix or sensor-covariance matrix, which usually takes tens of seconds or less. In contrast, the analysis time of Standard-VESTAL is proportional to either the number of time-samples in time-domain MEG data or frequency bins in frequency domain MEG data. The time for solving one L1-minimum norm problem is almost the same for one spatial mode in Fast-VESTAL, for one time-sample in time-domain Standard-VESTAL, and for one frequency-bin in frequency-domain Standard-VESTAL. Consequently, it took tens of seconds for Fast-VESTAL to obtain high-resolution MEG source images when processing datasets containing ~100–1000 (evoked MEG response) to ~100,000 (spontaneous MEG data) time samples. The processing time using Standard-VESTAL can be orders of magnitude longer.

The step of using temporal projection Eq. (4) in Fast-VESTAL is similar to the temporal dimension reduction in the Multiple Sparse Priors (MSP) method of Friston and colleagues (Friston et al., 2008). Both approaches adopted the temporal projection and used sensor covariance matrix for dimension reduction. One difference is that Fast-VESTAL explicitly obtains the minimum L1-norm solution for dominate spatial modes in the sensor waveforms after the temporal projection using Eq. (4), whereas MSP performs both temporal and spatial projections and seeks the hyperparameters using the iterative expected maximization (EM) approach. A unique feature of Fast-VESTAL is that the process of obtaining the minimum L1-norm solution for dominate spatial modes is 1) guaranteed to converge and 2) non-iterative, without the need for controlling the converging process / criteria. Another unique feature of Fast-VESTAL is that an inverse operator Eq. (12) was explicitly provided to faithfully recover the source time-courses with the same temporal resolution as the original sampling rate (e.g., in millisecond) even under extremely poor SNR conditions. It is also important to note that dimension reduction using Eq. (4) is not limited to the minimum L1 norm solution. In fact, the minimum L2-norm solution can also be used to solve Eq. (4) if a widely distributed non-sparse solution is desired.

Objective Pre-whitening Method for Removing Correlated Brain Noise

The present study also developed an objective approach (i.e., OPWM) to effectively remove correlated brain noise (Fig. 2). OPWM provided 1) an objective way to measure the efficacy of the pre-whitening step, when the estimated correlated noise matrix was constructed using incomplete or non-real time information; 2) an additional procedure to further remove residual correlated noise when pre-whitening step is not completely successful, which was based on the plots of SQRT of eigenvalues of the daughter pre-whitening correlated noise covariance matrices; and 3) an objective way to identify noise subspace in the pre-whitened signal covariance matrix. A unique feature of OPWM is that it uses the second-order derivatives of the SQRT of the eigenvalues from the daughter pre-whitened noise covariance matrices. This feature was discovered based on the fact that in cases of pure white noise, the SQRT of the eigenvalues from noise subspace should be exactly zero. In correlated brain-noise cases, the second-order derivatives of the SQRT of the eigenvalues from the daughter pre-whitened noise covariance matrices was shown to be an effective way to differentiate noise subspace from residual signal subspace after pre-whitening. OPWM was applied extensively in the present study to remove correlated brain noise before the MEG signals were processed by Fast-VESTAL, Standard-VESTAL, and the beamformer methods. The high similarity of the results from these three inverse source imaging methods for white-noise and brain-noise conditions underscores the good performance of OPWN (Fig. 3 versus Fig. 7; upper panels versus lower panels in Fig. 5; and left versus right panels in Table). We believe that the OPWM approach for removing correlated noise from the data is not inherently limited to Fast-VESTAL or MEG signal processing, but rather could be applied to any time-series analysis.

Median-nerve Responses

The application of Fast-VESTAL to the median-nerve MEG response of a single subject demonstrated the strength of this method in localizing multiple sources in human brain responses that are highly correlated. The cSI source from primary somatosensory cortex and its time-course, which exhibited initial sharp transient components at 20 and 30 ms followed by slow later components, are consistent with the known neurophysiology of the somatosensory system and previous studies (Wood et al., 1985; Davidoff, 1990; Hari et al., 1993; Forss et al., 1994; Baldissera and Leocani, 1995; Kawamura et al., 1996; Mauguiere et al., 1997a; Mauguiere et al., 1997b; Jousmaki and Forss, 1998; Forss and Jousmaki, 1998; Hari and Forss, 1999; Spiegel et al., 1999; Boakye et al., 2000; Huang et al., 2000; McGlone et al., 2002; Waberski et al., 2002; Huang et al., 2004a; Huang et al., 2005; Huang et al., 2006). Since a relatively large time-window of 15 to 500 ms post-stimulus interval was used in this analysis, the cluster of cSI sources from Fast-VESTAL covered Brodmann areas (BA) 1, 2, and 3b (Fig. 9), which are all part of the hand representation of the primary somatosensory cortex and are highly contiguous in space. The cluster did not further differentiate the sub-regions of the cSI cortex (e.g., BA 3b from BA 1 and 2) as they do in conventional VESTAL analysis using individual time samples from a much shorter post-stimulus interval (Huang et al., 2006). Likewise the cSI time course shown in Figure 9(A) actually represented the combined activities from BA 3b, 1, and 2, namely, the early transient 20 ms and 30 ms activities from BA 3b plus the later ~60 ms and ~150 ms activities from BA 1 and 2. Responses from these sub-regions within SI were originally revealed using the Standard-VESTAL algorithm when analyzing individual time samples in a much shorter poststimulus interval (Huang et al., 2006). In fact, Fast-VESTAL was applied to the analysis of a shorter period (i.e., 15 – 150 ms) and indeed, two sub-clusters within cSI cortex were identified, one in BA 3b and another in BA 1 and 2. The time course of the BA 3b sub-cluster showed strong transient 20 ms and 30 ms activity, and the time course of the BA 1 and 2 sub-clusters showed later ~60 ms and ~150 ms activities (figure not shown).

The contralateral and ipsilateral SII and SMA responses obtained from Fast-VESTAL (Fig. 9) also agreed well with previous findings (Hari et al., 1993; Forss and Jousmaki, 1998; Hari and Forss, 1999; Fujiwara et al., 2002; Simoes et al., 2003; Huang et al., 2005; Huang et al., 2006). It was notable that there were two sources in the cSII region, one slightly more posterior (cSII-b, green arrow) than the other (cSII-a, blue arrow). The cSII-b source is also designated ventral parietal cortex by others (Disbrow et al., 2001). The source time-courses obtained from Fast-VESTAL further revealed that the 6 sources were inter-correlated with correlation coefficients ranging from 10% to 98%. Altogether, these findings demonstrate Fast-VESTAL’s ability to localize highly-correlated sources and resolve source time-courses, which is vital for a more complete understanding of the neurophysiology of the somatosensory system. In addition, the cSI source preceded the other sources in contralateral and ipsilateral hemispheres (Fig. 9). Activity in cSIIs and cSMA of the contralateral hemisphere was earlier than those from corresponding areas in the ipsilateral hemisphere (i.e., iSII and iSMA). These findings are highly consistent with the known neurophysiology of the somatosensory system (Kandel et al., 2000).

In contrast, the beamformer solution was only able to find one obvious local maximum in the cSI (Fig. 9, second row). The absence of the other sources that are known to exist was striking, and underscores the beamformer’s difficulty in source detection under the conditions examined in present study. To our knowledge, in all published studies that used beamformer for analyzing median nerve responses, cSII, iSII, and other non-primary somatosensory sources were not reported (Hashimoto et al., 2001; Hirata et al., 2002; Gaetz and Cheyne, 2003; McCubbin et al., 2004; Gaetz et al., 2009; Hillebrand et al., 2013). We believe this was due to the high intersource cross correlations, which substantially violate the basic beamformer assumption that the sources must be uncorrelated. Our explanation was supported by a close analysis of the cross correlations in Table 2 in which 8 out of the 15 cross-correlation coefficients from Fast-VESTAL were above 50%. Furthermore, the early transient activity at 20–30 ms post-stimulus from the beamformer source time-courses (location seeded by Fast-VESTAL solutions) in cSII-a (Fig. 9(M), cSII-b (Fig. 9(N)), cSMA (Fig. 9(P)), and iSMA (Fig. 9(R)) was inconsistent with known neurophysiology of the somatosensory system, owing to a lack of direct thalamo-cortical projections to these non-primary somatosensory areas (Kandel et al., 2000).

A previous study (Hymers et al., 2010) suggested that the use of un-averaged individual trials rather than trial-averaged responses to construct the signal covariance matrix may improve the localization of correlated sources, assuming that inter-regional source correlations are attenuated in the un-averaged trials. However, no difference was found between these two approaches in our beamformer analyses of median nerve data. This result suggests that the neuronal sources evoked by median-nerve stimuli are actually highly time-locked to the electric stimuli, such that the beamformer solution will have problems localizing the correlated time-locked sources.

Source Amplitude Images of Human Resting-state Activity

The present study also assessed the performance of Fast-VESTAL relative to the beamformer method in reconstructing resting-state MEG source amplitude images for each standard frequency band. To our knowledge, this is one of the first comprehensive MEG/EEG source amplitude (power) imaging studies for resting-state signal that covers the entire brain for multiple frequency bands. The MEG source-amplitude imaging method (or the square-root of the source power images) in the present study for the human resting-state rhythms is different from the MEG source covariance / functional connectivity source analysis. Here, the strength of the neuronal sources was assessed for different frequency bands, whereas the MEG source covariance/ functional connectivity source analysis examines the similarity of the shapes of the source time-courses (Brookes et al., 2011a; Brookes et al., 2011b; Hipp et al., 2012; Soto and Jerbi, 2012; Hall et al., 2013). Therefore, it should not be surprising that the resting-state source amplitude images from Fast-VESTAL look significantly different from the functional connectivity source images.

On the other hand, a high degree of similarity was apparent between Fast-VESTAL source-amplitude images and the most recent source amplitude images from Hall and colleagues (Hall et al., 2013). In their study, the use of variance information (i.e. data that have not been variance normalized) in source-space projected Hilbert envelope time series yields important spatial information. They showed that employing the variance information improves the spatial delineation of network nodes. Additional analyses are needed to explore the similar findings across the two different approaches (i.e., Fast-VESTAL versus the use of variance information in source-space projected Hilbert envelope time series).

Resting-state alpha-band activity detected by EEG (Berger, 1929) and MEG (Cohen, 1968; Cohen, 1970) is known to be strong in the posterior half of the head (occipital, parietal, and posterior temporal regions), but may extend into the central areas in regions that generate the rolandic mu rhythm, see reviews in (Hari et al., 1997; Niedermeyer and Lopes da Silva, 2005). Our results obtained from Fast-VESTAL for the alpha-band were highly consistent with this neurophysiology. The present study builds upon this knowledge by providing a more refined analysis of the generators of human alpha-band activity. For example within the occipital lobe, activity from intracalcarine, supracalcarine, and lateral-occipital cortices was clearly distinguishable in the Fast-VESTAL source images (Fig. 11). Likewise, it has not been clear whether the alpha-band activities in the central sulcus area (i.e., the rolandic mu rhythm) are mainly from the postcentral gyrus (primary somatosensory cortex), the precentral gyrus (primary motor cortex), or both. The Fast-VESTAL source images in the alpha band showed that although alpha activity extended to the precentral gyrus, the dominant activity was clearly from the postcentral gyrus, more specifically from the hand representation area of the somatosensory cortex.

The Fast-VESTAL source-amplitude images for the generation of the beta-band MEG signals were also highly consistent with previous EEG and MEG findings. Beta-band activity from the pre- and postcentral gyri are part of the rolandic mu rhythm (Niedermeyer and Lopes da Silva, 2005). The Fast-VESTAL source images further showed that the postcentral gyri beta-band (mu) activity is mainly from the hand representation area of the somatosensory cortex, consistent with previous MEG research (Manshanden et al., 2002).

Our gamma-band source amplitude images from Fast-VESTAL also clearly showed larger involvement of frontal generators, different from those previously observed in alpha or beta bands (Fig. 11). Interestingly, gamma-band activity was also found in the anterior hippocampi, the amygdala, and the temporal pole. These results suggest that MEG resting-state gamma-band signal may be useful for studying memory and emotion processing. Fast-VESTAL-based MEG source amplitude images were also derived for low-frequency bands: delta (1–4 Hz) and theta (4–7 Hz) bands. The locations of midline frontal activity in paracingulate gyrus, medial frontal cortices, and subcallosal cortices appear to be consistent with theta activity seen in EEG, even though most of EEG studies were task-activated (e.g., problem solving) and provided no specific information on source locations (Mizuki et al., 1980; Mizuki et al., 1984; Mizuki et al., 1992; Takahashi et al., 1997; Niedermeyer and Lopes da Silva, 2005). Another interesting finding from the Fast-VESTAL result is the high degree of similarity between gamma band and delta-theta band for the inferior frontal and anterior temporal regions (Fig. 11). We are in the process of analyzing the functional connectivity of these regions across these frequency bands.

The results of source amplitude resting-state images from the beamformer solution were markedly different from those that employed Fast-VESTAL. The beamformer method showed little spatial differentiation among the different frequency bands. Although the neurophysiology of the human somatosensory system has been well studied, an understanding of the source amplitude images for different frequency bands is limited. As such, the quality of the beamformer source amplitude images for resting-state data cannot be assessed with certainty, which is a limitation of the present study. Additional information from techniques such as electrocorticography will be needed to address this issue.

In summary, the Fast-VESTAL MEG source imaging algorithm obtains L1-minimum-norm solutions for the sensor-waveform covariance matrix. Computer simulations demonstrated that Fast-VESTAL localizes correlated sources and accurately reconstructs their source time-courses even at poor signal-SNR conditions. A new objective pre-whitening method, OPWM, was also developed and used in Fast-VESTAL to objectively remove correlated brain noise. The application of Fast-VESTAL to human MEG median-nerve responses further demonstrated its power in reconstructing source time-courses that were highly consistent with known electrophysiology of the human somatosensory system. Furthermore, Fast-VESTAL provided the first set of comprehensive MEG source-amplitude images that covered the entire brain in standard atlas coordinates for different frequency bands of resting-state signals. Lastly, the Fast-VESTAL solution also has a low computational cost.

Highlights.

• A new MEG imaging method for obtaining accurate source locations and time-courses

• This new MEG imaging method, Fast-VESTAL, is highly robust to white and brain noise

• We develop a new objective pre-whitening method to remove correlated brain noise

• We examine the performance of Fast-VESTAL using median-nerve responses

• We obtain the first source amplitude image for all frequency bands in resting-state