Aris-Taylor dispersion in tubes with dead ends

Abstract

This paper deals with transport of point Brownian particles in a cylindrical tube with dead ends in the presence of laminar flow of viscous fluid in the cylindrical part of the tube (Poiseuille flow). It is assumed that the dead ends are identical and are formed by spherical cavities connected to the cylindrical part of the tube by narrow necks. The focus is on the effective velocity and diffusivity of the particles as functions of the mean flow velocity and geometric parameter of the tube. Entering a dead end, the particle interrupts its propagation along the tube axis. Later it returns, and the axial motion continues. From the axial propagation point of view, the particle entry into a dead end and its successive return to the flow is equivalent to the particle reversible binding to the tube wall. The effect of reversible binding on the transport parameters has been previously studied assuming that the particle survival probability in the bound state decays as a single exponential. However, this is not the case when the particle enters a dead end, since escape from the dead end is a non-Markovian process. Our analysis of the problem consists of two steps: First, we derive expressions for the effective transport parameters in the general case of non-Markovian binding. Second, we find the effective velocity and diffusivity by substituting into these expressions known results for the moments of the particle lifetime in the dead end [L. Dagdug, A. M. Berezhkovskii, Yu. A. Makhnovskii, and V. Yu. Zitserman, J. Chem. Phys. 141, 224712 (2007)]. To check the accuracy of our theory, we compare its predictions with the values of the effective velocity and diffusivity obtained from Brownian dynamics simulations. The comparison shows excellent agreement between the theoretical predictions and numerical results.

I. INTRODUCTION

The effect of a retaining boundary on the overall transport of Brownian particles advected by a confined flow is of significant importance for a number of fields of science and technology. Examples include chemical engineering (microfluidics,^1,2 heterogeneous catalysis,^3,4 chromato-graphy^5,6), biophysics (blood circulation,⁷ airflow in lungs,⁸ targeted drug delivery^9,10), and transport processes in geophysical systems (mixing in atmosphere and ocean,^11,12 flow of gas and water in hydraulically fractured wells,¹³ colloid filtration and water purification^14,15). It has been well recognized^1,16–19 that specifically engineered boundaries can provide an effective means for control of the transport of tracer particles in the confined flow. Among a variety of flow systems, the dispersion of Brownian particles in the Poiseuille flow (laminar flow in a cylindrical tube) has been traditionally the focus of research efforts due to its importance for many practical applications. In his well-known work,²⁰ Aris extended the seminal Taylor result on the particle dispersion in the Poiseuille flow in a tube with a reflecting wall^21,22 to the case where the particle can reversibly bind to the tube wall. Since then, the effect of reversible binding to the boundary on the particle transport in the flow has been extensively investigated, and there is a vast amount of literature on this subject (see Refs. ^23–34 and references therein). Some of the relevant results are summarized below.

When a point Brownian particle is advected by a uniform flow of a constant velocity v in a tube with reflecting walls, the probability density p(x, t) of finding the particle at position x measured along tube axis at time t satisfies the one-dimensional advection-diffusion equation

$$\frac{\partial p}{\partial t}=D\frac{{\partial }^{2}p}{\partial x^2}-v\frac{\partial p}{\partial x},$$ (1.1)

where D is the particle diffusivity in the absence of the flow. In a laminar stationary flow of viscous fluid in a cylindrical tube of radius a the flow velocity is not uniform. It is a function of distance r from the tube axis. The velocity profile, v_f(r), is given by the well known formula

$$v_{\mathit{f}}\left(r\right)=2{\overline{v}}_{\mathit{f}}\left(1-\frac{r^2}{a^2}\right),$$ (1.2)

where ${\overline{v}}_{\mathit{f}}$ is the velocity averaged over the tube cross-section, ${\overline{v}}_{\mathit{f}}=(2/a^2){\int }_0^a{v}_{\mathit{f}}\left(r\right)rdr$. Velocity v_f(r) vanishes at the tube wall (r = a) and has a maximum in the center of the tube (r = 0). The celebrated result obtained by Taylor^21,22 states that Eq. (1.1) remains valid in the presence of the flow with v and D replaced by the effective drift velocity v_eff and diffusivity D_eff. These effective transport parameters are related to ${\overline{v}}_{\mathit{f}}$, D, and the tube radius, a, by the relations

$$v_{\mathit{eff}}={\overline{v}}_{\mathit{f}},$$ (1.3)

$$D_{\mathit{eff}}=D+\frac{{\overline{v}}_{\mathit{f}}^2{a}^2}{48D}.$$ (1.4)

The ability of the tube wall to retain (reversibly bind) the particle results in significant enrichment of the transport phenomenology. Such binding may be caused by a variety of mechanisms including physical adhesion, reversible chemical reactions (particle absorption and desorption), and trapping by geometric heterogeneities of the tube surface (roughness, cavities, fjords, etc., see Refs. 1 and 16–19, and references therein). Since all these mechanisms interrupt the particle propagation along the tube axis, they can be treated in the framework of the same formalism. The specificity of each binding mechanism manifests itself in the statistics of the particle lifetime in the bound state.

All binding processes mentioned above can be described by the kinetic scheme (see Fig. 1),

$$\mathrm{flow}\rightleftarrows \mathrm{bound}.$$ (1.5)

Let $P_b^{eq}$ and $P_f^{eq}$ be the equilibrium probabilities of finding the particle in the bound state and in the flow, $P_b^{eq}+P_f^{eq}=1$. They can be written in terms of the mean lifetimes ⟨τ⟩_b and ⟨τ⟩_f spent by the particle in each state:

$$P_b^{eq}=\frac{{⟨\tau ⟩}_b}{{⟨\tau ⟩}_f+{⟨\tau ⟩}_b},P_{\mathit{f}}^{eq}=\frac{{⟨\tau ⟩}_f}{{⟨\tau ⟩}_f+{⟨\tau ⟩}_b}.$$ (1.6)

The ratio of these probabilities is the equilibrium constant

$$\frac{P_b^{eq}}{P_f^{eq}}=\frac{{⟨\tau ⟩}_b}{{⟨\tau ⟩}_f}=K.$$ (1.7)

This allows to express $P_b^{eq}$ and $P_f^{eq}$ in terms of K,

$$P_b^{eq}=\frac{K}{1+K},P_f^{eq}=\frac{1}{1+K}.$$ (1.8)

Using $P_f^{eq}$ and K, the effective drift velocity and diffusivity in a tube with retaining wall can be written as^{5,16,20,23,28,34}

$$v_{\mathit{eff}}={\overline{v}}_{\mathit{f}}{P}_f^{eq},$$ (1.9)

$$D_{\mathit{eff}}=D{P}_{\mathit{f}}^{eq}+▵D.$$ (1.10)

When the particle has zero velocity and diffusivity in the bound state, △D is given by^{5,16,20,23,28,34}

$$\begin{array}{ccc}\hfill ▵D& =& {\left(P_f^{eq}\right)}^3{\overline{v}}_{\mathit{f}}^2\left[{⟨\tau ⟩}_{b}K+\frac{a^2}{48D}(1+6K+11K^2)\right]\hfill \\ & =& \frac{{\overline{v}}_{\mathit{f}}^2}{{(1+K)}^3}\left[{⟨\tau ⟩}_{b}K+\frac{a^2}{48D}(1+6K+11K^2)\right].\hfill \end{array}$$ (1.11)

The above results were obtained assuming that the particle survival probability in the bound state decays as a single exponential. This is not always the case. Revealing examples are retaining systems with multilevel binding or tubes with dead ends considered below. To overcome this limitation we develop a theory for the non-Markovian case, i.e., when the probability density of the particle lifetime in the bound state is not necessarily single-exponential. We show that in this case Eqs. (1.9) and (1.10) remain unchanged with a modified expression for △D, which is given in Eq. (4.37).

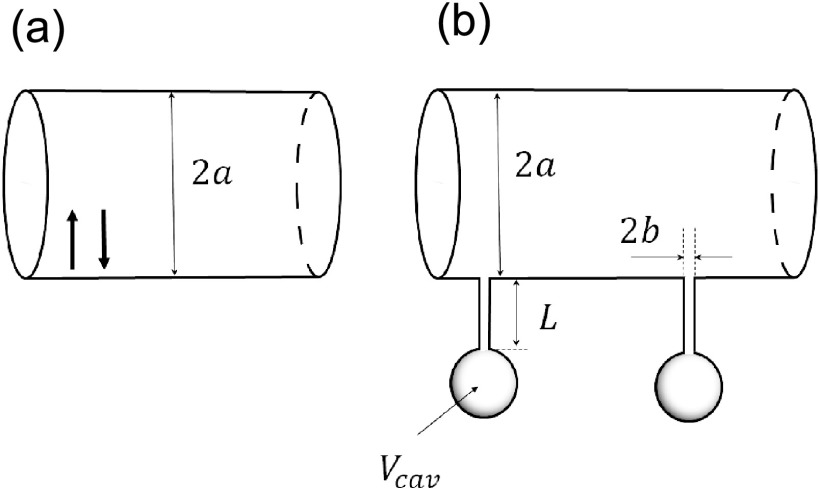
FIG. 1.

Schematic representations of a tube with reversible binding of particles to the tube wall (panel (a)) and a tube with dead ends (panel (b)).

The developed formalism is applied to study particle transport by the Poiseuille flow in a tube with dead ends. We assume that all dead ends are identical, and that a dead end is formed by a cavity of volume V_cav connected to the cylindrical part of the tube by a narrow cylindrical “neck” of radius b and length L (see Fig. 1(b)). Both L and V_cav can be equal to zero that corresponds to the “no neck” and “no cavity” cases, respectively. It is additionally assumed that (i) the dead ends are uniformly distributed over the tube wall, and (ii) the neck radius b is much smaller than tube radius a and the mean distance l between neighboring dead ends, measured along the tube axis. As a result, the surface fraction σ occupied by the dead end entrances, which is equal to the ratio of the dead end entrance area, πb², to the mean surface area per one dead end, πa²l, is negligibly small,

$$\sigma =b^2/\left(2al\right)\ll 1.$$ (1.12)

In view of this circumstance, we ignore the effect of dead ends on the Poiseuille flow and assume that the velocity profile is given by Eq. (1.2).

The outline of this paper is as follows. The general formalism is developed in Secs. II–IV. Its application to the particle transport in tubes with dead ends is discussed in Sec. V. To test the accuracy of our approximate theory we compare its predictions with the results obtained from Brownian dynamics simulations. The comparison demonstrates excellent agreement between the two. Some concluding remarks are made in Sec. VI.

II. MODEL

Consider transport of particles by the Poiseuille flow in a cylindrical tube of radius a with reversible binding of the particles to the tube wall (Fig. 1(a)). Let p_f (x, r, t) be the probability density of finding a particle in the flow at point (x, r) at time t, where the x-coordinate is measured along the tube axis and r is the distance from the tube axis, and p_b(x, t) be the probability density of finding the particle bound to the wall at a given value of x at time t. The probabilities of finding the particle bound to the wall and in the flow at time t, P_b(t), and P_f(t), respectively, are

$$P_b\left(t\right)={\int }_{-\infty }^{\infty }{p}_b(x,t)dx$$ (2.1)

and

$$P_f\left(t\right)=2\pi {\int }_{-\infty }^{\infty }dx{\int }_0^a{p}_f(x,r,t)rdr=2\pi {\int }_0^a{p}_r(r,t)rdr,$$ (2.2)

where 2πrp_r(r, t) is the probability density of finding the particle in the tube at distance r from the tube axis at time t,

$$p_r(r,t)={\int }_{-\infty }^{\infty }{p}_f(x,r,t)dx.$$ (2.3)

Because of the probability conservation,

$$P_b\left(t\right)+P_f\left(t\right)=1.$$ (2.4)

We assume that initially (at t = 0) the starting position of the particle is uniformly distributed over a tube cross-section, which is chosen as the origin of the x-coordinate. Thus,

$$p_f(x,r,0)=\frac{1}{\pi a^2}\delta \left(x\right),p_b(x,0)=0.$$ (2.5)

For methodological purposes, in this section and Secs. III and IV we assume that diffusion in the flow may be anisotropic, namely, the particle diffusivities along the tube axis, D_x, and in the radial direction, D_r, may be different. Then the two probability densities satisfy

$$\frac{\partial p_f}{\partial t}=D_x\frac{{\partial }^2{p}_f}{\partial x^2}-v_f\left(r\right)\frac{\partial p_f}{\partial x}+\frac{D_r}{r}\frac{\partial }{\partial r}\left(r\frac{\partial p_f}{\partial r}\right),$$ (2.6)

$$\begin{array}{ccc}\hfill \frac{1}{2\pi a}\frac{\partial p_b}{\partial t}& =& -D_r{\left.\frac{\partial p_f}{\partial r}\right|}_{r=a}\hfill \\ & =& \kappa p_f(x,a,t)-\kappa {\int }_0^t{\Psi }_b(t-t^{\prime })p_f(x,a,t^{\prime })d{t}^{\prime },\hfill \end{array}$$ (2.7)

where Ψ_b(t) is the probability density of the particle lifetime in the bound state and κ is the trapping rate that characterizes the binding efficiency of the tube wall (κ = 0 and κ = ∞ correspond to perfectly reflecting and absorbing walls, respectively). The first equation describes variation of the probability density of the particle in the flow, while the second equation describes the variation of the probability density of the particle bound to the wall. The terms κp_f (x, a, t) and $\kappa {\int }_0^t{\Psi }_b(t-t^{\prime })p_f(x,a,t^{\prime })d{t}^{\prime }$ in the second equation are the probability fluxes due to the particle binding to the wall and its escape from the bound state at time t, respectively. The later term accounts for that the particle, returning to the flow at time t, binds to the wall at some earlier time t^′, t^′ ⩽ t. Equation (2.7) simplifies in the Markovian case, when the probability density of the particle lifetime is a single exponential, ${\Psi }_b\left(t\right)={⟨\tau ⟩}_b^{-1}\exp (-t/{⟨\tau ⟩}_b)$ (see Appendix A). The second equation provides the boundary condition for the probability density p_f (x, r, t) at r = a. At r = 0 this probability density satisfies the reflecting boundary condition

$${\left.\frac{\partial p_f}{\partial r}\right|}_{r=0}=0.$$ (2.8)

Finally, Eq. (2.5) provides the initial conditions for Eqs. (2.6) and (2.7).

Integrating Eqs. (2.6) and (2.7) over x from minus to plus infinity, we find that p_r(r, t) and P_b(t) satisfy

$$\frac{\partial p_r}{\partial t}=\frac{D_r}{r}\frac{\partial }{\partial r}\left(r\frac{\partial p_r}{\partial r}\right),$$ (2.9)

$$\begin{array}{ccc}\hfill \frac{1}{2\pi a}\frac{d{P}_b}{dt}& =& -D_r{\left.\frac{\partial p_r}{\partial r}\right|}_{r=a}\hfill \\ & =& \kappa p_r(a,t)-\kappa {\int }_0^t{\Psi }_b(t-t^{\prime })p_r(a,t^{\prime })d{t}^{\prime }.\hfill \end{array}$$ (2.10)

As follows from Eqs. (2.5) and (2.8), the initial and boundary conditions for these equations, respectively, are

$$p_r(r,0)=\frac{1}{\pi a^2},P_b\left(0\right)=0,$$ (2.11)

and

$${\left.\frac{\partial p_r}{\partial r}\right|}_{r=0}=0.$$ (2.12)

Finally, the probability conservation condition, Eq. (2.4), written in terms of p_r(r, t) and P_b(t) takes the form

$$P_b\left(t\right)+2\pi {\int }_0^a{p}_r(r,t)rdr=1.$$ (2.13)

At long times, P_b(t) and P_f (t) approach their equilibrium values given by Eq. (1.8), while p_r(r, t) tends to $p_r^{eq}$ given by

$$p_r^{eq}=\frac{1}{\pi a^2}{P}_f^{eq}.$$ (2.14)

It can be shown (see Appendix B) that the mean particle lifetime in the flow is given by

$${⟨\tau ⟩}_f=a/\left(2\kappa \right).$$ (2.15)

Then the equilibrium constant, Eq. (1.7), is

$$K=\frac{2\kappa }{a}{⟨\tau ⟩}_b.$$ (2.16)

We take advantage of this formula later to eliminate κ from the final expressions using the relation κ = aK/(2⟨τ⟩_b).

III. MEAN DISPLACEMENT AND EFFECTIVE DRIFT VELOCITY

By definition, the mean displacement of the particle, ⟨x(t)⟩, is given by

$$\begin{array}{c}\hfill ⟨x\left(t\right)⟩={\int }_{-\infty }^{\infty }x\left[2\pi {\int }_0^a{p}_f(x,r,t)rdr+p_b(x,t)\right]dx.\end{array}$$ (3.1)

Here the angular brackets, ⟨...⟩, denote averaging over realizations of the particle trajectory. This notation should not be confused with the notations ⟨...⟩_{b, f}, which denote averaging over realizations of the random particle lifetimes in the bound state and in the flow. Taking the derivative of Eq. (3.1) with respect to time and using Eq. (2.6), we obtain

$$\begin{array}{ccc}\hfill \frac{d⟨x\left(t\right)⟩}{dt}& =& {\int }_{-\infty }^{\infty }x\left[2\pi {\int }_0^a\frac{\partial p_f(x,r,t)}{\partial t}rdr+\frac{\partial p_b(x,t)}{\partial t})\right]dx\hfill \\ & =& {\int }_{-\infty }^{\infty }x\left\{2\pi {\int }_0^a\left[D_x\frac{{\partial }^2{p}_f}{\partial x^2}-v_f\left(r\right)\frac{\partial p_f}{\partial x}\right.\right.\hfill \\ & & \left.\left.+\frac{D_r}{r}\frac{\partial }{\partial r}\left(r\frac{\partial p_f}{\partial r}\right)\right]rdr+\frac{\partial p_b}{\partial t}\right\}dx.\hfill \end{array}$$ (3.2)

To simplify the above equation we use the relations

$${\int }_{-\infty }^{\infty }x\frac{{\partial }^2{p}_f}{\partial x^2}dx=0,$$ (3.3)

$${\int }_{-\infty }^{\infty }x\frac{\partial p_f}{\partial x}dx=-{\int }_{-\infty }^{\infty }{p}_f(x,r,t)dx=-p_r(r,t),$$ (3.4)

$${\int }_0^a\frac{\partial }{\partial r}\left(r\frac{\partial p_f}{\partial r}\right)dr=D_{r}a{\left.\frac{\partial p_f}{\partial r}\right|}_{r=a}=-\frac{1}{2\pi }\frac{\partial p_b}{\partial t},$$ (3.5)

which allows us to write Eq. (3.2) as

$$\frac{d⟨x\left(t\right)⟩}{dt}=2\pi {\int }_0^a{v}_f\left(r\right)p_r(r,t)rdr.$$ (3.6)

After the Laplace transformation, this equation takes the form

$$⟨\widehat{x}\left(s\right)⟩=\frac{2\pi }{s}{\int }_0^a{v}_f\left(r\right){\widehat{p}}_r(r,s)rdr,$$ (3.7)

where s is the Laplace parameter, and $\widehat{f}\left(s\right)$ is the Laplace transform of function f (t), $\widehat{f}\left(s\right)={\int }_0^{\infty }\exp (-st)f\left(t\right)dt$. The long-time behavior of the mean particle displacement can be obtained from the small-s expansion of its Laplace transform. The latter can be derived from Eq. (3.7) using the small-s limiting behavior of function ${\widehat{p}}_r(r,s)$. We find this limiting behavior by solving Eqs. (2.9)–(2.13) by a perturbation theory using s as a small parameter.

Laplace transforming Eqs. (2.9), (2.10), (2.12), and (2.13) we obtain

$$s{\widehat{p}}_r-\frac{1}{\pi a^2}=\frac{D_r}{r}\frac{d}{dr}\left(r\frac{d{\widehat{p}}_r}{dr}\right),$$ (3.8)

$$\frac{s}{2\pi a}{\widehat{P}}_b=-D_r{\left.\frac{d{\widehat{p}}_r}{dr}\right|}_{r=a}=\kappa (1-{\widehat{\Psi }}_b){\left.{\widehat{p}}_r\right|}_{r=a},$$ (3.9)

$${\left.\frac{\partial {\widehat{p}}_r}{\partial r}\right|}_{r=0}=0,$$ (3.10)

$${\widehat{P}}_b+2\pi {\int }_0^a{\widehat{p}}_r(r,s)rdr=\frac{1}{s}.$$ (3.11)

As s → 0, ${\widehat{P}}_b\left(s\right)$ and ${\widehat{p}}_r(r,s)$ can be approximately written as

$$\begin{array}{c}\hfill {\widehat{P}}_b\left(s\right)\simeq \frac{1}{s}{P}_b^{eq}+P_b^{\left(0\right)},\end{array}$$ (3.12)

$$\begin{array}{c}\hfill {\widehat{p}}_r(r,s)\simeq \frac{1}{s}{p}_r^{eq}+p_r^{\left(0\right)}\left(r\right),\end{array}$$ (3.13)

where $P_b^{eq}$, $p_r^{eq}$ are given by Eqs. (1.8) and (2.14), and $P_b^{\left(0\right)}$, $p_r^{\left(0\right)}\left(r\right)$ are independent of s. Substituting the above expressions for ${\widehat{P}}_b\left(s\right)$ and ${\widehat{p}}_r(r,s)$ into Eqs. (3.8)–(3.11), we arrive at

$$\frac{D_r}{r}\frac{d}{dr}\left(r\frac{d{p}_r^{\left(0\right)}}{dr}\right)=p_r^{eq}-\frac{1}{\pi a^2}+s{p}_r^{\left(0\right)},$$ (3.14)

$$\begin{array}{ccc}\hfill \frac{1}{2\pi a}\left(P_b^{eq}+s{P}_b^{\left(0\right)}\right)& =& -D_r{\left.\frac{d{p}_r^{\left(0\right)}}{dr}\right|}_{r=a}\hfill \\ & =& \kappa (1-{\widehat{\Psi }}_b)\left(\frac{1}{s}{p}_r^{eq}+p_r^{\left(0\right)}\left(a\right)\right),\hfill \end{array}$$ (3.15)

$${\left.\frac{\partial p_r^{\left(0\right)}}{\partial r}\right|}_{r=0}=0,$$ (3.16)

$$P_b^{\left(0\right)}+2\pi {\int }_0^a{p}_r^{\left(0\right)}\left(r\right)rdr=0.$$ (3.17)

The small-s expansion of ${\widehat{\Psi }}_b\left(s\right)$ is given by

$${\widehat{\Psi }}_b\left(s\right)\simeq 1-s{⟨\tau ⟩}_b+\frac{s^2}{2}{⟨{\tau }^2⟩}_b,$$ (3.18)

where ⟨τ²⟩_b is the second moment of the particle lifetime in the bound state. Substituting this into Eq. (3.15) and neglecting the terms proportional to s², we obtain

$$\begin{array}{ccc}\hfill \frac{1}{2\pi a}\left(P_b^{eq}+s{P}_b^{\left(0\right)}\right)& =& -D_r{\left.\frac{d{p}_r^{\left(0\right)}}{dr}\right|}_{r=a}=\kappa \left[{⟨\tau ⟩}_b{p}_r^{eq}\right.\hfill \\ & & \left.+s\left({⟨\tau ⟩}_b{p}_r^{\left(0\right)}\left(a\right)-\frac{{⟨{\tau }^2⟩}_b}{2}{p}_r^{eq}\right)\right].\hfill \end{array}$$ (3.19)

This allows us to establish a relation between $P_b^{\left(0\right)}$ and $p_r^{\left(0\right)}\left(a\right)$,

$$P_b^{\left(0\right)}=\kappa \left[2\pi a{⟨\tau ⟩}_b{p}_r^{\left(0\right)}\left(a\right)-\frac{{⟨{\tau }^2⟩}_b}{a}{P}_f^{eq}\right],$$ (3.20)

which is used below. Then neglecting the term proportional to s in the right-hand side of Eq. (3.14), integrating the resulting equation, and taking into account the boundary condition in Eq. (3.16), we find that

$$p_r^{\left(0\right)}\left(r\right)=p_r^{\left(0\right)}\left(0\right)-\frac{r^2}{4\pi a^2{D}_r}{P}_b^{eq}.$$ (3.21)

The expression for $p_r^{\left(0\right)}\left(0\right)$ can be obtained from Eq. (3.17) with $P_b^{\left(0\right)}$ given by Eq. (3.20). The result is

$$p_r^{\left(0\right)}\left(0\right)=\frac{1}{8\pi D_r}\left(1+2K+\frac{4D_r{⟨{\tau }^2⟩}_b}{a^2{⟨\tau ⟩}_b}\right)P_f^{eq}{P}_b^{eq},$$ (3.22)

where we have used the expression for K given in Eq. (2.16).

Finally, substituting ${\widehat{p}}_r(r,s)$ in Eq. (3.13) into Eq. (3.7) and performing the integration, we arrive at

$$⟨\widehat{x}\left(s\right)⟩=\frac{1}{s^2}{\overline{v}}_{\mathit{f}}{P}_f^{eq}+\frac{1}{s}▵x,$$ (3.23)

where △x is given by

$$▵x=\frac{a^2{\overline{v}}_{\mathit{f}}}{24D_r}{P}_b^{eq}\left(1+3P_b^{eq}+\frac{12D_r{⟨{\tau }^2⟩}_b}{a^2{⟨\tau ⟩}_b}{P}_f^{eq}\right).$$ (3.24)

Eventually, we find two leading terms of the long time behavior of the mean particle displacement by inverting the Laplace transform in Eq. (3.23),

$$⟨x\left(t\right)⟩\simeq {\overline{v}}_{\mathit{f}}{P}_f^{eq}t+▵x,t\to \infty .$$ (3.25)

This leads to the following expression for the effective velocity

$$v_{\mathit{eff}}={\left.\frac{d⟨x\left(t\right)⟩}{dt}\right|}_{t\to \infty }={\overline{v}}_{\mathit{f}}{P}_f^{eq}.$$ (3.26)

The expressions in Eqs. (3.24)–(3.26) are the main results of this section. They are used below when deriving the expression for the effective diffusivity. The expression for v_eff, Eq. (3.26), and, hence, the leading term of the long time behavior of ⟨x(t)⟩, Eq. (3.25), can be written on the basis of intuitive arguments. However, the expression for the constant term, Eq. (3.24), cannot be obtained this way.

IV. EFFECTIVE DIFFUSIVITY

The effective diffusivity is defined as

$$D_{\mathit{eff}}=\frac{1}{2}\underset{t\to \infty }{\lim }\frac{d}{dt}\left(⟨x^2\left(t\right)⟩-{⟨x\left(t\right)⟩}^2\right),$$ (4.1)

where ⟨x(t)²⟩ is the second moment of the particle displacement along the tube axis,

$$\begin{array}{c}\hfill ⟨x{\left(t\right)}^2⟩={\int }_{-\infty }^{\infty }{x}^2\left[2\pi {\int }_0^a{p}_f(x,r,t)rdr+p_b(x,t)\right]dx.\end{array}$$ (4.2)

Using Eqs. (3.24)–(3.26), we can write D_eff as

$$D_{\mathit{eff}}=\underset{t\to \infty }{\lim }\left[\frac{1}{2}\frac{d⟨x^2\left(t\right)⟩}{dt}-v_{\mathit{eff}}\left(v_{\mathit{eff}}t+▵x\right)\right].$$ (4.3)

In the Laplace space the above definition of D_eff takes the form

$$D_{\mathit{eff}}=\underset{s\to 0}{\lim }\left[\frac{s^2}{2}⟨{\widehat{x}}^2\left(s\right)⟩-v_{\mathit{eff}}\left(\frac{1}{s}{v}_{\mathit{eff}}+▵x\right)\right].$$ (4.4)

Differentiating ⟨x²(t)⟩, Eq. (4.2), with respect to time and using Eq. (2.6), we obtain

$$\begin{array}{ccc}\hfill \frac{d⟨x^2\left(t\right)⟩}{dt}& =& {\int }_{-\infty }^{\infty }{x}^2\left[2\pi {\int }_0^a\frac{\partial p_f}{\partial t}rdr+\frac{\partial p_b}{\partial t}\right]dx\hfill \\ & =& {\int }_{-\infty }^{\infty }{x}^2\left\{2\pi {\int }_0^a\left[D_x\frac{\partial p_f^2}{\partial x^2}-v_f\left(r\right)\frac{\partial p_f}{\partial x}\right.\right.\hfill \\ & & \left.\left.+\frac{D_r}{r}\frac{\partial }{\partial r}\left(r\frac{\partial p_f}{\partial r}\right)\right]rdr+\frac{\partial p_b}{\partial t}\right\}dx.\hfill \end{array}$$ (4.5)

Next we use Eq. (3.5) and the relations

$${\int }_{-\infty }^{\infty }{x}^2\frac{\partial p_f^2}{\partial x^2}dx=2{\int }_{-\infty }^{\infty }{p}_f(x,r,t)dx=2p_r(r,t),$$ (4.6)

$${\int }_{-\infty }^{\infty }{x}^2\frac{\partial p_f}{\partial x}dx=-2{\int }_{-\infty }^{\infty }x{p}_f(x,r,t)dx\equiv -2f(r,t)$$ (4.7)

to write Eq. (4.5) as

$$\frac{d⟨x^2\left(t\right)⟩}{dt}=4\pi {\int }_0^a[D_x{p}_r(r,t)+v_f\left(r\right)f(r,t)]rdr.$$ (4.8)

The second equality in Eq. (4.7) provides the definition of function f (r, t).

After the Laplace transformation, Eq. (4.8) takes the form

$$s⟨{\widehat{x}}^2\left(s\right)⟩=4\pi {\int }_0^a[D_x{\widehat{p}}_r(r,s)+v_f\left(r\right)\widehat{f}(r,s)]rdr.$$ (4.9)

Substituting this into Eq. (4.4) we arrive at

$$\begin{array}{ccc}\hfill D_{\mathit{eff}}& =& \underset{s\to 0}{\lim }\left[2\pi s{D}_x{\int }_0^a{\widehat{p}}_r(r,s)rdr+2\pi s\right.\hfill \\ & & \left.\times {\int }_0^a{v}_f\left(r\right)\widehat{f}(r,s)rdr-v_{\mathit{eff}}\left(\frac{1}{s}{v}_{\mathit{eff}}+▵x\right)\right].\hfill \end{array}$$ (4.10)

As follows from Eq. (3.13), the first term in the square brackets tends to $D_x{P}_f^{eq}$, as s → 0. Therefore, we can write D_eff as

$$D_{\mathit{eff}}=D_x{P}_f^{eq}+▵D,$$ (4.11)

where

$$\begin{array}{c}\hfill ▵D=\underset{s\to 0}{\lim }\left[2\pi s{\int }_0^a{v}_f\left(r\right)\widehat{f}(r,s)rdr-v_{\mathit{eff}}\left(\frac{1}{s}{v}_{\mathit{eff}}+▵x\right)\right].\end{array}$$ (4.12)

To evaluate the first term in the square brackets in Eq. (4.12), we first derive an evolution equation for function f (r, t), defined in Eq. (4.7). Differentiating f (r, t) with respect to time and using Eq. (2.6) we obtain

$$\begin{array}{ccc}\hfill \frac{\partial f}{\partial t}& =& {\int }_{-\infty }^{\infty }x\frac{\partial p_f}{\partial t}dx\hfill \\ & =& {\int }_{-\infty }^{\infty }x\left[D_x\frac{\partial p_f^2}{\partial x^2}-v_f\frac{\partial p_f}{\partial x}+\frac{D_r}{r}\frac{\partial }{\partial r}\left(r\frac{\partial p_f}{\partial r}\right)\right]dx.\hfill \end{array}$$ (4.13)

Using the relations in Eqs. (3.3) and (3.4), we can write the above equation as

$$\frac{\partial f}{\partial t}=\frac{D_r}{r}\frac{\partial }{\partial r}\left(r\frac{\partial f}{\partial r}\right)+v_f\left(r\right)p_r.$$ (4.14)

The initial condition for function f (r, t) follows from Eq. (2.5):

$$f(r,0)={\int }_{-\infty }^{\infty }x{p}_f(x,r,0)dx=0.$$ (4.15)

At r = 0 and r = a this function satisfies boundary conditions

$${\left.\frac{\partial f}{\partial r}\right|}_{r=0}=0,$$ (4.16)

and

$$-D_r{\left.\frac{\partial f}{\partial r}\right|}_{r=a}=\kappa f(a,t)-\kappa {\int }_0^t{\Psi }_b(t-t^{\prime })f(a,t^{\prime })d{t}^{\prime },$$ (4.17)

which follow from Eqs. (2.7) and (2.8).

Equation (4.14) is an inhomogeneous linear equation. Its general solution can be written in terms of the radial propagator (Green's function), g(r, t|r^′), as

$$f(r,t)=2\pi {\int }_0^{t}d{t}^{\prime }{\int }_0^{a}g(r,t-t^{\prime }|r^{\prime })v_f\left(r^{\prime }\right)p_r(r^{\prime },t^{\prime })r^{\prime }d{r}^{\prime }.$$ (4.18)

The propagator satisfies

$$\frac{\partial g}{\partial t}=\frac{D_r}{r}\frac{\partial }{\partial r}\left(r\frac{\partial g}{\partial r}\right),$$ (4.19)

subject to the initial condition

$$g(r,0|r^{\prime })=\frac{1}{2\pi r}\delta (r-r^{\prime })$$ (4.20)

and boundary conditions

$${\left.\frac{\partial g}{\partial r}\right|}_{r=0}=0$$ (4.21)

and

$$\begin{array}{ccc}\hfill -D_r{\left.\frac{\partial g}{\partial r}\right|}_{r=a}& =& \kappa g(a,t|r^{\prime })-\kappa {\int }_0^t{\Psi }_b(t-t^{\prime })g(a,t^{\prime }|r^{\prime })d{t}^{\prime }\hfill \\ & =& \frac{1}{2\pi a}\frac{d}{dt}{P}_b\left(t\right|r^{\prime }).\hfill \end{array}$$ (4.22)

Here we have introduced the probability of finding the particle in the bound state at time t, P_b(t|r^′), conditional on that the particle starts at distance r^′ from the tube axis at t = 0. Because of the probability conservation, we have

$$P_b\left(t\right|r^{\prime })+2\pi {\int }_0^{a}g(r,t|r^{\prime })rdr=1.$$ (4.23)

The Laplace transform of f (r, t), Eq. (4.18), is

$$\widehat{f}(r,s)=2\pi {\int }_0^a\widehat{g}(r,s|r^{\prime })v_f\left(r^{\prime }\right){\widehat{p}}_r(r^{\prime },s)r^{\prime }d{r}^{\prime }.$$ (4.24)

Substituting this into the integral in Eq. (4.12), we obtain

$$\begin{array}{ccc}& & {\int }_0^a{v}_f\left(r\right)\widehat{f}(r,s)rdr\hfill \\ & & =2\pi {\int }_0^a{\int }_0^a{v}_f\left(r\right)\widehat{g}(r,s|r^{\prime })v_f\left(r^{\prime }\right){\widehat{p}}_r(r^{\prime },s)r{r}^{\prime }drd{r}^{\prime }.\hfill \end{array}$$ (4.25)

As t → ∞, the propagator g(r, t|r^′) tends to $p_r^{eq}$, Eq. (2.14). Therefore, it can be written as

$$g(r,t|r^{\prime })=p_r^{eq}+u(r,t|r^{\prime }),$$ (4.26)

where function u(r, t|r^′) vanishes as t → ∞. In the Laplace space Eq. (4.26) is translated into

$$\widehat{g}(r,s|r^{\prime })=\frac{1}{s}{p}_r^{eq}+\widehat{u}(r,s|r^{\prime }).$$ (4.27)

Using this we can write the integral in the right-hand side of Eq. (4.25) as a sum of two integrals,

$${\int }_0^a{v}_f\left(r\right)\widehat{f}(r,s)rdr=I_1\left(s\right)+I_2\left(s\right),$$ (4.28)

where

$$I_1\left(s\right)=\frac{2\pi }{s}{p}_r^{eq}\left({\int }_0^a{v}_f\left(r\right)rdr\right)\left({\int }_0^a{v}_f\left(r\right){\widehat{p}}_r(r,s)rdr\right)$$ (4.29)

and

$$I_2\left(s\right)=2\pi {\int }_0^a{\int }_0^a{v}_f\left(r\right)\widehat{u}(r,s|r^{\prime })v_f\left(r^{\prime }\right){\widehat{p}}_r(r^{\prime },s)r{r}^{\prime }drd{r}^{\prime }.$$ (4.30)

In view of Eq. (3.7), $I_1\left(s\right)=v_{\mathit{eff}}⟨\widehat{x}\left(s\right)⟩/\left(2\pi \right)$, and Eq. (4.28), takes the form

$${\int }_0^a{v}_f\left(r\right)\widehat{f}(r,s)rdr=\frac{1}{2\pi }{v}_{\mathit{eff}}⟨\widehat{x}\left(s\right)⟩+I_2\left(s\right).$$ (4.31)

This allows us to write △D, Eq. (4.12), as

$$\begin{array}{ccc}\hfill ▵D& =& 2\pi \underset{s\to 0}{\lim }s{I}_2\left(s\right)\hfill \\ \hfill & =& \frac{4\pi }{a^2}{P}_f^{eq}{\int }_0^a{\int }_0^a{v}_f\left(r^{\prime }\right)\widehat{u}(r,0|r^{\prime })v_f\left(r^{\prime }\right)r{r}^{\prime }drd{r}^{\prime },\hfill \end{array}$$ (4.32)

where we have used the small-s asymptotic behavior of ${\widehat{p}}_r(r,s)$, Eq. (3.13).

Introducing an auxiliary function w(r) defined by

$$w\left(r\right)=2\pi {\int }_0^a\widehat{u}(r,0|r^{\prime })v_f\left(r^{\prime }\right)r^{\prime }d{r}^{\prime },$$ (4.33)

we can write △D, Eq. (4.32), in the form

$$▵D=\frac{2}{a^2}{P}_f^{eq}{\int }_0^a{v}_f\left(r\right)w\left(r\right)rdr.$$ (4.34)

Function w(r) is found in Appendix C:

$$w\left(r\right)=w\left(0\right)+\frac{{\overline{v}}_f}{8a^2{D}_r}\left[r^4-2\left(1+P_b^{eq}\right)a^2{r}^2\right],$$ (4.35)

where w(0) is

$$\begin{array}{c}\hfill w\left(0\right)=v_{\mathit{eff}}\left\{\frac{{⟨{\tau }^2⟩}_b}{2{⟨\tau ⟩}_b}K{P}_f^{eq}+\frac{a^2}{24D_r}[2+3K+3(1+2K)P_b^{eq}]\right\},\end{array}$$ (4.36)

and K is given by Eq. (2.16).

Now we can find △D by substituting w(r) into Eq. (4.34) and performing the integration. The result is

$$\begin{array}{c}\hfill ▵D=v_{\mathit{eff}}^2{P}_f^{eq}\left[\frac{{⟨{\tau }^2⟩}_b}{2{⟨\tau ⟩}_b}K+\frac{a^2}{48D_r}\left(1+6K+11K^2\right)\right].\end{array}$$ (4.37)

This eventually allows us to find the effective diffusivity, Eq. (4.11), as a function of the system parameters

$$\begin{array}{ccc}\hfill D_{\mathit{eff}}& =& D_x{P}_{\mathit{f}}^{eq}\hfill \\ & & +{\left(P_f^{eq}\right)}^3{\overline{v}}_{\mathit{f}}^2\left[\frac{{⟨{\tau }^2⟩}_b}{2{⟨\tau ⟩}_b}K+\frac{a^2}{48D_r}(1+6K+11K^2)\right],\hfill \end{array}$$ (4.38)

which is the main result of this section.

Concluding this section, consider some limiting cases of the obtained results for D_eff. When Ψ_b(t) is a single exponential, ${\Psi }_b\left(t\right)={⟨\tau ⟩}_b^{-1}\exp (-t/{⟨\tau ⟩}_b)$, there is a simple relation between the first two moments of the particle lifetime in the bound state: ${⟨{\tau }^2⟩}_b=2{⟨\tau ⟩}_b^2$. Due to this relation, Eq. (4.38) simplifies and reduces to the expression³⁴

$$\begin{array}{c}\hfill D_{\mathit{eff}}=D_x{P}_{\mathit{f}}^{eq}+{\left(P_f^{eq}\right)}^3{\overline{v}}_{\mathit{f}}^2\left[{⟨\tau ⟩}_{b}K+\frac{a^2}{48D_r}(1+6K+11K^2)\right].\end{array}$$ (4.39)

When D_x = D_r = D this is identical to the expression given in Eq. (1.10), with △D given by Eq. (1.11).

As D_r → ∞, the particle velocity in the flow becomes uniform and is equal to ${\overline{v}}_{\mathit{f}}$. As a consequence, the second term in the square brackets in Eq. (4.38), responsible for particle dispersion due to the velocity gradient, vanishes. In addition, in this case the survival probability of the particle in the flow decays exponentially with the rate constant equal to 1/⟨τ⟩_f = 2κ/a. As a result, Eq. (4.38) simplifies and takes the form

$$D_{\mathit{eff}}=D_x{P}_{\mathit{f}}^{eq}+{\left(P_f^{eq}\right)}^3{\overline{v}}_{\mathit{f}}^{2}K\frac{{⟨{\tau }^2⟩}_b}{2{⟨\tau ⟩}_b}.$$ (4.40)

This is a generalization of the known expression^34–36 for the effective diffusivity D_eff of a particle that can jump between two states: a mobile state when it moves with constant velocity ${\overline{v}}_{\mathit{f}}$, and an immobile bound state. The previously published result was obtained assuming a single-exponential distribution of the particle lifetime in the bound state. The new expression for D_eff is applicable when dissociation of the bound state is a non-Markovian process.

V. TRANSPORT IN TUBES WITH DEAD ENDS

In this section, we apply the general theory developed above to a particular case of a tube with dead ends described in the Introduction (Fig. 1(b)), assuming that D_x = D_r = D. We present analytical results for the effective drift velocity and diffusivity in terms of the geometric parameters of the system (a, l, b, L, and V_cav) and validate them by comparison with the results obtained from Brownian dynamics simulations.

A. Analytical results

To apply the above theory to transport in a tube with dead ends, we describe the entry of the particle into a dead end as trapping by a perfectly absorbing disk of radius b on the otherwise reflective tube wall. For a particle diffusing in the flow, the boundary conditions on the tube wall are non-uniform: perfectly absorbing on the dead end entrances and perfectly reflecting on the rest of the wall. Using boundary homogenization (see Refs. ^37–39 and references therein) we can replace these non-uniform boundary conditions by an effective uniform partially absorbing boundary condition. Since the surface fraction σ of the absorbing disks is small, Eq. (1.12), the trapping rate entering into the effective boundary condition is given by^37–39

$$\kappa =\frac{4D}{\pi b}\sigma =\frac{2Db}{\pi al},$$ (5.1)

as discussed in Appendix D. Taking advantage of the relation between the mean particle lifetime in the flow and κ, ⟨τ⟩_f = a/(2κ), we can write ⟨τ⟩_f in terms of the tube parameters,

$${⟨\tau ⟩}_f=\frac{\pi a^{2}l}{4Db}.$$ (5.2)

Note that the particle enters the dead ends by diffusion rather than advection by the flow.

Entering a dead end, the particle interrupts its propagation along the tube axis. The particle lifetime in the dead end is a random variable described by the probability density function Ψ_b(t). An approximate expression for the Laplace transform of Ψ_b(t) was obtained in Ref. 40. This expression shows how ${\widehat{\Psi }}_b\left(s\right)$ depends on the geometric parameters of the dead end (b, L, and V_cav). It can be used to find moments of the particle lifetime in the bound state

$${⟨{\tau }^m⟩}_b={\int }_0^{\infty }{t}^m{\Psi }_b\left(t\right)dt={(-1)}^m{\left.\frac{d^m}{d{s}^m}{\widehat{\Psi }}_b\left(s\right)\right|}_{s=0}.$$ (5.3)

According to Eqs. (3.26) and (4.38), only the first two moments are required for the evaluation of the effective transport parameters. These moments are given by⁴⁰

$${⟨\tau ⟩}_b=\frac{V_{de}}{4Db},{⟨{\tau }^2⟩}_b=2{⟨\tau ⟩}_b^{2}F(b,L,V_{cav}),$$ (5.4)

where function F(b, L, V_cav) is

$$F(b,L,V_{cav})=1+{\left(\frac{V_{cav}}{V_{de}}\right)}^2+\frac{4L}{\pi b}\left[\frac{V_{cav}}{V_{de}}+\frac{1}{3}{\left(\frac{V_{neck}}{V_{de}}\right)}^2\right].$$ (5.5)

Here V_neck = πb²L is the volume of the neck connecting the cylindrical part of the tube with the dead end cavity, and V_de is the total dead end volume,

$$V_{de}=V_{neck}+V_{cav}.$$ (5.6)

Substituting ⟨τ⟩_f and ⟨τ⟩_b given in Eqs. (5.2) and (5.4) into Eq. (1.7), we arrive at the following expression for the equilibrium constant

$$K=\frac{V_{de}}{\pi a^{2}l}=\frac{V_{de}}{V_{tube}},$$ (5.7)

where V_tube = πa²l is the mean tube volume per a dead end. This leads to the following expression for $P_f^{eq}$, Eq. (1.8),

$$P_f^{eq}=\frac{1}{1+K}=\frac{V_{tube}}{V_{tube}+V_{de}},$$ (5.8)

which can be written based purely on geometric reasoning. Finally, we use $P_f^{eq}$ in Eq. (5.8) to find v_eff by means of Eq. (3.26). The result is

$$v_{\mathit{eff}}=\frac{{\overline{v}}_{\mathit{f}}}{1+K}={\overline{v}}_{\mathit{f}}\frac{V_{tube}}{V_{tube}+V_{de}}.$$ (5.9)

This expression shows how the effective particle velocity in a tube with dead ends depends on the geometric parameters of the system.

Next we find the effective diffusivity as a function of the geometric parameters. To this end, we use Eq. (4.38) with ⟨τ⟩_b and ⟨τ²⟩_b given in Eq. (5.4). As a result, we obtain

$$D_{\mathit{eff}}=\left[D+\frac{a^2{\overline{v}}_{\mathit{f}}^2}{48D}\frac{1+6K+11Q{K}^2}{{(1+K)}^2}\right]\frac{1}{1+K},$$ (5.10)

where we have used the expression for $P_f^{eq}$ in Eq. (1.8), and factor Q is given by

$$Q=1+\frac{12\pi }{11}\frac{l}{b}F(b,L,V_{cav}).$$ (5.11)

Note that this factor is always large, Q ≫ 1, because function F(b, L, V_cav), Eq. (5.5), is larger than unity, and it is assumed that b ≪ l. The expression in Eq. (5.10) is one of the main results of the present paper, which shows how the effective diffusivity of the particles in the tube with dead ends (Fig. 1(b)) depends on the geometric parameters of the system.

Finally, we consider two limiting cases in which the general formula in Eq. (5.10) significantly simplifies. The first case corresponds to dead ends without necks, i.e., when L = 0 and V_de = V_cav. Then from Eqs. (5.5) and (5.11) it follows that F(b, L = 0, V_cav) = 2 and

$$Q=1+\frac{24\pi }{11}\frac{l}{b}.$$ (5.12)

Interestingly, factor Q in this case is independent of the dead end dimensions (cavity size). The second limiting case corresponds to dead ends without cavities, i.e., V_cav = 0, V_de = V_neck = πb²L. In this case F(b, L, V_cav = 0) = 1 + 4L/(3πb) and

$$Q=1+\frac{24\pi }{11}\frac{l}{b}\left(\frac{1}{2}+\frac{2L}{3\pi b}\right).$$ (5.13)

In contrast to Eq. (5.12), now parameter Q depends on the dead end dimensions since it is a linear function of the dead end length L.

B. Numerical test

To test the accuracy of the proposed theory we compare the values of the effective drift velocity and diffusivity predicted by Eqs. (5.9) and (5.10) with those obtained from Brownian dynamics simulations. This is done for tubes with dead ends without necks, i.e., where factor Q is given by Eq. (5.12). We consider spherical cavities of radius R, so that the cavity volume is V_cav = 4πR³/3. The cavity radius is much larger than radius b of the apertures connecting cavities with the cylindrical part of the tube, R ≫ b. Since in the absence of the neck V_de = V_cav, the equilibrium constant in Eq. (5.7) takes the form

$$K=\frac{V_{cav}}{V_{tube}}=\frac{4R^3}{3a^{2}l}.$$ (5.14)

The comparison is made for four sets of values of the parameters a, l, and R (all values are given in dimensionless units): (1) a = l = R = 1; (2) a = l = 1, R = 2; (3) a = R = 1, l = 2; and (4) a = 2, l = R = 1. For these sets of the parameters the maximum and minimum values of the equilibrium constant, Eq. (5.14), are K_max ≃ 10.66 (a = l = 1, R = 2) and K_min ≃ 0.33 (a = 2, l = R = 1). For each set of parameters a, l, and R, we took two values of the aperture radius: b = 0.05 and b = 0.1. As a result, factor Q, Eq. (5.12), ranges from Q ≃ 72 (l = 1 and b = 0.1) to Q ≃ 290 (l = 2 and b = 0.05). We compare the theoretical predictions and simulation results at four values of the mean flow velocity: ${\overline{v}}_{\mathit{f}}=5,10,15$, and 20 (also in dimensionless units). Since K ranges from 0.33 to 10.66, the effective velocity v_eff, Eq. (5.9), varies from $0.09{\overline{v}}_{\mathit{f}}$ to $0.75{\overline{v}}_{\mathit{f}}$.

The effect of the dead ends on the effective diffusivity depends on the mean flow velocity ${\overline{v}}_{\mathit{f}}$. In the simulations, we take the particle initial diffusivity to be equal to unity in dimensionless units, D = 1. Then the maximum value of the effective diffusivity, D_eff ≈ 2500, is achieved at a = R = 1, l = 2, b = 0.05, and ${\overline{v}}_{\mathit{f}}=20$. Note that in a tube without dead ends, the effective diffusivity, Eq. (1.4), at ${\overline{v}}_{\mathit{f}}=20$ and a = 1 is D_eff ≃ 9.33, which is much smaller than D_eff ≈ 2500 in the tube with dead ends.

When the surface fraction σ of the dead end entrances on the tube wall is small, Eq. (1.12), the effect of randomly distributed dead ends on transport is the same as that of periodic dead ends separated by distance l. In view of these circumstances, we ran simulations in tubes with periodically distributed dead ends. In the simulations, we monitored positions of 10⁴ particles during 100 dimensionless time units (the dimensionless simulation time step was 10⁻⁶). Particle coordinates at time t and t + △t were related by the following relationships:

$$x(t+▵t)=x\left(t\right)+H(a-r\left(t\right))v_{\mathit{f}}\left(r\left(t\right)\right)▵t+{▵}_x\left(▵t\right),$$ (5.15)

$$y(t+▵t)=y\left(t\right)+{▵}_y\left(▵t\right),$$ (5.16)

$$z(t+▵t)=z\left(t\right)+{▵}_z\left(▵t\right),$$ (5.17)

where $r\left(t\right)=\sqrt{y^2\left(t\right)+z^2\left(t\right)}$, H(ξ) was the Heaviside step function, and △_x(△t), △_y(△t), and △_z(△t) were random increments generated with a Gaussian distribution

$$p\left({▵}_i\right|▵t)=\frac{1}{\sqrt{4\pi ▵t}}\exp \left(-\frac{{▵}_i^2}{2▵t}\right),i=x,y,z.$$ (5.18)

Particle collisions with the wall were treated as perfectly elastic. Particle initial positions were uniformity distributed in the cylindrical part of the tube over one tube period which contained the dead end entrance in its center.

Particle positions were used to find the effective velocity and diffusivity as functions of time, which reached plateau values at sufficiently long times. These plateau values were compared with their theoretically predicted counterparts found from Eqs. (5.9) and (5.10). The results of the comparison are summarized in Tables I and II, which give relative errors of the theoretical predictions in percent. One can see that the theoretically predicated values of v_eff and D_eff are in very good agreement with the values of the effective transport parameters obtained from the simulations.

Table I.

Relative errors in the effective velocity in percent defined as $100|v_{\mathit{eff}}^{sim}-v_{\mathit{eff}}^{theory}|/v_{\mathit{eff}}^{sim}$, where $v_{\mathit{eff}}^{sim}$ and $v_{\mathit{eff}}^{theory}$ are the effective velocities obtained from the simulations and given by Eq. (5.9), respectively.

b	0.05				0.1
${\overline{v}}_{\mathit{f}}$	5	10	15	20	5	10	15	20
a = l = R = 1	0.81	0.95	0.85	0.92	1.28	1.31	1.32	1.26
l = R = 1, a = 2	0.95	0.89	0.83	0.89	0.72	1.23	1.16	1.41
a = R = 1, l = 2	0.87	0.97	0.95	0.82	1.24	1.29	1.17	1.11
a = l = 1, R = 2	0.77	0.88	0.86	0.81	1.45	1.55	1.18	1.43

Table II.

Relative errors in the effective diffusivity in percent defined as $100|D_{\mathit{eff}}^{sim}-D_{\mathit{eff}}^{theory}|/D_{\mathit{eff}}^{sim}$, where $D_{\mathit{eff}}^{sim}$ and $D_{\mathit{eff}}^{theory}$ are the effective diffusivities obtained from the simulations and given by Eq. (5.10), respectively.

b	0.05				0.1
${\overline{v}}_{\mathit{f}}$	5	10	15	20	5	10	15	20
a = l = R = 1	1.49	2.23	2.06	2.18	1.92	2.30	1.82	1.82
l = R = 1, a = 2	1.46	0.83	1.11	2.10	0.84	1.13	1.10	1.17
a = R = 1, l = 2	1.46	0.89	1.04	0.85	0.65	0.55	0.76	0.91
a = l = 1, R = 2	2.57	2.17	2.25	2.29	2.95	3.86	3.13	2.66

In the simulations we studied dead ends with no necks. The reason is that obtaining reliable numerical results when the dead ends have necks, which are longer than their radius, takes much more time than it takes in the case of dead ends without necks. This happens because entering a dead end neck the particle mainly returns rather than goes through and escapes on the opposite side of the neck. The dependence of the translocation probability, P_tr, on the neck length, L, has the form⁴¹

$$P_{tr}=\frac{1}{2+4L/\left(\pi b\right)}.$$ (5.19)

In the absence of the neck (L = 0), P_tr = 1/2, as might be expected based on common-sense arguments, whereas for a long neck (L ≫ b), P_tr ≃ πb/(4L) ≪ 1.

VI. CONCLUDING REMARKS

The present paper is devoted to the Aris-Taylor dispersion in tubes with dead ends. Entering a dead end the particle interrupts its propagation along tube axis. Later it escapes from the dead end and returns to the flow. The particle escape from the dead end is a non-Markovian process. Therefore, to analyze the effect of dead ends on the effective velocity and diffusivity, we first developed a theory of transport in the Poiseuille flow with reversible non-Markovian binding of the particle to the tube wall. This has been done in Secs. III and IV. In Sec. V, the obtained results were used to find the effective velocity and diffusivity as functions of the geometric parameters of the system. To check the accuracy of our theory we compared its predictions with the values of the effective velocity and diffusivity obtained from Brownian dynamic simulations. The comparison (Sec. V) showed excellent agreement between the two for the considered range of the system parameters.

Finally, we summarize the conditions under which the proposed theory is valid. First, the radius of the dead end neck, b, should be much smaller than the tube radius, a, and the distance between neighboring dead ends, l. Second, the flow in the tube should be laminar and have the Poiseuille profile, Eq. (1.2). This means that the mean flow velocity, ${\overline{v}}_{\mathit{f}}$, should not be too high, so that the Reynolds number, $Re={\overline{v}}_{\mathit{f}}a/\nu$, where ν is the kinematic viscosity of the fluid, should not exceed its critical values, R < 1800.^1,3,42

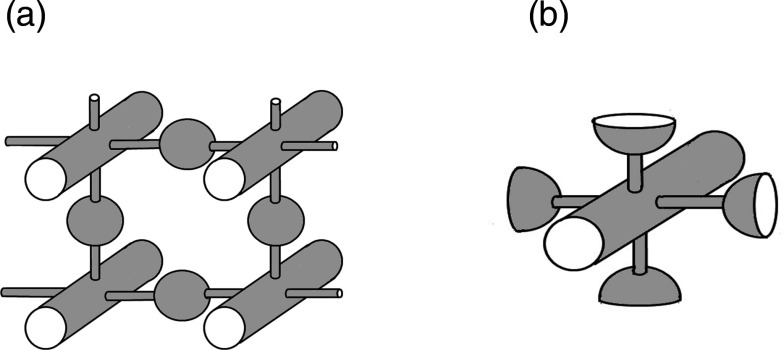
Our approach to the problem involves two main ingredients: (i) homogenization of the boundary conditions on the tube wall containing the dead end entrances (which is the replacement of the nonuniform boundary conditions on the wall by an effective uniform one) and, (ii) the description of the particle escape from the dead end using the results obtained in Ref. 40. This approach with minor modifications can be used to find the effective transport parameters, v_eff and D_eff, in systems of more complex geometries, like the periodic one depicted in Fig. 2, which is often used in modeling transport in porous media^13,43,44 and multi-compartment environments.⁴⁵

FIG. 2.

A periodic model of porous media (panel (a)) and its elementary cell (panel (b)).

Unbiased diffusion in such systems is anisotropic and characterized by two effective diffusiveness, $D_{\mathit{eff}}^{\left(x\right)}$ in the x-direction, which is parallel to the wide tube axes, and $D_{\mathit{eff}}^{(\perp )}$ in the plane normal to the x-direction. These two diffusivities can be found by extending formalisms developed in Refs. 40 and 46, respectively. The effect of the Poiseuille flow in the wide tube on the particle transport can be incorporated by using the formalism developed in the present study. To do this one has to consider transport in a tube with four periodic dead ends, elementary cell of which is shown in Fig. 2 (panel (b)). When the necks are narrow enough, the dead ends of the elementary cell work independently in the sense that the presence of one dead end does not affect the particle entry into the others. Using this assumption one can find v_eff and D_eff in such a tube with periodic dead ends following the way similar to the one described above.

APPENDIX A: EQUATION (2.7) IN THE MARKOVIAN CASE

In the Markovian case the probability flux escaping from the bound state is local in time. As a consequence, Eq. (2.7) can be written as

$$\frac{1}{2\pi a}\frac{\partial p_b}{\partial t}=-D_r{\left.\frac{\partial p_f}{\partial r}\right|}_{r=a}=\kappa p_f(x,a,t)-\frac{1}{2\pi a{⟨\tau ⟩}_b}{p}_b.$$ (A1)

This leads to the following simple relation between the Laplace transforms of the probability densities p_b(x, t) and p_f (x, a, t),

$$\frac{1}{2\pi a}\left(s+\frac{1}{{⟨\tau ⟩}_b}\right){\widehat{p}}_b(x,s)=\kappa {\widehat{p}}_f(x,a,s).$$ (A2)

One can check that this relation can be obtained from Eq. (2.7) with ${\Psi }_b\left(t\right)={⟨\tau ⟩}_b^{-1}\exp (-t/{⟨\tau ⟩}_b)$.

APPENDIX B: MEAN PARTICLE LIFETIMEIN THE FLOW

The mean particle lifetime in the flow, τ(r), considered as a function of the particle initial distance r from the tube axis, satisfies^47,48

$$\frac{D_r}{r}\frac{d}{dr}\left(r\frac{d\tau }{dr}\right)=-1,$$ (B1)

subject to the boundary conditions

$${\left.\frac{D_r}{r}\frac{d\tau }{dr}\right|}_{r=a}+\kappa \tau \left(a\right)=0,{\left.\frac{d\tau }{dr}\right|}_{r=0}=0,$$ (B2)

where κ is the boundary trapping rate. Solving Eq. (B1) we find

$$\tau \left(r\right)=\frac{a^2-r^2}{4D_r}+\frac{a}{2\kappa }.$$ (B3)

For a particle entering the flow from the wall, the mean lifetime in the flow is ⟨τ⟩_f = τ(a) = a/(2κ). This is the expression for the mean lifetime given in Eq. (2.15).

APPENDIX C: DERIVATION OF EXPRESSION FOR FUNCTION w(r), EQ. (4.35)

After the Laplace transformation, Eqs. (4.19) and (4.21)–(4.23) take the form

$$\frac{D_r}{r}\frac{d}{dr}\left(r\frac{d\widehat{g}}{dr}\right)=s\widehat{g}-\frac{1}{2\pi r}\delta (r-r^{\prime }),$$ (C1)

$${\left.\frac{d\widehat{g}}{dr}\right|}_{r=0}=0,$$ (C2)

$$-D_r{\left.\frac{d\widehat{g}}{dr}\right|}_{r=a}=\kappa ({\left.1-{\widehat{\Psi }}_b)\widehat{g}\right|}_{r=a}=\frac{1}{2\pi a}s{\widehat{P}}_b\left(s\right|r^{\prime }),$$ (C3)

$${\widehat{P}}_b\left(s\right|r^{\prime })+2\pi {\int }_0^a\widehat{g}(r,s|r^{\prime })rdr=\frac{1}{s}.$$ (C4)

The probability P_b(t|r^′) at long times approaches its equilibrium value $P_b^{eq}$. Therefore, it can be written as

$$P_b\left(t\right|r^{\prime })=P_b^{eq}+U\left(t\right|r^{\prime }),$$ (C5)

where U(t|r^′) vanishes as t → ∞. Using Eqs. (4.27) and (C1)–(C4), and the Laplace transform of Eq. (C5), it can be shown that functions $\widehat{u}(r,s|r^{\prime })$ and $\widehat{U}\left(s\right|r^{\prime })$ satisfy

$$\frac{D_r}{r}\frac{d}{dr}\left(r\frac{d\widehat{u}}{dr}\right)=p_r^{eq}-\frac{1}{2\pi r}\delta (r-r^{\prime })+s\widehat{u},$$ (C6)

$${\left.\frac{d\widehat{u}}{dr}\right|}_{r=0}=0,$$ (C7)

$$-D_r{\left.\frac{d\widehat{u}}{dr}\right|}_{r=a}=\kappa (\left.1-{\widehat{\Psi }}_b){\left(\frac{1}{s}{p}_r^{eq}+\widehat{u}\right|}_{r=a}\right)=\frac{1}{2\pi a}\left(P_b^{eq}+s\widehat{U}\right),$$ (C8)

$$\widehat{U}\left(s\right|r^{\prime })+2\pi {\int }_0^a\widehat{u}(r,s|r^{\prime })rdr=0.$$ (C9)

Taking the limit of s tending to zero, we find that function $\widehat{u}(r,0|r^{\prime })\equiv u_0\left(r\right|r^{\prime })$ satisfies

$$\frac{D_r}{r}\frac{d}{dr}\left(r\frac{d{u}_0}{dr}\right)=p_r^{eq}-\frac{1}{2\pi r}\delta (r-r^{\prime }),$$ (C10)

$${\left.\frac{d{u}_0}{dr}\right|}_{r=0}=0,$$ (C11)

$$a\kappa {⟨\tau ⟩}_b{u}_0\left(a\right|r^{\prime })+{\int }_0^a{u}_0\left(r\right|r^{\prime })rdr=\frac{\kappa {⟨{\tau }^2⟩}_b}{2\pi a}{P}_f^{eq},$$ (C12)

where we have used the expression for $p_r^{eq}$ in Eq. (2.14).

Multiplying both sides of Eqs. (C10)–(C12) by 2πr′v_f(r′) and then integrating the results over r^′ from zero to a, we find that function w(r) defined in Eq. (4.33) satisfies

$$\frac{D_r}{r}\frac{d}{dr}\left(r\frac{dw}{dr}\right)=v_{\mathit{eff}}-v_f\left(r\right),$$ (C13)

$${\left.\frac{dw}{dr}\right|}_{r=0}=0,$$ (C14)

$$a\kappa {⟨\tau ⟩}_{b}w\left(a\right)+{\int }_0^{a}w\left(r\right)rdr=\frac{1}{2}a\kappa {⟨{\tau }^2⟩}_b{v}_{\mathit{eff}}.$$ (C15)

Integrating Eq. (C13), we eventually obtain the expression for w(r) given in Eq. (4.35).

APPENDIX D: TRAPPING OF DIFFUSING PARTICLES BY PATCHY SURFACES

The steady-state flux J₁ of diffusing particles trapped by the only perfectly absorbing disk of radius b located on the otherwise reflecting flat wall is given by the Hill formula,⁴⁹ J₁ = 4Dbc, where c and D are the bulk concentration and diffusivity of the particles. Correspondingly, the steady-state flux J_N trapped by N identical absorbing disks of the same radius, located sufficiently far from each other, is the sum of the fluxes trapped by individual disks, J_N = J₁N. When the entire wall is randomly covered by the disks, and the disk surface concentration, n, is very low (n → 0), the steady-state flux J_A trapped by the disks located in a large area A of the wall, is given by J_A = J₁nA. Then the flux per unit area is J = J₁n = 4Dbcn. This flux can be interpreted as a steady-state flux trapped by a uniform partially absorbing flat wall, trapping rate of which is low enough and given by κ = 4Dbn. Introducing the disk surface fraction on the wall, σ = πb²n, we can write the trapping rate, κ, in the form given by Eq. (5.1)