Abstract
In this paper, we introduce the Hosoya-Spectral indices and the Hosoya information content of a graph. The first measure combines structural information captured by partial Hosoya polynomials and graph spectra. The latter is a graph entropy measure which is based on blocks consisting of vertices with the same partial Hosoya polynomial. We evaluate the discrimination power of these quantities by interpreting numerical results.
Introduction
Structural differentiation entails the classification of graphs according to structural features captured by quantitative measures, see, e.g., [1]–[5]. One way to demonstrate a classification procedure is to apply a measure (or index) to a special class of graphs and show that the measure discriminates between non-isomorphic graphs with high probability. A prominent example is the Balaban  index [6]–[8] which is highly discriminating on chemical graphs. However, this index has limitations as shown by Dehmer et al. [2] by means of a statistical analysis of the performance of the
index [6]–[8] which is highly discriminating on chemical graphs. However, this index has limitations as shown by Dehmer et al. [2] by means of a statistical analysis of the performance of the  and other indices on an exhaustively generated set of graphs without structural constraints, see [2]. This analysis shows that the discrimination power (also called uniqueness [2]) of graph measures depends on the underlying class of graphs [2].
and other indices on an exhaustively generated set of graphs without structural constraints, see [2]. This analysis shows that the discrimination power (also called uniqueness [2]) of graph measures depends on the underlying class of graphs [2].
This paper is an investigation of the discriminating power of structural indices based on the zeros of partial Hosoya polynomials and graph spectra. Also, we introduce and evaluate the Hosoya information content of a graph. To position this investigation we begin with a survey of literature dealing with eigenvalues and entropy-based measures of graphs. Classical results in the theory of graph spectra are due to Cvetković et al. [9]. The main concern of this theory is to explore structural properties of graphs and complex networks captured by graph spectra [10]. More recent results have been presented and surveyed by Chung [11] and Cioab [12]. Interdisciplinary applications of graph spectra, e.g., the analysis of biological networks and web graphs can be found in [10], [13]. Various graph measures incorporating eigenvalues have been discussed by Randić et al. [14] and Dehmer et al. [15]. One example of a measure is defined as the sum of the moduli of non-zero eigenvalues of the adjacency matrix of a graph; another is given by graph entropies based on the eigenvalues of matrices associated with a graph [14]–[16]. Yet another well-known measure is the Estrada index [17]–[20] which has been explored in bioinformatics, mathematical chemistry and applied mathematics. A more recent review of this quantity is due to Gutman et al. [21]. Variants of this measures using other matrices have been discussed by Li et al. [22]. A related measure is the so-called energy of a graph is an important quantity defined in relation to the eigenvalues of matrices associated with a graph, see [23]–[25]. Extremal properties of graph energy have been studied by [23]–[25]. A recent book on graph energy summarizing classical and new results is [26]. Inequalities for eigenvalue-based graph measures have been discussed in [12]. Elphick and Wocjan [27] analyzed a novel spectral measure for determining network irregularity [27].
[12]. Interdisciplinary applications of graph spectra, e.g., the analysis of biological networks and web graphs can be found in [10], [13]. Various graph measures incorporating eigenvalues have been discussed by Randić et al. [14] and Dehmer et al. [15]. One example of a measure is defined as the sum of the moduli of non-zero eigenvalues of the adjacency matrix of a graph; another is given by graph entropies based on the eigenvalues of matrices associated with a graph [14]–[16]. Yet another well-known measure is the Estrada index [17]–[20] which has been explored in bioinformatics, mathematical chemistry and applied mathematics. A more recent review of this quantity is due to Gutman et al. [21]. Variants of this measures using other matrices have been discussed by Li et al. [22]. A related measure is the so-called energy of a graph is an important quantity defined in relation to the eigenvalues of matrices associated with a graph, see [23]–[25]. Extremal properties of graph energy have been studied by [23]–[25]. A recent book on graph energy summarizing classical and new results is [26]. Inequalities for eigenvalue-based graph measures have been discussed in [12]. Elphick and Wocjan [27] analyzed a novel spectral measure for determining network irregularity [27].
Graph entropy measures have been explored extensively in various disciplines. Rashevsky and Mowshowitz did seminal work when developing the first graph entropy measures based on vertex orbits [28], [29]. Körner introduced a graph entropy measure that has been used in information theory [30]. Bonchev et al. developed the magnitude-based information indices and various others based on graph invariants such as vertex degrees and distances in graphs [31]–[34]. Also, Bonchev et al. [1] proposed an information index for graphs which is based on the Hosoya graph decomposition. However, this information index (using Hosoya index  [35] to define the probabilities of the induced partition) is quite different from the one we introduce here in section ‘Hosoya-based Indices’. Many other graph entropy measures can be found in [36]–[38]. To study results towards the Hosoya polynomial, we refer to [39], [40].
[35] to define the probabilities of the induced partition) is quite different from the one we introduce here in section ‘Hosoya-based Indices’. Many other graph entropy measures can be found in [36]–[38]. To study results towards the Hosoya polynomial, we refer to [39], [40].
In an earlier paper [3], we explored the discrimination power of measures (see section ‘Hosoya-based Indices’) that are based on the moduli of the zeros of the partial Hosoya polynomial. The main contribution of this paper is to define the Hosoya-Spectral indices combining structural information captured by partial Hosoya polynomials with graph spectra. Also, we examine the discrimination power of these indices and of the Hosoya information content of a graph. We discuss and compare the numerical results with the earlier ones produced in [3]. Further we elaborate on the usage of these measures as highly discriminating graph invariants.
Methods and Results
Hosoya-Based Indices
In this section, we reproduce the graph indices based on partial Hosoya polynomials, see [3]. As outlined in [3], the partial Hosoya polynomial of a vertex 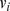 in the graph
in the graph 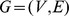 is given by [41], [42]
is given by [41], [42]
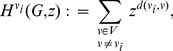 |
(1) |
where 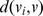 is the distance (i.e., length of a shortest path) between the vertices
is the distance (i.e., length of a shortest path) between the vertices 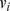 and
and  . Solving the equation
. Solving the equation
| (2) |
yields the complex zeros 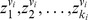 which are not equal to zero. We infer
which are not equal to zero. We infer 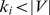 by applying the well-known fundamental theorem of Algebra [43], [44] stating that a complex polynomial
by applying the well-known fundamental theorem of Algebra [43], [44] stating that a complex polynomial
| (3) |
with degree 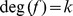 has
has 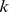 complex zeros.
complex zeros.
Also in [3], Dehmer et al. introduced the following indices:
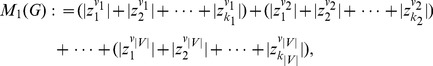 |
(4) |
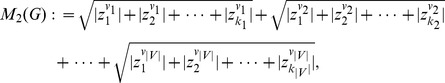 |
(5) |
and
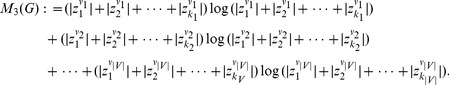 |
(6) |
Here, 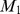 is the sum of the sums of the moduli of all partial Hosoya polynomials
is the sum of the sums of the moduli of all partial Hosoya polynomials 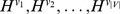 .
. 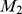 is the sum of the square roots of the sums of the moduli of all partial Hosoya polynomials.
is the sum of the square roots of the sums of the moduli of all partial Hosoya polynomials. 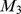 represents an entropy-like measure taking the sums of the moduli of all partial Hosoya polynomials into account.
represents an entropy-like measure taking the sums of the moduli of all partial Hosoya polynomials into account.
Spectra of graphs have been investigated extensively [9], [12]. As already mentioned, well-known spectral based indices are the Estrada index [18]–[20] and various forms of graph energy due to Gutman, see [23]–[25]. Since Hosoya polynomials and graph spectra capture different aspects of graph structure, we propose to combine the two in one index. So, let  be the eigenvalues of
be the eigenvalues of 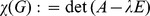 ;
; 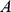 the adjacency matrix of
the adjacency matrix of 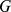 . The Hosoya-Spectral indices
. The Hosoya-Spectral indices
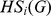 are defined as follows:
are defined as follows:
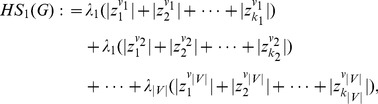 |
(7) |
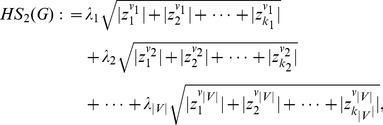 |
(8) |
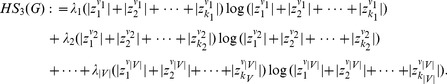 |
(9) |
Inspired by studying information-theoretic complexity measures [1], [28], [31]–[33], [45], we define the Hosoya information content of a graph 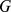 . Let
. Let 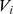 for
for 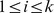 be the set of all vertices in
be the set of all vertices in 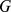 with the
with the 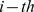 of
of 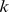 partial Hosoya polynomials of the vertices of
partial Hosoya polynomials of the vertices of 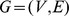 ;
; 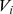 is then the
is then the  -th block in a partition of
-th block in a partition of 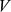 . The Hosoya information content of
. The Hosoya information content of 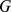 is defined by
is defined by
| (10) |
In the next section, we evaluate the discrimination power of this new measure and the Hosoya-Spectral indices on exhaustively generated graphs.
Numerical Results
As in [3], we present the numerical values resulting from the evaluation of the discrimination power of the Hosoya-Spectral indices and the Hosoya information content. In order to do so, we use the same graph classes in order to make direct comparisons [3]; 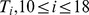 are the sets of all non-isomorphic trees with
are the sets of all non-isomorphic trees with  vertices.
vertices. 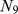 is the set of all non-isomorphic graphs with 9 vertices, see [2].
is the set of all non-isomorphic graphs with 9 vertices, see [2].
To evaluate the discrimination power quantitatively, we use the same measures as in [3]: ndv stands for the number of non-distinguishable graphs according to the values of the indices. From this, we also compute 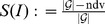 where
where 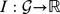 , see [46].
, see [46].
As in [3], the measures 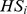 are fully unique on
are fully unique on  , see Table 1. We obtain the same result by applying the Hosoya-Spectral indices to
, see Table 1. We obtain the same result by applying the Hosoya-Spectral indices to  , see Table 2. See also [3]. Moreover, the Hosoya-Spectral indices can discriminate the tree class
, see Table 2. See also [3]. Moreover, the Hosoya-Spectral indices can discriminate the tree class 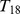 uniquely (see Table 3). Note that the earlier defined measures
uniquely (see Table 3). Note that the earlier defined measures 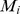 (see Equation 4–6) [3] produced the first degeneracies on the set
(see Equation 4–6) [3] produced the first degeneracies on the set 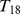 .
.
Table 1. Exhaustively generated sets of non-isomorphic trees: 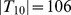 ,
, 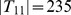 ,
, 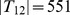 ,
, 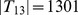 .
.
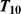
|
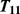
|
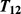
|
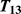
|
|||||
| Measure | ndv |
|
ndv |
|
ndv |
|
ndv |
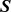
|
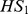
|
0 | 1,000000 | 0 | 1,000000 | 0 | 1,000000 | 0 | 1,000000 |
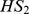
|
0 | 1,000000 | 0 | 1,000000 | 0 | 1,000000 | 0 | 1,000000 |
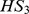
|
0 | 1,000000 | 0 | 1,000000 | 0 | 1,000000 | 0 | 1,000000 |
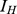
|
76 | 0,283018 | 201 | 0,144680 | 499 | 0,094373 | 1237 | 0,049192 |
Table 2. Exhaustively generated sets of non-isomorphic trees: 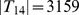 ,
, 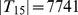 ,
, 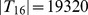 ,
, 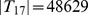 .
.
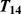
|
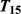
|
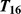
|
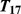
|
|||||
| Measure | ndv |
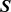
|
ndv |
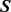
|
ndv |
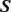
|
ndv |
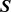
|
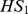
|
0 | 1,000000 | 0 | 1,000000 | 0 | 1,000000 | 0 | 1,000000 |
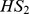
|
0 | 1,000000 | 0 | 1,000000 | 0 | 1,000000 | 0 | 1,000000 |
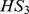
|
0 | 1,000000 | 0 | 1,000000 | 0 | 1,000000 | 0 | 1,000000 |
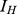
|
3067 | 0,029123 | 7637 | 0,013434 | 19178 | 0,007349 | 48629 | 0,003783 |
Table 3. Exhaustively generated sets of non-isomorphic trees and graphs: 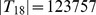 ,
,  .
.
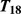
|
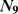
|
|||
| Measure | ndv |

|
ndv |
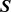
|
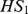
|
0 | 1,000000 | 24 | 0,999908 |

|
0 | 1,000000 | 18 | 0,999931 |

|
0 | 1,000000 | 12393 | 0,952723 |

|
123512 | 0,001979 | 261080 | 0,000000 |
The exhaustively generated graphs with 9 vertices (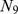 ) warrants special attention. In contrast to the previously introduced measures
) warrants special attention. In contrast to the previously introduced measures 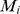 , Table 3 shows that the uniqueness of
, Table 3 shows that the uniqueness of 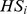 is high. More precisely,
is high. More precisely, 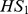 and
and 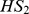 can discriminate 99% of the graph uniquely. The discrimination power of
can discriminate 99% of the graph uniquely. The discrimination power of 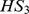 is approximately 95%. This marks a considerable improvement compared with the measures
is approximately 95%. This marks a considerable improvement compared with the measures 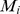 evaluated in [3] on the same classes of graphs. The improvement of the discrimination power of the new measures can be explained by the fact that partial Hosoya polynomials and graph spectra capture quite different aspects of graph structure. In particular, the partial Hosoya polynomial captures local graph properties related to distances in a graph, and the indices
evaluated in [3] on the same classes of graphs. The improvement of the discrimination power of the new measures can be explained by the fact that partial Hosoya polynomials and graph spectra capture quite different aspects of graph structure. In particular, the partial Hosoya polynomial captures local graph properties related to distances in a graph, and the indices 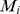 take account of the moduli of the zeros of these polynomials. By contrast, the spectrum of a graph captures connectivity properties linked to its adjacency matrix. The combination of these graph properties in the measures
take account of the moduli of the zeros of these polynomials. By contrast, the spectrum of a graph captures connectivity properties linked to its adjacency matrix. The combination of these graph properties in the measures 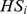 plausibly accounts for their superior performance over the single property measures (
plausibly accounts for their superior performance over the single property measures (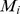 ).
).
Evidently, the discrimination power of 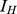 declines as the graph classes grow in size, i.e., the greater the cardinality of the graph class, the lower is index's discrimination power (measured by ndv and
declines as the graph classes grow in size, i.e., the greater the cardinality of the graph class, the lower is index's discrimination power (measured by ndv and 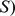 , see Table 1–3. Even for small classes, the degeneracy is high. For
, see Table 1–3. Even for small classes, the degeneracy is high. For 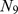 , the Hosoya information content
, the Hosoya information content 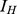 cannot discriminate at all and, hence,
cannot discriminate at all and, hence, 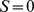 . These results are not surprising in view of the definition of Hosoya information content. The blocks of the partitions consist of vertices with the same partial Hosoya polynomial. Thus, the more cycles in a graph, the greater the likelihood of obtaining large blocks of vertices with the same partial Hosoya polynomial. The occurrence of such large blocks results in high values for the quantity ndv (and low values for
. These results are not surprising in view of the definition of Hosoya information content. The blocks of the partitions consist of vertices with the same partial Hosoya polynomial. Thus, the more cycles in a graph, the greater the likelihood of obtaining large blocks of vertices with the same partial Hosoya polynomial. The occurrence of such large blocks results in high values for the quantity ndv (and low values for 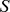 ).
).
Summary and Conclusions
In this paper, we defined the Hosoya-Spectral indices as well as the Hosoya information content of a graph. The former measures combine structural information captured by partial Hosoya polynomials and graph spectra. It is evident that those two graph features capture structural information differently and, hence, the resulting measures may be more unique than the ones (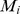 ) used in earlier work, see [3]. The numerical study reported here has confirmed this conjecture for both trees and graphs. Finally, as expected, the discrimination power of Hosoya information content was found to be very low.
) used in earlier work, see [3]. The numerical study reported here has confirmed this conjecture for both trees and graphs. Finally, as expected, the discrimination power of Hosoya information content was found to be very low.
In future research, we plan to explore extremal properties of both measures. In particular, Hosoya information content is related to the orbit structure of a graph, and this calls for studying the automorphism groups of certain classes of graphs.
Acknowledgments
We thank Lukas Huber for help regarding the data analysis and fruitful discussions
Data Availability
The authors confirm that, for approved reasons, some access restrictions apply to the data underlying the findings. The data sets (graphs) can be generated by using the papackage Nauty (subpackage geng) by McKay.
Funding Statement
Matthias Dehmer thanks the Austrian Science Funds for supporting this work (project P26142). Matthias Dehmer gratefully acknowledges financial support from the German Federal Ministry of Education and Research (BMBF) (project RiKoV, Grant No. 13N12304). Yongtang Shi are supported by NSFC, PCSIRT, China Postdoctoral Science Foundation and China Scholarship Council. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Bonchev D, Mekenyan O, Trinajstić N (1981) Isomer discrimination by topological information approach. J Comp Chem 2: 127–148. [Google Scholar]
- 2. Dehmer M, Grabner M, Varmuza K (2012) Information indices with high discriminative power for graphs. PLoS ONE 7: e31214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dehmer M, Mowshowitz A, Shi Y (2014) Discrimination power of graph measures based on complex zeros of the partial Hosoya polynomial. submitted for publication.
- 4. Konstantinova EV, Paleev AA (1990) Sensitivity of topological indices of polycyclic graphs. Vychisl Sistemy 136: 38–48. [Google Scholar]
- 5. Petrov E, Stoyanov B, Kochev N, Bangov I (2014) Use of cti index for perception of duplicated chemical structures in large chemical databases. MATCH Commun Math Comput Chem 71: 645–656. [Google Scholar]
- 6. Balaban AT (1982) Highly discriminating distance-based topological index. Chem Phys Lett 89: 399–404. [Google Scholar]
-
7.
Randić M (2013)
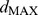 matrix of dominant distances in a graph. MATCH Commun Math Comput Chem
70: 221–238. [Google Scholar]
matrix of dominant distances in a graph. MATCH Commun Math Comput Chem
70: 221–238. [Google Scholar] -
8.
Randić M, Orel R, Balaban AT (2013)
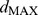 matrix graph invariants as graph descriptors. graphs having the same balaban
matrix graph invariants as graph descriptors. graphs having the same balaban 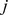 index. MATCH Commun Math Comput Chem
70: 239–258. [Google Scholar]
index. MATCH Commun Math Comput Chem
70: 239–258. [Google Scholar] - 9.Cvetković DM, Doob M, Sachs H (1980) Spectra of Graphs. Theory and Application. Deutscher Verlag der Wissenschaften. Berlin, Germany.
- 10.Estrada E (2011) The Structure of Complex Networks. Theory and Applications.. Oxford University Press.
- 11.Chung F (1997) Spectral Graph Theory, volume 12 of Cbms Regional Conference Series in Mathematics. American Mathematical Society.
-
12.Cioab
 SM (2010) Some applications of eigenvalues of graphs. In: Dehmer M, editor, Structural Analysis of Complex Networks, Boston/Basel: Birkhäuser. pp. 357–379. [Google Scholar]
SM (2010) Some applications of eigenvalues of graphs. In: Dehmer M, editor, Structural Analysis of Complex Networks, Boston/Basel: Birkhäuser. pp. 357–379. [Google Scholar] - 13.Wu J, Deng HZ, Tan YJ (2010) Spectral measure of robustness for internet topology. In: 2010 3rd IEEE International Conference on Computer Science and Information Technology (ICCSIT). volume 6 , pp. 50–54. [Google Scholar]
- 14.Randić M, Vracko M, Novic M (2001) Eigenvalues as molecular descriptors. In: Diudea MV, editor, QSPR/QSAR Studies by Molecular Descriptors, Nova Publishing. pp. 93–120. Huntington, NY, USA.
- 15. Dehmer M, Sivakumar L, Varmuza K (2012) Uniquely discriminating molecular structures using novel eigenvalue-based descriptors. MATCH Communications in Mathematical and in Computer Chemistry 67: 147–172. [Google Scholar]
- 16.Janežić D, Miležević A, Nikolić S, Trinajstić N (2009) Topological complexity of molecules. In: Meyers R, editor, Encyclopedia of Complexity and System Science, Springer, volume 5 . pp. 9210–9224. [Google Scholar]
- 17. Das KC, Lee SG (2009) On the Estrada index conjecture. Linear Algebra and its Applications 431: 1351–1359. [Google Scholar]
- 18. Estrada E (2000) Characterization of 3d molecular structure. Chemical Physics Letters 319: 713–718. [Google Scholar]
- 19. Estrada E (2002) Characterization of the folding degree of proteins. Bioinformatics 18: 697–704. [DOI] [PubMed] [Google Scholar]
- 20. Gutman I, Estrada E, Rodriguez-Velázquezc JA (2007) On a graph-spectrum-based structure descriptor. Croatica Chemica Acta 80: 151–154. [Google Scholar]
- 21.Gutman I, Deng H, Randenković S (2011) The Estrada index: An updated survey. In: Cvetković D, Gutman I, editor, Selected Topics on Applications of Graph Spectra, Mathematical Institute of the Serbian Academy of Sciences and Arts, Belgrade. pp. 155–174. [Google Scholar]
- 22. Li J, Shiu WC, Chan WH (2011) Note on the Laplacian Estrada Index of a Graph. MATCH Commun Math Comput Chem 6: 777–784. [Google Scholar]
- 23.Gutman I (2001) The energy of a graph: Old and new results. In: Betten A, Kohnert A, Laue R, Wassermann A, editor, Algebraic Combinatorics and Applications, Springer Verlag. pp. 196––211. Berlin. [Google Scholar]
- 24. Gutman I, Zhou B (2006) Laplacian energy of a graph. Linear Algebra and its Applications 414: 29–37. [Google Scholar]
- 25.Gutman I, Li X, Zhang J (2009) Graph energy. In: Dehmer M, Emmert-Streib F,editor, Analysis of Complex Networks: From Biology to Linguistics, Wiley-VCH. pp. 145–174. [Google Scholar]
- 26.Li X, Shi Y, Gutman I (2012) Graph Energy. Springer.
- 27. Elphick C, Wocjan P (2014) New measures of graph irregularity. Electronic Journal of Graph Theory and Applications 2: 52–65. [Google Scholar]
- 28. Mowshowitz A (1968) Entropy and the complexity of the graphs I: An index of the relative complexity of a graph. Bull Math Biophys 30: 175–204. [DOI] [PubMed] [Google Scholar]
- 29. Rashevsky N (1955) Life, information theory, and topology. Bull Math Biophys 17: 229–235. [Google Scholar]
- 30.Körner J (1973) Coding of an information source having ambiguous alphabet and the entropy of graphs. Transactions of the 6-th Prague Conference on Information Theory: 411–425.
- 31. Bonchev D, Trinajstić N (1977) Information theory, distance matrix and molecular branching. J Chem Phys 67: 4517–4533. [Google Scholar]
- 32. Bonchev D (1979) Information indices for atoms and molecules. MATCH Commun Math Comp Chem 7: 65–113. [Google Scholar]
- 33.Bonchev D (1983) Information Theoretic Indices for Characterization of Chemical Structures. Research Studies Press, Chichester.
- 34. Bonchev D (2000) Overall connectivities and topological complexities: A new powerful tool for QSPR/QSAR. J Chem Inf Comput Sci 40: 934–941. [DOI] [PubMed] [Google Scholar]
- 35. Hosoya H (1971) Topological index. A newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons. Bull Chem Soc Jpn 44: 2332–2339. [Google Scholar]
- 36. Dehmer M, Mowshowitz A (2011) A history of graph entropy measures. Information Sciences 1: 57–78. [Google Scholar]
- 37.Devillers J, Balaban AT (1999) Topological Indices and Related Descriptors in QSAR and QSPR. Gordon and Breach Science Publishers. Amsterdam, The Netherlands.
- 38. Mehler A, Weiβ P, Lücking A (2010) A network model of interpersonal alignment. Entropy 12: 1440–1483. [Google Scholar]
- 39.Gutman I, Zhang Y, Dehmer M, Ilić A (2012) Altenburg, Wiener, and Hosoya polynomials. In: Gutman I, Furtula B,editor, Distance in Molecular Graphs - Theory, Univ. Kragujevac.pp. 49–70. Kragujevac. [Google Scholar]
- 40. Deutsch E, Klavžar S (2013) Computing the hosoya polynomial of graphs from primary subgraphss. MATCH Commun Math Comput Chem 70: 627–644. [Google Scholar]
- 41. Došlić T (2008) Vertex-weighted Wiener polynomials for composite graphs. Ars Math Contemp 1: 66–80. [Google Scholar]
- 42. Hosoya H (1988) On some counting polynomials. Discrete Applied Mathematics 19: 239–257. [Google Scholar]
- 43. Dehmer M, Mowshowitz A (2011) Bounds on the moduli of polynomial zeros. Applied Mathematics and Computation 218: 4128–4137. [Google Scholar]
- 44.Fricke R (1924) Lehrbuch der Algebra. Friedrich Vieweg & Sohn Verlag. Braunschweig, Germany.
- 45. Dehmer M, Borgert S, Emmert-Streib F (2008) Entropy bounds for molecular hierarchical networks. PLoS ONE 3: e3079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Konstantinova EV, Skorobogatov VA, Vidyuk MV (2002) Applications of information theory in chemical graph theory. Indian Journal of Chemistry 42: 1227–1240. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The authors confirm that, for approved reasons, some access restrictions apply to the data underlying the findings. The data sets (graphs) can be generated by using the papackage Nauty (subpackage geng) by McKay.


