Noise and Analyzer-Crystal Angular Position Analysis for Analyzer-Based Phase-Contrast Imaging

Abstract

The analyzer-based phase-contrast X-ray imaging (ABI) method is emerging as a potential alternative to conventional radiography. Like many of the modern imaging techniques, ABI is a computed imaging method (meaning that images are calculated from raw data). ABI can simultaneously generate a number of planar parametric images containing information about absorption, refraction, and scattering properties of an object. These images are estimated from raw data acquired by measuring (sampling) the angular intensity profile (AIP) of the X-ray beam passed through the object at different angular positions of the analyzer crystal. The noise in the estimated ABI parametric images depends upon imaging conditions like the source intensity (flux), measurements angular positions, object properties, and the estimation method. In this paper, we use the Cramér-Rao lower bound (CRLB) to quantify the noise properties in parametric images and to investigate the effect of source intensity, different analyzer-crystal angular positions and object properties on this bound, assuming a fixed radiation dose delivered to an object. The CRLB is the minimum bound for the variance of an unbiased estimator and defines the best noise performance that one can obtain regardless of which estimation method is used to estimate ABI parametric images. The main result of this manuscript is that the variance (hence the noise) in parametric images is directly proportional to the source intensity and only a limited number of analyzer-crystal angular measurements (eleven for uniform and three for optimal non-uniform) are required to get the best parametric images. The following angular measurements only spread the total dose to the measurements without improving or worsening CRLB, but the added measurements may improve parametric images by reducing estimation bias.

Next, using CRLB we evaluate the Multiple-Image Radiography (MIR), Diffraction Enhanced Imaging (DEI) and Scatter Diffraction Enhanced Imaging (S-DEI) estimation techniques, though the proposed methodology can be used to evaluate any other ABI parametric image estimation technique.

1. Introduction

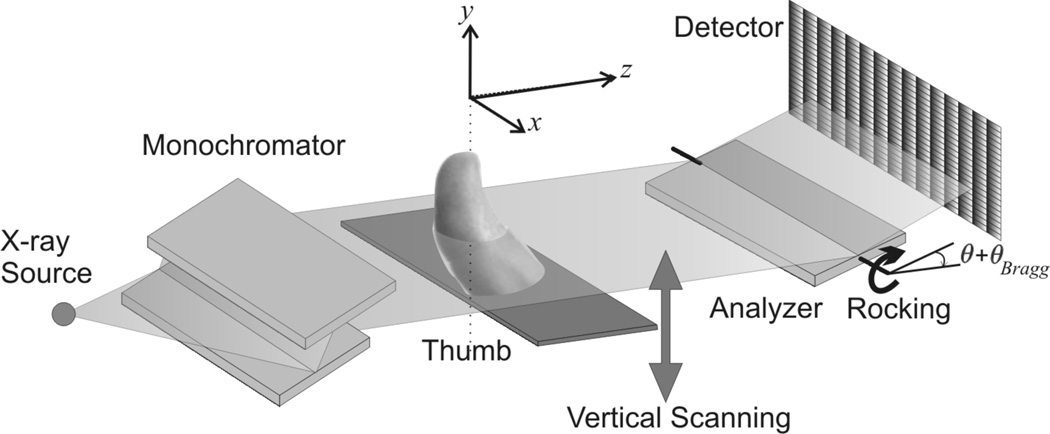
Analyzer-based phase-contrast imaging (ABI) utilizes the Bonse-Hart camera (Bonse and Hart, 1965), which is schematically shown in Figure 1. This system uses a system of diffracting crystals to make precise measurements of the angular content of an X-ray beam after it traverses an object. Specifically, the Bonse-Hart camera allows one to measure the beam angular intensity profile (AIP), i.e. X-ray beam intensity as a function of the angular direction of propagation at each pixel. To achieve this, the ABI system uses a highly collimated (directional) and quasi-monochromatic imaging beam that is obtained by the use of a double crystal monochromator. As the collimated X-ray beam passes through the object (e.g., a patient’s body), the beam will be attenuated by absorption processes, deflected due to refraction, and directed into a broadened range of angular directions due to ultra small-angle X-ray scattering (USAXS). After passing through the object, the beam strikes the analyzer-crystal, which diffracts the beam traveling in a specific narrow direction according to Bragg’s law. This beam is then detected by a pixelated X-ray detector. The imaging beam at the location of the object is usually wide (i.e. size in x axis direction) but only several millimeters in the vertical height (i.e. size in y axis direction). Therefore the object is mounted on a scanning stage driven by a stepping motor, thus allowing object scanning in the vertical direction. Next, by changing angular position (rocking) of the analyzer-crystal (in short analyzer), a number of raw images are acquired and used to calculate parametric images describing object properties.

Figure 1.

Schematic diagram of ABI imaging system (not drawn to scale). In this paper, we investigate the effect of the analyzer position on the noise performance.

For example, in the well-known diffraction enhanced imaging technique (DEI) (Chapman et al., 1997), the acquisition is done at two angular analyzer positions and it can therefore simultaneously estimate two parametric images, which contain information about refraction and absorption properties of the object. In multiple image radiography (MIR) (Wernick et al., 2003), which is an improvement upon the DEI, the acquisition is done at a number - larger than three - of angular analyzer positions; therefore, in addition to the previous two planar parametric images, MIR can also estimate ultra small-angle X-ray scattering (USAXS).

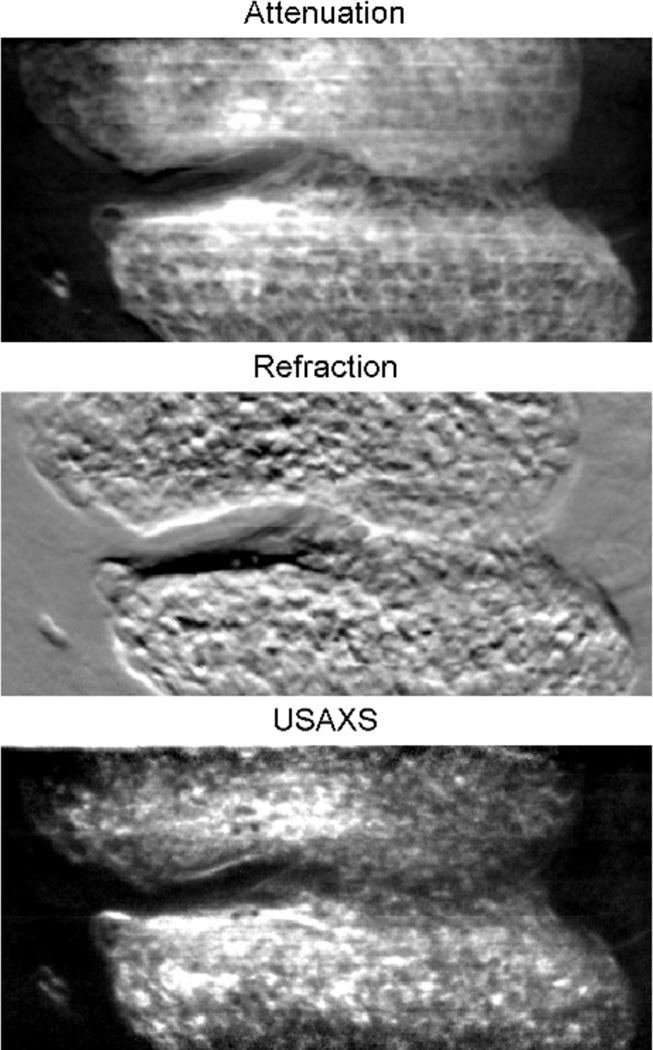
Examples of MIR images for formalin fixed human thumb tissue are shown in Figure 2. The attenuation image shows the absorption and Compton scatter rejection together (Chapman et al., 1997). The refraction image in MIR shows the integrated effect of refractive index variations along the beam path, and the USAXS image represents the sub-pixel textural structure of the object.

Figure 2.

MIR projections of a human thumb. The images are acquired with the beam energy of 40keV at 25 analyzer positions ranging from −4.8 to 4.8 μrad with 0.4 μrad increments (see experimental sections for acquisition details).

Because the contrast of the refraction and USAXS images does not rely on the absorption of X-ray by the object, ABI can be performed at X-ray energies higher than conventional radiography where radiation exposure to the patient can be low. In addition, ABI parametric images are virtually immune to degradation due to Compton scatter at higher angles and have good contrast, which can help to eliminate breast compression as in conventional mammography. For these reasons, ABI is emerging as a potential alternative to conventional radiography (Faulconer et al., 2009; Faulconer et al., 2010; Kitchen et al., 2011; Honnicke et al., 2012; Zhao et al., 2012). As additional reading see (Brankov and Zysk, 2012; Suortti et al., 2013) for a border overview of ABI and (Zhou and Brahme, 2008; Coan et al., 2009; Anastasio and La Riviere, 2012; Bravin et al., 2013; Coan et al., 2013; Lider and Kovalchuk, 2013; Liu et al., 2013) for phase-sensitive imaging in general.

Like many other modern imaging systems, ABI is an indirect imaging method, meaning that one must process the measured data in order to obtain the final parametric images. Therefore, the noise properties in ABI parametric images depend on the imaging conditions and the estimation method.

In the past, experimental ABI investigations were limited to synchrotron facilities due to the need for a very bright synchrotron X-ray radiation source that allows collimatization and monochromtization of the beam, with double crystal monochromator, while still having sufficient number of photons for imaging. Recently, efforts have been underway to implement ABI with a bench-top system employing conventional X-ray tube sources (Chapman et al., 2006; Vine et al., 2007; Nesch et al., 2009; Connor et al., 2011) in which the source photon flux is the major performance constraint.

Therefore, in this paper, we will quantify the parametric images noise due to two major causes: limited source intensity and analyzer angular positions by using the Cramér-Rao lower bound (CRLB) (Kay, 1993). CRLB is the minimum bound for the variance of any unbiased estimator and defines the best noise performance that one can obtain in parameter estimation from the raw data. The CRLB methodology unfortunately does not provide the minimum variance unbiased (MVU) estimator.

The work presented here is an extension of preliminary conference results (Majidi et al., 2008b; Marquet et al., 2006) where we used simulated phantom data. In (Brankov and Zysk, 2012) we presented some theoretical results, but in this paper we take this approach a step further including two experimental data sets, providing the full derivation, and clearly identifying source intensity and analyzer angular position impact on parametric images. In addition to MIR we also provide findings for analyzer angular positions selected in DEI (Chapman et al., 1997) and scatter-DEI (Rigon et al., 2003).

The idea of assessing the quality of the raw data by quantifying the parametric image quality is not new. For example, in (Pagot et al., 2005) the authors evaluated the best angular measurement positions for the refraction and scattering signals, as defined by area contrast, for a scenario where only two images were acquired. In our approach we define a more general statistical approach, based on CRLB, to assess the quality of the raw data. We also go a step further and present methodology to optimize the analyzer angular positions at which we measure beam’s AIP. Finally we finish by using CLRB to evaluate the performance of three estimation methods, in this work that is MIR (Wernick et al., 2003), DEI (Chapman et al., 1997) and scatter-DEI (Rigon et al., 2003). The presented evaluation methodology can be directly used on other estimation methods like extended-DEI (Chou et al., 2007; Rigon et al., 2007) and model based MIR (Majidi et al., 2008a). The purpose of this work is not to fully evaluate MIR or any other technique or to prove conclusively that any estimation methods will always perform best. The study is merely an illustration of the proposed procedure for quantifying noise and selecting analyzer angular positions by utilizing CRLB. The illustration reveals pitfalls and gains that one can encounter during this process.

First, we present the ABI image formation model (Khelashvili et al., 2006) based on radiative transfer theory (Ishimaru, 1997), followed by derivation of the CRLB in section 3. In section 4, we use CRLB as a guide to optimize the set of analyzer angular positions while in section 5 we evaluate the performance of three previously mentioned estimation methods. The conclusions are given in section 6.

2. Image formation model

In (Khelashvili et al., 2006), the image formation model was derived using radiative transfer theory. According to this model the AIP of the beam after passing through the object can be written as the following convolution:

$$g(\theta ;\mathbf{\nu })=I_{0}R(\theta )*f(\theta ;\mathbf{\nu }),$$ (1)

where R(θ) is the AIP of the beam that would be measured in absence of any object on the detector plane, * denotes one-dimensional convolution, and I₀ is the total number of photons per pixel for a preset total radiation exposure. The function R(θ) is called the intrinsic rocking curve as it is an inherent property of the imaging system and can be accurately measured and modeled as a Pearson type VII function which we will show later.

In ABI, the object is characterized by a hypothetical quantity called the object function, f (θ;ν), where θ is the angular direction of propagation and ν is a vector containing the parameters that define object interaction with the X-ray beam.

The full object model given in (Khelashvili et al., 2006) and summarized in Appendix A, is derived using radiative transfer theory where the object is modeled as a scattering, stratified medium. The full object function given in Eq A-3 is uniquely described by eight object parameters. Fortunately the approximate simplification of the full image formation model, also shown in Appendix A, yields to the following Gaussian curve for the object function defined by only three parameters:

$$f(\theta ;\mathbf{\nu })=\text{exp}(-{\nu }_1)\frac{1}{\sqrt{2\pi {\nu }_3}}\text{exp}(-\frac{{(\theta -{\nu }_2)}^2}{2{\nu }_3}).$$ (2)

Now, at each pixel the object is characterized by a parameter vector, ν = [ν₁,ν₂,ν₃]^T, containing the following parameters: ν₁, which conveys information about total attenuation by the object, ν₂ is the angle of refraction caused by the object, and ν₃ is the angular beam divergence (analogous to variance) induced by the object. This object function is the AIP that would result from illuminating the object with a unit intensity, perfectly collimated beam, i.e., a beam having its initial AIP described by a Dirac delta function δ(θ). In this context, the effect of the object on the X-ray beam is a convolution in terms of the propagation direction θ, and in this sense, the object function plays the role of an angular impulse-response (aka Green’s) function. By measuring the parameters of this impulse response function, one can obtain attenuation, refraction, and USAXS parameters, which can be displayed in the form of images.

The image formation model given in Eq (1) and object function given in Eq (2) was previously used in (Wernick et al., 2003; Rigon et al., 2003; Rigon et al., 2007) in an add-hoc fashion. For other image formation models see (Suhonen et al., 2007; Diemoz et al., 2010; Pavlov et al., 2001; Arfelli et al., 1998) where the authors usually assume a bell-shaped rocking curve such as Gaussian or Lorentzian convolved with an object function but no derivation of the object function was provided such as in (Khelashvili et al., 2006). All image formation models listed above are defined on a pixel-by-pixel basis; see (Wernick et al., 2003) for the justification; hence, ν denotes the values for any arbitrary pixel in the image.

In practice, measurements of g(θ;ν) are made on a digital detector for different angular positions of the analyzer crystal that will be denoted as g[l]. The expected value of the measured discrete AIP on the detector can be modeled as:

$$g_l\triangleq E[g[l]]=[\frac{I_0}{L}R{(\theta )}^{*}f(\theta ;\mathbf{\nu })]{|}_{\theta ={\theta }_l},$$ (3)

where l = 1,2,…,L represents the index of the analyzer angle θ_l, E[·] denotes the expected value, and I₀ / L represents the division of total exposure dose among L measurements.

In practical implementation of ABI using conventional X-ray tubes, photon flux will be the performance constraint; therefore, we can assume that the measured data is photon-limited, so Poisson noise will be the dominant noise source in raw ABI images (Wernick et al., 2003). Under this noise model, the likelihood function of the raw data is given by:

$$p(\mathbf{g};\mathbf{\nu })=\prod _{l=1}^L\frac{g_l^{g[l]}{e}^{-g_l}}{g[l]!},$$ (4)

where g = [g[1],g[2],…,g[l]]^T is a vector containing measured data.

3. Cramér-Rao lower bounds

To investigate the fundamental noise properties of ABI, we next consider the theoretical limit on the noise variance in estimation of the parametric images. This can serve as a foundation for optimizing the data acquisition procedure, as well as evaluation and comparisons of estimation algorithms. In ABI, we have three parameters to estimate simultaneously. The CRLB theorem for vector estimations (Kay, 1993) states that the variance of any unbiased estimator of the i^th element of the vector ν, denoted ν̂_i, is bounded as follows:

$$\mathit{\text{var}}({\mathrm{\nu ̂}}_i)\ge {\{{\mathbf{I}}^{-1}(\mathbf{\nu };\mathbf{\Theta })\}}_{i,i},$$ (5)

in which Θ = {θ₁,θ₂,…,θ_L} is a set of analyzer angular positions, {․}_i,i denotes i^th diagonal matrix element and I(ν;Θ) is a Fisher information matrix. This matrix has its i^th column and j^th row elements defined by:

$${\{\mathbf{I}(\mathbf{\nu };\mathbf{\Theta })\}}_{i,j}=-E[\frac{{\partial }^2}{\partial {\nu }_i\partial {\nu }_j}\text{ln}p(\mathbf{g};\mathbf{\nu })].$$ (6)

Substituting (1)–(4) into (6) yields to the following Fisher information matrix, which is derived in Appendix B:

$$\mathbf{I}(\mathbf{\nu };\mathbf{\Theta })=I_0\frac{1}{L}\sum _{l=1}^L\mathbf{I}\prime (\mathbf{\nu };{\theta }_l),$$ (7)

where $\mathbf{I}\prime (\mathit{\nu };{\theta }_l)={\mathbf{a}}_l{\mathbf{a}}_l^T$, and

$${\mathbf{a}}_l={\left[\sqrt{g_l^{\prime }}\frac{{\nu }_2{g}_l^{\prime }-h_l^{\prime }}{{\nu }_3\sqrt{g_l^{\prime }}}\frac{{\nu }_3{g}_l^{\prime }-q_l^{\prime }}{2{{\nu }^2}_3\sqrt{g_l^{\prime }}}\right]}^T,$$ (8)

where

$$g_l^{\prime }\triangleq [R{(\theta )}^{*}f(\theta ;\mathbf{\nu })]{|}_{\theta ={\theta }_l},$$ (9)

$$h_l^{\prime }\triangleq [R{(\theta )}^{*}\theta f(\theta ;\mathbf{\nu })]{|}_{\theta ={\theta }_l},$$ (10)

$$q_l^{\prime }\triangleq [R{(\theta )}^{*}{(\theta -{\nu }_2)}^{2}f(\theta ;\mathbf{\nu })]{|}_{\theta ={\theta }_l}.$$ (11)

Here, we note that the I′(ν;θ_l) matrix has rank one, so the inverse of the Fisher information matrix, I⁻¹(ν;Θ), exist only and only if at least three independent angular measurements are acquired. Though the CRLB expressions are complicated, one can compute these bounds numerically for any given set of analyzer angular measurements.

Here we will rewrite Eq (5) using result in Eq (7) as:

$$\mathit{\text{var}}({\mathrm{\nu ̂}}_i)\ge \mathrm{C}\mathrm{R}\mathrm{L}{\mathrm{B}}_i(\mathbf{\Theta }),$$ (12)

where:

$$\mathrm{C}\mathrm{R}\mathrm{L}{\mathrm{B}}_i(\mathbf{\Theta })=\frac{L}{I_0}{\left\{{[\sum _{l=1}^L\mathbf{I}\prime (\mathbf{\nu };{\theta }_l\left)\right]}^{-1}\right\}}_{i,i},$$ (13)

Here one can note that the estimator variance bound is inversely proportional to the total exposure dose I₀ and directly to the number of angular measurements. This expression shows that information given by one angular measurement can be interpreted independently from the total exposure dose and the total number of angular measurements. Therefore the results and conclusions obtained using a high flux source, like synchrotron, can be translated to a low flux source, like a conventional X-ray tube. This equation also points out that the estimators’ variance is a function of intrinsic system rocking curve and the object function and not only system rocking curve as sometimes assumed in literature (Kitchen et al., 2010; Pagot et al., 2005).

Now we would like to point out that Eq (13) is strictly valid only for equal acquisition time at each analyzer angular position. If one desires to modify acquisition times this can be easily incorporated into CRLB as:

$$\mathrm{C}\mathrm{R}\mathrm{L}{\mathrm{B}}_i(\mathbf{\Theta })=\frac{T}{I_0}{\left\{{[\sum _{l=1}^L{t}_l\mathbf{I}\prime {(\mathbf{\nu };{\theta }_l)}_l]}^{-1}\right\}}_{i,i},$$ (14)

where t_l is acquisition time for each individual angular position and $T=\sum _{l=1}^L{t}_l$ is the total acquisition time needed to acquire I₀ photons. Optimization of t_l is left for future research.

Note that the specific form of rocking curve and object function does not affect the CRLB equations derived in (13); therefore, the CRLB equations are general. Also note that considerations in this paper do not take into account the effect of a finite source spot size. This secondary effect is also left for future research.

If one considers methods like DEI (Chapman et al., 1997) or scatter-DEI (Rigon et al., 2003) that only estimate two parameters and use a specific analyzer angular positions one needs to modify bounds as follows. For DEI CRLB will become:

$$CRL{B}_i^{DEI}([{\theta }_H,{\theta }_L])=\frac{2}{I_0}{\left\{{\left[\right\{{\mathbf{I}}_{DEI}^{\prime }({\mathbf{\nu }}_{DEI};{\theta }_H)+{\mathbf{I}}_{DEI}^{\prime }({\mathbf{\nu }}_{DEI};{\theta }_L)\left\}\right]}^{-1}\right\}}_{i,i},$$ (15)

where ${\mathbf{I}}_{DEI}^{\prime }(\mathit{\nu };{\theta }_l)={\mathbf{a}}_l^{DEI}{\left({\mathbf{a}}_l^{DEI}\right)}^T$,

$${\mathbf{a}}_l^{DEI}={\left[\sqrt{g_l^{\prime }}\frac{{\nu }_2{g}_l^{\prime }-h_l^{\prime }}{{\nu }_3\sqrt{g_l^{\prime }}}\right]}^T,$$ (16)

and ν_DEI = [ν₁,ν₂] assuming ν₃ = 0.

Here we note that DEI is using angular measurements obtained at half of the rocking curve full with at the half maximum (FWHM) as noted by θ_H, and θ_L in later figures.

For scatter-DEI we will have:

$$CRL{B}_i^{S-DEI}([{\theta }_{TOP},{\theta }_{TOE}])=\frac{2}{I_0}{\left\{{\left[\right\{{\mathbf{I}}_{S-DEI}^{\prime }({\mathit{\nu }}_{S-DEI};{\theta }_{TOP})+{\mathbf{I}}_{S-DEI}^{\prime }({\mathit{\nu }}_{S-DEI};{\theta }_{TOE})\left\}\right]}^{-1}\right\}}_{i,i},$$ (17)

where ${\mathbf{I}}_{S-DEI}^{\prime }(\mathit{\nu };{\theta }_l)={\mathbf{a}}_l^{S-DEI}{\left({\mathbf{a}}_l^{S-DEI}\right)}^T$,

$${\mathbf{a}}_l^{S-DEI}={\left[\sqrt{g_l^{\prime }}\frac{{\nu }_3{g}_l^{\prime }-q_l^{\prime }}{2{{\nu }^2}_3\sqrt{g_l^{\prime }}}\right]}^T,$$ (18)

and ν_S−DEI = [ν₁,ν₃] assuming ν₂ = 0.

S-DEI is using angular measurements obtained at top and at the toe of the rocking curve as noted by θ_TOP, and θ_TOE in later figures.

It is well known that the DEI and S-DEI methods are prone to artifact and bias. However, DEI produces reasonably good images if the object is weakly scattering and S-DEI if the object is weakly refracting.

A. Effect of the analyzer crystal angular position on CRLB

In imaging an object, the most important factor affecting the parametric image noise, after the beam intensity I₀ and the number of angular measurements (as noted in the previous section), is the angular position of the analyzer crystal. In this section, we will analyze the effect of the analyzer angular position θ_l on CRLB. To gain intuition about the effect of the angular position, we approximate the true bounds, i.e. {I⁻¹(ν;Θ)}_i,i, with the inverse of the diagonal elements of the Fisher information matrix, i.e. ${\{\mathbf{I}(\mathit{\nu };\mathbf{\Theta })\}}_{i,i}^{-1}$. This would be equivalent to the estimation of each parameter individually, while the other two parameters are known. Now we can define the following information functions:

$$V_1({\theta }_l)={\{\mathbf{I}\prime (\mathit{\nu }\mathbf{;}{\theta }_l)\}}_{1,1}=g_l^{\prime },$$ (19)

$$V_2({\theta }_l)={\{\mathbf{I}\prime (\mathit{\nu };{\theta }_l)\}}_{2,2}={\left(\frac{{\nu }_2{g}_l^{\prime }-h_l^{\prime }}{{\nu }_3\sqrt{g_l^{\prime }}}\right)}^2,$$ (20)

$$V_3({\theta }_l)={\{\mathbf{I}\prime (\mathit{\nu };{\theta }_l)\}}_{3,3}={\left(\frac{{\nu }_3{g}_l^{\prime }-q_l^{\prime }}{2{{\nu }^2}_3\sqrt{g_l^{\prime }}}\right)}^2.$$ (21)

These functions show the amount of information we can acquire from a measurement at different analyzer angular positions. Since to visualize these functions one needs to know object parameters, we will examine these functions, for parameters obtained experimentally, in the experimental section.

B. CRLB for uniform set of analyzer angular positions

Next we will provide methodology to calculate and analyze the behavior of CRLB as we increase the number of angular measurements, i.e. analyzer angular positions. We can see in (3) that by increasing the number of measurements, L, we are decreasing the signal-to-noise ratio in each angular measurement, which represents the fixed total exposure dose to the tissue regardless of how many angular measurement are collected and equal acquisition time at each analyzer angular position.

First, we consider a uniform set of analyzer angular positions in the range of [θ_min,θ_max] so the angular positions are defined as following:

$${\theta }_l=(l-\frac{L+1}{2})\frac{{\theta }_{\text{max}}-{\theta }_{\text{min}}}{L},l=1,2,\dots ,L.$$ (22)

Now for a given set of analyzer angular positions, Θ_u = {θ₁,θ₂,…,θ_L}, we can estimate the expected CRLB as:

$${\overline{\mathrm{C}\mathrm{R}\mathrm{L}\mathrm{B}}}_i({\mathbf{\Theta }}_u)\simeq E{\left[{\{{\mathbf{I}}^{-1}(\mathit{\nu };{\mathbf{\Theta }}_u)\}}_{i,i}\right]}_{\mathrm{W}.\mathrm{r}.\mathrm{t}.\mathit{\nu }},$$ (23)

where E[·]_w.r.t.ν represents the expectation over the probability density function (pdf) of the parameter vector ν. Taking the expectation in (23) is an intractable problem. Therefore, we approximate the expectation by the arithmetic average over the parameters obtained from the experimental study:

$${\overline{\mathrm{C}\mathrm{R}\mathrm{L}\mathrm{B}}}_i({\mathbf{\Theta }}_u)\simeq \frac{1}{C}\sum _{c=1}^C{\{{\mathbf{I}}^{-1}({\mathit{\nu }}^c;{\mathbf{\Theta }}_u)\}}_{i,i},$$ (24)

where ν^c,c = 1,2,…,C represents the values of the parameter vector ν, at the c^th pixel in a pilot experimental study (e.g. human thumb or whole breast tissue study).

Now Eq (24) can serve as a basis for comparison of different sets of analyzer angular positions. It allows us to examine what is the impact of increasing the number of angular measurements, L, on estimated parametric images noise.

C. Optimal set of analyzer angular positions

In this section, we propose a method to investigate the possibility of further lowering the CRLB and hence achieving better estimation performance by using non-uniform analyzer angular positions.

To find a better set of non-uniform analyzer angular positions (denoted Θ^*) with respect to uniform angular positions, Θ_u, we define the following minimization problem:

$${\mathbf{\Theta }}^{*}=\text{arg}\underset{\mathbf{\Theta }}{\text{min}}J(\mathbf{\Theta }),$$ (25)

where

$$J(\mathbf{\Theta })=\sum _{i=1}^3\frac{{\overline{\mathrm{C}\mathrm{R}\mathrm{L}\mathrm{B}}}_i(\mathbf{\Theta })}{{\overline{\mathrm{C}\mathrm{R}\mathrm{L}\mathrm{B}}}_i({\mathbf{\Theta }}_u)}.$$ (26)

The main idea is: since the magnitude scales of the parametric images average CRLB are different, we normalize each ${\overline{\mathrm{C}\mathrm{R}\mathrm{L}\mathrm{B}}}_i(\mathbf{\Theta })$ by ${\overline{\mathrm{C}\mathrm{R}\mathrm{L}\mathrm{B}}}_i({\mathbf{\Theta }}_u)$, which is the average CRLB obtained for the uniform set of analyzer angular positions Θ_u with the same number of angular measurements.

4. Experimental analysis of CRLB

As we pointed out earlier, to visualize Eqs (19)–(21) or to take the expectation in Eq (23) or (26) one needs the probability density function (pdf) of the parameter vector. In general, this is unmanageable, however one can estimate these quantities from an experimental study.

We want to stress that the purpose of experimental studies is not to fully evaluate ABI imaging or to fully quantify noise and select a set of analyzer angular positions in general. The study is purely an example to illustrate the proposed procedure of utilizing CRLB. The results presented in this paper will be valid only for a similar imaging system, beam energy and tissue types as in our experiments.

A. Experimental studies

Experimental data was acquired using a synchrotron light source at Brookhaven National Laboratory; X15A beamline. A double Si (333) crystal was used for beam monochromatization, and one Si (333) crystal was used as the analyzer.

1. A formalin fixed human thumb was imaged with the beam energy of 40keV and angularly oversampled at 25 analyzer positions ranging from −4.8 to 4.8 μrad with 0.4 μrad increments.

2. An uncompressed, formalin fixed medium size breast was imaged with the beam energy of 60keV and angularly oversampled at 21 analyzer positions ranging from −2.4 to 2.4 μrad with 0.2 μrad increments.

Both data sets are measured with long exposure time approximately 10 hours per tissue; therefore, achieving a high signal-to-noise ratio (>35dB) in the raw data. Next, using an MIR estimation method (Wernick et al., 2003), we extract three parametric images.

B. Intrinsic rocking curve – Pearson type VII approximation

In (Suhonen et al., 2007; Diemoz et al., 2010; Pavlov et al.; Arfelli et al., 1998) the authors assume a bell-shaped rocking curve such as Guassian or Lorentzian. In (Hall et al., 1977; Kitchen et al., 2010; Kitchen et al., 2007) the authors have determined experimentally that for the ABI system as in Figure 1 the rocking curve can be accurately modeled better using a Pearson type VII function as:

$$R(\theta )=c{(1+\frac{{\theta }^2}{m{a}^2})}^{-m},$$ (27)

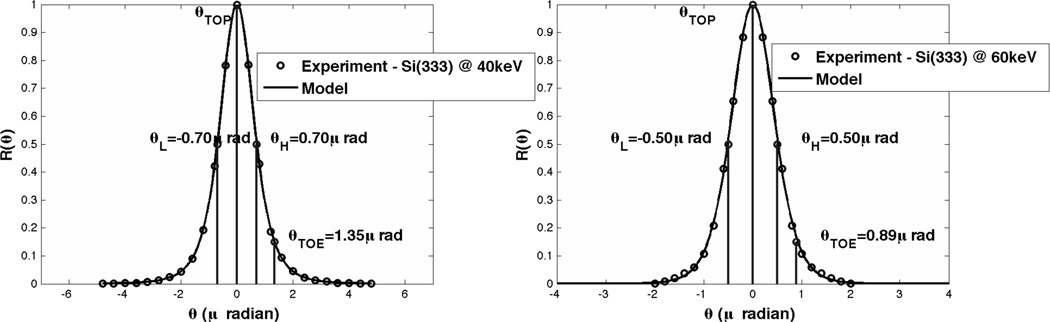
where in our experiments using three Si (333) crystals and for the incident photon energy of 40keV, a = 0.7146, and m = 2.3737, and of 60keV, a = 0.5355, and m = 4.3005. In both cases we assumed c = 1.0. Here c defines the curve amplitude, m governs the rate of decay of the tails, and both a and m determine the profile width. This Pearson type VII function has limits of the Gaussian (m = 1), modified Lorentzian (m = 2) and Cauchy (m = ∞) distributions (Hall et al 1977). Given the variety of functions the Pearson type VII function encompasses, it can provide a superior fit to near-perfect crystal reflections rocking curves. The shapes of these rocking curves can be seen in Figure 3.

Figure 3.

Example of a Rocking Curve for Si (333) Crystal at beam energy of (a) 40 keV (FWHM = 1.4μrad); (b) 60keV (FWHM = 1.0μrad).

In Figure 3 we also indicated analyzer angular positions used in DEI (Chapman et al., 1997) θ_L,θ_H and scatter-DEI (Rigon et al., 2003) θ_TOP,θ_TOE defined earlier.

C. Effect of the analyzer angular position

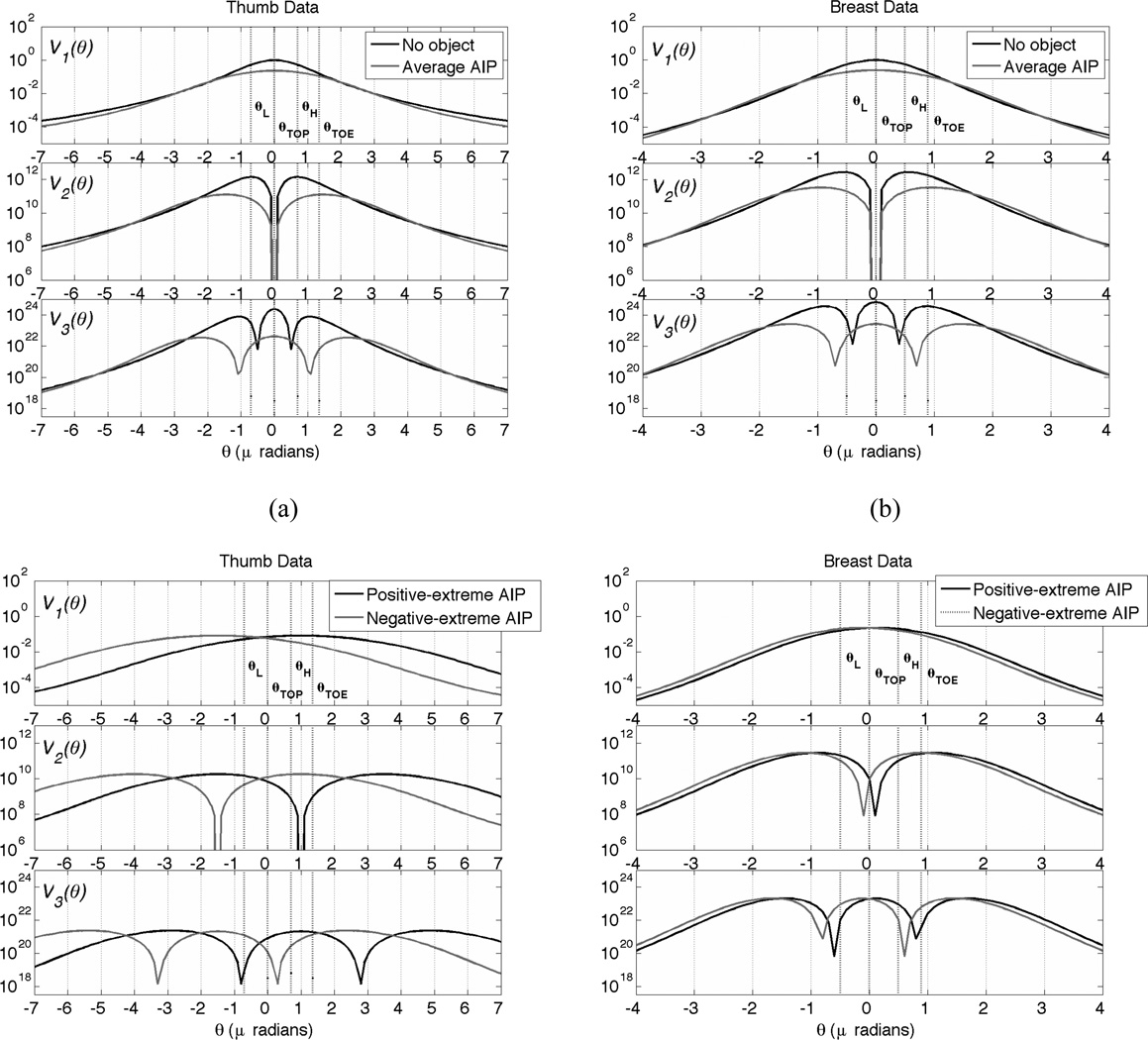
Examples of functions, defining the effect of the analyzer angular position θ_l on CRLB, as defined by Eqs (19)–(21) for four different object parameter vectors are given in Figure 4. The parameter vectors in use are extracted from two formalin-preserved human tissue samples (details are given in the experimental section): a human thumb (shown in Figure 2) and a whole breast. Each point at these functions shows the relative information at that analyzer angular position.

Figure 4.

Examples of information functions for parameter plotted on the logarithmic scale. Each function indicates the relative value of obtaining an angular measurement at a given angular analyzer position θ_l in regard to estimation of one of the object parameters. (a) For thumb sample imaged at 40 keV, (b) for breast data imaged at 60keV, in c) and d) we show information functions for extreme object parameters.

In short, if we desire to minimize CRLB (i.e. noise) in ν_i parameter estimation, using L angular measurements, we should acquire these measurement at analyzer positions, Θ = {θ₁,θ₂,…, θ_L}, so that $\sum _{l=1}^L{V}_i({\theta }_l)$ is maximized.

In addition to V_i (θ) functions, Figure 4 shows analyzer angular positions as defined in DEI, θ_H,θ_L, and S-DEI, θ_TOP,θ_TOE. If we look at the V₁(θ) function of the absorption parameter in Figure 4 a) and b), we can see that the maximum amount of information is at θ = 0μrad in both graphs. If we are concerned with the refraction parameter, we should look at V₂(θ) function for the average object AIP, where it is easy to observe that the maximum for different imaging setup and tissues combination occurs at different angular positions. For the thumb sample imaged at 40keV this is at θ = ±1.9 μrad, and for the breast sample imaged at 60keV this is at θ = ±0.9 μrad. Here it is worth noting that the “No object” V₂ (θ) function would indicate θ_H,θ_L, as the best measuring positions. Finally, for the USAXS parameter we should consider the V₃(θ) function. Two graphs indicate three regions with almost equal importance for the thumb sample: this is at θ = 0, and ± 2.9μrad and for the breast tissue at θ = 0, and ±1.6μrad. Here it is worth noting that the “No object” V₃(θ) function would approximately give θ_TOP,θ_TOE as the best measuring positions.

Next in Figure 4 c) and d) we show information functions for extreme object parameters. These graphs indicate that different regions in the object may provide a very different object AIP, and therefore, optimal set of analyzer angular positions. More sophisticated angular position selection methods that can take this variability into account are left for future research.

From the considerations above, it is clear that in order to optimize the set of analyzer angular positions, one needs to consider and know in advance: 1) which parameter or combination of parameters are of interest, 2) the tissue type, 3) tissue region of interest, 4) imaging energy and intrinsic system rocking curve.

Let us stress one additional result evident from Figure 4, that is, if one would optimize the analyzer angular positions only considering intrinsic system rocking curves (“No object” curves), suboptimal angular positions would be chosen. To correctly choose analyzer angular positions one needs to incorporate the object effect. To our knowledge, this paper is the first to point this out obviously. Other authors considered parametric image information content and quality based on the rocking curve only (Rigon et al., 2003; Pagot et al., 2005; Pagot et al., 2003; Chapman et al., 1997).

D. Experimental optimization of the number of analyzer angular measurements

The behavior of CRLB as we increase the number of angular measurements is given by Eq (24). As this equation indicates, we will use an average over the object parameters for the whole sample (thumb or breast), however it is important to note that different regions in the object may provide very different parameters (see Figure 4 for example), and therefore, results. For example, the structure’s boundaries will give much larger refraction than other points in the image. This means that very different results could be obtained in the various areas. Therefore, as we pointed out earlier, the results presented in this paper could be directly used only for a similar imaging system and tissue properties, however the present methodology can be used for optimizing any ABI system/imaging setup.

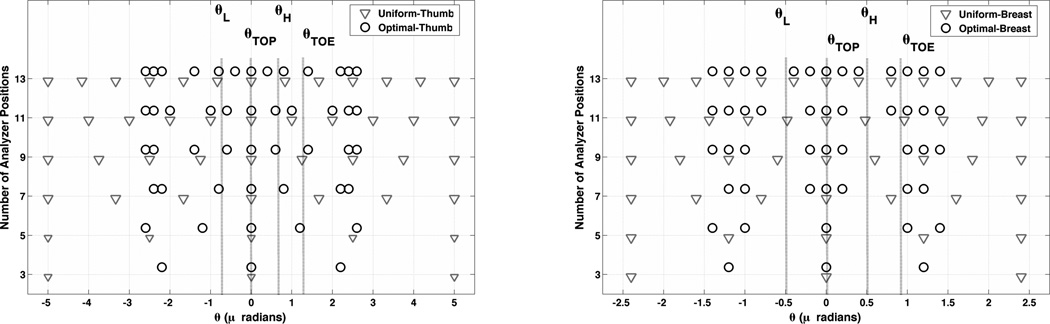
In the presented experiments we will consider a uniform set of analyzer angular positions in the range of [−5,5]μrad for thumb tissue and [−2.4,2.4]μrad for breast tissue (see Eq. (22) and Figure 7a) and b) to visualize the proposed set of analyzer angular positions).

Figure 7.

Analyzer angular positions in optimal and uniform set of analyzer angular positions for different number of angular measurements. (a) For thumb sample imaged at 40 keV, (b) for breast data imaged at 60keV.

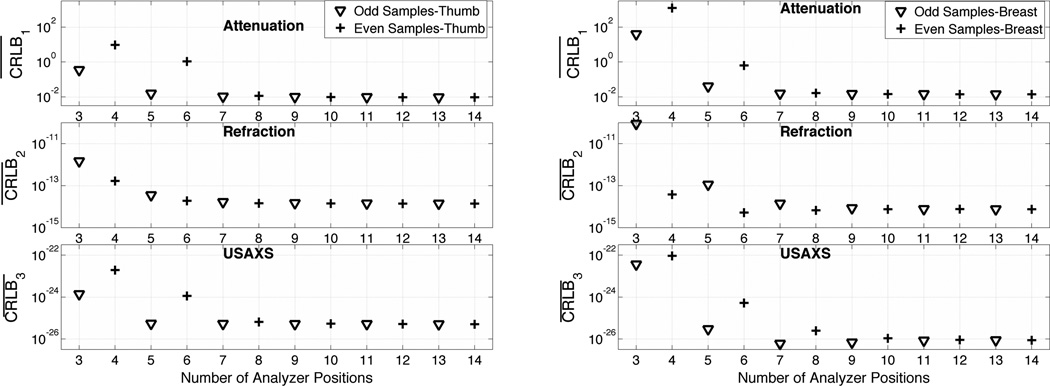
First, from Figure 5, we can see the improvement in average CRLB as we increase the number of analyzer angular measurements. We can observe that for lower numbers of angular measurements, the attenuation and USAXS parameter bounds are higher for L even numbers than for L odd numbers. This is because the maximum amount of information for attenuation and USAXS, as measured by V₁(θ) and V₃(θ) (see Figure 4), is at θ = 0 μrad, which is not sampled when using an even number of measurements. On the other hand, measuring at θ = 0 μrad does not contain any information about refraction (see V₂ (θ) in Figure 4) and that is why the average CRLB for the refraction image lies on almost the same curve for odd and even numbers of angular measurements.

Figure 5.

CRLB for an unbiased estimator vs. number of angular measurements using a uniform set of analyzer angular positions. (a) For thumb sample imaged at 40 keV, (b) for breast data imaged at 60keV.

Another observation that can be made from Figure 5 is that after a certain number of angular measurements (11 for both data sets), there is almost no improvement or loss in the average CRLB bounds. Therefore, in the case of a Minimum Variance Unbiased (MVU) estimator, there is neither benefit nor loss in acquiring more than 11 images at uniformly spaced analyzer angular positions for a fixed total radiation dose.

At this point we would like to stress that the Cramér-Rao lower bound (CRLB) is used to quantify the noise properties in parametric images of an unbiased estimator and defines the best noise performance that one can obtain regardless of which method is used to estimate ABI parametric images.

E. Experimental optimization of the analyzer angular positions

Here we will investigate the possibility of lowering the CRLB and hence achieving better estimation performance by using a set of non-uniform analyzer angular positions Θ^* according Eq. (25). For Θ_u, we used a uniform angular positions in the same range of [−5,5]μrad and [−2.4,2.4]μrad as before depending on the tissue type.

To optimize the objective function in (26), we used the exhaustive search method. For every number of angular measurements, we evaluated J(Θ) at every possible combination of analyzer angular positions (with minimum spacing of 0.2 μrad) and we defined the best set of positions as the one that has the smallest value of J (Θ).

In order to decrease computation time, we limited the number of possible patterns by imposing two constraints: We always measure at θ = 0, and our angular-sampling positions are always symmetrical around zero since V_i(θ_l), on average, is always symmetrical around zero. We selected an exhaustive search method for it simplicity, and also since it guarantees a globally optimal solution. The needed computational time needed for this optimization was 8 hours on a iMAC with Intel Core i5 2.9 GHz with 16 GB RAM. Other gradient type of optimization methods (Chong and Żak, 2008) may be used in future.

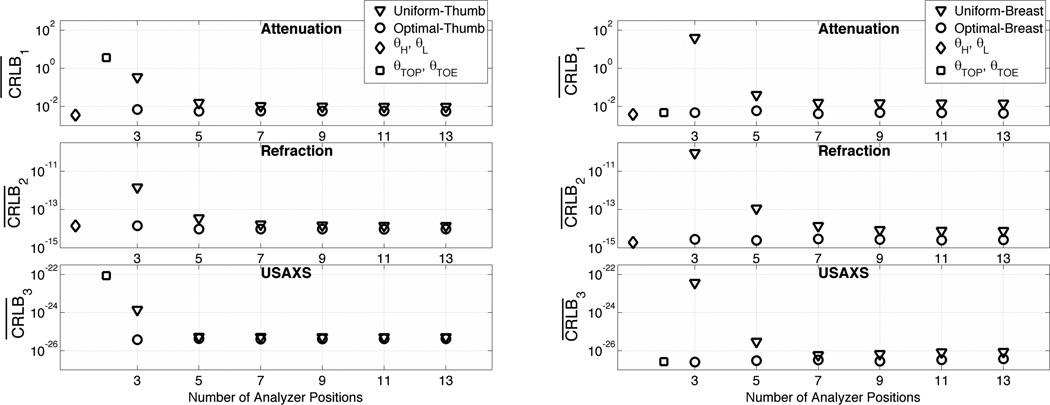
The resulting average CRLBs of optimal non-uniform and uniform set of analyzer angular positions are shown in Figure 6. One can observe that the attenuation and refraction CLRBs can be significantly improved over uniform angular positions while the USAXS parameter CRLB shows minor improvement. The presented results indicate that one can reduce estimator variance considerably by using a non-uniform set of analyzer angular positions that is optimized for the tissue of interest and a given ABI system.

Figure 6.

CRLB for an unbiased estimator vs. number of angular measurements for both optimal and uniform set of analyzer angular positions. (a) For thumb sample imaged at 40 keV, (b) for breast data imaged at 60keV.

Figure 6 also show CRLBs for analyzer angular positions as proposed in the DEI and S-DEI methods. Here we can see that for a weakly scattering and refracting object, like breast tissue, DEI and S-DEI angular positions seem to achieve optimal CRLB as one would expect bearing in mind the curves shown in Figure 4 b) and d).

The key result of this section is that only three angular measurements are required to get the best parametric images. As before, the second intriguing observation is that the successive angular measurements only spread the total dose to the additional measurements without improving or worsening CRLB.

The optimal set of analyzer angular positions for different numbers of angular positions and the two tissue samples are shown in Figure 7. As we can see, the angular measurements tend to converge to three dominant angular positions. These positions approximately correspond to the locations with the maximum information measured by V_i(θ_l), for the averaged AIP, in Figure 4.

5. DEI, S-DEI and MIR estimator comparison to CRLB

The graphs in Figure 5 and Figure 6 can be used as a benchmark, that is a lower bound, to evaluate the performance of ANY estimator. In this section, we will investigate the performance of the multiple-image radiography estimator (MIR) as described in (Brankov et al., 2006), DEI (Chapman et al., 1997) and scatter-DEI (Rigon et al., 2003) with respect to CRLB. The presented evaluation methodology can be directly used on other estimation methods like extended-DEI (Chou et al., 2007; Rigon et al., 2007) and model based MIR (Majidi et al., 2008a).

Specifically we will evaluate the MIR, DEI and S-DEI estimators by calculating estimators’ variance, squared bias, and Mean Square Error (MSE) and comparing it to CRLB. The purpose of this section is not to fully evaluate MIR, DEI or S-DEI but it is merely an example to illustrate the proposed evaluation procedure.

It is worth noting that the images estimated using the DEI and S-DEI method are prone to artifacts that are, most of the time, mitigated in the MIR method (as shown in (Wernick et al., 2003)). Similar methods to MIR have also been proposed independently in (Pagot et al., 2003) and (Rigon et al., 2003). Other ABI methods like extended-DEI (Chou et al., 2007; Rigon et al., 2007) use different assumptions about image formation, different number and location of the angular measurements.

A. Simulated data

To evaluate the estimation methods’ variance, squared bias, and Mean Square Error (MSE) we need to use simulated data for which true values of the parametric images are known. First, parametric images are estimated using experimental data described in the Experimental study section. Note that these raw images are acquired by angular oversampling and under high beam intensity, and as such, they result in accurate, low noise and bias, parametric images. Now we use these parametric images as true values to simulate AIPs according to the image formation model as given in (3). After simulating the angular sampling, we simulate the effect of noise by generating Poisson distributed values, i.e.

$$g[l]~P\text{oisson}\{g({\theta }_l)\},$$ (28)

where ~ denotes distributed according and we assume that I₀ = 1800 photons, which is a reasonable number of photons. To reduce statistical variations we generated 1000 independed noise realizations. Note that, according CRLB equation given in (13), the number assumed photons will only change graphs scale and not general conclusions.

B. Image acquisition using a uniform set of analyzer angular positions

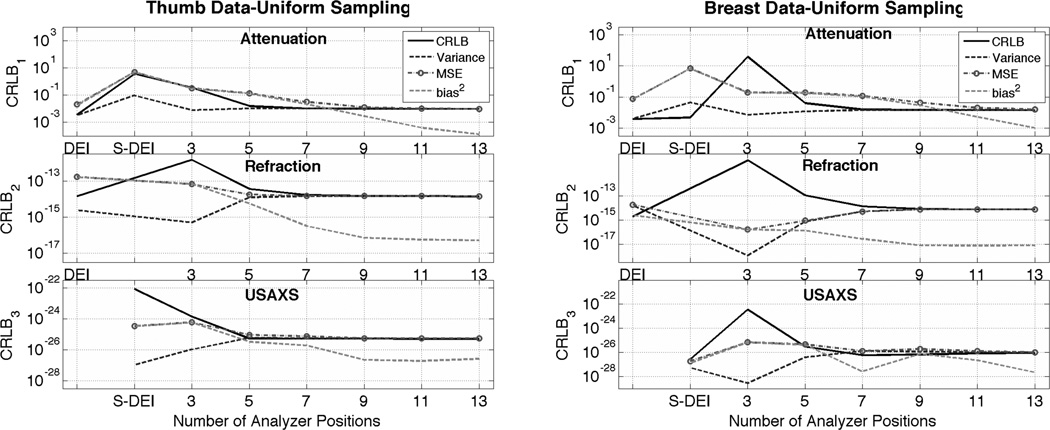
The results for the human thumb study are shown in Figure 8 a). We can see that DEI and SDEI estimator are highly biased. The same can be said for MIR for a low number of angular measurements (less than 7) where MIR occasionally even has variance lower than the average CRLB. However after 11 angular measurements, the bias of the estimation becomes negligible compared to the variance and MIR becomes approximately, for tested tissue, an MVU estimator, meaning that it achieves the best performance possible as defined by the CRLB for an unbiased estimator. Similar results are obtained for the breast study, which are shown in Figure 8 b).

Figure 8.

Variance, MSE, squared bias, and CRLB vs. number of angular measurements for optimized set of analyzer angular positions. (a) For thumb sample imaged at 40 keV, (b) for breast data imaged at 60keV.

Note that in (Huang et al., 2007; Diemoz et al., 2010) the authors showed that if the object scatter and refraction is sufficiently larger MIR methods still could have unwanted artifacts and, as such, may not becoming MVU. The origin of this is probably two fold: 1) small range of the analyzer angular-sampling and 2) insufficient angular-sampling density. This consideration is left for future research.

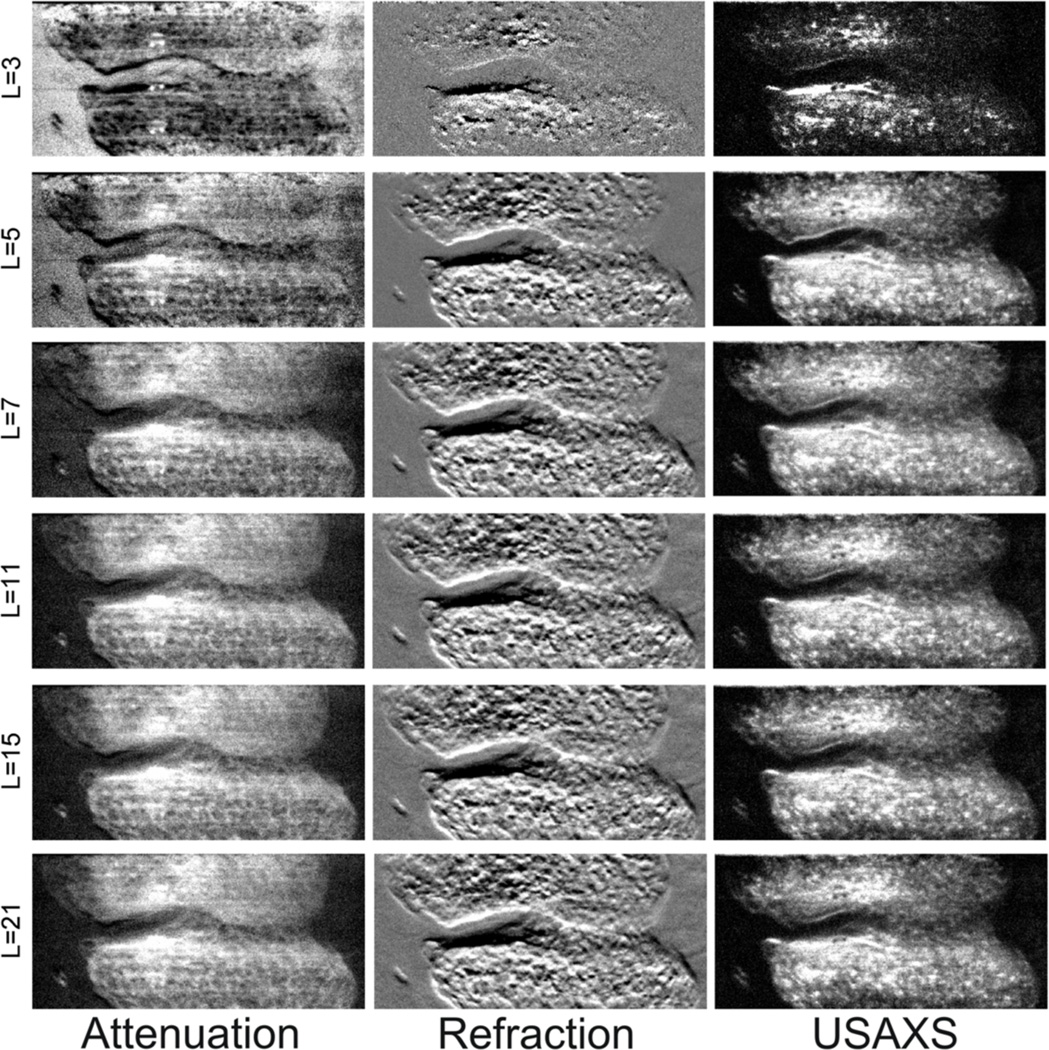
In order to evaluate the above results visually, we presented images for six different numbers of angular measurements in Figure 9. Visual inspection of images also confirms that 11 angular measurements seem sufficient for good parametric image estimation.

Figure 9.

Estimated MIR images using uniform set of analyzer angular positions with different number of angular measurements. Observe that there is little or no improvement after L>11.

Note that the above concepts of bias, variances or MSE are hard to demonstrate visually by the images as in Figure 9, as for example a potential bias is likely not to be noticed by the eye. However, since images are usually evaluated visually, their visual appearance is important.

One should note that we did not specify which estimator could achieve average CRLB for a non-uniform set of analyzer angular positions. The MIR estimator in (Brankov et al., 2006) is designed for a uniform set of analyzer angular positions and cannot be directly applied to a nonuniform set of positions. The problem of finding an MVU estimator for the non-uniform set of analyzer angular positions is left for future research.

6. Conclusion

In this work we derived the Cramér-Rao lower bound (CRLB) for analyzer-based phase-contrast imaging using the image formation model based on radiative transfer theory (Khelashvili et al., 2006). The CRLB is the minimum bound for the variance of any unbiased estimator and defines the best noise performance that one can obtain. We analyzed a situation in which the total exposure dose to the imaged object remains fixed regardless of the number of angular measurements. The results in this paper show that for a minimum-variance unbiased (MVU) estimator, only a limited number of angular measurements (eleven for uniform and three for optimal non-uniform set of analyzer angular positions) are required to get the best parametric images. The second intriguing observation is that the successive angular measurements only spread the total radiation dose to the additional measurements without improving or worsening the CRLB, however the added measurements usually can improve parametric images by reducing estimation bias.

The presented analysis is performed using data from two tissue samples. The findings obtained for these two particular tissue samples and imaging energies cannot be generalized, as the results are dependent on the tissue type, on the crystal reflection, energy, analyzer angular-sampling range, etc. Very different results could, in principle, be obtained in other conditions. For example, tissue with very large refraction and scattering angles could require a larger number of angular measurement steps. However the purpose of this work is not to fully evaluate any particular ABI technique or to prove conclusively that any methods or a set of analyzer angular positions will always perform the best. This study is merely an example to illustrate the proposed procedure for a given imaging system setup and tissue type.

We also showed that it is possible to minimize average CRLB (average over the whole image) further by deforming the set of analyzer angular positions from uniform. However, the problem of finding an MVU for the non-uniform analyzer angular positions is still an open research problem.

Last, we evaluated the MIR (Brankov et al., 2006) DEI (Chapman et al., 1997) and scatter-DEI (Rigon et al., 2003) estimators. MIR becomes an MVU estimator, which achieves average CRLB, when more than 11 uniformly spaced angular measurements are used.

Appendix

A. Approximation of the Object Function

Here we review the image formation model proposed in (Khelashvili et al., 2006). The image formation model is based on radiative transfer theory and the object is modeled as a stratified medium where the stratum is characterized by a linear absorption coefficient μ(r⃑) = μ(z) and by a spatially varying refractive index n(r⃑) = n₀ + n_y (z)y where r⃑ = (x, y, z)^T is the spatial coordinate of the system and the z coordinate is the direction of X-ray beam propagation. Furthermore, the object is assumed to have identical scattering centers distributed in the medium with the density ρ_n(r⃑) = ρ_n (z). Each scatter center is characterized by its extinction cross section σ_ext, which is defined as the sum of the scattering cross section σ_s and the absorption cross section σ_a. Next, we use a quantity called albedo (Khelashvili et al., 2006), defined as

$$W_0\triangleq \frac{{\sigma }_s}{{\sigma }_a+{\sigma }_s}.$$ (A-1)

And for each scattering center we also define:

$${\alpha }_p={\left[4{\delta }^2\text{ln}\right(\frac{2}{\delta }+1\left)\right]}^{-1},$$ (A-2)

where α_p is the beam broadening due to a single scattering center (von Nardroff, 1926) and δ is the difference between the refractive indices of the medium and the scatters. Now, by using the equation presented in (Khelashvili et al., 2006), we can write the object function for this stratum as

$$f(\theta )=e^{-\underset{0}{\overset{z}{\int }}\mathrm{\mu ̅}(\vec{r})dz}\sum _{k=0}^{\infty }\left[\frac{{(\tau (Z)W_0)}^k}{k!}{e}^{-\tau (Z)W_0}\sqrt{\frac{{\alpha }_p}{k\pi }}{e}^{(-\frac{{\alpha }_p}{k}{(\theta -\mathrm{\Delta }\theta )}^2)}\right],$$ (A-3)

where μ̅(z) ≜ ρ_n(z)σ_a + μ(z), and

$$\tau (Z)=\underset{0}{\overset{Z}{\int }}({\rho }_n(z){\sigma }_{\mathit{\text{ext}}}+\mu (z))dz,$$ (A-4)

$$\mathrm{\Delta }\theta (\vec{\rho })=\underset{0}{\overset{Z}{\int }}\frac{\partial }{\partial y}\text{ln}(n(x,y,z))dz=\underset{0}{\overset{Z}{\int }}\frac{n_y(z)}{n_0}dz,$$ (A-5)

where Z is the thickness of the medium. We can relate the terms in the summation of Eq. (A-3) to an expectation of a Gaussian curve with k /α_p variance over a Poisson probability distribution function of k. Interestingly, the summation in Eq (A-3) can be derived by statistical argument in which the random distribution of scatterers is modeled by the Poisson process. Here is it interesting to note that the full model is defined by eight model parameters σ_s,σ_a,ρ_n,μ,α_p,n₀,n_y,Z.

For large values of τ(Z)W₀, we can accurately approximate this object function by the dominant term that is a Gaussian curve, where k = τ(Z)W₀. Then we can rewrite (A-3) in the following form:

$$f(\theta ;\mathit{\nu })=\text{exp}(-{\nu }_1)\frac{1}{\sqrt{2\pi {\nu }_3}}\text{exp}(-\frac{{(\theta -{\nu }_2)}^2}{2{\nu }_3}),$$ (A-6)

where:

$${\nu }_1=\underset{0}{\overset{Z}{\int }}({\rho }_n(z){\sigma }_a+\mu (z))dz,$$ (A-7)

$${\nu }_2=\underset{0}{\overset{Z}{\int }}\frac{n_y(z)}{n_0}dz,$$ (A-8)

$${\nu }_3=\frac{1}{2}\frac{\tau (Z)W_0}{{\alpha }_p}=\frac{1}{2}\underset{0}{\overset{Z}{\int }}\frac{{\rho }_n(z){\sigma }_s}{{\alpha }_p}dz.$$ (A-9)

and ν₁ describes the net linear absorption of the medium (including absorption in scattering centers), ν₂ is the scaled refractive index gradient, and ν₃ can be interpreted as USAXS parameter of the medium.

B. Derivation of Cramér-Rao Lower Bounds

From (8) we have:

$${\{\mathbf{I}(\mathbf{\nu };\mathbf{\Theta })\}}_{i,j}=-E[\frac{{\partial }^2}{\partial {\nu }_i\partial {\nu }_j}\text{ln}p(\mathbf{g};\mathbf{\nu })].$$ (B-1)

The log-likelihood function of the data is given by

$$\text{ln}p(\mathbf{g};\mathbf{\nu })=\sum _{l=1}^L[g[l]\text{ln}{g}_l-g_l-\text{ln}(g[l]!)].$$ (B-2)

By taking the derivatives we have:

$$\frac{\partial }{\partial {\nu }_i}\text{ln}p(\mathbf{g};\mathbf{\nu })=\sum _{l=1}^L\left[\right(\frac{g[l]}{g_l}-1\left)\frac{\partial g_l}{\partial {\nu }_i}\right],$$ (B-3)

$$\frac{{\partial }^2}{\partial {\nu }_i\partial {\nu }_j}\text{ln}p(\mathbf{g};\mathbf{\nu })=\sum _{l=1}^L\left[\right(\frac{g[l]}{g_l}-1)\frac{{\partial }^2{g}_l}{\partial {\nu }_i\partial {\nu }_j}-\frac{g[l]}{g_l^2}\frac{\partial g_l}{\partial {\nu }_i}\frac{\partial g_l}{\partial {\nu }_j}].$$ (B-4)

By taking the expected value of (B-4) and substituting (3) and (4) into the result, noticing that g_l ≜ E [g[l]], we get:

$$\mathbf{I}(\mathbf{\nu };\mathbf{\Theta })=\sum _{l=1}^L\mathbf{I}(\mathbf{\nu };{\theta }_l),$$ (B-5)

$$\mathbf{I}(\mathbf{\nu };{\theta }_l)=\left[\begin{array}{ccc}\hfill g_l\hfill & \hfill \frac{{\nu }_2{g}_l-h_l}{{\nu }_3}\hfill & \hfill \frac{{\nu }_3{g}_l-q_l}{2{\nu }_3^2}\hfill \\ \hfill \frac{{\nu }_2{g}_l-h_l}{{\nu }_3}\hfill & \hfill \frac{{({\nu }_2{g}_l-h_l)}^2}{{\nu }_3^2{g}_l}\hfill & \hfill \frac{({\nu }_2{g}_l-h_l)({\nu }_3{g}_l-q_l)}{2{\nu }_3^3{g}_l}\hfill \\ \hfill \frac{{\nu }_3{g}_l-q_l}{2{\nu }_3^2}\hfill & \hfill \frac{({\nu }_2{g}_l-h_l)({\nu }_3{g}_l-q_l)}{2{\nu }_3^3{g}_l}\hfill & \hfill \frac{{({\nu }_3{g}_l-q_l)}^2}{4{\nu }_3^4{g}_l}\hfill \end{array}\right],$$ (B-6)

where:

$$g_l\triangleq E[g[l]]=[\frac{I_0}{L}R{\left(\theta \right)}^{*}f(\theta ;\mathbf{\nu })]{|}_{\theta ={\theta }_l},$$ (B-7)

$$h_l\triangleq [\frac{I_0}{L}{R(\theta )}^{*}\theta f(\theta ;\mathbf{\nu })]{|}_{\theta ={\theta }_l},$$ (B-8)

$$q_l\triangleq [\frac{I_0}{L}R{(\theta )}^{*}{(\theta -{\nu }_2)}^{2}f(\theta ;\mathbf{\nu })]{|}_{\theta ={\theta }_l}.$$ (B-9)

Alternatively, we can rewrite (B-6) in normalized from as:

$$\mathbf{I}(\mathbf{\nu };{\theta }_l)=\frac{I_0}{L}\mathbf{I}\prime (\mathbf{\nu };{\theta }_l),$$ (B-10)

where $\mathbf{I}\prime (\mathit{\nu };{\theta }_l)={\mathbf{a}}_l{\mathbf{a}}_l^T$, and

$$\mathbf{a}={\left[\sqrt{g_l^{\prime }}\frac{{\nu }_2{g}_l^{\prime }-h_l^{\prime }}{{\nu }_3\sqrt{g_l^{\prime }}}\frac{{\nu }_3{g}_l^{\prime }-q_l^{\prime }}{2{{\nu }^2}_3\sqrt{g_l^{\prime }}}\right]}^T,$$ (B-11)

where

$$g_l^{\prime }\triangleq [R{(\theta )}^{*}\theta f(\theta ;\mathbf{\nu })]{|}_{\theta ={\theta }_l},$$ (B-12)

$$h_l^{\prime }\triangleq [R{(\theta )}^{*}\theta f(\theta ;\mathbf{\nu })]{|}_{\theta ={\theta }_l},$$ (B-13)

$$q_l^{\prime }\triangleq [R{(\theta )}^{*}{(\theta -{\nu }_2)}^{2}f(\theta ;\mathbf{\nu })]{|}_{\theta ={\theta }_l}.$$ (B-14)