Heterogeneity of intrinsic biophysical properties among cochlear nucleus neurons improves the population coding of temporal information

Abstract

Reliable representation of the spectrotemporal features of an acoustic stimulus is critical for sound recognition. However, if all neurons respond with identical firing to the same stimulus, redundancy in the activity patterns would reduce the information capacity of the population. We thus investigated spike reliability and temporal fluctuation coding in an ensemble of neurons recorded in vitro from the avian auditory brain stem. Sequential patch-clamp recordings were made from neurons of the cochlear nucleus angularis while injecting identical filtered Gaussian white noise currents, simulating synaptic drive. The spiking activity in neurons receiving these identically fluctuating stimuli was highly correlated, measured pairwise across neurons and as a pseudo-population. Two distinct uncorrelated noise stimuli could be discriminated using the temporal patterning, but not firing rate, of the spike trains in the neural ensemble, with best discrimination using information at time scales of 5–20 ms. Despite high cross-correlation values, the spike patterns observed in individual neurons were idiosyncratic, with notable heterogeneity across neurons. To investigate how temporal information is being encoded, we used optimal linear reconstruction to produce an estimate of the original current stimulus from the spike trains. Ensembles of trains sampled across the neural population could be used to predict >50% of the stimulus variation using optimal linear decoding, compared with ∼20% using the same number of spike trains recorded from single neurons. We conclude that heterogeneity in the intrinsic biophysical properties of cochlear nucleus neurons reduces firing pattern redundancy while enhancing representation of temporal information.

our seemingly effortless ability to distinguish sound features within an everyday cacophony of background noise belies the computational difficulty of representing a complex auditory scene. Temporal envelope modulations in the sound amplitude across the frequency spectrum are fundamental for distinguishing and categorizing human speech, birdsong, and background textural sounds (Joris et al. 2004; Shannon et al. 1995; Singh and Theunissen 2003). Many of the mechanisms involved in the encoding of acoustic temporal phase cues, or “fine structure,” have been elucidated in the avian brain stem neural pathways responsible for calculating interaural time differences involved in sound localization (Carr and Konishi 1990; Overholt et al. 1992; Sullivan and Konishi 1984; Takahashi et al. 1984; for reviews, see Burger and Rubel 2008 and Kuba 2007). In contrast, the spectrotemporal information processing that underlies sound recognition is more poorly understood, but in birds this process begins with cochlear nucleus angularis (NA), which is also the start of the parallel ascending pathway for binaural sound intensity comparisons (Adolphs 1993; Köppl and Carr 2003; Manley et al. 1988; Soares and Carr 2001; Sullivan and Konishi 1984; Takahashi et al. 1984; Warchol and Dallos 1990). Detailed studies of how temporal envelope features are encoded in NA and its ascending targets are key for understanding the encoding of birdsong and other communication and environmental signals (Keller and Takahashi 2000; Narayan et al. 2006; Schneider and Woolley 2010; Steinberg and Peña 2011; Woolley and Casseday 2005; Woolley et al. 2005). Here, we investigated the mechanisms that underlie the temporal reliability of NA neurons during naturalistic input stimulation.

Neurons in NA respond with highly reliable patterns when presented with repeated white noise current stimuli in vitro (Bryant and Segundo 1976; Kreeger et al. 2012), and in vivo when presented with repeated frozen acoustic stimulation (Steinberg and Peña 2011), like neurons in other brain areas in vitro (Mainen and Sejnowski 1995; Tripathy et al. 2013) and in vivo (Butts et al. 2010; de Ruyter van Steveninck et al. 1997; Reinagel and Reid 2002). One prediction from these findings is that any two neurons receiving identical, or nearly identical, input should respond with highly correlated spike patterns, assuming these neurons have similar intrinsic properties (Bryant et al. 1973; Ermentrout et al. 2008; Galán et al. 2006; Reyes 2003; Street and Manis 2007). However, if every neuron responded with an identical pattern to a given input, then the information encoded by a population of neurons receiving similar inputs would be highly redundant. A solution to this problem is to introduce some form of neural heterogeneity among the set of synaptic inputs, network connectivity, or intrinsic properties (Friedrich and Laurent 2001; Gupta 2000; Padmanabhan and Urban 2010; Tripathy et al. 2013).

Identified neuronal cell types in auditory and other brain areas show an extraordinary diversity of firing properties (Connors and Gutnick 1990; Hodgkin 1948; Markram et al. 2004; Peruzzi et al. 2000), and the cochlear nucleus is no exception (Carr and Soares 2002; Fukui and Ohmori 2003; Golding et al. 1995; Hirsch and Oertel 1988; Oertel et al. 1988, 1990, 2011; Rothman and Manis 2003; Soares et al. 2002; Wu and Oertel 1984). We therefore investigated the relationship between the diversity of the biophysical properties of cochlear nucleus neurons and their encoding of complex stimuli.

Using an in vitro brain slice preparation and direct current (DC) injection, we tested how reliably and coherently a pseudo-population (henceforth “population”) of avian cochlear nucleus neurons responded when the neurons were presented with identical fluctuating noise stimuli. We found that the firing correlations across neurons were high, but heterogeneity in the intrinsic properties led to idiosyncratic spike trains in individual neurons. Variations in the spike trains across neurons significantly improved encoding using population information. Thus heterogeneity in the intrinsic biophysical properties of neurons in the cochlear nucleus effectively balances reliability, high population correlation and efficient coding of temporal information in the inputs.

MATERIALS AND METHODS

Brain slice preparation.

All animal procedures were reviewed and approved by the University of Maryland Institutional Animal Care and Use Committee. Chicken auditory brain stem slices were prepared as described previously (Kreeger et al. 2012). Briefly, chicken embryos incubated 17–18 days were rapidly decapitated, the brain stem was submerged in chilled and oxygenated low sodium artificial cerebral spinal fluid (ACSF) (in mM: 97.5 NaCl, 3 KCl, 2.5 MgCl₂, 26 NaHCO₃, 2 CaCl₂, 1.25 NaH₂PO₄, 10 dextrose, 3 HEPES, 230 sucrose), and transverse slices (250 μm) were made on a vibrating tissue slicer (Leica Microsystems, Wetzler, Germany). Slices were incubated in oxygenated ACSF (in mM: 130 NaCl, 3 KCl, 2 MgCl₂, 26 NaHCO₃, 2 CaCl₂, 1.25 NaH₂PO₄, 10 dextrose, 3 HEPES) for 30 min at 34°C then held in solution at room temperature. Slices were submerged in a recording chamber and continuously perfused with warmed (29.6 ± 1.4°C), oxygenated ACSF (1–2 ml/min). No synaptic channel blockers were used.

Patch-clamp electrophysiology.

Whole cell patch-clamp recordings were made from NA cells using infrared/differential interference contrast video microscopy. Initial micropipette resistances were 4–8 MΩ with an internal solution consisting of the following (in mM): 110 potassium-gluconate, 20 KCl, 1 EGTA, 2 MgCl₂, 10 HEPES, 2 Na₂ATP, 0.3 Na₂GTP, 10 phosphocreatine, and 0.1% biocytin. Recordings were made with a Multiclamp 700B patch clamp amplifier (Molecular Devices, Sunnyvale, CA) in current-clamp mode. Stimulation and recordings were controlled by a PC running custom software in IGOR Pro (Wavemetrics, Lake Oswego, OR).

Current stimulation and data collection protocols.

Flat current steps and noisy current steps were produced using custom routines written in IGOR Pro. The white noise current stimulus S(t) was generated by convolving Gaussian white noise with an exponential function (time constant, 3 ms), which was chosen to simulate the arrival of many small, stochastic and statistically independent synaptic currents, both excitatory and inhibitory (see Kreeger et al. 2012). Briefly, a Gaussian, exponential-filtered (τ = 3 ms) noise stimulus was generated using the same “random” seed to generate the same noise token for all experiments (two seeds, one for each noise token). For each neuron in the main data set in this paper (n = 60 NA neurons, data set in Table 1), we calibrated the stimulus to account for cell-to-cell variation in input resistance and the DC level to fall within the dynamic range of the neuron (Higgs et al. 2006; Kreeger et al. 2012). To determine whether difference in the DC amplitude across neurons influenced the correlation, we collected a data set (n = 10) using stimuli with identical DC level (300 pA) and observed no differences of the correlation index (CI) using this set vs. the main data set (see methods below).

Table 1.

Shuffled autocorrelogram and cross-correlogram summary statistics

	Peak CI	Delay, ms	Width, ms	n
All SAC	15.5 ± 8.7	NA	1.4 ± 0.7	60 neurons
Population SAC	2.63	NA	4.55
Pairwise CC, all	4.61 ± 2.64	2.04 ± 1.54	3.84 ± 1.70	1,660 pairs

Values are means ± SD. CI, correlation index; SAC, shuffled autocorrelation; CC, cross-correlation.

Cell classification.

Offline analysis was performed using custom procedures and functions using IGOR Pro, Matlab (Mathworks, Natick, MA) and Microsoft Excel. Classification was determined using physiological firing responses to 400- to 500-ms steps and 50- to 100-pA step amplitude intervals (Kreeger et al. 2012; Soares et al. 2002).

Shuffled autocorrelation and cross-correlation analysis.

To quantify the reliability of spiking by a neuron across repeated trials, we calculated a CI using a shuffled autocorrelation (SAC) analysis (Joris et al. 2006; Street and Manis 2007). The SAC analysis is an all-intervals histogram across all trials, excluding intervals taken from within the same trials, and divided by the normalizing factor (NF):

$$\text{NF}=N\cdot (N-1)\cdot r^2\Delta \tau D$$

where N is the number of trials, r is the mean firing rate, Δτ is the bin width of the correlation function (0.2 ms), and D is duration of the stimulus epoch (4 s). The central peak maximum is reported as the CI, and the width was full-width at half-maximum of the Gaussian fit of the shuffled auto- or cross-correlation (CC) function.

To compare firing across neurons or across different noise tokens, we performed CCs that were normalized to firing rate in an analogous method to the SAC, but as a one-sided function to determine lead/lag times, and the delay reported in the text was the peak location along the x-axis. Summary histograms and statistics include results of correlations with central peaks twice the baseline noise amplitude, true of >93% of possible pairwise combinations (1,660 of 1,770).

Spike distance metric.

The pseudo-population responses generated by two different noise tokens were tested for discriminability using a spike distance metric (van Rossum 2001) in which the “cost” of transforming one train into the other was calculated. To quantify discrimination at different time scales, the time constant of the exponential that was convolved with the spike train was varied (0.01 ms to 1,000 ms). The median Euclidean difference between the two filtered spike trains was used to assign trains to noise 1 or noise 2, and percentage of correctly classified tabulated. The whole procedure was repeated 30 times, and the mean and standard deviation of the classification percentages plotted.

Clustering analysis.

The neuronal activity was examined for evidence of clustering based on CC data using standard algorithms in MATLAB (Mathworks, Natick, MA). Dendrograms were constructed from the matrix of interneuron “distances,” where the distance was 1/log(CI) of the pairwise CC, and were optimized using the Ward linkage method and divided using the MATLAB default linkage threshold (0.7).

Stimulus reconstruction.

We used recorded spike trains to infer the stimulus using a standard optimal linear reconstruction approach (Bialek et al. 1991; Borst and Theunissen 1999; Butts et al. 2007; Stanley et al. 1999). To estimate the optimal linear filters, we used the last 32 of 40 repeat trials (discarding the first 8) and 7.2 s of the 8 s of recording over both 4-s stimulus blocks. The remaining 0.8 s was set aside for cross-validation, which we used to reconstruct the stimulus, given the recorded spike trains over this time. For single neurons, the optimal linear filter h(τ) is calculated from the spike triggered average k(τ), adjusted by the neuron's response autocorrelation function C(τ), such that k(τ) = ∑_τ′ C(τ − τ′) h(τ′). The reverse filter h(τ) can be solved for by expressing k(τ) and h(τ) as vectors: e.g., k = [k(0) k(1) k(2) . . . ] and h = [h(0) h(1) h(2) . . . ], where we are using boldface to denote a vector quantity. Expressing the autocorrelation function as a matrix C with corresponding entries that keep the above equation in register, the optimal linear reconstruction is given by:

$$h={\text{C}}^{-1}k$$

where C⁻¹ is the matrix inverse of C.

For each stimulus reconstruction, we used 30 of the 32 spike trains. Because these spike trains are from the same neuron, the optimal linear filter h_i corresponding to the ith spike train r_i(t) is simply h_i = h/30, and the linear reconstruction is then given by

$$s\text{*}(t)={\sum }_i{h}_i(\tau )r_i(t-\tau )$$

This estimated stimulus is compared with the actual stimulus to calculate quantities such as r². Because we use 30 repeats to perform each reconstruction (to compare to population reconstructions, below), the values of r² that we report is the median of 16 different samples of 30 spike trains (from the 32 available). Because 0.8 s is not enough data to calculate reliable measures of the coherence γ²(f), we use the full 8 s of data for this. Although this quantity is not cross-validated, we expect that it does not represent overfitting, because of the overall agreement of r² calculated between cross-validated and non-cross-validated datasets (data not shown). The reconstruction information I_rec is then calculated from the coherence using I_rec = ∑_f log₂ [1 − γ²(f)] (Borst and Theunissen 1999).

We performed pseudo-population reconstructions using the same approach, although, in this case, the optimal linear filters must take into account response CCs between neurons in addition to their autocorrelations. This involves modifying the vectors k and h and correlation matrix C in Eq. 1 as follows. Given that the spike-triggered average of the ith neuron is written k_i, the vector K = [k₁ k₂ k₃ . . . ] represents the concatenation of all spike-triggered averages, and likewise with H, which is composed of individual reconstruction filters h_i. The overall correlation matrix Q is then block-constructed by placing autocorrelation matrices Cⁱⁱ along the diagonal, and CC matrices C^ij between ith and jth neurons at their corresponding locations, such that Q = [C¹¹ C¹² C¹³ . . . ; C²¹ C²² C²³ . . . ; C³¹ . . . ]. The individual reconstruction filters h_i can then be extracted from H = Q⁻¹ K (which is identical form to h).

RESULTS

Reliable firing to temporally modulated stimuli elicits correlated activity across the ensemble of neurons.

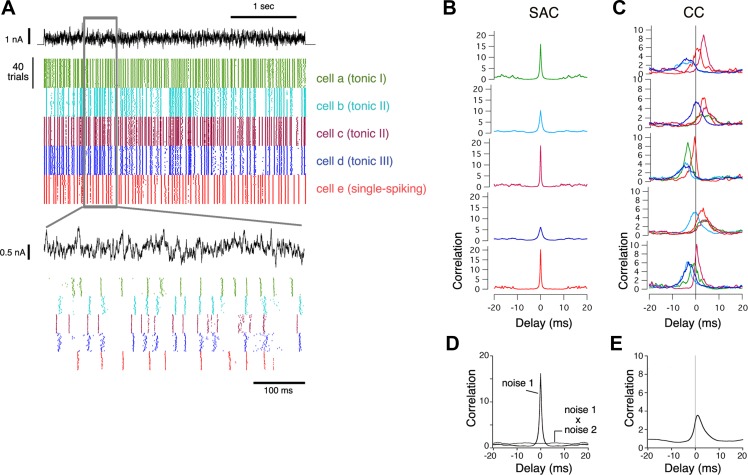
To determine whether different neurons would respond with temporally correlated spike train patterns when provided identically fluctuating input, we made sequential whole cell patch-clamp recordings from neurons in the avian cochlear NA while directly injecting a current stimulus composed of exponentially-filtered frozen noise superimposed on a DC step. Spike trains from single neurons showed a high degree of reliability across trials with repeated stimulation (Fig. 1A). To quantify this reliability, we computed the CI, taken as the peak value of the SAC (Joris et al. 2006; Street and Manis 2007), an all-interval histogram normalized to the firing rate. Consistent with previous results (Kreeger et al. 2012), the CIs of the SACs were large for all neurons (15.5 ± 8.7, mean ± SD, n = 60, Fig. 1, B and D), and peak widths were narrow (1.4 ± 0.7 ms).

Fig. 1.

Identical noise current stimulation in different neurons in nucleus angularis (NA) results in correlated firing activity. A: spike train response rasters for five different NA neurons to repeated presentations of the 4-s long, filtered Gaussian noise stimulus (top black trace), color coded for each separate neuron, 40 trials each. Bottom: expanded time scale. B: shuffled autocorrelation (SAC) functions corresponding to neurons a–e, top to bottom. Color coding is as in A. Correlations are normalized by firing rate to facilitate comparison across neurons; a value of one indicated uncorrelated spike timing from one trial to the next (see materials and methods). C: pairwise shuffled cross-correlation (CC) functions. Traces in each plot show the CC between a given neuron (corresponding to the SAC to its left) vs. the other four neurons in this figure (color coded according to second neuron in each pair). D: mean SAC averaged across all 60 neurons to noise 1 shows a large peak (“noise 1”). Responses of single neurons to two uncorrelated noise stimuli show no correlation (flat curve, “noise 1 × noise 2”). E: mean CC of all pairwise comparisons (n = 1,770 combinations; CCs with negative delays were flipped to be positive).

By treating this group of neurons as a “pseudo-population” (or simply “population”), we can then investigate how a similar population of neurons would have functioned if recorded simultaneously in the intact brain. We compared the sets of spike trains recorded in different neurons to identically fluctuating repeated stimuli. These fluctuations were superimposed on a current pedestal appropriate to the input resistance of each neuron. Close inspection of the spike trains revealed many alignments across cells, but also that each cell responded with its own idiosyncratic response pattern (Fig. 1A, bottom). We quantified the relative spike timing across neurons with a CC function in an analogous manner to the SAC. Pairwise CC analyses showed large, near-zero delay central peaks for a large majority (>93%; see materials and methods) of all possible combinations (Fig. 1C) with CIs ranging from 1.63 to 27.4 (Fig. 2Ai, Table 1). The CIs of the CCs had a median of 3.87, while the median CC width was 3.47 ms (Fig. 2Aii). A consistent lead or lag in the relative spike times resulted in nonzero peak delays, but most peak delays were close to zero: 75% of correlograms had peak delays smaller than 3 ms, with a median peak delay of 1.72 ms (Fig. 2Aiii). When correlograms were averaged across all pairwise combinations, the resulting function had a CI of 3.6, a width of 3.8 ms and a peak delay of 1.0 ms (Fig. 1E). Similar levels of correlation were observed under two conditions: when stimuli were varied across neurons (0.2–04 nA) to fall in the steepest part of the neuronal dynamic ranges, as shown here, or when DC level was held constant (data not shown).

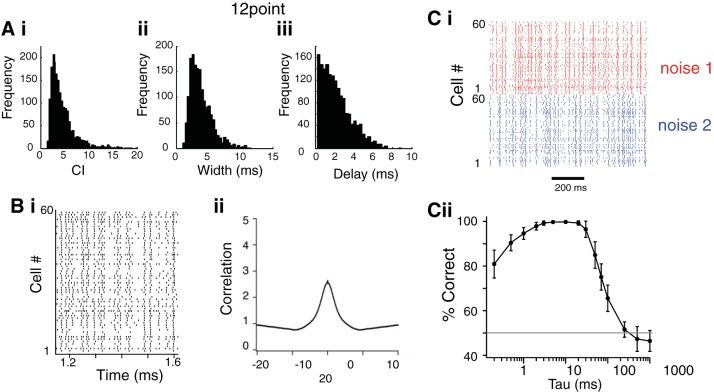
Fig. 2.

Summary analysis of correlations across neurons in response to identical noise stimuli. A: histograms of peak correlation index (CI; i), width (ii), and peak delay (iii) of the CC functions (n = 1,660 pairwise comparisons). Bi: population raster composed of spike trains from 60 different NA neurons. Bii: average population correlogram (n = 100 random iterations). C: responses to two different uncorrelated noise stimuli were discriminable. Ci: population rasters (1 spike train per neuron randomly selected) for noise 1 (red) and noise 2 (blue). Cii: classification of spike trains based on spike distance metric (van Rossum 2001). Values are means ± SD of 30 repeated analyses. Chance classification is 50% correct (gray line).

To compare the spike trains across the entire neural ensemble, we assembled a “population raster” by randomly selecting single trains from each neuron's set (Fig. 2Bi). We then calculated the shuffled correlogram of the population raster. The peak of the “population” correlogram had a CI of 2.63 and width of 4.55 ms (Fig. 2Bii). These data indicate that, based on intrinsic properties alone, a high degree of cross-neuronal correlation in firing is likely across pairs or groups of neurons receiving identical inputs.

We then asked whether the temporal patterning in the neural ensemble was sufficient for discriminating between different input patterns, and, if so, what is the optimal time scale for discrimination? To test this, a second noise stimulus was presented to each neuron with equal fluctuation and DC amplitude but was temporally uncorrelated to the first. This second noise stimulus also evoked reliable and correlated population firing responses (“noise 2” in Fig. 2C), and, as expected, the two sets of spike trains recorded in the same neuron to the different stimuli showed no correlation whatsoever (“noise 1 × noise 2”, Fig. 1D).

To quantify discrimination, we used a spike distance metric and classification procedure on population rasters for each noise stimulus, created as described previously (Fig. 2Ci) (Narayan et al. 2006; Schneider and Woolley 2010; van Rossum 2001). A cost function procedure that converts one spike train to another was used to calculate spike distances between a given train and every other train elicited by each stimulus. Each spike train was classified as “belonging” to noise 1 or noise 2 based on the distance, and the proportion of trains correctly classified was determined. The analysis was repeated while varying the time window of the cost function, which allows the sensitivity of the discrimination for time scale of the firing patterns to be determined: with short time windows the metric behaves like a “coincidence detector,” while with long time windows only differences in mean firing rate are counted. Different stimuli could be classified with >99% accuracy when time windows of 3 to 20 ms were used and fell to chance with time windows greater than 200 ms (Fig. 2Cii). These results indicate that the two ensembles are completely discriminable when temporal information in the spike trains is considered, but not when firing rate alone is considered.

Does cell type define correlated ensembles?

One previously documented aspect of heterogeneity among NA neurons is the division of these neurons into cell types based on their in vitro physiological responses to current step stimuli (for detailed descriptions of cell types in NA, see Carr and Soares 2002; Kreeger et al. 2012; Soares et al. 2002). Our laboratory's previous study showed that the different cell types affected how the input-output functions changed with noise stimuli (Kreeger et al. 2012). To investigate whether these physiological differences influenced the spike patterns in response to the noise stimuli, we assigned 54 NA neurons to one of the five cell types, Tonic I (n = 9), Tonic II (n = 20), Tonic III (n = 10), Damped (n = 10) and Single-Spiking (n = 5), while 6 neurons were excluded from analysis as ambiguous. Representative voltage responses to step currents that illustrate each type are shown in Fig. 3A.

Fig. 3.

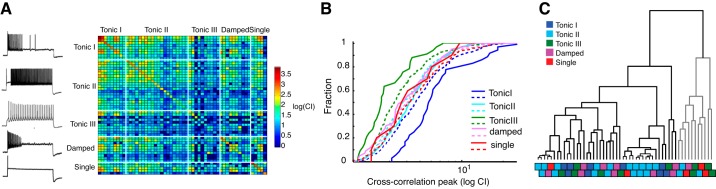
A: correlation matrix of the CI for all pairwise comparisons. Each row and column represents a single neuron (n = 54), grouped by cell type and ordered by the amplitude of the autocorrelations along the diagonal; CCs are symmetrical above and below the diagonal. Hot/cool colors indicate high/low CI. B: cumulative histograms of CI, color-coded by cell type. Solid lines represent the CIs of CCs between the same cell types (within-group); dashed lines represent the CIs of CCs between neurons of one given cell type (color coded) and all other cell types (across-group). C: cluster analysis of the correlation matrix showed two large clusters: one with significant CCs (black lines) and one with poor CCs (gray lines). Each terminal branch corresponds to a neuron and box below, color-coded by cell type as in B.

Were the neurons that were classified as the same cell type more highly correlated than neurons classified as different cell types? To examine this question we looked at the data three ways. First, to visually inspect the data we plotted the CIs from the SAC and pairwise CC analyses in a correlation matrix, with each of the neurons represented in one column and one row and each box representing a pairwise comparison (Fig. 3A). Second, we grouped the CIs of the CCs into cumulative histograms to determine whether the overall distribution of CIs differed between the within-cell-type pairings vs. the across-cell-type pairings (Fig. 3B). Third, we performed a cluster analysis to look for groupings of neurons based on their CC CIs unbiased by cell type (Fig. 3C).

The correlation matrix in Fig. 3A grouped the neurons by cell type and then further ordered the rows and columns by the CI of the autocorrelation (Fig. 3A). The CIs of the SACs, represented along the diagonal, were largest for Tonic I and Single spiking neurons and lowest for Tonic III neurons, comporting with previous work (Kreeger et al. 2012). The remainder of the correlation matrix above and below the diagonal contains the CIs of the CCs.

To test whether cell type was a factor in the correlations between neurons, we examined the distribution of pairwise correlations between the same cell types (“within-type”, solid lines in Fig. 3B) vs. those between different cell types (“across-type”, dashed lines in Fig. 3B). We performed this analysis separately for each cell type (i.e., Tonic I/Tonic I pair distribution vs. Tonic I/non-Tonic I distribution). We found the distributions largely overlapped, suggesting there were no within-type correlation preferences, with the exception of the Tonic I neurons (solid blue line vs. dashed blue lines in Fig. 3B, P < 0.05, Kolmogorov-Smirnov test). A leftward shift for the within-type distribution was observed for Tonic III neurons, which also had the lowest CI distribution (solid green line in Fig. 3B). The larger correlations amongst Tonic I neurons and the lower correlations amongst Tonic III neurons suggests that the amplitude of the CC is limited by the intrinsic reliabilities of any two individual neurons, rather than due to cell-type-specific similarities in particular firing patterns. While these data suggest that Tonic I neurons, as a group, may fire together as a correlated ensemble, it is not an exclusive ensemble, since Tonic I neurons also correlated strongly with subsets of neurons classified as other cell types.

Visually, the correlation matrix in Fig. 3A did not show any obvious patterning that might indicate clustering of the correlations into subpopulations. To test for correlation groupings unbiased by cell type, we performed a clustering analysis using the CI of the pairwise CC (or more precisely, the inverse of the CI) as an estimate of “distance”. The results of this clustering can be pictured with a “dendrogram” plotted in Fig. 3C. The dendrogram is a visual representation of the results of a minimization procedure that grouped neurons based on their distance to one another (see materials and methods). Each tip, or twig, of the tree represents an individual neuron, and the vertical height of the branch at intersection with the next twig represents the distance between them. Two large “clusters” (indicated by black and gray coloring of the sub-trees) were found.

The smaller of the two clusters (containing 11 out of the 54 neurons in the analysis) comprised neurons with the weakest CCs (tallest twigs), including a number of “below criterion” correlation indexes. The larger cluster of neurons (43/54) comprised neurons that had relatively high CCs. We examined the clusters post hoc to determine there was any pattern related to cell type. For visualization, each twig was color-coded by cell type (colored boxes in two staggered rows correspond to the “twigs” in the dendrogram directly above). The large cluster included all five cell types, while the small cluster included four cell types and did not include any Tonic I neurons. Within the larger cluster, there was no evidence of subclustering related to cell type. We will note, however, a small nearest-neighbor effect: neurons that form pairs of “twigs” tended to be of the same cell type (12 of 18 twig pairs) at a rate above chance.

Decoding of the temporal fluctuations by individual neurons: optimal linear stimulus reconstruction.

The high degree of reliability in the firing of individual neurons suggests they are responding to temporal events in the stimulus, yet each neuron responded somewhat differently. These differences could potentially reduce the redundancy of information carried by different neurons to allow a more complete encoding of the stimulus by the population.

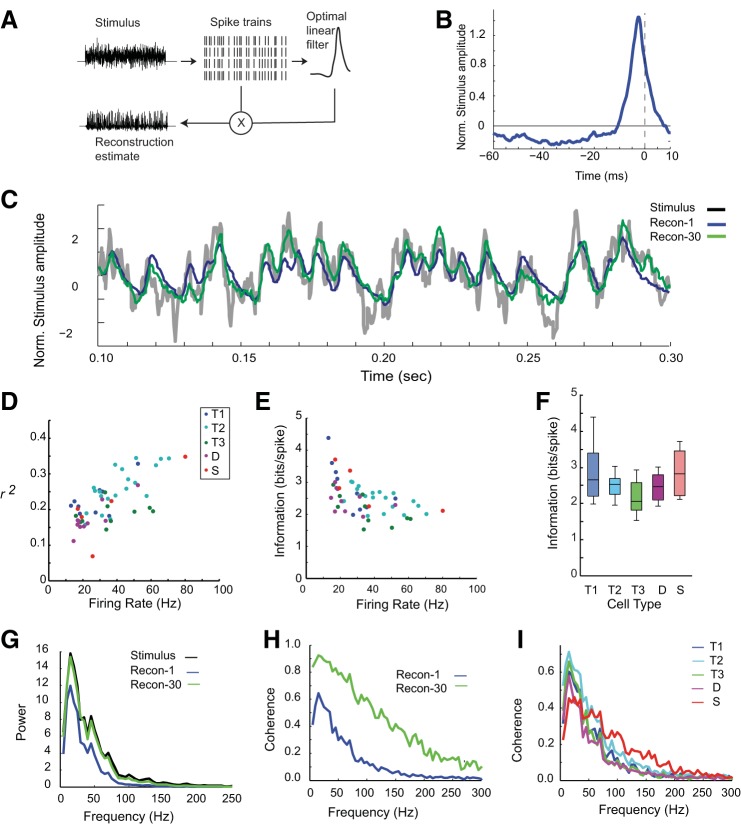
To investigate how information about the stimulus is encoded in the firing activity of individual neurons, we used optimal linear reconstruction (Bialek et al. 1991; Borst and Theunissen 1999) to produce an estimate of the original current stimulus from the spike trains (Fig. 4A). For each neuron, the stimulus reconstruction was created using its optimal linear filter (see materials and methods). These “reverse filters” were generated from a subset of the spike train data and corresponding current stimulus (7.2 of 8 s total of data; Fig. 4B), and then the reconstructed estimate of the stimulus during a reserved 0.8 s of data was generated by convolving each optimal filter with the corresponding spike train data (Fig. 4C, “Recon-1”). Goodness of fit was determined as the CC of the reconstruction and the original stimulus and reported as an “r²” value (coefficient of determination; Fig. 4D). Reconstructions using single neurons accounted for 7–35% of the variation in the stimulus with an average of 22% (SD ± 6%, n = 60, Fig. 4C). To determine what frequencies the reconstruction estimates were capable of coding, we measured the power spectra and coherence between the noise stimulus and single-neuron reconstructions (Fig. 4, G and H). Coherence was highest at ∼25 Hz with a peak amplitude of 0.6 (relative to a maximum possible of one) and low beyond 80 Hz (Fig. 4H, blue line).

Fig. 4.

Stimulus reconstruction using reverse correlation noise analysis. A: reconstruction procedure: an optimal linear filter was calculated from the spike trains in response to repeated noisy stimulus; the filter was convolved with each spike train and then averaged to generate a reconstructed estimate of the stimulus. B: optimal linear filter for a typical neuron. Spike occurred at 0 ms. C: original stimulus current (gray) and the corresponding reconstruction estimates based on the same neuron as in B (Recon-1, blue) or population of 30 neurons (Recon-30, green). D: reconstruction fits (r²) for single neurons increased with mean firing rate elicited by the stimulus for that neuron. Color coding is by cell type: T1, Tonic I neurons; T2, Tonic II neurons; T3, Tonic III neurons; D, Damped neurons; S, Single-spiking neurons. E: reconstruction information in bits/spike for the same neurons in D, colored by cell type. F: information rates by cell type. Most neurons carried similar information rates, except for lower rate in the Tonic III neurons (P < 0.05, ANOVA; Tonic III significantly different from Tonic I, P < 0.05 multiple-comparisons test). Box plot shows the median, interquartile range and extrema. G: power spectra of the original noise stimulus (black) and the reconstruction estimates in C (blue: single neuron; green: 30 neuron population). H: coherence of the reconstruction estimates with the original stimulus (blue: single neuron; green: 30 neuron population). I: coherence plotted by cell type shows similar curves for the Tonic neurons, while single-spiking neurons had better high-frequency coherence and worse lower-frequency coherence.

To determine whether different cell types carried different amounts of information about the stimulus, we analyzed coherence and information rate by cell type (Fig. 4I). The accuracy of the reconstruction estimate is strongly influenced by firing rate (Fig. 4D, n = 60, linear regression, Pearson's R = 0.67, P < 0.001). To adjust for firing rate, we calculated the reconstruction information using the cross-coherence (see materials and methods) and calculated the information per spike for each cell type (see materials and methods) (Fig. 4E), revealing that the information rate differed by cell type (Fig. 4F; P = 0.0162, one-way ANOVA, degrees of freedom = 4, F = 3.37). Tonic III neurons carried the lowest per spike information content (median, 2.06 bits/spike) compared with rates carried by Tonic I and Single-Spiking neurons (2.65 and 2.8 bits/spike, respectively; significantly different from Tonic I under multiple-comparisons test, Bonferroni correction, α = 0.05). The mean information rate over all neurons was 2.48 ± 0.54 bits/spike (n = 60).

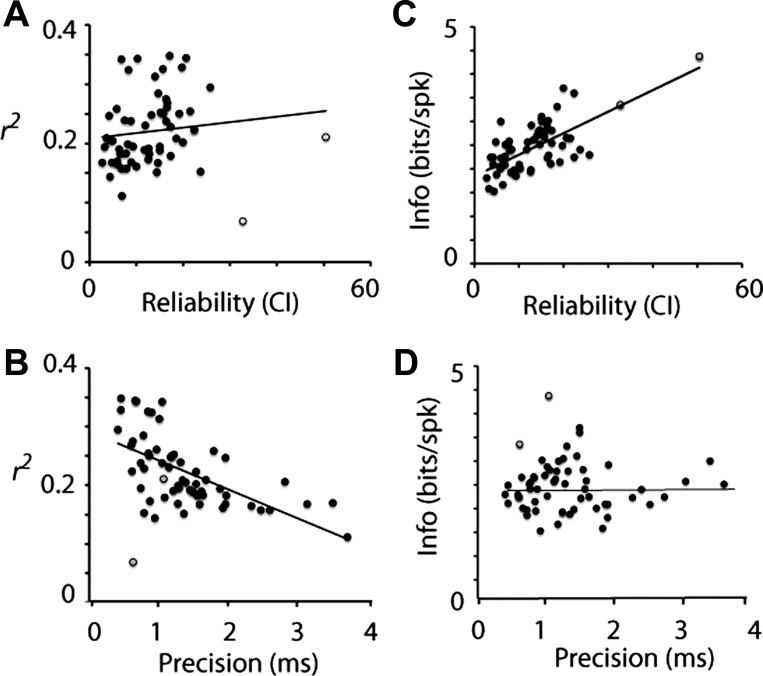
Given that Tonic III neurons had the lowest, and Tonic I neurons the highest, per-spike information rate as well as spike reliability (data not shown; see also Kreeger et al. 2012), we explicitly investigated the relationship between stimulus coding and spike reliability. We compared the reconstruction outcomes with the SAC analysis for each cell. When the fit of the reconstruction (r²) was plotted against reliability (CI of the SAC) for each cell, only a weak correlation was observed (Fig. 5A, all data: Pearson's R = 0.122, P > 0.05; excluding two outliers: Pearson's R = 0.349, P < 0.05), indicating that reliability was a weak predictor of reconstruction fit, while spike precision (width of the SAC) was a better predictor (Fig. 5B, Pearson's R = −0.527, P < 0.01). On the other hand, the per-spike information was highly correlated with reliability (Fig. 5C, Pearson's R = 0.685, P < 0.01), but uncorrelated with precision (Fig. 5D, Pearson's R = 0.010, P > 0.05). These data suggest that reliable spikes are informative spikes, but that overall reconstruction of the stimulus by individual neurons is limited by the firing rate and spike timing precision.

Fig. 5.

Stimulus reconstruction and spike timing reliability. Quality of the single-neuron reconstruction (r²) plotted against reliability (A) and timing precision for each neuron (B) is shown. Reliability was the CI, and timing was the width of the SAC for that neuron. The quality of reconstruction was strongly correlated with timing (Pearson's R = −0.527), but only weakly correlated with the reliability (R = 0.122). In contrast, information per spike was correlated with reliability (R = 0.685; C), but not with timing precision (R = 0.010; D).

Heterogeneity in spike firing properties leads to improved encoding of temporal fluctuations using population information.

Despite high reliability in the firing of individual neurons and high interneuronal correlation, there was also a notable heterogeneity in the spike patterns across neurons. To test whether the heterogeneity would improve stimulus encoding, we generated a reconstruction estimate of the stimulus based on a set of spike trains drawn from the population to compare with that generated from the same number of spike trains sampled from single neurons. We constructed optimal linear filters for each neuron in the context of the population by taking into account the response CCs in addition to its autocorrelation (see materials and methods), such that each optimal linear filter depends on the other neurons included in the population. One example reconstruction using a population of 30 neurons is shown in Fig. 4 (green traces labeled “Recon-30” in panels C, G, and H). The population estimate showed clear improvement over the estimate based on the same number of spike trains from a single neuron (Fig. 4C) and recovered a broader range of the frequency response (Fig. 4H). The population reconstruction coherence reached a maximum of >90% at ∼20 Hz, but the largest relative improvement over the single neuron reconstruction occurred between 50 and 150 Hz.

To investigate how the reconstruction improved with spike pattern heterogeneity, we created populations by varying the number of different neurons represented in the pool from 1 to 30 while keeping the total number of spike trains constant (Fig. 6A). As the number of unique neurons in the pool increased, the fit of the reconstruction improved significantly over single-neuron reconstructions, from a mean r² value of 0.22 ± 0.6 for single neurons to 0.31 ± 0.6 for pairs of neurons, to 0.53 ± 0.03 for a population of 30 neurons (Fig. 6B; P < 0.05, one-way ANOVA). The information rate also showed a threefold increase using the population spike trains over single-neuron spike trains (data not shown). Using spike trains from pairs of neurons classified as the same cell type improved the reconstruction equally well as using pairs classified as different cell types (data not shown). These data suggest that the heterogeneity in the spiking responses across individual neurons contributes to the encoding of the stimulus by reducing redundancy across the population.

Fig. 6.

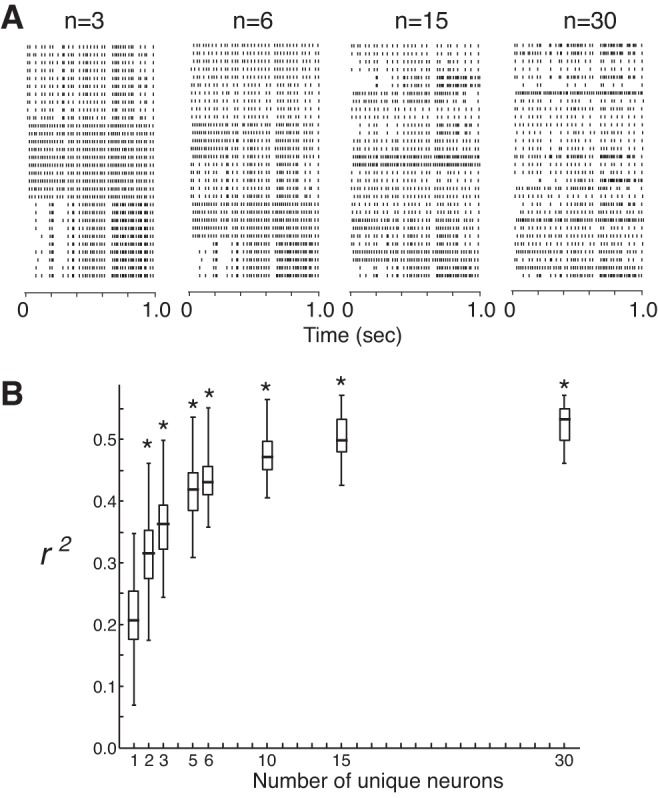
Population coding improves the stimulus reconstruction. A: population rasters drawn from different neuron pool number for a total of 30 trials show increasing heterogeneity in the firing patterns. B: reconstruction fit (r²) vs. number of unique neurons in the population group used in the reconstruction estimate (n = 120 repeated runs per group containing ≥ 2 unique neurons; n = 60 for single-neuron group). Increased heterogeneity results in improved reconstruction fit [one-way ANOVA using Welch's test assuming unequal variances, F(7,313) = 4.9, P < 0.001; all groups of n ≥ 2 neurons were significantly different from single-neuron group, *P < 0.05, Dunnett multiple-comparisons test]. Box plot represents the median, interquartile range and extrema.

Robust population coding of a common signal using nonidentical input fluctuations.

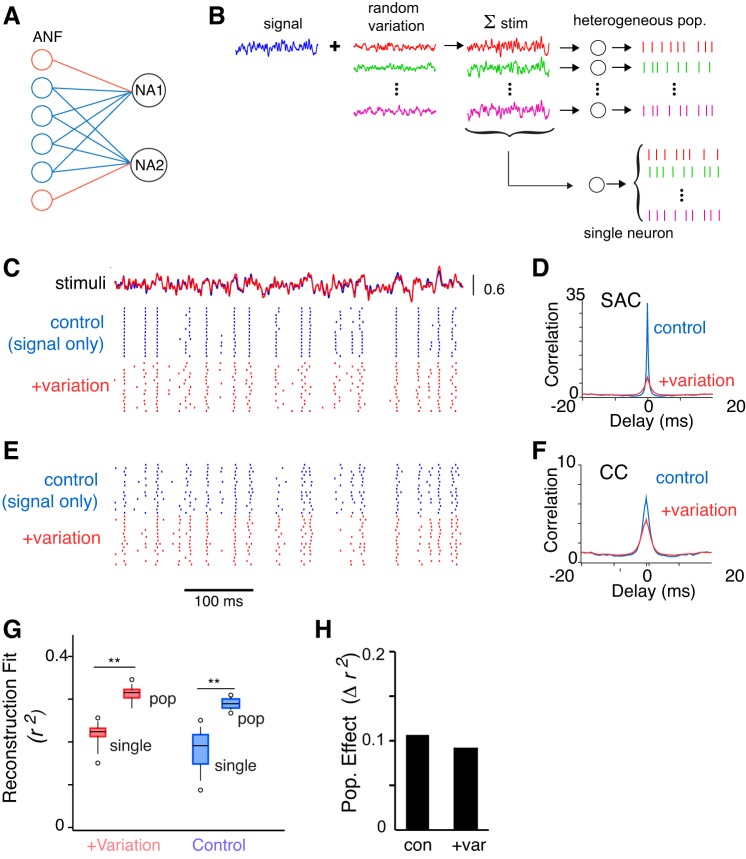
Our experiments providing each NA neuron with identically fluctuating inputs allowed us to isolate the effects of intrinsic firing properties on the spiking responses. Several limitations of this experimental approach, however, should be acknowledged. First, only repeated presentations of a stimulus to an individual neuron were truly identical and resulted in extremely high reliability. During sequential recordings, however, all neurons received identical temporal modulations, but the mean current amplitudes were calibrated individually based on each neuron's input resistance and input-output function (i.e., “f–I curve”). It was possible that these amplitude differences contributed to the spike train variation only indirectly as a result of differences of the intrinsic properties: controlling for absolute stimulus amplitude resulted in slightly worse, although still high, correlations across neurons (data not shown). Second, we were interested as to whether population coding would be improved due to biophysical differences under more naturalistic conditions. During natural auditory processing, any two neurons are unlikely to experience identical synaptic drive, since realistically they receive only partially overlapping sets of inputs (Fig. 7A).

Fig. 7.

Robust stimulus coding in the presence of interneuronal input variations. A: each NA neuron sums multiple small inputs that may partially overlap with inputs to other NA neurons. B: schematic of experimental protocol using varied input. A standard noisy current (“signal”) was summed with a set of randomly varying noise currents (“random variation”) to generate the set of stimuli presented to the neurons (“∑ stim”). A “heterogeneous” population response was constructed by selecting a single response from each neuron (n = 15 sequential recordings) presented with a different variation of the ∑ stim (see data shown as red dot raster in E). For comparison, a “homogeneous” population response was constructed from the responses of a single neuron to 15 trials each with a different variation of the ∑ stim (red dot raster in C). “Control” heterogeneous and homogeneous population responses were constructed using the signal alone (not shown in B; blue dot rasters in C and E). C: single-neuron effects of random variation. Top traces: control noise stimulus (blue) overlaid with one example of a noise stimulus with added random variation (red) (signal/noise, 4:1). Rasters show that random variation in the stimulus introduced variability in the timing and likelihood of spiking (red) compared with control (blue). Rows in each condition correspond to different trains from a single neuron. D: average SAC (n = 15) showed a large decrease in peak amplitude and increase in width with random added noise. E: effect of random variation on population correlations. Stimuli are as in C. Population rasters are in response to presentation of identical signal stimulus (blue). Addition of random variation to the stimulus resulted in some additional variation (red). Rows in each condition correspond to different neurons. F: average cross-correlograms of responses (CC, n = 105 pairwise comparisons) collected during control stimulation (blue) and during stimulation with added random variation (red). G: optimal linear reconstruction analysis in the presence of random noise variation (+variation, red) show a population effect, with larger r² values for the heterogeneous population (“pop”) than for a homogeneous population of responses from single neurons (“single”) (**P < 0.001), similar to the population effect seen under control stimulation for these neurons (control, **P < 0.001) (n = 15 neurons). H: absolute population effect size (Δr² = mean population r² − mean single neuron r²) was similar in the two conditions.

To investigate the effect of nonidentical, but correlated, input stimulation on reliability and signal coding, we analyzed the responses of neurons that were stimulated with either repeated presentations of the “signal” alone, or with a set of stimuli generated by adding random current noise to the signal (signal-to-noise ratio, 4:1; see materials and methods; Fig. 7B). The addition of random noise variation effectively “roved” the amplitude of the stimulus, allowing a test of the hypothesis that biophysical heterogeneity contributes to improved coding, rather than differences in mean level amplitude that were a limitation in the previous experiments.

For single neurons, the addition of random noise variation to the stimulus decreased spike reliability by nearly 80% (Fig. 7, C and D). In contrast, for population responses, the addition of random variation decreased the average CC by 42% (Fig. 7, E and F). In the presence of random noise variation, the CI values were similar for single neurons (SACs had a mean CI of 6.52 ± 4.86) and for CCs (mean CI was 4.60 ± 1.39); thus the addition of random noise to the set of responses in single neuron mimicked the level of correlation and spike time jitter found in the population using similar stimuli.

If the improvements in population coding were due to biophysical diversity among NA neurons, then we would expect that reconstructions using the “heterogeneous” population (15 different sequentially recorded neurons) would be improved relative to a “homogeneous” population (single neurons presented with signal + random noise variation, i.e., “∑ stim”; Fig. 7B). If the improvements in coding observed in experiments using identical stimuli were partly or wholly an artifact of uncontrolled variations in amplitude, then we would expect the population effect to be small; that is, the quality of the reconstructions using the heterogeneous and homogeneous (single cell) populations should be similar. When we analyzed the reconstructions in the presence of random noise variation, we found a large population effect: the fit improved using the heterogeneous population by 42% relative to homogeneous (r² values: heterogeneous, 0.32 ± 0.02 vs. homogeneous/single, 0.22 ± 0.03, P < 0.001; Fig. 7G). The population effect observed using stimuli with random variation was nearly as large as that using control stimuli with no random variation (Δr² for +variation, 0.09; control, 0.11; Fig. 7H). These data support the contention that biophysical heterogeneity amongst neurons contributes to improved encoding in the cochlear nucleus.

DISCUSSION

Temporally fluctuating current stimuli elicit highly reliable firing in neurons of the avian cochlear nucleus. We have shown here that the firing was tightly correlated across the population and also found a high degree of heterogeneity between the spike patterns of different neurons. Stimulus-driven spike trains from individual neurons encoded a substantial portion of the temporal modulations in the stimulus. Pooling information across the population improved the coding more than twofold. The improvements in encoding increased with increasing heterogeneity in the spike patterning, due to variations in the spiking responses across different neurons that spanned a greater proportion of the stimulus, reduced redundancy and combined for a more accurate stimulus reconstruction. These experiments using DC injection allowed us to show that the differences in the patterning were largely due to variation in intrinsic firing properties. These results suggest that biophysical heterogeneity in the firing properties of cochlear nucleus neurons within and across cell type is an important potential mechanism for the efficient coding of auditory stimuli.

Reliable firing and temporal correlations across neurons efficiently encode salient stimulus components.

Highly reliable, stimulus-driven firing suggests that activity faithfully encodes the dynamic fluctuations in the inputs. Our laboratory's previous study showed that when presented with frozen white-noise current stimuli, NA neurons fired with reliable, stimulus-locked spike patterns (Kreeger et al. 2012), similar to neurons in other brain areas (Mainen and Sejnowski 1995; Street and Manis 2007). In this study we showed that information about the stimulus was efficiently encoded in the firing patterns using optimal linear reconstruction methods (Bialek et al. 1991; Borst and Theunissen 1999; Butts et al. 2007; Stanley et al. 1999). Spiking activity by individual neurons could account for ∼22% of the stimulus variance, with high coherence with the stimulus in the frequency range of 10–80 Hz. Individual neurons had an average information rate of ∼2.5 bits/spike, comparable to estimates of coding efficiency in other peripheral, auditory or sensory areas (Bialek et al. 1991; Borst and Theunissen 1999; Butts et al. 2010; Rieke et al. 1997; Tripathy et al. 2013). There was a strong positive correlation between a neuron's reliability and how much information each spike carried: the more reliable the firing, the more informative was each spike.

Highly reliable firing has been observed in vivo during recordings of spiking activity in barn owl NA in response to acoustic noise stimuli (Steinberg and Peña 2011). The reliable firing in NA in vivo was related to the extraction of the acoustic envelope, while the cochlear nucleus in the “temporal” pathway, nucleus magnocellularis, had comparatively less reliable firing but was better phase-locked to the fine structure. Neural activity in NA is the likely source, via direct or indirect ascending projections, of reliable temporal inputs to higher order auditory nuclei that also demonstrate good envelope coding (Keller and Takahashi 2000). Reliable temporal patterning is observed also in the neural activity recorded in vivo in midbrain and forebrain auditory areas in zebra finch and mouse in response to natural communication signals. When temporal information in the neighborhood of 10 ms is used, the neural activity can be used to distinguish between stimuli, whereas rate information is comparatively uninformative (Holmstrom et al. 2010; Narayan et al. 2006; Schneider and Woolley 2010). These studies suggest that the highly reliable temporal patterning is critical to processing the spectrotemporal envelope information so characteristic of natural communication signals.

One would naturally conjecture that, if different reliable neurons were presented with the same temporally modulated stimulus, they should respond similarly, and their patterns of activity would be correlated in time. Our results show that neurons do, in fact, respond with correlated firing to a precision of 3–5 ms. Similar levels of population correlations have been observed among pyramidal neurons of the mammalian dorsal cochlear nucleus (Street and Manis 2007). The reliable firing and correlations occur during the rising phase and peaks of temporal activity. Previous work showed that many NA neurons are particularly sensitive to these rapid fluctuations and fire more when steep fluctuations occur (Kreeger et al. 2012). Similarly, mammalian cochlear nucleus neurons are sensitive to the rate of rise in the voltage and have narrow temporal integration windows, although stellate cells (analogous to the tonic firing neurons in NA) have been described as integrators (McGinley and Oertel 2006). Because NA neurons receive many small inputs from auditory nerve fibers, rapid fluctuations would be expected to arise when there are correlations across the input population. Correlations in the input array are, therefore, propagated to the next level with increased firing and correlations in the cochlear nucleus population output activity. This suggests that cochlear nucleus neurons show synchrony transfer, such that receipt of coactivated inputs results in correlated outputs (Ratté et al. 2013; Reyes 2003).

Evidence from in vivo recordings has shown that sound stimulation can drive stimulus-driven synchronous firing (Shivdasani et al. 2009; Woolley et al. 2006). Stimulus correlations in the temporal domain convey salient features in the sounds, such as onsets and amplitude modulations, and, therefore, carry information about the statistical structure of natural auditory scenes. Psychophysical experiments have shown that coincident onsets or rapid coherent amplitude and frequency modulations act as grouping cues to unify a perception of distinct acoustic components as arising from a single source, promoting streaming and segregation (Bregman 1990; McAdams 1989). The physiological basis of these psychoacoustic effects is not yet understood, but temporal coherence in the spiking activity across a wide range of neuronal populations encoding different features could provide a binding cue (Malsburg and Schneider 1986; Shamma et al. 2011).

Biophysical heterogeneity reduces information redundancy and improves temporal envelope coding.

Highly reliable firing and population correlations indicate efficient coding of salient temporal features. However, if all neurons responded reliably and identically to the same stimulus, resulting in strong temporal correlations, high redundancy would curtail the information transmitted across the population (Sompolinsky et al. 2001; Zohary et al. 1994). Heterogeneity of response or network properties can improve information processing using population codes (Chelaru and Dragoi 2008; Osborne et al. 2008; Shamir and Sompolinsky 2006). Using identical fluctuating stimuli and DC injection in an in vitro preparation, we show that cochlear nucleus neurons demonstrate a remarkable degree of heterogeneity in the firing patterns across different cells; remarkable since individually, each neuron's firing activity was exceptionally reliable, precise and fluctuation-driven. Using optimal linear decoding, in this study we showed that pooling the information across populations of auditory neurons improved stimulus coding of the temporal fluctuations, explaining >50% of the stimulus variance with a population of 30 neurons. Furthermore, under more realistic scenarios using inputs that were highly similar but not identical, heterogeneity among the neuronal firing responses still improved the neural coding of a common signal. Studies in the olfactory bulb have shown similar effects that we show here, such that the diversity of the intrinsic properties of mitral cells receiving common inputs improved coding by reducing redundancy and generating heterogeneity in the temporal patterning of activity (Padmanabhan and Urban 2010; Tripathy et al. 2013). Intrinsic biophysical heterogeneity may thus be a common mechanism for improved sensory coding.

Heterogeneity within and across physiological cell type.

Based on their physiological firing properties in response to step currents, neurons in NA can be divided into five classes: a single-spiking type and several types of repetitive firing neurons (Fukui and Ohmori 2003; Soares et al. 2002). These cell types, however, had relatively little influence on the neuronal firing correlations when stimulated with noisy currents. Instead of grouping into correlated subensembles of similar neurons, the heterogeneity in firing resulted in a correlational structure was distributed and not clustered. The hypothesis that groups of neurons with similar intrinsic properties would selectively form coherently firing ensembles distinct from other neurons with different intrinsic properties (Ermentrout et al. 2008) did not bear out in our data. Pairwise combinations of neurons of the same “cell type” generate reconstruction estimate improvements of equal magnitude as pairwise combinations of neurons from different cell types. The lack of clustering even when ignoring cell type designations suggested that the variation might be more continuous than discrete. These results underscore the idea that, even within defined cell types, there can also lurk substantial variability in the details of the biophysics (Marder and Goaillard 2006).

In summary, the reliability of firing and efficient encoding of temporally modulated stimuli by neurons in the avian cochlear nucleus appear to be balanced with the pressure for redundancy reduction achieved through the expression of continuous heterogeneity in the intrinsic biophysical properties within and across cell classes. The intrinsic heterogeneity of membrane mechanisms, as shown here, along with variation in the synaptic input strength, short-term synaptic plasticity and other network heterogeneities could all independently contribute to improving coding at the single neuron and population level.

GRANTS

This work was supported by funding by the National Institute of Deafness and Other Communication Disorders Grant DC10000 (K. M. MacLeod), a grant from the National Organization for Hearing Research (K. M. MacLeod), and a Howard Hughes Undergraduate Research Fellowship (L. J. Kreeger).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.A., L.J.K., S.T.L., and K.M.M. performed experiments; J.A., L.J.K., S.T.L., D.A.B., and K.M.M. analyzed data; J.A., D.A.B., and K.M.M. edited and revised manuscript; J.A., L.J.K., S.T.L., D.A.B., and K.M.M. approved final version of manuscript; L.J.K., D.A.B., and K.M.M. conception and design of research; D.A.B. and K.M.M. interpreted results of experiments; D.A.B. and K.M.M. prepared figures; D.A.B. and K.M.M. drafted manuscript.