Metabolic resource allocation in individual microbes determines ecosystem interactions and spatial dynamics

Summary

The inter-species exchange of metabolites plays a key role in the spatio-temporal dynamics of microbial communities. This raises the question whether ecosystem-level behavior of structured communities can be predicted using genome-scale models of metabolism for multiple organisms. We developed a modeling framework that integrates dynamic flux balance analysis with diffusion on a lattice, and applied it to engineered consortia. First, we predicted, and experimentally confirmed, the species-ratio to which a 2-species mutualistic consortium converges, and the equilibrium composition of a newly engineered 3-member community. We next identified a specific spatial arrangement of colonies, which gives rise to what we term the “eclipse dilemma”: does a competitor placed between a colony and its cross-feeding partner benefit or hurt growth of the original colony? Our experimentally validated finding, that the net outcome is beneficial, highlights the complex nature of metabolic interactions in microbial communities, while at the same time demonstrating their predictability.

Introduction

Although often studied alone in well-mixed flasks, most microbial organisms live in multi-species, structured, highly dynamic consortia (Denef et al., 2010; Dethlefsen et al., 2007; Lozupone et al., 2012; Ramette and Tiedje, 2007; Xavier and Foster, 2007). Interactions of microbes with each other and with the environment play a fundamental role in the evolution and dynamics of these communities. Many of these interactions are mediated by the uptake and excretion of small molecules, produced and degraded by the metabolic network encoded within each organism. In turn, the ensuing spatio-temporal changes of nutrients and byproducts in the environment continually modify the conditions sensed by individual cells, causing transient niches and context-dependent inter-species interactions.

Given this complexity, one may ask whether a suitable mathematical modelling framework could help bridge the gap between metabolic strategies of individual species and ecosystem-level dynamics. Such a framework would be a powerful instrument for microbial ecology, with potential impact on research areas as diverse as biogeochemical cycles (Falkowski et al., 2008), the health-balancing role of the human microbiome (Lozupone et al., 2012; Turnbaugh et al., 2007), and synthetic ecology (Klitgord and Segrè, 2011; Park et al., 2011; Shou et al., 2007). Moreover, fundamental questions on the stability (May, 1973; Mougi and Kondoh, 2012) and diversity (Curtis et al., 2002; Gudelj et al., 2010) of microbial ecosystems, the evolution of cooperation (Harcombe, 2010; Xavier and Foster, 2007) and the emergence of multicellularity (Pfeiffer and Bonhoeffer, 2003) lie precisely at the boundary between the metabolic requirements of individual species and the community-level implications of shared resources.

The past decade has seen the emergence of several novel experimental systems for investigating the dynamics of structured microbial consortia. For example, spatial structure was shown to be critical for maintaining diversity in systems with antagonistic interactions, ranging from chemical warfare (Kerr et al., 2002) to predator-prey behavior (Balagaddé et al., 2008), as well as beneficial interactions (Kim et al., 2008). In terms of metabolism, a variety of novel, engineered mutualisms between co-dependent strains have been developed (Harcombe, 2010; Hillesland and Stahl, 2010; Shou et al., 2007). These include a laboratory-evolved costly cooperation between Salmonella enterica Serovar typhimurium LT2 and an auxotrophic Escherichia coli K12 strain (Harcombe, 2010), which we use as a starting point in the current work.

While some qualitative results, such as the importance of spatial structure in a two-species system, are consistent with theory on the evolution of cooperation (Sachs et al., 2004), broader and more quantitative predictions such as species ratios, or interactions between a larger number of players are unexplored experimentally and computationally. How predictable are consortia compositions in spatially structured environments, and how strongly are they affected by initial species frequencies? Can stable systems be engineered with more than two species? Can inter-species interactions in synthetic microbial consortia emerge as a consequence of individual species solving their own metabolic resource allocation problem?

From a theoretical perspective, these questions bridge multiple distinct scales, from individual intracellular reactions, up to the spatial distributions of multiple species and environmental metabolites (Gudelj et al., 2010; MacLean and Gudelj, 2006). Classical ordinary differential equation (ODE) models have been shown to recapitulate colony diameter and height as a function of time (Kamath and Bungay, 1988; Pipe and Grimson, 2008; Pirt, 1967; Rieck et al., 1973). Agent-based models have successfully shown how colony morphology arises as an emergent property of the behavior of individual cells or clusters of cells (Ben-Jacob et al., 1998; Kreft et al., 1998, 2001; Xavier et al., 2005). However, these approaches typically assume simple inter-species interaction rules rather than computing them based on detailed representations of intracellular biochemical networks.

In contrast, stoichiometric modeling, a class of systems biology methods with roots in metabolic engineering, has been shown to provide testable predictions of metabolic activity at the whole genome scale, with no need for the hundreds of differential equations and kinetic parameters typical of classical kinetic models. One of the most broadly used methods, flux balance analysis (FBA) (Orth et al., 2010) assumes steady state and optimality to predict metabolic rates (fluxes) of all reactions in the cell, including uptake and secretion fluxes, and the amount of microbial growth (Harcombe et al., 2013; McCloskey et al., 2013; Segrè et al., 2002). It is important to keep in mind that the simplifications that make FBA efficient and useful are also among the main reasons for its limitations, including the incapacity to predict intracellular metabolite concentrations, the reliance on a pre-defined metabolic objective and the need for prior knowledge of biomass composition. Alternative uses of stoichiometric constrains (e.g. sampling of the feasible space (Bordel et al., 2010)), integration with high-throughput data (Becker and Palsson, 2008; Collins et al., 2012) and economy-inspired theory (Fleming, 2011; De Martino et al., 2012; Reznik et al., 2013; Schuetz et al., 2012) are among the new directions being sought in order to overcome some of these limitations.

Recent efforts have shown how FBA can be extended to model metabolite-mediated interactions between different species in microbial consortia (Klitgord and Segrè, 2011), e.g., by searching for syntrophic compositions (Stolyar et al., 2007), interaction-inducing environments (Klitgord and Segrè, 2010), competition/cooperation balances (Freilich et al., 2011; Wintermute and Silver, 2010), or multi-level optima (Zomorrodi and Maranas, 2012) in multi-species joint stoichiometric models, or by implementing dynamic flux balance modeling of cocultures (Khandelwal et al., 2013; Salimi et al., 2010). Some of these approaches require a priori assumptions on how two species interact, e.g. a tunable ratio of the biomass production rates (Stolyar et al., 2007), a minimal growth rate for each species (Klitgord and Segrè, 2010), or different types of joint or multilevel objective functions (Freilich et al., 2011; Wintermute and Silver, 2010; Zomorrodi and Maranas, 2012). Most importantly, to our knowledge, these approaches have not been extended to multi-species communities in a structured environment, although a single-species model has been previously coupled with reactive transport (Scheibe et al., 2009).

Here we introduce a multi-scale modeling framework that computes ecosystem-level spatio-temporal dynamics based on detailed intracellular metabolic stoichiometry, without any a priori assumption on whether and how different species would interact. Our approach, named Computation Of Microbial Ecosystems in Time and Space (COMETS), implements a dynamic FBA algorithm on a lattice, making it possible to track the spatio-temporal dynamics of multiple microbial species in complex environments with complete genome scale resolution. We apply COMETS to the study of a previously built E. coli/S. enterica synthetic consortium (Harcombe, 2010), and to a new three-member consortium that incorporates Methylobacterium extorquens AM1 into the E. coli/S. enterica system.

Results

From genome-scale to ecosystem-level spatio-temporal models

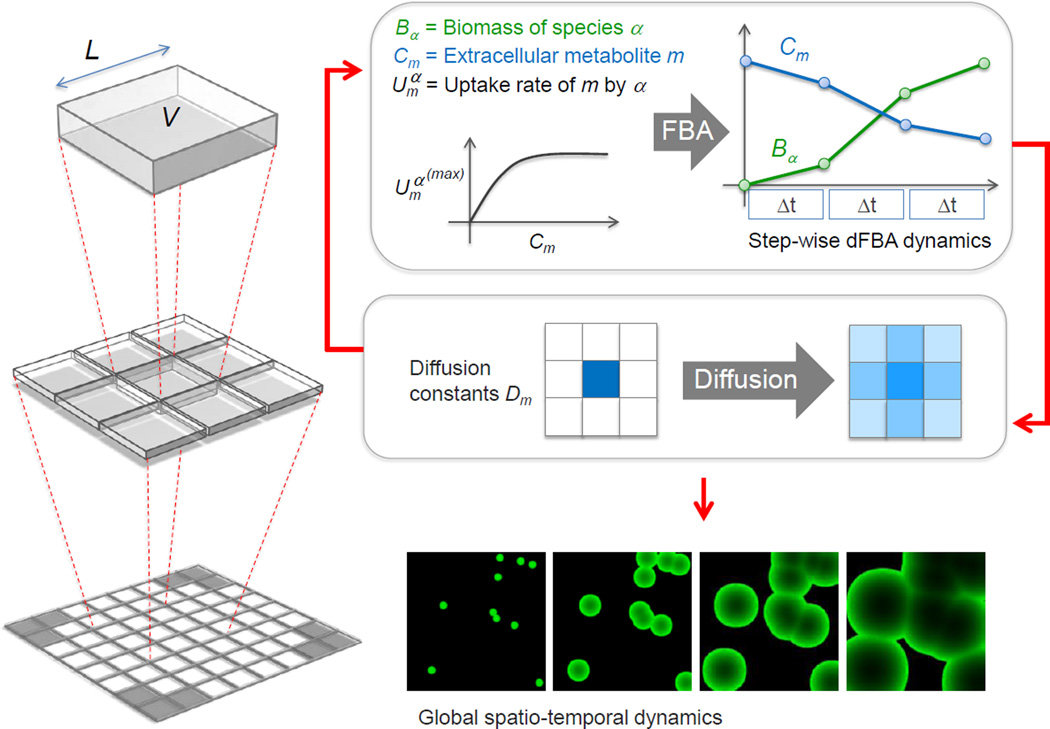
COMETS uses dynamic flux balance analysis (dFBA) (Mahadevan et al., 2002) to perform time-dependent metabolic simulations of microbial ecosystems, bridging the gap between stoichiometric and environmental modeling. Simulations occur on a spatially structured lattice of interacting metabolic subsystems (“boxes”), providing at the same time insight on intracellular metabolic fluxes and on ecosystem-level distributions of microbial populations and nutrients. COMETS incorporates two fundamental steps (Fig. 1 and Methods). The first step, cellular growth, is modeled as an increase of biomass at different spatial locations, using a hybrid kinetic-dFBA algorithm. Each box may contain biomass for an arbitrary number of different species. The second step consists of a finite differences approximation of the diffusion of extracellular nutrients and byproducts in the environment, and of the expansion of biomass (see Methods). Simple diffusion simulations in absence of growth behave as expected (Fig. S1, Related to Fig. 1). We have incorporated multiple species into COMETS by importing the corresponding stoichiometric models, either from manually curated reconstructions, or from automated pipelines that construct models from annotated genomes and highthroughput data, such as Model SEED (Henry et al., 2010). In addition, both spatially and molecularly complex environments can be designed by the user through an interactive toolbox (Fig. S2, Related to Fig. 1) and simulation outcomes can be analyzed through a visualization tool (Fig. S3, Related to Figs. 1 and 4).

Figure 1.

A schematic representation of the key steps of COMETS simulations, from the level of individual boxes (top) to a whole lattice (bottom). Within each box, dFBA is solved for each species, with uptake set by Michaelis-Menten equations (top right). These calculations amount to piecewise linear approximations of the growth and environmental metabolites as a function of time. Classical discretization of the diffusion equation gives local rules for updating biomass and nutrients in each box (middle). The ensuing algorithm computes ecosystem dynamics (bottom) as a function of intracellular metabolism of individual species.

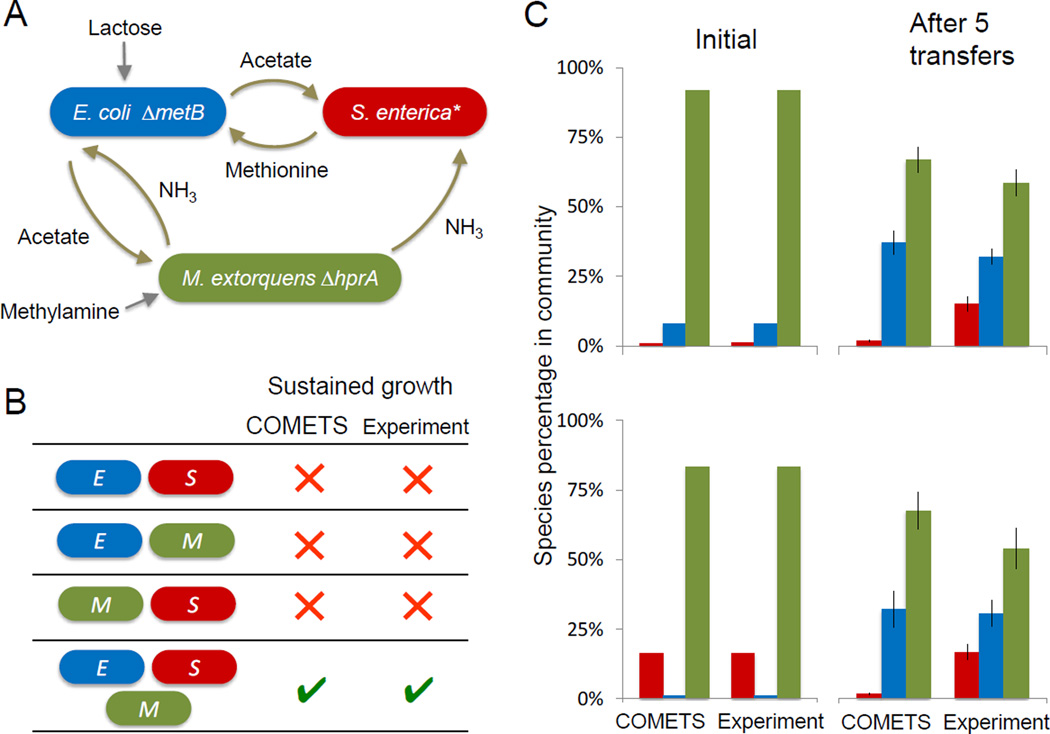
Figure 4.

COMETS predictions of growth for a novel 3-species consortium. A) A mutant M. extorquens AM1 was added to the 2-species system. The M. extorquens lacks hprA, so it relies on carbon from E. coli, while providing the other two species with a source of nitrogen. B) COMETS correctly predicts that all three members of the consortium are necessary for growth on lactose/methylamine minimal medium. C) Species frequencies before and after 5 transfers. Blue bars correspond to E. coli, red bars to S. enterica and green bars to M. extorquens. COMETS ratios (left) represent biomass; observed values (right) are based on CFU. Error bars are standard deviations.

COMETS recapitulates E. coli colony growth on different substrates

A key step toward modeling growth of spatially-structured communities is to make sure that the basic dynamics of colony growth can be well-captured by our computational approach, with parameter values estimated from the literature (Table 1). As in any FBA model, COMETS does not require intracellular kinetic parameters. However, in analogy with previous dFBA formulations, COMETS estimates the upper bounds to metabolite uptake rates using a saturation curve, described through standard kinetic parameters V_max and K_M. In the simulations presented below, we assumed these parameters to be the same for all metabolites. Substrate-specific values can be easily introduced if known (see Methods), though theoretical considerations based on the diffusion-limited nature of uptake kinetics suggests limited substrate-to-substrate variation (Berg and Purcell, 1977). The effects of variations of either universal or substrate-specific uptake kinetics parameters are illustrated in Fig. S4 (Related to Figs. 1 and 2), along with sensitivity to all free parameters in COMETS. Moreover, we show that COMETS simulations are invariant relative to small rescaling of the space and time units (Fig. S5, Related to Figs. 1 and 2).

Table 1.

Like any stoichiometric model, COMETS does not require kinetic for intracellular reactions. However, it does require a few parameters associated with the processes of diffusion, nutrient uptake, and carrying capacity of individual boxes. We set all these basic parameters based on values found in the literature.

Parameter	Value	Citation
Uptake Vmax	10 mmol/g/hr	Gosset 2005
Uptake Km	10 µM	Gosset 2005
Death rate	1%	Saint-Ruf et al 2004
Metabolite diffusion	5 × 10−6 cm2/sec	Stewart 2003
Biomass diffusion	3 × 10−9 cm2/sec*	Korolev et al 2011
Max colony height	200 µm	Lewis & Wimpenny 1981
Oxygen concentration	250 µmol/cm2	Peters et al 1987

^*The E. coli colony growth simulations were run with a biomass diffusion of 3×10⁻¹⁰ because the laboratory experiments carried out by Lewis and Wimpenny 1981 used plates made with 1.5% agar rather than the 0.8% agarose used in all other experiments.

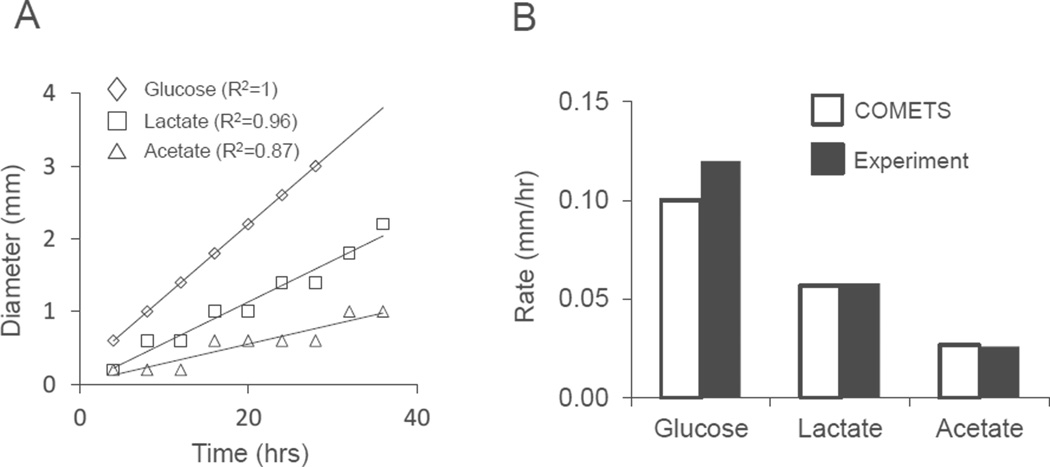
Figure 2.

COMETS predictions of E. coli colony growth on various carbon sources. A) COMETS predicts that colony diameter increases linearly on glucose (diamonds), lactate (squares) and acetate (triangles). B) COMETS predictions of the rate of colony expansion (white bars) compared to the values reported by Wimpenny (black bars, no error estimate available). Predicted colony expansion on glucose was 16.7% slower than observed, while predicted growth on lactate and acetate deviated by 2.7% and 2.2% respectively.

As a first benchmark for COMETS we tested its capacity to reproduce the observation that colonies increase linearly in diameter over time (Cooper et al., 1968; Palumbo et al., 1971; Pirt, 1967; Wimpenny, 1979). Simulated colonies of E. coli followed this growth pattern with only small deviations from linearity as result of lattice discreteness (Fig 2A). Importantly, COMETS accurately predicted the rate of diameter increase on a variety of carbon sources (Fig 2B) as compared to previously published data by Lewis and Wimpenny (Lewis and Wimpenny, 1981). These simulations with different carbon sources required only changes in the initial environmental conditions, with no need for parameter tuning.

Species ratio convergence in a co-dependent, two-species consortium

We next tested the ability of COMETS to predict interactions between members of the E. coli/S. enterica synthetic consortium mentioned above (Harcombe, 2010). In lactose medium, Salmonella enterica Serovar typhimurium LT2 relies on carbon byproducts from an Escherichia coli K12 metB mutant. Reciprocally, this auxotrophic E. coli requires methionine from its partner in order to grow in minimal medium. Stoichiometric models of each partner were modified to incorporate known genetic constraints (Fig. 3A). For the E. coli strain, the metB mutation was incorporated by constraining to zero the flux through the corresponding reaction (cystathionine γ-synthase). In S. enterica, methionine excretion requires gain-of-function mutations in metA (homoserine transsuccinylase) (SM Douglas, WRH, CJM, unpublished). This excretion was modeled as coupled to biomass, so that as cells grew they excreted observed levels of the amino acid. These genetic alterations created an obligate mutualistic interaction in silico consistent with that observed in the laboratory; neither species was able to grow in isolation on lactose minimal media, but growth was observed when both species were present (Fig 3B).

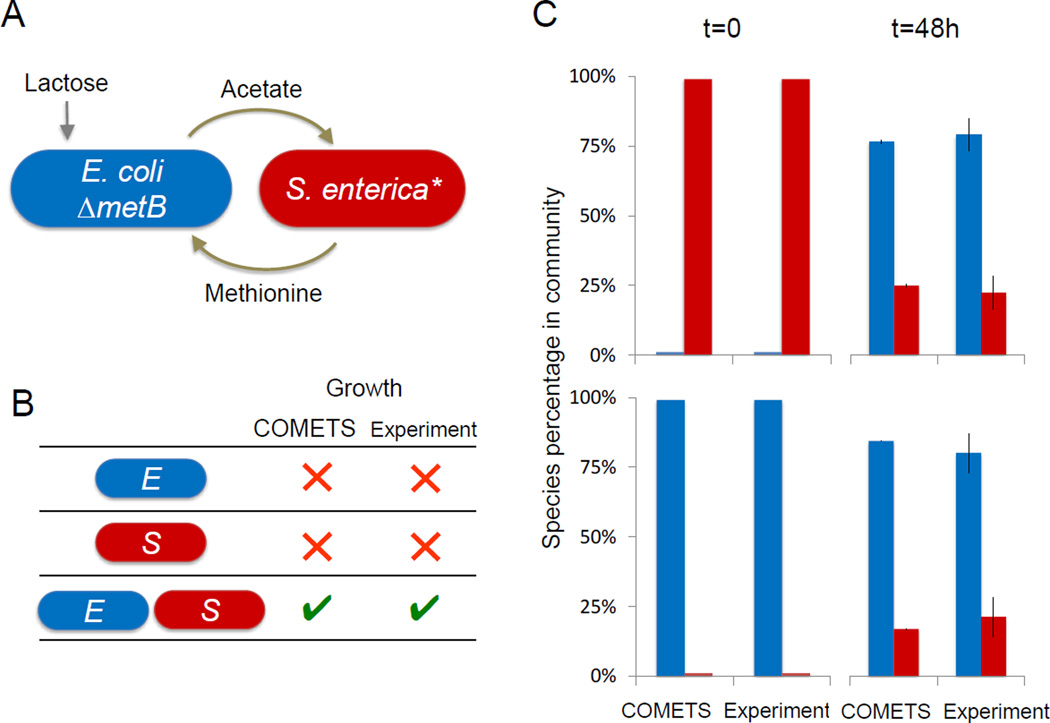
Figure 3.

COMETS predictions of growth for a two-species synthetic consortium. A) The consortium consists of a mutant S. enterica that provides methionine to an auxotrophic E. coli, obtaining carbon byproducts in return. B) COMETS correctly predicts that co-culture is necessary for growth on lactose minimal medium. C) Predicted and observed species frequencies before and after 48 hours of growth. Blue bars correspond to E. coli, red bars to S. enterica. COMETS ratios (left) represent biomass; observed values (right) are based on CFU. Error bars are standard deviations.

In order to test whether COMETS could quantitatively capture community level behavior, we tested its ability to predict the impact of starting conditions on species ratio in our two-species consortium grown on solid medium (Fig 3C). COMETS predicted that, following a single 48-hour growth cycle, communities would converge in composition even when initial frequencies differed by two orders of magnitude (1%-99% E. coli). This convergence was indeed observed experimentally over 48 hours, in agreement with previous observations in other model ecosystems (Estrela and Brown, 2013; Shou et al., 2007). More surprisingly, COMETS also correctly predicted the species ratio to which the communities converged in the laboratory. COMETS predicted a composition of 79±4% E. coli, which is not significantly different than the experimentally observed frequency of 78±6% (mean±standard deviation, p=0.67 with a 2-tailed t-test). As illustrated for example in (Kerner et al., 2012), predicting species stability and convergence to specific ratios based on simple kinetic models is not a trivial challenge. Furthermore, previous implementations of constraint-based metabolic modeling have struggled to predict which pairs of E. coli mutants would co-exist, let alone their equilibrium ratios (Wintermute and Silver, 2010).

An engineered three-species consortium converges to a stable composition

As described above, one of the strengths of COMETS is its ability to handle arbitrarily complex ecosystems. We therefore challenged COMETS to predict the behavior of a tri-partite obligate mutualism. Towards this goal, we experimentally engineered a new synthetic consortium, which incorporates M. extorquens AM1 into the previous E. coli/S. enterica system. This represents a significant advance in complexity relative to obligate consortia that have been previously engineered (Harcombe, 2010; Shou et al., 2007). M. extorquens is the best-studied model system for C₁ metabolism (Chistoserdova et al., 2009; Vuilleumier et al., 2009) and has the ability to obtain energy, carbon and nitrogen from methylamine. Here we used a ΔhprA strain (Marx, 2008) that lacks a key enzyme (hydroxypyruvate reductase) for assimilating carbon from methylamine. In media with lactose and methylamine, the ΔhprA M. extorquens strain relies on acetate from E. coli, while providing the other two species with a source of nitrogen due to dissimilation of methylamine (Fig 4A). To our knowledge this is the first metabolically-engineered obligate mutualism between three species (but see (Miller et al., 2010) and (Kim et al., 2008) for systems that were not metabolically engineered, and (Hernández-Sánchez et al., 2013) for a non-obligate system).

COMETS again made accurate predictions about the obligate nature of species interactions in the consortium (Fig. 4B). Similarly to the E. coli mutant, a model of the engineered M. extorquens was created by constraining flux through HprA to zero. COMETS correctly predicted that no species – nor species pair – was capable of growth in lactose-methylamine media. Only when all three species were present was sustained growth observed both in the laboratory and in simulations.

Extending the analysis presented above for the two-species system, we investigated the ability of COMETS to predict the stability and steady-state community composition in our novel three-species mutualism. COMETS predicted that the community would converge to very similar species ratios from different starting conditions (Fig 4C); after 5 growth cycles each lasting 96 hours, there was no significant difference between species ratios (E. coli p= 0.48, S. enterica p = 0.91, M. extorquens p=0.50 with a 2-tailed t-test). Interestingly, COMETS predicted that M. extorquens would dominate the community despite having the lowest maximal growth rate. Experimental observation supported the predicted convergence of community composition over 5 growth cycles, and the dominance of M. extorquens (see also Fig. S3, Related to Figs. 1 and 4).

The metabolic eclipse dilemma: benefit of a competitor in spatially-structured mutualism

We used the two-species consortium to investigate the influence of spatial structure on competition in mutualistic systems. As a first step, we tested the growth of each partner as a function of increasing distance between them. Consistent with expectations, both the modeled colonies and the observations of the pair exhibited decreased growth as they were initiated further apart (Fig. S6, Related to Fig. 5).

Figure 5.

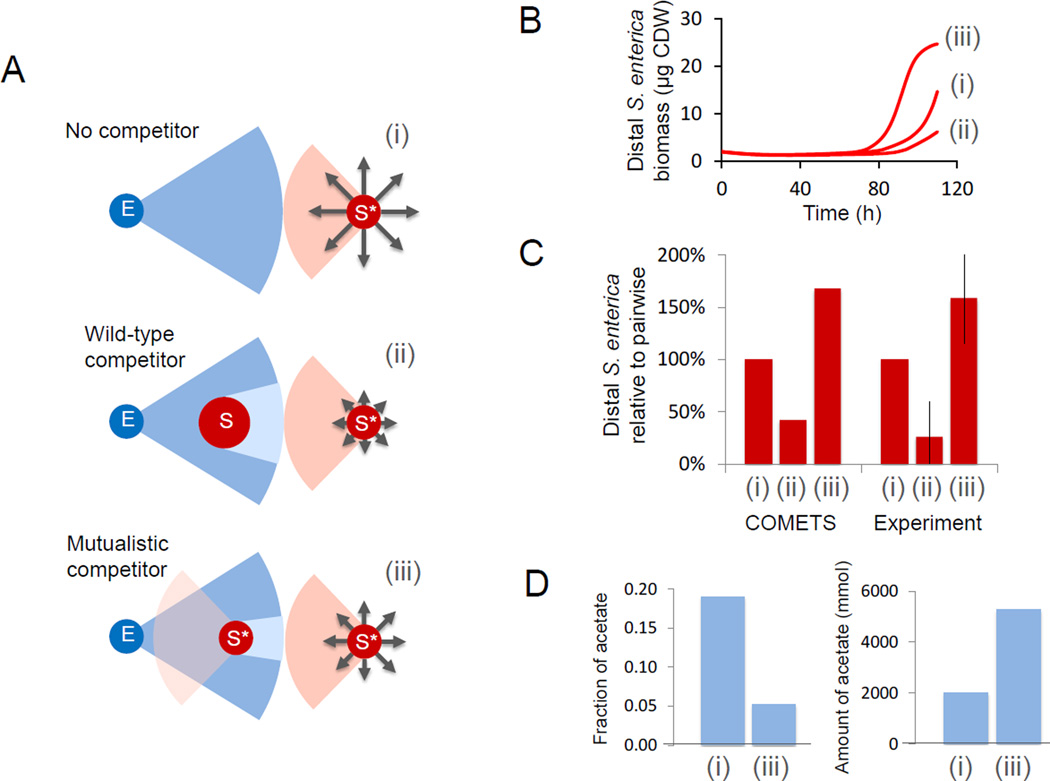
The impact of competition on focal colony growth. A) Naïve expectation that growth of focal S. enterica colonies (red circles next to numerals) would be reduced by placement of a competitor between the focal S. enterica and its obligate mutualistic partner E. coli (blue circles). Relative anticipated growth is represented by grey arrows, methionine diffusing from S. enterica colonies is displayed in red, carbon byproducts diffusing from E. coli are displayed in blue. B) COMETS predicted that wildtype S. enterica between E. coli and the focal colony would reduce its growth (line ii) as compared to the no competitor scenario (line i). However, if a second colony of the same methionine-excreting S. enterica is placed in the middle, it increases growth of the distal colony (line iii). C) Growth of the distal colonies standardized to scenario i for the case with no competitor (i), wildtype competitor (ii), and mutualistic competitor (iii). COMETS ratios (left three bars) represent biomass; experimental values (right three bars) are based on CFU. Error bars are standard deviations. D) Acetate uptake of distal colonies i and iii in COMETS. The fraction of acetate is the total uptake of the distal colony divided by the total acetate excretion of its partner. The amount of acetate is the total moles taken up by each colony during the first 89 hours (i.e. before any E. coli start to utilize acetate).

As growth of communities will rarely be as simple as pairwise interactions between micro-colonies, we then asked how additional colonies influence pairwise interactions. When essential metabolites diffuse from a point source one might expect that colonies have an “eclipse” effect, casting a resource shadow that reduces the metabolites available to more distant colonies. Based on this logic, one would expect that the growth rate of a colony would be reduced if a competitor colony is placed between the colony and a mutualistic partner (Fig 5A). The extent of negative impact should scale with the rate at which the intermediate colony removes metabolites from the environment. On the other hand, one could argue for an opposite outcome, i.e. that the newly interposed colony, by helping the mutualistic partner, will ultimately benefit the original colony. Intuition alone cannot provide an answer to this conundrum, as its solution depends on the balance between the metabolic rates of the different species, the spatial organization of the colonies, and the diffusion rates.

We used COMETS to simulate the outcome of this gedanken experiment. COMETS predicted that a colony of wildtype S. enterica (whose model lacks the imposed methionine excretion of the mutualistic strain) would rapidly remove carbon from its surroundings and diminish the growth of a more distant colony of mutualistic S. enterica (Fig 5B). However, if the intermediate colony were another mutualistic S. enterica, then, based on COMETS, the growth of the distal colony would end up being larger than in the absence of an interfering colony. Though this effect is predicted to be time dependent, it holds over a substantial temporal window (Fig 5B).

We then tested the computational predictions experimentally, and found that after 10 days a colony of S. enterica eclipsed by a methionine-excreting competitor produced more biomass than in the absence of a competitor (Fig 5C, p=0.02 with a 2-tailed t-test). The intermediate colony increased the growth and excretion of a mutualistic partner, and this amplifying effect outweighed the influence of competition for carbon. In addition to correctly predicting these qualitative behaviors, COMETS also predicted the ratio of distal colony biomasses in the three scenarios (Fig 5C). The difference in the timing at which these ratios were observed (experiment, 240 hours; model, 110 hours) may be partially ascribed to the fact that COMETS does not take into account lag time nor changes in diffusion due to plate drying over this long period.

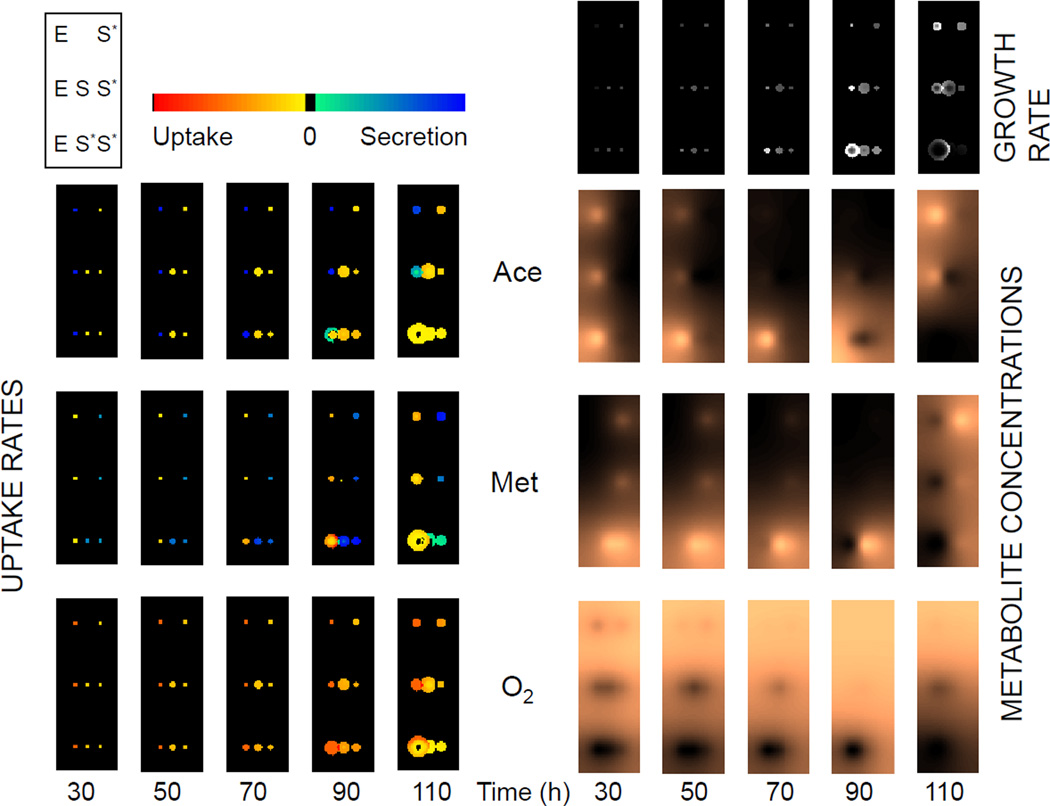
Thus, based on both the model and the experiment, the metabolic eclipse has the non-intuitive outcome of benefiting the colony that is being eclipsed. Additional insight on the details of this phenomenon would require experimental measurements of metabolite concentrations at different points in space and time, e.g. using imaging mass spectrometry (Louie et al., 2013; Watrous and Dorrestein, 2011). While this is beyond the scope of the current work, we can use COMETS to provide some preliminary theoretical insight, by taking advantage of its capacity to record simulated fluxes and metabolites at any given time and location for all organisms. This is best illustrated in the heatmaps of Fig 6, which display snapshots of key intracellular transport fluxes (for acetate, methionine and oxygen), and of the corresponding environmental metabolite concentrations, across different organisms, spatial locations and time points. The maps provided putative mechanistic insight into how heterogeneity in metabolic phenotypes determined local community composition and function, ultimately driving ecosystem-level dynamics. For example, is it possible to see how acetate uptake/secretion rates diverge over time, matched by methionine fluxes in the opposite directions, and rising levels of oxygen consumption. Helpful insight on the eclipse dilemma can be obtained by further elaboration of the computational data illustrated in Fig. 6. In particular, by using the flux values across the different colonies and time points, we were able to determine that the distal S. enterica colony took up a lower percentage - but a greater amount - of the acetate excreted by its partner when a competitor was present (Fig 5D).

Figure 6.

Heatmaps of the spatial distributions of exchange fluxes (left-side, 3 by 5 set of heatmaps), metabolite concentrations (right-side, copper-toned, 3 by 5 set of heatmaps) and growth rates (top-right, gray-shaded heatmaps) are shown at different time points during the “metabolic eclipse” simulation described in Fig. 5. The legend in the top-left corner shows the relative positions of the simulated colonies (E = E. coli; S = S. enterica). Fluxes (left) are scaled from excretion (blue) to uptake (red) for each lattice box at each of five time points for three key metabolites (acetate, methionine and oxygen). Metabolite concentrations scale from low (dark) to high (bright). Fluxes are normalized across all time points; metabolites are normalized within each time point (to make early low concentration levels visible).

Discussion

Our results demonstrate that inter-species interactions and microbial community dynamics can emerge as the consequence of individual species locally optimizing intracellular resource allocation. We have used synthetic two- and three-species consortia whose growth depends upon metabolic exchange to experimentally test the predictions of a computational framework that is based entirely on this individual optimality postulate. This approach requires very few free parameters and no a priori assumptions on whether or how species would interact. One notable exception is the need to impose that S. enterica secretes methionine as it grows. This requirement, not unlike other flux constraints added in FBA models to match empirical knowledge (such as the maintenance flux), is a consequence of the fact that the specific strain used in the experiment has evolved this secretion capacity as a new trait. Such a trait could not possibly be captured by the standard S. enterica FBA model. This current limitation could be addressed by adding in COMETS the capacity for organisms to evolve, i.e. undergo mutations (e.g. in the form of random changes in constraints) and selection (competition between newly emerged variants).

Data from both two- and three-species consortia confirmed predictions that they would repeatedly converge to a steady-state composition even from different starting conditions. The convergence of the two-species consortium is similar to observations with auxotrophic yeast (Shou et al., 2007); our results indicate that this robust behavior extend to the three-species consortium. Here there was a potential tension between mutualistic interactions and direct competition for limiting nutrients, such as S. enterica and M. extorquens competing for acetate, and E. coli and S. enterica competing for ammonia. Particularly surprising was the accuracy of the prediction that the three-species consortium would be dominated by M. extorquens – the strain with the slowest maximal growth rate. Whereas the potentially rapid E. coli and S. enterica faced dual limitations (methionine and N or acetate and N, respectively), M. extorquens could access N and energy from methylamine, and the limiting acetate was only required for assimilation. These results are noteworthy in light of the exciting possible opportunities of using synthetic ecology to design microbial consortia for biomedical and metabolic engineering applications. For this goal to come to fruition it is critical to be able to predict how synthetic communities behave through time, even in heterogeneous environments, such as the lining of a human gut, or the architecture of a leaf. We demonstrated here that the dynamics are repeatable not only within replicates, but between treatments with different starting conditions.

Our experiment on the metabolic eclipse provided a specific, subtle example of COMETS arbitrating between the positive and negative effects that arise from the spatial organization of colonies. That proximity of a conspecific competitor could be an advantage due to the stimulation of a shared mutualistic partner highlights the utility and importance of spatially-explicit experiments when investigating the nature of interactions in microbial communities. More broadly, the balance between positive and negative effects that arise from local interactions determines changes in community properties such as composition and function, and has important implications for the evolutionary dynamics of microbial systems. For example, whether cooperation is selected in structured environments critically depends not only on the qualitative existence of benefits and costs, but on the quantitative balance between these interactions (Bull and Harcombe, 2009). COMETS has the capacity to evaluate the impact of conflicting types of interactions. For example, the observed dichotomy between fractions and amounts of exchanged nutrients between different species (Fig. 5D) may provide a useful starting point for studying the complexity of cross-feeding interactions in natural ecosystems. Moreover, while in this work we focus on inter-species interactions, COMETS can be used to study phenotypic diversity and metabolic heterogeneity within individual colonies. The 3D version of COMETS (under development) will enhance this type of analysis, as it will explicitly account for changes in diffusivity for different molecules (including oxygen) through the colony itself.

The prominent role of optimization in flux balance in general, and in COMETS in particular, deserves further reflection. In COMETS, each organism operates based on its own objective (maximization of biomass, in the current work) given the surrounding nutrient availability. Note that the same species in different spatial locations (in the same in silico experiment) may utilize resources differently (e.g. oxygen-limited biomass in one location will have different physiology than carbon-limited biomass in another). This is an important difference from approaches that optimize the interests of the group, and is a central component of COMETS’ ability to accurately predict species ratios. However, even the assumption that evolution has acted on a population to optimize a simple objective has been challenged by new data and analyses (Harcombe et al., 2013; Schuetz et al., 2012). Indeed it is unlikely that any single objective function could faithfully represent the possible spectrum of metabolic strategies across many different conditions. Future work could explore how COMETS predictions change upon implementing alternative conditiondependent objective functions. Such objective functions could be linear or quadratic (Segrè et al., 2002), and could include constraints associated with genetic regulation (Becker and Palsson, 2008; Collins et al., 2012).

Future elaborations of COMETS can be envisioned to incorporate additional aspects of microbial physiology that play an important role in microbial ecosystems, such as chemotaxis, quorum sensing, and antibiotic warfare. For example, chemotaxis could be modeled using non-isotropic diffusion, as a function of specific metabolite gradients. Toxins or antibiotics could be modeled as additional diffusible molecules that affect the death rate of specific organisms. The fact that COMETS performed so well despite lacking these important components is likely a consequence of our use of communities designed to strongly rely on metabolic-based interactions. At the same time, metabolism plays a fundamental role in many microbial systems, and it will be interesting to use COMETS as a null model to explore whether metabolic interactions are sufficient to explain ecosystem dynamics. Since no preliminary assumption needs to be made about which nutrients may mediate an interaction, COMETS can be extended to arbitrarily complex metabolic interdependencies. For example, as shown here, extending a consortium from two-way to three-way requires no additional assumptions or effort, other than modifying the initial conditions. Along the same line, COMETS can be extended to any number of species (including genetically modified strains), while increasing at most linearly in computational complexity.

The increasing flow of metagenomic sequencing data provides top-down observational insight into the taxonomic and functional dynamics of microbial communities in different environments. Our work shows that there is a complementary, mechanistic, bottom-up way of studying how ecosystem dynamics may be ultimately understood in terms of its constituents’ genomes. This approach is directly amenable to experimental testing, and paves the way for new computationally-driven directions in synthetic ecology. Despite the fact that our current work has been focused on small engineered communities, the concepts and algorithms we developed should be applicable and relevant to natural microbial consortia as well.

Methods

COMETS variables

COMETS simulates the biomass and metabolite dynamics of multiple microbial species in physical space. Physical space (in 2D) is discretized into what could be thought of as an N by M grid of “boxes” whose location is defined by a pair of coordinates (x,y), with x=1,…,N and y=1,…,M. Each box corresponds to a square of size L by L, where L is the minimal length scale, or the spatial resolution of COMETS (see Supplemental Experimental Procedures).

Each box can contain different microbial species and extracellular metabolites. Microbial species’ abundances are described as the amounts of the corresponding biomass in each box. We denote with B^α_(x,y) the amount (in g dry cell weight) of biomass of species α present in a box at position (x,y), and with Q^m_(x,y) the amount (in mmoles) of metabolite m present in a box at position (x,y). Note that both biomass and metabolite abundances are time dependent variables, i.e. Q^m_(x,y)=Q^m_(x,y)(t) and B^α_(x,y)=B^α_(x,y)(t). For each metabolite in each box we can define a concentration C^m_(x,y)=Q^m_(x,y)/V in mmoles/ml.

Biomass in each box can increase due to cellular growth, or decrease due to microbial death. In addition, upon growth, biomass can expand from a given box to a neighboring one, a process that we currently model as slow diffusion. Metabolite levels in each box can change due to secretion or uptake by the microbial biomass present in the same box, or due to diffusion in/from neighboring boxes. The details of how biomass and metabolite levels change are described next.

COMETS biomass dynamics

The amount of biomass produced by a given population of microbes per unit time is estimated based on the nutrients available in the environment, and on the capacity of the organism’s metabolism to transform such nutrients into biomass. Towards this goal, we employ a pseudo-dynamic version of FBA known as dynamic FBA, or dFBA (Mahadevan et al., 2002; Orth et al., 2010).

Following a standard notation, we call S^α the stoichiometric matrix of a species α. Matrix element S^α_i,j denotes the number of molecules of intracellular metabolite i that participate in reaction j (positive if metabolite i is a product, negative if it is a reactant). Each reaction is associated with a flux v^α_j (measured in mmol/(gDW*h), giving rise to a vector v^α. The basic Linear Programming problem of FBA (for species α) can be written as follows:

$$\text{Maximize \hspace{1em}}{\mathit{Z}}^T{\mathit{v}}^{\alpha }\text{Subject to \hspace{1em}}{\mathit{S}}^{\alpha }{\mathit{v}}^{\alpha }=0{\mathit{\text{LB}}}^{{\alpha }_j}\le v^{\alpha }\le {\mathit{\text{UB}}}^{{\alpha }_j}=1,\dots ,n$$ Eq. 1

where Z defines the objective function, taken to be by default maximization of biomass production (see Discussion). The vectors LB^α and UB^α correspond to the lower and upper bounds to all fluxes respectively. As detailed below, the dynamic calculation of these bounds is an important aspect of COMETS.

In the dFBA formulation of COMETS, each step, for each species, consists of two main processes:

1. Calculation of upper bounds for uptake rates In line with previous FBA computations, exchange fluxes balance flow in and out of each model (see (Orth et al., 2010) for additional discussion). What is unique to the dFBA formulation of COMETS is the implementation of additional environment-dependent constraints on these uptake/secretion fluxes. Upper bounds on uptake fluxes for the dFBA calculation are estimated based on a concentration-dependent saturating function, in analogy with Michaelis-Menten kinetics (Feng et al., 2012). Given an environmental concentration C^m of m (in a given box), the upper bound to u_m is given by the following saturation curve:

   $$U{B}_m^{\alpha }=\frac{V_{\text{max}}^{\alpha ,m}{[C_m]}^n}{{[C_m]}^n+K_M^{\alpha ,m}}$$ Eq. 2

   where n is a Hill coefficient (currently set to 1), $V_{\text{max}}^{\alpha ,m}$ is the maximal rate, and $K_M^{\alpha ,m}$ is a binding constant.
2. Solution of FBA problem and update of biomass and extracellular metabolite levels Upon setting all upper bounds based on the dynamically changing environmental concentrations, an FBA problem is solved for each species in each box, as described in Eq. 1. Next, the abundance of biomass (for all species) and environmental metabolites are updated in each box, according to the following discrete update rules:

   $$B_{(x,y)}^{\alpha }(t+\mathrm{\Delta }t)=B_{(x,y)}^{\alpha }(t)+B_{(x,y)}^{\alpha }(t)·v_{\mathit{\text{growth}}}^{\alpha }·\mathrm{\Delta }t{Q}_{(x,y)}^m(t+\mathrm{\Delta }t)=Q_{(x,y)}^m(t)+u_m^{\alpha }·B_{(x,y)}^{\alpha }(t)·\mathrm{\Delta }t$$

   where $v_{\mathit{\text{growth}}}^{\alpha }$ is the growth rate of the corresponding species (in that specific box, (x,y)), and $u_m^{\alpha }$ is the rate of uptake/secretion of metabolite m by species α.

Thus, starting with a user-defined initial condition, a dFBA time step is performed on each box in the grid. Each box is updated independently. If there are multiple species present in a single box, they compete for media and space (i.e. a preset total carrying capacity per box). In this case, the order in which FBA is done is randomized among the species in each box.

In addition to biomass increase due to cellular growth, at each time cycle COMETS evaluates the extent of biomass reduction, due to dilution or cell death.

Diffusion

Diffusion steps are alternated with growth steps, predicting how biomass and extracellular metabolites propagate across the lattice. COMETS numerically computes approximate solutions to the standard two-dimensional diffusion equation on a 2D lattice, by using an alternating direction implicit (ADI) scheme with a central difference formulation (Peaceman and Rachford, Jr., 1955) as used in similar individual-based models (Chung et al., 2010; Gerlee and Anderson, 2008) (see Figure S1). This diffusion step is applied to biomass and media with substantially different diffusion coefficients. If the different species in the model are not allowed to exist in the same box (an option set by the user), then they undergo diffusion in random order; all boxes occupied by other species are treated as Neumann boundaries. Diffusion is applied separately to each medium component. While metabolite-specific diffusion constants may be introduced if known, here we use the same value for all metabolites. Some boxes may represent physical barriers, which could be used to model different environmental topologies (e.g Petri dish or a microfluidic device).

COMETS download

COMETS executables, code, instructions and examples can be downloaded at http://www.bu.edu/segrelab/comets (see also Fig. S2, Related to Fig. 1).

In silico experiments

We tested the predictive power of COMETS with metabolic models of E. coli (iJO_1366) (Orth et al., 2011), S. enterica (iRR_1083) (Raghunathan et al., 2009) and M. extorquens AM1 (Klitgord and Segrè, 2010). Standard FBA models were converted to COMETS format with the script provided on the COMETS website. Mutant E. coli and M. extorquens models were constructed by constraining flux through knocked out reactions to zero. A mutant S. enterica model was constructed that excreted methionine at a rate consistent with empirical observations. To achieve this we added on the right side of the growth reaction 0.5 mmol/gDW of excreted extracellular methionine, balanced by an equal amount of intracellular methionine consumed (at the left side of the reaction equation). A ΔhprA M. extorquens model was constructed by constraining flux through the knocked out reaction to zero.

In silico environments were consistent with carbon limited minimal media (Table S1). Square lattices were constructed with individual boxes either 0.02 (Figure 2) or 0.05 cm a side (Figures 3–6). The amount of carbon under each box was calculated based on standard 25 ml plates (for example 5g/L glucose media was implemented as 0.0088 mmol/cm²). Oxygen depletion has been observed inside colonies (Peters et al., 1987; Wimpenny and Coombs, 1983) so oxygen concentrations were constrained to 0.25 mmol/cm². Trace metals and other minor components of media were provided at a concentration of 1000 mmol/box so that they were not limiting.

Simulations were executed with parameters based on published values (see also Table 1). Metabolite diffusion was set to 5×10⁻⁶ cm²/sec in agreement with sugar diffusion in (Stewart, 2003). Biomass diffusion was set to 3×10⁻⁹ cm²/sec for most simulations based on (Korolev et al., 2011). The colony expansion simulations were run with a biomass diffusion of 3×10⁻¹⁰ cm²/sec because they were carried out on 1.5% agar plates rather than the 0.8% agarose used in all other experiments. Michaelis-Menten parameters were set to canonical values of K_m = 0.01 mM and V_max= 10 mmol g⁻¹ hr⁻¹ for all metabolites, well within the range of observed values (Gosset, 2005). An upper bound on biomass per box on the lattice was set based on the observation that E. coli colonies do not exceed a height of approximately 0.2 mm (Lewis and Wimpenny, 1981). Cell death rate was set to 1% per time step (Saint-Ruf et al., 2004). The time step for all simulations was 0.1 hr.

Strains used experimentally

The experimental data we collected involved strains of E. coli K-12, S. enterica LT2 and M. extorquens AM1. The E. coli was an isolate from the Keio collection (ΔmetB CGSC# 10824, (Baba et al., 2006), erroneously referred to as ΔmetA in (Harcombe, 2010)) with the lac operon replaced via conjugation with E. coli HfrH PO1 relA1 thi-1 spoT supQ80 nad57::Tn10. The methionine excreting S. enterica LT2 mutant was created through a combination of engineering and selection (Harcombe 2010). The ΔhprA M. extorquens was created previously (Marx, 2008).

Colony expansion comparisons

The E. coli colony growth dynamics were compared to results from (Lewis and Wimpenny, 1981). They made minimal media plates with 15 g/L bacto-agar and 0.5% (w/v) of glucose, lactate or acetate. Plates were inoculated with a glass needle technique, incubated at 37 °C and measured microscopically. Average profiles were determined and used to calculate the radial growth rate. This data was compared against COMETS, by simulating growth of a colony on each of the carbon sources. Colonies were initiated with 3×10⁻⁷ g biomass in the center of a 50x50 lattice with a box width of 0.02 cm. The diameter at various time points was based on the number of boxes with more than 10⁻⁷ g biomass/box along a horizontal line through the center of the colony.

Two-Species Consortium

The two-species ratio tests involved mixed cultures grown as a lawn on petri dishes or in simulations. Experimentally, E. coli and S. enterica were grown overnight in permissive media and then mixed at a ratio of 1:99 and 99:1. Five µl of these mixtures were spread on 5 mm plates of lactose Hypho minimal media (2.92 mM lactose, 7.26 mM K₂HPO₄, 0.88 mM NaH₂PO₄, 1.89 mM (NH₄)₂SO₄, 0.41 mM MgSO₄, 1 mL of a metal mix based on (Delaney et al., 2013) (recipe in Table S2). The plates were allowed to grow for 2 days at 37 °C. At the end of this time, CFU were determined by washing and scraping plates with 720 μL of minimal media, and then spreading dilutions on LB plates. On LB both E. coli and S. enterica can grow independently, and X-gal (5-bromo-4-chloro-3-indolyl-β-D-galactopyranoside) was included in the plates so that blue E. coli colonies could be distinguished from white S. enterica colonies. Comparison to COMETS was carried out by randomly distributing 100 boxes in the relevant species ratios each with 3×10⁻⁷ biomass across a 25×25 lattice (individual box width=0.05 cm). Cell overlap was allowed and the total biomass of each type was determined after 48 hours of simulated growth. Three replicate simulations were carried out for each treatment.

The impact of space and orientation on the consortium involved detailed placement of cells. Wet lab experiments were carried out with overnight cultures of E. coli and S. enterica that were washed and concentrated to ~10⁹ cells/mL. Cells were added to wells in a 384 well plate in the desired layout. A 384-pin head was then used to stamp the cells onto a petri dish so that E. coli was inoculated 10 mm from focal S. enterica, and when relevant intermediate S. enterica was exactly half way between. Different treatments were separated by 30 mm. These plates were grown at 37 °C with high humidity for 10 days. The biomass produced in the eclipse experiment was assayed by cutting colonies out of the plate, breaking up the agar, vortexing extensively, plating on permissive LB plates and counting colonies. COMETS comparisons were carried out in a 50×140 lattice of 0.05 cm boxes. Boxes were inoculated with 2×10⁻⁶ g of biomass at the appropriate distances.

Three-species consortium

Experiments with the three-species consortium involved very similar protocols to those with the two-species consortium. Each species was grown in permissive media and then the species were combined volumetrically at ratios of 1:100:100 or 100:1:100 E. coli:S. enterica:M. extorquens. 10 μL of one of the mixtures was added to each of three replicate methylamine-lactose minimal medium plates ((NH₄)₂SO₄ replaced with 1.9 mM Na₂SO₄, and 2.51 mM methylamine·HCl added). After 96 hrs incubation the surface of the plates was scrubbed with 720 μL of minimal media. An aliquot of 5 μL of the resultant suspension was then transferred to a fresh plate, spread and incubated for 96 hrs. A total of five transfers were completed and at each transfer the ratios of the three species were determined from their CFU concentrations.

This process was emulated in COMETS by randomly distributing 100 boxes in the relevant species ratios each with 3×10⁻⁷ biomass across a 15x15 lattice (individual box width=0.05 cm). The initial ratios based on CFU data were 1:8:92 and 16:1:83 E. coli:S. enterica:M. extorquens. The simulations were carried out for 96 hours at which point the species ratios were calculated. A new lattice was then randomly populated with the initial amount of biomass in the new ratios to mimic the laboratory transfer regime. Three replicate simulations were carried out for each of the treatments.

Highlights.

Microbial community dynamics can be inferred from intracellular metabolism

Metabolic interactions drive synthetic microbial consortia to predictable equilibria

The “metabolic eclipse”: how spatial organization shapes the dynamics of mutualism

Computation of Microbial Ecosystems in Time and Space (COMETS): a flexible tool