Cerebral TOF Angiography at 7T: Impact of B₁⁺ Shimming with a 16-Channel Transceiver Array

Abstract

Purpose

Time-of-flight (TOF) MR imaging is clinically among the most common cerebral non-contrast enhanced MR angiography techniques allowing for high spatial resolution. As shown by several groups TOF contrast significantly improves at ultra-high field (UHF) of B₀=7T, however, spatially varying transmit B₁ (B₁⁺) fields at 7T reduce TOF contrast uniformity, typically resulting in sub-optimal contrast and reduced vessel conspicuity in the brain periphery.

Methods

Using a 16-channel B₁⁺ shimming system we compare different dynamically applied B₁⁺ phase shimming approaches on the RF excitation to improve contrast homogeneity for a (0.5 mm)³ resolution multi-slab TOF acquisition. In addition, B₁⁺ shimming applied on the venous saturation pulse was investigated to improve venous suppression, subcutaneous fat signal reduction and enhanced background suppression originating from MT effect.

Results

B₁⁺ excitation homogeneity was improved by a factor 2.2 to 2.6 on average depending on the shimming approach, compared to a standard CP-like phase setting, leading to improved vessel conspicuity particularly in the periphery. Stronger saturation, higher fat suppression and improved background suppression were observed when dynamically applying B₁⁺ shimming on the venous saturation pulse.

Conclusion

B1⁺ shimming can significantly improve high resolution TOF vascular investigations at UHF, holding strong promise for non contrast-enhanced clinical applications.

Introduction

It has been shown over the last years that non contrast-enhanced (CE) MR angiography (MRA) techniques, including time-of-flight (TOF), can benefit from using MR scanners operating at 7T (1–4). The main sources of gain in angiogram quality at ultra-high field (UHF), i.e. field strengths of 7T and above, include an increase in intrinsic signal-to-noise ratio (SNR) and longer T₁ relaxation constants in brain tissues (5). The latter provides stronger suppression of static spins (dark background), which is at the core of TOF contrast with fresh blood flowing into the excitation slab yielding high intensity signal (bright blood). Consequently, several patient studies have already been conducted, benefiting from the superior TOF contrast at 7T (6–9). However, one of the main challenges associated with UHF relates with higher RF power required to achieve a given flip angle, resulting in higher SAR values (10,11). To reduce SAR at UHF, RF peak power can be reduced by extending RF pulse duration, or by using the VERSE technique (12), to the cost however of increased sensitivity to B₀ inhomogeneity which may distort excitation profiles. Another challenge at UHF derives from shorter RF wavelengths that result in significantly higher spatial heterogeneity in transmit B₁ magnitude (|B₁⁺|), yielding contrast and signal variations (10,13,14) that can be deleterious for clinical applications. When a single channel volume coil is used for RF transmission in the head at UHF, the B₁⁺ pattern typically includes strong magnitude in the center of the brain, and much weaker magnitude in the periphery. Corresponding excitation attenuation may reduce locally angiographic contrast between bright vessel and dark static background, particularly for smaller vessels, thus negatively affecting one of the primary targets expected to benefit from TOF at UHF (2,3). There are several approaches that can be used in order to improve the excitation pattern, among those are B₁⁺ shimming (14–16), parallel transmission (17,18) or the use of dielectric pads (19,20).

In this work we investigate the benefits and limits of using B₁⁺ shimming with a 16-channel transceiver array to reduce the inhomogeneity of the excitation patterns in cerebral multi-slab 3D TOF imaging at 7T, with an emphasis on the impact of the number of B₁⁺ calibration slices. We also evaluate the impact of increasing B₁⁺ efficiency for saturation RF pulses that are used to reduce venous contribution and subcutaneous fat signal.

Methods

B₁⁺ phase shimming: principle

The spatial, complex transmit B₁ field of a K-channel transmit (TX) array for a given driving voltage can be expressed as:

$$B_1^{+}(r)={\sum }_{k=1}^K{B}_{1,k}^{+}(r)={\sum }_{k=1}^K\mid B_{1,k}^{+}(r)\mid ·e^{i({\phi }_k(r)+{\phi }_{0,k})},$$ (1)

where $B_{1,k}^{+}(r)=\mid B_{1,k}^{+}(r)\mid ·e^{i({\phi }_k(r)+{\phi }_{0,k})}$ is the spatially dependent complex field generated by transmit channel k for the given transmitter voltage, r the spatial coordinates, φ_k(r) the spatially varying phase, and φ_0,k a user-defined spatially constant zero-order phase applied to channel k in a given B₁⁺ shim setting (13). In this work, only B_1,k⁺ phases (not magnitude) are modulated (through φ_0,k) for shimming purpose whereas a uniform transmit voltage (driving B_1,k⁺ magnitude) is always applied through all channels; thus Eq. [1] does not include channel-specific magnitude coefficients. The circular polarized (CP) mode commonly realized in a single-channel transmit volume coil can be approximated in a TX array by a set of incremental phases φ_0,k (k=1,2,…K), determined by the azimuthal position of each channel (13). Alternatively, a CP-like mode with similar B₁⁺ distribution (i.e. bright in the brain center and dark in the periphery) can be obtain by different B₁⁺ shimming methods (21,22). A typical approach (15,21,23–25) to improve excitation homogeneity consists in finding a set of φ_0,k phases that minimize the coefficient of variation (CV) of |B⁺₁(r)|, defined as the standard deviation (std) over the mean through a region of interest (ROI):

$${CV}_{B_1^{+}}=\frac{\mathit{std}(\mid B_1^{+}(r)\mid )}{\mathit{mean}(\mid B_1^{+}(r)\mid )}$$ (2)

where r ∈ ROI. A well-known caveat with this approach, however, is that minimizing ${CV}_{B_1^{+}}$ in a large ROI may come at the cost of a significant reduction in B₁⁺ efficiency defined as the ratio of the magnitude of the sum over the sum of the magnitude of B⁺_1,k (13,21,23,26):

$${\eta }_{B_1^{+}}=\frac{\mid {\sum }_{k=1}^K{B}_{1,k}^{+}(r)\mid }{{\sum }_{k=1}^K\mid B_{1,k}^{+}(r)\mid }$$ (3)

where, by definition, $0\le {\eta }_{B_1^{+}}\le 1$. In such case, minimizing ${CV}_{B_1^{+}}$ may require too high RF peak power and/or too high SAR levels. Alternative approaches have been proposed to lower SAR while relaxing constraints on |B₁⁺| homogeneity, such as maximizing the average value of B₁⁺ efficiency through the ROI: $\overline{n_{B_1^{+}}}=\frac{1}{N}{\sum }_{r=1}^N{\eta }_{B_1^{+}}$, with N the number of voxels within the ROI, or computing a compromise where |B₁⁺| homogeneity is relaxed until a maximum distance between the smallest and largest pixel-wise |B₁⁺| values through the ROI is reached (21,26).

With regards to B₁⁺ shimming the study is organized in two steps. First, different B₁⁺ shim solutions were applied to optimize the slab selective RF excitation pulse (yielding angiogram signals), while one CP-like mode B₁⁺ shim setting (described later in the Methods section) was constantly applied to the saturation pulse. Second, different B₁⁺ shim solutions were, instead, used to optimize the slab selective RF saturation pulse (yielding venous saturation in a slab positioned above the imaging slab), while a same CP-like mode B₁⁺ shim setting was constantly applied to the excitation pulse.

Hardware and experimental setting

Eleven healthy subjects, who signed a consent form approved by a local Institutional Review Board, were imaged in supine position on either of two whole body 7T systems (Siemens Magnetom 7T, Erlangen, Germany) using a homebuilt 16 channel transceiver coil, designed similarly as in (27), powered by 16×1kW RF amplifiers (CPC, Hauppauge, NY, USA). Both systems were equipped with a remotely controlled, 16-channel RF phase and gain control unit that allows for dynamically applying different B₁⁺ shim solutions on different RF pulses in a same MR sequence as detailed in (21). The transmitter voltage was calibrated based on 3D flip angle maps acquired before collecting TOF images (see acquisition parameters below).

B₁⁺ mapping

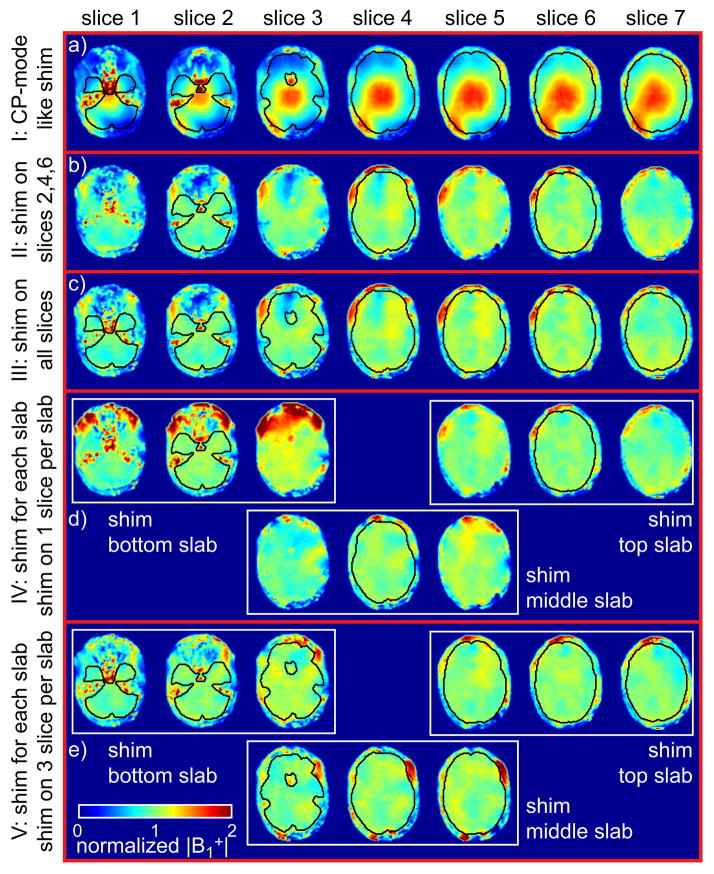
Complex B_1,k⁺ maps for the K=16 transmit channels were obtained with a hybrid B₁⁺ mapping technique as described in (26) which consists in merging one absolute large flip angle |B₁⁺| map measured with all coils transmitting together in a known B₁⁺ shim setting, with 16 complex, relative B_1,k⁺ maps derived from small flip angle, multi-slice gradient echo (GRE) images acquired with only one coil element transmitting at a time. The large flip angle map was measured with the 3D actual flip angle (AFI) technique (28) with TE/TR1/TR2=1.9ms/20ms/120ms, nominal α=60°, resolution=4×4×4.5 mm³. GRE images were collected in 7 equidistant axial slices, 9 mm apart between slice centers, TE/TR = 2.6ms/50ms, α=8°, resolution=2×2×6 mm³. As shown in Fig. 1, the even slices were positioned at the center of three overlapping, 24 mm thick TOF slabs (with 25% overlap), while the odd slices were positioned on the edges of the slab, so that slice #5 belongs to both slabs #2 and #3, while slice #3 belongs to both slabs #1 and #2.

Figure 1.

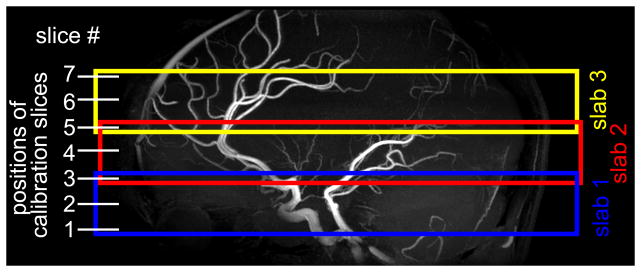
Location of the 3 overlapping TOF slabs, indicated in colored boxes, and corresponding positions of the 7 B₁⁺ calibration slices. 3 slices are located within each TOF slab while slices 3 and 5 are shared by two TOF slabs each.

CP-like mode B₁⁺ shim setting

The baseline B₁⁺ shim setting labeled CP-like mode, used as a comparison reference throughout step I of the study, consisted of either: 1) a set of incremental φ_0,k phases, with a 22.5° increment between neighboring channels aiming at approximating the azimuthal position of the coil elements about the z axis, or 2) a particular B₁⁺ shimming solution, obtained in one subject, maximizing constructive interference between TX channels while constraining the solution to a maximum deviation between min(|B₁⁺|) and max(|B₁⁺|), which consistently provided a typical CP-like |B₁⁺| pattern through subjects. These two pre-determined CP-like modes did not rely on the B₁⁺ calibrations acquired during a particular session. Throughout step II of the study, the CP-like mode was obtained with choosing the B₁⁺ shimming solution providing the best fit between the resulting $\overline{{\eta }_{B_1^{+}}}$ map and a user-defined 2D Gaussian shape (22).

Step 1: B₁⁺ shimming for slab selective excitation RF pulses

In eight subjects, |B₁⁺| homogeneity was optimized by minimizing ${CV}_{B_1^{+}}$, using the Optimization Toolbox in Matlab (The MathWorks, Nattick, MA, USA), comparing 5 different B₁⁺ shim settings (I,II,III,IV,V) described below, while venous saturation RF pulses were always applied in CP-like mode. In order to spatially determine the B₁⁺ shimming targets, 7 ROIs were manually drawn on the 7 calibration slices (see Fig. 2), encompassing parts of the cerebrum, cerebellum and brain stem. As previously mentioned, 3 out of the 7 calibration slices, respectively, were included in each of the three TOF 3D slabs. To reduce the likelihood of approaching a sub-optimal local minimum for ${CV}_{B_1^{+}}$ by the optimization, each minimization was run 100 times using randomly distributed sets of 16 B_1,k⁺ phases (over the range 0 – 2π) as starting phase values for φ_0,k (the same table of 16 × 100 starting random phase sets was used for each B₁⁺ shim computation); Among the 100 optimizations the resulting optimized B₁⁺ phase shim setting with lowest corresponding ${CV}_{B_1^{+}}$ value was finally used.

Figure 2.

|B₁⁺| maps calculated for subject 3 for the different shim settings (I-V), normalized by the mean |B₁⁺| within the ROI of each shim setting.

The first B₁⁺ shim setting out of the 5 settings used for the excitation RF pulse is the CP-like mode as described above which served as a baseline for the comparison:

• Setting I: CP-like mode B₁⁺ shim set applied on all excitation slabs

Then, we compared two B₁⁺ shimming strategies: either a single B₁⁺ shim solution was calculated and applied for the 3 excitation slabs as a whole, or three different B₁⁺ shim solutions were calculated and applied for each TOF slab. Within these two strategies, we also investigated the impact of using a different number of B₁⁺ calibration slices to optimize B₁⁺, resulting in four experimental B₁⁺ shim settings:

Using a single B₁⁺ shim set calculated for all slabs at once

• Setting II: optimization performed using three B₁⁺ calibration slices (#2, #4 and #6) located at the center of each TOF slab

• Setting III: optimization performed using all B₁⁺ calibration slices (from #1 to #7)

Using three B₁⁺ shim sets specifically calculated for each individual TOF slab

• Setting IV: optimization performed using only the B₁⁺ calibration slice positioned at the center of each TOF slab (slice #2 for slab #1, slice #4 for slab #2, slice #6 for slab #3)

• Setting V: optimization performed using, for each TOF slab, the three B₁⁺ calibration slices overlapping the latter (slices #1, #2 and #3 for slab #1, slices #3, #4 and #5 for slab #2, slices #5, #6 and #7 for slab #3).

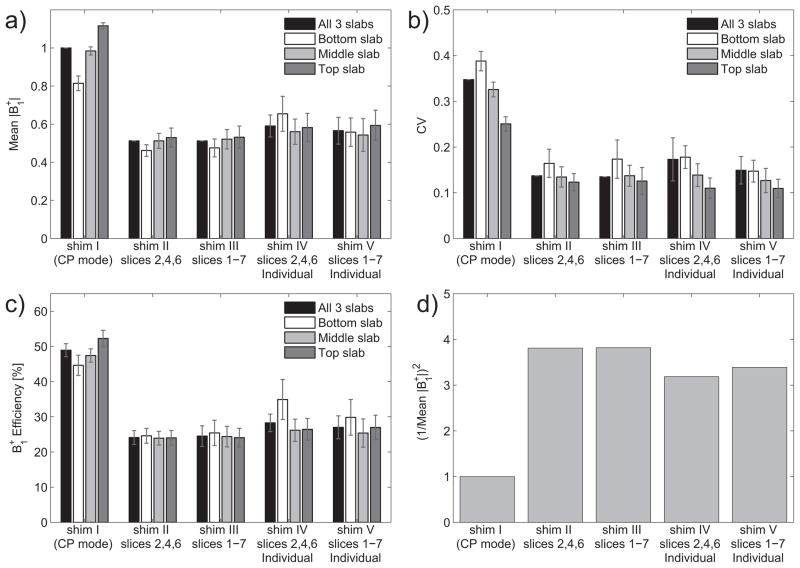
Estimated |B₁⁺| patterns of each subject were normalized by the mean |B₁⁺| value measured in CP-like mode, averaged over all 7 ROIs. Then, for each subject and each of the five B₁⁺ shim settings, the mean value of these normalized |B₁⁺| patterns was calculated: i) over each of the 7 ROIs, ii) over the 3 ROIs covering each TOF slab, and iii) for all 7 ROIs at once. Similar calculations were performed for standard deviation, for ${CV}_{B_1^{+}}$ and for $\overline{{\eta }_{B_1^{+}}}$. Furthermore, in order to estimate the corresponding variations in global SAR, the RF energy required to achieve a given average flip angle with each of the B₁⁺ shim solutions was compared to the corresponding RF energy required in CP-like mode.

Step 2: B₁⁺ shimming for selective saturation RF pulse

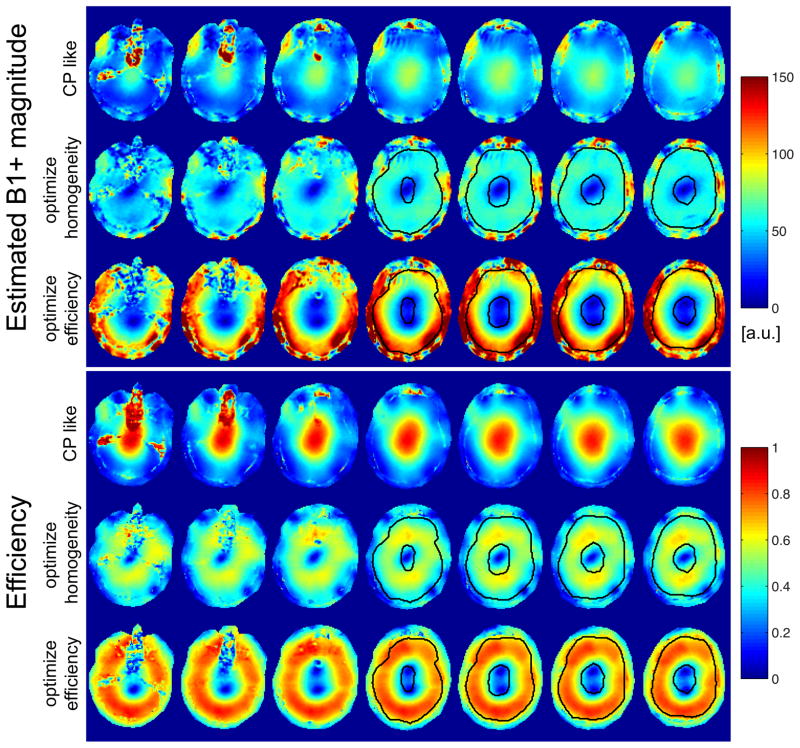
In three subjects, B₁⁺ shimming was specifically optimized for the selective saturation RF pulse, targeting a slab positioned above the TOF imaging slab for the purpose of saturating fresh venous blood flowing downwards and entering the imaging slab. In order to achieve a strong |B₁⁺| in the periphery of the brain, 4 elliptical ring-shaped ROIs were drawn on the 4 uppermost calibration slices, covering the entire brain tissue with the exclusion of a circle drawn at the center of the brain (see. Fig. 6). The rationale for strengthening |B₁⁺| in the periphery is multifold: 1) as the main sources of venous signal contribution originate in the periphery of the axial slabs considered here, including notably the sagittal sinus, their saturation does not require high |B₁⁺| in the center; 2) because of strong sensitivity to chemical shift, the VERSE transformed saturation RF pulses, targeting proton signals above the imaging slab, can also saturate to a certain degree fat signal within the imaging slab (3), which is of high interest for improving TOF MIP reconstruction; here again, with the subcutaneous fat layer contained in the periphery of the axial TOF imaging slabs, no high |B₁⁺| in the center is required for fat saturation; 3) saturation pulses are especially demanding in term of RF energy, thus it is strongly desirable to achieve high $\overline{{\eta }_{B_1^{+}}}$ when applying such pulses; and much higher $\overline{{\eta }_{B_1^{+}}}$ can be achieved in the periphery of the brain with B₁⁺ shimming solutions that ignore, thus allow for a very weak |B₁⁺| in the center (the latter resulting from localized, strongly destructive B_1,k⁺ interferences).

Figure 6.

Estimated B₁⁺ magnitude and corresponding efficiency for the different B₁⁺ shim settings (A–C) applied on the venous saturation RF pulse. All B₁⁺ shim settings were calculated based on ROIs (indicated in black) drawn in the upper 4 slices; the inner ROI indicates a region which was excluded for optimization.

Three different B₁⁺ shim settings for the saturation RF pulses were then compared:

• Setting A: CP-like mode

• Setting B: |B₁⁺| homogeneity maximized (i.e. ${CV}_{B_1^{+}}$ minimized) over the ring shaped saturation ROIs

• Setting C: $\overline{{\eta }_{B_1^{+}}}$ maximized over the ring shaped saturation ROIs

For setting A, the reference voltage was the same as for the previous experiments, preserving a target flip angle of 60° in the Circle of Willis, and determined using the AFI maps. For setting B and C, the voltage for the saturation pulses was recalibrated in order to achieve an average flip angle of 60° within the saturation ring-shaped ROIs.

RF power calibration and TOF acquisition

Prior to each TOF acquisition, the flip angle pattern effectively generated by each B₁⁺ shim setting previously calculated was measured using 3D AFI maps. The reference RF voltage of the console was then set based on the average flip angle value within the ROIs. For those TOF acquisitions where different B₁⁺ phase sets were applied on each TOF excitation slab (setting IV and V), slab-specific voltage attenuation coefficients were applied in order to obtain the same average flip angle in all slabs.

VERSE RF Pulse transformation

In order to reduce SAR, the VERSE algorithm (12) was implemented in the TOF sequence as described in a previous study (3), limiting the maximum RF peak voltage of the excitation pulse and of the saturation pulse, to 50% and 30% of their initial maximum peak voltage, respectively, while preserving same total duration for each RF pulse. Although the VERSE transformation inherently increases the sensitivity of RF pulses to ΔB₀-induced and chemical shift-induced off-resonance, potentially resulting in excitation pattern distortion (3,12), we have previously shown at 7T that, when applied to the saturation RF pulse, this phenomenon can be explicitly exploited to also saturate, in addition to the venous signal within the saturation slab, the subcutaneous fat signal within the imaging (i.e. excitation) slab (3). This explains the more aggressive level of VERSE transformation applied to the saturation pulse (70% of RF voltage reduction) than to the excitation pulse voltage (50% of RF voltage reduction) in order to preserve satisfactory excitation pattern fidelity for the latter. To further reduce SAR, the nominal saturation flip angle was set to 60° in all experiments, still providing substantial saturation, while reducing the corresponding SAR contribution by about ~44% compared with a nominal saturation flip angle of 90°.

TOF acquisition

3D time-of-flight images were acquired with following parameters: 3 slabs of 24 mm thickness, 25% overlap, FOV = 220×172×60 mm³, resolution = 0.49×0.49×0.50 mm³, TR/TE = 25 ms/2.9 ms, flip angle = 20º, GRAPPA=3, 25% slice oversampling, 6/8 slice partial Fourier. In order to investigate potential intensity changes induced by different B₁⁺ shimming solutions at the junction of adjacent TOF slabs, we did not use tilted optimized non-saturating excitation (TONE) pulses (29) and we limited the flip angle to 20° for a TR of 25 ms to reduce saturation effects of arterial blood flowing through the excitation slab.

In all acquisitions, a 40 mm thick travelling venous saturation RF slab was placed cranially with a gap of 13 mm to the excitation slab using a nominal flip angle of 60°. Maximum intensity projection (MIP) maps were generated from the native TOF images over full 3-slabs thickness (axial orientation) and over 40 mm thickness (sagittal and coronal), unless otherwise specified. Beside MIP images, the impact of B₁⁺ shimming on the angiogram quality was further investigated, using the native TOF data sets, in several arterial branches of the Posterior Cerebral Artery (Parieto-occipital Artery and Calcarine Artery), in the insular segment of the Middle Cerebral Artery, and in the Basilar Artery. In each of these locations, one ROI was carefully drawn within the vessel, covering a line segment approximately 1cm long, and one ROI was drawn in the background tissue in the vicinity of the vessel. The artery-to-background contrast was then computed by dividing the average signal of the two ROIs, and the contrast ratio, i.e. contrast variation due to B₁⁺ shimming, was obtained by dividing artery-to-background contrast after/before B₁⁺ shimming.

Results

B₁⁺ optimization for the excitation RF pulse

Figure 2 shows, in one representative subject (S3), the resulting |B₁⁺| maps obtained with the five different B₁⁺ shim settings applied to the excitation RF pulse, normalized by the mean value of |B₁⁺| within the ROIs. Thus, the normalized value of 1 corresponds to the target flip angle of 20° that was used in the TOF acquisition. The corresponding ${CV}_{B_1^{+}}$ values are tabulated in Table 1, together with the average ${CV}_{B_1^{+}}$ values (in brackets) obtained through all subjects.

Table 1.

CV values of measured |B₁⁺| maps for different slices and different B₁⁺ shim strategies for Subject 3. The corresponding values averaged over all 9 subjects are given in brackets. The grey shaded cells indicate for each setting which calibration slices were used for B₁⁺ shimming computation. The CP-like mode was determined by incremental RF phases through channels, without using the measured B₁⁺ maps.

B1 Shim Setting	Nb of Shim computation slabs†	Shim ROI slices	slice 1	slice 2	slice 3	slice 4	slice 5	slice 6	slice 7	average
Setting I: CP-like mode	1	n/a	42.0% (41.7%)	35.9% (37.5%)	38.5% (35.8%)	34.3% (32.5%)	30.6% (28.5%)	26.4% (24.5%)	22.9% (21.1%)	33.4% (32.7%)
Setting II	1	2,4,6	13.7% (17.8%)	9.8% (14.0%)	16.1% (15.2%)	11.9% (13.1%)	9.6% (10.8%)	8.6% (11.1%)	11.1% (14.3%)	12.4% (14.9%)
Setting III	1	1–7	14.4% (19.7%)	10.2% (16.1%)	15.6% (15.3%)	12.0% (13.3%)	9.8% (11.6%)	8.4% (11.5%)	10.1% (13.8%)	12.4% (15.1%)
Setting IV	3	2	10.8% (14.0%)	7.1% (10.7%)	19.0% (19.6%)					13.8% (14.1%)
		4			11.4% (14.6%)	8.6% (11.3%)	10.6% (12.8%)
		6					9.0% (11.5%)	6.7% (9.4%)	10.0% (11.6%)
Setting V	3	1–3	10.9% (15.8%)	8.3% (12.1%)	10.5% (13.8%)					10.0% (12.6%)
		3–5			9.6% (13.3%)	9.0% (11.5%)	10.2% (11.5%)
		5–7					9.6% (11.5%)	7.3% (9.5%)	10.9% (11.1)

^†when a single shim computation slab is used it covers the 3 TOF imaging slab

In setting I, the typical |B₁⁺| pattern observed in CP mode in the human brain at 7T is easily recognized with strong B₁⁺ magnitude in the center of the brain and reduced magnitude in the periphery, with a center-to-periphery ratio up to 5.4. The corresponding ${CV}_{B_1^{+}}$ value within the ROIs through the 7 slices amounts to 33.4%. By comparison, when a single B₁⁺ shimming solution is calculated based on slices #2, #4 and #6 (setting II, Fig. 2b) or on all 7 slices (Setting III, Fig. 2c), the average ${CV}_{B_1^{+}}$ value through all 7 slices dropped to 12.4% in both cases. Similar results were observed through all subjects, as reflected by the group averaged ${CV}_{B_1^{+}}$ values (see Table 1). A noticeable absence of significant difference between the |B₁⁺| patterns obtained with settings II and III, shown for subject S3 in Figs. 2b and 2c, was also observed through all volunteers (data not shown).

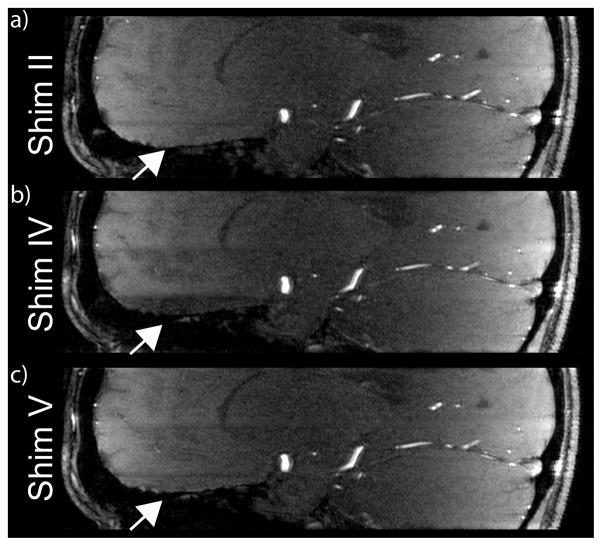
As shown in Fig. 2d with B₁⁺ shim setting IV, by using slab-specific B₁⁺ shimming solutions, each based on one calibration slice, |B₁⁺| homogeneity is further improved at the level of each calibration slice (center of slab) with average ${CV}_{B_1^{+}}$ value dropping down to 7.1%, 8.6% and 6.7% for the bottom, middle and top slabs. However, by using only one calibration slice at the slab center, larger |B₁⁺| heterogeneity can be expected at the top or the bottom of a given slab, which is indeed observed: for example, for subject S3, in slice #3, which is the upper slice of the bottom slab, ${CV}_{B_1^{+}}$ reaches 19.0% (or 19.6% for all subjects) when applying the B₁⁺ shimming solution of the bottom slab (based on slice #2), with a local increase of |B₁⁺| in the frontal lobe (up to 2.2 times greater than |B₁⁺| averaged through the slice) clearly seen in Fig. 2d. This same slice #3, however, is also the bottom slice of the middle slab, and when B₁⁺ shimming is applied on the middle slab, based on calibration slice #4, a lower |B₁⁺| value is now observed in the frontal lobe slice #3 from the bottom slab. A predictable issue with such opposite variations of |B₁⁺| values on the same slice for two overlapping slabs is that different resulting TOF contrast may occur within the junction between two TOF slabs. This is highlighted in Fig. 3 showing coronal views of native TOF images with shim settings II, IV and V, where much stronger background tissue attenuation can be seen in the bottom slab with setting IV (Fig. 3b). It seems reasonable to expect that using 3 calibration slices per slab for B₁⁺ shim calculation could mitigate this issue, and this is indeed demonstrated in Fig. 2e, Table 1 and Fig. 3c, showing that, when using 3 calibration slices per slab (setting V), ${CV}_{B_1^{+}}$ dropped from 19.0% to 10.5% (14.7% for the group average), resulting in improved contrast homogeneity at the slab junction. Even though residual local TOF contrast variations could still be observed at the slab junctions in some volunteers with setting V, these variations were much less pronounced than with B₁⁺ shim setting IV.

Figure 3.

Native sagittal TOF images of subject 3 for B₁⁺ shim settings II, IV and V. A high B₁⁺ magnitude in the frontal brain area for the lowest slab (compare Fig. 2) reduces the static tissue signal for shim IV and introduces a significant intensity change between bottom and middle slab. This was recovered using 3 calibration slices for each TOF slab (setting V) as demonstrated in c). In comparison, a constant shim setting used for all 3 TOF slabs (setting II) avoids intensity variations at the junction of 2 adjacent slabs.

Overall, ${CV}_{B_1^{+}}$ values calculated, for each slab, over the 3 slices, tend to increase when going from the top to the bottom slab, regardless of the shim setting. Interestingly, when using slab-specific B₁⁺ shimming this effect could already be partly reduced by simply adjusting the relative voltage applied on each slab, i.e. multiplying all channel voltages by a same scalar.

As expected, improving |B₁⁺| homogeneity with B₁⁺ shimming always translates in reduced mean |B₁⁺| for a given transmitter voltage (Fig. 4a), due to a lower $\overline{{\eta }_{B_1^{+}}}$ (Fig. 4c) that results in an inverse quadratic increase in RF power (thus in global SAR) for a given average flip angle, of up to 3.8 times for settings II and III when compared to CP-like mode (see Fig. 4d).

Figure 4.

a–c) Quantitative summary of mean |B₁⁺|, CV and efficiency for different B₁⁺ shim settings (I–V), averaged over each of the 3 TOF slabs (white+gray bars) and average over all slabs (black bars) for all subjects. Diagram d) displays the squared inverse of the mean |B1+| of all three slabs relative to the CP mode, a quantity that is proportional to the global SAR for a given flip angle.

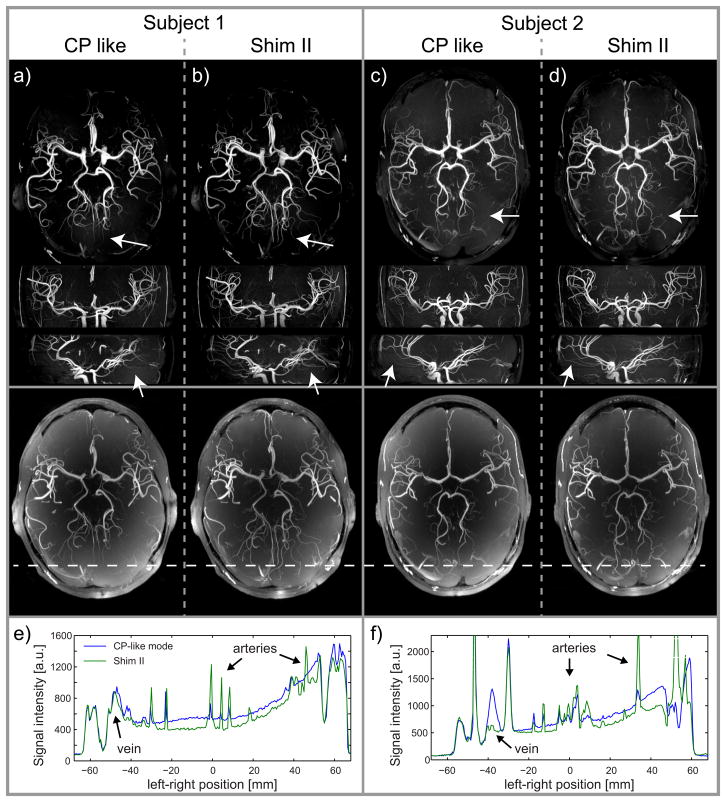
Fairly substantial gains in TOF contrast when using B₁⁺ shimming, however, can be appreciated in Fig. 5, showing MIP images in two subjects with side-to-side comparison between CP-like mode and B₁⁺ shim setting II. In order to better appreciate the nature of TOF contrast improvement, resulting images in Figure 5 are shown both after (upper row with 3-axis MIP views) and before (bottom row with axial MIP views) correction for receive sensitivity profile field bias. Consistent with the spatial pattern of gain in |B₁⁺|, smaller vessel conspicuity increases in the periphery of the brain (see arrows). This is also illustrated in Figures 5e+f, which show horizontal line plots through the MIP images in the bottom row of Fig 5a-d) at the location indicated by the horizontal dashed line. It can be seen on these line plots that, overall, the background signal is reduced whereas signal intensity in the arteries clearly increases after B₁⁺ shimming (green line) compared with CP-like mode (blue line). When further quantifying these changes in native TOF images for the two subjects shown in Fig. 5, for small arteries in the brain periphery (Parieto-occipital Artery, Calcarine Artery, Middle Cerebral Artery) the contrast was found to increase (between +21% and +63%) compared to CP-like mode. This improvement is particularly beneficial for the fairly small PCA branches in which a vessel-to-background contrast as low as 1.2 was measured in CP-like mode. On the other hand, the vessel-to-background contrast in the center of the brain (Basilar Artery) was reduced (between −25 and −38%) with setting II compared with CP-like mode, which is naturally explained by the larger flip angle obtained in the center of the brain in CP-mode. This local contrast reduction with B₁⁺ shimming, however, was not deleterious since a high vessel-to-background signal ratio (>4) was still preserved in the Basilar Artery with setting II.

Figure 5.

50 mm thick axial, coronal and sagittal MIP views obtained from receive profile corrected native TOF images in 2 subjects performed with saturation RF pulses applied in CP-like B1+ shim setting and with (a+c): CP like B1+ shim setting I and (c+d) with B1+ shim setting II used for the excitation RF pulse. Stronger contrast in particular for the smaller vessels can be appreciated when using shim setting II (see arrows). The last row in (a–d) shows thinner (30 mm) axial MIP images of the same datasets but without correction of the receive profile. The diagrams in (e+f) show line plots through the MIP images at the location indicated by the white horizontal dashed line.

B₁⁺ optimization for saturation RF pulse

Drastically different |B₁⁺| patterns were achieved with B₁⁺ shimming for saturation pulse, computed within elliptical ring shaped ROIs on the 4 top slices, as seen in Fig. 6 showing, in one subject, |B₁⁺| (top) and $\overline{{\eta }_{B_1^{+}}}$ (bottom) maps obtained with settings A, B and C, assuming constant RF input voltage.

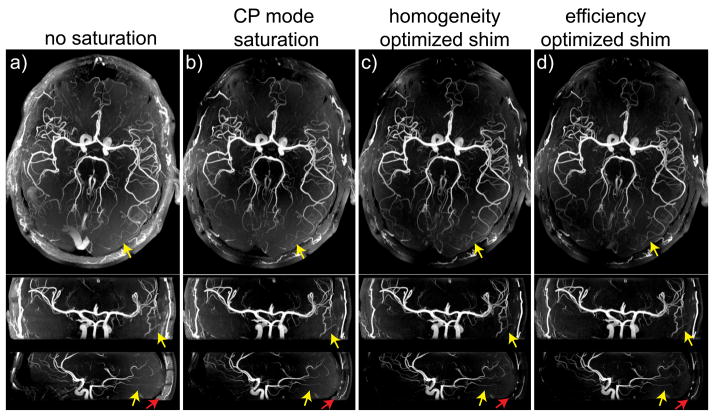
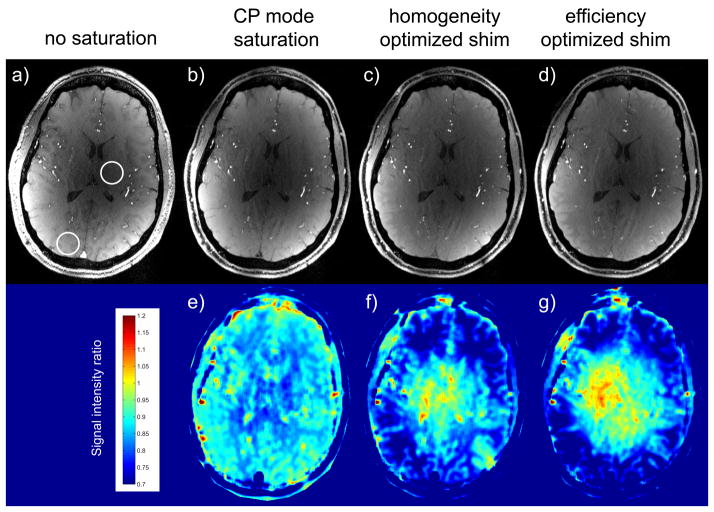
Averaged over three subjects, $\overline{{\eta }_{B_1^{+}}}$ over the 4 ROIs increases from 40.5% in setting A (CP-like mode) to 56.8% in setting B (maximizing |B₁⁺| homogeneity) and to 65.8% in setting C (maximizing $\overline{{\eta }_{B_1^{+}}}$), with the estimated average flip angle multiplied by a factor of 1.45 in setting B and of 1.78 in setting C when compared with setting A. As can be seen in Fig. 7, showing, in one representative subject, 3-axis MIP views of TOF data sets obtained without (Fig. 7a) and with saturation pulse using B₁⁺ shim settings A, B and C (Figs. 7b–d), venous and subcutaneous fat signals are clearly reduced in the presence of saturation pulses, with stronger signal suppression for settings B and C especially visible on fat signal suppression (red arrows). In order to investigate the impact of B₁⁺ shimming on the MT effect associated with saturation pulses, we measured the reduction in background signal averaged over circular ROIs. In an ROI positioned close to the center of the brain but excluding ventricle areas (see Fig. 8a), and compared with the absence of a saturation pulse, the background signal was reduced by 17%, 10% and 6% when applying settings A, B and C on the saturation pulse, respectively. The opposite trend was observed within an ROI positioned in the periphery (see Fig. 8a), with corresponding background signal reduction of 15%, 32% and 35%. The spatial patterns of these variations are easier to identify in Figs. 7e–g, showing the corresponding images normalized by Fig. 8a. Note in Fig. 7 improved vessel conspicuity in the periphery in those locations where a stronger background signal reduction was achieved with B₁⁺ shimming on saturation pulses.

Figure 7.

Axial, coronal and sagittal MIP images of TOF acquisitions with CP-like shim used for excitation and a) without venous saturation applied (a), and with saturation applied using B₁⁺ shim setting A (b), setting B (c) and setting C (d). Red arrows signal suppression of subcutaneous fat signal. Yellow arrows indicate area with background signal reduction through MT.

Figure 8.

Top row: native TOF images acquired with a CP-like shim setting. a) no saturation was applied, b–c) B₁⁺ shim settings A–C were applied for the saturation pulse. Bottom row: signal intensity ratio images of images b–c) normalized by image a).

Discussion

Higher SNR and longer T₁ relaxation constants in brain tissues at ultra-high magnetic field are particularly beneficial for TOF angiography, resulting in excellent vessel-to-background contrast, as demonstrated by several groups (1–4,30,31). However, to the best of the authors’ knowledge, only single TX channel volume coils or multi-channel TX coils operating in a fixed CP-like mode have been used so far in TOF studies at UHF, with a corresponding |B₁⁺| distribution, higher in the center of the brain and lower in the periphery, that preserves strong angiographic contrast in the center, but potentially results in a significant reduction of contrast in the periphery. (Throughout the study, this so-called CP-like mode pattern is used as a starting point reference to evaluate potential gains with B₁⁺ shimming).

B₁⁺ shimming, where only a channel-specific constant RF phase (or phase and magnitude) term is applied on a given RF TX channel for the entire duration of a pulse, is a relatively inexpensive technique, potentially accessible by retrofitting MR scanners, yet capable of providing highly significant improvement in |B₁⁺| distribution; as such, B₁⁺ shimming is already utilized in a variety of biomedical research projects and in multiple anatomical targets, a few examples of which can be found in (21,23,26,32–35). By comparison, full range pTX techniques (17,18), where different RF pulse shapes are plaid on different TX channels, rely on fairly expansive hardware, require more sophisticated methods (especially for large flip angles), and, until now, have been used in demonstration of principle studies (36–39) rather than in actual applications, with, as of today, only a few MR centers capable of running full pTX protocols in-vivo. Even though such full range pTX methods, including for TOF (40), are expected to further benefit from their additional degrees of freedom, this context provides solid rationale to this study, aiming at evaluating the benefit of B₁⁺ shimming to mitigate deleterious consequences of |B₁⁺| inhomogeneity in TOF imaging at 7T. The current study focused on phase-only RF modulation, a widely used version of B₁⁺ shimming techniques, which also is the least demanding one hardware-wise.

In the first part of the study, aiming at a more homogeneous excitation flip angle through the three overlapping TOF imaging slabs, B₁⁺ strategies were compared at two levels: firstly, either a unique B₁⁺ shim solution (over the three slabs) or three different, slab-specific solutions were applied, and, secondly, different number of B₁⁺ calibration slices were used for B₁⁺ shimming computation. Importantly, the first and very clear result consistently observed through all subjects is a significant improvement of the overall |B₁⁺| homogeneity, when using any of the proposed B₁⁺ shimming approaches, by comparison to a CP-like mode, translating in more homogeneous TOF contrast and better vessel conspicuity, with reduced disparity between brain center and periphery. Comparing single B₁⁺ shim solutions (settings II and III) with multiple slab-specific solutions (settings IV and V) indicates that additional gains are obtained with the slab-specific solutions, as CV_B1 values were further reduced. Choosing a different number of B₁⁺ calibration slices for B₁⁺ shimming calculation plaid a significant role only when using multiple slab-specific solutions. Indeed, when applying a single B₁⁺ solution (settings II and III), using either 3 or 7 calibration slices for calculation did not result in significant difference between corresponding |B₁⁺| patterns. However, with slab-specific B₁⁺ solutions (settings IV and V), using only the slice at each slab center for B₁⁺ shim computation could result, for some given location at the junction between two slabs, in substantial variations of |B₁⁺| between the two corresponding B₁⁺ shim solutions; this in turn can yield improper TOF MIP reconstruction. These observations suggest that the best results may be obtained by dynamically applying slab-specific B₁⁺ shimming solutions that use all three calibration slices in each slab to calculate each slab solution. The fact that applying a global relative voltage factor (through all channels) for each of the three slab, already improves |B₁⁺| homogeneity through all slices, could be interpreted as a consequence of the generic distribution of |B₁⁺| along z-axis in microstrip elements; investigating these profiles, however, is beyond the scope of the present study. It will also be interesting in further developments to evaluate the impact on TOF imaging at UHF of using both phase and magnitude B₁⁺ shimming, instead of phase-only B₁⁺ shimming.

A well-known issue when reducing CV_B1 over large size ROIs with B₁⁺ shimming is a corresponding reduction in B₁⁺ efficiency, which, as expected, was observed for the excitation pulses with all B₁⁺ shimming settings compared with the CP-like mode. This can rapidly become a limiting factor because of a concomitant increase in the required RF power for a given average flip angle (up to a factor of 4 in our results). Thus, although this technique is in general not limited to gradient echo sequences or to small flip angle RF pulses and can be applied to spin echo sequences with (multiple) refocusing RF pulses, as demonstrated with localized B₁⁺ shim optimization in spin echo fMRI (41), the corresponding increase in SAR may however limit such applications to only a few slices when a uniform |B₁⁺| is required over a large region of the brain. Several SAR reduction techniques, however, can be used to address this limitation and, in the current study, we implemented the VERSE approach for this purpose, as previously demonstrated in TOF acquisitions at 7T (3). As a result, to achieve an excitation flip angle of 20°, the peak B₁⁺ magnitude was reduced from 7.2 μT with the original RF pulse to 3.6 μT with the VERSE transformed RF excitation pulse.

In the second part of the study, B₁⁺ shimming was only applied to the saturation RF pulse, taking advantage, in order to achieve higher $\overline{{\eta }_{B_1^{+}}}$, of using ROIs that exclude the brain center. Here, two different algorithms were compared to the CP-like mode setting, aiming at either minimizing CV_B1 (setting B), or maximizing $\overline{{\eta }_{B_1^{+}}}$ (setting C), through ROIs drawn on the 4 uppermost calibration slices. The noticeable gains in $\overline{{\eta }_{B_1^{+}}}$, readily obtained by simply excluding a circle form the center of the ROI used for B₁⁺ shimming computation, resulted in average flip angle values multiplied by 1.45 and 1.78, in settings B and C, respectively. Such gains have significant consequences as they substantially reduce the RF energy required to suppress venous and fat signals with RF saturation pulses (as shown in Fig. 7), the latter being often excluded from TOF protocols at 7T because of SAR limits. Note that an additional SAR mitigation measure, applied for all saturation pulses in this study, consists in using a nominal saturation flip angle of 60° instead of 90°, thereby reducing RF energy by more than 50%, while preserving the bulk part of spin saturation. In addition, the peak |B₁⁺| values for a target flip angle of 60° were reduced from 9.1 μT to 2.7 μT by using the VERSE transformation. Being able to include saturation pulses also provide improved vessel-to-background contrast resulting from the MT component of these pulses. When applying different B₁⁺ shim settings to the saturation pulse, the spatial patterns of background signal reduction (Fig. 8) were consistent with the |B₁⁺| maps of the corresponding shim settings. This, we hypothesized, was a direct expression of the MT component of the saturation pulse, which depends on the corresponding spatial distribution of |B₁⁺|, helping further to increase vessel-to-background contrast (contrary to background signal, bright signal from fresh arterial spins entering the slab are not affected by the saturation pulses) and vessel conspicuity in the periphery of the brain as illustrated in Fig. 7. It is interesting to note that with a nominal flip angle of 60° for the saturation pulse, improvement in vessel conspicuity mediated through MT was still preserved.

Conclusion

B₁⁺ shimming solutions dynamically applied in TOF angiography at 7T successfully reduce angiographic contrast heterogeneity resulting from |B₁⁺| heterogeneity, and help improving venous and fat saturation, as well as MT-based background signal attenuation relying on saturation RF pulses, while limiting corresponding required RF energy. The resulting improvements in vessel conspicuity hold strong promises for future high resolution vascular investigations at UHF, including non contrast-enhanced clinical applications.