Experimental Validation of Displacement Underestimation in ARFI Ultrasound

Abstract

Acoustic radiation force impulse (ARFI) imaging is an elastography technique that uses ultrasonic pulses to both displace and track tissue motion. Previous modeling studies have shown that ARFI displacements are susceptible to underestimation due to lateral and elevational shearing that occurs within the tracking resolution cell. In this study, optical tracking was utilized to experimentally measure the displacement underestimation achieved by acoustic tracking using a clinical ultrasound system. Three optically translucent phantoms of varying stiffness were created, embedded with sub-wavelength diameter microspheres, and ARFI excitation pulses with F/1.5 or F/3 lateral focal configurations were transmitted from a standard linear array to induce phantom motion. Displacements were tracked using confocal optical and acoustic methods. As predicted by earlier FEM studies, significant acoustic displacement underestimation was observed for both excitation focal configurations; the maximum underestimation error was 35% of the optically measured displacement for the F/1.5 excitation pulse in the softest phantom. Using higher F/#, less tightly focused beams in the lateral dimension improved accuracy of displacements by approximately 10 percentage points. This work experimentally demonstrates limitations of ARFI implemented on a clinical scanner using a standard linear array and sets up a framework for future displacement tracking validation studies.

I. Introduction

Acoustic radiation force impulse (ARFI) ultrasound is a non-invasive imaging technique that is used to investigate the mechanical properties of internal tissues.¹ Fundamentally, ARFI works by employing a long duration ultrasonic pulse that, through transfer of momentum, generates a force in the propagating medium. This force displaces the underlying tissue in a highly localized manner serving as a precise, virtualized form of palpation.

The physics behind acoustic radiation force (ARF) have been extensively studied, and in an absorbing media, under simplified plane wave assumptions, the force has been shown to be proportional to the intensity of the acoustic pulse as follows:

$$F=\frac{2\alpha I}{c}$$ (1)

where α is the absorption coefficient of the medium, I is the temporal-average beam intensity, and c is the speed of the sound through the medium.^{2, 3} When applied impulsively, this force creates a μm-order, uniaxial deformation in the direction of wave propagation that can be tracked using various ultrasound-based time delay estimators (TDEs).⁴ In practice, the same transducer can be used to generate both the ARF pulse and the tracking pulses. This ensures that the tracking pulses are co-located with the induced motion, thereby increasing the accuracy of displacement estimation by largely eliminating decorrelation from off-axis motion. Decorrelation has been shown to be a key source of variance in ultrasound-based motion tracking as predicted by the Cramér-Rao lower bound.⁵

Using the same transducer for both pushing and tracking is elegant in design, but not without side effect. Namely, the displacement estimates are susceptible to another form of decorrelation called shearing artifact. Shearing artifact is the result of non-uniform, on-axis scatterer displacement within the tracking point spread function (PSF) that is caused by the gradient of force induced by the pushing pulse. Because some scatterers are not moving as far as others under the tracking PSF, averaging occurs and the final displacement estimates do not depict the full extent of tissue motion. An analytic expression for the magnitude of this type of decorrelation was derived by McAleavey et al.⁶, which mitigated this effect by modifying the focal configuration, or F/# (defined as the ratio of aperture width, z, to focal depth, d), of the pushing and tracking pulses appropriately. It was concluded that a broad defocused pushing pulse combined with a narrow focused tracking pulse will yield both the highest correlations and the highest ARFI displacement estimates. Furthermore, it was predicted that in a common imaging scenario (1D linear array) where control over F/# can only be exerted in the lateral dimension, ARFI displacement could, at most, be only $1∕\sqrt{2}$ of the true peak displacement.

A number of studies have since been published that have investigated the impact of shearing decorrelation using finite element method (FEM) modeling.^{7, 8} In Palmeri et al.⁷, ultrasonic tracking of an ARFI induced deformation with a 1D linear array was simulated in homogenous media with various elastic constants. It was shown that underestimation due to shearing was not constant over time (i.e. underestimation was worst in the early time points, as low as ~50% of the true induced motion) and the accuracy of estimation improved more rapidly with stiffer material. The reason ARFI displacement estimation improves over time is that shear waves radiate out from the region of excitation (ROE) and the distortive shear wave front is no longer within the tracking PSF. The stiffer the material, the faster the shear waves are able to traverse the resolution cell, and the accuracy of the estimation is improved at a correspondingly higher rate. In Dhanaliwala et al.⁸, an expression for signal-to-noise ratio (SNR) in an ARFI image was derived by extending the original McAleavey derivation for shearing decorrelation, and FEM experiments were performed with a 1.5D linear array. The authors show that using a smaller elevational aperture for the pushing pulse results in ARFI images with higher SNR due to the improvements in the shearing decorrelation.

While shearing artifact has been comprehensively studied in the literature with FEM, there is a notable lack of experimental measurements of the phenomenon. To our knowledge, the only published data in this regard is from McAleavey et al.⁶ in which the TDE correlation values taken in a single phantom were shown to change as a function of the ratio of pushing to tracking elements. The fact that experimental measurements are sparse is not entirely surprising due to the inherent complexity of developing an apparatus that can truly measure ARF-induced dynamics; displacements are usually very small (μm-order), the motion fast (msec-order recovery times), and ROEs located deep (cm-order) within tissue. A number of groups have approached this problem using optically-based techniques^9–12, the most recent of which includes tracking ARF-induced motion with a high-speed camera.^{13, 14} In Bouchard et al.¹³, two opposing piston transducers (one to push and one to track) were confocally aligned on a metal wire embedded near the surface of a phantom, and the motion induced by the pushing piston was then simultaneously tracked with a high-speed camera. These methods were further refined by Bouchard et al.¹⁴, where instead of a metallic marker, small sub-wavelength size (10 μm diameter) polystyrene beads were embedded in a translucent phantom to provide a more realistic ARFI imaging scenario. ARFI displacements, again induced by a single element piston transducer, were motion tracked optically to investigate the dynamics of an ARFI excitation at depth within a phantom but were not simultaneously tracked acoustically as done previously.

In the following work, the high-speed camera framework proposed by Bouchard et al. is extended and utilized to experimentally validate ARFI displacement estimates taken with a clinical imaging system. A conventional linear array transducer is confocally aligned with a high-speed camera to simultaneously capture ARFI displacements measured acoustically and optically in translucent phantoms. The acoustically tracked displacements are then validated using the optical gold standard to experimentally measure the displacement underestimation previously demonstrated with FEM simulations. In addition, experiments are performed on phantoms with varying material stiffness using different excitation focal configurations to investigate the impact of these parameters on acoustic displacement tracking.

II. Methods

A. Optical Phantom Construction

Three custom, translucent, gelatin-based, tissue-mimicking phantoms were constructed adapting the formulation of Bouchard et al.¹⁴ The phantom recipes consisted of the following ingredients: type-A gelatin (Acros Organics, Geel, Belgium), agar (Fisher Scientific, Fair Lawn, NJ, USA), black polystyrene microspheres (10-μm, Polysciences Inc., Warrington, PA, USA), n-propanol, and de-ionized water (concentrations are given in Table 1). The agar powder was added to each phantom for acoustic scattering while the polystyrene beads served as markers for optical tracking. The diameter of the agar particles was not published by the manufacturer and was measured experimentally with an Accusizer 780A (Particle Sizing Systems, Santa Barbara, CA, USA) system to be 28.4 ± 33.5 μm. The estimated concentration for the polystyrene bead suspension given by the manufacturer was 4.55 × 10⁷ particles/mL.

Table 1.

Recipes and material parameters for the phantoms investigated in this study. Young's modulus values were measured using shear wave velocimetry. Values for speed of sound, attenuation, and Young's modulus are reported as mean ± one standard deviation.

Ingredient	Phantom 1	Phantom 2	Phantom 3
Type-A gelatin (g)	12.9	22	34
n-propanol (mL)	10	10	10
Water (mL)	190	190	190
Agar (g)	1	1	1
Polystyrene microspheres (drops)	10	10	10

Parameter	Phantom 1	Phantom 2	Phantom 3
Speed of sound (m/s)	1521.9 ± 0.26	1533.7 ± 0.44	1555.9 ± 0.32
Attenuation (dB/cm @ 3.5 MHz)	0.25 ± 0.05	0.51 ± 0.05	0.44 ± 0.04
Young's Modulus (kPa)	6.6 ± 0.49	19.8 ± 0.93	30.2 ± 1.48
Speckle SNR	1.89± 0.11	1.82 ± 0.08	1.84 ± 0.07

To evaluate the scattering of the two different particles (agar versus polystyrene), the estimated differential scattering cross-section (σd) was computed for each using the following formula¹⁵:

$${\sigma }_d\left(\theta \right)=\left(\frac{{\left(\frac{\omega }{c_0}\right)}^4{a}^6}{9}\right){\left(\frac{\left(\frac{1}{{\rho }_v{c}_v^2}-\frac{1}{{\rho }_o{c}_o^2}\right)}{\frac{1}{{\rho }_o{c}_o^2}}+\frac{3({\rho }_v-{\rho }_o)}{2{\rho }_v+{\rho }_o}\cos \theta \right)}^2$$ (2)

where ω is the angular acoustic center frequency, a is the radius of the scatterer, c_o and c_v are the speeds of sound in the background and scatterer respectively, ρ_o and ρ_v are the densities of the background and scatterer respectively, and θ is the angle of the scatterer with respect to the center of the transducer (assumed to be 180°). The density (ρ_v) and speed of sound (c_v) values for agar and polystyrene were assumed to be 1.04 g/cm³ and 1500 m/s, and 1.05 g/cm³ and 2350 m/s, respectively. The values for ρ_o and c_o were assumed to be 0.98 g/cm³ and 1540 m/s respectively for the gelatin background. Using these parameters, the differential scattering cross-section was estimated to be higher for the agar (2.98 × 10⁻⁹ cm² sr⁻¹) compared to the polystyrene (8.39 × 10⁻¹³ cm² sr⁻¹). The backscatter coefficient (η_BS) was also calculated with the following equation:

$${\eta }_{BS}=n{\sigma }_d$$ (3)

where n is the number density of the scatterers. The number density of agar was measured by the Accusizer to be 3.50 × 10⁵ particles/mL, while the number density of polystyrene beads was estimated to be 1.14 × 10⁵ particles/mL based on the manufacturer's reported concentration. Therefore, the backscatter coefficient was calculated as 1.04 × 10⁻³ cm⁻¹ sr⁻¹ for agar, and 9.54 × 10⁻⁸ cm⁻¹ sr⁻¹ for polystyrene.

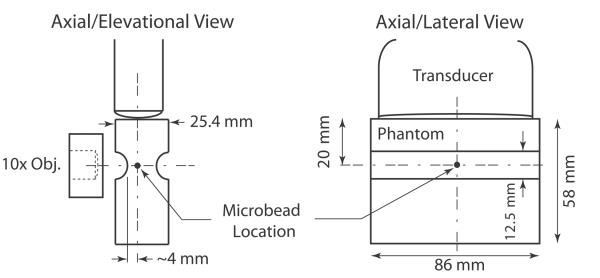
Three phantoms were heated to 40°C and congealed in a rectangular acrylic cast (inner dimensions: 86 × 86 × 25.4 mm); their elasticity was varied by adjusting the amount of gelatin powder. A cylindrical acrylic piece with a diameter of 12.5 mm was cut in half and glued to the top and bottom of the acrylic cast to create a groove in each phantom that improved light transmission and ensured uniform sound transmission elevationally. Approximately 28 mm of phantom was cut with a wire in order to situate the groove ~20 mm (the desired axial focal depth) from one edge of the phantom. Figure 1 depicts the phantom design, showing close-up schematics of the phantom, transducer, and microscope objective.

Figure 1.

Schematics of phantom design and confocal alignment of optical and acoustic foci showing the axial/elevational view and the axial/lateral view. Although only one microbead is shown in these schematics, many microbeads (~2.28 × 10⁷ beads) were dispersed throughout the whole volume of the phantom.

B. Experimental Setup

The general experimental setup is shown in Figures 2(a) and (b). Ultrasonic imaging was performed with a Siemens Acuson Antares™ imaging system (Siemens Medical Solutions USA, Ultrasound Division), equipped with the Axius Direct Ultrasound Research Interface (URI) that allowed customizable beam sequencing and access to the raw radiofrequency (RF) data, and a VF7-3 linear array transducer. The transducer was secured in a holder connected to a digital three-axis motion controller mounted on an optical air table (Newport Corp., Irvine, CA, USA). A custom acrylic water tank was constructed and mounted on an Olympus IX71 microscope (Olympus America Inc., Melville, NY, USA) fitted with a 10× objective and opposing, coaxial, 100-W halogen illumination source (U-LH100L-3, Olympus America Inc., Melville, NY, USA). A Fastcam SA1 high-speed camera (Photron USA Inc., San Diego, CA, USA) was coupled to the microscope for digital frame capture.

Figure 2.

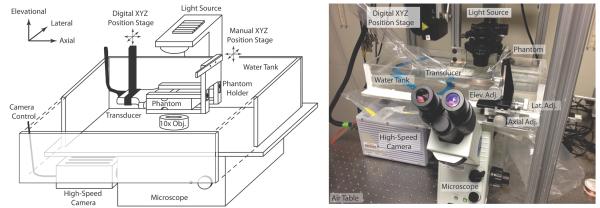
Schematic of experimental set up is shown in (a) with a photograph of the actual set up in (b).

Alignment of the optical and acoustic foci was achieved following methods similar to Bouchard et al.¹⁴ First, an Onda HNC-0400 needle hydrophone (Onda Corp., Sunnyvale, CA, USA) was mounted on a manual micro-positioning stage, and the tip was aligned to the optical focus of the microscope. Next, the needle hydrophone was connected to a Signatec PDA14A analog-to-digital (A/D) convertor (Signatec Inc., Newport Beach, CA, USA), and, using a custom program developed in LabVIEW (National Instruments, Austin, TX, USA), the transducer was swept across the hydrophone in the lateral/elevational dimensions while transmitting a single A-line to generate a 2D map of the acoustic point spread function (PSF). Using the 2D PSF map as a guide, the transducer was then positioned such that the peak amplitude was centered on the hydrophone. This process of mapping the PSF and positioning the transducer was repeated iteratively with smaller ranges and finer step resolutions to achieve precise lateral/elevational alignment of the transducer.

Due to the difference in the speed of sound (SOS) in water and the phantoms, axial alignment was not performed by measuring acoustic intensity with the hydrophone, but rather by positioning the transducer a known distance away from the optical focus (in this case, 20 mm). This positioning was achieved ultrasonically, using the pulse-echo RF data of a single A-line captured by the ultrasound scanner; the tip of the needle hydrophone (i.e. the optical focus) served as a strong reflector, and the transducer was positioned accordingly after measuring the SOS in water.

With the acoustic and optical foci aligned, the needle hydrophone was removed and replaced with a phantom held in an acrylic holder. At the back of the holder, a piece of strong attenuating rubber was placed to minimize sound reflections. Finally, the phantom was translated laterally and elevationally, using the manual positioning stage, until a polystyrene bead was centered in the microscope's FOV, after which data collection began.

C. Data Collection

ARFI ensembles consisted of two reference pulses, one acoustic radiation force (ARF) excitation pulse, and 500 tracking lines with an 11 kHz pulse repetition frequency (PRF). ARFI excitations were 300 cycles at 4.21 MHz, and both tracking and reference lines were two cycles at 6.15 MHz. Two different focal configurations (F/#) were used for the excitation pulse (F/1.5 or F/3), while the reference/tracking pulses always used an F/1.5 configuration on transmit and dynamic focusing and aperture growth (F/0.75) on receive. The focus in elevation, set by a cylindrical lens, was 3.8 cm. For each acquisition, a single ensemble was captured, spatially corresponding to the line that was used when mapping the PSF. Prior to each ARFI ensemble, a matched B-mode was also acquired (220 RF lines spaced 0.18 mm apart).

The high-speed camera was configured to acquire frames at a 150 kHz frame rate, across a 128 × 128 pixel FOV. To synchronize the ultrasound system and the camera, the electrocardiogram (ECG) triggering features on the Antares were utilized. An ECG simulator was connected via a standard three wire ECG cable to the Antares ECG input port, and the camera's “trigger in” port was connected to the Antares' auxiliary ECG output port. When the ECG simulator was switched on, the Antares simultaneously triggered ARFI acquisition and output a trigger pulse that synchronized the camera. In this manner, optical and acoustic data was captured for 10 different beads in each phantom, with 3 matched acquisitions per bead for a total of 180 data sets (3 phantoms × 2 F/#'s × 10 beads × 3 repeated acquisitions).

In order to control for displacement magnitude decorrelation, the output power of the Antares was empirically calibrated such that the maximum displacement magnitude was normalized across all phantom stiffnesses and focal configurations. Starting with the stiffest phantom and F/3 pushing pulse, the scanner was arbitrarily set to a high output power (90%), and the displacement of the bead was tracked optically, yielding a peak displacement of ~18 μm (see “Data Processing” for description of optical tracking methods). The output power for all other phantoms and focal configurations was then scaled down appropriately by iteratively searching for a setting that resulted in an optically tracked peak displacement matching ~18 μm. Table 2 shows the empirically determined power settings used for every phantom and focal configuration combination.

Table 2.

Empirically determined power settings for the Antares for each phantom and pushing pulse focal configuration (F/#) to yield the equivalent displacement.

	Output Power Setting
F/#	Phantom 1	Phantom 2	Phantom 3
F/1.5	28.3%	38.0%	47.0%
F/3	43.6%	70.0%	90.0%

Elasticity of each phantom was measured using ultrasonically based shear wave velocimetry.^{16, 17} The beam sequence used to perform these measurements consisted of 40 ARFI ensembles (300 cycle, F/1.5 pushing pulse) spaced 0.53 mm apart laterally with a stationary region of excitation (ROE) positioned at the center of the lateral FOV. Shear wave group velocity was computed from this data using lateral time to peak (TTP) methods, and subsequently related to Young's modulus following previously derived equations.¹⁷

D. Data Processing

Acoustic motion tracking was performed by one-dimensional normalized cross correlation (kernel length = 4.5λ ≈ 1.1 mm, where λ is the wavelength of the tracking pulses) applied to the raw RF data. As demonstrated by Palmeri et al.⁷, a kernel size of up to 5λ reduces noise from jitter without significantly changing mean displacement estimates, which was desirable for this study due to the relatively small sample size of beads per phantom. Optical motion tracking was performed by two-dimensional normalized cross correlation. Two-stage interpolation was used in both the acoustic and optical data to track sub-sample displacements; the first stage included upsampling the raw RF data (or raw grayscale pixel data) by a factor of 4 with spline interpolation, while the second included fitting a parabola to the maximum of the correlation function in the case of the acoustic data, and upsampling the correlation curve by a factor of 4 in the optical case.^{4, 14} Finally, acoustically tracked displacements were scaled by the measured SOSs in the phantoms (see “Speed of Sound and Attenuation Measurements” for SOS measurement methods) to convert time delays to distance measurements.

To validate acoustic displacement measurements and compute displacement underestimation a number of steps were performed to align the acoustic and optical data. First, to reduce experimental noise, the median displacement curve was computed from the three matched acquisitions taken from each bead (this was done for the three acoustic acquisitions as well as the three optical acquisitions). Next, a time correction factor was computed for the optical data to correct for a small delay that occurred between the trigger and the start of the ARFI acquisition (the delay was caused by dummy frames that had to be added to the beam sequence to allow proper ECG synchronization). This was done by identifying the frame in which the camera first saw motion (axial displacement ≥ 1 μm), and setting the time of this frame equal to the time of ARF pulse plus the time-of-flight (TOF) to the bead. The time correction (Δt) was calculated using the following equation:

$$\Delta t=\frac{i_0}{\mathit{FPS}}-(t_{\mathit{ARF}}+t_{\mathit{TOF}})$$ (4)

$$t_{\mathit{TOF}}=\frac{z}{c_p}$$ (5)

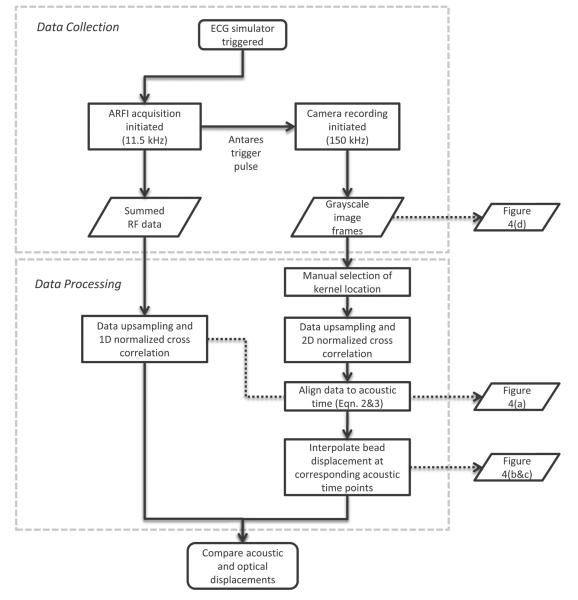
where i₀ is the index of the camera frame where motion is first observed, FPS is the frame rate of the camera acquisition, t_ARF is the time the ARF pulse is fired and t_TOF is the time of flight of the ARF pulse to the microbead (defined as the distance to the bead from the transducer, z, divided by the measured SOS in the phantom, c_p). With the optical and acoustic data aligned in time, linear interpolation was used on the optical displacement curves to get the true displacement at each acoustic time point. This interpolation was necessary because the PRF of the ultrasonic scanner was not an integer multiple of the camera framerate, and therefore the clocks were not synchronized perfectly sample for sample. Finally, with the optical and acoustic data aligned, two-sample Wilcoxon rank sum tests (α = 0.01) were performed at each time step to test for statistical difference between the optical and acoustic displacement measurement. A flow chart of the data collection and data processing steps is given in Figure 3.

Figure 3.

Flow chart describing data collection and data processing steps.

To ensure the phantoms exhibited fully developed speckle, speckle signal-to-noise ratio (SNR) was computed over a 4 × 4 mm region of interest (ROI) centered at the location of each bead on the envelope detected B-mode data (calculated as the absolute value of the Hilbert transformed RF data). The measured speckle SNR values are reported in Table 1.

E. Speed of Sound and Attenuation Measurements

The SOS for each phantom was measured with a 0.5” (1.27 cm) diameter element, 2” (5.08 cm) spherically focused Panametrics-NDT 3.5 MHz piston transducer (Olympus, Waltham, MA, USA) in a custom-built water tank. First, an aluminum plate reflector was positioned approximately 5 cm from the transducer face. Using a Panametrics-NDT Pulser/Receiver (Olympus, Waltham, MA, USA) in pulse-echo mode (negative impulse), two different A-lines were obtained at precisely 10 mm apart using a Newport motion-stage with micron resolution (Newport Corp., Irvine, CA, USA). The SOS in water, c_w, was calculated using the following equation:

$$c_w=\frac{2\left(\Delta d\right)}{\mid t_1-t_2\mid }$$ (6)

where Δd is the distance the transducer was moved between A-lines, t₁ is the time of peak negative pressure of the first A-line and t₂ is the time of peak negative pressure of the second A-line. The measured SOS (1496.8 m/s) was subsequently verified using a Fluke 51 II Thermometer (Fluke Corp., Everett, Washington, USA) to determine the water bath temperature (24.6°C) and compared to published data.¹⁸

Using the empirically determined SOS in water, the piston transducer was positioned precisely 5.08 cm from the plate reflector by aligning the peak negative pressure to the time (67.9 μsec) associated with a distance of 5.08 cm. Ten different A-lines were acquired with each phantom positioned between the transducer and the plate reflector. Since the phantom width was constructed to be 2.54 cm, each A-line would travel through 5.08 cm of phantom and 5.08 cm of water in one round-trip path. Thus, the SOS measurements in each phantom, c_p, were calculated using the following equations:

$$c_p=\frac{2\left(d_p\right)}{(t_{p+w}-t_w)}$$ (7)

$$t_w=\frac{2\left(d_w\right)}{c_w}$$ (8)

Where d_p is distance the sound traveled in the phantom, t_p+w is the time associated with the peak negative pressure of each acquired A-line, t_w is the calculated round-trip time that it takes the sound wave to travel through water, d_w is distance the sound traveled in water.

Attenuation, α, was measured directly after measuring SOS using the same pulse-echo experimental set up and was calculated using the following formula:

$$\alpha =\frac{20{\mathit{log}}_{10}\left(\frac{V_w}{V_{p+w}}\right)}{2\left(d_p\right)}$$ (9)

where V_w and V_p+w are the peak negative echo voltage amplitudes from water only and phantom and water, respectively.

III. Results

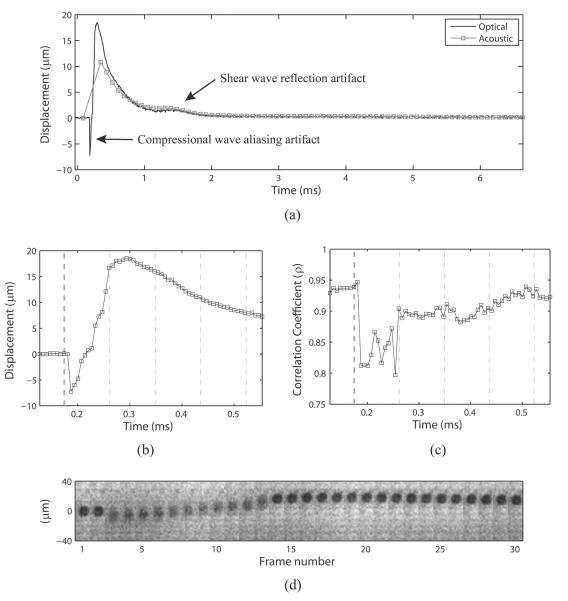
Figure 4 shows an example of the raw data taken from the 30.2 kPa phantom with an F/1.5 pushing pulse focal configuration. Panel (a) shows the optically and acoustically tracked data, in their native sample rates, plotted on top of each other. Two artifacts can be seen in this plot: first, a broad, low displacement peak appears in both the optical and acoustic traces at ~1.5 msec, and second, a sharp, negative displacement peak (suggesting significant motion towards the transducer) appears in the optical trace at 0.19 msec. The broad, low-displacement artifact was observed previously by Bouchard et al.¹⁴ and is the result of a shear wave reflection off of the proximal (w.r.t. the camera) edge of the phantom. The sharp negative displacement, on the other hand, is due to the high frequency compressional motion that the microbead experiences as the ARF pulse passes through it. The reason this motion is misregistered as a bulk negative motion is that the high frequency (4.21 MHz) compressional displacement is severely undersampled by the camera (150 kHz) and aliasing occurs. This phenomenon is shown more clearly in panels (b), (c), and (d), which show zoomed in versions of displacement, correlation coefficient (ρ), and filmstrip of the raw camera data, respectively. Looking at panel (d) first, the bead appears blurry for 11 frames (73.3 μsec) at the beginning of displacement, which corresponds to the duration of a 300 cycle ARF pulse oscillating at 4.21 MHz (71.3 μsec). During this time, the edges of the bead appear smeared over the axial extent of compressional vibration, and the correlation coefficient (panel (c)) drops significantly (ρ ≈ 0.8). Callé et al.¹¹ reported similar findings using an optical interferometric technique, which was not limited by frame rate and could fully sample the compressional motion of an ARF pulse as it passed through a Mylar sheet embedded in a phantom. In the context of this study, the negative tracking artifact was disregarded because no acoustic tracking data was taken at time points coinciding with the compressional motion.

Figure 4.

(a) Example of displacement profiles tracked optically and acoustically in the 30.2 kPa phantom with an F/1.5 ARF pulse focal configuration. Note two anomalous displacements: a broad, low displacement occurring at ~1.5 msec corresponding to a shear wave reflection off the proximal phantom boundary, and a sharp, negative displacement occurring before the first acoustically tracked point at ~0.19 msec corresponding to aliased compressional motion from the high frequency 300 cycle ARF pulse. (b) Zoomed in version of the optical displacement vs. time trace. (c) Zoomed in time scale showing the maximum correlation coefficients calculated for each optical time point. Vertical lines in both (b) and (c) depict timing of acoustic pulses: thicker black line indicates the ARF pulse, while thinner black lines indicate tracking pulses. (d) Filmstrip showing the camera frames over time. Note that the bead appears blurry while the ARF pulse oscillates the bead at the carrier frequency (4.21 MHz) in frames 3–13. During this time, the correlation coefficient of optical tracking drops significantly (c), and a negative displacement artifact appears in the optical trace (b).

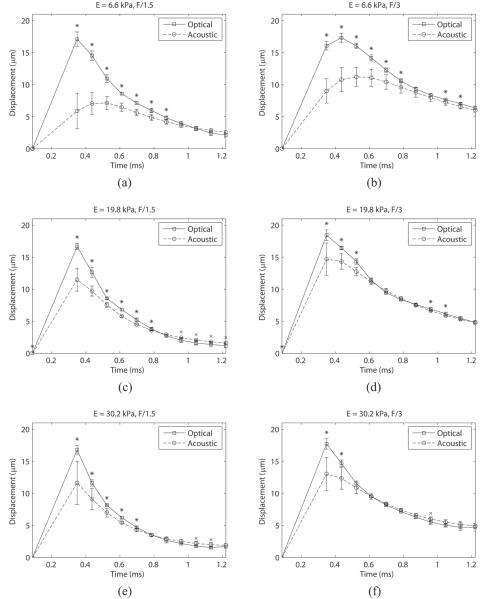
Figure 5 shows how the displacement estimate varies as a function of time using both optical and acoustic tracking methods, which are matched sample for sample for all experiments. The top row corresponds to displacements tracked in the 6.6 kPa phantom, while the center and bottom rows correspond to the 19.8 kPa and 30.2 kPa phantoms, respectively. The left column shows the results using an F/1.5 focal configuration for the ARF pulse, with the right showing F/3. Each data point represents the mean displacement measured across 10 beads with error bars showing one standard deviation. Statistical differences (p < 0.01) between mean optical and acoustic displacements are indicated with an asterisk when the optical mean is higher and a cross when the acoustic mean is higher. Note that as the stiffness of the phantom or F/# increases, the mean displacements measured acoustically match the optical displacements at earlier time points (listed in Table 3).

Figure 5.

Displacement through time measured both acoustically and optically for the 6.6, 19.8, and 30.2 kPa phantoms with F/1.5 ((a), (c), and (e)) and F/3 ((b), (d), and (f)) excitation pulse focal configurations. The tracking transmit pulse focal configuration was F/1.5 for all cases. Error bars indicate one standard deviation. Statistical significance (p < 0.01) is indicated by a black asterisk or cross for higher optical or acoustic values, respectively. Note that as the phantom gets stiffer or F/# increases, the time over which the acoustic and optical measurements are statistically different decreases.

Table 3.

Time points at which mean acoustic and optical displacements become non-significantly different in Figure 5.

Stiffness	Excitation F/#
	F/1.5	F/3
6.6 kPa	0.96 msec	0.87 msec
19.8 kPa	0.87 msec	0.61 msec
30.2 kPa	0.78 msec	0.52 msec

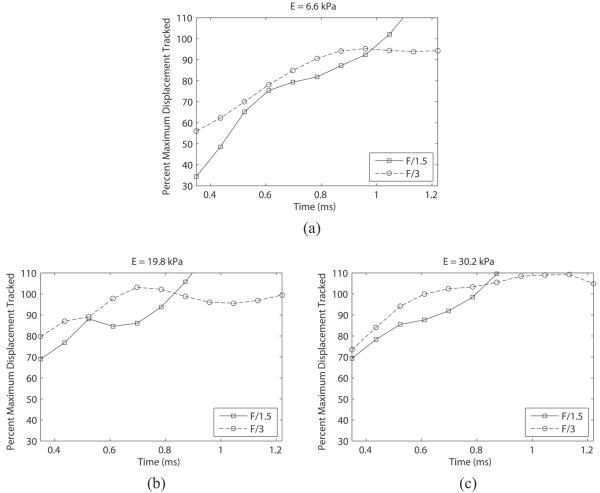
Figure 6 shows the mean acoustic displacement as a percentage of the mean optical gold standard over time for the 6.6 kPa (a), 19.8 kPa (b), and 30.2 kPa (c) phantoms. Note that the underestimation is worst in the first time step, and the accuracy improves with time until ultimately reaching 100% of the optical measurement.

Figure 6.

Percentage of optical displacement tracked acoustically in phantoms of 6.6 kPa (a), 19.8 kPa (b), and 30.2 kPa (c) with two different excitation pulse focal configurations (F/1.5 and F/3). The tracking transmit pulse focal configuration was F/1.5 for all cases. Note that the F/1.5 excitation results in a larger displacement underestimation at the early time points. Percentage values were calculated from the mean displacement values at each time point in Figure 5.

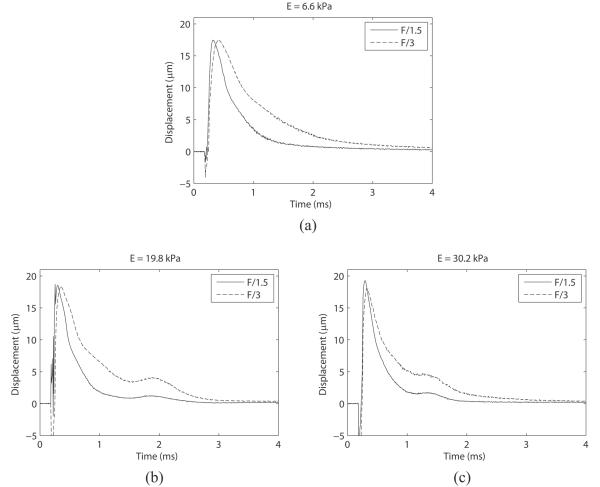
Finally, Figure 7 shows the mean optical displacement traces for each phantom, with different F/# excitations plotted on top of each other. This data is re-plotted in order to illustrate the effect of F/# on the recovery profile of the phantom; namely, as the F/# is increased, the recovery time (RT) and time-to-peak (TTP) is observed to elongate. Table 4 lists the measured values of peak displacement, recovery time, and TTP across F/# and phantom stiffness for comparison.

Figure 7.

Mean optically traced displacements with F/1.5 and F/3 ARF pulse focal configurations plotted on top of each other to show the effect of pushing F/# on phantom recovery time. In each phantom, time to 67% recovery of maximum displacement and time to peak is elongated when a less focused pushing pulse is utilized.

Table 4.

Mean peak displacement, time to 67% recovery, and time to peak measured optically across 10 beads (± 1 standard deviation).

Parameter	F/#	Phantom
		6.6 kPa	19.8 kPa	30.2 kPa
Peak (μn)	F1.5	17.7 ± 1.6	18.5 ± 1.3	19.8 ± 1.7
	F3	17.6 ± 0.8	18.5 ± 0.8	18.2 ± 0.9
Recov. (msec)	F1.5	0.46 ± 0.04	0.35 ± 0.03	0.3 ± 0.03
	F3	0.87 ± 0.05	0.69 ± 0.05	0.56 ± 0.04
TTP (msec)	F1.5	0.14 ± 0.012	0.11 ± 0.014	0.10 ± 0.007
	F3	0.22 ± 0.013	0.16 ± 0.005	0.14 ± 0.005

IV. Discussion

Previous analytical and FEM studies have shown that ultrasonic motion tracking of ARF-induced displacements is subject to underestimation due to scatterer shearing in the lateral and elevational dimension.^{6, 7} This underestimation is dependent on the underlying material stiffness and can be mitigated by beamforming the excitation PSF to encompass the tracking PSF (i.e. defocus the pushing beam laterally/elevationally and/or lower its center frequency). Material stiffness impacts underestimation because it affects the speed at which shear waves propagate away from the ROE. The faster the shear wave, the more quickly the displacement field broadens over time in the lateral and elevational dimensions, making the scatterer motion under the tracking PSF more uniform and reducing the underestimation error. In the same respect, defocusing the excitation beam also reduces displacement underestimation by increasing the cross-sectional area over which force is initially deposited and broadening the extent of the displacement field relative to the tracking PSF.

Figure 5 and Figure 6 confirm the FEM predicted phenomena, showing improvement in the accuracy of acoustically-derived displacements as either the stiffness of the phantom or the excitation F/# is increased. Figure 6 shows that the first acoustic time point, which coincides with the highest optical displacement in almost all cases, has the greatest underestimation. This underestimation then resolves with time at a rate governed by the stiffness of the phantom, which is depicted numerically in Table 3. As expected, the stiffest phantom matches the optical displacement at the earliest time point. Figure 6 and Table 3 also show that doubling the F/# of the excitation pulse in the lateral dimension results in improved displacement estimation accuracy and shorter times to non-significant difference from optically measured displacements. The acoustic estimates with F/3 excitations were on average 7.7, 10.4, and 7.7% closer to the optical measurements for the 6.6, 19.8, and 30.2 kPa phantoms, respectively (over the time period that it takes F/1.5 to reach non-significant difference). Finally, the variance (i.e. jitter) of the acoustic displacement estimates was observed to be worst in the earliest time points, consistent with previously simulated data.

Figure 6 also shows that the F/1.5 excitation resulted in a small amount (~10 to 20%) of acoustic overestimation of the measured displacement in all three phantoms (at ~0.9 msec and later), which was generally not observed with the F/3 excitation. This overestimation, like the underestimation at the earlier time points, could occur if the scatterers at the edge of the PSF are displacing more than the scatterers in the center of the PSF. Due to the large −6 dB elevational beamwidth (~2.4 mm) at an axial focus of 20 mm, this could conceivably occur if either the shear wave front has not entirely left the PSF at the time the center scatterers begin to recover, or if the shear wave reflection artifact has returned into the PSF. Figure 7 suggests that the shear wave reflection does not coincide with the time of overestimation in the 6.6 and 19.8 kPa phantoms, but could coincide in the 30.2 kPa phantom. A more in-depth investigation that is not confounded by shear wave reflections is needed to conclusively determine the mechanisms underlying displacement overestimation.

Figure 7 and Table 4 show an interesting phenomenon associated with increasing the F/# of the excitation pulse; the RT and TTP of the phantoms are both elongated. In all three stiffnesses, the optically measured RT was increased by a factor of 2, while the TTP was increased by a factor of 1.5 when the excitation F/# was increased from F/1.5 to F/3. Elongated TTP by F/# was previously reported by Palmeri et al.¹⁹ in FEM studies and was attributed to the broader cross-sectional area of the pushing beam, but the effect on RT was either not observed or not reported. It would be expected that the same inertial (mass) effects described by Palmeri et al.¹⁹ that explain the increase in TTP would increase RT as well, but it was outside of the scope of this study to investigate these dynamics in further detail.

There were a number of potential sources of error in this study that could have contributed to erroneous measurement of displacement underestimation: focal alignment mismatch between optical and acoustic data sets, jitter in optical displacement estimation, and sample-for-sample timing uncertainty. As described previously, focal alignment was carried out in water, which had a slightly different SOS than the gelatin phantoms. Because of this, the axial focus of the transducer was not precisely positioned on the microbead when the experiments were carried out. For the purpose of this study, though, it was not critical that the microbead be precisely at the acoustic focus axially, only that the position of the bead relative to the transducer be known so that it could be located within the range of the acoustic A-line. Therefore, to discern the axial position of the microbead two empirical SOS measurements had to be made, both subject to experimental error; the first was a measurement in water to precisely position the transducer 20 mm from the needle hydrophone, and the second was a measurement in each phantom in order to calibrate the fast-time dimension of the acoustic RF data. If either of these measurements was incorrect, the acoustic data would be slightly misaligned axially and the measured underestimation erroneous. The standard deviation on both SOS measurements was generally small though (< 1 m/s) and would result in a one or two sample axial shift (~20 to 40 μm) that was not expected to have a significant impact on the results of this study.

Jitter in the optical measurements was another possible source of error. Like acoustic displacement estimation, optical displacement estimation was subject to jitter errors arising from limited camera pixel resolution and electronic noise from camera components. To quantify the impact of optical jitter error, the standard deviation was calculated on the last 100 samples of every optical data set and averaged together resulting in an empirical jitter error of 0.11 μm on optical measurements, which is low compared to the displacements induced in this study. Finally, timing uncertainty could have impacted the sample-per-sample alignment of the optical and acoustic data. One of the consequences of this experimental design is that the camera and the ultrasound system run on different clocks, and the Antares scanner did not output a trigger with every ultrasonic pulse. Therefore, optical data had to be interpolated when the time step of the acoustic pulse did not align precisely with the optical sample. Any error arising from this interpolation step, though, was deemed to be insignificant due to the high frame rate of the camera acquisition (150 kHz).

Understanding displacement underestimation is important in the context of imaging mechanically heterogeneous tissues because of its potential to impact contrast. The most common 2D parametric images created from an ARFI acquisition show peak displacement values measured at each pixel. In this type of image, areas of low peak displacement represent stiffer tissues while areas of high displacement represent softer tissues. The underestimation phenomenon, though, works in the opposite direction; the stiffer structures have higher shear wave speeds and are less underestimated (i.e. have higher displacement) while the softer structures have slower shear wave speeds and are more underestimated (i.e. have lower displacement). Therefore, correcting displacement underestimation, either through excitation pulse geometry and transducer design⁸ or filtering and motion tracking techniques^{20, 21}, could have major impact on the field of ARFI imaging. This work presents an experimental framework for testing and validating these novel approaches to reducing displacement underestimation.

Conclusion

Acoustic displacement underestimation in ARFI, previously predicted by theory and FEM modeling, was validated experimentally. A high F/# excitation pulse was seen to reduce the amount of displacement underestimation due to lateral shearing. Likewise, a dependence on material stiffness was observed, where stiffer phantoms showed less underestimation and faster times to matching the true displacements. These experiments set up a framework for future displacement tracking validation studies using relevant diagnostic ultrasound hardware.