Motion-compensated compressed sensing for dynamic contrast-enhanced MRI using regional spatiotemporal sparsity and region tracking: Block LOw-rank Sparsity with Motion-guidance (BLOSM)

Abstract

Purpose

Dynamic contrast-enhanced MRI of the heart is well-suited for acceleration with compressed sensing (CS) due to its spatiotemporal sparsity; however, respiratory motion can degrade sparsity and lead to image artifacts. We sought to develop a motion-compensated CS method for this application.

Methods

A new method, Block LOw-rank Sparsity with Motion-guidance (BLOSM), was developed to accelerate first-pass cardiac MRI, even in the presence of respiratory motion. This method divides the images into regions, tracks the regions through time, and applies matrix low-rank sparsity to the tracked regions. BLOSM was evaluated using computer simulations and first-pass cardiac datasets from human subjects. Using rate-4 acceleration, BLOSM was compared to other CS methods such as k-t SLR that employs matrix low-rank sparsity applied to the whole image dataset, with and without motion tracking, and to k-t FOCUSS with motion estimation and compensation that employs spatial and temporal-frequency sparsity.

Results

BLOSM was qualitatively shown to reduce respiratory artifact compared to other methods. Quantitatively, using root mean squared error and the structural similarity index, BLOSM was superior to other methods.

Conclusion

BLOSM, which exploits regional low rank structure and uses region tracking for motion compensation, provides improved image quality for CS-accelerated first-pass cardiac MRI.

INTRODUCTION

Compressed sensing (CS), an acceleration technique of growing importance, is making a major impact on MRI (1). Using CS, high-quality images can be recovered from data sampled well below the Nyquist rate provided that the sampling pattern is incoherent, the images are sparse in a transform domain, and a sparsity-promoting iterative reconstruction is used (1). Because of the high temporal and spatial redundancy inherent to dynamic contrast-enhanced MRI, these data can be represented sparsely in a transform domain and are well-suited for acceleration by CS (2). However, patient motion due to respiratory or other factors reduces the spatiotemporal redundancy of the data and, if not corrected, leads to image artifacts (3–11). The problem of imperfect breathholding and associated respiratory motion presents a major challenge to CS-acceleration of first-pass cardiac MRI, where, even when patients are instructed to suspend respiration for 15–20 seconds, they are often unable to comply fully with instructions and they breathe during the scan.

A number of CS methods have been developed to accelerate dynamic MRI. Early studies such as k-t SPARSE showed that sparsity in the spatial and temporal-frequency (x-f) domain could be exploited to accelerate cine MRI using CS (2,12). The k-t FOCal Underdetermined System Solver (k-t FOCUSS) method made improvements to x-f domain approaches by separating the data into predicted and residual signals, where the predicted signal served as a baseline signal and sparsity was exploited for the residual signal (4). While x-f domain methods combined with parallel imaging have been successfully used for dynamic contrast-enhanced MRI (3), the non-periodic nature of dynamic contrast-enhanced MRI leads to a broader band of temporal frequencies than cine MRI, thus these applications present less x-f sparsity than cine MRI. For these cases, data-driven spatiotemporal basis functions such as those used in Partially Separable Functions (13) and the k-t Sparsity and Low-Rank (k-t SLR) method (6) may have advantages. For example, the k-t SLR method, which is applied in the image-time domain and exploits matrix rank sparsity by decomposing the signal using singular value decomposition (SVD), has provided quite good image quality for accelerated contrast-enhanced cardiac perfusion imaging (6). However, even while advanced sparsifying transforms such as SVD provide improved image quality, these approaches are still subject to artifacts when respiratory motion or other patient movement occurs.

One approach to handle complex dynamics such as breathing is to extract motion information from the acquired data and apply motion compensation during CS reconstruction. Some studies (7,14) base their work on Batchelor’s motion matrix method (15) to correct for respiratory motion in free-breathing or real-time cine imaging. While this approach carefully separates cardiac and respiratory motion, the data binning step limits its extension to wider applications such as dynamic perfusion imaging and relaxation imaging. Another approach is to compensate the image dataset for motion and then apply a CS sparsity transform to the motion-compensated data, such as in k-t FOCUSS with motion estimation and compensation (4) and the recent method of Motion-Adaptive Spatio-Temporal Regularization (MASTeR) (16), as well as other methods (10,11). To date, these methods have employed the temporal difference or x-f methods as the sparsifying transform, and the results clearly demonstrate the advantages afforded by motion compensation.

We sought to develop and evaluate a CS method for first-pass contrast-enhanced cardiac perfusion MRI that combines the advantages of data-driven spatiotemporal basis functions and regional motion tracking. Specifically, we propose a method that divides images into regions, tracks the regions over time, and applies SVD to the tracked regions. Using this approach, our method can both account for regional non-periodic variations in motion and can exploit regional spatiotemporal sparsity. In our present implementation, the regions are square blocks and we exploit matrix low rank sparsity, thus we have coined the term Block LOw-rank Sparsity with Motion-guidance (BLOSM) to describe this method.

METHODS

BLOSM Overview

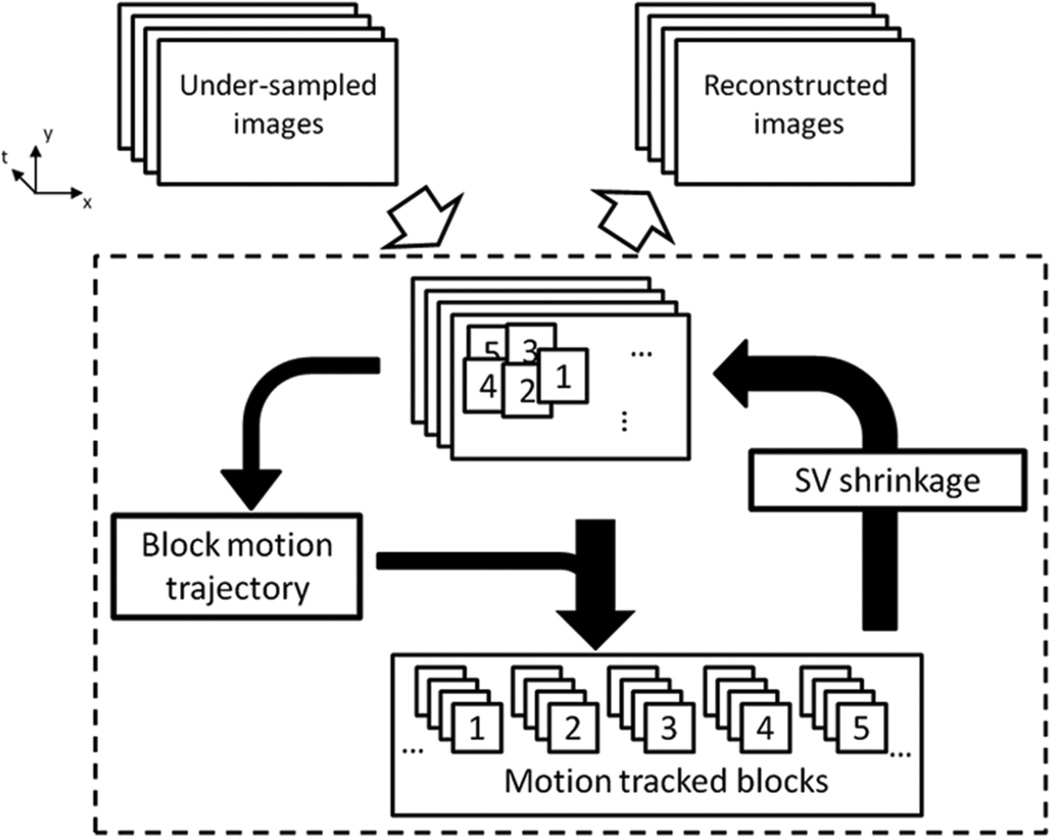
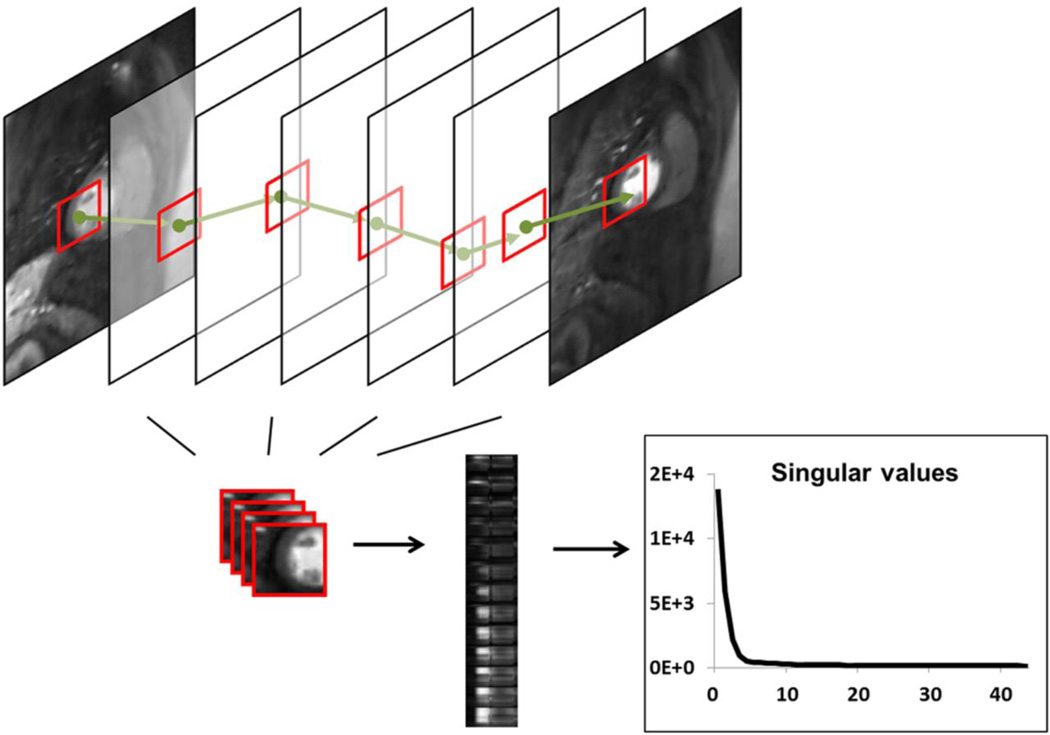
The proposed BLOSM method is based on the concept of motion-guided compressed sensing using a regional approach to motion tracking and spatiotemporal sparsity. In BLOSM (as shown in Fig. 1), blocks of image pixels are defined on one image and tracked through time using motion maps extracted from the image data itself (not using separately acquired training data). The tracked blocks are then grouped into clusters which contain structurally-similar and temporally-related content. The clusters undergo SVD, image estimates are re-computed, and the algorithm iterates as shown. Because the clusters contain motion-tracked blocks, we expect them to exhibit decreased dynamic complexity and, correspondingly, increased matrix low-rank sparsity (17). Specifically, referring to Fig. 2, a block (red box) is initiated on the first image and is tracked to the succeeding images. Next, as also illustrated, the tracked blocks are gathered into a 3D cluster and rearranged into a 2D matrix, where each block becomes one column and blocks corresponding to separate time points are placed into separate columns. The 2D matrix is then subject to SVD to exploit low-rank sparsity. The 2D matrix is expected to have greater spatiotemporal sparsity compared to the whole image or to untracked blocks because the blocks have a smaller scope with decreased spatiotemporal variations, and motion tracking leads to less motion contamination.

Figure 1.

General description of Block LOw-rank Sparsity with Motion-guidance (BLOSM). A set of undersampled dynamic images are divided into blocks (labeled 1 to 5 as an example). Motion trajectories for each block are obtained from the current image estimation and used to track each block through time. The motion-tracked blocks are stacked together to form a cluster for each group of blocks. Each cluster then undergoes a singular value shrinkage step and the resulting blocks are merged into a new estimated image. The iterations continue for a fixed number of iterations or until a stopping criteria is met.

Figure 2.

BLOSM tracks blocks of pixels through time and exploits regional low-rank sparsity. An example block of pixels (red square) is tracked through all the frames. These temporally related blocks with similar spatial contents are gathered together to form a 3D (N_b×N_b×N_t) cluster. The cluster is rearranged into a 2D matrix (N_s×N_t, N_s = N_b×N_b), which has high spatiotemporal correlations. Singular value decomposition is applied to the matrix, and only a few of the singular values have significantly higher values than the others, thus the data present low-rank sparsity.

The CS reconstruction problem of BLOSM can be framed as the following constrained optimization problem:

$${\mathit{\text{minimize}}}_{m,R}{\Vert {\mathrm{\Phi }}_{ℛ}\mathbf{m}\Vert }_{p*}s.t.{\Vert {ℱ}_{\mathrm{u}}\mathbf{m}-\mathbf{d}\Vert }_2<\in$$ [1]

where m represents the estimated dynamic images, d is the acquired undersampled k-space data, and ℱ_u is the undersampled Fourier transform which only takes values at the k-space positions where the d are acquired. Φ_ℛ represents the operator for block tracking and creation of rearranged clusters, after m is divided into blocks which are tracked using displacement maps. ‖*‖_p* is a joint Schatten p-norm that exploits the regional low rank property.

Block motion tracking

There are several techniques that may be used to extract motion information from images (18–22), where displacements of moving objects relative to a reference image can be obtained. In this study, displacement maps were computed using the Advanced Normalization Tools (ANTS) registration toolbox (23,24) which includes a set of state-of-the-art image registration methods. The inputs to ANTS are the complex images. From these inputs, the registration toolbox takes the magnitude of the complex images and outputs pixel-by-pixel displacement maps. For block tracking, the displacement Δu of each pixel was obtained as Δu = ℛ(u) ≡ (Δx, Δy, Δt) where u = (x, y, t) is the pixel space-time position and the displacement operator ℛ is obtained using ANTS.

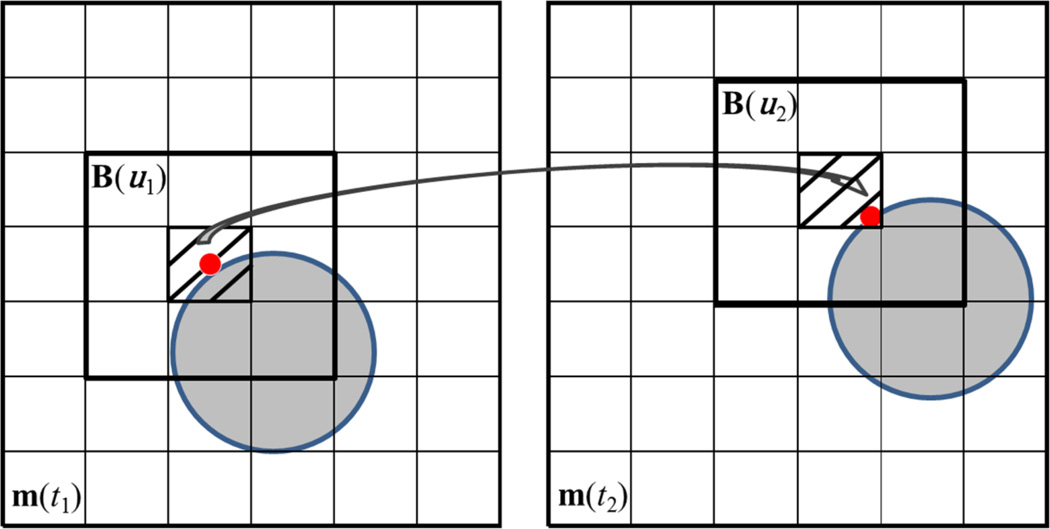
In BLOSM, blocks were initiated on the first image and motion tracking was applied to each block. For example, consider one block B(u₁) ∈ ℂ^N_b×N_b, where u₁ = (x₁, y₁, t₁) indicates that the block center was at position (x₁, y₁) at time frame t₁. The displacement Δu₁ of the block center pixel was obtained from the displacement map as ℛ(u₁) and the tracked pixel location would then be u₁ + ℛ(u₁). Note that the displacement operator ℛ is calculated globally using the whole image and that ℛ(u₁) and u₁ + ℛ(u₁) may be non-integer numbers. Instead of performing a spatial interpolation to get the tracked pixel location as in conventional image registration, the tracked center from u₁ was taken as u₁ = {u₁ + ℛ(u₁)}, where “{}” takes the integer. A new block B(u₂) was defined to include all neighboring pixels around u₂ with the same block size, as illustrated in Fig. 3. B(u₂) was then motion tracked to succeeding frames with the block center at u_n = {u_n−1 + ℛ(u_n−1)} on the n_th frame. The tracked blocks were collected as a cluster Ξ=[B(u₁), B(u₂), … B(u_Nt)] with dimension of N_b×N_b×N_t. Φ_ℛm yields a set of clusters Ξ=[Ξ₁, Ξ₂, …] and was obtained by performing the block motion tracking procedure for each block defined on the first frame and tracked through all subsequent frames. This approach avoids spatial interpolation, which often leads to image blurring (25).

Figure 3.

Illustration of BLOSM block tracking. m(t₁) and m(t₂) are two consecutive images. An object (gray circle) is displayed on both images which underwent a translational shift (rightward and upward) from frame to frame. A red point is labeled on the circle to represent part of the object. A block B(u₁) centered at the red point is initiated on m(t₁). The red point is tracked from m(t₁) to m(t₂) using the ANTS toolbox, as shown by the arrow. Note that the tracked point on m(t₂) is not at the center of the pixel. Instead of using spatial interpolation, the pixel containing the red dot (the shaded pixel) is selected as the new center pixel for the block. Then the neighboring pixels are included to form a tracked block on m(t₂) as B(u₂) where u₂ = {u₁ + Δu₁}.

Regional sparsity

Matrix rank sparsity has been used previously for dynamic CS reconstruction (6,26–28), with one example being the k-t SLR method. In these studies matrix rank sparsity was applied to the entire image dataset. In addition, recent studies such as Low-dimensional-structure Self-learning and thresholding (LOST) (29,30) and compartment-based k-t Principal Component Analysis (31) showed that separating an image dataset into different regions could increase spatiotemporal sparsity and improve reconstruction quality. Along these lines, we explored the use of matrix rank sparsity applied regionally by using SVD on tracked regions of dynamic datasets. Specifically, SVD was applied separately on each cluster Ξ ∈ ℂ^{N_b×N_b×N_t}. Each Ξ was rearranged into a matrix Z ∈ ℂ^N_s×N_t (N_s=N_b×N_b) where each block becomes one column. Then, Z was decomposed as Z = U∑V* by SVD. The diagonal of ∑ ∈ ℂ^N_s×N_t consists of singular values γ which, if the block is truly low rank, will have fewer significant values than the rank of Z.

Coarse-to-fine strategy

We used a variable-density sampling pattern with full sampling of the central phase-encode lines and random undersampling of the outer phase-encode lines. The total number of collected k_y lines was the fully sampled number divided by the acceleration rate, and 50% of the total acquired lines were sampled around the center of k-space. Using this approach, the initial image estimate has very low spatial resolution, and, as the algorithm iterates, the spatial resolution increases. We developed a coarse-to-fine strategy to take advantage of this behavior, where smaller blocks and finer motion tracking (i.e., registration methods) were used as the algorithm iterated and image resolution improved. Specifically, an initial reconstruction was performed where no motion estimation was used for the first 50 iterations. Through the subsequent iterations, smaller block sizes and a finer registration method were used for motion estimation. Given the dimensions of the images as N_x×N_y×N_t, the initial block size was set as 1/5 of the shorter spatial dimension. After 50 iterations, a mutual-information-based rigid registration method embedded within ANTS was performed to obtain global translational shifts. After subsequent sets of 50 iterations, the block size was decreased 1.5 times until the final block size reached 5×5 pixels. Motion information was updated every 50 iterations. After 150 iterations, the rigid registration was replaced with a cross-correlation-based non-rigid registration method using ANTS.

Avoidance of gaps

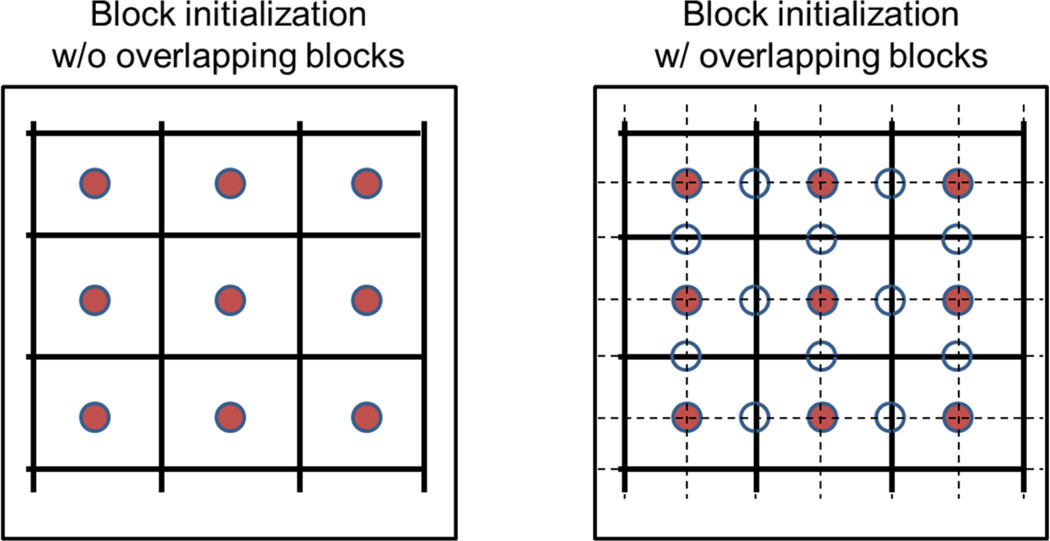
To ensure that gaps are not left between tracked blocks, we used highly overlapping blocks and a gap detection and filling method. After defining the initial blocks, a second set of blocks, shifted by half the block size, was also defined and used (Fig. 4). In addition, during execution of BLOSM, images are automatically inspected for gaps and additional blocks are generated to cover gaps if they appear. Specifically, on the n_th frame after block motion tracking, a mask of uncovered areas or “gaps” is calculated as G_n. A “common” gap mask G_c is generated by taking the union set (along the temporal direction) of all the gap masks: G_c = G₁ ∪ G₂ ∪ … G_Nt. G_c is then used for each frame to get the pixels belonging to the gaps. Spatially discontinuous gaps are separated using connected component analysis (32) and are treated as different gap blocks at different spatial locations. Gap blocks at the same spatial location on different frames are gathered together into a 3D block cluster, which is further transformed into a 2D matrix and subjected to SVD, in the same manner as the other block clusters. No motion tracking is performed for the gap blocks in order to avoid potential additional gaps that might occur if the gap blocks were tracked.

Figure 4.

In BLOSM, overlapping blocks are used to avoid gaps. The circles in the figure represent block centers. The solid red centers represent initial blocks that cover the whole image, and the unfilled circles represent additional blocks. The initial blocks are demarcated by solid lines, and the additional blocks, which overlap the initial blocks, are demarcated by dashed lines.

Optimization method

A solution to the constrained optimization problem of Eq. 1 can be obtained by solving the following unconstrained Lagrangian problem using a diminishing λ through the iterations (33)

$${\mathbf{m}}^{*}={\text{arg min}}_{\mathbf{m},ℛ}{\Vert {ℱ}_{\mathrm{u}}\mathbf{m}-\mathbf{d}\Vert }_2+\lambda {\Vert {\mathrm{\Phi }}_{ℛ}\mathbf{m}\Vert }_{p*}$$ [2]

An iterative soft-thresholding (IST) algorithm (34) was adopted to solve Eq.2. Specifically, for the i_th iteration, the following steps were taken:

$$1.{\mathbf{m}}^{\text{'}i}={𝓢}_{\mathrm{W}}({𝓓}_{\lambda ,p}({\mathrm{\Phi }}_{ℛ}{\mathbf{m}}^i))$$ [3]

$$2.{\mathbf{m}}^i={\mathbf{m}}^{i-1}+\delta {𝓕}^{-1}(\mathbf{d}-𝓕{\mathbf{m}}^{\text{'}i})$$ [4]

where 𝓓_λ,p is a singular value soft thresholding operator defined as

$${𝓓}_{\lambda ,p}(\mathbf{Z})={𝓓}_{\lambda ,p}(\mathbf{U}\sum \mathbf{V}*)=\mathbf{U}\text{soft}(\text{diag}(\sum ),\lambda p{|\text{diag}(\sum )|}^{p-1})\mathbf{V}*$$ [5]

and soft() is the well-known soft thresholding operation defined as

$$\text{soft}(\gamma ,\lambda p{|\gamma |}^{p-1})=\text{signum}(\gamma )\text{max}(0,\gamma -\lambda p{(\gamma )}^{p-1})$$ [6]

𝓓_λ,p was applied to every cluster generated by Φ_ℛmⁱ. 𝓢_w is a weighted averaging operator (35) which merges the blocks to form images. The weighting was calculated as the reciprocal of the number of times one pixel was overlapped by different blocks. m' is an auxiliary variable and δ is a fixed value step size. Currently, the calculation was set to have a fixed number of iterations.

Evaluation of BLOSM

To evaluate the BLOSM method, we used computer simulations and experimental first-pass contrast-enhanced cardiac MRI of human subjects. In both settings, retrospectively rate-4 undersampled images reconstructed using BLOSM were compared to fully-sampled data and to other CS methods. Since BLOSM uses SVD applied to motion-tracked regions, we compared it to conventional k-t SLR (which uses SVD applied to non-motion-compensated whole images), BLOSM without block motion-guidance (BLOSM w/o MG), and k-t SLR with global motion-guidance (k-t SLR w/ gMG). The implementation of BLOSM w/o MG was straightforward. The blocks were treated as static and motion information was not estimated. Overlapping blocks were still generated. SVD was applied to each cluster of blocks. The implementation of k-t SLR was treated as BLOSM without motion guidance or blocks. k-t SLR w/ gMG exploited sparsity of the registered/motion compensated whole images. Specifically, for one iteration, the images were first compensated for motion by registering them to one reference image, which was the temporal average of the last 10 images. SVD was applied on the registered images. After the singular value shrinkage, the de-noised images were “registered back” for fidelity calculations since the original acquired data contained motion. These algorithms were all solved using IST, and no additional sparsity constraints were used. The weighting factor λ in front of the sparsity term was optimized independently for each of these three methods, as it was for BLOSM. Other parameters such as the norm p and the block size N_b were selected to be the same as those used for BLOSM. BLOSM was also compared to k-t FOCUSS with motion estimation and compensation (k-t FOCUSS with ME/MC), since this is a motion-compensated CS method. The program code of k-t FOCUSS with ME/MC was obtained online (36). The five CS methods: BLOSM, k-t FOCUSS with ME/MC, k-t SLR, BLOSM w/o MG and k-t SLR w/ gMG were systematically compared.

Image quality for the various reconstruction algorithms was quantified using the root mean square error (RMSE) and the structure similarity (SSIM). RMSE measures the direct difference between the two images and is widely used for the assessment of CS methods (3–7,37,38). In this study, we used the relative RMSE (rRMSE) defined as

$$\mathrm{r}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\frac{1}{N}\sqrt{\sum \frac{{|\mathbf{x}-\mathbf{y}|}^2}{{|\mathbf{x}|}^2}}$$ [7]

where N = N_x×N_y×N_t, x are the fully-sampled images and y are the reconstructed images. We also used the structural similarity index (SSIM), which is a more comprehensive measurement of the similarity between two images, and includes measurement of structure, intensity and contrast, representing human perception more closely (39). The equation for SSIM is

$$\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}(\mathbf{x},\mathbf{y})=\frac{(2{\mu }_{\mathbf{x}}{\mu }_{\mathbf{y}}+c_1)(2{\sigma }_{\mathbf{x}\mathbf{y}}+c_2)}{({\mu }_{\mathbf{x}}^2+{\mu }_{\mathbf{y}}^2+c_1)({\sigma }_{\mathbf{x}}^2+{\sigma }_{\mathbf{y}}^2+c_2)}$$ [8]

where x and y are the two images undergoing comparison, μ_x and σ_x are the average and variance of x, σ_xy is the covariance of x and y, and c₁ and c₂ are variables that stabilize the division with a weak denominator, chosen as described by Wang et al (39).

Computer-simulated phantoms

Computer simulations of heart-like phantoms with complex motions and signal intensity variations were used to evaluate BLOSM. Specifically, we simulated objects undergoing rigid translational shifts along the phase-encoding and readout directions, objects undergoing both abrupt and gradual changes in size (which can be interpreted as either through-plane motion or cardiac contraction), objects undergoing appearance and disappearance (i.e., non-permanent features) and an object undergoing counterclockwise rotation. Motions were combined with temporally quadratically changing signal intensity.

The images were Fourier transformed to generate k-space data, undersampled at acceleration rate 4 using the variable density k_y-t mask described above, and then reconstructed using various CS algorithms.

First-pass cardiac perfusion imaging

All imaging was performed on a 1.5T MR scanner (Avanto, Siemens, Erlangen, Germany). Eight different subjects with suspected heart disease were studied in accordance with protocols approved by our institutional review board after informed consent was obtained. For each subject a 5-channel phased-array RF coil was used and 1–4 short-axis slices were acquired each heartbeat for 50 repetitions during infusion of 0.075 mmol/kg gadopentetate dimeglumine (Magnevist, Bayer HealthCare, Montvale, NJ). A saturation-recovery Turbo FLASH sequence was used with parameters as follows: nonselective 90° saturation pulse with a saturation recovery time of 100–120 ms, field of view = 240–315×370–410 mm², matrix = 86–152×128–200, slice thickness = 8 mm, flip angle = 8–15°, TR = 1.9–2.2 ms, and TE = 0.9–1.4 ms. Immediately prior to initiating the perfusion scan, each subject was instructed to suspend respiration during the scan using our standard instructions for breathholding. If the subjects could not hold their breath for the entire scan, they were instructed to breathe lightly for the remainder of the scan. As is typical for first-pass perfusion MRI of the heart, even with proper instructions about breathing, many patients do not comply well with the instructions, and various breathing patterns occur during perfusion imaging. The datasets collected and used in this study all present prominent respiratory motion, even though the patients were instructed not to breath. From the 8 patients studied, a total of 26 slices were collected, and each slice was treated as a distinct dataset. All data were acquired without prospective undersampling. Among the 26 datasets, 14 of them were fully-sampled sum-of-squares (SoS) combined magnitude-valued images and 12 of them were fully-sampled multi-coil complex-valued k-space data. In this study, we focused our efforts on evaluating BLOSM and other CS methods using only single-coil data. To serve this purpose, we combined the 12 multi-coil complex-valued k-space datasets into 12 single-coil magnitude-valued image data using SoS. The resulting 26 magnitude-valued datasets were transformed into k-space and retrospectively undersampled at acceleration rate 4 using the variable density k_y-t mask described above, and then reconstructed using various CS algorithms.

Evaluation of initial block size, initial block positions, the coarse-to-fine strategy, and the use of motion compensation

Systematic experiments were performed to determine whether the initial block size or block positions have an effect on image quality. For these studies, the same datasets were reconstructed using different initial block sizes or positions. Specifically block size factors of 2, 3, 4, …,10 were chosen, which correspond to initial block sizes of 51, 35, 27, …, 11 for an image matrix of 102*128. Due to the usage of the coarse-to-fine (CTF) strategy, where the block size decreases through the iterations and the registration method varied with iteration, the final block size was kept constant (5 for all settings), and the total iteration number was the same for different initial settings. Relative RMSE was calculated to perform a quantitative evaluation comparing the initial block sizes. Reconstruction time was also recorded. To assess whether there is a dependence on the initial block positions, BLOSM reconstructions using the original initial block positions and using shifted initial block positions (shifted by up to one quarter of the initial block size) were compared to reference images, where the reference images were fully-sampled 2DFT-reconstructed images. Experiments were also performed to demonstrate the utility of the CTF strategy. For these studies, both simulated and human datasets were reconstructed using BLOSM with and without the CTF strategy. In BLOSM without the CTF strategy, a constant block size and rigid registration method were used through all the iterations. Studies were also performed to show that motion guidance within BLOSM improves image quality. Both simulated and human datasets were used for these studies, which compared BLOSM with and without motion tracking.

Computation time

Benchmark tests for BLOSM, k-t SLR and k-t FOCUSS with ME/MC were performed. All tests were performed in MATLAB on a desktop computer (3.4GHz Intel(R)i7 CPU with 12GB RAM). A human perfusion dataset with a matrix size of 102×128 and 44 time frames was used. A fixed number of 200 iterations was used for BLOSM and k-t SLR, and the k-t FOCUSS with ME/MC method used a convergence metric to terminate the algorithm.

RESULTS

Comparison of BLOSM and other CS reconstruction methods using computer simulations

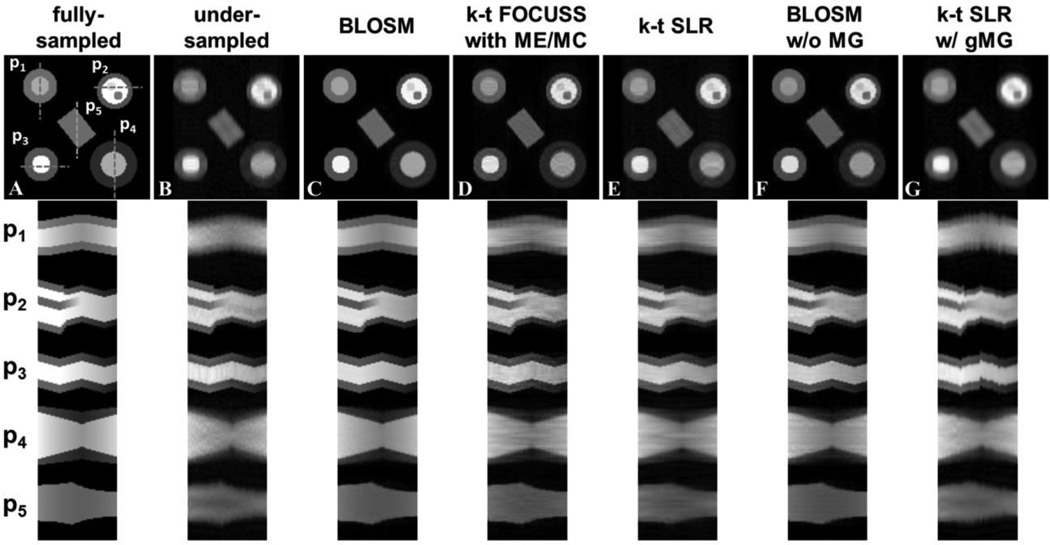
Fig. 5 shows the comparison of BLOSM to other reconstruction algorithms for the computer-simulated phantoms. Example rate-4 accelerated CS-reconstructed images at one time point along with the fully-sampled reference and under-sampled FFT reconstructed images are shown on the top row. In Fig. 5 various motions were presented: rigid translational shifts along the phase-encoding direction (phantom 1, or P1) and readout direction (P3); translational shifts combined with an abrupt change in size and appearance/disappearance of non-permanent features (P2) and gradual change in size (P4), both of which can be interpreted as either through-plane motion or cardiac contraction; and object rotation (P5). Corresponding position-time (x-t) profiles are shown on the bottom row for each of the simulated phantoms. In the presence of object motion, signal intensity variation, and the appearance and disappearance of objects, visual inspection shows that images reconstructed using BLOSM most closely resemble the fully sampled images, as compared to the other CS methods. k-t FOCUSS with ME/MC and conventional k-t SLR had substantial residual artifact as well as some blurring. Some artifacts were more severe on k-t FOCUSS with ME/MC. BLOSM w/o MG removed more artifacts than conventional k-t SLR, which supports the concept of exploiting regional instead of global spatiotemporal sparsity. However, edge artifacts along the direction of motion can be seen on BLOSM w/o MG, which are attributed to the lack of motion correction. k-t SLR w/ gMG had substantial smoothing effects. Relative RMSE and SSIM analysis showed that BLOSM achieved the minimum error and the maximum similarity (rRMSE=2.85E-8, SSIM=0.89) compared to k-t FOCUSS with ME/MC (rRMSE=6.30E-8, SSIM=0.66), k-t SLR (rRMSE=8.85E-8, SSIM=0.49), BLOSM w/o MG (rRMSE=6.50E-8, SSIM=0.78) and k-t SLR w/ gMG (rRMSE=8.28E-8, SSIM=0.57).

Figure 5.

Reconstruction of retrospectively rate-4 undersampled images from computer-simulated phantoms that undergo translational shifts, rotation, deformation/TPM and variable signal intensity over time. Example reconstructed images at one time frame are shown in the top row. Phantom 1 (P1) undergoes rigid translational shifts along the phase-encoding direction. P2 has an abrupt change in size as well as appearance/disappearance of features to mimic through plane motion combined with translational shifts in the readout direction. P3 undergoes rigid translational shifts along the readout direction. P4 undergoes a gradual change in size which can be interpreted as either cardiac contraction or through-plane motion. P5 rotates counterclockwise through time to mimic object rotation motion. All the phantoms also have quadratically changing signal intensity over time. Corresponding x-t profiles for each phantom (P1–P5) are shown on the bottom panel, where the profile locations are indicated by dashed lines on the fully-sampled image. The first column shows fully-sampled data reconstructed by FFT and serves as a reference. The other columns display undersampled data reconstructed using conventional FFT and the CS methods: BLOSM, k-t FOCUSS with ME/MC, k-t SLR, BLOSM without motion guidance (BLOSM w/o MG) and k-t SLR with global motion guidance (k-t SLR w/ gMG). BLOSM provided the most accurate recovery of the fully sampled images. For k-t FOUCSS with ME/MC, k-t SLR and BLOSM w/o MG, residual artifacts and moderate motion blurring can be observed, especially on P4.

Comparison of BLOSM and other CS reconstruction methods for accelerated first-pass cardiac perfusion imaging of human subjects

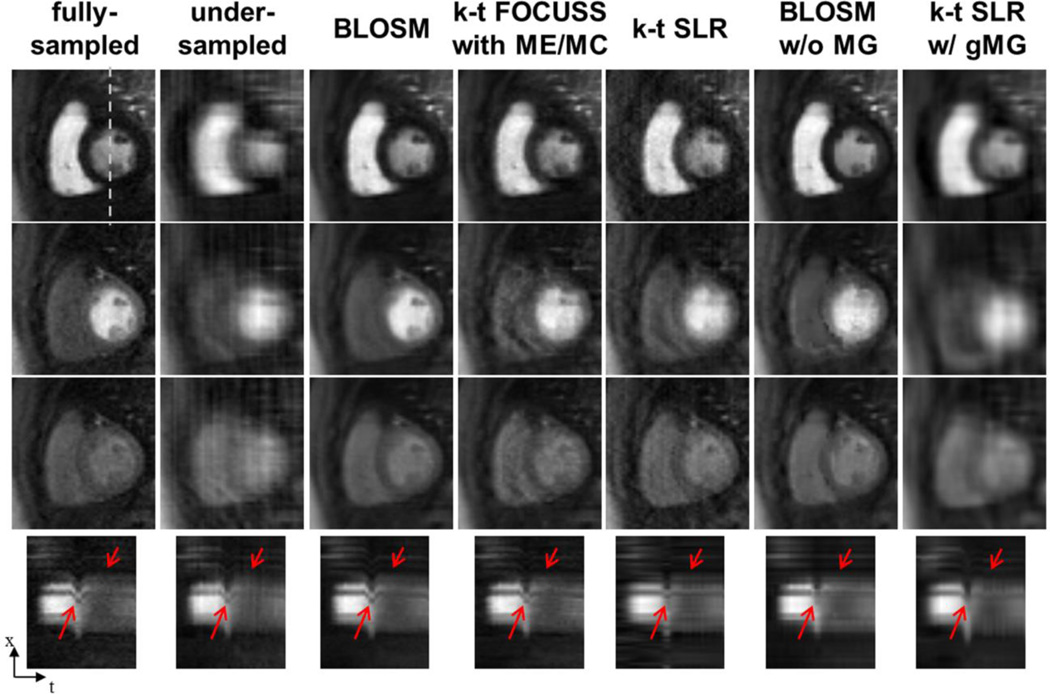
Fig. 6 shows representative results from first-pass contrast-enhanced perfusion images of the heart using different CS reconstruction methods. Images acquired at early, middle, and late phases of contrast enhancement are shown in different rows. Due to patient respiration, the heart shifted downward (~16 mm) in the middle row. Images from fully-sampled k-space data as well as rate-4 retrospectively-accelerated images reconstructed using conventional FFT, BLOSM and other CS methods are shown in separate columns. Visual inspection shows that BLOSM-reconstructed images resemble the fully-sampled data at all phases better than the other CS methods. Reconstruction methods without motion guidance, namely k-t SLR and BLOSM w/o MG (columns 3 and 4), show the inability to recover artifact-free images when motion occurs (row 2). k-t FOCUSS with ME/MC (row 2) had blurring and lower SNR as compared to BLOSM. k-t SLR w/ gMG had excessive blurring, similar to that seen in the simulated phantom, which propagated through many phases including phases with little or no motion.

Figure 6.

Comparison of BLOSM with other CS algorithms using retrospectively rate-4 undersampled first-pass contrast-enhanced MRI of the heart. Example frames are presented in different rows representing early, mid and late phases of contrast passage. Undersampled data are reconstructed by conventional FFT, BLOSM, k-t FOCUSS with ME/MC, k-t SLR, BLOSM without motion guidance (w/o MG) and k-t SLR with global motion guidance (w/ gMG). Respiratory motion occurred to a large degree during the middle phase (second row) and to a lesser degree at the late phase (third row). BLOSM provided the best image quality for all the phases and very closely matched the fully-sampled images. k-t FOCUSS with ME/MC, k-t SLR and BLOSM w/o MG performed fairly well for phases where there was no or little motion. For the mid phase, severe artifacts can be seen for k-t FOCUSS with ME/MC, k-t SLR and BLOSM w/o MG. k-t SLR w/ gMG resulted in blurred images for all phases. x-t profiles showing similar results are shown on the bottom row, with important dynamic features highlighted by red arrows.

Motion recovery can also be appreciated by observation of the x-t profiles. As highlighted by the red arrows, noise and artifacts were mostly removed without over-smoothing using BLOSM, while all the other methods showed various artifacts and did not recover x-t profiles when motion occurred as accurately as BLOSM.

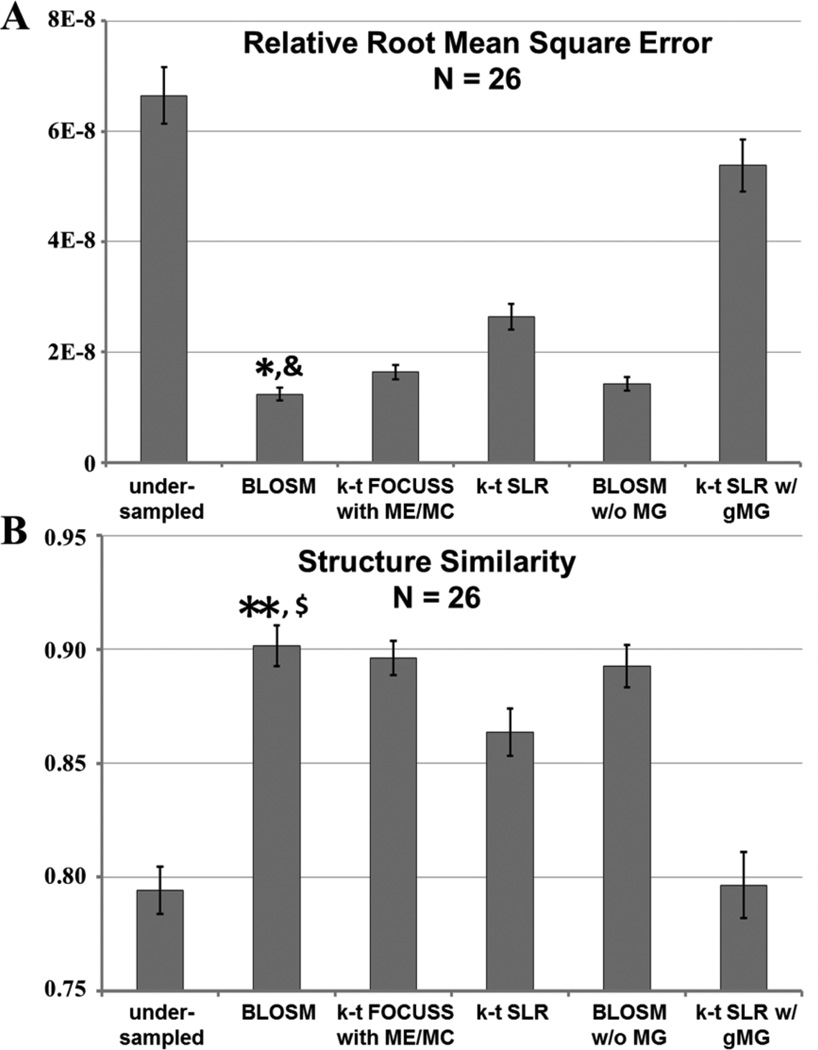
The reconstructed images were analyzed quantitatively using rRMSE and SSIM. Values for 26 slices are shown in Fig. 7. BLOSM demonstrated the best reconstruction quality with the minimum rRMSE and the maximum value of SSIM (p<0.05 vs. all other methods, ANOVA)

Figure 7.

Quantitative analysis of the performance of various reconstruction methods applied to rate-4 accelerated first-pass contrast-enhanced MRI of the heart. Average relative root mean square error (rRMSE) and structural similarity (SSIM), averaged over time, of the CS-reconstructed images were compared to fully-sampled reference images. BLOSM achieved the lowest error (rRMSE) and highest similarity (SSIM) of all the CS methods. (* P<0.01 v.s. undersampled, k-t FOCUSS with ME/MC, k-t SLR and k-t SLR w/ gMG; & P<0.05 v.s. BLOSM w/o MG; ** P<0.01 v.s. undersampled, k-t SLR, and k-t SLR w/ gMG; $ P<0.05 v.s. k-t FOCUSS with ME/MC).

Evaluation of initial block size, initial block positions, the coarse-to-fine strategy, and the use of motion compensation

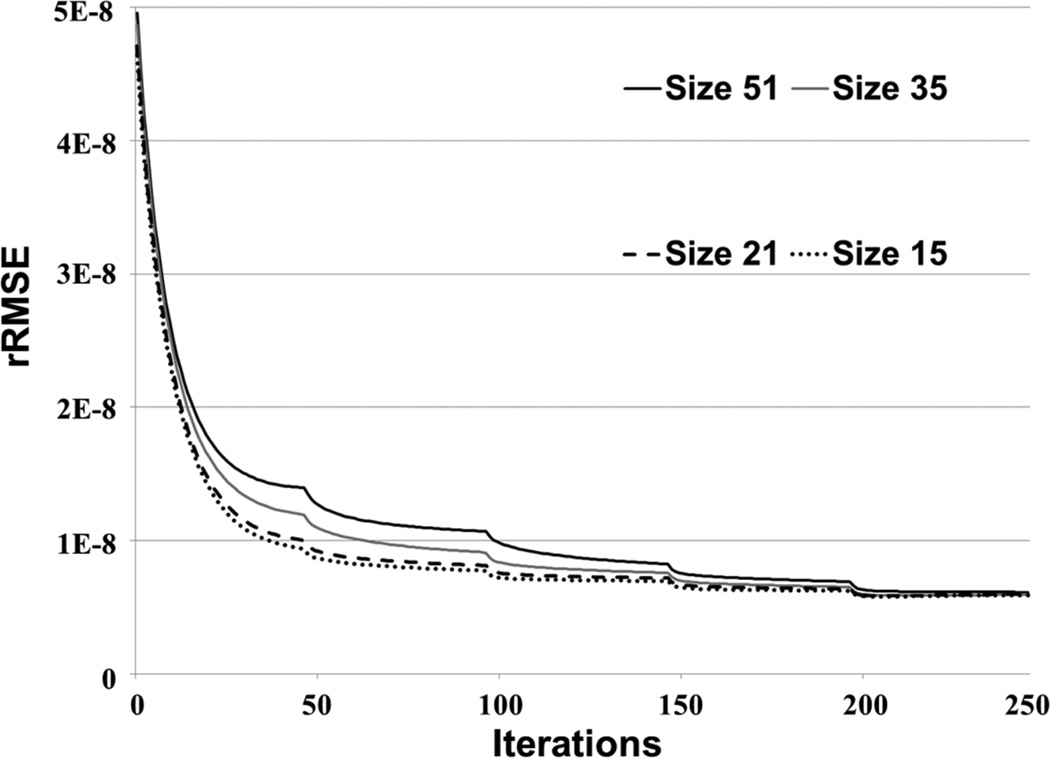
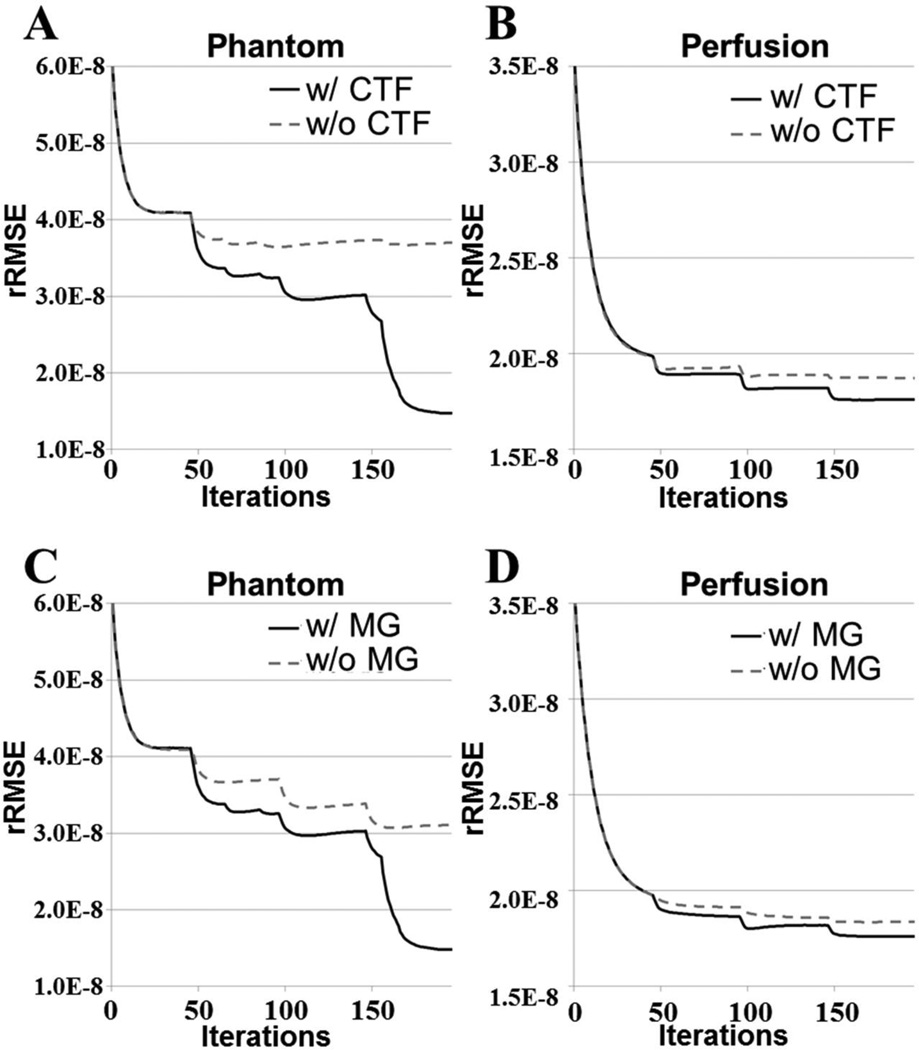
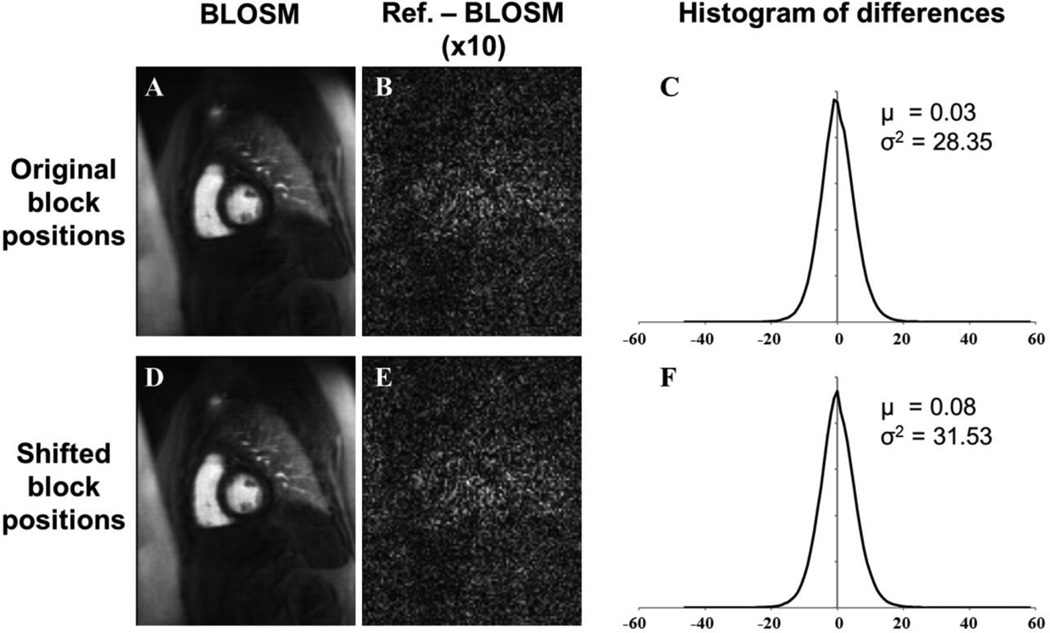
Fig. 8 plots rRMSE as a function of the BLOSM iteration number for different initial block sizes, and shows that BLOSM converges to a single rRMSE value independent of the initial block size. Thus, no single initial block size is optimal for BLOSM. Using similar plots, Figs. 9A–B demonstrate the benefits of the coarse-to-fine strategy, as use of the coarse-to-fine strategy reduces rRMSE in both phantom and human data. Lastly, Figs. 9C–D show the benefits of motion guidance, as BLOSM with motion tracking leads to reduced rRMSE as compared to BLOSM w/o MG. A number of abrupt transitions in rRMSE as a function of iteration are observed in Fig. 8, and correspond to coarse-to-fine adjustments of block size, registration method, and iterative soft threshholding values as BLOSM iterates. To quantify potential differences related to initial block positions, BLOSM using the original block positions and BLOSM using the shifted block positions were both compared to a reference image (a fully-sampled 2DFT-reconstructed image). As shown in Fig. 10, we found a nearly identical difference distribution compared to the reference image for BLOSM using the original block positions and BLOSM using the shifted block positions.

Figure 8.

Convergence of BLOSM for different initial block sizes. BLOSM using different initial block sizes was used to reconstruct a first-pass perfusion dataset. These rRMSE vs. iteration curves demonstrate that the convergence of BLOSM is essentially independent of the initial block size (not all tested initial block sizes are shown, but all had similar behavior).

Figure 9.

Convergence of BLOSM under various conditions. Panels (A and B) show for both computer simulated phantoms and in vivo perfusion imaging that the coarse-to-fine strategy provides lower rRMSE compared to not using this strategy. Similarly, panels (C and D) show that for both computer simulated phantoms and in vivo perfusion imaging the use of motion guidance reduces rRMSE compared to not using motion guidance.

Figure 10.

Image reconstruction using BLOSM is not highly dependent on the initial block positions. Images were reconstructed using BLOSM with original initial block positions (A) and with shifted initial block positions (D). The difference between a fully-sampled 2DFT-reconstructed image (Reference image) and (A) is shown in (B), and the difference between the reference image and (D) is shown in (E). Histograms from multiphase difference images using the original initial block positions and the shifted initial block positions are shown in (C) and (F), respectively. Using either the original initial block positions or the shifted initial block positions results in the same difference distribution (Gaussian distribution verified using the Jarque-Beta test) compared to the reference images. μ is the mean and σ² is the variance.

Computation time

Benchmark tests showed the total computation times for BLOSM, k-t SLR and k-t FOCUSS with ME/MC for a given dataset were 986, 32, and 142 seconds, respectively. For BLOSM, 647 seconds were spent on motion estimation, 93 seconds on computing sparsifying transforms (SVD) and 210 seconds on block handling. Due to the coarse-to-fine strategy, BLOSM iterations were divided into 4 stages, where stage 1 had 60 blocks of size 21×21 pixels, stage 2 had 90 blocks of size 17×17, stage 3 had 154 blocks of size 13×13 and stage 4 had 216 blocks of size 11×11. The average computation times per iteration were 1.1±0.04, 1.5±0.04, 1.9±0.05 and 2.3±0.05 seconds for each stage, respectively.

DISCUSSION

We developed a novel CS reconstruction technique, termed BLOSM, that exploits regional spatiotemporal sparsity and compensates for the effects of respiratory motion by embedding motion tracking within the reconstruction algorithm. Experiments comparing different reconstruction algorithms demonstrated that the regional approach with motion compensation combine to contribute to the superior performance of BLOSM. Visual inspection of images as well as quantitative assessments of image quality (rRMSE and SSIM) demonstrated the advantages of BLOSM.

The two key components of BLOSM, namely the use of both regional sparsity and motion tracking, work together to achieve improved image quality. The finding that BLOSM without motion guidance performed better than global k-t SLR demonstrated that regional sparsity has advantages over global sparsity when using SVD. This finding was also observed in previous work where compartment-based k-t PCA separated perfusion images into different parts (right ventricular blood pool, left ventricle, etc.) and achieved better image quality than conventional k-t PCA (31). In addition, BLOSM with motion guidance performed better than BLOSM without motion guidance, showing the advantage of the motion-guided regional approach.

Adequate motion tracking is central to the performance of BLOSM. We chose to use the ANTS toolbox because it can handle various types of motion and deformation, even with changing signal intensity (23,24). It is worth pointing out that although in BLOSM blocks are tracked, the motion information used for block tracking is obtained by registering whole images, not by using a block matching algorithm, such as in k-t FOCUSS with ME/MC. We used the displacement of the central pixel of the block to represent the whole block motion. The displacements in a region are expected to be smoothly changing, so the center pixel should be representative of the block. Also, our method for tracking blocks in BLOSM avoided the use of spatial interpolation. In contrast, our implementation of k-t SLR with global motion guidance included spatial interpolation steps in the sparsity calculation and in the fidelity calculation, and lead to blurring and smoothing. BLOSM was designed to avoid spatial interpolation, which contributed to its lack of blurring. BLOSM was evaluated using 2D imaging, and may be subject to errors when through-plane motion occurs. Therefore, we used computer simulations to investigate the behavior of BLOSM with through-plane motion and found that, while some minor blurring can occur, BLOSM still performed better than the other CS methods under these conditions. This result held even when objects completely disappeared and appeared over time. In the future we may investigate a frame rejection scheme and/or a 3D acquisition to better deal with throughplane motion. While motion tracking within BLOSM will never be perfect, we combined motion tracking with SVD, which is known to be fairly tolerant to misregistration of serial images (6,13,40). Also, the use of a block-tracking approach could potentially lead to image regions that are not covered by tracked blocks, i.e., gaps. To avoid such a situation, we use highly overlapping blocks and, if gaps do occur, they are detected and patched with additional blocks. Our results also showed that BLOSM converges to a common RMSE independent of the initial block size, and that there is little effect of using different initial block positions on the resulting reconstructed images.

Our data also support the use of the coarse-to-fine strategy for BLOSM. As the BLOSM algorithm iterates, the spatial resolution of the estimated image improves and supports the use of finer motion estimation and use of smaller blocks. When comparing BLOSM with and without the coarse-to-fine strategy, rRMSE is lower when using this strategy. In the current implementation of BLOSM, the block size decreased and the registration method updated once for every fifty iterations, and these settings achieved good results. However, a better approach to consider in the future may be to include an estimate of displacement accuracy into the cost function and to adaptively weight motion-guidance. In that case, when the displacement estimation accuracy is low, less trust will be given to the current estimate and the previous estimate would be used instead. Such a strategy would be similar to the approach used with Kalman filters and may improve tolerance to motion estimation error (41).

Free parameters for the CS problem were empirically varied to find a set that achieved low rRMSE. The Schatten norm, p, threshold value, λ, and block size, N_b, were optimized separately while fixing the other parameters. Parameter optimization was done for phantom and human data, and the optimal values were similar for both types of data, indicating that the algorithm is stable. With Schatten norm p<=1, Eq.1 becomes a non-convex problem. We found that optimal image quality was achieved with p=0.9, and this agrees with other results using the same Schatten norm applied to MR images of the brain (33). The threshold value for each block at singular value γ is calculated as λ p(γ)^p−1 and the selection of p=0.9 enables a block-specific regularization since different blocks have different values of γ. Singular values which contain most of the energy and contrast will receive low penalties while small singular values which mainly correspond to noise and artifacts will receive higher penalties. When p is fixed, the weighting factor λ in Eq.6 controls the threshold and has a high impact on reconstruction quality. For each of the CS methods (BLOSM, BLOSM w/o MG, k-t SLR and k-t SLR w/ gMG) a range of λ (0~2000) was independently tested using a couple of datasets to find the optimal λ that gave the minimum rRMSE. For the IST algorithm and using a diminishing of λ through iterations, we found that the final image quality was stable for a range of λ values (20~200) even with changes in other experimental parameters, such as the norm p. When an aggressive λ value (>500) was chosen, over-regularization was observed as block-like artifacts. Other recent methods exploiting regional sparsity (29,31,35) also have different regularization of different regions. A moderate filtering or denoising step is taken in these studies to ease the block artifacts. Our use of overlapping blocks is similar to these strategies. In our study, all images were scaled to have a maximum value of 250 and no block artifacts were observed for a wide range of λ (0~500) with our experimental settings. Most of the datasets tested showed optimal behavior at λ=50. Thus a λ value of 50 was chosen to reconstruct all the datasets.

BLOSM is a motion-adaptive regional-sparsity-based CS method. Other methods such as k-t FOCUSS (4) and, recently, MASTeR (16) also incorporate motion compensation into a CS reconstruction. In k-t FOCUSS with motion estimation and compensation, although motions are estimated on a regional basis, x-f sparsity is exploited. In MASTeR, motion estimation varies regionally and temporal-difference sparsity is used. In contrast, BLOSM uses regional motion estimation and exploits regional matrix low-rank structure. Also, these three methods differ in the details of the motion estimation algorithms, which likely effects resulting image quality. Previously, most CS methods for dynamic imaging have exploited sparsity using either whole images (such as k-t SLR) or single pixels (such as temporal difference or x-f sparsity). BLOSM, which exploits regional sparsity, is in between these two extremes, and provides the advantages of greater flexibility (compared to whole images) and use of more information (compared to single pixels). The k-t SLR method used in this study for comparison was modified to use the IST optimization algorithm and excluded the spatiotemporal total variance reported by Lingala et al (6). The modified k-t SLR method was used in order to make a fair comparison with BLOSM. Like k-t SLR, BLOSM could be extended to include extra sparsity constraints and could be solved by alternating direction algorithms (42). In this manuscript, we focused our efforts on evaluating BLOSM and other CS methods using only single-coil data. In the future we plan to combine BLOSM with parallel imaging such as SENSE (43) and Self-consistent Parallel Imaging (SPIRiT) (44) by exploiting joint sparsity (3,45–47) to achieve higher acceleration rates and better reconstruction quality. BLOSM is also compatible with non-Cartesian k-space trajectories. A limitation of our study was that, when comparing various reconstruction methods, we used magnitude-only datasets, thus phase effects were not accounted for.

The present study focused on using BLOSM to reconstruct high-quality accelerated contrast-enhanced first-pass cardiac perfusion images, even in the presence of respiration due to imperfect breathholding. However, using the concepts of regional motion tracking and regional sparsity, BLOSM may also be applicable to other dynamic MRI such as cardiac cine imaging, T1 mapping, multi-TI arterial spin labeling, and other methods. Acceleration of these applications with BLOSM may be the subject of future studies. The computation time of BLOSM could also be improved in the future. The time consumed by the motion estimation (65% of total time) and block handling (21% of total time) can be decreased through better parallelization of the code and implementation using a graphics processing unit.

In summary, BLOSM makes use of data-driven spatiotemporal basis functions applied to regions and achieves motion compensation by embedding regional motion tracking into the iterative CS image reconstruction algorithm. With this combination, BLOSM attains the benefits of data-driven spatiotemporal basis functions while reducing artifacts from non-periodic motion such as breathing.