Direct Characterization of Arterial Input Functions by Fluorescence Imaging of Exposed Carotid Artery to Facilitate Kinetic Analysis

Abstract

Purpose

With the goal of facilitating tracer kinetic analysis in small-animal planar fluorescence imaging, an experimental method for characterizing tracer arterial input functions is presented. The proposed method involves exposing the common carotid arteries by surgical dissection, which can then be imaged directly during tracer injection and clearance.

Procedures

Arterial concentration curves of IRDye-700DX-carboxylate, IRDye-800CW-EGF, and IRDye-800CW conjugated to anti-EGFR Affibody are recovered from athymic female mice (n=12) by directly imaging exposed vessels. Images were acquired with two imaging protocols: a slow-kinetics approach (temporal resolution=45 s) to recover the arterial curves from two tracers simultaneously, and a fast-kinetics approach (temporal resolution=500 ms) to characterize the first-pass peak of a single tracer. Arterial input functions obtained by the carotid imaging technique, as well as plasma curves measured by blood sampling were fit with a biexponential pharmacokinetic model.

Results

Pharmacological fast- and slow-phase rate constants recovered with the proposed method were 0.37±0.26 and 0.007±0.001 min⁻¹, respectively, for the IRDye700DX-C. For the IRDye800CW-EGF, the rate constants were 0.11±0.13 and 0.003±0.002 min⁻¹. These rate constants did not differ significantly from those calculated previously by blood sampling, as determined by an F test; however, the between-subject variability was four times lower for arterial curves recovered using the proposed technique, compared with blood sampling.

Conclusions

The proposed technique enables the direct characterization of arterial input functions for kinetic analysis. As this method requires no additional instrumentation, it is immediately deployable in commercially available planar fluorescence imaging systems.

Introduction

Fluorescence imaging is increasingly being used to study tissue dynamics and biodistribution of optical probes in preclinical disease models [1–3]. Leveraging decades of research in more established fields such as positron emission tomography (PET), computed tomography (CT), and magnetic resonance imaging (MRI), quantitative optical tracer kinetic methods have emerged as powerful tools to quantify hemodynamics, leakage [4], and receptor concentration through tracer-binding models [5–7]. Although traditionally, research has focused on using fluorescent probes to maximize molecular-specific contrast, the use of quantitative tracer kinetics to study tissue dynamics is relatively nascent. This increased interest is primarily attributable to a few important advantages that optical methods have over PET, CT, and MRI. First, images can be acquired with high temporal resolution—in some cases, on the order of milliseconds [8]—and acquisitions can be made over the course of hours. Second, fluorescent probes can be produced for a wide assortment of applications—including targeted fluorescent agents to study drug distribution and receptor binding and enzyme-activatable probes capable of reporting on intracellular processes [9]. The recent emergence of dual-tracer receptor concentration imaging (DT-RCI), in particular, has made feasible the nondestructive quantification of surface receptor concentration in a tissue region of interest (ROI), providing the potential for longitudinal study of drug delivery and cancer treatment in the same animal.

In tracer kinetic theory, the time-dependent concentration of tracer in a tissue ROI is given by the concentration of tracer delivered to the tissue region (i.e., the arterial input function) convolved with some characteristic kinetic function (i.e., the distribution of the tracer within the tissue compartments). Despite the existence of both model-based and nonparameteric kinetic analysis methods, the accurate recovery of meaningful kinetic parameters in small-animal imaging has been hampered by the lack of adequate methods to characterize arterial concentration. For this reason, fluorescence imaging of tracer distribution is often limited to semiquantitative assessments of tissue uptake and retention based on images acquired hours after tracer injection. The fluorescence intensity provides an indication of the molecular affinity of a targeted tracer to a particular tissue region, but also contains information about nonspecific uptake and retention. Alternatively, a reference tissue model such as DT-RCI [7] can be used, but an implicit assumption of this technique is that the arterial input functions of the two tracers are identical.

Here, an experimental method is presented to measure the arterial input function that does not require blood sampling or any additional instrumentation, and is independent of the choice of tracer being used. The approach involves surgically exposing a large artery (i.e., the carotid artery) by separating it from the surrounding tissue and inserting a black nonreflecting piece of polyvinyl cloth behind the artery to block fluorescence from the underlying and surrounding tissue. Following data acquisition, ROI corresponding to the exposed artery are selected from the image using a semiautomatic segmentation procedure, and concentration curves are calculated from the region-averaged fluorescence signal recovered for each time point. The approach was evaluated in vivo using female athymic nude mice and results were compared with previously reported direct blood sampling methods. As a corollary, the imaging approach was used to recover curves with high “first-pass” temporal resolution (500 ms). These methods are the first reporting of this approach and as is shown, will likely have significant utility in a range of applications.

Materials and Methods

Tracer Kinetic Theory

In tracer kinetics, the uptake of a tracer by the tissue can be described by the following convolution [10, 11]:

$$Q(t)=F[C_a(t)\ast R(t)]$$ (1)

where C_a(t) is the time-dependent arterial concentration of the tracer, F is the blood flow and R(t) is the impulse residue function which describes the fraction of tracer remaining in the elemental imaging volume at time, t, following an idealized bolus injection; in other words, R(t) is equal to Q(t) in the theoretical case where C_a(t) is a Dirac-delta function produced by administering a unit mass of tracer directly into the feeding artery of the ROI in a single instant of time.

The convolution in Eq. 1 forms the basis of modern tracer kinetic methods; analytical approaches can be further subdivided into parametric and nonparametric methods. Parametric methods explicitly model R(t) as a mathematical function—e.g., a single- or biexponential function or a more complex function such as the tissue homogeneity model [12] or the gamma capillary transit time model [4, 13]. Nonparametric methods recover the R(t) function without any prior mathematical definition of R(t) [14, 15] but are less stable than parametric methods for similar signal-to-noise ratio and temporal resolution. Both methods require that the time-dependent change in contrast for a tissue region/voxel, Q(t), and the artery, C_a(t), be characterized.

A third category of kinetic analysis has emerged first in PET, and then more recently in the case of optical DT-RCI, when C_a(t) is unavailable. In these “reference tissue” models, the molecular binding of a targeted tracer can be separated from the delivery and uptake of that tracer by using a reference region where tracer is known not to bind. The reference region can be spatially distinct (in the case of PET imaging [16, 17]) or can be made spectrally distinct through the dual injection of tracers fluorescing at different wavelengths [18, 19], as is the case in DT-RCI [6, 7, 19].

Animal Experiments

All animal experiments were carried out under an approved protocol from the Dartmouth Institutional Animal Care and Use Committee. Arterial input functions were characterized in a total of 12 female nude mice (Strain 01B74, National Cancer Institute, Frederick, MD) in this nonsurvival study. Animals were randomly placed into a slow-kinetics group (n=7) or a fast-kinetics group (n=5) to investigate two different imaging protocols, as described in the next section. Following induction of a surgical plane of anesthesia using 1.5–2 % isofluorane and oxygen, mice were surgically prepped for the imaging study. A sharp dissection of the neck was performed, and superficial tissue was removed to enable access to the underlying vasculature. Blunt dissection was performed with forceps, exposing both common carotid arteries by separating them from the connective and other surrounding tissue. Next, a piece of black polyvinyl cloth was placed behind the carotid arteries, occluding all tissue in the neck except for the two exposed arteries (Fig. 1). The arteries were irrigated with phosphate-buffered saline (PBS) and the entire neck area was covered in a transparent plastic wrap (Anchor Packaging, St. Louis, MO) to maintain moisture levels in the tissue. The animal was placed supine on the heated imaging bed of the imaging system, anesthesia was maintained, and all four limbs were restrained using medical tape.

Fig. 1.

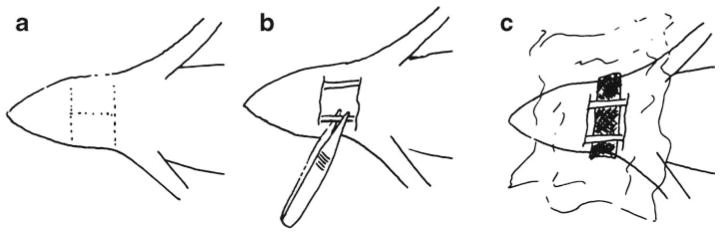
The surgical procedure used in the carotid imaging method. a First, the incisions are made in the skin, which is folded back or removed, creating a surgical window. b Lymph nodes, fat and other tissues are blunt dissected with forceps to expose the carotid arteries. c Black polyvinyl cloth that is optically opaque is placed behind the two carotid arteries. The surgical area is irrigated with PBS and covered with polyethylene film.

For animals in the fast-kinetics group, the tail vein was catheterized so that the bolus of tracer could be administered via plastic tubing while the animal was inside the closed imaging system. This was imperative for the fast-kinetics imaging protocol so that the first-pass curve could be properly characterized. Catheterization required a 30-Ga needle (BD Medical, East Rutherford, NJ) to be disassembled from the plastic female Luer taper fitting, and inserted into medical tubing about 0.5 m in length with a nominal inner diameter of approximately 0.3 mm (corresponding to the nominal outer diameter of a 30-Ga needle). The needle was heparinized, inserted into the tail vein of the mouse, and fixed in place by tape and surgical glue (Vetbond, 3 M, St. Paul, MN). To inject the optical tracer the IV line was loaded with PBS (approximately 75 μl). Then, 50 μl of tracer was pushed into the tubing, followed by a flush of 150 μl PBS, causing the tracer to be injected in its entirety in a single bolus. The amount of fluid introduced to the animal was limited to 200 μl, enabling complete injection of the tracer material without causing side-effects owing to hypervolemia. For the slow imaging group, injections were performed directly into the tail vain while the animal was supine on the imaging stage, and then the stage was moved into the scanner and closed within 30 s of the injection. Injections were performed over a duration of less than 3 s.

Data Acquisition

Images were acquired on a planar fluorescence imaging device (Pearl® Impulse, LI-COR Biosciences, Lincoln, NE) during injection (fast-kinetics group) and clearance of tracer (both groups). Two imaging protocols were examined—fast- and slow-kinetics protocols—with five animals in the fast-kinetics group, and seven animals in the slow-kinetics group. In the slow-kinetics protocol, fluorescence images were acquired every 30–35 s for 50 images, and then every 3 min for the remainder of the 2 h imaging time at a spatial resolution of 85 μm. At each time point, a white light image and two fluorescence images (700 and 800 nm emission wavelength) were acquired sequentially. In the fast-kinetics protocol, images were acquired at 255 μm resolution in three timing phases: every 0.5 s for 3.5 min, every 15 s for 8.5 min, and every 3 min for the remainder of the 2-h imaging time. In this case, only a single fluorescence image (800 nm emission wavelength) was acquired at each time point.

In the slow-kinetics group, 0.2 nmol of untargeted IRDye-700DX-C (LI-COR Biosciences) and 0.2 nmol of targeted IRDye800CW-EGF (LI-COR Biosciences) were administered simultaneously in 200 μl of PBS directly into the tail vein. In the fast-kinetics group, 0.1 nmol of anti-EGFR Affibody (Affibody Ab, Solna, Sweden) labeled with IRDye-800CW (LI-COR Biosciences) in 50 μl of PBS was administered in a single bolus injection using the catheterization method described in the previous section.

Blood sampled plasma curves for IRDye-700DX-C and IRDye-800CW-EGF, which have been previously published [20], were reanalyzed using the same biexponential model described below, so that they could be directly compared with the carotid imaging measurements. Collection of blood samples was performed following the tail vein injection of 1 nmol of each dye in 75 μl at selected time points. For each sample, 100 μl of blood were extracted via submandibular bleeding with a 5 mm lancet (Goldenrod; MEDIpoint, Mineola, NY) into a hepranized vial (Hospira, Lakeforest, IL). The blood samples were centrifuged (SD110; Marsh Bio Products, Rochester, NY) and fluorescence analysis was performed on the supernatant plasma using a spectrofluorometer (Fluoromax-3; Horiba Scientific, Edison, NJ). The plasma curves were characterized from 13 mice, but as blood could only be extracted three or four times per animal without altering the physiology of the animal, each time point reflected measurements acquired from only three mice. To minimize between-subject variability due to differences in bolus injection, all mice had a blood sample acquired at the 1-min time-point, to which the data were normalized. To allow proper comparison with the data collected from carotid imaging, blood-sampled curves were scaled by the difference in administered dose, which was five times higher than in the present study, and converted to arterial concentration by using an assumed hematocrit ratio of 0.45 [21].

Image Processing

Fluorescence images were imported into MATLAB (Version R2008a, MathWorks, Natick, MA) using an in-house developed routine. Images were preprocessed to remove autofluorescence by subtracting a pre-injection image from all subsequent images. Subsequent denoising of the images was performed by applying a 3×3 pixel 2D median filter (medfilt2 in MATLAB). A vessel segmentation algorithm was used to extract the pixels within the time series of images whose time-varying change in intensity was most strongly associated with the arterial concentration curve, C_a(t). This was done using a multistep process. First, a polygon ROI was manually drawn on the white light image around the region corresponding to the vessel. The centroid of the polygon was determined, and the time-dependent change in fluorescence at this single centroid point was used as a rough estimate for the arterial curve. Then, each fluorescence image in the time series was segmented into two regions (foreground and background) by thresholding, so that the region corresponding to the higher fluorescence values within the polygon ROI were averaged at each time point to recover an arterial curve. This procedure was repeated for 20 threshold values. The best threshold value was selected by minimizing the following cost function:

$$H(\tau ,\lambda )={\Vert \frac{C_{\tau }(t)-C_C(t)}{max(C_{\tau })}\Vert }_2+\lambda {\Vert \frac{\mathrm{d}{C}_{\tau }(t)/\mathrm{d}t}{max(C_{\tau })}\Vert }_2$$ (2)

where τ is the threshold level, C_τ(t) is the C_a(t) calculated from the region thresholded at τ, and C_C(t) is the C_a(t) calculated from the centroid point only. The second term of the cost function is a smoothness penalty scaled by λ (controlling the relative contribution of smoothness to the optimization) and is in unit of seconds. The value of λ was determined empirically, and λ=10 s was used to process all datasets.

To enable direct comparison between arterial input functions measured using the proposed technique, and plasma concentration data obtained by blood sampling, it was necessary to convert the relative fluorescence units measured by the imaging system to units of molar concentration. The placement of black cloth behind the vessel effectively reduces fluorescence originating from nonvessel tissue elements but increases the sensitivity of depth-dependent effects that arise in wide-field planar fluorescence imaging due to its inherent lack of depth resolution. Relative fluorescence units were therefore divided by the imaging element volume, to account for the differences in RFUs that arise when vessels of different volumes but identical dye concentrations are imaged. The volume was approximated by measuring the vessel diameter directly from the average enhancement image. This was used to determine the average vessel thickness in the direction into the plane of the image, which was subsequently multiplied by the voxel area (determined by the resolution of the system). Following the volumetric correction, molar concentration was calculated using dye-specific calibration curves of volume-normalized RFUs versus concentration.

Biexponential Fit of Recovered Arterial Curves

Excepting the first-pass component, the arterial curves were fit to the biexponential pharmacokinetic model of type: ae^−bt+ce^−dt. Optimization was performed using the lsqcurvefit function in MATLAB which implements a trust-region-based nonlinear minimization method [22]. Nonnegative constraints were placed on all parameters, and stopping criteria based on the minimum parameter step size of 1×10⁻⁶ (‘TolX’) and minimum change in the objective function of 1×10⁻⁶ (‘TolFun’) were used. All values are presented as group mean±standard deviation (SD) unless otherwise indicated.

Results and Discussion

A representative example of an image acquired with the slow-kinetics protocol for a single time point (1 min postinjection; 15 s integration time; and 85 μm spatial resolution) during tracer circulation is shown in Fig. 2. Note the enhancement of the vessel, which shows good signal-to-background contrast over the inserted black fabric backing. Images acquired with the fast-kinetics protocol demonstrated diminished signal-to-noise characteristics; however, this was reduced with median filtering, and did not appreciably affect the performance of the vessel segmentation algorithm.

Fig. 2.

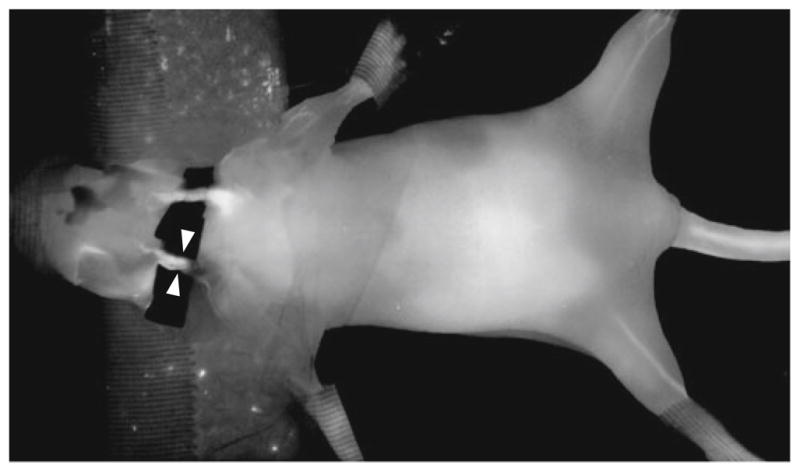
A single time point image acquired on the LI-COR Pearl fluorescence imaging system during injection of tracer (t = 1 min), showing carotid artery enhancement (arrows).

Following preprocessing, vessel segmentation, and calibration, the vessel pixels were averaged to obtain concentration curves for each channel. The curves obtained with the slow-kinetics protocol for the two tracers, injected simultaneously, is depicted in Fig. 3. To facilitate comparison with the blood sample measurements, biases in the data were estimated and subtracted based on the assumption that the arterial concentration after five half-lives is zero. For the carotid imaging technique, a high degree of reproducibility was observed across all time points for both tracers; across all animals (n=7) and time points, the mean coefficient of variation was 5.0±1.4 % for the IRDye700DX-C and 4.4±1.3 % for the IRDye800CW-EGF. By comparison, the mean coefficient of variation for the blood sampling technique was 22.5±17.5 and 13.7±10.0 % for the IRDye700DX-C and IRDye800CW-EGF, respectively. In other words, the variability of the carotid imaging data was about four times less than the blood sampling data.

Fig. 3.

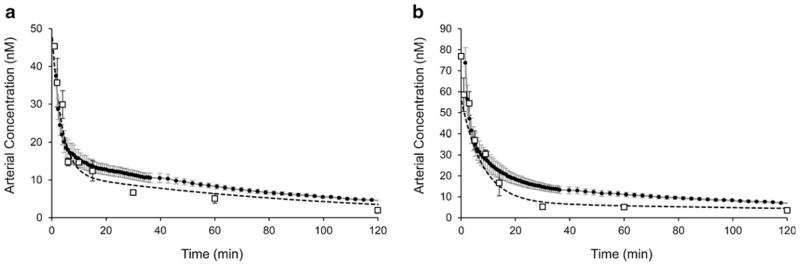
Arterial input functions measured by carotid imaging (solid circles) compared with blood sampled measurements (open squares) for a IRDye700DX-C and b IRDye800CW-EGF. Dashed lines represent the curves of best fit to the blood sampled data and correspond to the biexponential model values reported in the text. Error bars for the carotid imaging technique (gray bars) and the blood sample technique (black bars) are standard deviation.

The biexponential pharmacokinetic model was used to assess the distribution and elimination characteristics of the arterial curves obtained with the two methods, and for the two tracers. The biexponential model was fit to arterial curves recovered for each animal, and group averages were computed. In addition, the group average arterial curve recovered from blood sampling was fit with the biexponential model. The distribution and elimination rate constants (corresponding to model parameters b and d, respectively) recovered from arterial curves measured by carotid imaging were 0.37±0.26 and 0.007±0.001 min⁻¹ for the IRDye700DX-C. For the IRDye800CW-EGF, the rate constants were 0.11±0.13 and 0.003±0.002 min⁻¹, respectively. In comparison, the parameters recovered from fitting the blood sampling data were 0.28±0.05 and 0.01±0.006 min⁻¹ for the IRDye700DX-C and 0.13±0.01 and 0.004±0.002 min⁻¹ for the IRDye800CW-EGF. The pharmacokinetic parameters obtained with the two techniques were not significantly different for either the IRDye700DX-C (F_{2, 10}=0.67, p=0.47) or the IRDye800CW-EGF (F_{2, 10}=0.84, p=0.39), as determined by an F test of the error norms between the blood sampled data and the curves generated by the two sets of kinetic parameters [23]. This suggests that the differences in rate constants were due to variability in the data and not model-dependent differences. The normalization and bias subtraction previously described did not affect the recovered parameters or the results of the rate constant comparisons.

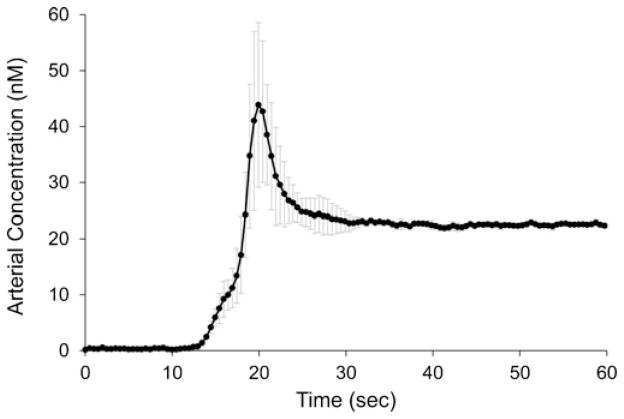
The mean arterial input function obtained with the fast-kinetics protocol for the anti-EGFR Affibody IRDye800CW is presented in Fig. 4. The first-pass peak—which is necessary to calculate of blood flow, extraction fraction, and blood volume [12]—is clearly discernible in these measurements. This is of particular significance given the high heart rates of mice (about 900 beats/min), which reduces the width of the arterial peak [24]. A high degree of reproducibility was also observed for the distribution and elimination phases of the arterial curves collected with the fast-kinetics protocol; the coefficient of variation after the first-pass and recirculation (t>1 min) was 2.5 %. The coefficient of variation during the first-pass (t≤1 min) was much higher at 51 %, owing to the variability in bolus injections, as well as the technique itself. The large variability in how the injection is administered suggests that first-pass kinetic analysis depends on proper characterization of the arterial input function. Given the ability to capture the first-pass dynamics of the arterial input function, more complex tracer kinetic methods can be utilized. In particular, methods that enable the recovery of blood volume and extraction fraction could provide new information in preclinical studies [4].

Fig. 4.

Mean anti-EGFR affibody IRDye800 arterial input function for the first 60 s acquired with the fast-kinetics protocol. Values are the means from n=5 mice, and error bars are the standard deviation. The temporal resolution during this phase was 500 ms.

The results of the semiautomatic vessel segmentation procedure are depicted in Fig. 5. Arterial curves obtained in this representative sample varied substantially across threshold values. The biexponential model was fit to the arterial curve recovered with each threshold value; coefficients of variation for the pharmacokinetic rate constants were 115 and 27 %, for b and d, respectively. The large variability dependent on grayscale threshold value highlights the importance of proper vessel segmentation. By optimizing the threshold value according to the procedure described above, vessel boundaries that were too conservative (resulting in a noisy curve) and vessel boundaries that were too liberal (resulting in background pixels that contribute to a deviation from the centroid arterial curve) were avoided. The result is a lower coefficient of variation because of the extravascular tissue that could not be completely removed during the surgical process.

Fig. 5.

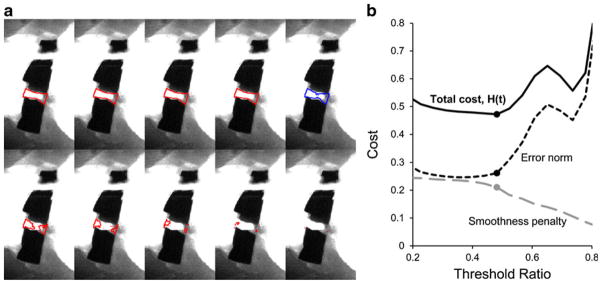
a Segmented vessel region based on a range of threshold values (increasing in value). The lowest threshold values accept the largest area of pixels but begin to deviate from the true plasma curve due to partial volume errors with the background pixels. Highest threshold values accept only a small number of pixels of greatest mean intensity, resulting in a nonsmooth plasma curve. b The cost function (H(τ)) seeks to minimize the error norm while maximizing smoothness.

A major limitation of the proposed technique is that it is highly invasive: it requires surgical exposure of major blood vessels and therefore cannot be used repeatedly in the same animal. Furthermore, owing to the complexity of the surgical intervention, the mortality rate from surgical complications (principally, accidental severing of the carotid artery leading to exsanguination) was approximately 12 %. Therefore, the invasiveness of this method may limit its use in certain applications, such as in longitudinal studies. However, there are possible solutions which can be considered on a case-by-case basis. For instance, it may be possible to use a population-averaged arterial input function in the kinetic analysis; in this case, a subgroup of animals are used to characterize the arterial input functions for one or more tracers, and then these curves are used in the kinetic analysis of data collected longitudinally, from the other animals. Further work is necessary to determine the effect of using a population-averaged arterial curve, versus individually characterized ones, for a given kinetic analysis. An additional limitation of this method is that it requires highly sensitive planar imaging equipment with high dynamic range. This was achievable using the Pearl Impulse device, which reports a dynamic range of approximately 10⁴–10⁶ [25]. The extension of this technique to other imaging modalities requires careful evaluation. One limitation that must be considered in some applications is whether the receptor targeted by the tracer is expressed on the vessel wall, or whether any ubiquitous receptors on the vessel wall might bind the tracer nonspecifically. In this case, the clearance rate constants determined from vessel measurements will be slower than the actual values. Finally, although the validation portion of this study showed that rate constants recovered by fitting the data acquired with the two techniques were statistically equivalent, the real test for this method will be the degree to which it enables quantitative kinetic analysis of tissue ROI.

Despite these limitations, there are some important benefits to using the proposed technique. In particular, arterial input functions collected directly from planar fluorescence images are characterized in the same measurement space as the rest of the image. A common problem in fluorescence imaging is how to relate measured fluorescence intensity to actual fluorophore concentration. Therefore, it is not trivial to combine plasma or arterial input functions measured in absolute concentration units (e.g., nM)—such as those obtained with blood sampling or a pulse dye densitometer—with fluorescence imaging data in units of intensity. Proper calibration requires correcting for the detector efficiency, fluorophore quantum efficiency, autofluorescence, and surface light absorption and scatter. Furthermore, plasma concentration and arterial concentration differ by a scaling factor that is related to the hematocrit ratio if there is no blood–cell-specific binding. By acquiring input functions in the same measurement space as the optical image data, quantitative binding and retention kinetics can be performed without extensive calibration of optical images, since the same scaling factors will influence the arterial and tissue curves equally. Alternatively, the approach used in this paper can be used to convert fluorescence measurements to arterial or plasma concentration units, for applications where quantification of those functions—and additionally, blood flow, blood volume, and the leakage rate constant (K₁)—is desired.

In addition, the current gold standard—blood sampling—can be problematic in small animals. Only a limited number of samples can be acquired from each animal, and thus a large number of animals are often required to properly characterize a population plasma curve for a given combination of optical tracers. Furthermore, the processing of the blood samples, which involves centrifugation and separation from red blood cells, can introduce a number of potential experimental errors. In fact, a constant bias observed between the two techniques (representing approximately 5 % of the maximum) was removed before data were plotted in Fig. 3. It was not known whether this bias was attributable to blood sample processing, or an error present in the carotid imaging data.

Finally, as the proposed technique does not require additional instrumentation, it can be readily implemented into existing small animal imaging frameworks. When combined with more advanced kinetic analysis methods, the proposed technique has the potential to improve the quantification of molecular expression and kinetics. Additionally, the use of the fast-kinetics protocol may enable characterization of kinetic parameters that have not been previously accessible in preclinical imaging. Extension of this imaging approach could be done for other major vessels as well, which has not been explored here, but depending upon the application may be important to consider.

Conclusions

Quantitative tracer kinetics analysis is a relatively nascent field of optical imaging; however, methods are emerging that could provide important insight into cancer biology, drug distribution, and disease progression. The quantification of kinetic parameters depends in part on the proper characterization of tracer arterial input functions. This proof-of-principle study demonstrates that a surgically exposed major artery, such as the common carotid artery, can be imaged directly using current planar fluorescence systems to characterize arterial concentration curves.