Fast and Accurate Calculation of Protein Depth by Euclidean Distance Transform

Abstract

The depth of each atom/residue in a protein structure is a key attribution that has been widely used in protein structure modeling and function annotation. However, the accurate calculation of depth is time consuming. Here, we propose to use the Euclidean distance transform (EDT) to calculate the depth, which conveniently converts the protein structure to a 3D gray-scale image with each pixel labeling the minimum distance of the pixel to the surface of the molecule (i.e. the depth). We tested the proposed EDT method on a set of 261 non-redundant protein structures. The data show that the EDT method is 2.6 times faster than the widely used method by Chakravarty and Varadarajan. The depth value by EDT method is also highly accurate, which is almost identical to the depth calculated by exhaustive search (Pearson’s correlation coefficient≈1). We believe the EDT-based depth calculation program can be used as an efficient tool to assist the studies of protein fold recognition and structure-based function annotation.

1 Introduction

For a given protein tertiary structure, many residue level attributions can be extracted, such as the secondary structure type, dihedral angle and solvent accessibility. Those structural features help establish the properties of different amino acid types and categorize protein structure folds. For example, Ramachandran plot [1] revealed that the distribution of backbone dihedral angles (or the secondary structure) was highly regulated. Solvent accessibility (SA) evaluates the hydrophobicity of amino acids in different protein structures, which can be calculated accurately by EDTSurf [2] or approximately by DSSP [3].

However, SA usually specifies the residues in a binary form. For the residues that are completely buried in protein, it does not describe where the residues locate inside the molecule. Depth, which measures the distance of each atom/residue to the solvent accessible surface in a continuous form, greatly complements the missing information by SA. In fact, the depths of residues in a protein are highly related to their effects of mutations on protein stability and on protein-protein interactions [4]. The residue depth has also been widely used to specify protein folds in protein structure prediction [5–7] and assist structure-based protein function annotation [8].

Despite the importance, by far there are very few methods which can calculate the depth for protein structures efficiently at either an atom level or a residue level. In Ref. [4], Chakravarty and Varadarajan proposed to calculate the residue depth by rotating the protein in a box where the closest water molecule is identified for each atom in the protein. The accuracy of the method is compromised since the calculated depth value depends on the positions of the water molecules. One can also calculate the depth by first generating the explicit solvent accessibility surface (e.g. by EDT-Surf or MSMS [9]) and then identifying the vertex on the triangulated surface which is the closest one to the atom [10–11]. However, the computation of this kind of method is quite time-consuming since all the atoms in the protein need to be searched against the huge number of vertices on the surface.

In a recent study, we have established the relationships between the three kinds of macromolecular surfaces and Euclidean distance transform (EDT) theoretically and developed a fast algorithm for generating their triangulated surfaces precisely [2]. In this work, we apply the EDT technique to the calculation of protein atom depth and residue depth. The algorithm is fast since the explicit triangulated surface is not required. To investigate the efficiency and accuracy of this method, we compare the computational time and depth value with that by Chakravarty and Varadarajan (CV). We also analyze the relations of the depth with the commonly-used radius of gyration and solvent accessibility. The source code and executable program are freely available at http://zhanglab.ccmb.med.umich.edu/EDTSurf/.

2 Material and Method

2.1 Depth Definition

Atom depth is the shortest distance between the center of the atom and the outer solvent accessible surface (SAS) of the molecule, as illustrated in Fig. 1. SAS is the area traced out by the center of a probe sphere when it is rolled over the whole molecule [12]. When one atom is exposed (e.g. atom i in the figure), its depth will equal to the sum of the van de Waals radius and the radius of the probe sphere r_p which is often set to 1.4 Å. For atoms which are completely buried inside (e.g. atoms j and k in the figure), their solvent accessibilities are all equal to zero, but their depths may be different. Residue depth is the average value of the atom depths of all the atoms in a residue.

Fig. 1.

Illustration of three atoms with different depth values in a 2D plane. The outside boundary stands for the solvent accessible surface

The definition of depth by Chakravarty and Varadarajan is a little different, which is the shortest distance to the explicit bulk water rather than the solvent accessible surface. Since water molecules don’t have spherical shapes and may have different poses around the molecule, this difference will result in the slightly different depth values.

2.2 Euclidean Distance Transform

Euclidean distance transform (EDT) is the transformation that converts a digital binary image to another gray-scale image where the value of each pixel is the minimum Euclidean distance between that pixel and the boundary. We have developed a fast algorithm which can conduct EDT in arbitrary dimensional space [13]. EDT has been widely used in the fields of image processing and computer graphics, such as skeleton extraction [14], shortest path planning [15] and geometric shape description [16].

Given a protein structure, we suppose it has N atoms, each of which locates at p_i and has a van der Waals radius r_i. To calculate the atom depth in this protein, we first build the solvent accessible solid using equation (1), which is the union of all the spheres with radius equal to the sum of the van der Waals radius and the radius of the probe sphere. The union operation is conducted in the discrete 3D space using space-filling technique, with each sphere represented by a set of grid points.

$$O_{SA}=\underset{i=1}{\overset{N}{\cup }}\mathit{\text{sphere}}(p_i,r_i+r_p)$$ (1)

Then we can easily determine the outer shell of the solvent accessible solid, which is the discrete representation of solvent accessible surface. We do the EDT transform to the shell and can get the shortest Euclidean distance of each point to the shell, which happens to be the depth value of this point. Although there are other distance functions, such as City-block distance and Chessboard distance, only Euclidean distance has the direct relationship to the three macromolecular surfaces as well as the depth.

In the original CV method and its recent extension [17], non-bulk water molecules are removed in the regions of narrow cavities and internal voids. Otherwise, atoms around those regions will have small values of depths. Using equation (1), the solvent accessible solid has already filled most of the empty space in the same regions since the radius of each atom is enlarged by the radius of the probe sphere. Therefore, the two methods have consistent depth values in those special regions.

Fig. 2 shows an example of the EDT result to the same shape of the SAS in Figure 1, where the red curve stands for the SAS. After the EDT transform, every position has a shortest distance to the SAS, as represented by the gray-scale pixel value in the image. The lighter the point is, the longer distance to the surface it will have. Based on the definition of the depth, we can see that the gray-scale pixel value calculated by the EDT at each point exactly is the depth value of that point. In the figure, the centers of the three atoms, as represented by the blue dots, have different depth values.

Fig. 2.

Illustration of the EDT to the solvent accessible surface (in red) in a 2D plane. Centers of the three atoms are marked in blue.

Solvent accessibility of each residue is defined as the ratio of the total SAS area of all the atoms in the residue to the maximum SAS area of that residue type. Hence, we have to build the explicit triangulated surface from the discrete shell by surface triangulation algorithms such as the Marching Cube method [18]. Different to the solvent accessibility derivation, depth calculation doesn’t require the generation of the explicit triangulated SAS.

Given the shell of the discrete SAS, we can also calculate the depth of each atom by exhaustive search (ES). That is to say, we search for the point on the shell which is the closest to the center of the atom.

3 Result and Discussion

3.1 Visualization of Depth

In order to visually check the depth information generated by the method described above, we have embedded the EDT-based depth calculation algorithm into our Macromolecular Visualization and Processing (MVP) program, which can be downloaded at http://zhanglab.ccmb.med.umich.edu/MVP/.

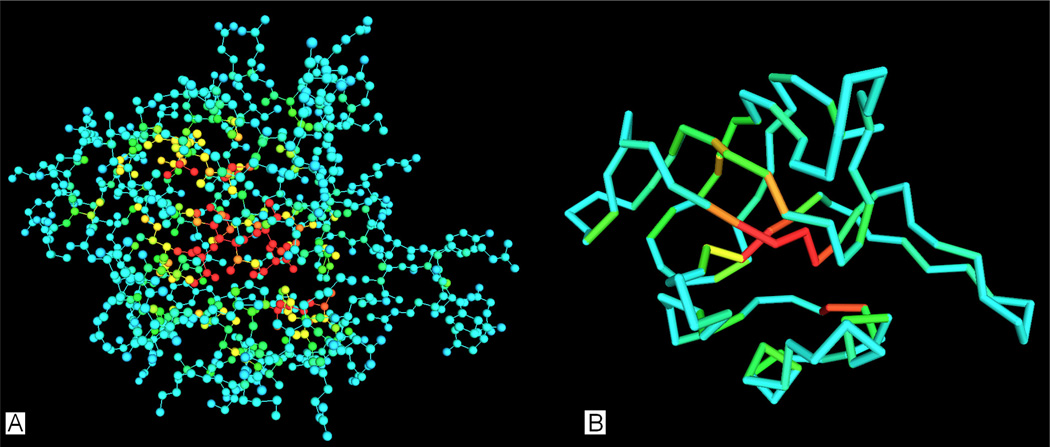
Fig. 3 shows two snapshots of the MVP visualization result of a hypothetical protein from thermus thermophilus HB8 (PDB ID: 1whz, chain A), which contains 122 residues and 937 atoms. Atoms in the left figure are in the ball-stick style. Red color means high value of atom depth while blue means low. In the right image, we show the protein backbone structure where the color of each residue is also correlated with its residue depth. From both images, we can clearly see the layers of the protein structure, especially the hydrophobic core which is in red.

Fig. 3.

(A) atom depth (B) residue depth of the protein 1whz chain A

3.2 Depth Distributions of Different Residue Types

Since different residue types have different hydrophobicities, their depth distribution should also be different. Therefore, we choose 36,556 protein domains used by our threading programs [6,19] for validation, which can be downloaded at http://zhanglab.ccmb.med.umich.edu/library/. Those structures are non-homologous to each other with sequence identity cutoff 70%. Protein chains which contain multiple domains are discarded from the list in this test, because multiple-domain proteins are often not well-packed.

The distributions of residue depths of the 20 residue types are summarized in Fig. 4, which are arranged in the order of their hydrophobicity scales [20]. Residue depths normally are in the range of 2.9 Å and 8.9 Å. Almost all the residue depths are less than 5 Å for the 8 hydrophillic residues on the top 2 rows. TRP and SER have similar hydrophobicities, but TRP has more depths which are deeper than 5 Å. This is probably because TRP has a longer side-chain and its depth can be large even part of the residue is exposed. For the 6 most hydrophobic residues on the bottom two rows, more depth values are around 6 Å than the hydrophillic residues. However, majority of the depths are still close to 3.1 Å, which means many hydrophobic residues still locate around the surface of the domain structures. It is understandable if the protein is stable only in the complex form instead of the monomeric form. Hydrophobic residues in the interface will have deep residue depths if we treat the complex as a whole.

Fig. 4.

distributions of residue depths for the 20 residue types

3.3 Comparison of Depth Generation Methods

We compare the depth results by the algorithm described by Chakravarty and Varadarajan (CV) and exhaustive search (ES) and EDT-based method (EDT) mentioned above. The test set here we choose contains 261 non-homologous protein chains randomly selected from the PISCES list [21]. We rotate each protein at 25 different orientations and find the shortest distance to the outer water molecule for each atom in the CV algorithm. For both ES and EDT, we first enlarge each protein 4 times and put it into a bounding box. Then we create the voxel shell which represents the solvent accessible surface. ES method directly searches the closest voxel for each atom without using EDT. EDT method only requires the EDT to the voxel shell to get the depth value for each atom.

We first compare the similarities of the depth values generated by the three methods. The Pearson’s correlation coefficients (PCC) of the depth values by the three kinds of methods are shown in Table 1. Results by ES and EDT methods are highly close to each other. Although CV method is quite different to the other two, it still has a high correlation (>0.90) with them.

Table 1.

Comparison of the residue depths by methods of Chakravarty and Varadarajan (CV), exhaustive search (ES) and EDT-based method (EDT)

		CV	ES	EDT
	CV	1.00	0.91	0.90
PCC	ES	0.91	1.00	1.00
	EDT	0.90	1.00	1.00
Time(sec)		2.23	1.69	0.88

The difference of the depth values by CV and EDT mainly comes from two sources. First, the depth definitions by the two methods are slightly different, which have been described before. Second, since CV is an approximation method, depth value is highly dependent on the water molecules placed outside of the protein. Sometimes the depth value is close to the real depth if the water molecule happens to be the closest one while sometimes it doesn’t. In contrast, depth values calculated by ES and EDT are close to the real one. The only error is caused by the discretization of the protein which makes the discrete shell not exactly the same as the actually continuous SAS.

We then compare the average computational time by the three methods, which is listed in the last row of the Table 1. The calculation is performed on a single node with a 2.27 GHZ Intel E5520 Xeon processor and 24 GB memory. EDT method is 2.6 times faster than CV and 1.9 times faster than ES. We can imagine the CPU time taken by the ES method will increase rapidly if we increase the scale factor to get more accurate SAS shell. We have also tried the new version of the DEPTH program using the CV method in [17], which takes even longer time (data not shown) due to the extensive search for the non-bulk water molecules.

Compared with the accuracy, speed may be not an issue if we only calculate the depth once for a given protein structure. However, a lot of computational resources could be saved if depth information of thousands of structures has to be calculated. For example, in the application of protein fold recognition, the non-redundant template library often contains more than 30,000 protein chains/domains extracted from the Protein Data Bank (PDB) [22].

3.4 Depth vs. Radius of Gyration

The radius of gyration (RG) refers to the root mean square distance of the protein atoms from the center of gravity. Due to the simplicity of calculation, RG has been widely used to characterize the global shape and compactness of protein tertiary structures in protein structure prediction [23] and function annotation [24]. However, due to the high specificity of protein tertiary structure packing, the simple RG calculation cannot precisely reflect the shape and residue distribution related to the exposed surfaces on specific proteins. In this section, we examine the quantitative relation of RG and depth calculated from EDT technique which highlights the advantage of depth in characterizing the overall shape of protein tertiary structures.

We compare the radius of gyration with the maximum residue depth (MD) and the average residue depth (AD) in Fig. 5(A) and 5(B) separately. The data are acquired still based on the 36,556 domain structures in our threading template library. In the left figure, we can see that the two features have some correlation in most of the regions. Most times, when the radius of gyration is large, the maximum depth will also be high. Especially when the protein structure is compact and has a globular shape, its maximum depth will be highly correlated with its radius of gyration, such as the protein in Fig. 6(A). It is the chain A of the Desulfovibrio vulgaris apoflavodoxinriboflavin complex (PDB ID: 1bu5), which has the radius of gyration around 14 Å. Since the five beta-strands and four helices are densely organized, the maximum depth is also very high and very close to the radius of gyration.

Fig. 5.

Comparison of the radius of gyration with the maximum residue depth in (A) and the average residue depth in (B). Reduced number of points are shown in the figure by Origin

Fig. 6.

Cartoon style of two protein chains with color representing the residue depth. (A) 1bu5 chain A, radius of gyration=13.840Å, maximum depth=10.459Å (B) 1ijg chain L, radius of gyration=30.428Å, maximum depth=7.603Å.

There are also exceptions where the radius of gyration is high but the maximum depth is extremely low. This is because some single-domain proteins (e.g. a superlong helix) have a loose shape which makes the depth values of most residues very low. Fig. 6(B) shows the chain L of the Bacteriophage phi29 head-tail connector protein (PDB ID: 1ijg). If we solely consider this chain, only one end is well-shaped. There are three other helices in the middle, which connect the other end with two short beta-strands and one short helix. This structure has an extremely large radius of gyration of 30 Å. However, since this chain is not compact and most of the residues are exposed, the maximum depth is only 7.603 Å.

The scatter plot between the average depth and the radius of gyration in the Fig. 5(B) has the similar distribution to that between the maximum depth and the radius of gyration in Fig. 5(A). This is because the Pearson’s correlation coefficient between the maximum depth and the average depth is very high (0.92 in Table 2).

Table 2.

Pearson’s correlation coefficients between the four global features

	RG	RS	MD	AD
RG	1.00	0.96	0.07	0.02
RS	0.96	1.00	0.05	−0.02
MD	0.07	0.05	1.00	0.92
AD	0.02	−0.02	0.92	1.00

Another measurement of the overall shape is the radius of the bounding sphere (RS), which is the minimum radius of the sphere which could cover all the atoms in the protein structure. It has a very high correlation (0.96) to the radius of gyration, which is probably because the center of the bounding sphere is close to the center of gravity for most proteins.

All the PCC values between the four global structural features are listed in Table 2. Due to the irregular shapes of some proteins, RG and RS have no obvious correlations with the maximum and average depths. For RG and RS, distance calculations are between the positions of all the residues and one fixed point (e.g. the center of gravity or the center of the bounding sphere). Those distances have no strong physical meaning when the protein has non-globular shape and residues are far away from this point. For depth, different atoms have different closest points on the SAS.

From the above analysis, we can draw the conclusion that RG and RS are very rough measurements of protein shapes. The maximum/average residue depth provides non-redundant information to RG/RS. They can help characterize the unique features of protein tertiary structures including the overall 3D shape and in particular the residue distribution relative to the surface exposition.

3.5 Depth vs. Solvent Accessibility

The range of solvent accessibility value is in [0, 1] after we normalize the SAS area by the maximum SAS area of each residue type. For the residues which are partially exposed to solvation, they may have the same solvent accessibility but different depth values due to the various sizes of the different residue types. By comparing the nonzero solvent accessibility and residue depth for each residue type based on the 36,556 protein domains, we find that SA and RD follow an exponential function:

$$RD=y+A\times e^{-SA/t}$$ (2)

In Table 3, we list values of the three parameters in equation (2) for all the 20 amino acids. As expected, those parameters are different for different residue types. The amplitude parameter A seems proportional to the size of each amino acid. For example, small amino acids GLY and AlA have small amplitudes while large amino acids ARG and TRP have big amplitudes. Hydrophillic residues tend to have a larger t parameter, such as ARG and LYS while more hydrophobic residues have a higher y parameter, e.g. PHE and ILE.

Table 3.

Parameters of the exponential functions for the 20 amino acid types

	y	A	t		y	A	t
ARG	2.96	1.20	0.14	SER	2.89	0.84	0.11
LYS	2.96	1.18	0.16	THR	2.97	0.90	0.12
ASN	2.93	0.98	0.11	GLY	2.87	0.64	0.06
ASP	2.91	0.97	0.11	ALA	2.96	0.77	0.07
GLU	2.92	1.09	0.12	MET	3.08	1.17	0.08
GLN	2.95	1.09	0.12	CYS	2.93	0.98	0.11
HIS	3.00	1.20	0.11	PHE	3.17	1.29	0.07
PRO	3.04	0.83	0.11	LEU	3.16	1.05	0.06
TYR	3.08	1.35	0.10	VAL	3.13	0.95	0.07
TRP	3.12	1.44	0.10	ILE	3.18	1.05	0.06

In Fig. 7, we compare the solvent accessibility and residue depth for aspartic acid as an example. Generally, points in the scatter plot follow the exponential function, as illustrated by the black fitting curve. Depth difference is not significant when the solvent accessibility is high, which means that the majority of the residue is exposed. However, when SA is low (majority is buried), depth values can be quite different. Two reasons may cause the diversity of the depth values. The first one is the different relative positions and orientations of the residue to the solvent accessible surface while the other is the different side-chain conformations. The shape of each residue type is not unique due to the degrees of freedom of the side-chain torsion angles.

Fig. 7.

Scatter plot of the solvent accessibility and residue depth for aspartic acid. Black curve is the fitting curve by an exponential function. Reduced number of points are shown in the figure by Origin.

4 Conclusions

We have developed a computational algorithm for the fast and accurate calculation of the atom/residue depth through Euclidean distance transform. The method was tested on a set of 261 non-redundant protein structures. It was shown that EDT-based method is 2.6 times faster than the widely-used method developed by Chakravarty and Varadarajan but the accuracy of the EDT-based method is higher than that of the latter compared to the actual depth from exhaustive search.

The depth data are systematically analyzed in the large-scale proteins that cover the entire PDB library at the sequence identity cutoff of 70%. It is found that the maximum/ average residue depth has no obvious correlation with the commonly-used radius of gyration and radius of the bounding sphere. Hence, the maximum/average depth could be considered as a new geometric feature for describing the global shape of a protein tertiary structure. It is of potential use for protein fold classification and structure comparison.

When the residue is not completely buried inside of the protein molecule, solvent accessibility and residue depth follow an exponential relation. Different residue types have different parameters of the fitting functions and different distributions of residue depths even their hydrophobic scales are close to each other. The various sizes of the amino acids seem to be the major factor which causes the difference.

When the residue is completely buried inside of the protein, residue depth becomes a useful measurement as the solvent accessibility remains zero in this situation. It could be used as a complementary feature to the solvent accessibility for improving the fold recognition and the structure-based protein function annotation.

The source code and executable program for computing the atom depth and residue depth are freely available at http://zhanglab.ccmb.med.umich.edu/EDTSurf/. The associated software MVP (Macromolecular Visualization and Processing) for visualizing the depth information is at http://zhanglab.ccmb.med.umich.edu/MVP/.