REDUCED INTENSITY IN GAIT-SLIP TRAINING CAN STILL IMPROVE STABILITY

Abstract

Perturbation training with “free” slips (i.e., with long slip distance) has been able to successfully improve stability and to reduce the incidence of falls among older adults. Yet, it is unclear whether a highly constrained training with reduced slip distance (and hence training intensity) can achieve similar effects. The purpose of this study was to investigate whether short-distance slips could also improve the control of stability, and whether such improvements could be generalized to a novel, “free” slip. Thirty-six young subjects were randomly assigned to either one of the two training groups, which underwent seven training trials with constrained slips of either 12-cm or 18-cm in distance before encountering a novel, “free” slip (up to 150cm) in the test trial; or the control group, which only experienced the same test trial of a novel, “free” slip. The results showed that while both training groups were able to significantly improve their control of stability in training; the 18-cm group had significantly better reactive control of stability than the 12-cm group. During the “free” slip, such advantage enabled the 18-cm group to exhibit significantly less balance loss incidence than 12-cm group (58.3 vs. 83.3%) and the controls (100%). These differences could be fully accounted for when we assume that the central nervous system directly controls slip velocity or slip distance during adaptation, whereby the level of similarity between training trials and the test trial governs the degree of generalization. The findings that low intensity training may still improve stability warrant further investigations among older adults.

INTRODUCTION

Falls are among the most serious problems facing older adults, which can cause injuries and even death (Nyberg et al., 1996). Slips comprise 40% of outdoor falls among older adults (Luukinen et al., 2000). Therefore an effective training program to prevent sliprelated falls is highly desired. An emerging paradigm relies on perturbation training to reduce fall-risk (Bhatt et al., 2006; Parijat and Lockhart, 2012; Shimada et al., 2004). Repeated-slip exposure, for instance, forces the central nervous system (CNS) to adopt proactive (feed-forward) and reactive control strategies that, even if unconscious, can improve the control of the center of mass (COM) stability relative to the slipping base of support (BOS), and consequently lead to the reduction in the likelihood of falls. Such training-induced adaptive changes can reduce fall incidence by nearly 50% among older adults (Pai et al., 2010).

While these results are very promising, inducing slips-and-falls might be of some concern among frail elderly or those who are not in physical conditions to tolerate such training. The first novel slip can travel up to 0.7m (Yang and Pai, 2007) at a peak speed of 2.51m/s (Yang et al., 2009). It is unknown whether and to what degree that repeated slips with short-distance (constrained) could still elicit training adaptation and the generalization of such training effects to a different context upon encountering a novel and “free” slip in real-life. Logically, low intensity training with shorter slip distance and lower peak slip velocity could be more conducive and likely safer among frail older adults.

The purpose of this study was, therefore, to investigate whether short-distance slips could also improve the control of stability, and whether such improvements could be generalized to a novel, “free” slip. Two training groups first underwent training with short-distance slips (12-cm or 18-cm), and were then exposed to a novel, unconstrained, “free” slip with a maximum allowable slip distance up to 150cm. We hypothesized that both training groups could generalize the improved response to the “free” slip in comparison to the control group’s response to the same “free” slip. Because 18-cm slip would have closer resemblance to the “free” slip than did the 12-cm slip, we also expect the former group will perform better than did the latter during slip recovery upon the novel “free” slip.

METHODS

Subjects and experimental setup

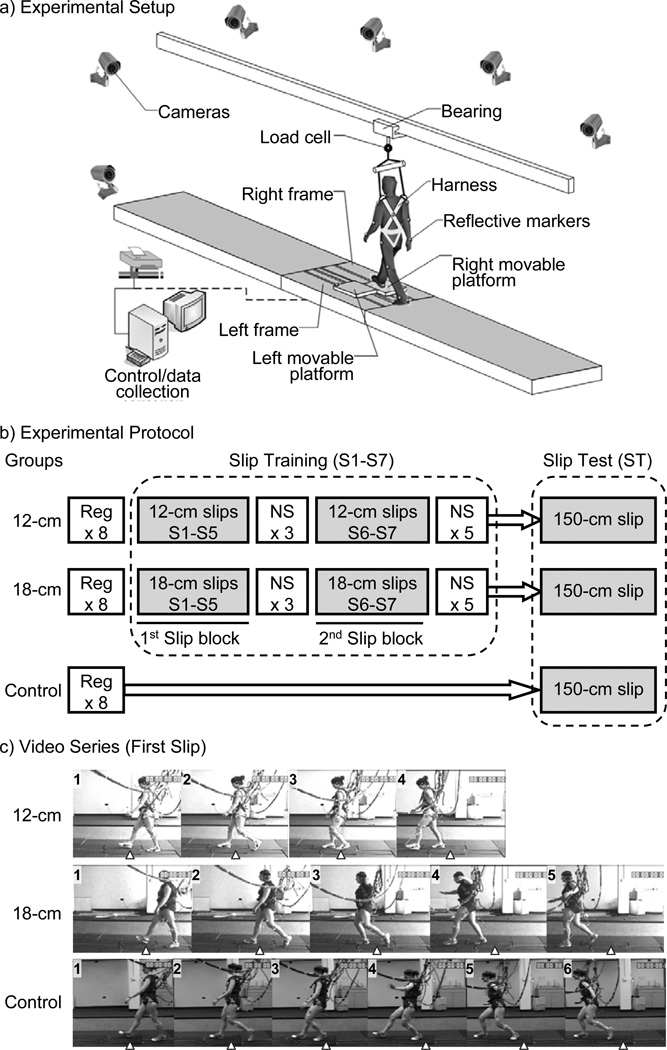
Thirty-six healthy young adults (24.9±3.7 years) participated in the institutionally approved study (Table 1). Unexpected slip perturbations were induced as subjects walked along a 7-m walkway in which a sliding device was embedded (Fig. 1a). The device consisted of a pair of low-friction, passively movable platforms each mounted upon a metal frame supported by two individual force plates (AMTI, Watertown, MA) for recording the ground reaction force (Yang and Pai, 2007). Only the right platform was used to induce slip in the present study. Once released on slip trials, the platform was “free” to smoothly slide forward up to 1.5m without the stoppers installed on the tracks. During the training, the stoppers were installed along these tracks to reduce the slip distance under the constrained conditions. The platform release was automatically achieved by a computer-controlled program. All subjects wore a safety harness, which was linked through a load cell to a ceiling-mounted beam during walk (Fig. 1a).

Table 1.

The demographics in mean ± SD for two training groups (12-cm and 18-cm) and the control group.

Groups	12-cm	18-cm	Control	p value	Pooled
	(n = 12)	(n = 12)	(n = 12)		(n = 36)
Age (years)	24.4 ± 3.2	23.6 ± 3.4	26.6 ± 4.0	0.12	24.9 ± 3.7
Height (cm)	169.7 ± 8.0	170.8 ± 6.3	174.8 ± 7.2	0.20	171.8 ± 7.3
Mass (kg)	64.2 ± 8.4	68.0 ± 8.0	69.6 ± 11.1	0.36	67.3 ± 9.3
Sex (female)	6 (50.0%)	7 (58.3%)	10 (83.3%)	0.21*	23 (63.9%)

^*χ² test was used.

Figure 1.

Schematics of a) the experimental setup inducing a slip during gait and b) the experimental protocol of the present study, and c) video sequences show the first slip trial for three groups. A slip is induced by releasing a slipping device consisting of two low-friction movable platforms. Each of the two moveable platforms is mounted on a frame with four linear bearings, and the frame was bolted to two force plates to measure the ground reaction force. The low-profile movable platforms (and the force plates beneath, not shown here) were embedded in a 7-m walkway with decoy platforms (not shown) to reduce its visibility. The right- and left-side moveable platforms can be unlocked electronically after the landing of the corresponding foot. Only the right platform was released in the present study. A set of 28 light-reflective markers were placed on bilateral upper and lower extremities, torso, and platforms. Their spatial positions were captured by an 8-camera motion capture system. The subjects were required to wear a safety harness which is individually adjusted to prevent a fall to the ground. A load cell was used to measure the force exerted on the harness. The testing protocol for the 12-cm group consisted of 8 regular walking trials (Reg) followed by a block of five 12-cm training slips (S), a block of 3 nonslips (NS), a second block of two 12-cm training slips, a second block of 5 nonslips, and a 150-cm slip test (ST). The protocol for the 18-cm group was similar to that for the 12-cm group, except that the maximum distance of the training slip was 18 cm. The protocol for the control group consisted of 8 regular walking trials followed by a 150-cm ST slip. For the video sequences, the first three frames for all groups show the instants of right (slipping) foot touchdown that triggered the onset of the slip, left (recovery) foot liftoff and its touchdown. The fourth frame in 12- and 18-cm groups is the instant of the next left foot touchdown. The fifth frame in 18-cm group is the instant of right foot liftoff. For the control group, the fourth, fifth, and sixth frames respectively represent the instant of right foot liftoff, right foot touchdown, and left foot liftoff. The triangle on each frame marks the location of the heel at the onset of the slip.

Experimental protocol

Subjects were randomly and evenly assigned to three groups: two training groups and a control group. Subjects in both training groups received slip training with reduced slip distances before exposed to a “free” slip; while the control group only experienced the “free” slip without any training (Fig. 1b). One of the training groups experienced slips with maximum distance of 12cm during the training session (the 12-cm group), while the other experienced slips with maximum distance of 18cm (the 18-cm group). Other than the different maximum slip distance (12 or 18cm), the training protocols were identical between these two groups (Fig. 1b). Subjects were informed that they would be performing normal walking initially and would experience simulated slips later without knowing when, where, and how that would happen. They were also told to try to recover their balance on any slip incidence and then to continue walking forward. A slip was induced on the ninth trial, which was followed by four consecutive slip trials, a block of three nonslips, and the second block of two re-slips for a total seven slips (S1-S7). Finally, after another five trials of unperturbed walking, they experienced the unconstrained slip test (ST). The subjects in the control group received the same instruction while they only experienced the ST after eight unperturbed trials (Fig. 1b).

Data collection

Full body kinematic data from 28 retro-reflective markers placed on the subjects’ body and platforms were gathered using an 8-camera motion capture system (MAC, Santa Rosa, CA) at 120Hz. Marker paths were low-pass filtered at marker-specific cut-off frequencies (ranging from 4.5 to 9Hz) using fourth-order, zero-lag Butterworth filters (Winter, 2005). Force plate and load cell data were collected at 600Hz and synchronized with motion data. Three dimensional locations of joint centers, heels, and toes were computed from the filtered marker positions.

Trial outcomes, events, and kinematic variables

A fall was classified when the peak load cell force during slip exceeded 30% body weight; while a recovery was identified if the moving average load cell force did not exceed 4.5% body weight over any 1-second period after slip onset (Yang and Pai, 2011). When the recovery heel landed posterior to the slipping heel after the slip onset, the trials would be classified as backward balance loss trials. Conversely, trials with the recovery heel landing anterior to the slipping heel were classified as no balance loss trials (Bhatt et al., 2006). The events of interest included the instant of the slipping (right) limb touchdown (RTD), the instant of the recovery (left) limb liftoff (LLO), and the instant immediately prior to its touchdown (LTD). These events were determined from the vertical ground reaction force.

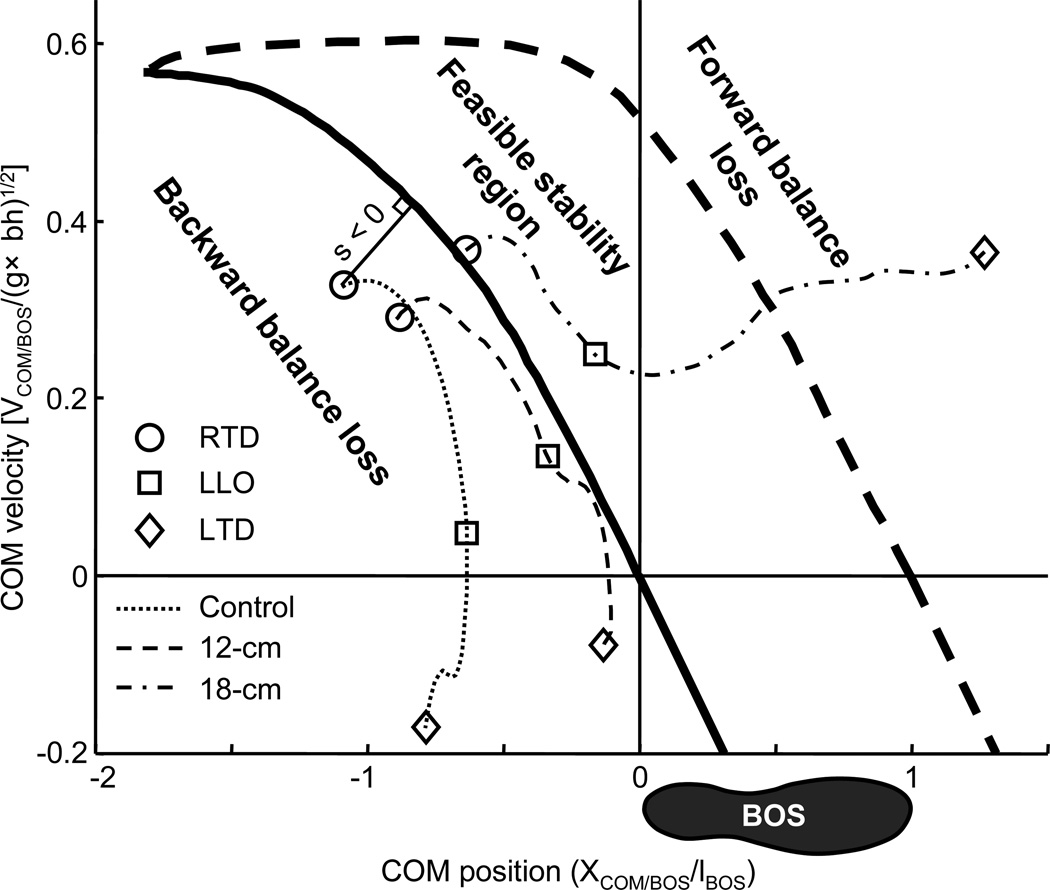
The body COM kinematics was calculated using a 13-segment rigid body model (de Leva, 1996). The two components of the COM motion state, i.e. its position and velocity were calculated relative to the rear of BOS (i.e. the right heel) and normalized by foot length (l_BOS) and $\sqrt{g\times bh}$, respectively, where g is the gravitational acceleration and bh the body height. The COM stability was evaluated by calculating the shortest distance from the COM motion state to the limits against backward balance loss (Fig. 2) (Yang et al., 2008a; Yang et al., 2008b). Preslip stability was obtained at RTD; post-slip stability was obtained at the instants of LLO and LTD.

Figure 2.

Schematic illustration of the stability measurement (s), in which representative trajectories from 12-cm (the dotted line), 18-cm (dash-dotted line), and control (dotted line) groups depict the center of mass (COM) motion state (i.e., the x-coordinates represents the COM anteroposterior position and the positive y-coordinates indicates its forward velocity) from right (slipping) foot touchdown (RTD, circle), through left (recovery) foot liftoff (LLO, square), to the instant of its touchdown (LTD, diamond) in the 150-cm slip test. The feasible stability region is enclosed by two boundaries: the limits of stability against backward balance loss (the thick solid line) and those against forward balance loss (the thick dashed line). When a COM motion state lies within the feasible stability region, balance loss is preventable. A motion state further below the lower boundary of the feasible stability region (i.e., a more negative value) is more unstable and a backward balance loss becomes inevitable because the initial forward momentum is insufficient to carry the COM forward to within the BOS. Conversely, when the motion state is further above the upper boundary (i.e. a more positive stability), a forward loss of balance becomes inevitable due to the excessive forward momentum. The thin solid line indicates the magnitude of the instantaneous COM stability, which was defined as the shortest distance from the given COM motion state at that instant to the limits of stability against backward balance loss. When the instantaneous COM motion state is below/above the limits, the stability value is negative/positive, respectively. Greater stability values indicate greater stability against backward balance loss (Pai, 2003). Position and velocity of the COM relative to the base of support (BOS) are dimensionless variables expressed as a fraction of l_BOS and $\sqrt{g\times bh}$, respectively, where l_BOS represents the foot length, g is gravitational acceleration, and bh the body height.

Several gait variables including preslip step length and foot angle, and BOS velocity at LLO were calculated to further understand the contributing factors to adaptive changes in the stability. Preslip step length was calculated as the anteroposterior distance measured between both heel markers at RTD. Foot angle was the angle between the sole and ground and was calculated at RTD. The BOS velocity at LLO was the platform’s speed at the instant of LLO. In addition, the peak BOS velocity and the maximum BOS travel distance were also analyzed for slip trials. The peak BOS velocity was calculated as the maximum BOS travel velocity during the slip. The maximum BOS travel distance was the longest forward displacement of the BOS during the period of the right stance phase. These variables were computed upon S1 and S7 for training groups; and upon ST for all groups.

To examine the differences of the slip training between two training groups, the following three additional variables characterizing the BOS kinematics were also analyzed upon the training slips for both groups. They included the travel distance of the platform from RTD to the instant of the peak BOS velocity (X_{BOS,T peak, VBOS}), the time instant when peak BOS velocity was reached relative to LLO (T_peak,VBOS), and the time instant when maximum BOS displacement achieved (T_max,XBOS). These variables were calculated on S1 and S7 for training groups. The improvements in the COM stability, the landing kinematics, and the BOS slip kinematics from S1 to S7 were calculated as the difference of these variables between trials for both groups.

Statistics

To assess demographic and age differences between three different groups, these variables were compared across all three groups using a one-way analysis of variance (ANOVA) (factor: group, 12-cm vs. 18-cm vs. control). The Generalized Estimating Equation (GEE) test, post-hoc Wilcoxon Signed-Rank test, and Mann Whitney test were applied to examine the training effect on backward balance loss reduction in each training group (the within-group factor: S1 vs. S7), and to examine the similarity of training effect across both training groups (the between-group factor: 12-cm vs. 18-cm). In parallel, ANOVA for repeated measures, with group (12-cm vs. 18-cm) as between group factor and trial (S1 vs. S7) as the within group factor was used to assess adaptive improvements in time elapsed during the single and double stance phase after slip onset, the stability control, preslip step length, preslip foot angle, BOS velocity at LLO, and BOS kinematics. Significant main effects and interactions were resolved with paired and independent t-tests using the proper corrections. The improvements in COM stability, BOS kinematics, and the landing kinematics were compared between groups (12-cm vs. 18-cm) using independent t-tests.

To investigate issues related to the generalization, χ² tests were performed to compare the backward balance loss incidence on ST among all three groups. Generalization effects were evaluated first by comparing the slip outcome and later by examining both proactive (preslip) and reactive (post-slip) control in slip responses. One-way ANOVAs (factor: group) with Tukey’s post-hoc tests were conducted to compare the differences among the three groups upon the ST slip in the following variables: durations of the single and double stance phases, the pre- and post-slip stability, the preslip step length and foot angle, BOS velocity at LLO, peak BOS velocity, and maximum BOS displacement. All analyses were performed using SPSS 19 (IMB Corp., Armonk, NY) with a significance level of 0.05.

RESULTS

Adaptation to slip training

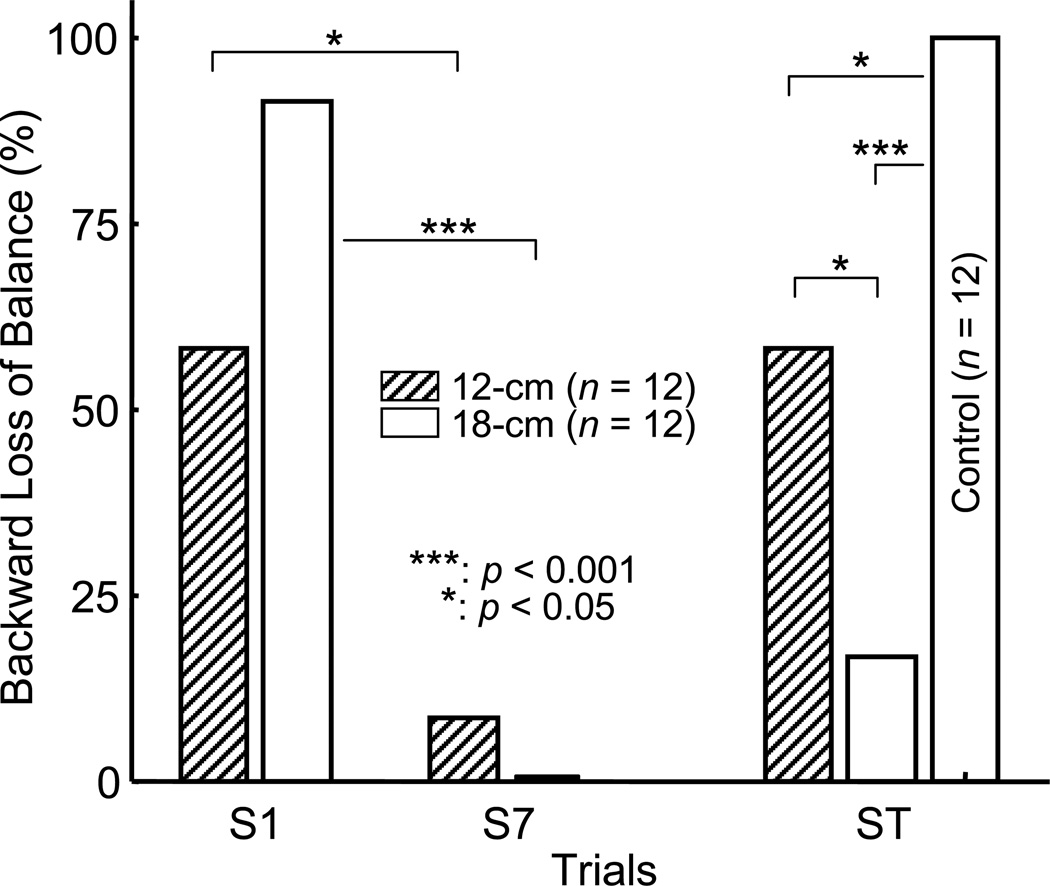
Although more subjects in the 18-cm group experienced backward balance loss on the first training slip (S1) than the 12-cm group (91.6% vs 58.3%, p=0.059, Fig. 3), both groups were able to significantly reduce incidence of balance loss at the end (S7) of training (0% for the 18-cm group, and 8.3% for the 12-cm group; p < 0.001 within group, p=0.204 between group, and group-by-trial interaction: p=0.012, Fig. 3). The significant group-by-trial interaction indicated that the reduction of the backward balance loss from S1 to S7 was greater in 18-cm group than in 12-cm group (p=0.025, Table 2).

Figure 3.

The rate of the backward loss of balance in percentage resulting from slips for both training groups (12-cm and 18-cm) upon their first (S1) and last (S7) training slips, and for both training groups and the control group on their 150-cm “free” slip test (ST).

Table 2.

Comparison of the improvements in variables including rate of balance loss, COM stability, landing kinematics, BOS slip kinematics, and temporal parameters from the first slip (S1) to the last slip (S7) during the training session between the 12-cm and 18-cm groups.

		Groups		p value
Variables		12-cm	18-cm
Rate of balance loss (%)		50.0	91.6	0.025
	RTD	0.043 ± 0.041	0.063 ± 0.028	0.183
Stability	LLO	0.227 ± 0.144	0.386 ± 0.157	0.016
	LTD	0.450 ± 0.356	0.886 ± 0.374	0.007
Step length at RTD (/bh)		−0.035 ± 0.025	−0.051 ± 0.033	0.194
Foot angle at RTD (deg)		−7.850 ± 5.615	−11.34 ± 7.162	0.193
COM position at RTD		0.156 ± 0.139	0.198 ± 0.084	0.373
BOS velocity at LLO (m/s)		−0.363 ± 0.487	−0.855 ± 0.412	0.014
Peak BOS velocity (m/s)		−0.556 ± 0.276	−0.874 ± 0.309	0.015
Maximum BOS displacement (m)		−0.019 ± 0.042	−0.088 ± 0.070	0.008
Durations (s)	RTD to LLO	0.019 ± 0.026	0.001 ± 0.036	0.170
	LLO to LTD	0.095 ± 0.202	0.202 ± 0.143	0.147

RTD: the slipping foot touchdown; LLO: the recovery foot liftoff; LTD: the instant immediately prior to the recovery foot touchdown.

The step length is the anteroposterior distance between heels at RTD and normalized to the body height (bh). The COM position is relative to the rear edge of the BOS and normalized by the foot length. Foot angle is the angle between the sole and ground where a flat foot corresponded to zero degrees with toe up as positive.

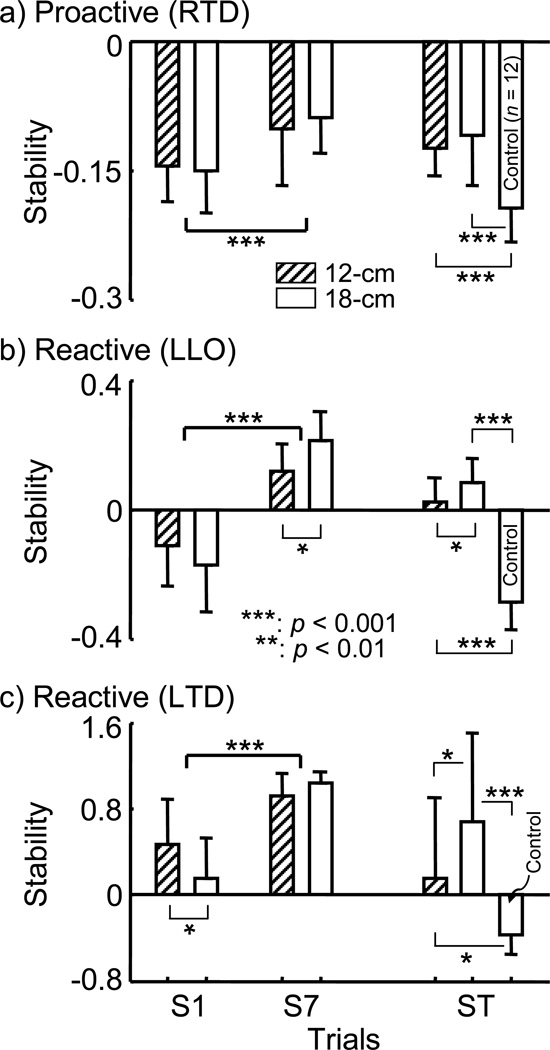
Both groups made similar improvements in the control of preslip stability (main trial effect: p < 0.001; but main group effect: p=0.84, and group-by-trial interaction: p=0.183, Fig. 4a, Table 2). A different picture emerged in the control of post-slip stability, whereby the 18-cm group was able to make significantly greater improvements from S1 to S7 than did the 12-cm group, both at LLO (main group effect: p=0.644, main trial effect: p < 0.001 group-by-trial interaction: p=0.017, Fig. 4b, Table 2) and at LTD (main group effect: p=0.373, main trial effect: p < 0.001and group-by-trial interaction: p=0.008, Fig. 4c, Table 2).

Figure 4.

Comparisons of dynamic preslip stability at slipping foot touchdown (RTD), b) post-slip stability at recovery foot liftoff (LLO), and c) post-slip stability at recovery foot touchdown (LTD) for both training groups (12-cm and 18-cm) upon their first (S1) and last (S7) training slips, and for both training groups and the control group on their 150-cm slip test (ST). The thick line indicates the p value for the main trial factor while thin line represents the p value for the post-hoc analysis.

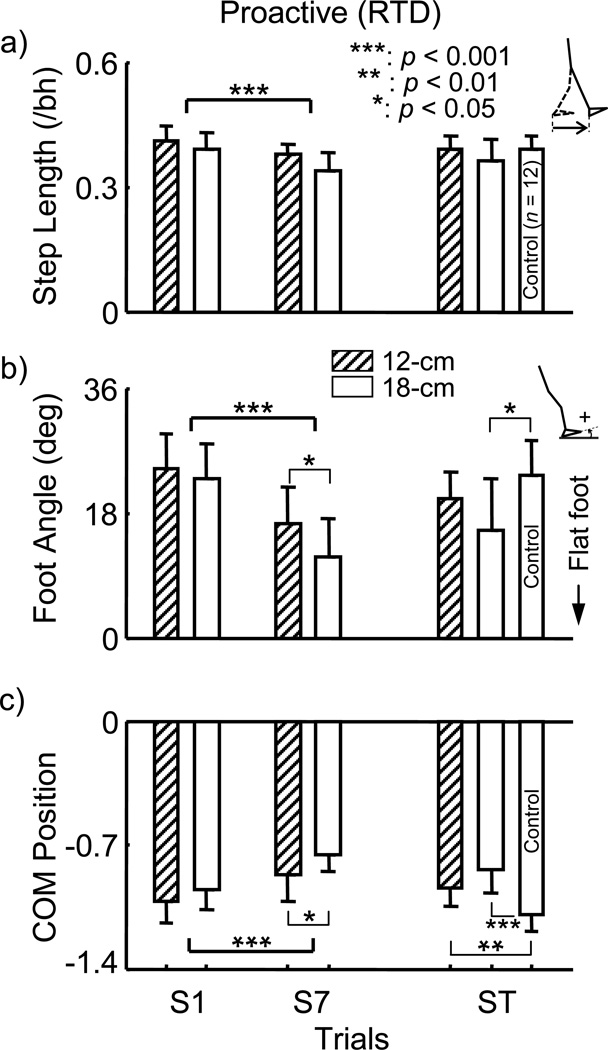
Adaptive adjustments were also made in landing kinematics, including shorter step length (main trial effect: p < 0.001, Fig. 5a) and more flat footed in landing angle at RTD (main trial effect: p < 0.001, Fig. 5b). There were significant difference associated with the foot angle at RTD groups (main group effect: p=0.041, and group-by-trial interaction: p=0.194 for step length, Fig. 5). However, the step length at RTD did not differ between groups (main group effect: p=0.083, and group-by-trial interaction: p=0.193, Fig. 5). The adaptive changes in landing kinematics from S1 to S7 led to the forward shift of the COM position that would increase the COM stability at RTD (main trial effect: p=0.001, main group effect: p=0.045; and group-by-trial interaction: p=0.193, Fig. 5c).

Figure 5.

Comparison of group means (± SD) for a) preslip step length at slipping foot touchdown (RTD), b) preslip slipping side foot angle at RTD, and c) the center of mass (COM) position relative to the base of support (BOS) at RTD for both training groups (12-cm and 18-cm) upon their first (S1) and last (S7) training slips, and for both training groups and the control group on their 150-cm slip test (ST). The step length is the anteroposterior distance between heels at RTD and normalized to the body height (bh). The COM position is relative to the rear edge of the BOS and normalized by the foot length. Foot angle is the angle between the sole and ground where a flat foot corresponded to zero degrees with toe up as positive. The thick line indicates the p value for the main trial factor while thin line represents the p value for the post-hoc analysis.

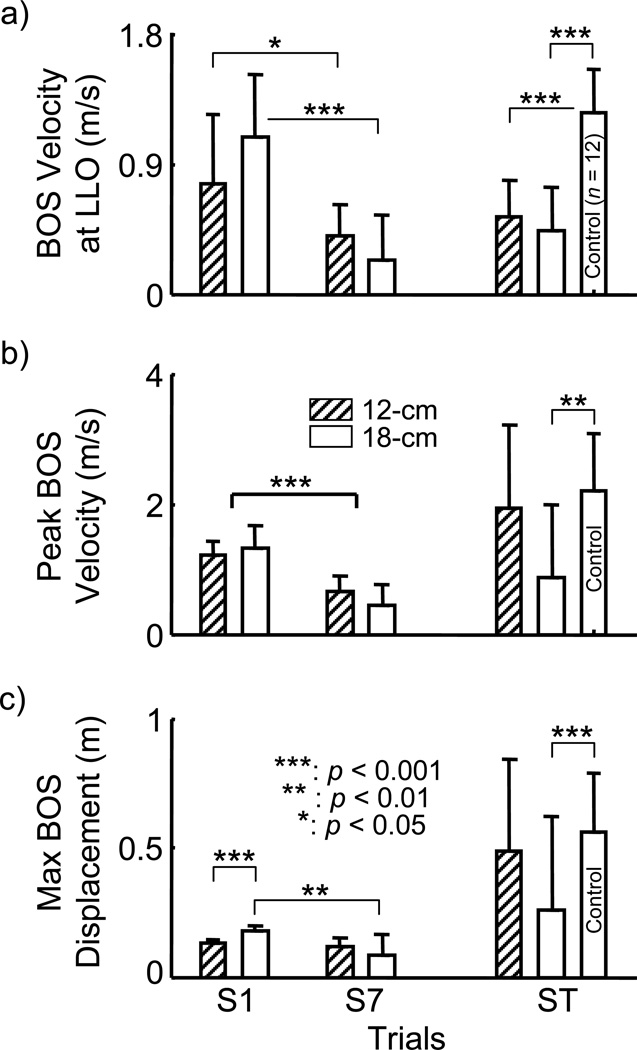
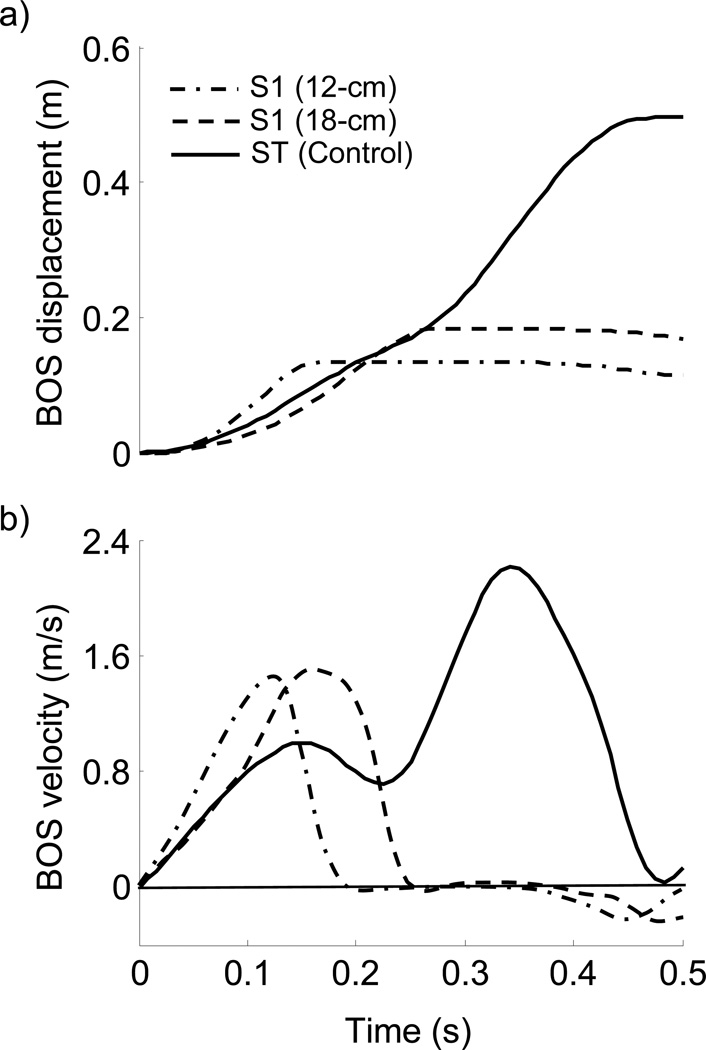
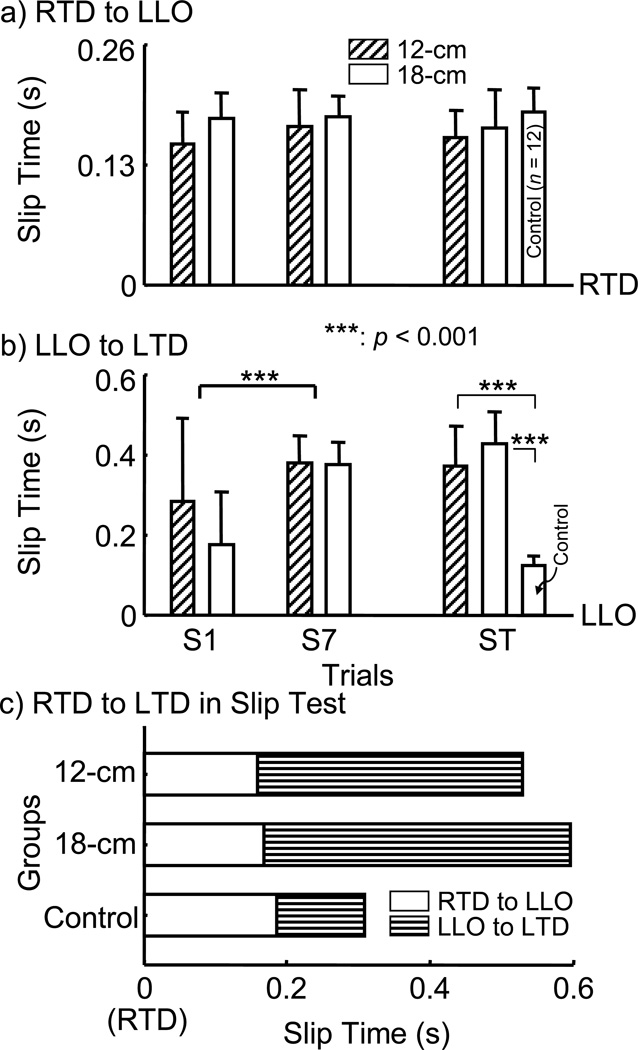
The BOS velocity at LLO (main trial effect: p < 0.001, Fig. 6a) as well as maximum BOS velocity (main trial effect: p < 0.001, Fig. 6b; Fig. 7b) were reduced from S1 to S7. Again, the 18-cm group was able to make greater improvements in both of these measurements than did the 12-cm (main group effect: p=0.519, and group-by-trial interactions: p=0.014 for BOS velocity at LLO; and main group effect: p=0.631, and group-by-trial interactions: p=0.015 for the peak BOS velocity, Fig. 6, Table 2). Notably, the 18-cm group was also able to significantly reduce the maximum BOS displacement (p < 0.001, Fig. 6c; Fig. 7a) from S1 to S7 while the 12-cm group did not display such change (p > 0.05, Fig. 6c). As result, the time to reach such distance after training was significantly extended for the 18-cm group than it did for the12-cm group (Table 3, p < 0.001), while both groups learned how to extend single stance phase from LLO to LTD (p < 0.001 for both, Fig. 8b).

Figure 6.

Group mean and standard deviation of a) base of support (BOS) velocity at left foot liftoff (LLO) after slip onset, b) peak base of support (BOS) velocity, and c) maximum BOS displacement for both training groups (12-cm and 18-cm) upon their first (S1) and last (S7) training slips, and for both training groups and the control group on their 150-cm slip test (ST). The thick line indicates the p value for the main trial factor while thin line represents the p value for the post-hoc analysis.

Figure 7.

Representative time history of base of support (BOS) a) displacement and b) velocity after slipping foot touchdown on the first slip for subjects from each group. For 12-cm and 18-cm training groups, the first slip is their first slip during training session (i.e. S1). For the control group, the first slip is their test slip (ST).

Table 3.

Comparison of group means (± SD) for the BOS characteristics of the first training slip (S1) between the 12-cm and 18-cm groups.

	12-cm		18-cm
Parameters	S1	S7	S1	S7
Tpeak,VBOS (s)	0.06 ± 0.06	0.09 ± 0.08	0.04 ± 0.04	0.11 ± 0.15
XBOS,T peak,VBOS (cm)	7.06 ± 0.86	6.69 ± 3.14	9.55 ± 2.27	4.37 ± 6.92*
Tmax,XBOS (s)	−0.13 ± 0.16	−0.14 ± 0.08	0.01 ± 0.08Δ	−0.20 ± 0.15&

X_{BOS,Tpeak,VBOS} Displacement of the BOS when peak BOS velocity was reached;

T_peak,VBOS Time when peak BOS velocity was reached (relative to LLO);

T_max,XBOS Time when maximum BOS displacement was reached (relative to LTD);

^*p < 0.05 vs. S1 of 18-cm group;

^Δp < 0.05 vs. S1 of 12-cm group;

^&p < 0.01 vs. S1 of 18-cm group.

Figure 8.

Elapsed time a) from slipping foot touchdown (RTD) and recovery foot liftoff (LLO), and b) from LLO to left foot touchdown (LTD) in seconds (mean ± SD) for both training groups (12-cm and 18-cm) upon their first (S1) and last (S7) training slips, and for both training groups and the control group on their 150-cm slip test (ST). The thick line indicates the p value for the main trial factor while thin line represents the p value for the post-hoc analysis. c) The elapsed time from RTD to LLO for three groups upon the ST trial.

Generalization effect

Although none of them fell during their training earlier, one subject in each training group (8.3%) fell during the ST slip in comparison to two subjects (16.7%) did from the control group in the same trial. Only 16.7% of the 18-cm group lost balance in this ST trial in comparison to 58.3% of the 12-cm group (p=0.035) and 100% of the control group did (p < 0.001, Fig. 3). Further, less subjects in the 12-cm group lost their balance than ones in the control group on ST trial (p=0.012, Fig. 3). Both groups had significantly greater preslip and post-slip stability in comparison to the control group (preslip: p < 0.001 for both groups; post-slip at LLO: p < 0.001 for both groups; post-slip at LTD: p < 0.05 for the 12-cm group and p < 0.001 for the 18-cm group, Fig. 4). While little difference was found between these two groups in the control of preslip stability (p > 0.05, Fig. 4a), the 18-cm group gained better control of post-slip stability (p < 0.05 for LLO and LTD, Fig. 4).

Only subjects in 18-cm group but not in 12-cm group exhibited a more flat-footed landing in comparison to the control group upon ST slip (p < 0.05, Fig. 4b). To account for these differences in the control of post-slip stability, the 18-cm group was able to significantly reduce the slip intensity as evidenced by reducing peak BOS velocity (p < 0.01, Fig. 6b; Fig. 7b) and shortening maximum slip distance (p < 0.001, Fig. 6c; Fig. 7a) than did both the 12-cm and control groups (Fig. 6). Both training groups were able to extend their single stance time during recovery after slip onset in comparison to the control group (p < 0.001 for both groups, Fig. 8).

DISCUSSION

This study investigated whether and to what degree that repeated slips with short-distance (constrained) could still elicit training adaptation and the generalization of such training effects to a different context upon the encountering of a novel and “free” slip. Our results indicated that motor adaptation did emerge during short-distance slips and such effects could indeed carryover to a novel, unconstrained slip. The adaptation and its generalization were made evident by the training groups’ reduced incidence of backward balance loss (in comparison to that of the control group) during the novel “free” slip. Such difference was a consequence of training-induced improvements in both proactive and reactive control of stability.

The results supported our first hypothesis that both training groups could generalize the improved response to slip during the “free” slip. While at the end of training both groups improved the control of stability, the 18-cm group was significantly less likely to experience balance loss and hence significantly greater generalized training effect than did the 12-cm group during the subsequent “free” ST. Apparently, the generalization of such gain in the control of stability was modulated by the level of similarity between the trained and untrained conditions. The findings also validated our second hypothesis that the 18-cm slip training was more effective than the 12-cm slip training in reducing backward balance loss and in improving the control of stability for slip recovery upon the long-distance slip. Nevertheless, pre-exposure to short-distance slips still contributed positively to the development of proper adaptive strategies, such that the training groups were able to respond better on a subsequent long-distance slip in comparison to the control group without any training. Such findings indicated that cautions should be exercised when adjusting the slip intensity for safety concern in order to optimize the training effect without depriving them appropriate adaptive learning experience.

Adaptation and generalization in proactive control

It is known that with proper training, humans are adaptable to sudden or unexpected changes in environmental constraints during a range of activities from standing to locomotion (Conditt et al., 1997; Wolpert and Ghahramani, 2000). In this adaptive process, the feed-forward control underlying successful proactive adjustments, occurring before perturbation onset and typically relying on previously acquired knowledge, can affect the movement outcomes in two different ways. First, feed-forward control can alter posture and limb control prior to an encounter with an environmental hazard (McIlory and Maki, 1993; Patla et al., 1991). Improved movement stability prior to the onset of perturbation resulted from the feed-forward adjustments can reduce the need for a reactive correction after the onset of the perturbation. Second, feed-forward control can modulate the feedback-control-related response to increase the likelihood of success of this reaction (Bhatt et al., 2006; Marigold and Patla, 2002; Pavol et al., 2002). Our results revealed that both mechanisms have been applied by the training groups. Both groups proactively improved their preslip stability resulting from their adaptive changes in landing kinematics at RTD. Specifically, they landed their leading feet more flat while shortened their step length (Cham and Redfern, 2002). Both adaptive changes resulted in the forward-shifted COM position at RTD. The improved preslip stability attributed to the significant reduction of the incidences of balance loss for both groups across the training trials (S1 through S7). These adaptive changes can also contribute to the reductions in BOS displacement and velocity during subsequent slip (Bhatt et al., 2006; Heiden et al., 2006).

During the training process, the CNS may shift from initially relying on context prediction based on sensory feedback for error correction to an emerging adaptive feed-forward control during later trials (Bastian, 2008). Interestingly, such adaptive adjustments were rather consistent between two training groups. In essence, the constraints (stoppers) that were placed at the end of the 12-cm and 18-cm slips abruptly terminated the forward slip in an effect equivalent to a “trip”. Because the sudden termination of the slip due to the stoppers during the training slips, the trailing limb was not fully engaged to recover the balance from slip perturbation (Table 3). Specifically, 9 subjects out of 12 for 12-cm group and 6 out of 12 for 18-cm group did land their recovery foot after the movable platform was terminated by the stoppers. Though the corrective reactions generated by the leading (or perturbed) limb are important to keep balance following a perturbation (Cham and Redfern, 2001; Lockhart and Kim, 2006), the trailing (or unperturbed) limb’s recovery stepping is also crucial in maintaining dynamic stability in responding to an unexpected destabilizing event such as a slip in gait (Marigold et al., 2003; Moyer et al., 2009). Therefore, this constraint-induced readjustment between the COM and its BOS could have lessened the initial disturbing effect from the slip; and hence lessened the training effect without fully involving the recovery stepping, especially for the 12-cm group. However, the errors emerged from the initial slip prior to its stop apparently had still provided the CNS the opportunity to recalibrate its stability limits under the slip condition (Pai and Iqbal, 1999). This recalibrated predictive control would enable this person to maintain stability regardless of whether, where, and how a slip occurs; hence reducing reliance on the reactive recovery response.

The repeated-slip training enabled young adults to proactively improve their stability before slip occurrence, which was consistent with previous findings (Bhatt et al., 2006). Subjects may adopt a more “cautious gait” with shorter step (Giladi et al., 2005). The shortened step length found in the present study also agrees with the previously reported relationship between step length and slip risk among both young (Cham and Redfern, 2002; Lockhart et al., 2003; McVay and Redfern, 1994; Moyer et al., 2006) and older adults (Lockhart et al., 2003). A flatfoot landing may also reduce the demand on friction from the ground reaction force (Cham and Redfern, 2002; Marigold and Patla, 2002). Such technique was thought to be another contributor to a reduced slip velocity, i.e., its severity (Cham and Redfern, 2002). The reduced foot angle reduces one’s reliance on floor friction for braking forward momentum when the slip occurs, thereby reducing the peak slip velocity the subject experiences during the slip (Chambers and Cham, 2007; Yang and Pai, 2013). The stability, step length, foot angle, and COM position at right foot touchdown upon S1, however, were not different from that of the control group during ST (p > 0.05 for all).

Adaptation and generalization in reactive control

The amount of improvements in reactive (at LTD) control from S1 to S7 was nearly 10- and 14- fold greater than that in proactive (at RTD) control respectively for 12- and 18- cm groups (Table 2, Fig. 4). It was the more robust improvements in the 18-cm group’s reactive control than that in the 12-cm group’s that likely contributed to the better overall generalization outcome of the former. The reactive adaptations differ importantly from proactive adaptations in that they can take place quickly in response to ongoing afferent input (Morton and Bastian, 2006). When feed-forward mechanism by itself is insufficient to eliminate the perturbation generated error, reactive feedback corrections must be critical in restoring and improving post-slip stability and these were the places where the 12- and 18-cm groups differed significantly (Figs. 4 and 5) (McIlory and Maki, 1993; Owings et al., 2001). Here, the 18-cm group acquired significantly better skills in the control of stability (that included a better reactive control of maximum slip velocity and slip distance) than did the 12-cm group and eliminated their need for any protective stepping response in the majority of them (83.3%) during the novel “free” slip. In contrast to the 12-cm group, a longer slip distance during the training had enabled the 18- cm group to develop better reactive skills that can be more readily generalized and applicable to the novel “free” slip in which the slip distance was not constrained, while both groups had already acquired similar feed-forward control skills.

Our study has limitations. First, because this is the first study of its kind, only healthy (no neurological musculoskeletal or other systemic disorder) young participants were included to reduce the risk of potential injury that can be caused by such large-scale perturbation to population with high risk of fracture. Because there were no older adults included, the findings might only have very limited implications. Second, while a pre- and post-training design can be desirable, a single slip for test before the training in itself can produce training effect that can mask the subsequent targeted training effect and hence contaminate the results (Bhatt and Pai, 2009). We therefore used the control group to represent the pre-training baseline for both training groups. Such alternative design is based on the assumption that the subjects in both training groups and in the control group would behave similarly to a novel slip. Because they were randomly assigned to any of the groups and all of them were healthy (i.e., lack of any predisposition to falls), we believe that such an assumption is acceptable.

In summary, inducing real-life like, large-scale (free) slips would carry certain risk of injury. It is attractive that subjects were able to acquire adaptive fall-resisting skills after undergoing short-distance-slip training, and such adaptive skills were generalizable such that they could better recover from a slip with longer distance. The findings that low intensity training may still improve stability warrant further investigations among older adults